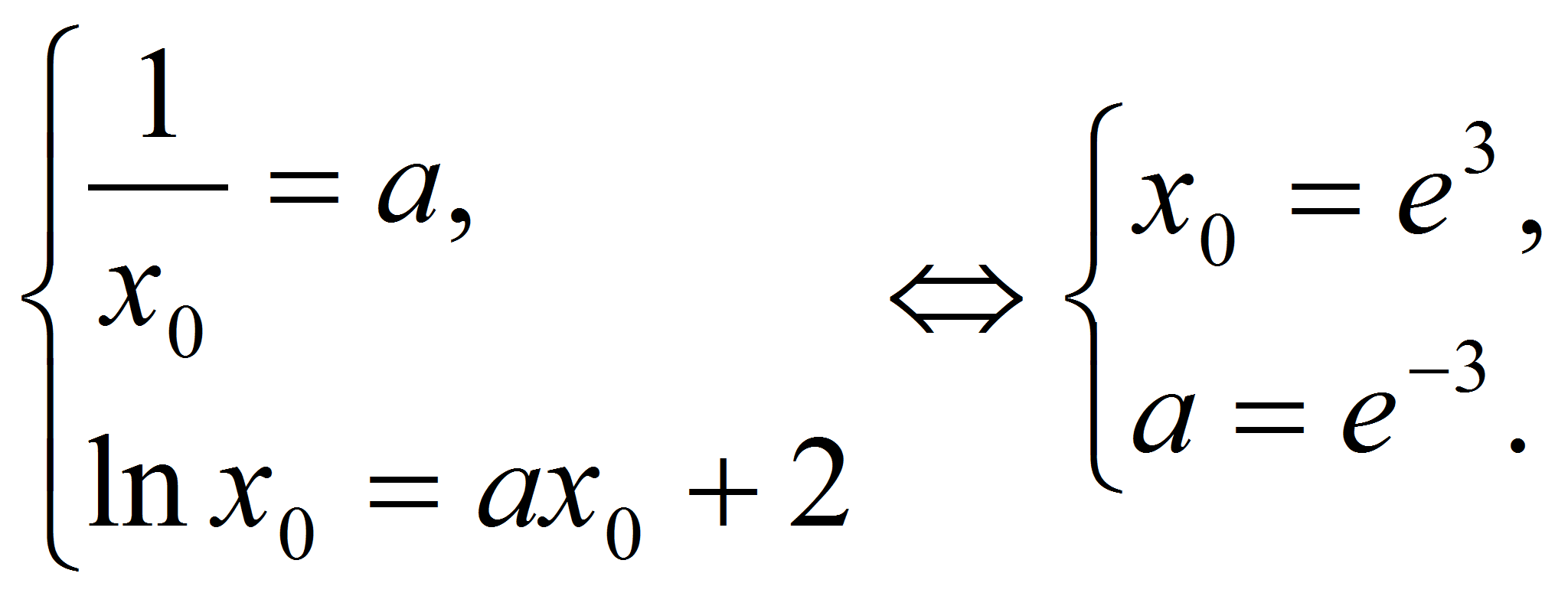егэ – Как найти ординату касательной?
|
Здравствуйте. Мне даны 2 функции, они паралелльны. Я нашёл абсциссу. Задание (ЕГЭ, часть B):
Я нашёл x. Она равна -0,5. Как найти ординату? Спасибо. |
1 ответ
|
Теперь, когда присутствует условие задачи, понятно, о чем идет речь. Параллельными должны быть касательная к графику функции и заданная прямая $%y=5x+11.$% |
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
отмечен:
егэ
×336
задан
16 Апр ’13 16:31
показан
14262 раза
обновлен
17 Апр ’13 17:33
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
- Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1–192-13 или y0=3·-1–192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания – 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Касательная и заданная кривая имеют общие точки -точки касания.
Угловой коэффициент касательной равен производной функции, вычисленной в
точке касания. С одной стороны этот коэффициент нам известен из уравнения касательной, он равен 66, к=66. С другой стороны, найдём производную и приравняем её числу 66.
Получили абсциссы двух точек касания. Найдём их ординаты, подставив найденные числа в уравнение.Причём и в уравнение касательной, и в уравнение кривой, ответ будет один и тот же,ведь точки касания общие для них.
Точка с абсциссой х=4 – точка касания другой касательной, не той которую задали в условии.
Точка(-3,-27)
Чтобы
правильно и рационально решать задачи, связанные
с уравнением касательной, нужно четко понимать, что такое
касательная, владеть техникой составления
уравнения касательной к графику функции и
представлять себе, для решения каких задач (в том
числе и задач с параметрами) можно использовать метод касательной.
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при
(рис. 1).
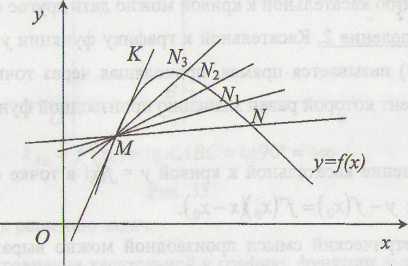
Рис. 1
Касательная к кривой может
иметь с ней несколько общих точек или пересекать ее. Можно дать и
другое определение касательной к кривой.
Опр.
2. Касательной к графику функции у
= f(x) в
точке A0(x0;
f(x0))
называется
прямая, проходящая через точку A0,
угловой
коэффициент которой
равен значению производной функции у
=f(x)
в точке
с абсциссой x0.
Уравнение
касательной
к кривой у =
f(x)
в точке с
абсциссой х0
имеет вид:
.
Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
,
причем ее
угловой коэффициент
равен
.
Вывод: если в точке х0
есть производная
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции
и наоборот; если
в точке х0
нет производной
функции
,
то в точке с
этой абсциссой нет касательной к графику функции
и наоборот.
Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).
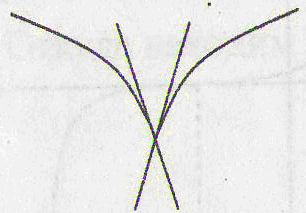
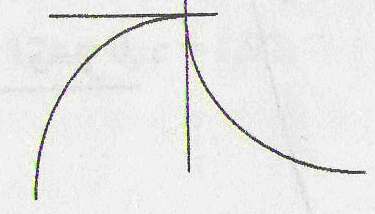
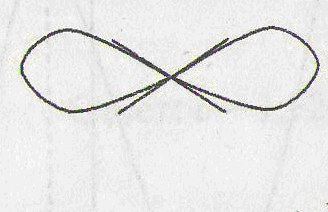
угловая точка
точка возврата узловая
точка
а) б) в) г)
Рис. 2
Рассмотрим решение
некоторых задач.
Задачи,
связанные с определением того, является ли прямая
у = kx
+ b
касательной к графику функции
у = f(x).
Можно указать два способа решения таких задач.
-
Находим общие
точки графиков, т. е. решаем уравнение f(x)
= kx
+ b,
а затем для каждого из его решений
вычисляем
.
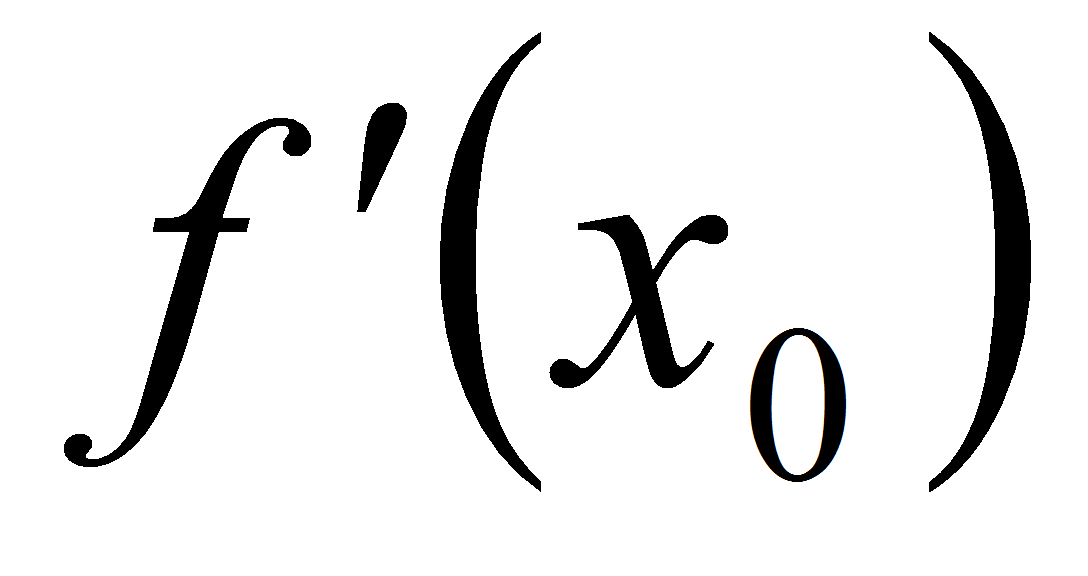В тех случаях, когда
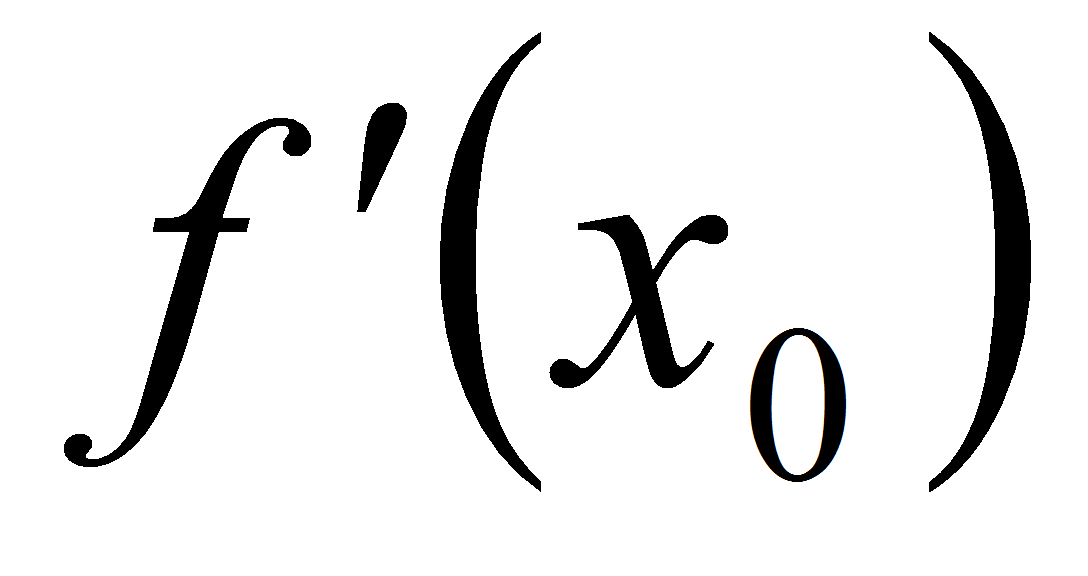
= k,
имеет место касание, в других —
пересечение. -
Находим корни
уравнения
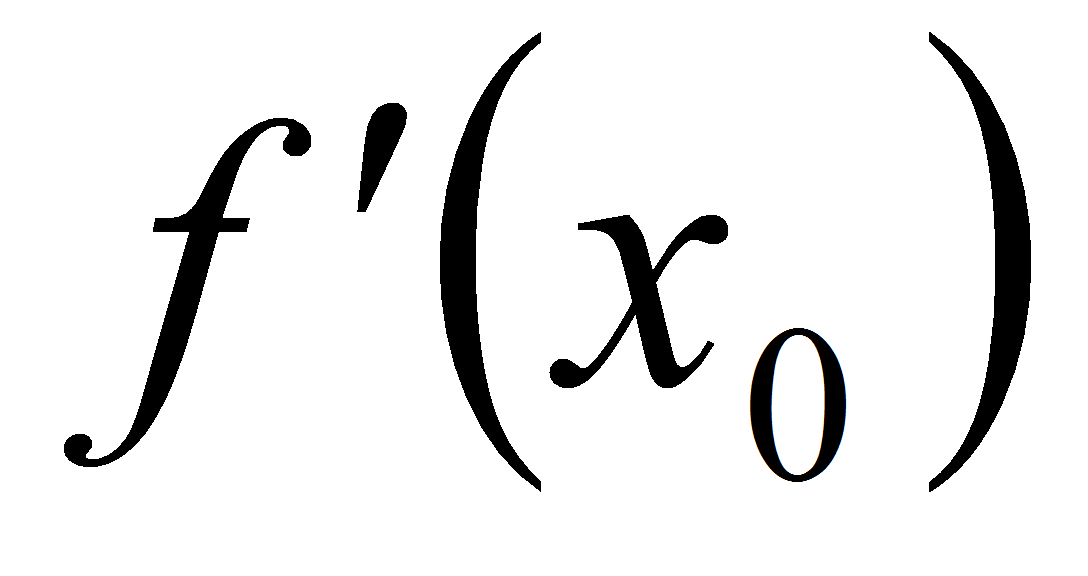
= k
и для каждого из них проверяем, выполняется ли
равенство f(x)
= kx
+ b.
При его выполнении получаем абсциссы точек
касания.
.Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система
-
При каких
значениях b
прямая у = 3х +b
является касательной к графику функции у
=
?
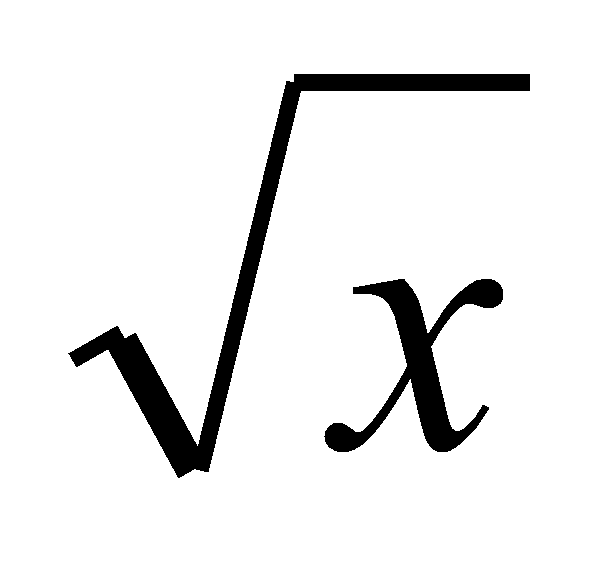?Решение.
Записав условие касания
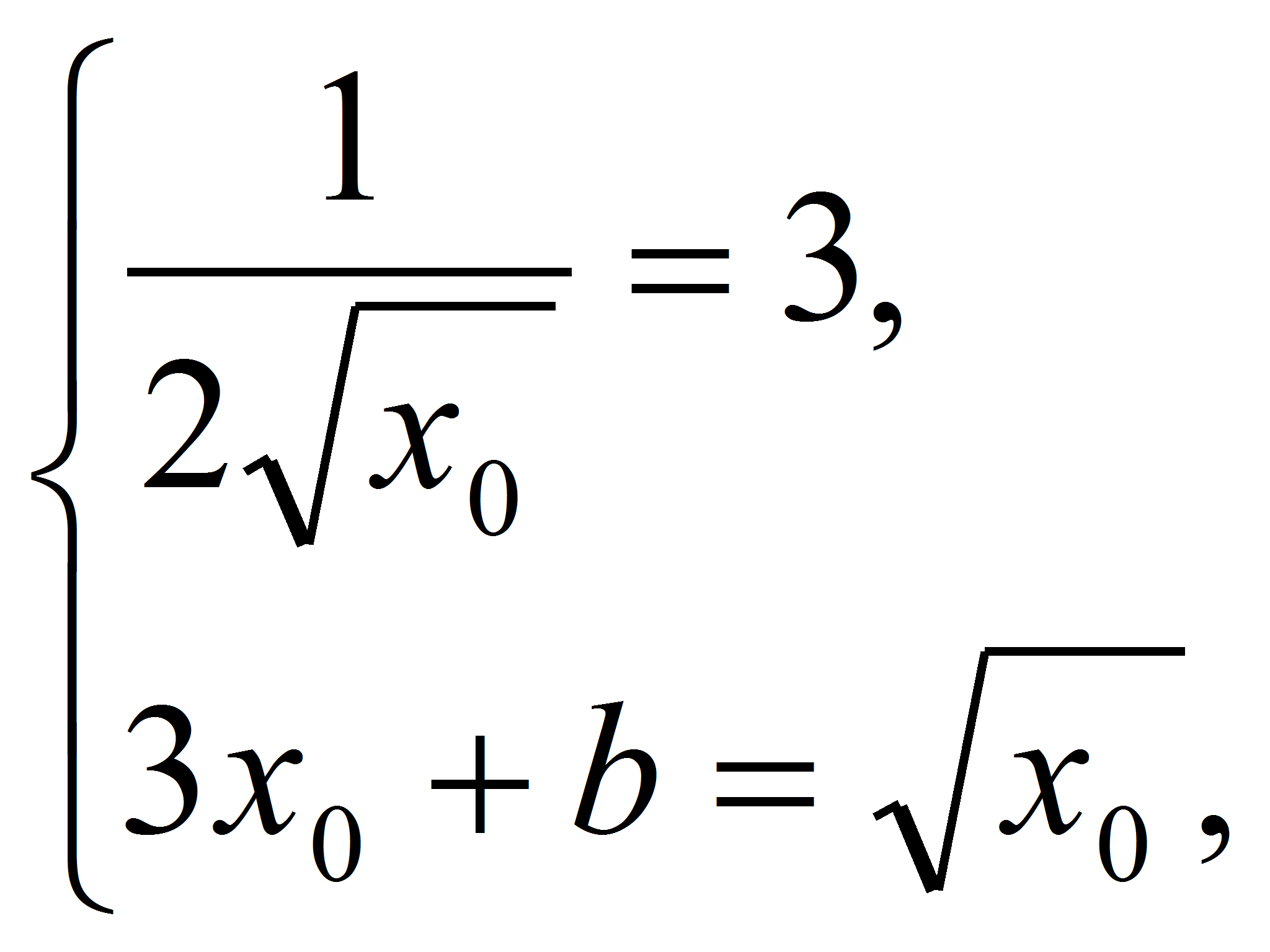
получим
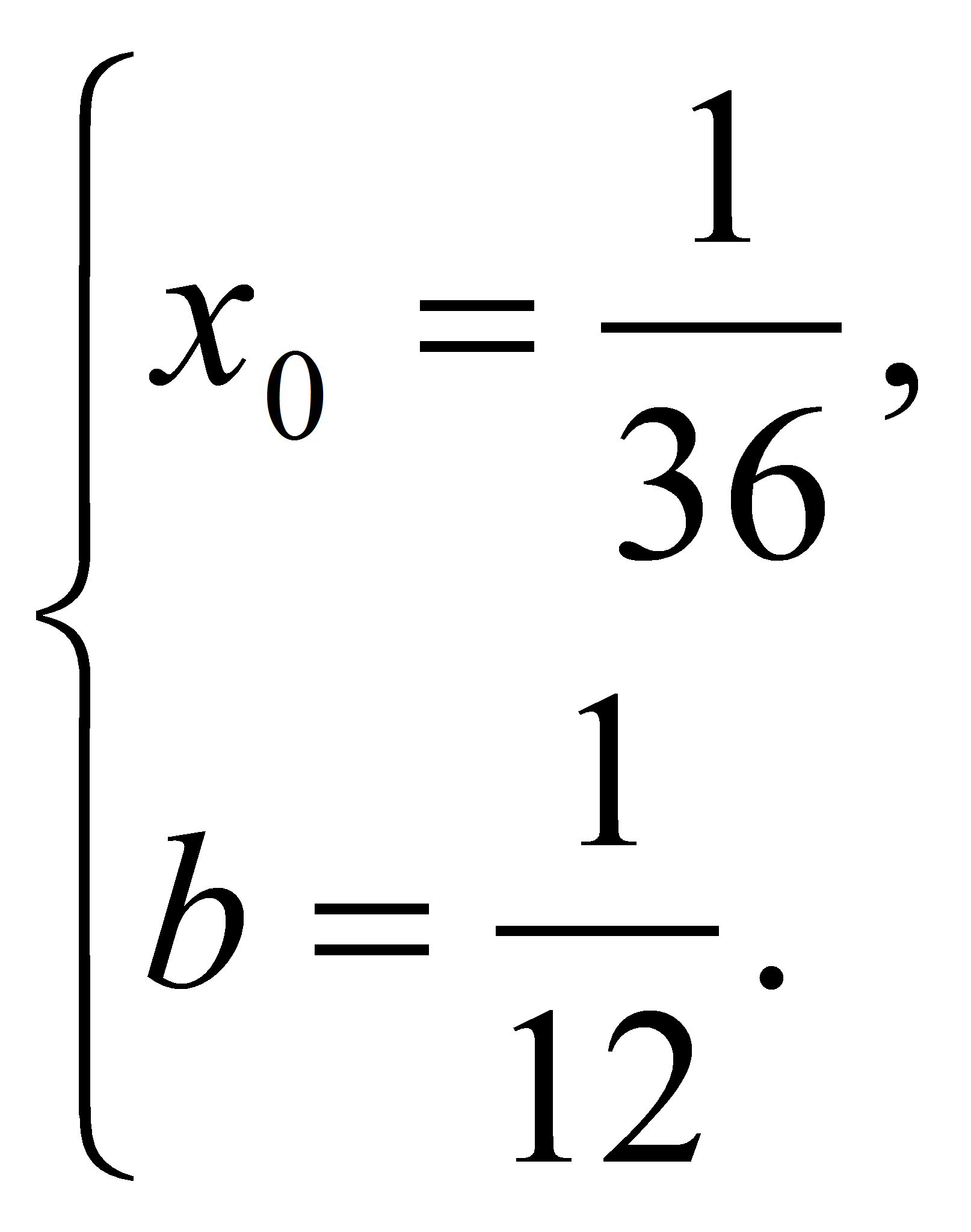
Ответ:
.
-
При каких
значениях а прямая
у=ах+2
является касательной к графику функции
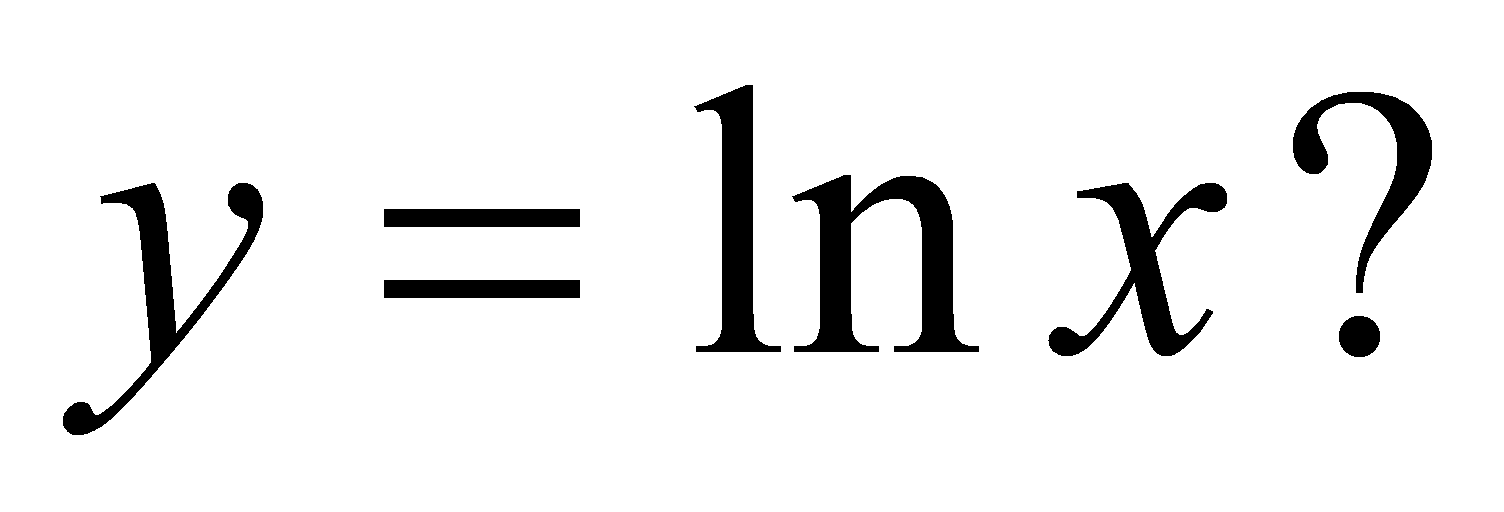
Указание.
Ответ:
а = e-3
-
При каких
значениях а прямая
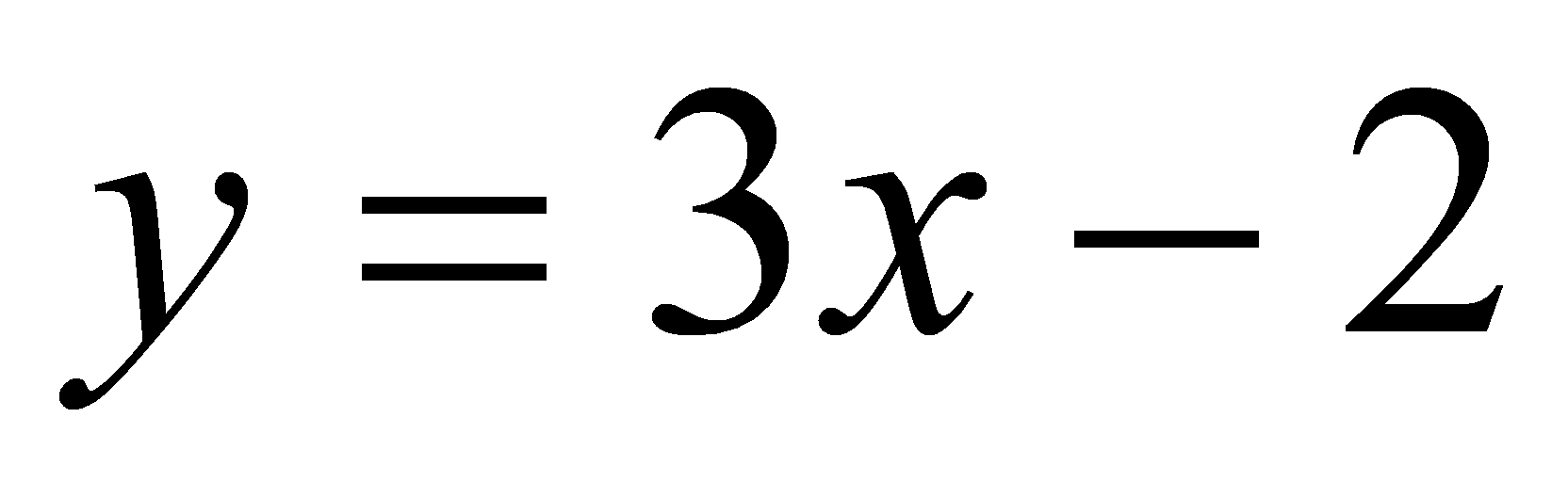
является касательной к графику функции
Указание.
Ответ:
а = 7 или а =
-1.
-
Является ли
прямая
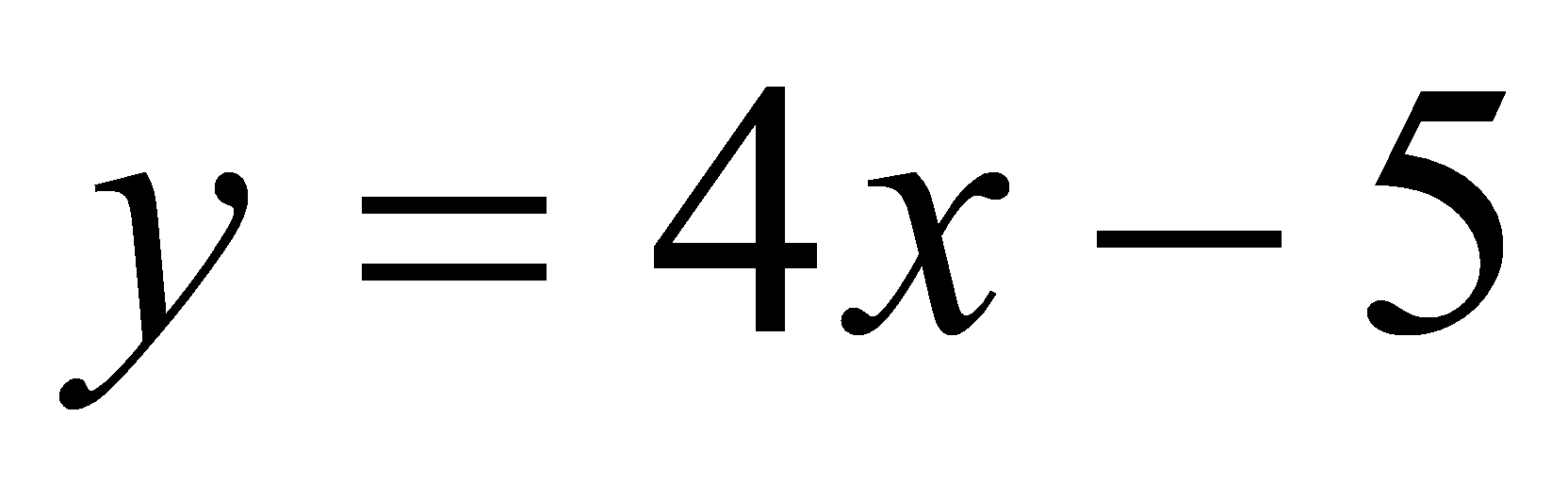
касательной к графику функции
?
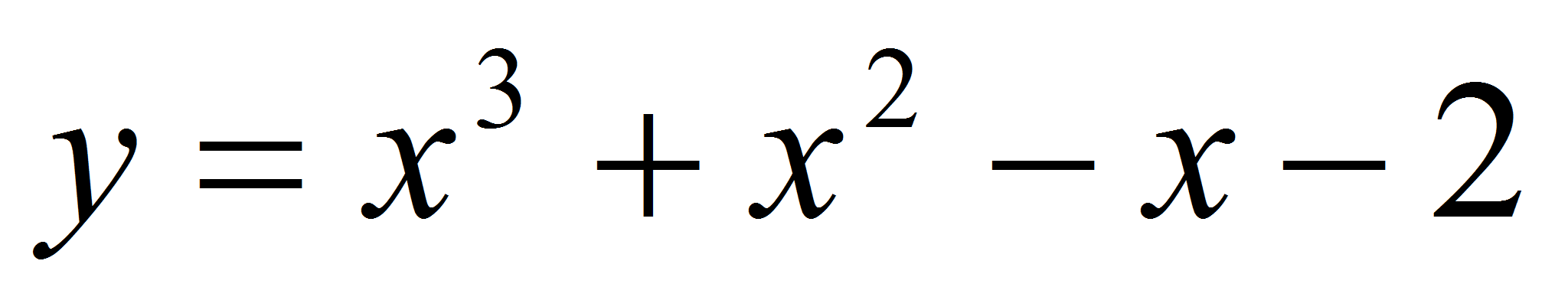Если является, то найти координаты точки касания.
?Решение.
Пусть
.
Из условия следует, что должны выполняться равенство
,
где
–
возможная абсцисса точки касания. Имеем:
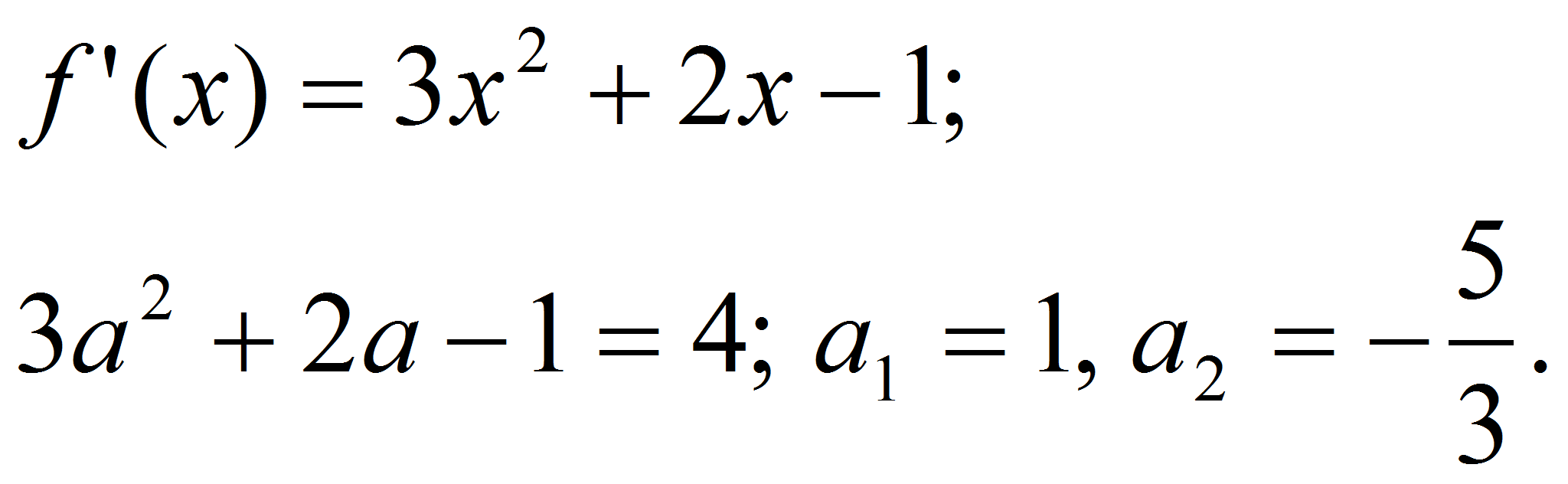
Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке
как раз и получится
.
Значит, точка касания имеет координаты (1;-1).
-
К графику
функции
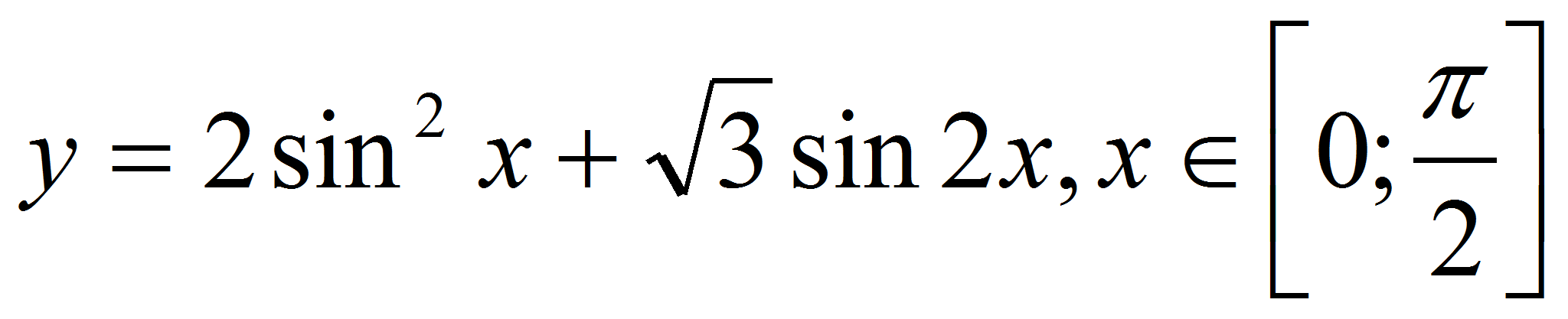проведена
касательная, параллельная прямой
.
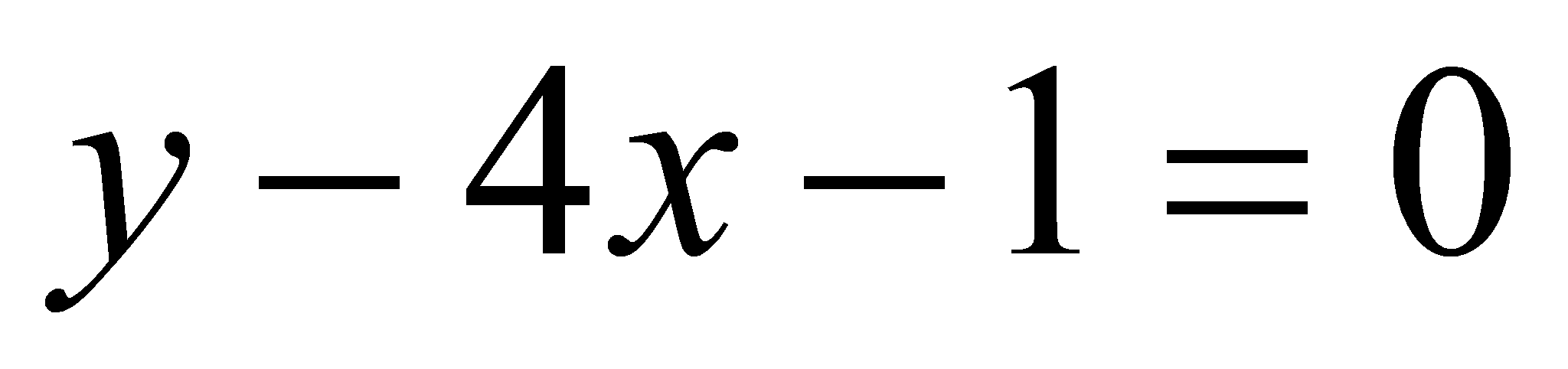Найти ординату точки касания.
проведена
.Решение.
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
.
Имеем:
Таким образом,
.
Значит,
–
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:
Ответ: 1.
-
Написать
уравнение всех касательных к графику функции
,
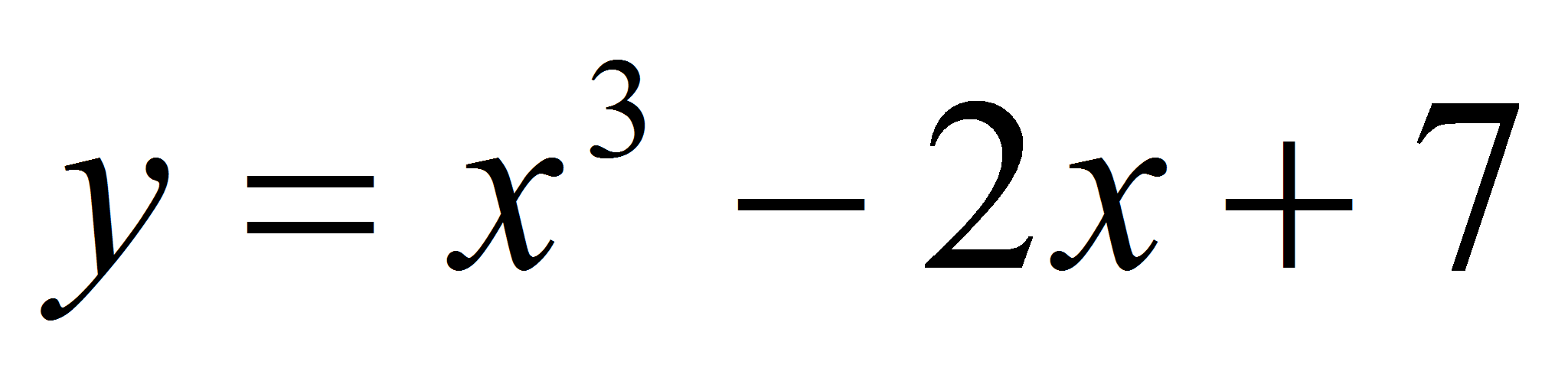параллельных прямой
.
,Решение.
Так как касательная должна быть параллельна прямой
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
.
Отсюда
или
.
Далее составляем уравнение касательной для каждой точки.
Ответ:
,
.
-
Найти все
значения
,
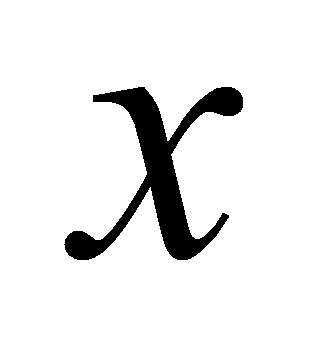при каждом из которых касательная к графикам функций
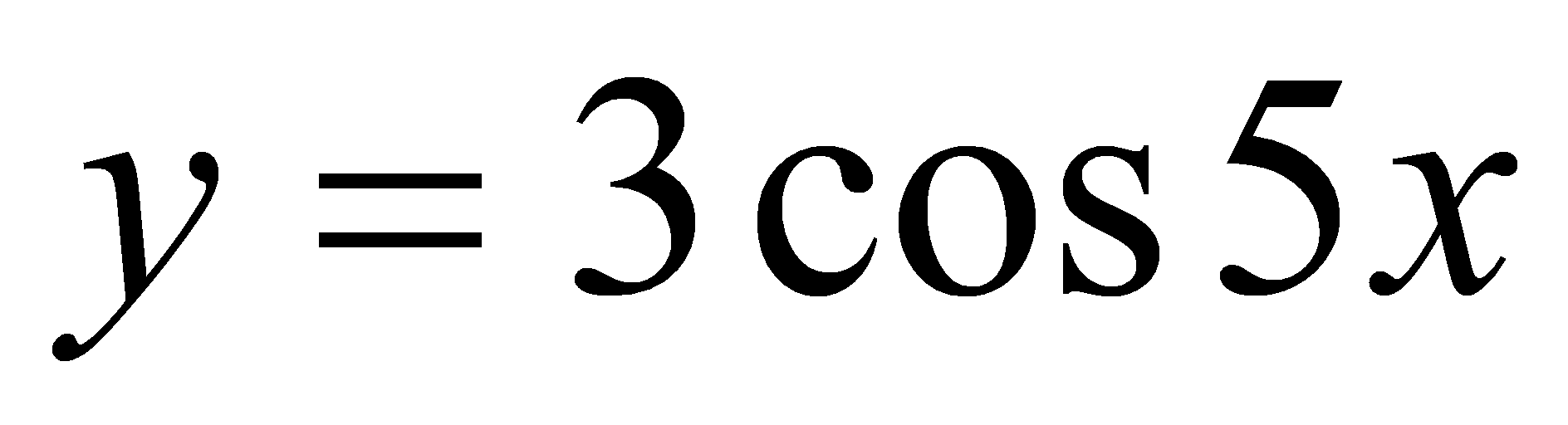
и
в
точках с абсциссой
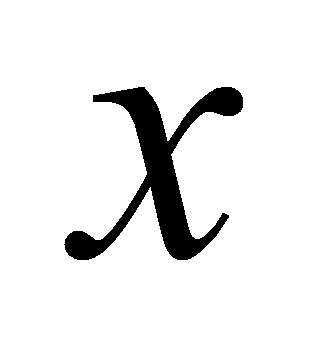
параллельны.
вРешение.
Известно, что тангенс угла наклона касательной к графику функций
в точке с абсциссой
равен
.
Следовательно, все искомые значения
будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем
-
Найти
расстояние между касательными к графику функции
,
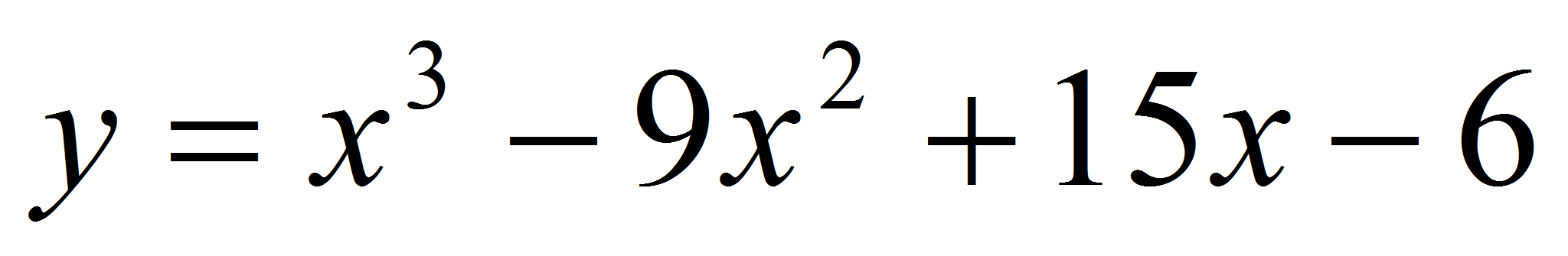расположенными параллельно оси
.
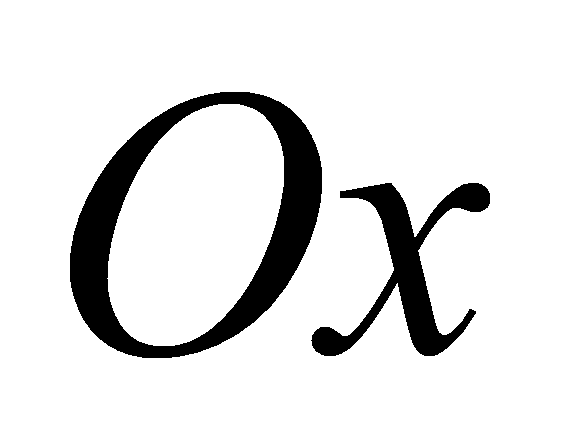,Решение.
Найдем критические точки заданной функции:
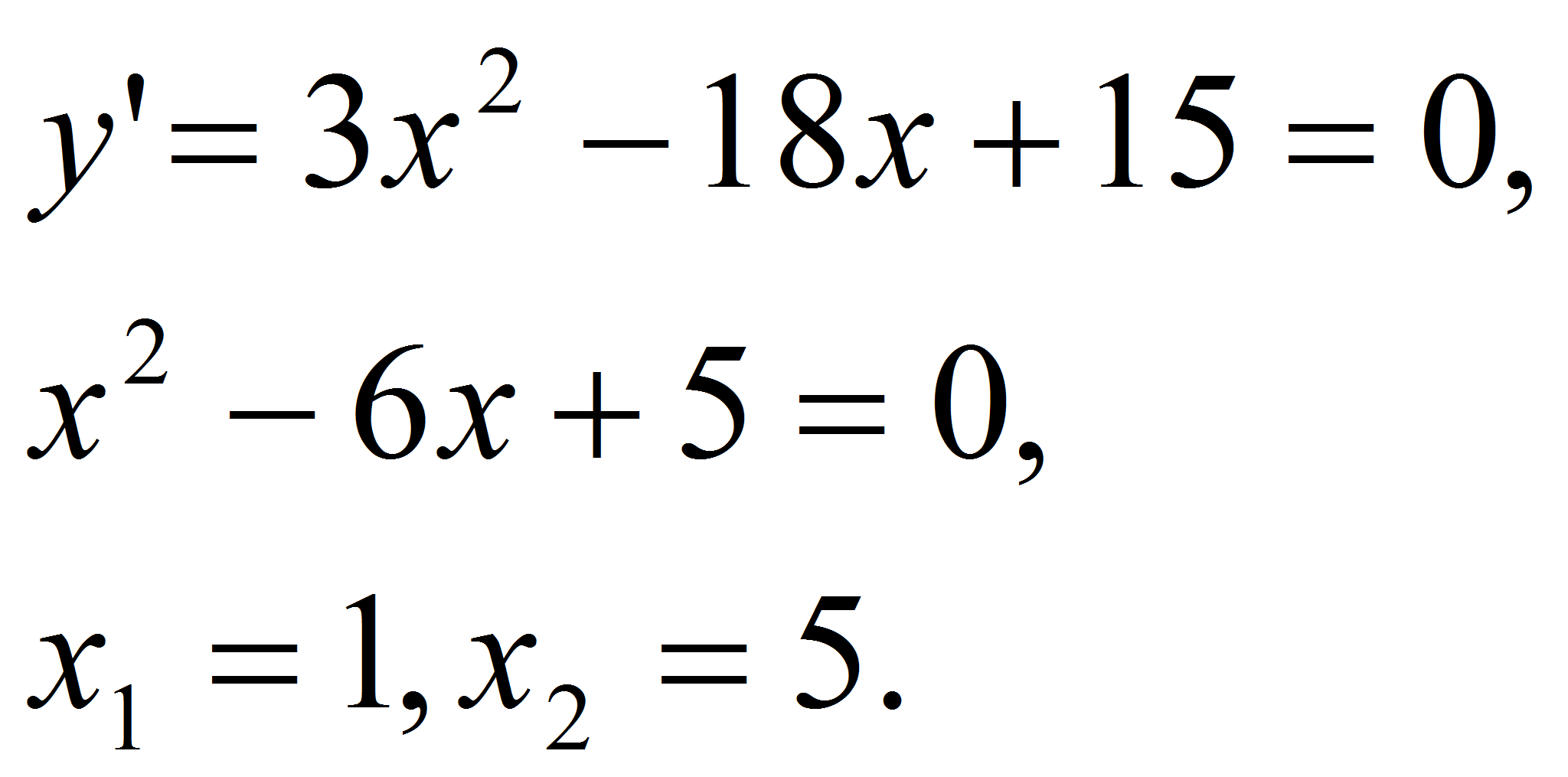
Так как,
производная в точках
и
равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
.
Найдем значения функций в этих точках.
Итак,
расстояние d
между касательными, параллельными оси
,
равно
С составлением
уравнения касательной, параллельной данной прямой, связана задача о
нахождении кратчайшего расстояния между графиком
некоторой функции f(x)
и прямой
.
Во многих
случаях удается найти касательную к графику
,
параллельную данной прямой
и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой
является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле
-
Найти
кратчайшее расстояние между параболой
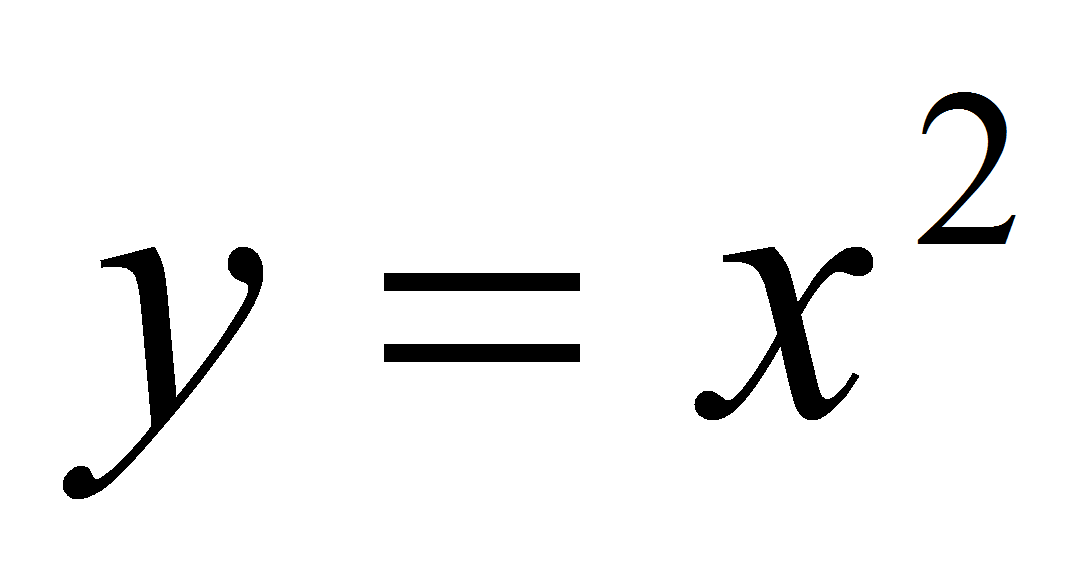
и прямой
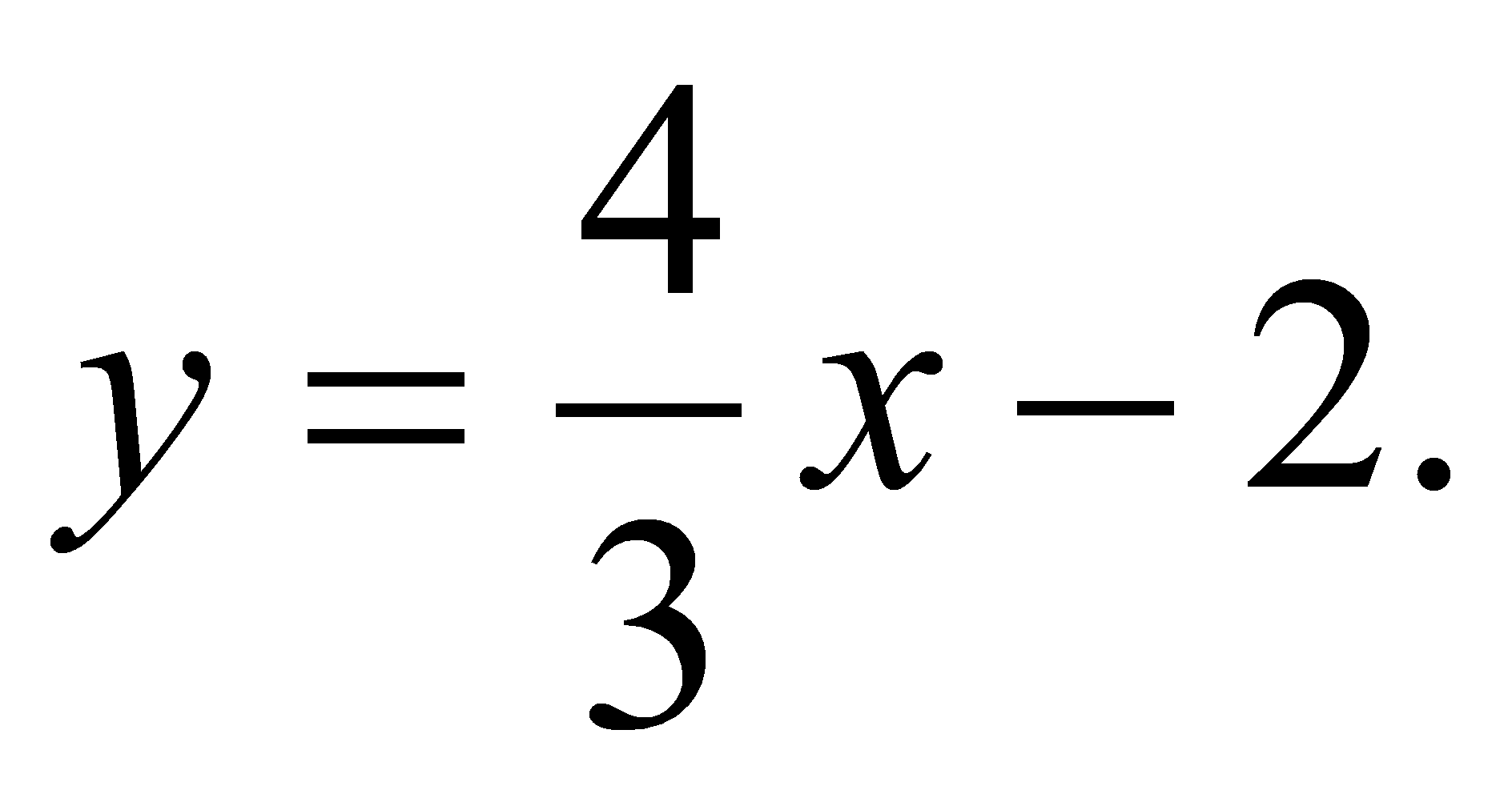
Решение.
Убедившись, что графики не имеют общих
точек (уравнение
не имеет решений), запишем
уравнение такой касательной к графику функции
,
которая параллельна прямой
Уравнение касательной имеет
вид
касание происходит в точке
Прямая у =
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
.
Ответ:
Довольно
сложной является задача составления уравнения всех касательных к
графику функции у = f(x),
проходящих через заданную точку М(х0;
у0),
вообще говоря, не лежащую на графике.
Приведем алгоритм решения этой задачи.
1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:
2. Решаем
относительно t
уравнение
и для каждого его
решения t
записываем
соответствующую
касательную в виде
.
-
Написать
уравнение всех касательных к графику функции
,
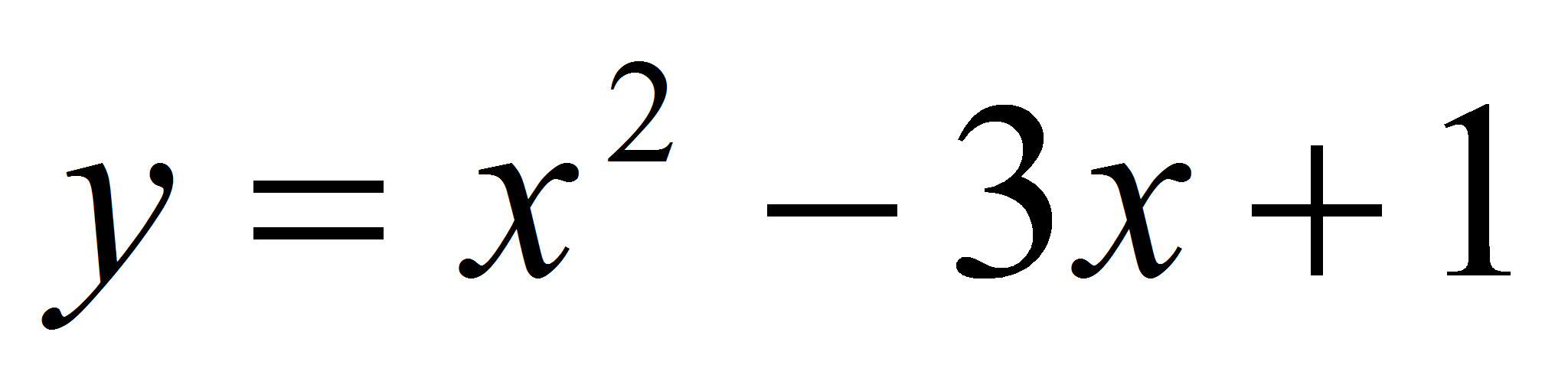проходящих через точку
М(2; -2).
,Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
.
Так как эта
касательная проходит через точку
(2; -2), то 
,
откуда
.
Ответ:
.
-
Найти
площадь треугольника, образованного касательными, проведенными
к графику функции
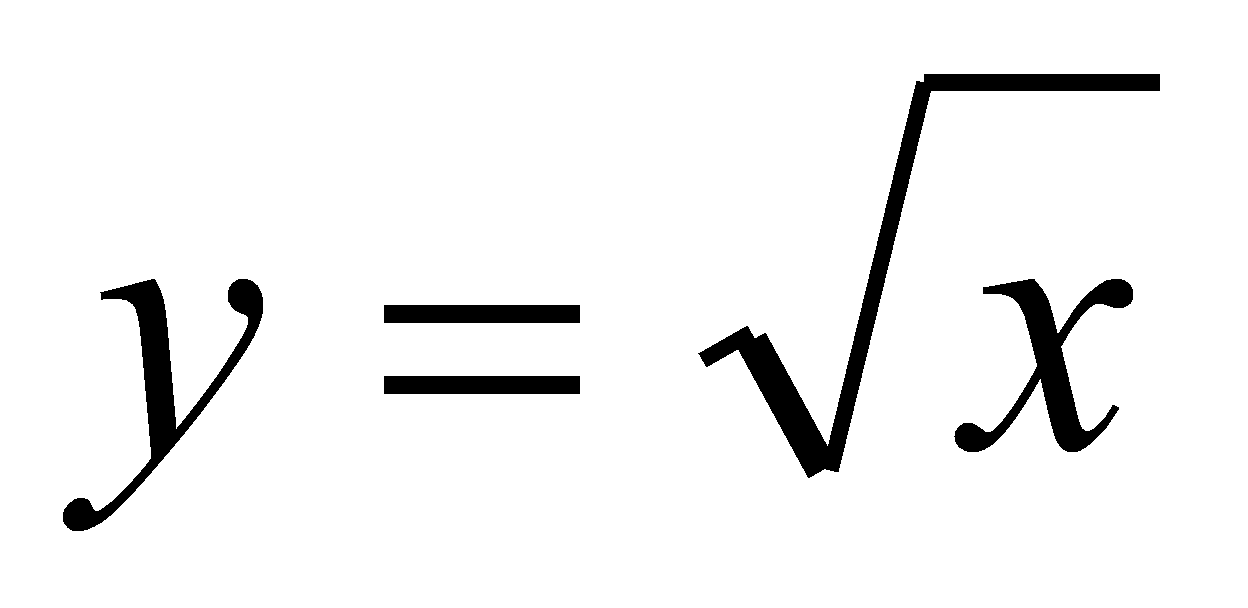
через точку
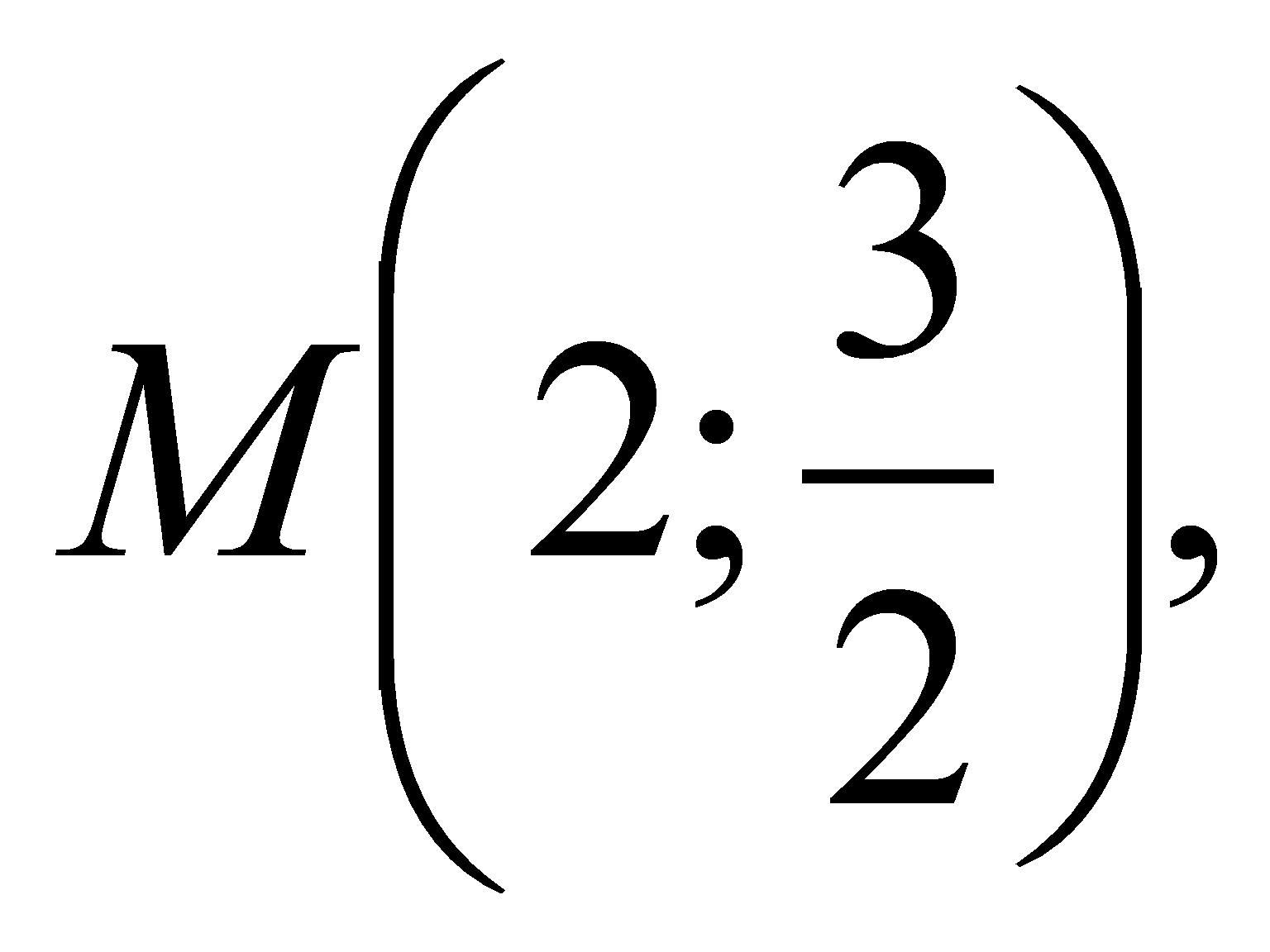
и секущей,
проходящей через точки касания.
Указание.
Уравнение
дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.
Ответ:
0,25.
Говорят, что
прямая
является общей касательной графиков функции
и
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая
является общей касательной графиков функций
(в точке М(2; 5) и
(в точке K(0,5;
-1)). Заметим, что графики функций
и
имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.
-
Доказать,
что параболы
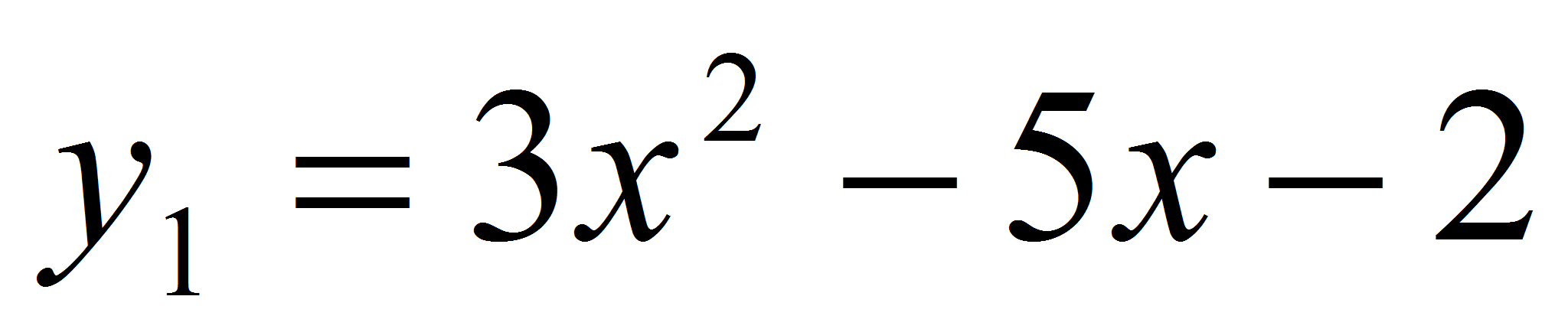
и
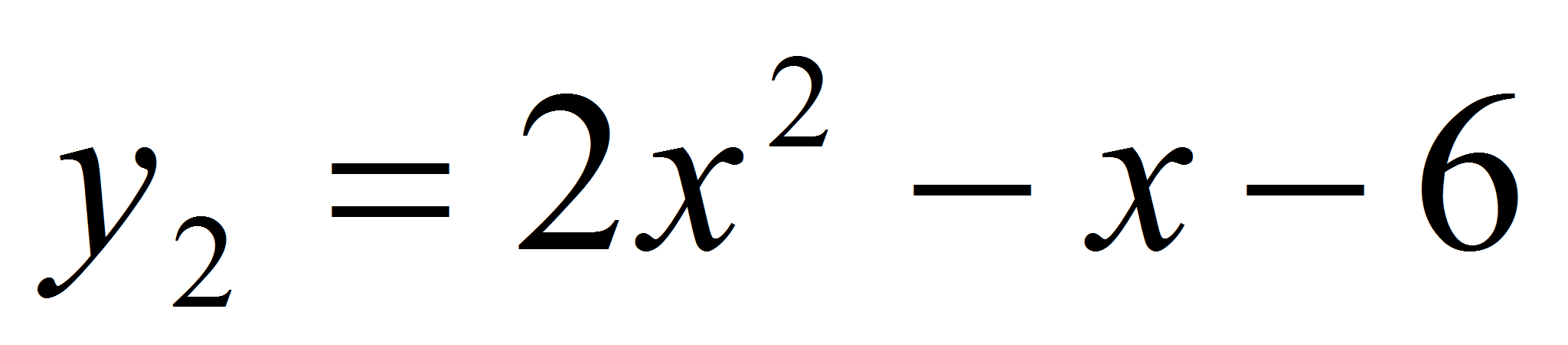имеют
в их общей точке общую касательную. Найти
уравнение этой общей касательной. Решение.
Уравнение
имеет
единственный корень х=2,
т. е. параболы имеют единственную общую точку
М(2;0). Убедимся, что значения производных для
обеих функций в точке х =
2 равны; действительно,
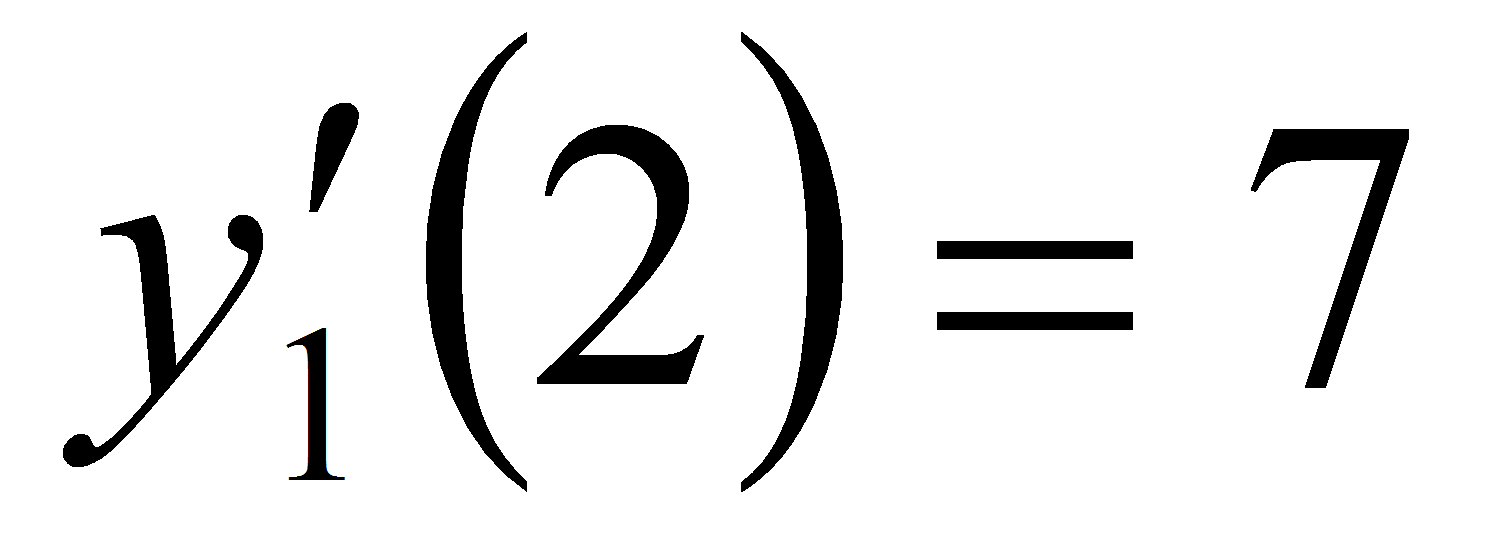и
.
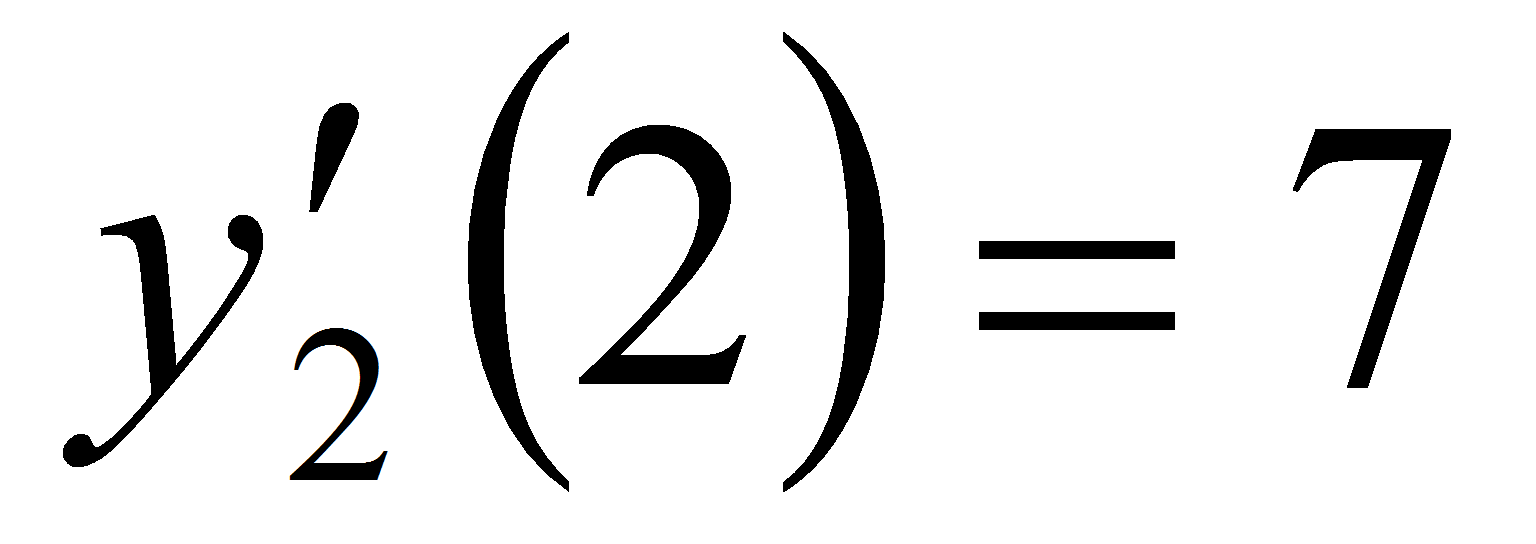Далее составляем уравнение касательной.
имеют
имеет
и
.Ответ:
.
В завершении рассмотрим
решение еще нескольких задач на касательную с параметром.
-
При
каких значениях параметра
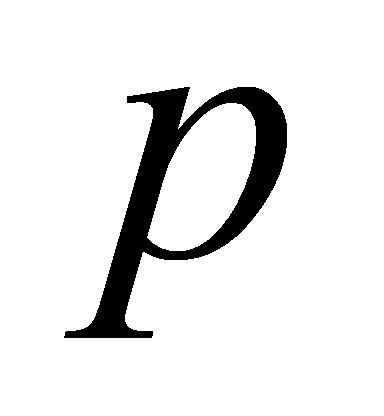касательная
к графику функции
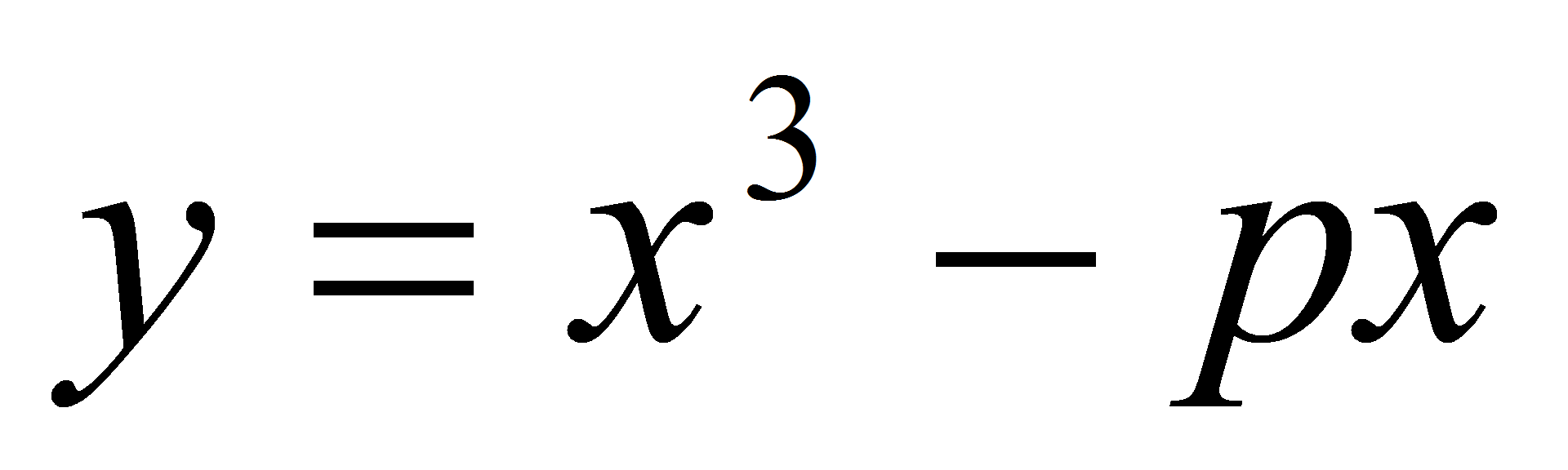
в точке
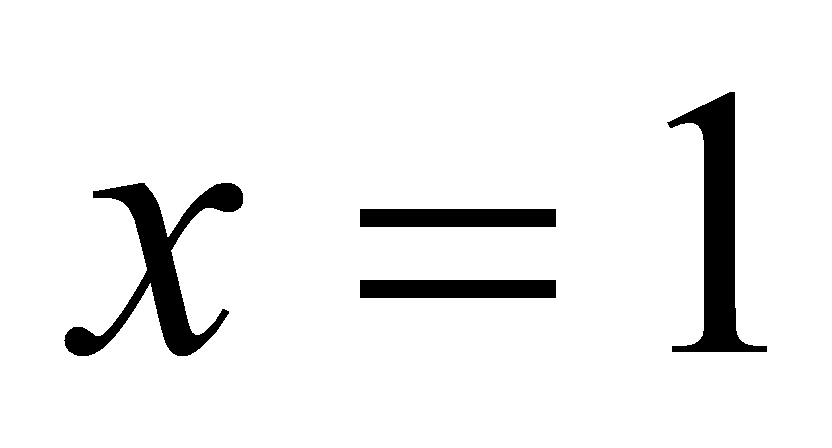
проходит через точку (2;3)?
касательная
Решение.
Составим уравнение касательной к графику заданной функции в точке
:
Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
.
-
Может ли
касательная к кривой
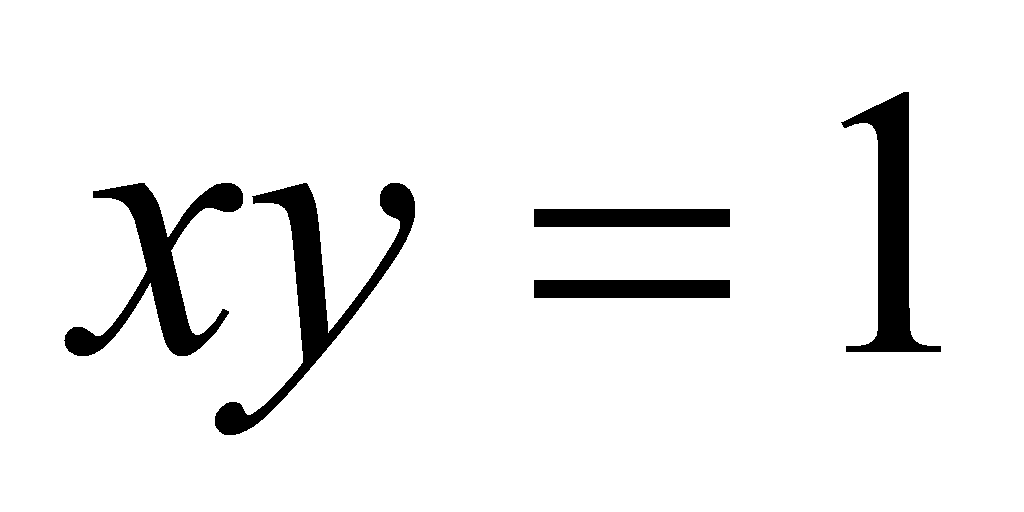
в какой-либо ее точке составлять острый угол с положительным
направлением оси
?
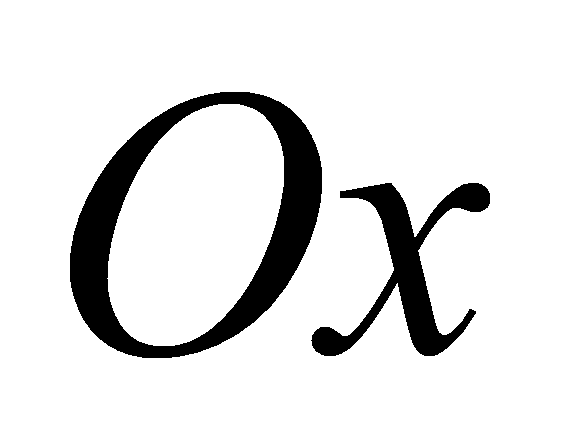Решение.
Найдем производную функции
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.
Ответ: Не
может.
-
Найти
значение параметра
,
при котором касательная к графику функции
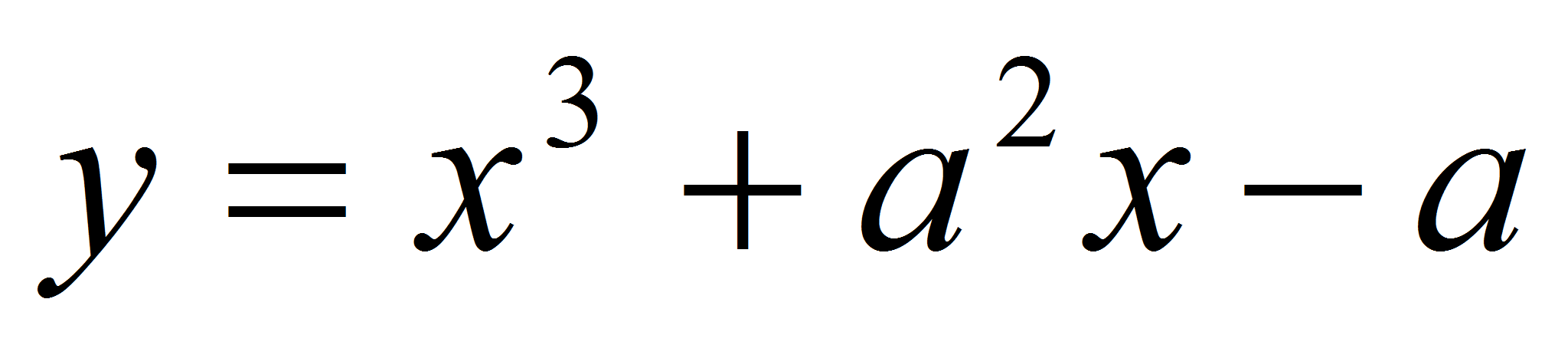
в точке
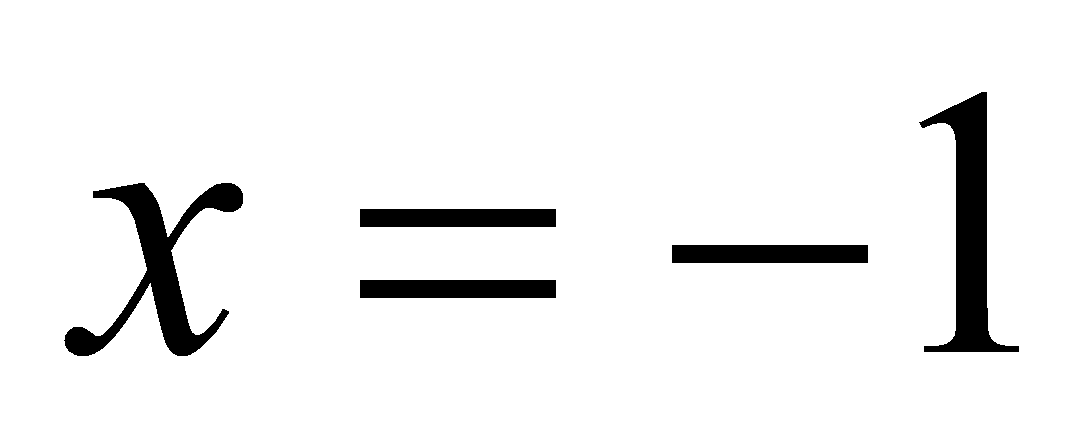
проходит через точку М(1;7).
Решение.
Пусть
тогда
.
Составим уравнение касательной:
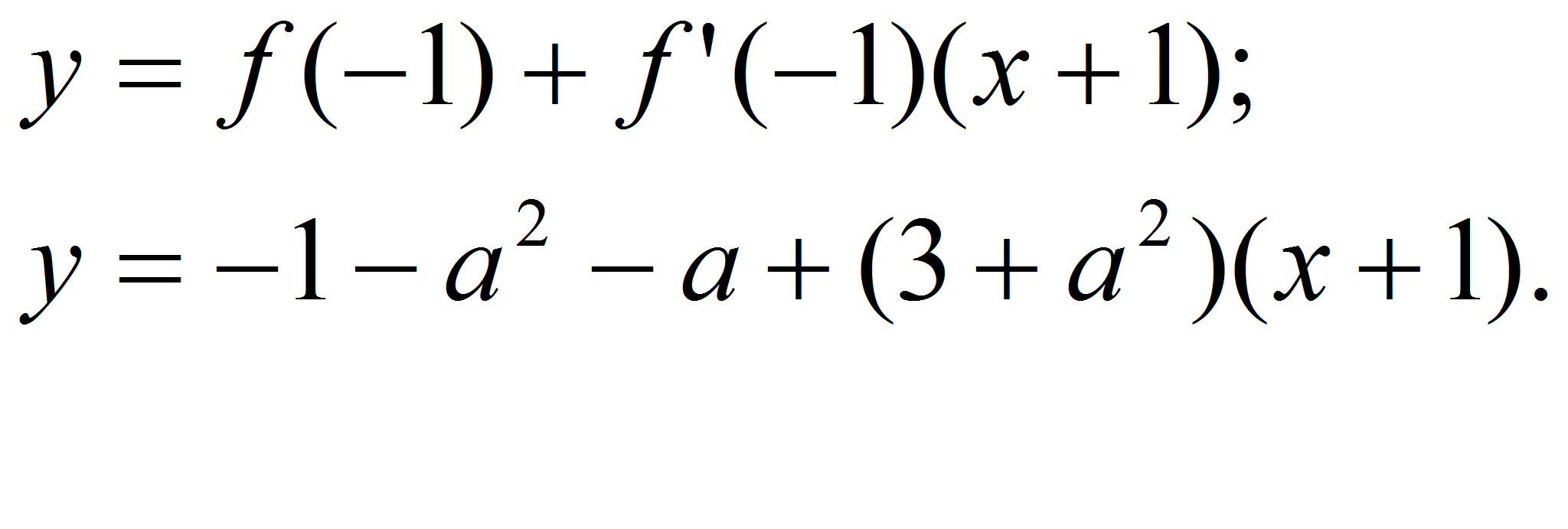
По условию эта
касательная проходит через точку М(1;7), значит,
,
откуда получаем:
-
При каких
значениях параметра
прямая
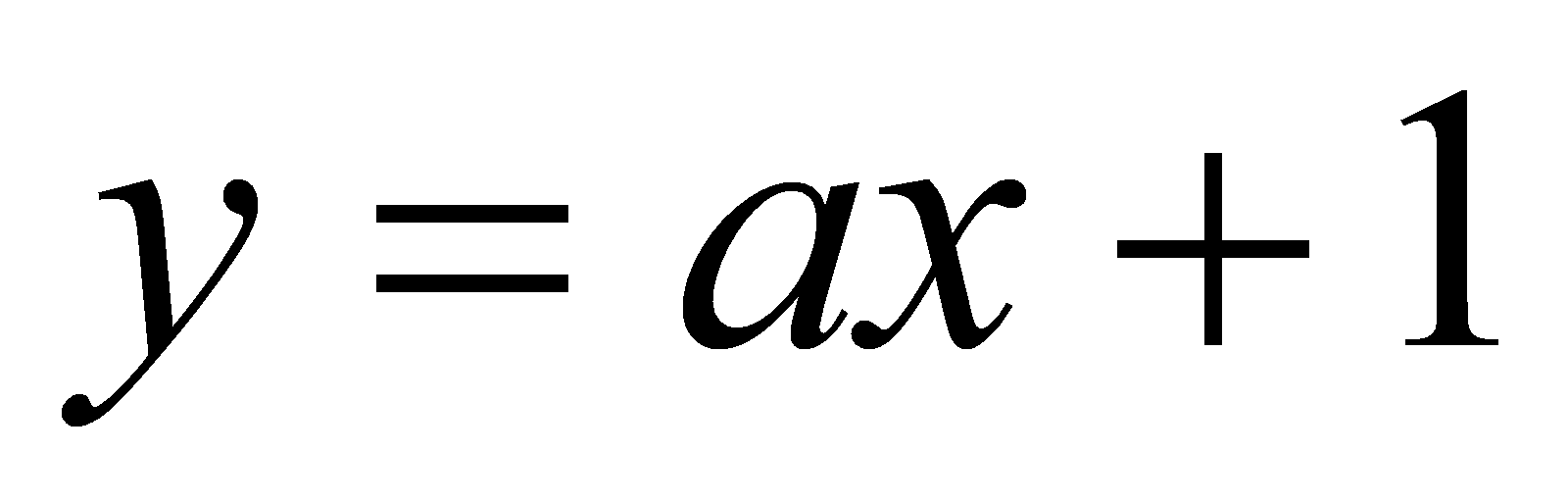
является касательной к графику функции
?
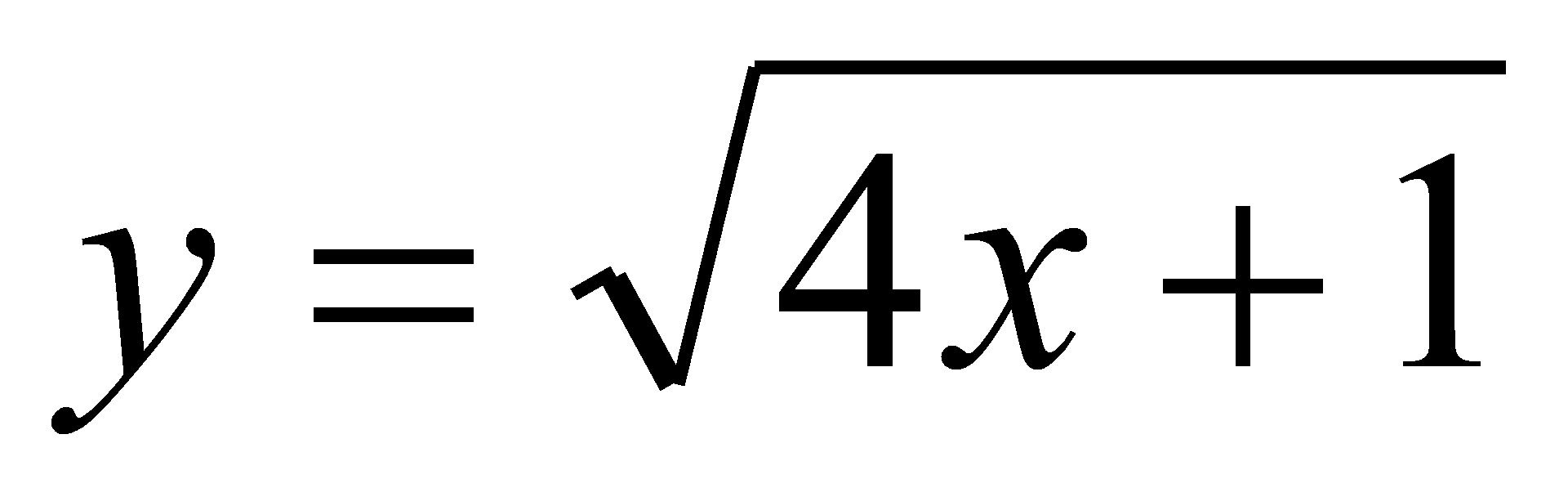?Решение.
Из условия следует, что должно выполнятся равенство
где
абсцисса
точки касания. Значит,
и
связаны между собой равенством
(1). Составим уравнение касательной к графику заданной функции в
точке
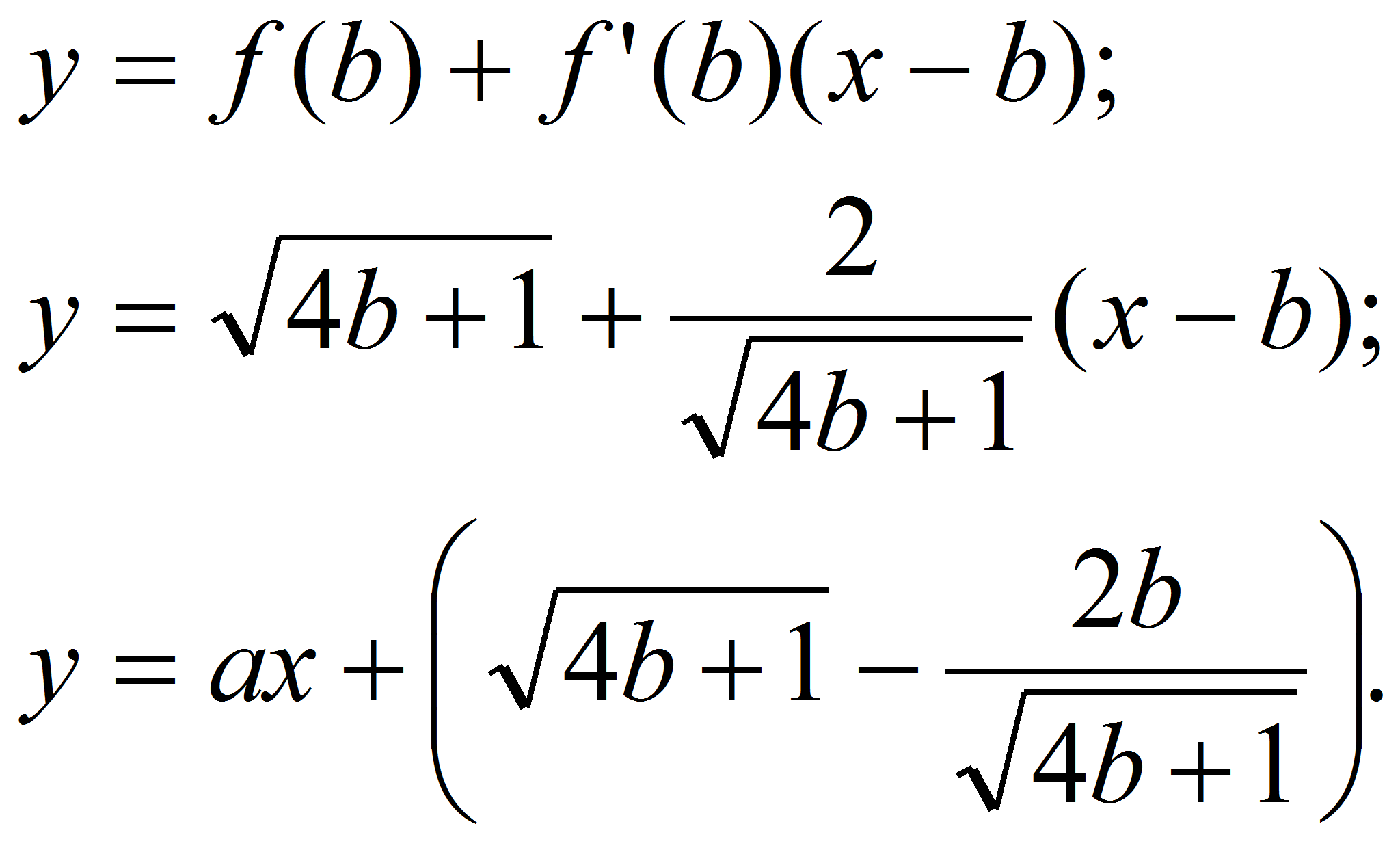
Из условия
следует, что должно выполняться равенство
.
Решив это уравнение, получим
.
Тогда из (1) получаем, что
.
-
При каком
значении
прямая
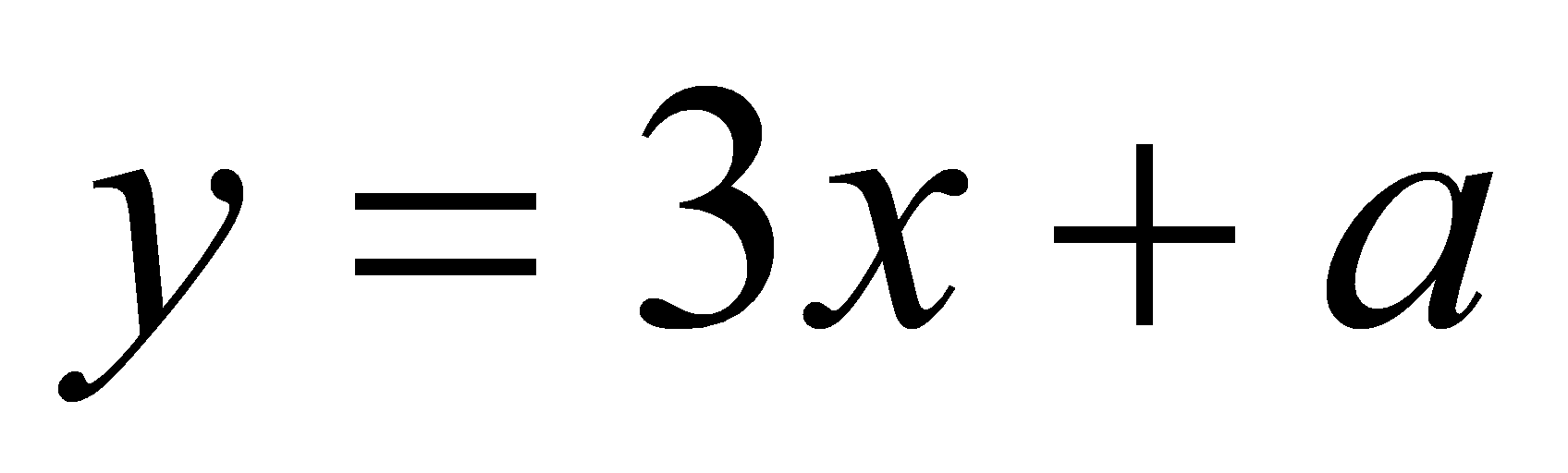
является касательной у графику
?
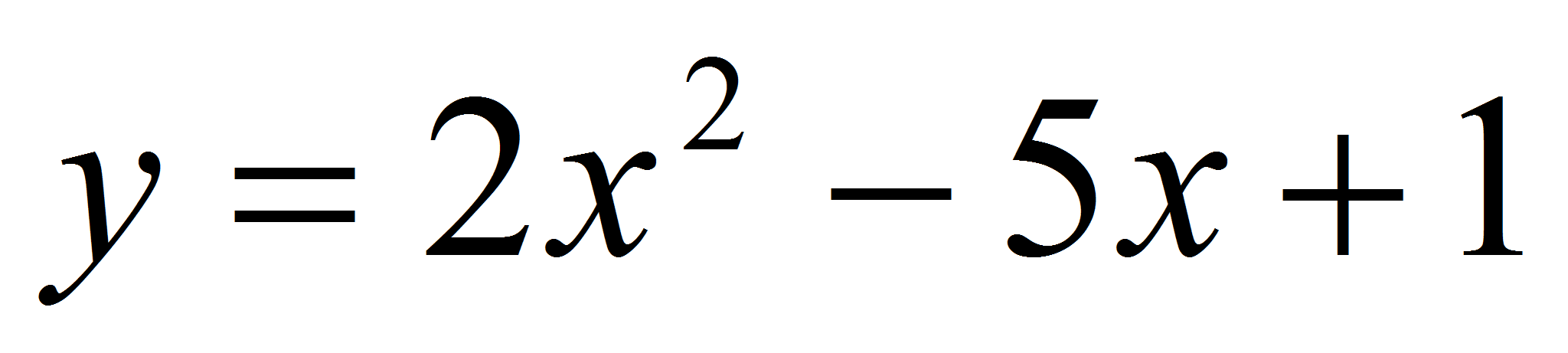Решение.
Так как прямая
является касательной к графику функции
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
откуда
,
следовательно,
–
абсцисса точки касания. Найдем теперь
из
условия равенства значений функций
и
при
.
Имеем
,
откуда
.
-
При каких
значениях параметра а касательные к графику функции
,
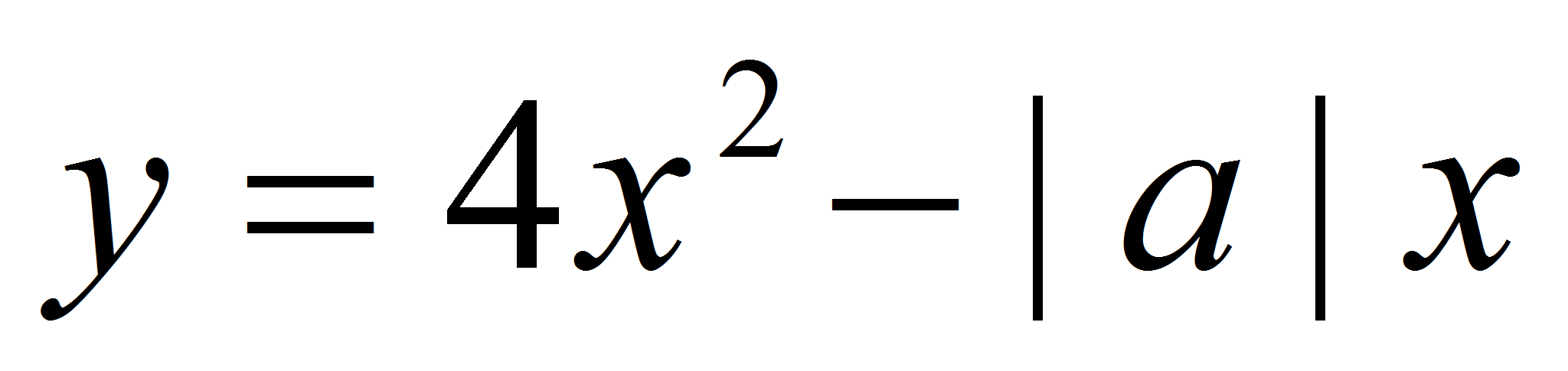проведенные в точках его пересечения с осью оx,
образуют между собой угол 60о?
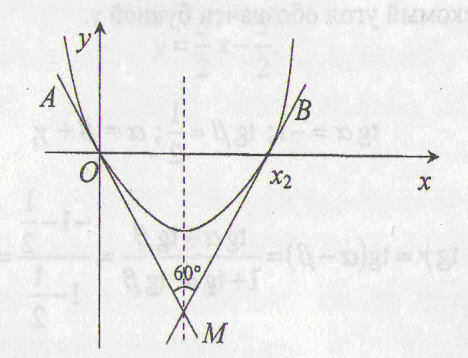
,Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):
и
учитываем,
что х2>0
(рис. 3)
-
Рис. 3
Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен
Далее имеем:
.
Таким образом, получаем, что
,
то
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Таким образом, получаем, что
,
то есть
Ответ:
.
Литература:
-
Далингер,
В.А. Начала математического анализа в задачах [Текст]: учебное
пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. –
312 с. -
Звавич, Л.И. Алгебра и
начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с
углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В.
Чинкина.– М.: Дрофа, 1999. – 352 с.
Основные термины (генерируются автоматически): график функции, касательная, уравнение касательной, прямая, решение, абсцисса, касание, график функций, кратчайшее расстояние, угловой коэффициент.
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Касательная – это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем – уравнение нормали к графику функции.
В нём k – угловой коэффициент.
Отсюда получаем следующую запись:
Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль – это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет “холодным душем”.
Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .
Решаем задачи вместе
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример – тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг – приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в “формулу-болванку” и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного “причесать”: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Снова решаем задачи вместе
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали – не заметить, что функция, данная в примере, – сложная и вычислять её производную как производную простой функции. Следующие примеры – уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Внимание! Данная функция – сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Как и в предыдущем примере, данная функция – сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Касательная и нормаль к графику функции
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
Касательная и нормаль к циссоиде в точке (2;2).
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) – абсциссу точки в которой нужно построить касательную Найти уравнение касательной
Немного теории.
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) – углом между этой прямой и осью Ox
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) – ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми
Касательная и нормаль к кривой
Касательная прямая – прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:
а уравнение нормали:
Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.
Решение. Находим значение функции в заданной точке:
Далее вычислим значение производной функции в точке $x_0=0$:
а тогда уравнение касательной запишется в виде:
или после упрощения:
$$y-4=-frac<1><-3>(x-0) Rightarrow x-3 y+12=0$$
Ответ. Уравнение касательной: $3x+y-4=0$
Уравнение нормали: $x-3y+12=0$
Угол между кривыми
Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_<1>x+b_<1>$ и $y=k_<2>x+b_2$, то тангенс угла между кривыми определяется соотношением:
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
Итак, искомый тангенс:
Ответ. $operatorname phi=frac<1><7>$
[spoiler title=”источники:”]
http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/
http://www.math-solution.ru/math-task/equation-tangent
http://www.webmath.ru/poleznoe/formules_8_10.php
[/spoiler]
