- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Прямоугольник – это четырехугольник, у которого все углы прямые.
На рис. 1 изображен прямоугольник АВСD.
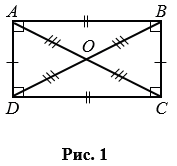
Отрезки АВ и СD, АD и ВС – противолежащие стороны прямоугольника. Противолежащие стороны прямоугольника не имеют общих точек. В прямоугольнике противолежащие стороны равны, тогда на рис. 1 в прямоугольнике АВСD: АВ = DС, АD = ВС.
Отрезки АВ и АD, АD и DC, DC и ВС, АВ и ВС – соседние или смежные стороны. Смежные стороны – стороны, которые имеют общую вершину. Смежные стороны прямоугольника имеют специальные названия: длина и ширина.
Отрезки АС и ВD – диагонали прямоугольника. Диагонали прямоугольника соединяют противолежащие вершины. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Так на рис. 1 АС = ВD и ОА = ОВ = ОС = ОD.
Периметр – это сумма длин всех сторон многоугольника. Обозначается периметр буквой 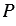 .
.
Учитывая, что в прямоугольнике противоположные стороны равны, его периметр вычисляется по формуле: 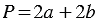 или
или 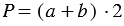 , где
, где 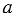 и
и 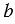 смежные стороны прямоугольника (длина и ширина).
смежные стороны прямоугольника (длина и ширина).
Площадь прямоугольника обозначается буквой 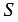 . Площадь прямоугольника равна произведению его смежных сторон, т.е. если
. Площадь прямоугольника равна произведению его смежных сторон, т.е. если 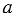 и
и 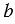 смежные стороны прямоугольника, то его площадь
смежные стороны прямоугольника, то его площадь 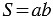 .
.
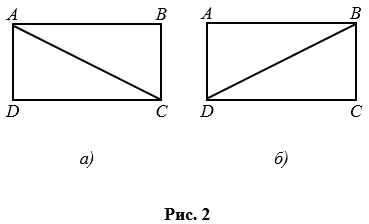
Каждая диагональ прямоугольника делит его на два равных треугольника. На рис. 2, 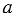 диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е.
диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е. 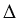 АВС =
АВС = 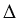 АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
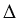 ВАD =
ВАD = 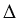 ВСD.
ВСD.
Прямоугольник, у которого все стороны равны, называют квадратом.
Ось симметрии
Прямоугольник имеет ось симметрии. Ось симметрии прямоугольника – это прямая, проходящая через средины противоположных сторон прямоугольника. У прямоугольника две оси симметрии, на рис. 3 прямые 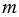 и
и 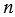 оси симметрии прямоугольника АВСD.
оси симметрии прямоугольника АВСD.
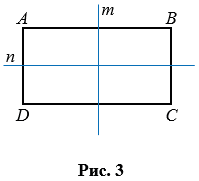
Если лист бумаги перегнуть по прямым 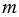 (или
(или 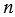 ), то две части прямоугольника, лежащие по разные стороны от прямой
), то две части прямоугольника, лежащие по разные стороны от прямой 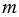 (или
(или 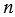 ), совпадут.
), совпадут.
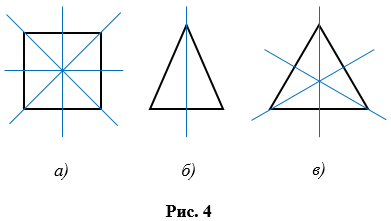
Существуют и другие фигуры, которые имеют ось симметрии, такие фигуры называют симметричными относительно прямой. Так, например, квадрат имеет четыре оси симметрии (рис. 4, 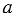 ), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 702,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 717,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 750,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1104,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1142,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Номер 546,
Мерзляк, Полонский, Якир, Учебник
Номер 573,
Мерзляк, Полонский, Якир, Учебник
Номер 579,
Мерзляк, Полонский, Якир, Учебник
Номер 1080,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Номер 412,
Мерзляк, Полонский, Якир, Учебник
Номер 662,
Мерзляк, Полонский, Якир, Учебник
Номер 757,
Мерзляк, Полонский, Якир, Учебник
Номер 1180,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 338,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 721,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 916,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1550,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 20,
Мерзляк, Полонский, Якир, Учебник
Номер 378,
Мерзляк, Полонский, Якир, Учебник
Номер 410,
Мерзляк, Полонский, Якир, Учебник
Номер 663,
Мерзляк, Полонский, Якир, Учебник
Номер 892,
Мерзляк, Полонский, Якир, Учебник
Номер 979,
Мерзляк, Полонский, Якир, Учебник
Номер 1111,
Мерзляк, Полонский, Якир, Учебник
Номер 1112,
Мерзляк, Полонский, Якир, Учебник
Задание 401,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 67,
Мерзляк, Полонский, Якир, Учебник
Номер 313,
Мерзляк, Полонский, Якир, Учебник
Номер 450,
Мерзляк, Полонский, Якир, Учебник
Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
Вычислить площадь фигуры, ограниченной линиями ![]() .
.
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая ![]() определяет ось
определяет ось ![]() , прямые
, прямые ![]() параллельны оси
параллельны оси ![]() и парабола
и парабола ![]() симметрична относительно оси
симметрична относительно оси ![]() , для неё находим несколько опорных точек:
, для неё находим несколько опорных точек:
![]()
Искомую фигуру желательно штриховать:
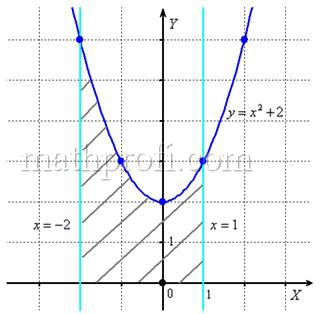
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке ![]() график функции
график функции ![]() расположен над осью
расположен над осью ![]() , поэтому искомая площадь:
, поэтому искомая площадь:
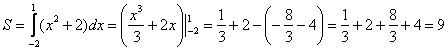
Ответ: ![]()
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями ![]() и осью
и осью ![]()
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью ![]() :
:
Пример 12
Вычислить площадь фигуры, ограниченной линиями ![]() ,
, ![]() и координатными осями.
и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
![]()
и выполним чертёж, получая фигуру площадью около двух клеток:
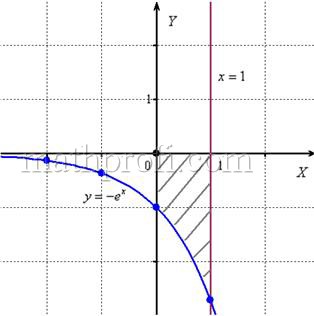
Если криволинейная трапеция расположена не выше оси ![]() , то её площадь можно найти по формуле:
, то её площадь можно найти по формуле: 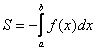 .
.
В данном случае: 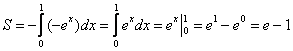
Ответ: ![]() – ну что же, очень и очень похоже на правду.
– ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями ![]() ,
, ![]() .
.
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы ![]() и прямой
и прямой ![]() , поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
, поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
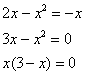
таким образом:
![]()
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой ![]() всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
![]() – именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
![]()
Выполним чертеж:
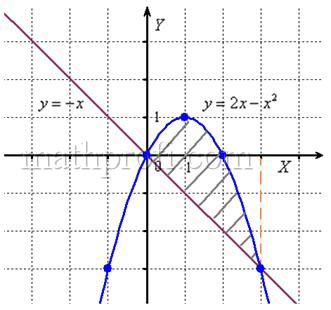
А теперь рабочая формула: если на отрезке ![]() некоторая непрерывная функция
некоторая непрерывная функция ![]() больше либо равна непрерывной функции
больше либо равна непрерывной функции ![]() , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых
, то площадь фигуры, ограниченной графиками этих функций и отрезками прямых ![]() , можно найти по формуле:
, можно найти по формуле:
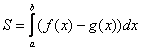
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке ![]() парабола располагается выше прямой, а поэтому из
парабола располагается выше прямой, а поэтому из ![]() нужно вычесть
нужно вычесть ![]()
Завершение решения может выглядеть так:
На отрезке ![]() :
: ![]() , по соответствующей формуле:
, по соответствующей формуле:
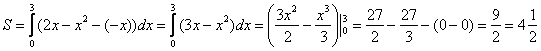
Ответ: ![]()
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 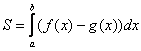 . Поскольку ось
. Поскольку ось ![]() задаётся уравнением
задаётся уравнением ![]() , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу
, то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу 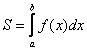 либо
либо 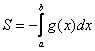
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) ![]() ,
, ![]() .
.
б) ![]() ,
, ![]() ,
, ![]()
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
Вычислить площадь фигуры, ограниченной линиями ![]()
Решение: выполним бесхитростный чертёж,
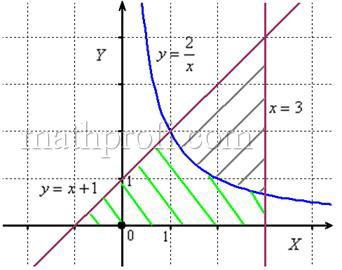
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую ![]() можно недочертить до оси
можно недочертить до оси ![]() , и тогда мы вовсе не увидим нужную фигуру.
, и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке ![]() над осью
над осью ![]() расположен график прямой
расположен график прямой ![]() ;
;
2) на отрезке ![]() над осью
над осью ![]() расположен график гиперболы
расположен график гиперболы ![]() .
.
Совершенно понятно, что площади можно (и нужно) сложить:
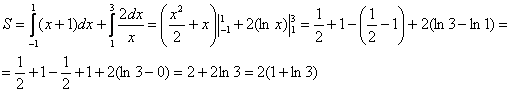
Ответ: ![]()
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]() и координатными осями.
и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс ![]() зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой ![]() и прямой
и прямой ![]() , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
, где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
![]()
и находим его корни:
![]() – нижний предел интегрирования,
– нижний предел интегрирования, ![]() – верхний предел.
– верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция ![]() (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
(Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле 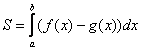 , все основные вариации мы разобрали выше.
, все основные вариации мы разобрали выше.
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!
 1.9. Объём тела вращения
1.9. Объём тела вращения
 1.7. Геометрический смысл определённого интеграла
1.7. Геометрический смысл определённого интеграла
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Учебник
Геометрия, 9 класс
Ромб: Формулы, Площадь, Вписанная Окружность
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
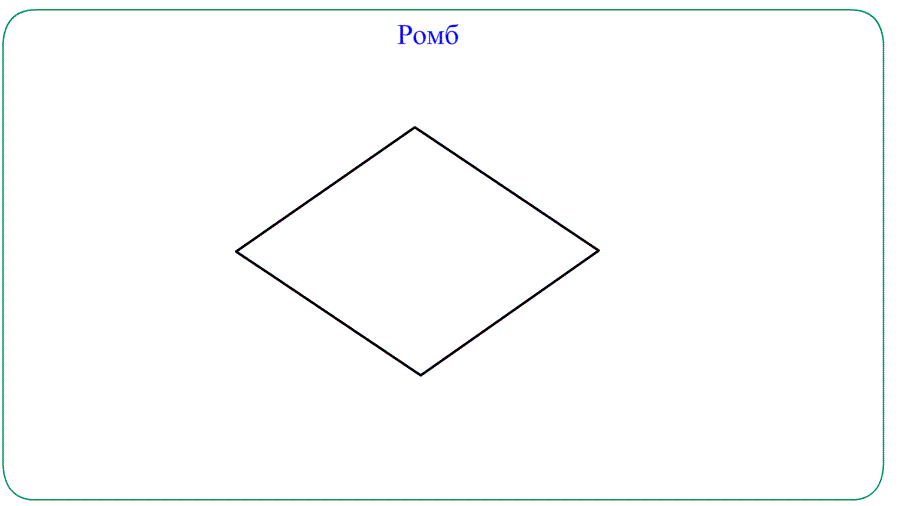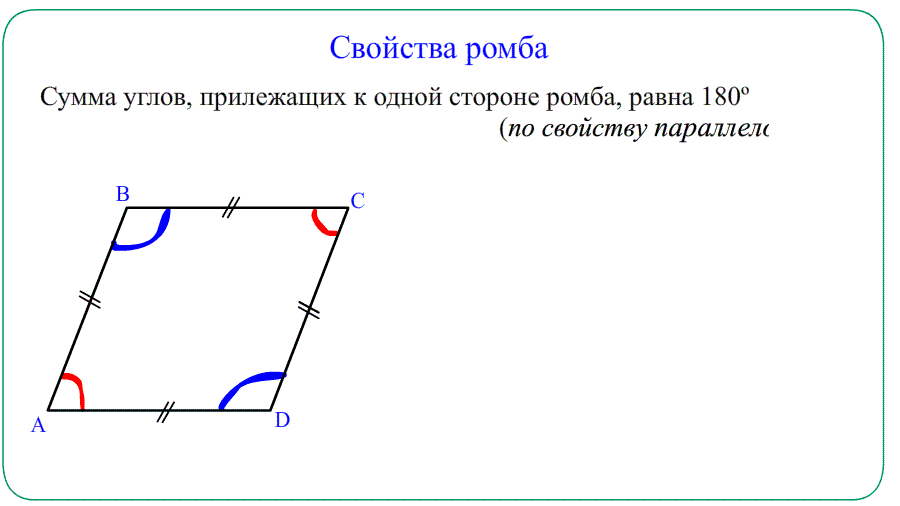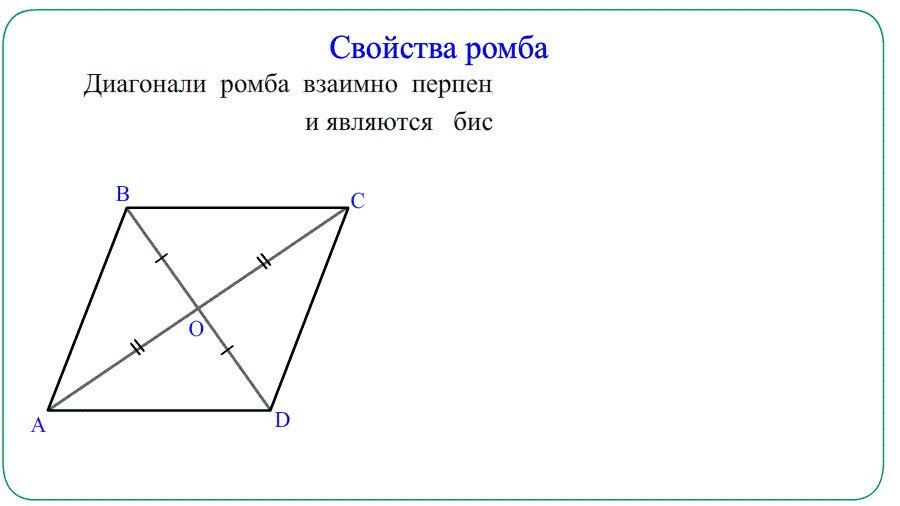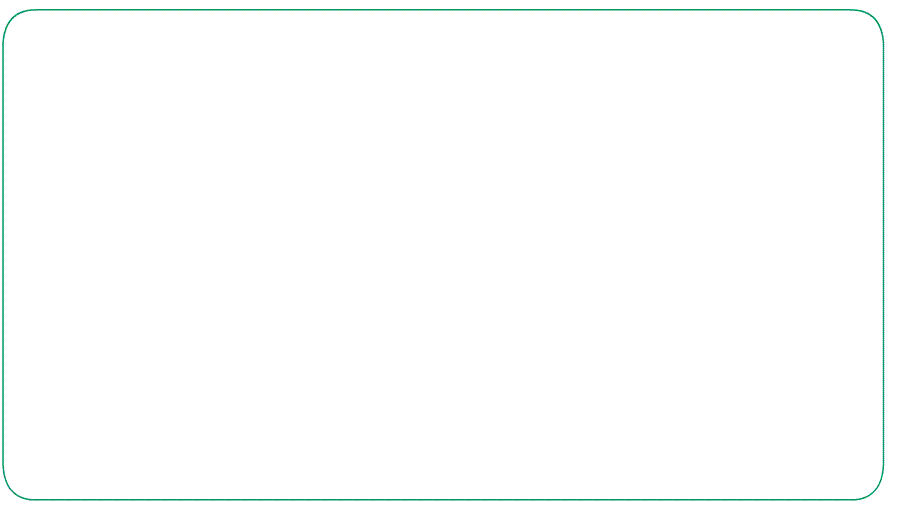
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая – $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . – половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ – пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
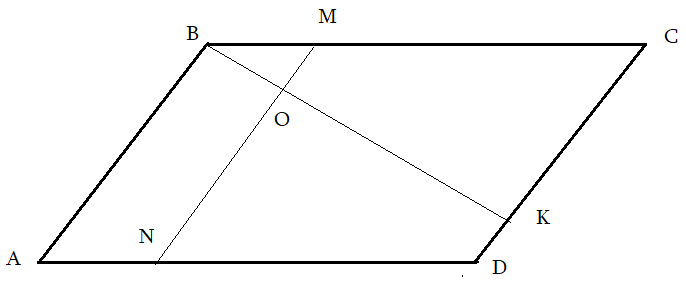
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ – параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ – квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто неподвижное – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Квадрат – одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: “В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник – стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Видео
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Теги
![]()
3 месяца назад
одной клетки равен 1.
Ответы2
Ответ:
S1 + S2 + S3
Объяснение:
Я ещё не изучал данную тему, но и так ясно что там дано 3 треугольника и ихние площади, следовательно площадь многоугольника равна сумме треугольников
Для решения рассмотрим рисунок (http://bit.ly/3wE8wdY).
Построим перпендикуляры из точек M и L к оси симметрии и определим площадь полученного многоугольника. Многоугольник состоит из 15 клеток, тогда его площадь равна 15 ед.
Площадь многоугольника симметричного данному так же равна 15 ед.
Тогда общая площадь полученной фигуры равна 2 * 15 = 30 ед.
Ответ: 30.
