| Квадрат | |
|---|---|
 Квадрат со стороной  и диагональю и диагональю  |
|
| Рёбра | 4 |
| Символ Шлефли | {4} |
| Вид симметрии | Диэдрическая группа (D4) |
| Площадь | a2 |
| Внутренний угол | 90° |
| Свойства | |
| Выпуклый многоугольник, Изогональная фигура, изотоксальная фигура | |
Квадра́т (от лат. quadratus, четырёхугольный[1]) — правильный четырёхугольник, то есть плоский четырёхугольник, у которого все углы и все стороны равны. Каждый угол квадрата — прямой 
Варианты определения[править | править код]
Квадрат может быть однозначно охарактеризован разными способами[3][4].
- Четырёхугольник, диагонали которого равны и взаимно перпендикулярны, причём точка пересечения делит их пополам.
- Четырёхугольник, являющийся одновременно прямоугольником и ромбом.
- Прямоугольник, у которого длины двух смежных сторон равны.
- Прямоугольник, у которого диагонали пересекаются под прямым углом.
- Ромб, у которого диагонали равны.
- Ромб, у которого два соседних угла равны.
- Ромб, один из углов которого — прямой (прочие углы, как легко доказать, тогда также прямые).
- Параллелограмм, у которого длины двух смежных сторон равны, а угол между ними — прямой.
- Параллелограмм, у которого диагонали равны, а угол между ними — прямой.
- Дельтоид, все углы которого прямые.
Свойства[править | править код]
Основной источник: [4]
Далее в этом разделе 



Стороны и диагонали[править | править код]
Диагонали квадрата равны, взаимно перпендикулярны, делятся точкой пересечения пополам и сами делят углы квадрата пополам (другими словами, являются биссектрисами внутренних углов квадрата). Длина каждой диагонали 
Периметр квадрата 
.
Вписанная и описанная окружности[править | править код]

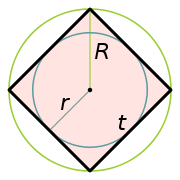
Вписанная и описанная окружности для квадрата
Центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей.
Радиус вписанной окружности квадрата равен половине стороны квадрата:
Радиус описанной окружности квадрата равен половине диагонали квадрата:
Из этих формул следует, что площадь описанной окружности вдвое больше площади вписанной.
Площадь[править | править код]
-

-
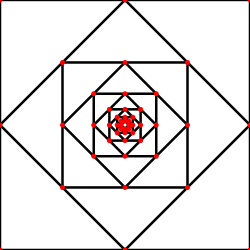
Соединив середины сторон квадрата, получаем квадрат вдвое меньшей площади
Площадь 
.
Из формулы 
Квадрат имеет два замечательных свойства[5].
- Из всех четырёхугольников с заданным периметром квадрат имеет наибольшую площадь.
- Из всех четырёхугольников с заданной площадью квадрат имеет наименьший периметр.

К уравнению квадрата; здесь
Уравнение квадрата[править | править код]
В прямоугольной системе координат уравнение квадрата с центром в точке 
где 




Уравнение квадрата с центром в начале координат и сторонами, параллельными осям координат (см. рисунок), может быть представлено в одной из следующих форм:
(легко получается применением поворота на 45° к предыдущему уравнению)
- (в полярных координатах[7])
Математические проблемы[править | править код]
С квадратами связаны ряд проблем, часть из которых до сих пор не имеет решения.
- Квадратура круга — древняя проблема построения циркулем и линейкой квадрата, равновеликого по площади заданному кругу. В 1882 году Фердинанд Линдеман доказал, что это невозможно.

Пример квадрирования квадрата
- Квадрирование квадрата — задача о разбиении квадрата на конечное число меньших квадратов, без «дырок», причём длины сторон квадратов должны отличаться друг от друга (в идеале должны быть все различны). Найден ряд решений этой задачи.
- Долгое время математики пытались доказать, что непрерывное отображение отрезка прямой в квадрат невозможно, пока Джузеппе Пеано не построил свой контрпример.
- Гипотеза Тёплица: на всякой замкнутой плоской жордановой кривой можно отыскать четыре точки, образующие вершины квадрата. Не доказана и не опровергнута.
- Разбиение квадрата сеткой одинаковых более мелких квадратов также приводит к множеству проблем, используемых, в частности, в теории латинских и греко-латинских квадратов, магических квадратов, в игре судоку.
Симметрия[править | править код]

Квадрат обладает наибольшей осевой симметрией среди всех четырёхугольников. Он имеет:
- одну ось симметрии четвёртого порядка — ось, перпендикулярную плоскости квадрата и проходящую через его центр;
- четыре оси симметрии второго порядка (то есть относительно них квадрат отражается сам в себя), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.
Применение[править | править код]
В математике[править | править код]
Единичный квадрат используется как эталон единицы измерения площади, а также в определении площади произвольных плоских фигур. Фигуры, у которых можно определить площадь, называются квадрируемыми.
Теорема Пифагора первоначально формулировалась геометрически: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Квадратами являются грани куба — одного из пяти правильных многогранников.
В математической физике символ квадрата может означать «оператор Д’Аламбера» (даламбериан) — дифференциальный оператор второго порядка:
Из теоремы Бойяи — Гервина следует, что любой многоугольник равносоставлен квадрату, то есть его можно разрезать на конечное число частей, из которых составляется квадрат (и обратно)[8].
Графы:
K4 полный граф часто изображается как квадрат с шестью рёбрами.
Орнаменты и паркеты[править | править код]
- Мозаики, включающие квадраты
-

-

-

Мозаики, орнаменты и паркеты, содержащие квадраты, широко распространены.
Другие применения[править | править код]
Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.
Квадратный флаг Лима поделён на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.
Графика[править | править код]
Символы со сходным начертанием: ロ · ⼝ · ⼞
Ряд символов имеют форму квадрата.
- Символы Юникода U+25A0 — U+25CF
- U+20DE ◌⃞ COMBINING ENCLOSING SQUARE
- ロ (Японский иероглиф «Ро» (катакана))
- 口 (Китайский иероглиф «рот»)
- 囗 (Китайский иероглиф «ограда»)
В Latex для вставки символа квадрата служат конструкции Box или square.
В HTML, чтобы заключить произвольный текст в квадрат или прямоугольник, можно использовать конструкцию:
- <span style=”border-style: solid; border-width: 1.5px 1.5px 1.5px 1.5px; padding-left: 4px; padding-right: 4px;”>text</span>; результат: text.
Вариации и обобщения[править | править код]
Многомерное пространство[править | править код]
Квадрат можно рассматривать как двумерный гиперкуб.
Неевклидова геометрия[править | править код]
В неевклидовой геометрии квадрат (в более широком смысле) — многоугольник с четырьмя равными сторонами и равными углами. По величине этих углов можно судить о кривизне плоскости — в евклидовой геометрии и только в ней углы прямые, в сферической геометрии углы сферического квадрата больше прямого, в геометрии Лобачевского — меньше.
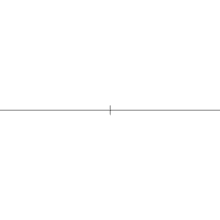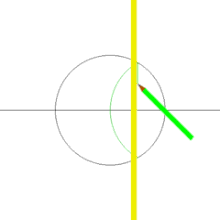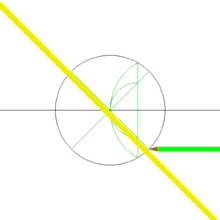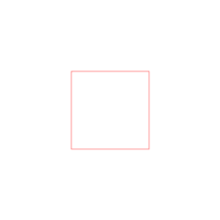
Построение квадрата с использованием циркуля и линейки

Складывание квадрата из произвольного куска бумаги
См. также[править | править код]
- Алгоритм «движущиеся квадраты»
- Квадрат Полибия
- Квадратная матрица
- Квадратриса
- Первая теорема Тебо
- Площадь произвольного четырёхугольника
Примечания[править | править код]
- ↑ Квадрат // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 561. — 1600 с.
- ↑ Квадрат // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 776. — 1184 с.
- ↑ Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
- ↑ 1 2 Каплун, 2014, с. 171—173.
- ↑ Понарин Я. П. Элементарная геометрия: В 2 т. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — С. 117, 119. — 312 с. — ISBN 5-94057-171-9.
- ↑ Уравнение квадрата в декартовой системе координат. Дата обращения: 9 ноября 2021. Архивировано 9 ноября 2021 года.
- ↑ What is the polar equation for a square, if any?
- ↑ Болтянский В. Г. Третья проблема Гильберта. — М.: Наука, 1977. — 208 с. Архивировано 28 июня 2021 года.
Литература[править | править код]
- Каплун А. И. Математика, Учебно-практический справочник. — Ростов н/Д.: ООО “Феникс”, 2014. — 240 с. — ISBN 978-5-222-20926-3.
Ссылки[править | править код]
- Квадрат, геометрическая фигура // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Какова симметрия квадрата? Сколько у квадрата осей симметрии? Есть ли у квадрата центр симметрии?
Утверждение
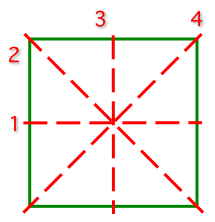
Квадрат имеет четыре оси симметрии.
Осями симметрии квадрата являются прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
 Две оси симметрии прямоугольника — прямые, проходящие через точку пересечения его диагоналей параллельно сторонам.
Две оси симметрии прямоугольника — прямые, проходящие через точку пересечения его диагоналей параллельно сторонам.
Две оси симметрии ромба — прямые, содержащие диагонали ромба.
Квадрат является и ромбом, и прямоугольником, а значит, все четыре прямые являются осями симметрии квадрата.
Утверждение
Квадрат является центрально-симметричной фигурой.
Центр симметрии квадрата — точка пересечения его диагоналей.
Параллелограмм — центрально-симметричная фигура, с центром симметрии в точке пересечения диагоналей.
Так как квадрат является параллелограммом, он также является центрально-симметричной фигурой. Центром симметрии квадрата является точка пересечения его диагоналей.
|
Квадрат имеет четыре оси симметрии второго порядка (т.е. для совпадения нужно повернуть квадрат вокруг этой оси на 1/2 полного оборота), в плоскости, в которой лежит квадрат, и одну ось симметрии четвёртого порядка, перпендикулярную плоскости, в которой лежит квадрат. автор вопроса выбрал этот ответ лучшим
СТЭЛС 6 месяцев назад Что такое ось симметрии? Правильно – это прямая (проведенная или воображаемая) которая разделяет фигуру на две одинаковые половины, которые как бы отражаются друг в друге, и в точность друг друга повторяют. Квадрат имеет все четыре стороны равные. Проведя через противоположные углы две прямых, мы имеем две оси. Проведя через цент квадрата две прямых, перпендикулярных противоположным сторонам, через которые они проходят, получаем еще две оси симметрии. Итого получается что у квадрата четыре оси симметрии.
КорнетОболенский более года назад Данный вопрос рассматривается, скорее всего, в курсе математики начальной школы. Поэтому и ответ будет интересен ученикам младших классов. У квадрата 4 оси симметрии.
На данном рис. показаны все оси симметрии с нумерацией от 1 до 4. Добавлю ещё, что точка пересечения этих осей будет центром симметрии квадрата. kellymilena более года назад Рассмотрим квадрат.У данной фигуры искомых осей симметрии будет сразу несколько. Во-первых, это диагональ первая и вторая, , соединяющие несмежные вершины. Также следует считать осью симметрии отрезок, который проходит перпендикулярно через центр квадрата. Также это которая аналогично горизонтальная прямая, через центр данной фигуры проходящая. Это прямые проходят прямо через точку, еде происходит пересечение диагоналей, лежащих параллельно его сторонам. Прямые, которые содержат диагонали квадрата , и проходят через его углы, лежащие напротив друг друга, (противоположные), являются осями симметрии квадрата. Итак,у квадрата получилось 4 оси симметрии.
Alex2837 6 месяцев назад Если не вдаваться в дословную терминологию, то можно сказать, что осью симметрии является прямая линия, которая разделяет геометрическую фигуру на две одинаковые по форме части. Что касается такой геометрической фигуры, как квадрат, то всем известно, что у него все стороны имеют равное значение. Поэтому, осей симметрии у квадрата может быть только четыре. Эти оси проходят от противоположных углов квадрата через центр, а также от середин противоположных сторон квадрата через центр. Других осей симметрии в квадрате, чтобы получить равные по форме части, провести невозможно. Поэтому, правильный ответ – четыре оси симметрии.
KillNUR 5 лет назад Квадрат – это прямоугольник у которого все стороны равны между собой, все углы прямые, диагонали равны. Поэтому помимо двух осей симметрии, которые есть у прямоугольника (делят противолежащие стороны пополам), добавляются еще две оси – проходящие по диагоналям квадрата Если вращать квадрат по любым из этих 4х осей, то получаемые разными частями квадрата фигуры будут совпадать
Чосик более года назад Прямоугольники имеют две оси симметрии, которые проходят через точку пересечения его диагоналей. Но если в случае обычного прямоугольника равны лишь противоположные стороны, то в случае с квадратом равны будут все стороны. Это приведет к тому, что число осей симметрии возрастает вдвое. Ведь помимо осей симметрии, что имеет прямоугольник, появляются еще две оси симметрии, свойственные ромбам. Потому ответ – четыре оси симметрии.
Dilyara K 5 лет назад У квадрата все четыре стороны равны между собой, все углы равны 90° (прямые). Из-за этого у квадрата равными оказываются еще и диагонали. Поэтому в отличие от прямоугольника, у которого всего две оси симметрии, у квадрата четыре оси симметрии. Две из них проходят по линиям, которые делят противоположные стороны квадрата пополам. Две другие оси проходят по диагоналям квадрата.
владсандрович более года назад Квадрат как мы знаем является такой фигурой, у которой все стороны равны, а потому в отличие от прямоугольника, у него осями симметрии будут еще и те, которые идут не только как прямые, но и по диагонали и в общей сложности, их будет в итоге 4.
Красное облако более года назад У квадрата (в отличие от прямоугольника) все стороны равны, это важный момент. Получается что у этой геометрической фигуры (квадрат) не две оси симметрии как у прямоугольника, а целых четыре и по диагонали в том числе. Ответ, 4 оси симметрии. Знаете ответ? |
| Квадрат | |
 |
|
| Рёбра | 4 |
|---|---|
| Символ Шлефли | {4} |
| Вид симметрии | Диэдрическая группа (D4) |
| Площадь | t2 |
| Внутренний угол (градусы) | 90° |
Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника.
Содержание
- 1 Свойства квадрата
- 2 Свойства
- 3 Периметр квадрата
- 4 Площадь квадрата
- 5 Неевклидова геометрия
- 6 Многообразие квадратов
- 7 См. также
- 8 Ссылки
Свойства квадрата
- Длины всех сторон равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов.
Свойства
- Пусть
— сторона квадрата,
— радиус описанной окружности,
— радиус вписанной окружности. Тогда центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей, и
- радиус вписанной окружности квадрата равен половине стороны квадрата:
,
- радиус описанной окружности квадрата равен половине диагонали квадрата:
,
- радиус вписанной окружности квадрата равен половине стороны квадрата:
- Квадрат обладает наибольшей симметрией среди всех четырёхугольников. Он имеет:
- одну ось симметрии четвёртого порядка (ось, перпендикулярная плоскости квадрата и проходящая через его центр);
- четыре оси симметрии второго порядка (что для плоской фигуры эквивалентно отражениям), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.
- Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Площадь квадрата и длина его сторон
Периметр квадрата
-
- периметр квадрата равен:
,
- периметр квадрата равен:
Площадь квадрата
- Здесь приведены формулы, свойственные именно квадрату. См. также формулы для площади произвольных четырёхугольников.
Неевклидова геометрия
В неевклидовой геометрии квадрат (более широко) — многоугольник с четырьмя равными сторонами и равными углами.

Построение квадрата с использованием циркуля и линейки

Складывание квадрата из произвольного куска бумаги
Многообразие квадратов
Квадратами являются грани куба — одного из пяти правильных многогранников.
Графы:
K4 полный граф часто изображается как квадрат с шестью рёбрами.
Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.
Квадратный флаг Лима поделен на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.
См. также
- Квадратом называют возведение в степень 2
- Квадратура круга
- Единичный квадрат
- Квадрирование квадрата
- Параллелограмм Вариньона
- Теорема Тебо 1
- Четырёхугольник
- Marching squares
Ссылки
| Фото на Викискладе |
- Квадрат, геометрическая фигура // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Видео
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.

Рис. 2 Графическое представление центральной симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.

То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.

Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.

Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.

Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.












