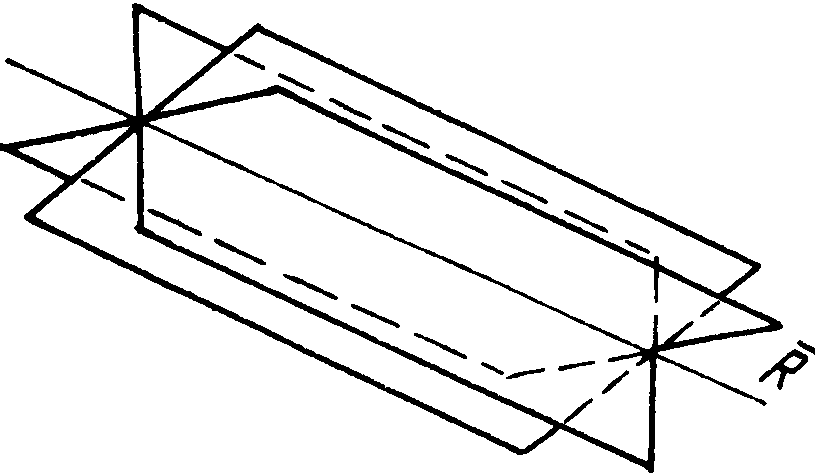
Кристаллографической
зоной называется совокупность плоскостей
или граней кристалла, параллельных
одному направлению, называемому осью
зоны (рис.1.15). Параллельным переносом
плоскости или грани одной зоны можно
заставить их пересечься друг с другом
по оси зоны. Любая зона однозначно
определяется осью зоны, которую можно
записать как вектор Rmnp: R=ma+nb+pc.
Найдем условие зональности плоскостей
относительно вектора Rв кубической
системе. Если плоскость параллельна
осиR, то нормаль к этой плоскости
всегда будет перпендикулярна оси зоны.
Последнее условие является необходимым
и достаточным, чтобы определить
принадлежность плоскости к данной
кристаллографической зоне.
Рис. 1.15.
Кристаллографическая зона.
Нормалью к
плоскости (hkl) является векторH
обратной решетки, равный H=ha*+kb*+lc*. Если (hkl)
принадлежит зоне с осьюR, тоHперпендикулярен R – значит должно
выполняться условие (HR)=0. Подставляя
значение векторовHиR, получим
условие зональности плоскостей в
кубической решетке
(HR) = hm+kn +lp = 0 . (1.30)
Определим индексы оси зоны по индексам
двух плоскостей зоны (h1k1l1)
и (h2k2l2).
Для обеих плоскостей условие зональности
определяет систему уравнений:
(1.31)
Решение этой системы дает:
,
,
, (1.32)
где
– общий множитель, равный =
Все
индексы прямойRможно сократить на
общий множитель 1/. При этом прежние и новые их значения
обозначают одну и ту же прямую. Если
определение ведется для какого-либо
известного кристалла, то мы получим
численные значения кристаллографических
индексов оси зоны.
Пример:
Найти индексы
оси зоны для плоскостей (111) и ()
кубической решетки.
Условие
зональности согласно (1.30)
откуда
=1,
=1
и
=
–2
Итак, индексы
кристаллографической зоны [mnp]=[].
Построение этой оси в элементарной
ячейке кубической решетки показано на
рис.1.11.
1.13. Кристаллографические проекции
При графическом
изображении кристаллов широко пользуются
различными их проекциями. Проекции
применяются для решения ряда задач
кристаллографии и рентгеноструктурного
анализа: определения ориентировки
кристаллов, индицирования рентгенограмм
и т.д. Обычно ими пользуются тогда, когда
нет необходимости определять межплоскостные
расстояния, а требуется установить лишь
взаимную ориентацию атомных плоскостей,
граней и ребер кристалла. Поскольку
расстояния между параллельными
плоскостями кристалла равны, то всю
совокупность параллельных плоскостей
при построении проекций заменяют одной
плоскостью, а все параллельные прямые
– одной прямой.
В целом весь проектируемый кристалл
заменяется пучком прямых и плоскостей,
проходящих через одну точку. Полученное
построение называют кристаллическим
комплексом.
Таким образом,
кристаллический комплекс – это совокупность
прямых и плоскостей, параллельных ребрам
и граням кристалла, проходящих через
одну точку. Эта точка называется центром
комплекса.
При
проектировании кристаллического
комплекса на плоскость получают линейнуюпроекцию кристалла; при проектировании
на сферу –сферическую. На линейной
проекции плоскость изобразится прямой,
являющейся ее следом; прямая – точкой.
Неудобство этой проекции состоит в том,
что для изображения всех плоскостей и
прямых необходима бесконечно большая
плоскость проекций. Поэтому линейная
проекция применяется очень редко.
При построении
сферической проекции центр сферы
совмещается с центром комплекса.
Очевидно, на сферической поверхности
все плоскости кристаллического комплекса
проектируются в виде больших кругов,
стягиваемых сферой, прямые – двумя
диаметрально противоположными точками.
Неудобством сферической проекции при
большом числе проектируемых плоскостей
является сложность и громоздкость
построения.
В кристаллографии,
при решении многих задач, пользуются
преимущественно обратным
кристаллографическим комплексом, в
котором плоскости заменяют нормалями
к ним, а прямые – перпендикулярными к
ним плоскостями. Полученная совокупность
прямых и плоскостей, проходящих через
одну точку 0, и носит название обратного
илиполярного комплекса. Точка 0 –
центр комплекса.
Все проекции,
полученные при проектировании полярного
комплекса, имеют приставку “гномо”.
Проекция полярного комплекса на плоскость
носит название гномонической проекции.
Плоскость(hkl) в ней изобразится
точкой. Недостаток этой проекции тот
же, что и у линейной, а именно для
построения всей совокупности проекций
плоскостей требуется очень большая
площадь проекций. Чтобы устранить этот
недостаток, плоскость проекций заменяют
сферой. В результате получаем
гномосферическиепроекции.
Проекцией
плоскости (hkl) здесь будет точка
пересечения M нормали со сферой. Положение
точки M на сфере описывается в
кристаллографии, выраженными в градусах:
полярным расстоянием,
и долготой. Полярное
расстояние или широта отсчитывается
обычно от полюса и меняется в пределах
от 0 до 180градусов.
Долготу
отсчитывают от некоторого начального
меридиана от 0 до 360градусов по часовой стрелке, если
смотреть с верхнего полюса.
Недостаток
гномосферической проекции состоит в
том, что определение положения точек
на сфере проекций и решение ряда задач
связано с гониометрическими измерениями
(на сфере). Это неудобно.
Наиболее
часто в кристаллографии пользуются
гномостерео-графическимипроекциями.
Они включают в себя достоинства,
свойственные линейным и гномоническим
проекциям, а именно: комплекс проектируется
на плоскость, которая ограничена кругом
проекций. Здесь так же, как и в предыдущих
случаях, центр полярного комплекса
совмещается с центром сферы (рис.1.16).
Через центр сферы проводится плоскость
проекции P, которая пересекает сферу по
большому кругу. Это сечение называется
основным кругом проекции.
Рис.1.16.
Гномостереографическая проекция.
Прямая,
перпендикулярная к плоскости P и
проходящая через центр О, пересекает
сферу в двух точках N и S, которые называют
полюсамипроекций. При построении
гномостереографической проекции
плоскости (hkl) точку выхода ее нормали
на сфере (точку M) соединяют с полюсом
проекций, расположенным по другую
сторону от плоскости Р. Точка пересечения
прямой MS с плоскостью P (точка Q) и будет
являться гномостереографической
проекцией плоскости (hkl).
Легко видеть,
что проекции всех плоскостей кристалла
находятся в пределах большего круга.
Таким образом, размеры проекции конечны
и определяются радиусом сферы. В этом
одно из достоинств гномостереографической
проекции.
Построение
гномостереографической проекции
кристалла проводят, взяв только один
из полюсов проекции, например S, и
рассматривая нормали, направленные в
одну сторону от плоскости проекций P.
Тогда для каждой плоскости (hkl)
получаем одну точку проекции(hkl),
которую называют полюсом плоскости.
Совокупность гномостереографических
проекций плоскостей кристалла набольшом
круге проекцийназывается егополюсной
фигурой(рис.1.17).
Рис. 1.17.
Полюсные фигуры.
Вид полюсной
фигуры зависит от симметрии кристалла,
а также от его установки относительно
плоскости проекций и прямой SN. При
изменении установки кристалла все точки
проекций на полюсной фигуре смещаются.
Плоскость
или грань кристалла, перпендикулярная
прямой SN, будет иметь проекцию в центре
большого круга; все плоскости, параллельные
прямой SN, спроектируются в виде точек
на большом круге проекций. Все другие
плоскости кристалла дадут точки проекций
на остальной площади большего круга.
Рассмотрим,
как будут располагаться на полюсной
фигуре точки гномостереографической
проекции какой-либо кристаллографической
зоны (рис.1.18).
Рис. 1.18.
Гномостереографическая проекция
плоскостей одной зоны.
Для этого
представим зону в виде полярного
комплекса, выбрав за центр комплекса
некоторую точку на оси зоны. В полярном
комплексе зона изобразится в виде прямых
– нормалей, лежащих в одной плоскости
(рис.1.18), перпендикулярной оси зоны. Эта
плоскость пересечет сферу по большому
кругу, следовательно, выходы всех
нормалей к плоскостям зоны будут также
располагаться на большем круге сферы
проекций.
Гномостереографической
проекцией большого круга будет дуга,
стягиваемая диаметром AA
(рис.1.18). Таким образом, все точки проекций
плоскостей одной кристаллографической
зоны будут располагаться по дуге,
стягиваемой на концах диаметром круга
проекций. Если ось зоны совпадает с
направлением SN, то ее проекция будет
представлять собой ряд точек, расположенных
по периметру большого круга проекций
P. На рис.1.18 ось зоны не совпадает с
направлением SN, а составляет с ней угол
90. Индексы оси этой
зоны для кубического кристалла совпадают
с индексами центральной точки полюсной
фигуры.
Соседние файлы в папке Підручники
- #
- #
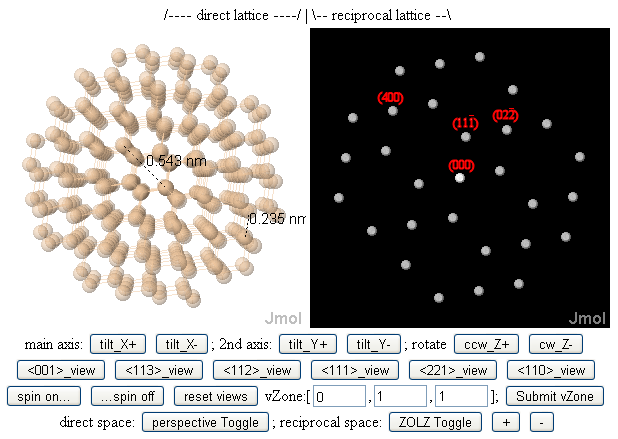
Нанокристаллы (слева), рисунки оси зон (справа)
Ось зоны – термин, который иногда используется для обозначения ориентации кристалла с «высокой симметрией», обычно относится к любому направлению, относящемуся к прямой решетке (в отличие от обратной решетки ) кристалла в трех измерениях. Поэтому он индексируется прямыми индексами решетки, а не индексами Миллера .
Оси высокосимметричных зон через кристаллическую решетку, в частности, часто лежат в направлении туннелей через кристалл между плоскостями атомов. Это связано с тем, что, как мы увидим ниже, такие направления осей зон обычно лежат в более чем одной плоскости атомов в кристалле.
Индексирование по оси зоны
Трансляционная инвариантность кристаллической решетки описывается набором базисных векторов элементарной ячейки прямой решетки (контрвариантных или полярных) a , b , c или, по сути, величинами этих векторов ( параметрами решетки a, b и c) и углы между ними (а именно α между b и c , β между c и a , и γ между a и b ). Компоненты векторов прямой решетки измеряются в единицах расстояния, таких как метры или ангстремы .
Эти векторы решетки индексируются путем перечисления одного (часто целого) множителя для каждого базисного триплетного компонента, который обычно помещается между квадратными [] или угловыми скобками. Таким образом, прямой вектор решетки s uvw или [u, v, w] определяется как u a + v b + w c . Угловые скобки используются, когда вы хотите ссылаться не на конкретный вектор решетки, а на симметрично эквивалентный класс векторов решетки. В случае кубической решетки, например, 100⟩ представляет [100], [010] и [001], потому что каждый из этих векторов симметрично эквивалентен.
Термин ось зоны, более конкретно, относится только к направлению вектора решетки в прямом пространстве. Например, так как [120] и решетка векторы [240] имеют общее направление, их ориентация и соответствуют [120] зона кристалла. Подобно тому, как набор плоскостей решетки в прямом пространстве соответствует вектору обратной решетки в дополнительном пространстве пространственных частот и импульсов, «зона» определяется как набор плоскостей обратной решетки в частотном пространстве, которые соответствует вектору решетки в прямом пространстве.
Аналогом оси зоны в обратном пространстве является «нормаль к плоскости решетки» или «направление g-вектора». Векторы обратной решетки (одноформные или аксиальные) индексируются по Миллеру с использованием вместо этого базис-триплета обратной решетки ( a *, b *, c *), обычно между круглыми () или фигурными {} скобками. Фигурные скобки используются, когда вы хотите ссылаться не на конкретный вектор обратной решетки, а на симметрично эквивалентный класс векторов обратной решетки.
Здесь, как обычно, a * ≡ b × c / V c , b * ≡ c × a / V c и c * ≡ a × b / V c , где объем элементарной ячейки равен V c = a • ( b × c ) . Таким образом, вектор обратной решетки g hkl или (h, k, l) = h a * + k b * + l c * имеет направление, перпендикулярное кристаллографической плоскости (hkl), и величина g hkl = 1 / d hkl равна обратно пропорционально расстоянию между плоскостями (hkl), измеренному в единицах пространственной частоты, например, в циклах на ангстрем.
| Объект | Общий тип | Конкретный экземпляр | Единицы | Трансформация |
|---|---|---|---|---|
| зона или вектор решетки s uvw |  |
![[uvw] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/13177fbadade7d0b9102ae9a6e5092f277dcbaa1) |
прямое пространство, например [метры] | противоположный вариант или полярный |
| плоскость или вектор g g hkl |  |
 |
обратное пространство, например [циклов / м] | ковариант или осевой |
Полезное и довольно общее правило кристаллографических «двойных векторных пространств в 3D» состоит в том, что условие для прямого вектора решетки [uvw] иметь направление (или ось зоны), перпендикулярное обратному вектору решетки [hkl], просто hu + kv + lw = 0. Это верно, даже если, как это часто бывает, набор базисных векторов, используемый для описания решетки, не является декартовым.
Шаблоны оси зоны
Таким образом, в более широком смысле [uvw] диаграмма оси зоны (ZAP) представляет собой дифракционную картину, полученную падающим пучком, например, электронов, рентгеновских лучей или нейтронов, движущихся вдоль направления решетки, заданного индексами оси зоны [uvw]. Из-за своей малой длины волны λ электроны с высокой энергией, используемые в электронных микроскопах, имеют очень большой радиус сферы Эвальда (1 / λ), так что дифракция электронов обычно «освещает» дифракционные пятна с g-векторами (hkl), которые перпендикулярны [ uvw], т.е. для которого hu + kv + lw = 0.
Алмазный атомный кластер кремния FCC (слева), вид вниз по зоне [011], с соответствующим рисунком оси зоны (справа).
Одним из результатов этого, как показано на рисунке выше, является то, что зоны с “низким индексом” обычно перпендикулярны плоскостям решетки с “низким индексом Миллера”, которые, в свою очередь, имеют небольшие пространственные частоты (g-значения) и, следовательно, большие периодичности решетки. (d-интервалы). Другими словами, в электронной микроскопии, если вы хотите, чтобы ваш электронный луч был направлен вниз по широким (а значит, легко видимым) туннелям между столбцами атомов в кристалле, направляя луч вниз по оси зоны с низким показателем преломления (и, соответственно, с высокой симметрией). может помочь в этом.
Смотрите также
- Кристаллография
- Двойная основа
- Обратная решетка
- Индекс Миллера
- Дифракция
- Электронная дифракция
- Просвечивающая электронная микроскопия
Сноски
внешние ссылки
- Международные таблицы для кристаллографии
Нанокристаллы (слева), рисунки оси зон (справа)
Ось зоны, термин, который иногда используется для обозначения “высокосимметричных” ориентаций в кристалле, чаще всего относится к любой направление относительно прямой решетки (в отличие от обратная решетка ) кристалла в трех измерениях. Поэтому он индексируется прямыми индексами решетки, а не Индексы Миллера.
Оси высокосимметричных зон через кристаллическую решетку, в частности, часто лежат в направлении туннелей через кристалл между плоскостями атомов. Это связано с тем, что, как мы увидим ниже, такие направления осей зон обычно лежат в пределах более чем одной плоскости атомов в кристалле.
Индексирование по оси зоны
Трансляционная инвариантность кристаллической решетки[1][2] описывается набором элементарных ячеек на прямой решетке (контрвариант[3] или полярные) базисные векторы а, б, c, или, по сути, величинами этих векторов ( параметры решетки a, b и c) и углы между ними (а именно α между б и c, β между c и а, и γ между а и б). Компоненты векторов прямой решетки измеряются в единицах расстояния, таких как метры или ангстремы.
Эти векторы решетки равны индексированный путем перечисления одного (часто целого) множителя для каждого базисного триплета, который обычно помещается в квадратные [] или угловые ⟨⟩ скобки. Таким образом, прямой вектор решетки suvw или [u, v, w] определяется как uа+ vб+ wc. Угловые скобки используются, когда вы хотите ссылаться не на конкретный вектор решетки, а на симметрично эквивалентный класс векторов решетки. В случае кубической решетки, например, 100⟩ представляет [100], [010] и [001], потому что каждый из этих векторов симметрично эквивалентен.
Термин ось зоны, более конкретно, относится только к направление вектора решетки в прямом пространстве. Например, поскольку векторы решетки [120] и [240] имеют общее направление, их ориентации обе соответствуют зоне [120] кристалла. Как только набор плоскостей решетки в прямом пространстве соответствует вектору обратной решетки в дополнительном пространстве пространственных частот и импульсов определяется “зона”[4][5] в качестве набор плоскостей обратной решетки в частотном пространстве, который соответствует вектору решетки в прямом космосе.
Аналогом оси зоны в обратном пространстве является «нормаль к плоскости решетки» или «направление g-вектора». Обратная решетка (одноформная[6] или аксиальный) векторы Индексированный по Миллеру используя базис-триплет обратной решетки (а*, б*, c*), как правило, в круглых () или фигурных {} скобках. Фигурные скобки используются, когда вы хотите ссылаться не на конкретный вектор обратной решетки, а на симметрично эквивалентный класс векторов обратной решетки.
Здесь как обычно а* ≡ б×c/ Vc, б* ≡ c×а/ Vc, и c* ≡ а×б/ Vc, где объем элементарной ячейки Vc = а•(б×c). Таким образом, вектор обратной решетки граммhkl или (h, k, l) = hа* + kб* + lc* имеет направление, перпендикулярное кристаллографической плоскости (hkl), и величину ghkl = 1 / дhkl равна обратной величине расстояния между плоскостями (hkl), измеренному в единицах пространственной частоты, например циклов на ангстрем.
| Объект | Общий тип | Конкретный экземпляр | Единицы | Трансформация |
|---|---|---|---|---|
| зона или решетка-вектор suvw |  |
![[uvw] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/13177fbadade7d0b9102ae9a6e5092f277dcbaa1) |
прямое пространство например [метры] | противоположный вариант или полярный |
| плоскость или g-вектор граммhkl |  |
 |
взаимное пространство, например [циклов / м] | ковариант или осевой |
Полезное и довольно общее правило кристаллографических “двойных векторных пространств в 3D” состоит в том, что условие для прямого вектора решетки [uvw] иметь направление (или ось зоны), перпендикулярное обратному вектору решетки [hkl], просто hu + kv + lw = 0. Это верно, даже если, как это часто бывает, набор базисных векторов, используемый для описания решетки, не является декартовым.
Шаблоны оси зоны
Таким образом, по расширению [uvw] схема оси зоны (ZAP) – это дифракционная картина, полученная падающим лучом, например электронов, рентгеновских лучей или нейтронов, движущихся вдоль направления решетки, определяемого индексами оси зоны [uvw]. Из-за их малой длины волны λ электроны высокой энергии, используемые в электронных микроскопах[7] иметь очень большой Сфера Эвальда радиус (1 / λ), так что дифракция электронов обычно “освещает” дифракционные пятна с g-векторами (hkl), которые перпендикулярны [uvw], т.е. для которых hu + kv + lw = 0.
Алмазный атомный кластер кремния FCC (слева), вид вниз по зоне [011], с соответствующим рисунком оси зоны (справа).
Одним из результатов этого, как показано на рисунке выше, является то, что зоны с «низким индексом» обычно перпендикулярны плоскостям решетки с «низким индексом Миллера», которые, в свою очередь, имеют небольшие пространственные частоты (значения g) и, следовательно, большие периодичности решетки. (d-интервалы). Другими словами, в электронной микроскопии[8][9][10][11] если вы хотите, чтобы ваш электронный луч был направлен вниз по широким (а значит, легко видимым) туннелям между столбцами атомов в кристалле, направление луча вниз по оси зоны с низким показателем преломления (и, как следствие, высокой симметрией) может помочь в этом.
Смотрите также
- Кристаллография
- Двойная основа
- Обратная решетка
- Индекс Миллера
- Дифракция
- Электронная дифракция
- Просвечивающая электронная микроскопия
Сноски
- ^ Дж. М. Зиман (1972 2-е изд) Основы теории твердого тела (Cambridge U. Press, Cambridge UK).
- ^ Збигнев Даутер и Мариуш Яскольски (2010) «Как читать (и понимать) Том A Международных таблиц по кристаллографии: введение для неспециалистов», J. Appl. Cryst. 43, 1150-1171 pdf
- ^ Джордж Арфкен (1970) Математические методы для физиков (Академик Пресс, Нью-Йорк).
- ^ Э. У. Наффилд (1966) Рентгеновские дифракционные методы (Джон Вили, Нью-Йорк).
- ^ Б. Э. Уоррен (1969) дифракция рентгеновских лучей (Эддисон-Уэсли, издание в мягкой обложке, Dover Books 1990) ISBN 0-486-66317-5.
- ^ ср. Чарльз В. Миснер, Кип С. Торн и Джон Арчибальд Уиллер (1973) Гравитация (В. Х. Фриман, Сан-Франциско, Калифорния).
- ^ Джон М. Коули (1975) Дифракционная физика (Северная Голландия, Амстердам).
- ^ П. Хирш, А. Хауи, Р. Николсон, Д. У. Пэшли и М. Дж. Уилан (1965/1977) Электронная микроскопия тонких кристаллов (Баттервортс / Кригер, Лондон / Малабар, Флорида) ISBN 0-88275-376-2
- ^ Дж. У. Эдингтон (1976) Практическая электронная микроскопия в материаловедении (Н. В. Филипс, Gloeilampenfabrieken, Эйндховен) ISBN 1-878907-35-2
- ^ Людвиг Реймер (1997 4-е изд) Просвечивающая электронная микроскопия: физика формирования изображений и микроанализ. (Шпрингер, Берлин) предварительный просмотр.
- ^ Дэвид Б. Уильямс и К. Барри Картер (1996) Просвечивающая электронная микроскопия: Учебник материаловедения (Plenum Press, Нью-Йорк) ISBN 0-306-45324-X
внешняя ссылка
- Международные таблицы для кристаллографии