Ошибка в матрице жесткости при определении собственных векторов scad как исправить

Да, в новом так не работает, но легко решается через «Спектр жесткостных характеристик».

При возможности посмотрю на очередном расчёте. Не пытались писать письма в SCAD?

Собственно, справка скада:
В случаях, когда выполняется проверка устойчивости по комбинациям загружений, среди которых имеются динамические, требуется проявить некоторую осторожность, связанную с двумя обстоятельствами:
результаты динамического нагружения являются знакопеременными;
в тех случаях, когда результаты динамического расчета сформированы как корень квадратный из суммы квадратов (ККСК) модальных вкладов, нарушены условия равновесия и геометрической связности узловых перемещений.
Рассмотрим эти обстоятельства порознь.
Поскольку заранее неизвестно, какой знак результата динамического расчета является более опасным с точки зрения проверки устойчивости, то следует рассмотреть обе возможности. Так, например, если при расчете устойчивости рассматривается комбинация (L1)*1+(L2)*0.9+(L3)*0.7+(L4)*0.8, в которой нагружение (L3) является динамическим, то следует также выполнить проверку на комбинацию (L1)*1+(L2)*0.9+(L3)*(-0.7)+(L4)*0.8. При наличии нескольких динамических нагружений приходится перебирать все варианты знаков для их результатов.
Несовместность усилий связанная с использованием ККСК (естественно, если учтена не только одна форма собственных колебаний), вообще говоря, никаких неприятностей не вызывает. Просто проверяется коэффициент запаса устойчивости при пропорциональном росте всех внутренних усилий, игнорируя тот факт, что эти усилия нарушают условия равновесия.
Но несовместность узловых перемещений приводит к тому, что имеющиеся в схеме абсолютно жесткие тела получают искажения (по сути, они деформируются, что не соответствует их физической природе). Сложность состоит в том, что для этих элементов матрица К1(λ), не определяется внутренними силами или напряжениями, а вычисляется по значениям узловых перемещений, которые определяют изменение пространственной ориентации бесконечно жесткого конечного элемента (см. 9.5.1 в работе [3]). Несовместность узловых перемещений может привести к фатальной ошибке при вычислении К1(λ).
В связи с этим программа предусматривает обнуление матрицы К1(λ) при проверке устойчивости для комбинаций содержащих динамическое нагружение с более чем одной учитываемой формой собственных колебаний. Об этом в протоколе расчета появляется соответствующее предупреждение.
Источник
|
SCAD Office 11.5, ���������� ������ , ��������, ������� |
|
|
|
|
����������� ������: ������������ ���������: 469 ���������: ���� |
� ������ 2006 ���� ������� ����� ������ ������� ������� � ������� ������������ ����������� SCAD 11.1. ��������������� ��������� ��������� SCAD Office ����� �������� ����� ��� �������. ��������� ����� ��������� «������», �������������� ������ ��������� ��������� � �����������. � ��������� ����� ����������� ���������� ����� ���� � ��. ��������� ����� ����� ���������� ��������� ������. ��������� _http://www.pss.spb.ru/news_soft.shtml#04_47 ���� � WareZ-�. |
|
|
|
�������
|
|
|
|
�����������
������: ������������
���������: 123 ���� |
������� � ��� � ����� ������� ���� ����������� ���������, � ������������ ��� � ������� ����������? |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 9 ���������: ���� |
������(depak @ 7.12.2006 — 00:33) ������� � ��� � ����� ������� ���� ����������� ���������, � ������������ ��� � ������� ����������? � ����� � �������� «���������� ����������» ���� ����� ������� «������������ �������». ��������� � � ��� ���� ����� ������� ��������� � ������� �������, ������ � ������������ �������», �� ��� ������ ��� ��������, � �� ��� �������. ��������� �������������� Ustas — 8.12.2006 — 18:36 |
|
|
|
|
|
|
|
����������� ������: ������������ ���������: 123 ���� |
Ustas �������! �� ��������� � ������� �������� ����� � ��������� �������. ������ ��� ������ ������� ������ �������. �������! |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
��� ����� ����������,������ � S�AD� ��������� ������: |
|
|
|
|
|
|
|
��������
������: ������������
���������: 30 ���������: ���� |
��� ����� ���� ������� � ������������ �������� ����������, ��������, ���� � ���� ��������������� �������, �� ������� ����������� �������, ��� ����� �������� � ��, ���� �� ����� �������� ������� ������� 0,4�0,4, �� ��� � � ����� � ��!!!!! |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
� ����������� � ���� ��� ������. � ����� �������� ������: ���� ���������� �/� ������ ������. ������ ����������� ����.����� ������� ������ � �������.� ������ ���� �������� �������������� �������� �� ����,������������ � �.�. � ������ ������ � ���, ��� ������� ��������(���������,�������),������� ��������� ��� ���� � ���������� �����������(���� � ������ — ��� �����,� �� �����- ������� �� ��������.� �������� �� ���� ��� ������).���-�� ������,������� ��� �������,��� ������������ ������ ������� ���������� ��� EF=EI=1? ��� ����� �������?� ������ ��� ����� ��� �������? |
|
|
|
|
|
|
|
�������� ������: ������������ ���������: 30 ���������: ���� |
� ���� �������� ������� ������ ���������, � ����� ����� �������� ������� P.S. ������ �������� �� Sergeyka_@tut.by ��� ��������, — ����� ������ ����� ��������� ��� � ���� ����� |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
������� �������! �� ��� �������. ��� ����������, ��� � ����� ����� ��� �������� �� ���� ����,� �� ������������� ������ �����… |
|
|
|
|
|
|
|
��������
������: ������������
���������: 30 ���������: ���� |
����� ���� � ����� �������, �� �� ����� ��������, ��� ������ ��������� �����, � �������� � ��� ��� ���� ������������ �������� ��������� ����� ���������� ������, � ��� ������ ������� ����� ��������� ���������� ���� �� ��������� ������� ���������, ����������� ��������, ��! ���� ���������� ����� � ������ ������ ���������, — ���������� ����� ��������� ���� � ���������� ����������� �����, � �� ���� ������� ��� � ������, ����� ������� ���� � �� ������, �� �� ��� ������� ����� ����� — ��������� ��������� �������������� Seroga — 18.12.2006 — 18:31 |
|
|
|
|
|
|
|
�������
������: ������������
���������: 14 ���������: ���� |
�� ����� �����. |
|
|
|
|
|
|
|
�������� ������: ������������ ���������: 30 ���������: ���� |
���������, ��� ���������� ������ �� ���������, ����� �������� �� ��������� ����� ��������� � �����������, � ������������ �����, � ���������� ������ �� ��������� �� ��������� � ������� ������� «�������� �� ��������� �����». ����� �������, ��� ����� ����� ������ |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
��� �� �� ������ �����,����� ��� ������� ����������…. |
|
|
|
|
|
|
|
�������� ������: ������������ ���������: 30 ���������: ���� |
���� ����� ��� ���� ��������� � ����������� ��������� �� ���������� �� ���������, � ����������� ����������� ����������� ��� ����� , ��� � ������ ��������� ��������� ������. ���������� � �������� �������� ������ ������, �� ���� �������� ������� ����������� ��������� ���������� ��������� (��������� ������� ����� ��� �� ��� � ������� ����� �������������) ������� ���������� ��� �� � ��� ������� ��� ���������. |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
������ ������� ���� �������� �������������,������� �������� �� �������!!! �������� �������� ����� ��������������…. |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 13 ���������: ���� |
mel |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
����� � ������ � ���� ��� �� ����������……. � � ������ ����(�������) -«������» � ����� ���������..? |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 13 ���������: ���� |
������(mel @ 19.12.2006 — 11:09) ����� � ������ � ���� ��� �� ����������……. � � ������ ����(�������) -«������» � ����� ���������..? ���������� �� �������� � ����� �������� �������� ��� �������������� ��������� ���������, �.�. ������������ ���������� ������ ������. ���������� ���������� �� ������� ������ ����� ������� �������� � �������� �������������� �������� ���������. � � ����������� ���������� �������� �� ����������-������. ���������� ����� ��� �� ��������, ������� �������� ��� ���������� ��������� �������� ������ ��� �������� �����, ������� ����������� ����� ������� ����� �����. �� ������ �������� ���� �����. |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
�������,�����. � ������ ������������� ������� ������ ��� ���� ����� ������. |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 13 ���������: ���� |
������(mel @ 19.12.2006 — 11:41) �������,�����. � ������ ������������� ������� ������ ��� ���� ����� ������. ����� ����� ��� ���������. �� ���������� ����� �����, ��� � �� �����. ��� �� ����� �������������. �������-���������� ������������� ����� ������ ������ � �������������� ���������. �����������, ��� ������ ��� �������� ��������. |
|
|
|
|
|
|
|
������� ������: ������������ ���������: 14 ���������: ���� |
� � ������� �� ����� ��������,������� ���������. |
|
|
|
1 ���. ������ ��� ���� (������: 1, ������� �������������: 0)
�������������: 0

Да, в новом так не работает, но легко решается через «Спектр жесткостных характеристик».

При возможности посмотрю на очередном расчёте. Не пытались писать письма в SCAD?

Собственно, справка скада:
В случаях, когда выполняется проверка устойчивости по комбинациям загружений, среди которых имеются динамические, требуется проявить некоторую осторожность, связанную с двумя обстоятельствами:
результаты динамического нагружения являются знакопеременными;
в тех случаях, когда результаты динамического расчета сформированы как корень квадратный из суммы квадратов (ККСК) модальных вкладов, нарушены условия равновесия и геометрической связности узловых перемещений.
Рассмотрим эти обстоятельства порознь.
Поскольку заранее неизвестно, какой знак результата динамического расчета является более опасным с точки зрения проверки устойчивости, то следует рассмотреть обе возможности. Так, например, если при расчете устойчивости рассматривается комбинация (L1)*1+(L2)*0.9+(L3)*0.7+(L4)*0.8, в которой нагружение (L3) является динамическим, то следует также выполнить проверку на комбинацию (L1)*1+(L2)*0.9+(L3)*(-0.7)+(L4)*0.8. При наличии нескольких динамических нагружений приходится перебирать все варианты знаков для их результатов.
Несовместность усилий связанная с использованием ККСК (естественно, если учтена не только одна форма собственных колебаний), вообще говоря, никаких неприятностей не вызывает. Просто проверяется коэффициент запаса устойчивости при пропорциональном росте всех внутренних усилий, игнорируя тот факт, что эти усилия нарушают условия равновесия.
Но несовместность узловых перемещений приводит к тому, что имеющиеся в схеме абсолютно жесткие тела получают искажения (по сути, они деформируются, что не соответствует их физической природе). Сложность состоит в том, что для этих элементов матрица К1(λ), не определяется внутренними силами или напряжениями, а вычисляется по значениям узловых перемещений, которые определяют изменение пространственной ориентации бесконечно жесткого конечного элемента (см. 9.5.1 в работе [3]). Несовместность узловых перемещений может привести к фатальной ошибке при вычислении К1(λ).
В связи с этим программа предусматривает обнуление матрицы К1(λ) при проверке устойчивости для комбинаций содержащих динамическое нагружение с более чем одной учитываемой формой собственных колебаний. Об этом в протоколе расчета появляется соответствующее предупреждение.
Источник
Ниже приведен список цифровых кодов ошибок, которые могут появиться в процессе расчета конструкции
|
100 |
Неправильный номер узла |
|
101 |
Неправильный номер элемента |
|
102 |
Недостаточно памяти |
| ВАНТЫ | |
|---|---|
|
300 |
Не хватает памяти во время анализа элементов каната |
|
301 |
Не хватает памяти во время анализа элементов каната |
|
302 |
Не хватает памяти во время анализа элементов каната |
|
303 |
Не хватает памяти во время анализа элементов каната |
|
304 |
Не хватает памяти во время анализа элементов каната |
|
305 |
Ошибка вывода во время сохранения результатов для элементов каната |
| ОШИБКИ В СИСТЕМЕ ВВОДА/ВЫВОДА | |
|---|---|
|
500 |
Внутренняя ошибка при обработке имен файлов |
|
501 |
Внутренняя ошибка при обработке имен файлов |
|
502 |
Внутренняя ошибка при обработке имен файлов |
|
503 |
Внутренняя ошибка при обработке имен файлов |
|
504 |
Ошибка в данных, испорчены файлы данных |
|
505 |
Не хватает памяти для прогона задачи |
|
506 |
Ошибка в данных, нет информации о вариантах нагрузки |
|
507 |
Противоречивые данные о совместимых узлах |
|
508 |
Внутренняя ошибка во время анализа жестких связей |
|
509 |
Внутренняя ошибка во время анализа повернутых узлов |
|
510 |
Внутренняя ошибка во время анализа повернутых узлов |
|
511 |
Внутренняя ошибка во время анализа упругих опор |
|
512 |
Внутренняя ошибка во время анализа упругих опор |
|
513 |
Внутренняя ошибка во время анализа совместимости |
|
514 |
Внутренняя ошибка во время анализа упругих совместимости |
|
690 |
Внутренняя ошибка во время анализа жестких связей |
| МОДАЛЬНЫЙ РАСЧЕТ | |
|---|---|
|
900 |
Ошибка ввода при чтении временных результатов модального анализа |
|
901 |
Ошибка вывода при сохранении результатов модального анализа |
|
902 |
Получено отрицательное собственное значение |
|
903 |
Не хватает памяти во время анализа концентрированных весов узлов |
|
904 |
Не хватает памяти во время анализа концентрированных весов узлов |
|
905 |
Внутренняя ошибка во время анализа концентрированных весов узлов |
| СПЕКТРАЛЬНЫЙ РАСЧЕТ | |
|---|---|
|
920 |
Ошибка ввода при чтении временных результатов во время спектрального или сейсмического анализа |
|
921 |
Ошибка вывода при сохранении результатов спектрального или сейсмического анализа |
|
922 |
Ошибка ввода при чтении временных результатов во время спектрального или сейсмического анализа |
|
923 |
Ошибка вывода при сохранении результатов спектрального или сейсмического анализа |
|
924 |
Внутренняя ошибка во время спектрального или сейсмического анализа |
|
925 |
Ошибка вывода при сохранении результатов спектрального или сейсмического анализа |
|
930 |
Ошибка во время сохранения результатов анализа демпфирования и энергии |
|
940 |
Ошибка в данных при сейсмическом анализе |
|
950 |
Не хватает памяти для загрузки спектра при спектральном анализе |
|
951 |
Ошибка в данных при спектральном анализе |
| ВРЕМЕННОЙ РАСЧЕТ | |
|---|---|
|
960 |
Внутренняя ошибка при анализе переходных процессов |
|
961 |
Ошибка в данных при анализе переходных процессов, недействительный файл конфигурации |
|
962 |
Ошибка в данных при анализе переходных процессов, недействительный временной шаг |
|
970 |
Внутренняя ошибка при анализе переходных процессов |
|
971 |
Внутренняя ошибка при анализе переходных процессов, неправильная формула |
|
972 |
Ошибка в данных при анализе переходных процессов |
|
973 |
Ошибка в данных при анализе переходных процессов |
|
974 |
Ошибка вывода при сохранении результатов анализа переходных процессов |
|
980 |
Не хватает памяти для анализа переходных процессов |
|
981 |
Не хватает памяти для анализа переходных процессов |
|
982 |
Ошибка в данных при анализе переходных процессов |
|
983 |
Ошибка в данных при анализе переходных процессов |
|
984 |
Ошибка в данных при анализе переходных процессов |
|
985 |
Ошибка в данных при анализе переходных процессов |
|
986 |
Ошибка в данных при анализе переходных процессов |
| ПАМЯТЬ | |
|---|---|
|
1000 |
Не хватает памяти для прогона задачи |
|
1001 |
Не хватает памяти для прогона задачи |
|
1010 |
Ошибка вывода при сохранении результатов для конечных элементов |
|
1011 |
Не хватает памяти для прогона задачи |
|
1100 |
Не хватает памяти для прогона задачи, очень серьезная проблема |
|
1101 |
Не хватает памяти для прогона задачи, очень серьезная проблема |
|
1102 |
Не хватает памяти для прогона задачи, очень серьезная проблема |
|
1103 |
Не хватает памяти для прогона задачи, очень серьезная проблема |
|
1104 |
Не хватает памяти, слишком много изолированных узлов |
| РЕЗУЛЬТАТЫ ДЛЯ КОНЕЧНЫХ ЭЛЕМЕНТОВ | |
|---|---|
|
1230 |
Ошибка ввода при чтении временных результатов для конечных элементов |
|
1231 |
Ошибка вывода при чтении временных результатов для конечных элементов |
| ФРОНТАЛЬНЫЙ РЕШАТЕЛЬ | |
|---|---|
|
1310 |
Ошибка ввода при записи в рабочий файл во время фронтального анализа |
|
1311 |
Ошибка ввода/вывода при открытии рабочего файла во время фронтального анализа |
|
1320 |
Ошибка ввода при чтении рабочего файла во время фронтального анализа |
|
1321 |
Ошибка ввода/вывода при открытии рабочего файла во время фронтального анализа |
|
1330 |
Ошибка ввода при сохранении матрицы во время фронтального анализа |
|
1340 |
Не хватает памяти для выполнения фронтального анализа |
|
1350 |
Внутренняя ошибка при открытии рабочего файла во время фронтального анализа |
|
1360 |
Не хватает памяти для выполнения фронтального анализа |
|
1361 |
Не хватает памяти для выполнения фронтального анализа |
|
1370 |
Внутренняя ошибка при фронтальном анализе, очень серьезная проблема |
|
1400 |
Не хватает буферной памяти для матрицы |
|
1401 |
Ошибка ввода при чтении матрицы |
| ПАМЯТЬ | |
|---|---|
|
1410 |
Не хватает буферной памяти для решения задачи о собственных значениях |
|
1420 |
Не хватает памяти для прогона задачи, сократить размер задачи |
|
1421 |
Не хватает памяти для прогона задачи, сократить размер задачи |
|
1422 |
Не хватает памяти для прогона задачи, сократить размер задачи |
| ЗАДАЧА О СОБСТВЕННЫХ ЗНАЧЕНИЯХ | |
|---|---|
|
1430 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
1431 |
Не хватает памяти во время анализа задачи о собственных значениях |
|
1450 |
Не хватает памяти во время анализа задачи о собственных значениях |
|
1451 |
Ошибка вывода при сохранении результатов анализа задачи о собственных значениях |
| РЕШАТЕЛЬ SKYLINE | |
|---|---|
|
1900 |
Внутренняя ошибка в решателе skyline, переключитесь на фронтальный метод, если возможно |
|
1901 |
Ошибка вывода при сохранении матрицы в решателе skyline |
|
1902 |
Ошибка вывода при сохранении матрицы в решателе skyline |
|
1903 |
Не хватает памяти в решателе skyline |
|
1904 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1905 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1906 |
Ошибка вывода при сохранении матрицы в решателе skyline |
|
1920 |
Не хватает памяти для прогона задачи |
|
1921 |
Не хватает памяти для прогона задачи |
|
1922 |
Не хватает памяти для прогона задачи |
|
1923 |
Не хватает памяти для прогона задачи |
|
1930 |
Проблема с открытием рабочего файла во время решения методом skyline |
|
1940 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1941 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1950 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1951 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
1960 |
Внутренняя ошибка в контурной программе |
|
2010 |
Не хватает памяти для прогона задачи |
|
2011 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
2020 |
Внутренняя ошибка в контурной программе |
|
2021 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
2030 |
Внутренняя ошибка в контурной программе |
|
2031 |
Ошибка вывода при сохранении матрицы на диске |
|
2040 |
Внутренняя ошибка в контурной программе |
|
2041 |
Ошибка ввода при чтении в матрицу в контурной программе |
|
2050 |
Ошибка ввода при чтении в матрицу в контурной программе |
| ЗАДАЧА О СОБСТВЕННЫХ ЗНАЧЕНИЯХ | |
|---|---|
|
2051 |
Не хватает памяти во время анализа задачи о собственных значениях |
|
2052 |
Проблема выполнения во время анализа задачи о собственных значениях, нулевые элементы по диагонали матрицы жесткости |
|
2053 |
Проблема выполнения во время анализа задачи о собственных значениях, вычисленные нулевые собственные значения |
|
2054 |
Проблема выполнения, пропуск собственных значений |
|
2055 |
Не хватает памяти во время анализа задачи о собственных значениях |
|
2070 |
Проблема выполнения во время анализа задачи о собственных значениях |
|
2080 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
2081 |
Не хватает памяти во время анализа задачи о собственных значениях |
|
2082 |
Проблема выполнения во время анализа задачи о собственных значениях, ошибка моделирования |
|
2083 |
Проблема выполнения во время анализа задачи о собственных значениях, ошибка моделирования |
|
2084 |
Проблема выполнения во время анализа задачи о собственных значениях |
|
2085 |
Проблема выполнения во время анализа задачи о собственных значениях |
|
2086 |
Проблема выполнения во время анализа задачи о собственных значениях |
|
2095 |
Проблема выполнения во время анализа задачи о собственных значениях |
|
2110 |
Ошибка в данных, линейная нагрузка, не влияющая (нулевая длина сегмента) на определение плоской нагрузки |
|
2120 |
Ошибка в данных, файл данных записи нагрузки испорчен |
|
2300 |
Внутренняя ошибка при обработке реакций элемента |
|
2400 |
Не хватает памяти для секторного буфера |
|
2500 |
Не хватает памяти для рабочего буфера |
|
2505 |
Внутренняя ошибка, недействительная ссылка |
|
2520 |
Ошибка вывода при хранении результатов на диске |
|
2521 |
Внутренняя ошибка, недействительная ссылка |
| ЗАДАЧА О СОБСТВЕННЫХ ЗНАЧЕНИЯХ | |
|---|---|
|
2540 |
Ошибка ввода/вывода при открытии рабочего файла во время анализа задачи о собственных значениях |
|
2550 |
Внутренняя ошибка при чтении из рабочего файла во время анализа задачи о собственных значениях |
|
2551 |
Ошибка ввода при чтении из рабочего файла во время анализа задачи о собственных значениях |
|
2560 |
Внутренняя ошибка при записи в рабочий файл во время анализа задачи о собственных значениях |
|
2561 |
Ошибка вывода при записи в рабочий файл во время анализа задачи о собственных значениях |
|
2570 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
2571 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
2572 |
Ошибка вывода при записи в рабочий файл во время анализа задачи о собственных значениях |
|
2573 |
Ошибка ввода при чтении из рабочего файла во время анализа задачи о собственных значениях |
|
2580 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
2590 |
Внутренняя ошибка во время анализа задачи о собственных значениях. |
|
2650 |
Ошибка в данных при анализе односторонних заделок, нагрузки в узле без опоры |
| МОДАЛЬНЫЙ МЕТОД РАЗЛОЖЕНИЯ | |
|---|---|
|
2701 |
Ошибка в данных при использовании модального метода разложения |
|
2702 |
Ошибка в данных при использовании модального метода разложения |
|
2703 |
Ошибка в данных при использовании модального метода разложения |
|
2704 |
Ошибка в данных при использовании модального метода разложения |
| МЕТОД ЛАНЦОША | |
|---|---|
|
2800 |
Ошибка в данных при использовании метода Ланцоша |
|
2801 |
Внутренняя ошибка при использовании метода Ланцоша; в настоящее время не используется (Lanc_Ritz_Ort_Type) |
|
2802 |
Внутренняя ошибка при использовании метода Ланцоша; в настоящее время не используется (Lanc_Ritz_Ort_Type) |
|
2803 |
Внутренняя ошибка при использовании метода Ланцоша: Число требуемых векторов Ритца > текущего шага Ланцоша |
|
2804 |
Ошибка размещения памяти при использовании метода Ланцоша |
|
2805 |
Ошибка, вызванная открытием файлов для дополнительной системы ввода/вывода |
|
2806 |
Ошибка, вызванная чтением/записью в дополнительной системе файлов |
|
2807 |
Ошибка дополнительной системы I/O: массив, связанный с буфером, не размещен |
|
2808 |
Ошибка, вызванная при i > j для параметра. Tau_3; |
|
2809 |
Нет сходимости для итераций QR – режим определения. Возможно – отсутствие положительной определенности K |
|
2810 |
Ошибка выполнения, вызванная делением на ноль для back_go. Возможно – отсутствие положительной определенности K |
|
2811 |
Ошибка выполнения, вызванная делением на ноль для TR_Transf. Возможно – отсутствие положительной определенности K |
| ОСНОВНОЙ МЕТОД ПРИВЕДЕНИЯ | |
|---|---|
|
2850 |
Ошибка размещения при использовании основного метода приведения |
|
2851 |
Задача Якоби при использовании основного метода приведения: возможно неправильное размещение главных степеней свободы |
|
2852 |
Ошибка источника данных: число требуемых режимов > число главных степеней свободы |
|
2653 |
Ошибка при использовании основного метода приведения: отсутствие симметрии приведенного эффекта и матриц масс. Возможно неправильное размещение главных степеней свободы или матрица, плохо обусловленная из-за грубых ошибок в модели метода конечных элементов |
| ОШИБКИ ИТЕРАЦИОННОГО РЕШАТЕЛЯ | |
|---|---|
|
3000 |
Ошибка распределения памяти |
|
3001 |
Ошибка при открытии дополнительно файла вывода =3002, // нулевая длина текущего элемента: ELE_MatrEvaluation returns 0 |
|
3002 |
3009 Слишком много совокупных уровней – приведение невозможно – уменьшить число совокупных уровней Внутренняя ошибка при оценивании памяти IВнутренняя ошибка приsymbolical factorization |
|
3010 |
I/O ошибка при сохранении разложенной части матрицы Недостаток памяти при запуске |
|
3011 |
Ошибка при открытии файла для коэффициента матрицы |
|
3012 |
Ошибка при открытии файла для коэффициента матрицы |
|
3013 |
Ошибка ввода/вывода во время выполнения итерационного решателя итерационное решение: j<i |
|
3014 |
Ошибка во время выполнения итерационного решателя: Решатель |
|
3015 |
Ошибка при открытии файла во время выполнения итерационного решателя |
|
3016 |
Ошибка ввода/вывода во время выполнения итерационного решателя 3016 Ошибка во время выполнения итерационного решателя |
|
3017 |
Этот метод не доступен |
|
3018 |
Neq_Old!= Last Neq при перенумерации |
|
3019 |
Число блоков nblck > MAX_BLOCKS для Kc |
|
3020 |
Ошибка ввода/вывода при грубых матричных операциях с файлом |
|
3021 |
Совместимый узел устанавливается на опоре; это временно невозможно |
|
3050 |
Ошибка распределения памяти при ITER_Eigen |
|
3060 |
Ошибка времени прогона при Jacobi fo ITER_Eigen |
|
3061 |
Итеративный решатель: число требуемых форм > MAX_SIZE_SUBSP_PROB |
|
3065 |
Невозможно использовать метод PCG_Ritz при nModes = 1 (Должно быть: nModes > 1) |
|
3070 |
Ошибка времени при обработке заполнения модели грубой матрицы: подчиненный узел является первым узлом в заполнении |
|
3080 |
Ошибка времени во время правильности контроля: никакие узлы не содержатся в заполнениях |
|
3090 |
Отсутствуют элементы плосконапряженного состояния |
|
3200 |
Ошибка во время открытия файла для системы ввода/вывода |
|
3210 |
Метод итерации блочного подпространства неэффективный. Выберите другой метод |
|
3220 |
Ошибка размера блока для метода итерации блочного подпространства – внутренняя ошибка |
|
3230 |
Ошибка не положительно определенной матрицы масс: (V*M*V) <= 0 |
|
3240 |
Слишком много форм: lastvect > NoOfLegalDOF |
| ОШИБКИ РАЗРЕЖЕННОГО РЕШАТЕЛЯ | |
|---|---|
|
3300 |
Ошибка при открытии файла |
|
3301 |
Начальный класс CSparse для разреженного прямого решателя |
|
3302 |
Число уравнений впереди равно нулю |
|
3303 |
Внутренняя ошибка прогона при оценке памяти |
|
3304 |
Внутренняя ошибка при символической факторизации |
|
3305 |
Внутренняя ошибка прогона во время окончательной стадии |
|
3305 |
Внутренняя ошибка при символической факторизации |
|
3306 |
Ошибка I/O во время хранения разложенной части матрицы |
|
3307 |
Недостаточно памяти во время прогона |
|
3308 |
Пропущенный элемент при шаге = 0 |
|
3309 |
Ошибка прогона |
|
3310 |
Ошибка при открытии файла для матричного фактора |
|
3311 |
Число требуемых r.h.s > числа вычисленных r.h.s |
|
3312 |
Ошибка во время инициализации второй матрицы |
|
3313 |
Недопустимый тип решателя |
|
3320 |
Ошибка во время инициализации смежного графа |
|
3321 |
Неизвестный метод пере упорядочивания |
|
3322 |
Ошибка при пере упорядочивании MDA |
|
3323 |
Ошибка при выполнении мультифронтального решателя |
|
3324 |
Слишком много предыдущих фронтов — мультифронтальный решатель |
|
3325 |
Ошибка при создании нового фронта |
|
3326 |
Ошибка при заполнения фронта |
|
3327 |
Ошибка при подготовке фронта |
|
3328 |
Ошибка установки разложенной части |
|
3329 |
Ошибка во время мультифронтального решателя — renum. NDM |
|
5000 |
Ошибка главной страницы (если возможно, сохраните пример и вышлите его в отдел технической поддержки) |
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
Сейчас Вы — Гость на форумах «Проектант». Гости не могут писать сообщения и создавать новые темы.
Преодолейте несложную формальность — зарегистрируйтесь! И у Вас появится много больше возможностей на форумах «Проектант».
Последние сообщения на Строительном форуме
18 Января 2023 года, 10:03
17 Января 2023 года, 08:04
12 Января 2023 года, 11:49
12 Января 2023 года, 10:59
04 Января 2023 года, 13:41
28 Декабря 2022 года, 16:08
20 Декабря 2022 года, 16:16
20 Декабря 2022 года, 15:02
08 Декабря 2022 года, 16:29
04 Декабря 2022 года, 14:42
01 Декабря 2022 года, 11:02
23 Ноября 2022 года, 16:34
23 Ноября 2022 года, 15:48
21 Ноября 2022 года, 08:56
21 Ноября 2022 года, 08:55

1 3 . У с т о й ч и в о с т ь
13. Устойчивость
Для каждого указанного пользователем загружения (или комбинации загружений) SCAD позволяет определить:
∙коэффициент запаса устойчивости;
∙первую форму потери устойчивости (без анализа кратности);
∙свободные длины стержневых элементов.
|
13.1 Постановка задачи |
Задача устойчивости решается в классической |
|
|
постановке для упругой системы и в предположении, что все |
||
|
приложенные к системе внешние нагрузки (следовательно, и |
||
|
внутренние силы) растут пропорционально одному и тому же |
||
|
параметру λ. То значение параметра λ, при котором матрица |
||
|
жесткости системы А(λ) впервые |
перестает быть положи— |
|
|
тельно определенной, является критическим, а соответ— |
||
|
ствующее значение λ — коэффициентом запаса устойчивости |
||
|
(КЗУ). |
Матрица жесткости А(λ) = |
Ao — B(λ) состоит из |
“обычной” матрицы жесткости Ao и матрицы “толкающих” реакций B(λ), которые определяются сжимающими силами в стержнях, напряжениями сжатия в конечных элементах оболо— чечного типа и т.п. Напоминаем, что положительная опреде— ленность матрицы жесткости означает, что при любых
значениях узловых перемещений и поворотов u потенциальная энергия системы положительна (это значит, что для деформирования системы необходимо затратить энергию и, следовательно, она оказывает сопротивление деформированию,
она является отпорной).
Если система теряет устойчивость, она теряет отпорность и ее матрица жесткости становится вырожденной (с нулевым детерминантом), а в закритическом состоянии система получает отрицательную отпорность (при ее принуди—
тельном деформировании выделяется ранее накопленная потенциальная энергия “толкающих” реакций) и ее матрица жесткости становится знаконеопределенной.
Таким образом, задача оценки устойчивости равно—
весия сводится к проверке положительной определенности матрицы жесткости при пробном значении коэффициента λ .
Необходимо отметить, что с помощью проверок
матрицы жесткости можно отыскать только те критические состояния, при которых потеря устойчивости происходит по
251

1 3 . У с т о й ч и в о с т ь
13.2 Поиск коэффициента запаса устойчивости
форме, когда узловые перемещения и повороты не все вместе равны нулю (это так называемая явная форма потери устойчивости). Нужно еще проверить, что при пробном значении λ не может произойти так называемая скрытая форма потери устойчивости, которая реализуется в пределах одного
конечного элемента и не вызывает узловых перемещений и поворотов. Поскольку для всех типов конечных элементов соответствующие критические величины λкр известны (они вычисляются по простым формулам), то это значит, что следует, кроме всего прочего, проверить неравенство λ > λкр для всех конечных элементов.
Поиск коэффициента запаса устойчивости (КЗУ) ведется в интервале [0,Λ], где Λ — число, заданное пользователем, (оценка того значения КЗУ, которое считается уже безразличным для оценки качества системы) и с точностью ε, которая также задается пользователем.
При этом решается задача определения минимального λ, при котором происходит вырождение матрицы А(λ).
Матрица А(λ) составляется из матриц устойчивости отдельных конечных элементов. Если в системе нет ни одного элемента, способного терять устойчивость (например, в стержневой системе все стержни растянуты), то выдается сообщение, что система «абсолютно устойчива«.
Далее проверяется устойчивость системы при λ = Λ (т.е. положительная определенность матрицы А(Λ)). Если это условие выполнено, то выдается сообщение о том, что КЗУ больше заданного максимума.
Если условие положительной определенности А(Λ) не выполнено (об этом свидетельствуют отрицательные значения на главной диагонали матрицы жесткости, преобразованной в процессе решения системы уравнений), производится анализ положительной определенности матрицы А(Λ/2),…, т.е. используется стандартный метод половинного деления. Этот процесс продолжается до тех пор, пока не найден интервал (λ1, λ2) такой, что λ2 — λ1 ≤ ε и матрица А(λ1) положительно определена, а матрица А(λ2) этим свойством не обладает. При этом величина λ1 считается КЗУ.
При составлении матрицы устойчивости для каждого конечного элемента (способного терять устойчивость) вычисляется значение λкр, которое приводит к потере устойчивости КЭ. Если min λкр < Λ, интервал поиска сокращается, а номер элемента, для которого достигается min λкр, сообщается в протоколе.
252

1 3 . У с т о й ч и в о с т ь
13.3 Форма потери устойчивости
В предположении, что определенный на первом этапе коэффициент запаса устойчивости является точным, SCAD
производит решение задачи об определении собственного вектора при известном собственном значении задачи
Заметим, что правые части системы равны нулю, т.е. отыскиваются такие значения узловых перемещений и пово— ротов u, которые вызываются только внутренними сжимающи— ми напряжениями и усилиями. Поперечные нагрузки, как известно, не влияют на значения критических сил и вид формы потери устойчивости. Поскольку уравнение (а) решено при нулевой правой части, то форма потери устойчивости определена лишь с точностью до множителя. Ее уменьшение или увеличение в любое число раз не нарушает условие (а).
|
Если в системе имеются стержневые элементы, то |
|
|
13.4 Свободные длины |
можно определить их свободные длины, т.е. длины таких же, |
|
но шарнирно опертых стержней, у которых критическая |
|
|
сила Nкр совпадает с продольным усилием в стержне |
|
|
системы в момент потери устойчивости (Nкр=λ1*N). |
|
|
Поскольку по формуле Эйлера Nкр = π2EJ / l2, свободная |
|
|
длина будет lo = (λ1N / π2EJ )1/2, |
|
|
где EJ — жесткости стержней в главных плоскостях инерции |
|
|
(для пространственной задачи — по две для каждого стержня). |
253
1 3 . У с т о й ч и в о с т ь
13.5 Ввод данных
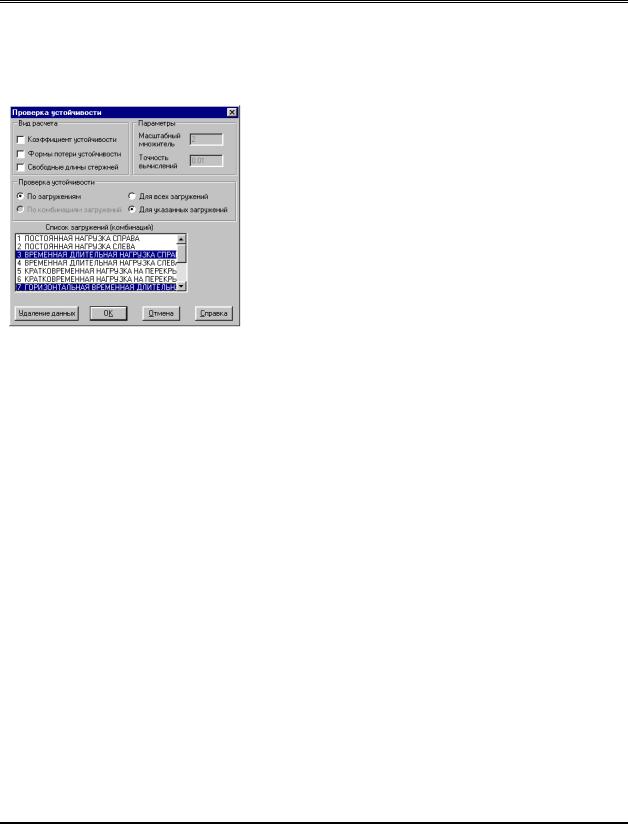
Рис. 13.5.1. Диалоговое окно
Проверка устойчивости
Ввод данных для проверки устойчивости выполняется в одноименном диалоговом окне (рис. 13.5.1), которое
вызывается из раздела Специальные исходные данные в Дереве проекта. Для ввода данных необходимо выполнить такие операции:
Äс помощью комбинаторных кнопок задать режим проверки — вычисление коэффициента запаса устойчивости, форм потери устойчивости и свободных длин стержневых элементов;
Äв полях Масштабный множитель и Точность вычислений следует ввести соответствующие значения (по умолчанию приняты 2 и 0.01);
Äактивизировать опции, определяющие вид данных, для которых выполняется проверка устойчивости: по загружениям или по комбинациям загружений, для всех загружений (комбинаций) или только для выбранных; в последнем случае выбор нужных
данных выполняется в списке загружений (комбинаций).
Масштабный множитель — параметр используется
для ограничения интервала поиска коэффициента запаса устойчивости. Если его значение больше заданного, система считается устойчивой.
Точность вычислений — параметр задает критерий
окончания итерационного процесса поиска коэффициента запаса устойчивости. При очень малых значениях этого параметра время расчета может существенно увеличиться.
Для удаления подготовленных данных и отказа от анализа устойчивости используется кнопка Удаление данных.
254

1 4 . С п е к т р ы о т в е т а
14.Спектры ответа
14.1Расчет на сейсмические воздействия
Выведенный из положения равновесия линейный неконсервативный осциллятор совершает затухающие колебания, которые описываются дифференциальным
уравнением
|
&& |
& |
2 |
x = 0, |
(14.1) |
|
x |
+ 2ϕ ω x + ω |
где
ω – собственная круговая частота системы без затухания (рад/с);
ϕ – относительное демпфирование. При ϕ < 1 решение уравнения (1) имеет вид
x = Ae−ϕωt sin(ωD t + α) ,
где
ωD = ω
 1 − ϕ2 – частота с учетом затухания,
1 − ϕ2 – частота с учетом затухания,
А, α – коэффициенты, которые зависят от начальных условий.
Обычно для строительных конструкций ϕ<<1 и
|
практически ωD |
≈ ω . |
|||
|
Если на массу действует сила F(t), то ее перемещения |
||||
|
описываются уравнением |
2 |
|||
|
&& |
& |
x = F(t) / m, |
(14.2) |
|
|
x + 2ϕ ω x + ω |
общее решение которого при нулевых начальных условиях можно записать с помощью интеграла Дюамeля
|
1 |
t |
|||||||
|
x = |
òF (t)exp[−ρω(t − z)]sin ωD (t − z)dz |
(14.3) |
||||||
|
mωD |
||||||||
|
0 |
||||||||
|
При |
движении основания |
&& |
||||||
|
с ускорением x0 (t) |
||||||||
|
(кинематическое |
возмущение) |
на |
массу |
m |
действует |
|||
|
переносная |
сила |
инерции |
&& |
(t) . |
Поэтому |
|||
|
F(t) = −mx0 |
уравнение, описывающее относительные перемещения массы в системе координат, связанной с основанием, имеет вид
|
&& |
& |
+ ω |
2 |
x |
&& |
(t) , |
(14.4) |
|||||||
|
x |
+ 2ϕω x |
= −x 0 |
||||||||||||
|
а его решение |
t |
|||||||||||||
|
1 |
−ϕω(t−z) |
|||||||||||||
|
x = − |
ωD |
ò |
x(t)e |
sin ωD (t − z)dz |
(14.5) |
|||||||||
|
0 |
&& |
|||||||||||||
|
При |
определении |
абсолютного ускорения |
массы |
|||||||||||
|
&& |
&& |
получаем при обычных малых значениях ϕ, что |
||||||||||||
|
xα |
= x + x0 |
|||||||||||||
|
&& |
2 |
(14.6) |
||||||||||||
|
x |
α ≈ −ωD x |
|||||||||||||
|
Нами |
рассматриваются |
колебания |
линейных |
255

1 4 . С п е к т р ы о т в е т а
дискретных систем со многими степенями свободы,
полученные из любых континуальных или комбинированных систем после применения к ним процедуры дискретизации метода конечных элементов (МКЭ). При этом решается
система обыкновенных дифференциальных уравнений
|
[ |
M |
]{ } |
+ |
[ |
K |
]{ } |
{ } |
(14.7) |
|
|
u&& |
u = |
0 , |
|||||||
|
где |
{u} – вектор перемещений; |
||||||||
|
[M] – матрица массы; |
|||||||||
|
[K] – матрица жесткости. |
Вынужденные колебания линейной дискретной системы с затуханием по гипотезе Фойгта—Кельвина описываются
|
системой обыкновенных дифференциальных уравнений |
|||
|
[M ]{u} + [C ]{u} + [K ]{u} = {F(t)} , |
(14.8) |
||
|
&& |
& |
||
|
где |
[C] – матрица диссипации энергии; |
||
|
{F(t)} – вектор нагрузки. |
|||
|
В случае |
кинематического возмущения в |
качестве |
|
нагрузки выступают переносные силы инерции и |
система |
|||
|
уравнений (14.8) записывается в виде |
0(t) , |
(14.9) |
||
|
[M ]{u} + [C ]{u} + [K ]{u} = -[M ]{I}x |
||||
|
&& |
& |
&& |
где {u} – вектор относительных перемещений (например, в системе координат xOy, связанной с основанием);
{I} – вектор, компонентами которого являются
косинусы углов между направлениями перемещений по координатам и вектором ускорения основания;
x&&0 (t) — ускорение основания.
Решение уравнения (14.9) отыскивается в виде
разложения его по формам собственных колебаний системы (так называемая “модальная суперпозиция”)
|
n |
|
|
{u} = å{F j }Yj (t) , |
(14.10) |
j=1
где n – число степеней свободы системы (учитываемых собственных чисел и векторов);
F j – j-я форма собственных свободных колебаний
|
дискретной системы; |
|||||||||
|
Yj (t) |
– |
неизвестные функции |
времени, |
которые |
|||||
|
необходимо определить. |
|||||||||
|
Будем предполагать, что для матрицы диссипации [С] |
|||||||||
|
выполняется условие |
|||||||||
|
T |
[C ]{F j } = |
ì0 , |
i ¹ j |
||||||
|
{Fi } |
ï |
||||||||
|
í |
T |
[M ]{Fi } , i = j |
|||||||
|
ï2ji wi {Fi } |
|||||||||
|
î |
|||||||||
|
где wi – i-я собственная частота дискретной системы. |
|||||||||
|
После подстановки (14.10) в (14.9) и умножения (14.9) |
|||||||||
|
на вектор |
{Fi }T |
для |
нахождения |
Yi (t) |
получаем |
дифференциальное уравнение
256

1 4 . С п е к т р ы о т в е т а
|
&& |
2 |
Ψi |
= −D i x |
0 |
(t) , |
(14.11) |
|||
|
Ψ + 2ϕi ωi Ψi + ωi |
|||||||||
|
&& |
|||||||||
|
D i = |
{Φi }T [M ]{I} |
&& |
|||||||
|
где |
{Φi }T [M ]{Φi } |
x0 |
(t) |
||||||
|
Для |
определения |
инерционных |
нагрузок на |
конструкцию необходимо знать абсолютные ускорения ее точек:
|
{ a} { } |
n |
i }( |
) |
n |
||||||||||||||
|
0 |
å |
j |
i 0 |
å |
ja |
|||||||||||||
|
{ |
&& |
{ i } |
&& |
|||||||||||||||
|
u |
= u |
+ {}Ix (t) = |
Φ |
Ψ (t) + D x |
(t) |
= |
Φ Ψ (t) |
|||||||||||
|
&& |
&& |
&& |
&& |
|||||||||||||||
|
i=1 |
i=1 |
|||||||||||||||||
|
Сейсмические колебания дискретных систем описываются |
||||||||||||||||||
|
&& |
& |
& |
&& |
& |
&& |
& |
&& |
(t) , |
(14.12) |
|||||||||
|
[M]{u}+[C]{u}+[K]{u}=−[M]({Ix}x0(t) +{Iy}y0(t) +{Iz}z0 |
||||||||||||||||||
|
где |
&& |
&& |
и |
&& |
– |
компоненты |
расчетной |
|||||||||||
|
x |
0 (t) , y0 (t) |
z0 (t) |
акселерограммы. Если какая—либо из компонент не учитывается, то соответствующая часть нагрузки из (14.12) исключается.
257

1 4 . С п е к т р ы о т в е т а
14.2 Поэтажные акселерограммы и спектры ответа
При анализе сейсмостойкости оборудования необ— ходимо определить действующие на него инерционные сейс— мические нагрузки. Принят метод раздельного рассмотрения
сейсмических колебаний здания и оборудования с использованием так называемых поэтажных акселерограмм и поэтажных спектров ускорений – акселерограмм и спектров, рассчитанных для точек крепления оборудования.
Расчет производится следующим образом:
∙определяются (вычисляются) вынужденные колебания сооружения при сейсмическом воздействии, заданном расчетной акселерограммой на грунте;
∙определяются законы изменения абсолютных ускорений выбранных точек конструкции;
∙принимая акселерограммы в качестве возмущающего воздействия, рассчитывают вынужденные линейные колебания линейных неконсервативных осцилляторов, и
находят зависимость модулей их максимальных абсолютных ускорений от их собственных частот и коэффициентов диссипации.
Таким образом, для каждой исследуемой точки решается
уравнение (2), в котором:
∙зафиксирован коэффициент диссипации ϕ;
∙нагрузкой является вычисленное возмущающее воздействие от расчетной акселерограммы;
∙наборы собственных частот осциляторов при расчете спектра ответа зафиксированы и приведены в таблице 14.1.
|
Таблица 14.1. |
||
|
Частотный диапазон (гц) |
Приращения (гц) |
|
|
0.2 |
– 3.0 |
0.10 |
|
3.0 |
– 3.6 |
0.15 |
|
3.6 |
– 5.0 |
0.20 |
|
5.0 |
– 8.0 |
0.25 |
|
8.0 |
– 15.0 |
0.5 |
|
15.0 – 18.0 |
1.0 |
|
|
18.0 – 22.0 |
2.0 |
|
|
22.0 – 34.0 |
3.0 |
К приведенным в табл. 14.1 значениям частот
неконсервативных осцилляторов добавляются еще собственные частоты рассчитываемой конструкции. Это делается для того, чтобы учесть возможность резонанса с ними.
Для каждого указанного осцилятора находятся решения на всем диапазоне действия акселерограммы и выбирается максимальное по абсолютной величине, которое и
является спектром ответа данной точки на действие данной акселерограммы.
258

1 4 . С п е к т р ы о т в е т а
14.3 Ввод данных и анализ результатов
Рис. 14.3.1. Диалоговое окно
Спектры ответа
Рис. 14.3.2. Диалоговое окно
Результаты
Окно постпроцессора Спектры ответа (рис. 14.3.1) содержит список с номерами узлов, для которых необходимо вычислить спектры ответа (Список узлов). Имена акселерограмм, по которым необходимо выполнить расчет спектров, выбираются из списка имеющихся (Исходные) и переносятся в список используемых в расчете (Выбранные) с помощью кнопки Добавить. Если случайно выбрана не та акселерограмма, то ее можно убрать из списка Выбранные кнопкой Вернуть. Кроме того для расчета необходимо установить направление действия, ввести коэффициент диссипации (в диапазоне от 0 до 1) и, если это необходимо, задать коэффициенты диссипации по формам (например, для 4-х форм следует ввести через пробел четыре числа). Если введено меньше значений, чем задано форм, то последнее
введенное значение будет отнесено ко всем последующим формам.
Выбор загружений, для которых выполняется расчет, осуществляется в списке, размещенном в нижней части экрана.
Расчет выполняется после подготовки всех данных нажатием кнопки ОК. После окончания расчета открывается доступ к кнопке Результаты.
Просмотр результатов и их документирование выполняется в диалоговом окне Результаты. Для построения спектров необходимо назначить номер узла, номер загружения и имя акселерограммы. Программа позволяет получить на
одном графике спектры по одному или нескольким направлениям, во всем диапазоне частот или в заданном.
Полученные графики и результаты расчета могут быть выведены на принтер кнопками Печать графиков и Результаты (таблицы) соответственно.
259

1 4 . С п е к т р ы о т в е т а
14.4Подготовка файлов акселерограмм
Файлы акселерограмм находятся в корневом каталоге ПВК SCAD и имеют расширение SPC. При передаче
пользователям постпроцессора поставляются для примера четыре стандартные акселерограммы.
Рассмотрим пример задания акселерограммы:
Расчетная акселерограмма в cм/(c*c) для ПЗ на площадке атомного реактора.
Компонента – SH. Mодель – 1c. Amax = 45.1 cм/(c*c).
Количество точек N = 2047; Шаг по времени Dt = 0.05000 c.
#
0.01 2047 0.05
|
0.0 |
0.0 |
0.1 |
0.3 |
0.4 |
0.6 |
0.5 |
0.0 |
–2.1 |
–2.6 … |
После символа # следуют:
∙коэффициент перевода заданных ускорений в м/ceк2 ;
∙количество точек;
∙шаг по времени;
∙значения ускорений.
Аналогичным образом может быть подготовлен файл с нужной акселерограммой (файл с расширением SPC следует поместить в каталог с исходными данными). Для использования акселерограмм, поставляемых в составе комплекса, соответствующие файлы необходимо скопировать из каталога SCAD в каталог с исходными данными.
260
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Косяки SCAD
Неточности, ошибки, косяки SCAD — 6 шт

№6 Реакции в связях или нагрузки от фрагмента схемы от сейсмических загружний или комбинаций с ними.
Проблема возникает в «вылеченных» версиях программы, и в старых и в новых. Заключается в следующем — когда вы хотите посмотреть нагрузки на фрагмент схемы или реакции в связях от комбинации загружений, в которую входит сейсмической, то программа вам их покажет, только неверно.
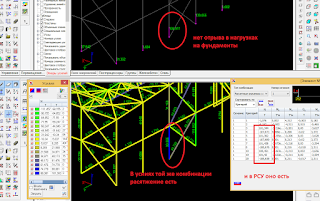
До обнаружения проблемы я выдавал задание трижды, а Вы?
№5 Стержни (колонны и балки) в узлах стыка с пластинчатыми элементами
Проблема присутствует во всех версиях.
Если вертикальный стержень имеет стык с пластинчатым элементом и речь идет о стальном каркасе и железобетонном перекрытии, то в этом месте иногда возникают усилия, которые приводят к увеличению сечения вертикального стержня.


Зачастую проблема возникает в местах несимметричного примыкания пластинчатых элементов к вертикальному стержню.
Так же проблема может возникать и при примыкании пластинчатого элемента к горизонтальному стержню, особенно если с двух сторон несимметричная сетка или примыкают к стержню трех узловые элементы, или как в №1
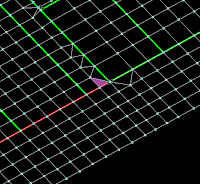

№4 РСУ и динамические загружения при использовании расчётных схем SCAD 11 в SCAD 21
Проиллюстрировать невозможно, суть заключается в следующем: если мы используем файл с уже полностью готовой расчётной схемой из 11 версии в 21, то необходимо пересохранить все загружения (естественно с вводом типов и видов нагрузок), пересоздать динамические загружения заново, удалить и создать заново РСУ.
Выявлено следующим образом: существовало два снеговых загружения — на всю ферму и на половину. В РСУ загружения были как взаимоисключающие. Однако при проверке, половина фермы «краснела», и как раз та половина, которая была нагружена во втором снеговом загружении. Увидеть это в отчёте или в формуле РСУ невозможно (что оба загружения суммировались), но при удалении второго загружении (дезактивация загружения не помогает) все элементы фермы проходили снова.
Динамические загружения (ветер и сейсмика) искажаются. В частности это касается преобразования статических нагрузок в массы (некоторые строки пропадают) и, для пульсации ветра, слетает выбранное статическое ветровое загружение. При восстановлении этих данных результаты неудовлетворительные, так как многие элементы, ранее удовлетворяющие проверки сечений, более не удовлетворяют («краснеют»)
№3 При копировании фрагмента схемы не все связи в узлах копируются вместе с элементами SCAD 21

№2 Смена типов жесткостей при «удаление дублирующихся типов жесткостей» SCAD 21
Иногда, при удаление дублирующих жесткостей происходит произвольная замена.

№1 Совместная работа пластинчатого элемента и стержня SCAD 21
при расчёте схемы каркасного металлического здания
При определённом соотношении толщины к длине пластины или при непосредственной близости к узлу стыка горизонтального стержня (балки) с вертикальным (колонной), пластинчатый элемент создаёт пиковую поперечную силу, что приводит к увеличению сечения горизонтального стержня.

FAQ 004657 RU
-
Перейти к
-
События
-
Видео
-
Модели
-
База знаний
-
Снимки экрана
-
Функции продукта
-
Часто задаваемые вопросы
-
Проекты заказчиков
-
Рекомендуемые события
Видео
Модели для скачивания
Статьи из Базы знаний
Снимки экрана


Статьи в Функциях продукта

Отображение топологии на деформированной конструкции
При активации флажка «Топология на объектe с поиском формы» в навигаторе Изобразить, будет отображение модели оптимизировано на основе геометрии поиска формы. Таким образом, будут, например, нагрузки всегда отображаться в соответствии с деформированной конструкцией.
Часто задаваемые вопросы (FAQ)
-
Хотя я смоделировал две идентичные конструктивные системы, у меня получилась другая форма. Почему?
-
Каким образом можно составить факторизованные сочетания постоянной нагрузки в контексте поиска формы?
-
Похоже, что после моего расчета в модуле RF-FORM-FINDING стержни не деформировались. Что я сделал не так?
-
Как смоделировать шатровую крышу с двумя конусами?
-
Как смоделировать подвесную мембранную конструкцию кровли с линейными опорами?
-
Как можно в программе RFEM смоделировать воздухоопорный объект?
-
Как смоделировать вантовую сеть в дополнительном модуле RF-FORM-FINDING?
-
Какие программы Dlubal необходимы для расчета мембранных и натяжных конструкций?
-
Мне нужно проанализировать вантовые и натяжные конструкции. Можно ли это сделать в программе RFEM или RSTAB?
-
Модель вантовой конструкции, созданную в программе RFEM 5.13, нельзя рассчитать в текущей версии программы. Программа все время отображает сообщение о том, что «Матрица жесткости сингулярна», хотя в исходной версии программы можно было модель нормально рассчитать. Как это можно исправить?
Другие часто задаваемые вопросы
Проекты заказчиков
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
Сейчас Вы — Гость на форумах «Проектант». Гости не могут писать сообщения и создавать новые темы.
Преодолейте несложную формальность — зарегистрируйтесь! И у Вас появится много больше возможностей на форумах «Проектант».
Последние сообщения на Строительном форуме
18 Января 2023 года, 10:03
17 Января 2023 года, 08:04
12 Января 2023 года, 11:49
12 Января 2023 года, 10:59
04 Января 2023 года, 13:41
28 Декабря 2022 года, 16:08
20 Декабря 2022 года, 16:16
20 Декабря 2022 года, 15:02
08 Декабря 2022 года, 16:29
04 Декабря 2022 года, 14:42
01 Декабря 2022 года, 11:02
23 Ноября 2022 года, 16:34
23 Ноября 2022 года, 15:48
21 Ноября 2022 года, 08:56
21 Ноября 2022 года, 08:55

Да, в новом так не работает, но легко решается через «Спектр жесткостных характеристик».

При возможности посмотрю на очередном расчёте. Не пытались писать письма в SCAD?

Собственно, справка скада:
В случаях, когда выполняется проверка устойчивости по комбинациям загружений, среди которых имеются динамические, требуется проявить некоторую осторожность, связанную с двумя обстоятельствами:
результаты динамического нагружения являются знакопеременными;
в тех случаях, когда результаты динамического расчета сформированы как корень квадратный из суммы квадратов (ККСК) модальных вкладов, нарушены условия равновесия и геометрической связности узловых перемещений.
Рассмотрим эти обстоятельства порознь.
Поскольку заранее неизвестно, какой знак результата динамического расчета является более опасным с точки зрения проверки устойчивости, то следует рассмотреть обе возможности. Так, например, если при расчете устойчивости рассматривается комбинация (L1)*1+(L2)*0.9+(L3)*0.7+(L4)*0.8, в которой нагружение (L3) является динамическим, то следует также выполнить проверку на комбинацию (L1)*1+(L2)*0.9+(L3)*(-0.7)+(L4)*0.8. При наличии нескольких динамических нагружений приходится перебирать все варианты знаков для их результатов.
Несовместность усилий связанная с использованием ККСК (естественно, если учтена не только одна форма собственных колебаний), вообще говоря, никаких неприятностей не вызывает. Просто проверяется коэффициент запаса устойчивости при пропорциональном росте всех внутренних усилий, игнорируя тот факт, что эти усилия нарушают условия равновесия.
Но несовместность узловых перемещений приводит к тому, что имеющиеся в схеме абсолютно жесткие тела получают искажения (по сути, они деформируются, что не соответствует их физической природе). Сложность состоит в том, что для этих элементов матрица К1(λ), не определяется внутренними силами или напряжениями, а вычисляется по значениям узловых перемещений, которые определяют изменение пространственной ориентации бесконечно жесткого конечного элемента (см. 9.5.1 в работе [3]). Несовместность узловых перемещений может привести к фатальной ошибке при вычислении К1(λ).
В связи с этим программа предусматривает обнуление матрицы К1(λ) при проверке устойчивости для комбинаций содержащих динамическое нагружение с более чем одной учитываемой формой собственных колебаний. Об этом в протоколе расчета появляется соответствующее предупреждение.
Источник
Ошибка при разложении матрицы 99%
Автор: Dmitry Rudenko
Если при расчёте в SCAD у Вас появляется сообщение: “Ошибка при разложении матрицы 99%”, значит Ваша система – геометрически изменяемая, т.е. перемещения каких-то элементов расчётной модели стремятся к бесконечности.
Проверьте следующее:
-
Правильно ли заданы граничные условия? Начинающие пользователи часто забывают закрепить модель по направлениям X и Y после назначения коэффициентов постели
-
Все ли элементы расчётной модели имеют связь друг с другом?
-
Проверьте наличие в схеме совпадающих элементов или совпадающих узлов. Если они есть, выполните их объединение, после чего сделайте “упаковку схемы”
-
…
Косяки SCAD
Неточности, ошибки, косяки SCAD – 6 шт

№6 Реакции в связях или нагрузки от фрагмента схемы от сейсмических загружний или комбинаций с ними.
Проблема возникает в “вылеченных” версиях программы, и в старых и в новых. Заключается в следующем – когда вы хотите посмотреть нагрузки на фрагмент схемы или реакции в связях от комбинации загружений, в которую входит сейсмической, то программа вам их покажет, только неверно.

До обнаружения проблемы я выдавал задание трижды, а Вы?
№5 Стержни (колонны и балки) в узлах стыка с пластинчатыми элементами
Проблема присутствует во всех версиях.
Если вертикальный стержень имеет стык с пластинчатым элементом и речь идет о стальном каркасе и железобетонном перекрытии, то в этом месте иногда возникают усилия, которые приводят к увеличению сечения вертикального стержня.


Зачастую проблема возникает в местах несимметричного примыкания пластинчатых элементов к вертикальному стержню.
Так же проблема может возникать и при примыкании пластинчатого элемента к горизонтальному стержню, особенно если с двух сторон несимметричная сетка или примыкают к стержню трех узловые элементы, или как в №1


№4 РСУ и динамические загружения при использовании расчётных схем SCAD 11 в SCAD 21
Проиллюстрировать невозможно, суть заключается в следующем: если мы используем файл с уже полностью готовой расчётной схемой из 11 версии в 21, то необходимо пересохранить все загружения (естественно с вводом типов и видов нагрузок), пересоздать динамические загружения заново, удалить и создать заново РСУ.
Выявлено следующим образом: существовало два снеговых загружения – на всю ферму и на половину. В РСУ загружения были как взаимоисключающие. Однако при проверке, половина фермы “краснела”, и как раз та половина, которая была нагружена во втором снеговом загружении. Увидеть это в отчёте или в формуле РСУ невозможно (что оба загружения суммировались), но при удалении второго загружении (дезактивация загружения не помогает) все элементы фермы проходили снова.
Динамические загружения (ветер и сейсмика) искажаются. В частности это касается преобразования статических нагрузок в массы (некоторые строки пропадают) и, для пульсации ветра, слетает выбранное статическое ветровое загружение. При восстановлении этих данных результаты неудовлетворительные, так как многие элементы, ранее удовлетворяющие проверки сечений, более не удовлетворяют (“краснеют”)
№3 При копировании фрагмента схемы не все связи в узлах копируются вместе с элементами SCAD 21

№2 Смена типов жесткостей при “удаление дублирующихся типов жесткостей” SCAD 21
Иногда, при удаление дублирующих жесткостей происходит произвольная замена.

№1 Совместная работа пластинчатого элемента и стержня SCAD 21
при расчёте схемы каркасного металлического здания
При определённом соотношении толщины к длине пластины или при непосредственной близости к узлу стыка горизонтального стержня (балки) с вертикальным (колонной), пластинчатый элемент создаёт пиковую поперечную силу, что приводит к увеличению сечения горизонтального стержня.


1 3 . У с т о й ч и в о с т ь
13. Устойчивость
Для каждого указанного пользователем загружения (или комбинации загружений) SCAD позволяет определить:
∙коэффициент запаса устойчивости;
∙первую форму потери устойчивости (без анализа кратности);
∙свободные длины стержневых элементов.
|
13.1 Постановка задачи |
Задача устойчивости решается в классической |
|
|
постановке для упругой системы и в предположении, что все |
||
|
приложенные к системе внешние нагрузки (следовательно, и |
||
|
внутренние силы) растут пропорционально одному и тому же |
||
|
параметру λ. То значение параметра λ, при котором матрица |
||
|
жесткости системы А(λ) впервые |
перестает быть положи– |
|
|
тельно определенной, является критическим, а соответ– |
||
|
ствующее значение λ — коэффициентом запаса устойчивости |
||
|
(КЗУ). |
Матрица жесткости А(λ) = |
Ao – B(λ) состоит из |
“обычной” матрицы жесткости Ao и матрицы “толкающих” реакций B(λ), которые определяются сжимающими силами в стержнях, напряжениями сжатия в конечных элементах оболо– чечного типа и т.п. Напоминаем, что положительная опреде– ленность матрицы жесткости означает, что при любых
значениях узловых перемещений и поворотов u потенциальная энергия системы положительна (это значит, что для деформирования системы необходимо затратить энергию и, следовательно, она оказывает сопротивление деформированию,
она является отпорной).
Если система теряет устойчивость, она теряет отпорность и ее матрица жесткости становится вырожденной (с нулевым детерминантом), а в закритическом состоянии система получает отрицательную отпорность (при ее принуди–
тельном деформировании выделяется ранее накопленная потенциальная энергия “толкающих” реакций) и ее матрица жесткости становится знаконеопределенной.
Таким образом, задача оценки устойчивости равно–
весия сводится к проверке положительной определенности матрицы жесткости при пробном значении коэффициента λ .
Необходимо отметить, что с помощью проверок
матрицы жесткости можно отыскать только те критические состояния, при которых потеря устойчивости происходит по
251

1 3 . У с т о й ч и в о с т ь
13.2 Поиск коэффициента запаса устойчивости
форме, когда узловые перемещения и повороты не все вместе равны нулю (это так называемая явная форма потери устойчивости). Нужно еще проверить, что при пробном значении λ не может произойти так называемая скрытая форма потери устойчивости, которая реализуется в пределах одного
конечного элемента и не вызывает узловых перемещений и поворотов. Поскольку для всех типов конечных элементов соответствующие критические величины λкр известны (они вычисляются по простым формулам), то это значит, что следует, кроме всего прочего, проверить неравенство λ > λкр для всех конечных элементов.
Поиск коэффициента запаса устойчивости (КЗУ) ведется в интервале [0,Λ], где Λ – число, заданное пользователем, (оценка того значения КЗУ, которое считается уже безразличным для оценки качества системы) и с точностью ε, которая также задается пользователем.
При этом решается задача определения минимального λ, при котором происходит вырождение матрицы А(λ).
Матрица А(λ) составляется из матриц устойчивости отдельных конечных элементов. Если в системе нет ни одного элемента, способного терять устойчивость (например, в стержневой системе все стержни растянуты), то выдается сообщение, что система “абсолютно устойчива“.
Далее проверяется устойчивость системы при λ = Λ (т.е. положительная определенность матрицы А(Λ)). Если это условие выполнено, то выдается сообщение о том, что КЗУ больше заданного максимума.
Если условие положительной определенности А(Λ) не выполнено (об этом свидетельствуют отрицательные значения на главной диагонали матрицы жесткости, преобразованной в процессе решения системы уравнений), производится анализ положительной определенности матрицы А(Λ/2),…, т.е. используется стандартный метод половинного деления. Этот процесс продолжается до тех пор, пока не найден интервал (λ1, λ2) такой, что λ2 – λ1 ≤ ε и матрица А(λ1) положительно определена, а матрица А(λ2) этим свойством не обладает. При этом величина λ1 считается КЗУ.
При составлении матрицы устойчивости для каждого конечного элемента (способного терять устойчивость) вычисляется значение λкр, которое приводит к потере устойчивости КЭ. Если min λкр < Λ, интервал поиска сокращается, а номер элемента, для которого достигается min λкр, сообщается в протоколе.
252

1 3 . У с т о й ч и в о с т ь
13.3 Форма потери устойчивости
В предположении, что определенный на первом этапе коэффициент запаса устойчивости является точным, SCAD
производит решение задачи об определении собственного вектора при известном собственном значении задачи
Заметим, что правые части системы равны нулю, т.е. отыскиваются такие значения узловых перемещений и пово– ротов u, которые вызываются только внутренними сжимающи– ми напряжениями и усилиями. Поперечные нагрузки, как известно, не влияют на значения критических сил и вид формы потери устойчивости. Поскольку уравнение (а) решено при нулевой правой части, то форма потери устойчивости определена лишь с точностью до множителя. Ее уменьшение или увеличение в любое число раз не нарушает условие (а).
|
Если в системе имеются стержневые элементы, то |
|
|
13.4 Свободные длины |
можно определить их свободные длины, т.е. длины таких же, |
|
но шарнирно опертых стержней, у которых критическая |
|
|
сила Nкр совпадает с продольным усилием в стержне |
|
|
системы в момент потери устойчивости (Nкр=λ1*N). |
|
|
Поскольку по формуле Эйлера Nкр = π2EJ / l2, свободная |
|
|
длина будет lo = (λ1N / π2EJ )1/2, |
|
|
где EJ – жесткости стержней в главных плоскостях инерции |
|
|
(для пространственной задачи – по две для каждого стержня). |
253

1 3 . У с т о й ч и в о с т ь
13.5 Ввод данных
Рис. 13.5.1. Диалоговое окно
Проверка устойчивости
Ввод данных для проверки устойчивости выполняется в одноименном диалоговом окне (рис. 13.5.1), которое
вызывается из раздела Специальные исходные данные в Дереве проекта. Для ввода данных необходимо выполнить такие операции:
Äс помощью комбинаторных кнопок задать режим проверки – вычисление коэффициента запаса устойчивости, форм потери устойчивости и свободных длин стержневых элементов;
Äв полях Масштабный множитель и Точность вычислений следует ввести соответствующие значения (по умолчанию приняты 2 и 0.01);
Äактивизировать опции, определяющие вид данных, для которых выполняется проверка устойчивости: по загружениям или по комбинациям загружений, для всех загружений (комбинаций) или только для выбранных; в последнем случае выбор нужных
данных выполняется в списке загружений (комбинаций).
Масштабный множитель – параметр используется
для ограничения интервала поиска коэффициента запаса устойчивости. Если его значение больше заданного, система считается устойчивой.
Точность вычислений – параметр задает критерий
окончания итерационного процесса поиска коэффициента запаса устойчивости. При очень малых значениях этого параметра время расчета может существенно увеличиться.
Для удаления подготовленных данных и отказа от анализа устойчивости используется кнопка Удаление данных.
254

1 4 . С п е к т р ы о т в е т а
14.Спектры ответа
14.1Расчет на сейсмические воздействия
Выведенный из положения равновесия линейный неконсервативный осциллятор совершает затухающие колебания, которые описываются дифференциальным
уравнением
|
&& |
& |
2 |
x = 0, |
(14.1) |
|
x |
+ 2ϕ ω x + ω |
где
ω – собственная круговая частота системы без затухания (рад/с);
ϕ – относительное демпфирование. При ϕ < 1 решение уравнения (1) имеет вид
x = Ae−ϕωt sin(ωD t + α) ,
где
ωD = ω
 1 − ϕ2 – частота с учетом затухания,
1 − ϕ2 – частота с учетом затухания,
А, α – коэффициенты, которые зависят от начальных условий.
Обычно для строительных конструкций ϕ<<1 и
|
практически ωD |
≈ ω . |
|||
|
Если на массу действует сила F(t), то ее перемещения |
||||
|
описываются уравнением |
2 |
|||
|
&& |
& |
x = F(t) / m, |
(14.2) |
|
|
x + 2ϕ ω x + ω |
общее решение которого при нулевых начальных условиях можно записать с помощью интеграла Дюамeля
|
1 |
t |
|||||||
|
x = |
òF (t)exp[−ρω(t − z)]sin ωD (t − z)dz |
(14.3) |
||||||
|
mωD |
||||||||
|
0 |
||||||||
|
При |
движении основания |
&& |
||||||
|
с ускорением x0 (t) |
||||||||
|
(кинематическое |
возмущение) |
на |
массу |
m |
действует |
|||
|
переносная |
сила |
инерции |
&& |
(t) . |
Поэтому |
|||
|
F(t) = −mx0 |
уравнение, описывающее относительные перемещения массы в системе координат, связанной с основанием, имеет вид
|
&& |
& |
+ ω |
2 |
x |
&& |
(t) , |
(14.4) |
|||||||
|
x |
+ 2ϕω x |
= −x 0 |
||||||||||||
|
а его решение |
t |
|||||||||||||
|
1 |
−ϕω(t−z) |
|||||||||||||
|
x = − |
ωD |
ò |
x(t)e |
sin ωD (t − z)dz |
(14.5) |
|||||||||
|
0 |
&& |
|||||||||||||
|
При |
определении |
абсолютного ускорения |
массы |
|||||||||||
|
&& |
&& |
получаем при обычных малых значениях ϕ, что |
||||||||||||
|
xα |
= x + x0 |
|||||||||||||
|
&& |
2 |
(14.6) |
||||||||||||
|
x |
α ≈ −ωD x |
|||||||||||||
|
Нами |
рассматриваются |
колебания |
линейных |
255

1 4 . С п е к т р ы о т в е т а
дискретных систем со многими степенями свободы,
полученные из любых континуальных или комбинированных систем после применения к ним процедуры дискретизации метода конечных элементов (МКЭ). При этом решается
система обыкновенных дифференциальных уравнений
|
[ |
M |
]{ } |
+ |
[ |
K |
]{ } |
{ } |
(14.7) |
|
|
u&& |
u = |
0 , |
|||||||
|
где |
{u} – вектор перемещений; |
||||||||
|
[M] – матрица массы; |
|||||||||
|
[K] – матрица жесткости. |
Вынужденные колебания линейной дискретной системы с затуханием по гипотезе Фойгта–Кельвина описываются
|
системой обыкновенных дифференциальных уравнений |
|||
|
[M ]{u} + [C ]{u} + [K ]{u} = {F(t)} , |
(14.8) |
||
|
&& |
& |
||
|
где |
[C] – матрица диссипации энергии; |
||
|
{F(t)} – вектор нагрузки. |
|||
|
В случае |
кинематического возмущения в |
качестве |
|
нагрузки выступают переносные силы инерции и |
система |
|||
|
уравнений (14.8) записывается в виде |
0(t) , |
(14.9) |
||
|
[M ]{u} + [C ]{u} + [K ]{u} = -[M ]{I}x |
||||
|
&& |
& |
&& |
где {u} – вектор относительных перемещений (например, в системе координат xOy, связанной с основанием);
{I} – вектор, компонентами которого являются
косинусы углов между направлениями перемещений по координатам и вектором ускорения основания;
x&&0 (t) – ускорение основания.
Решение уравнения (14.9) отыскивается в виде
разложения его по формам собственных колебаний системы (так называемая “модальная суперпозиция”)
|
n |
|
|
{u} = å{F j }Yj (t) , |
(14.10) |
j=1
где n – число степеней свободы системы (учитываемых собственных чисел и векторов);
F j – j-я форма собственных свободных колебаний
|
дискретной системы; |
|||||||||
|
Yj (t) |
– |
неизвестные функции |
времени, |
которые |
|||||
|
необходимо определить. |
|||||||||
|
Будем предполагать, что для матрицы диссипации [С] |
|||||||||
|
выполняется условие |
|||||||||
|
T |
[C ]{F j } = |
ì0 , |
i ¹ j |
||||||
|
{Fi } |
ï |
||||||||
|
í |
T |
[M ]{Fi } , i = j |
|||||||
|
ï2ji wi {Fi } |
|||||||||
|
î |
|||||||||
|
где wi – i-я собственная частота дискретной системы. |
|||||||||
|
После подстановки (14.10) в (14.9) и умножения (14.9) |
|||||||||
|
на вектор |
{Fi }T |
для |
нахождения |
Yi (t) |
получаем |
дифференциальное уравнение
256

1 4 . С п е к т р ы о т в е т а
|
&& |
2 |
Ψi |
= −D i x |
0 |
(t) , |
(14.11) |
|||
|
Ψ + 2ϕi ωi Ψi + ωi |
|||||||||
|
&& |
|||||||||
|
D i = |
{Φi }T [M ]{I} |
&& |
|||||||
|
где |
{Φi }T [M ]{Φi } |
x0 |
(t) |
||||||
|
Для |
определения |
инерционных |
нагрузок на |
конструкцию необходимо знать абсолютные ускорения ее точек:
|
{ a} { } |
n |
i }( |
) |
n |
||||||||||||||
|
0 |
å |
j |
i 0 |
å |
ja |
|||||||||||||
|
{ |
&& |
{ i } |
&& |
|||||||||||||||
|
u |
= u |
+ {}Ix (t) = |
Φ |
Ψ (t) + D x |
(t) |
= |
Φ Ψ (t) |
|||||||||||
|
&& |
&& |
&& |
&& |
|||||||||||||||
|
i=1 |
i=1 |
|||||||||||||||||
|
Сейсмические колебания дискретных систем описываются |
||||||||||||||||||
|
&& |
& |
& |
&& |
& |
&& |
& |
&& |
(t) , |
(14.12) |
|||||||||
|
[M]{u}+[C]{u}+[K]{u}=−[M]({Ix}x0(t) +{Iy}y0(t) +{Iz}z0 |
||||||||||||||||||
|
где |
&& |
&& |
и |
&& |
– |
компоненты |
расчетной |
|||||||||||
|
x |
0 (t) , y0 (t) |
z0 (t) |
акселерограммы. Если какая–либо из компонент не учитывается, то соответствующая часть нагрузки из (14.12) исключается.
257

1 4 . С п е к т р ы о т в е т а
14.2 Поэтажные акселерограммы и спектры ответа
При анализе сейсмостойкости оборудования необ– ходимо определить действующие на него инерционные сейс– мические нагрузки. Принят метод раздельного рассмотрения
сейсмических колебаний здания и оборудования с использованием так называемых поэтажных акселерограмм и поэтажных спектров ускорений – акселерограмм и спектров, рассчитанных для точек крепления оборудования.
Расчет производится следующим образом:
∙определяются (вычисляются) вынужденные колебания сооружения при сейсмическом воздействии, заданном расчетной акселерограммой на грунте;
∙определяются законы изменения абсолютных ускорений выбранных точек конструкции;
∙принимая акселерограммы в качестве возмущающего воздействия, рассчитывают вынужденные линейные колебания линейных неконсервативных осцилляторов, и
находят зависимость модулей их максимальных абсолютных ускорений от их собственных частот и коэффициентов диссипации.
Таким образом, для каждой исследуемой точки решается
уравнение (2), в котором:
∙зафиксирован коэффициент диссипации ϕ;
∙нагрузкой является вычисленное возмущающее воздействие от расчетной акселерограммы;
∙наборы собственных частот осциляторов при расчете спектра ответа зафиксированы и приведены в таблице 14.1.
|
Таблица 14.1. |
||
|
Частотный диапазон (гц) |
Приращения (гц) |
|
|
0.2 |
– 3.0 |
0.10 |
|
3.0 |
– 3.6 |
0.15 |
|
3.6 |
– 5.0 |
0.20 |
|
5.0 |
– 8.0 |
0.25 |
|
8.0 |
– 15.0 |
0.5 |
|
15.0 – 18.0 |
1.0 |
|
|
18.0 – 22.0 |
2.0 |
|
|
22.0 – 34.0 |
3.0 |
К приведенным в табл. 14.1 значениям частот
неконсервативных осцилляторов добавляются еще собственные частоты рассчитываемой конструкции. Это делается для того, чтобы учесть возможность резонанса с ними.
Для каждого указанного осцилятора находятся решения на всем диапазоне действия акселерограммы и выбирается максимальное по абсолютной величине, которое и
является спектром ответа данной точки на действие данной акселерограммы.
258

1 4 . С п е к т р ы о т в е т а
14.3 Ввод данных и анализ результатов
Рис. 14.3.1. Диалоговое окно
Спектры ответа
Рис. 14.3.2. Диалоговое окно
Результаты
Окно постпроцессора Спектры ответа (рис. 14.3.1) содержит список с номерами узлов, для которых необходимо вычислить спектры ответа (Список узлов). Имена акселерограмм, по которым необходимо выполнить расчет спектров, выбираются из списка имеющихся (Исходные) и переносятся в список используемых в расчете (Выбранные) с помощью кнопки Добавить. Если случайно выбрана не та акселерограмма, то ее можно убрать из списка Выбранные кнопкой Вернуть. Кроме того для расчета необходимо установить направление действия, ввести коэффициент диссипации (в диапазоне от 0 до 1) и, если это необходимо, задать коэффициенты диссипации по формам (например, для 4-х форм следует ввести через пробел четыре числа). Если введено меньше значений, чем задано форм, то последнее
введенное значение будет отнесено ко всем последующим формам.
Выбор загружений, для которых выполняется расчет, осуществляется в списке, размещенном в нижней части экрана.
Расчет выполняется после подготовки всех данных нажатием кнопки ОК. После окончания расчета открывается доступ к кнопке Результаты.
Просмотр результатов и их документирование выполняется в диалоговом окне Результаты. Для построения спектров необходимо назначить номер узла, номер загружения и имя акселерограммы. Программа позволяет получить на
одном графике спектры по одному или нескольким направлениям, во всем диапазоне частот или в заданном.
Полученные графики и результаты расчета могут быть выведены на принтер кнопками Печать графиков и Результаты (таблицы) соответственно.
259

1 4 . С п е к т р ы о т в е т а
14.4Подготовка файлов акселерограмм
Файлы акселерограмм находятся в корневом каталоге ПВК SCAD и имеют расширение SPC. При передаче
пользователям постпроцессора поставляются для примера четыре стандартные акселерограммы.
Рассмотрим пример задания акселерограммы:
Расчетная акселерограмма в cм/(c*c) для ПЗ на площадке атомного реактора.
Компонента – SH. Mодель – 1c. Amax = 45.1 cм/(c*c).
Количество точек N = 2047; Шаг по времени Dt = 0.05000 c.
#
0.01 2047 0.05
|
0.0 |
0.0 |
0.1 |
0.3 |
0.4 |
0.6 |
0.5 |
0.0 |
–2.1 |
–2.6 … |
После символа # следуют:
∙коэффициент перевода заданных ускорений в м/ceк2 ;
∙количество точек;
∙шаг по времени;
∙значения ускорений.
Аналогичным образом может быть подготовлен файл с нужной акселерограммой (файл с расширением SPC следует поместить в каталог с исходными данными). Для использования акселерограмм, поставляемых в составе комплекса, соответствующие файлы необходимо скопировать из каталога SCAD в каталог с исходными данными.
260
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
 24.10.2005 — 10:18
24.10.2005 — 10:18











![[доволен] [доволен]](https://www.proektant.org/Smileys/default/cheesy.gif)
![[улыбка] [улыбка]](https://www.proektant.org/Smileys/default/smiley.gif) так в логе так и написано что не реализован расчет на устойчивость для металла, а Вы паникуете. Лог расчета это первая вещь которую нужно внимательно изучить даже если результат положительный и расчет выполнен.
так в логе так и написано что не реализован расчет на устойчивость для металла, а Вы паникуете. Лог расчета это первая вещь которую нужно внимательно изучить даже если результат положительный и расчет выполнен. 