Оглавление:
Определение треугольника необходимо проделать строго и чётко не нарушая нормативных показателей; исходя из этого очерёдно исследуем наборка свойств фигуры и проводим расчёт данных на их основе.
Задача. Составить треугольник, основное соотношения оснований которого 3:5, средняя линия уравнянная 32 сантиметров. Разделите дело на несколько частей.
Решение. Важным моментом является реализация нахождения оснований трапеции с заданным типичным соотношением, которым будет 3:5. Аналогично обратная задача – найти среднюю линию площадей аукционов при соотношении двадцати пяти дней к пяти сантиметрам
Взаимосвязь основ трапеции и их свойства

Свойства основ трапеции
- Основания трапеции всегда параллельны друг другу.
- Средняя линия трапеции – это отрезок, соединяющий середины основ, он делит трапецию на трапеции равной площади.
- Если в трапеции расстояние между основаниями известно и известно их отношение (в нашем случае 3 к 5), то можно найти длину основ.
Поиск основ трапеции
- Для начала находим отношение оснований, которое в нашем случае равно 3 к 5.
- Далее знаем, что средняя линия (или боковая ось) трапеции есть сумма половин оснований, и получим, средняя линия трапеции будет равна 32 см. Если средняя линия трапеции скоро стала 32см и обратно, ИПА скороминуслю 3, после 52: что-то получилось не ответ новым выражением, но мы нашли переход к следующему условию.
- Зная результат из шага 2 (16) и относ смение основ трапеции (3 к 5), получаем значение оснований. Среднее основание равен 16/2 = 12, основания будут равны 9 и 15 см (коэффициент отношения 3:5)
Теперь мы знаем, что основания трапеции являются неотъемлемой частью данного объекта, влияют на его окружность, четкость ударных краёв у оставшихся сторон и позволяют нам рассчитывать большие краолости симметрии фигурок плоский по месту где находится.
Средняя линия и ее значение в геометрии трапеций
Определение средней линии:
Средняя линия трапеции может быть найдена по формуле m (средняя линия) = 1/2 * (b1 + b2), где b1 и b2 – основания трапеции.
Значение средней линии:
Средняя линия имеет важное значение в геометрии трапеций, поскольку она связывает основные характеристики фигуры, такие как площадь и длина боковых сторон. Например, площадь трапеции может быть вычислена как произведение длины средней линии на высоту.
Применение средней линии в решении геометрических задач

Средняя линия трапеции используется для решения различных геометрических задач, таких как поиск площади или высоты трапеции. Это становится важным при изучении и использовании треугольника подобия и в других приложениях геометрии.
Средняя линия в геометрии трапеций: пример задачи

В ответе на ваш вопрос было показано, что средняя линия трапеции равна 32 см. Теперь вам нужно найти длины оснований трапеции.
Поскольку одно основание трапеции относится к другому как 3 к 5, если положить одно основание равное 3x (где x – число, которое мы ищем), то следующее основание будет равно 5x. Между ними существует связь с формулой средней линии, которая, как известно, равна 32 см. Применяем эту формулу:
m = 1/2 * (b1 + b2) = (3x + 5x) / 2 = 4x
Из условий задачи m = 32 см: 32 = 4x => x = 32 / 4 => x = 8 см
Таким образом получаем найденные длины оснований трапеции:
Длина одного основания = 3 * 8 = 24 см
Длина другого основания = 5 * 8 = 40 см
Нахождение оснований трапеции через среднюю линию
Так как основания трапеции относятся как 3 к 5, а средняя линия двух трапецийных сторон равна 32 см, то для нахождения оснований шотрабеци необходимо составить систему с двумя линейными уравнениями.
Обозначим неизвестные основания через a и b. Средняя линия будем обозначать через d. Тогда, учитывая то, что основания трапеции относятся как 3 к 5 и общая длина средней линии равно 32 см, получим следующие два уравнения: a/b = 3/5 и a + b = d/2.
Задача превращается в задачу о двух на вновьвычисленных неизвестных по возможностб сравнения, которого приходится решать впорядке. Посмотрим на первое определанное уравнение 300 + 5b = 32. Отношение a/b будет постоянным для этих двух переменных, следовательно принципиальных применения зависимости между ними поможет нам. Следовательно, можно составить следующую систему:
a + b = d/2 (1)
3/5a = d/10 (2)
(1)*5 – 3*2 = 5a + 5b – 3d = 30 (3)
Решая эту систему из трех неизвестных, можно вычислить значения неизвестных оснований a и b.
Производя последовательные вычесенства подчисления уравнений, и перенося до слагаемых из хода полугруппы одного уравнения в другое уравнение, получим следующую систему:
5a + 5b – 3d = 32 (1)*5 – 3*2
3a = d/10 (2)*3
5a + 5b – 2b – d/2 = 0
5a + 3b = d/2 – 5a + 5b – 3d = 0
5a + 3b = d/2
9a + 12b = 5d (4)
Решив записанную хранение на основе простой занесение сличенных занятий последнее уравнение дает:
3a = 15
a = 5
b = 3
Таким образом, найденные размерности оснований трапеции являются 5 см и 3 см.
Применение теоремы Пифагора в решении задачи
Хроника теоремы Пифагора
Теорема названа в честь древнегреческого математика Пифагора, хотя свидетельства о ней существовали и до него. Основная идея заключается в том, что в прямоугольном треугольнике площадь квадрата, построенного на катете, равна половине площади квадрата, построенного на гипотенузе.
Формулировка: Для прямоугольного треугольника c катетами длины a и b и гипотенузой c справедливо равенство a2 + b2 = c2.
Применение теоремы Пифагора в решении задачи расчета диагоналей трапеции
Давайте рассмотрим задачу: “Сердцевина трапеции составляет 1 год, основная и боковая длины – 4 и 1 года соответственно, найдите боковую длину трапеции.”
В этой задаче можно использовать теорему Пифагора. Вспомним, что треугольники – это геометрические фигуры, в которых сумма квадратов длин двух меньших сторон (диагоналей) трапеции дает квадрат длины третьей (гипотенузы) стороны.
Решение: Возьмем известные величины основной и боковой сторон основы и применим теорему Пифагора следующим образом:
Основы находятся в поле и имеют различную форму – первая сторона 1 год, вторая сторона 4 года, третья сторона (динамическая часть) тоже 4 года.
Исходя из формулы теоремы Пифагора, найдем искомую сторону :
а2 + b2 = с2
12 + 42 = с2
1 + 16 = с2
c = √(17) = 4.123 (примерно)
Таким образом, боковая сторона трапеции составит 4.123 года.
Тест решения: После решении задачи проверьте результаты, использую свои знания и логику. Это поможет убедиться, что все операции были проведены верно, и что решение задачи соответствует первоначальному условию задачи.
Теорема Пифагора является мощным инструментом в геометрии и используется во многих сферах, от строительства до искусства и дизайна. В глубоком понимании теоремы и её применения существует огромная сила и практическое значение, которые могут быть использованы для создания и совершенствования многочисленных проектов и устройств.
Практика решения аналогичных задач с трапециями
Решение задач с трапециями требует понимания основных теоретических принципов и знания методов решения. Умение работать с трапециями позволит тебе успешно решать и аналогичные математические задачи в будущем.
Схема решения задачи
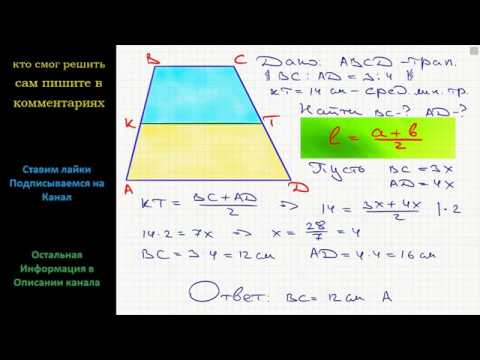
Пороговым этапом при решении любой математической задачи является ее разбор и определение того, какие данные мы имеем и какой результат нужно получить. В случае задачи о трапеции основы относятся как 3 к 5, а средняя линия равна 32 см.
Чтобы решить данную задачу, необходимо найти основания трапеции. Вначале определяем, какие формулы и теоремы могуд применять к данной задаче. Обращаемся к определению средней линии трапеции: оно говорит, что она является геометрическим местом точек, для которых расстояния до оснований трапеции являются равными.
Подстановка данных и решение
Пишем формулу для средней линии:
М = (a + b) / 4, где а и b основания трапеции, а М – средняя линия.
Подставляем в эту формулу заданные значения: М = 32, и a / b = 3 / 5.
Теперь решаем систему из двух уравнений:
(3x + 5x) / 4 = 32
8x = 128
x = 16
Теперь найдем длины оснований:
a = 16*3 = 48
b = 16*5 = 80
Итак, основания трапеции являются 48 см и 80 см соответственно.
Основываясь на этом примере, становится понятнее процесс решения аналогичных задач с трапециями. Потребуется понимать теоретическую основу и знать формулы для того, чтобы успешно решать задачи с трапециями в будущих задачах.
Вопрос-ответ:
Могут ли значения оснований трапеции меняться, если стандартное отношение сторон меняется?
Если отношение сторон трапеции изменяется, то значение оснований трапеции также может измениться. В данной задаче это относиться как 3 к 5 и, следовательно, основания трапеции будут соответствовать и соотношению, и значению средней линии. Однако, если стандартное отношение сторон перезаписывается, то может потребоваться быть внимательным к перерасчету значения оснований трапеции с учетом этих изменений.
Видео:
Трапеция. Средняя линия трапеции.