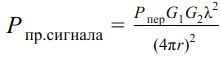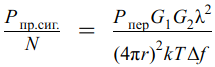Отношение сигнал шум как найти - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 февраля 2022 года; проверки требуют 2 правки.

Отношение сигнал/шум (ОСШ; англ. signal-to-noise ratio, сокр. SNR) — безразмерная величина, равная отношению мощности полезного сигнала к мощности шума:

${displaystyle mathrm {SNR} ={P_{mathrm {signal} } over P_{mathrm {noise} }}={A_{mathrm {signal} }^{2} over A_{mathrm {noise} }^{2}},}$

где

— средняя мощность,

— среднеквадратичное значение амплитуды. Оба сигнала измеряются в полосе пропускания системы.

Обычно отношение сигнал/шум выражается в децибелах (дБ):

${displaystyle mathrm {SNR(dB)} =10log _{10}left({P_{mathrm {signal} } over P_{mathrm {noise} }}right)=20log _{10}left({A_{mathrm {signal} } over A_{mathrm {noise} }}right).}$

Чем больше это отношение, тем меньше шум влияет на характеристики системы.

Основные причины плохих шумовых характеристик[править | править код]

Основные причины высокого уровня шума в сигнальных системах:

рассогласованные линии передачи сигнала,
тепловой шум и дробовой шум в компонентах системы,
недостаточная разрядность АЦП,
резонансные явления,
паразитные связи (паразитная ёмкость),
самовозбуждение системы,
нелинейность передаточных характеристик^{[уточнить]}.

Методы улучшения характеристик[править | править код]

Чаще всего улучшения шумовых характеристик системы можно добиться правильным согласованием входов и выходов её составных частей. Тогда паразитная ЭДС помехи, включённая последовательно с высоким внутренним сопротивлением источника шума, будет подавлена.

Снижение собственных шумов усилительного тракта (малошумящие усилители) достигается соответствующими схемотехническими решениями, в частности применением активных и пассивных компонентов с низким уровнем шума.

Если спектр полезного сигнала отличается от спектра шума, улучшить отношение сигнал/шум можно ограничением полосы пропускания системы.

Шум квантования устраняется повышением разрядности АЦП.

Для улучшения шумовых характеристик сложных комплексов применяются методы электромагнитной совместимости.

Измерение[править | править код]

В аудиотехнике отношение сигнал/шум определяют путём измерения напряжения шума и сигнала на выходе усилителя или другого звуковоспроизводящего устройства среднеквадратичным милливольтметром либо анализатором спектра. Современные усилители и другая высококачественная аудиоаппаратура имеет показатель сигнал/шум около 100—120 дБ.

В системах с более высокими требованиями используются косвенные методы измерения отношения сигнал/шум, реализуемые на специализированной аппаратуре.

В звукотехнике[править | править код]

Отношение сигнал/шум — параметр АЦП, ЦАП, микшера, микрофонного, предварительного или оконечного усилителя, например усилителя активных колонок. Он показывает, насколько сильно шумит звуковое устройство (обычно от 60 до 135,5 дБ) при отсутствии сигнала. Чем выше значение сигнал/шум, тем более чистый звук и больший динамический диапазон обеспечивается системой. Для музыкальных целей желательно, чтобы этот параметр был не менее 75 дБ, а для систем с высококачественным звучанием не менее 90 дБ.

Телефонный речевой канал имеет С/Ш около 30 дБ.

В видео[править | править код]

Отношение сигнал/шум — отношение уровня электрического сигнала к уровню шума этого сигнала, численно определяет содержание паразитных шумов в сигнале. Чем больше значение отношения сигнал/шум для видеосигнала, тем меньше помех и искажений имеет изображение на экране монитора. Значения отношения от 45 до 60 дБ соответствуют приемлемому качеству видеосигнала, значение менее 40 дБ означает высокий уровень шумов в видеосигнале и, как следствие, низкое качество видеоизображения.

См. также[править | править код]

Шумопонижение
Шум квантования
PSNR
SFDR
Коэффициент шума (шум-фактор, фактор шума)
Зашумленные данные (англ.) (рус.
Феномен информационного шума

Примечания[править | править код]

Источник

From Wikipedia, the free encyclopedia

Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in decibels. A ratio higher than 1:1 (greater than 0 dB) indicates more signal than noise.

SNR is an important parameter that affects the performance and quality of systems that process or transmit signals, such as communication systems, audio systems, radar systems, imaging systems, and data acquisition systems. A high SNR means that the signal is clear and easy to detect or interpret, while a low SNR means that the signal is corrupted or obscured by noise and may be difficult to distinguish or recover. SNR can be improved by various methods, such as increasing the signal strength, reducing the noise level, filtering out unwanted noise, or using error correction techniques.

SNR also determines the maximum possible amount of data that can be transmitted reliably over a given channel, which depends on its bandwidth and SNR. This relationship is described by the Shannon–Hartley theorem, which is a fundamental law of information theory.

SNR can be calculated using different formulas depending on how the signal and noise are measured and defined. The most common way to express SNR is in decibels, which is a logarithmic scale that makes it easier to compare large or small values. Other definitions of SNR may use different factors or bases for the logarithm, depending on the context and application.

Definition[edit]

Signal-to-noise ratio is defined as the ratio of the power of a signal (meaningful input) to the power of background noise (meaningless or unwanted input):

$mathrm{SNR} = frac{P_mathrm{signal}}{P_mathrm{noise}},$

where P is average power. Both signal and noise power must be measured at the same or equivalent points in a system, and within the same system bandwidth.

Depending on whether the signal is a constant (s) or a random variable (S), the signal-to-noise ratio for random noise N becomes:^[1]

${displaystyle mathrm {SNR} ={frac {s^{2}}{mathrm {E} [N^{2}]}}}$

where E refers to the expected value, i.e. in this case the mean square of N,
or

${displaystyle mathrm {SNR} ={frac {mathrm {E} [S^{2}]}{mathrm {E} [N^{2}]}}}$

If the noise has expected value of zero, as is common, the denominator is its variance, the square of its standard deviation σ_N.

The signal and the noise must be measured the same way, for example as voltages across the same impedance. The root mean squares can alternatively be used in the ratio:

$mathrm{SNR} = frac{P_mathrm{signal}}{P_mathrm{noise}} = left ( frac{A_mathrm{signal}}{A_mathrm{noise} } right )^2,$

where A is root mean square (RMS) amplitude (for example, RMS voltage).

Decibels[edit]

Because many signals have a very wide dynamic range, signals are often expressed using the logarithmic decibel scale. Based upon the definition of decibel, signal and noise may be expressed in decibels (dB) as

$P_{{mathrm {signal,dB}}}=10log _{{10}}left(P_{{mathrm {signal}}}right)$

and

$P_{{mathrm {noise,dB}}}=10log _{{10}}left(P_{{mathrm {noise}}}right).$

In a similar manner, SNR may be expressed in decibels as

${mathrm {SNR_{{dB}}}}=10log _{{10}}left({mathrm {SNR}}right).$

Using the definition of SNR

${mathrm {SNR_{{dB}}}}=10log _{{10}}left({frac {P_{{mathrm {signal}}}}{P_{{mathrm {noise}}}}}right).$

Using the quotient rule for logarithms

$10 log_{10} left ( frac{P_mathrm{signal}}{P_mathrm{noise}} right ) = 10 log_{10} left ( P_mathrm{signal} right ) - 10 log_{10} left ( P_mathrm{noise} right ).$

Substituting the definitions of SNR, signal, and noise in decibels into the above equation results in an important formula for calculating the signal to noise ratio in decibels, when the signal and noise are also in decibels:

${mathrm {SNR_{{dB}}}}={P_{{mathrm {signal,dB}}}-P_{{mathrm {noise,dB}}}}.$

In the above formula, P is measured in units of power, such as watts (W) or milliwatts (mW), and the signal-to-noise ratio is a pure number.

However, when the signal and noise are measured in volts (V) or amperes (A), which are measures of amplitude,^{[note 1]} they must first be squared to obtain a quantity proportional to power, as shown below:

$mathrm{SNR_{dB}} = 10 log_{10} left [ left ( frac{A_mathrm{signal}}{A_mathrm{noise}} right )^2 right ] = 20 log_{10} left ( frac{A_mathrm{signal}}{A_mathrm{noise}} right ) = 2 left ( {A_mathrm{signal,dB} - A_mathrm{noise,dB}}right ).$

Dynamic range[edit]

The concepts of signal-to-noise ratio and dynamic range are closely related. Dynamic range measures the ratio between the strongest un-distorted signal on a channel and the minimum discernible signal, which for most purposes is the noise level. SNR measures the ratio between an arbitrary signal level (not necessarily the most powerful signal possible) and noise. Measuring signal-to-noise ratios requires the selection of a representative or reference signal. In audio engineering, the reference signal is usually a sine wave at a standardized nominal or alignment level, such as 1 kHz at +4 dBu (1.228 V_RMS).

SNR is usually taken to indicate an average signal-to-noise ratio, as it is possible that instantaneous signal-to-noise ratios will be considerably different. The concept can be understood as normalizing the noise level to 1 (0 dB) and measuring how far the signal ‘stands out’.

Difference from conventional power[edit]

In physics, the average power of an AC signal is defined as the average value of voltage times current; for resistive (non-reactive) circuits, where voltage and current are in phase, this is equivalent to the product of the rms voltage and current:

$mathrm{P} = V_mathrm{rms}I_mathrm{rms}$

$mathrm{P}= frac{V_mathrm{rms}^{2}}{R} = I_mathrm{rms}^{2} R$

But in signal processing and communication, one usually assumes that ^[3] so that factor is usually not included while measuring power or energy of a signal. This may cause some confusion among readers, but the resistance factor is not significant for typical operations performed in signal processing, or for computing power ratios. For most cases, the power of a signal would be considered to be simply

${displaystyle mathrm {P} =V_{mathrm {rms} }^{2}}$

Alternative definition[edit]

An alternative definition of SNR is as the reciprocal of the coefficient of variation, i.e., the ratio of mean to standard deviation of a signal or measurement:^[4]^[5]

$mathrm{SNR} = frac{mu}{sigma}$

where is the signal mean or expected value and sigma is the standard deviation of the noise, or an estimate thereof.^{[note 2]} Notice that such an alternative definition is only useful for variables that are always non-negative (such as photon counts and luminance), and it is only an approximation since ${displaystyle operatorname {E} left[X^{2}right]=sigma ^{2}+mu ^{2}}$ . It is commonly used in image processing,^[6]^[7]^[8]^[9] where the SNR of an image is usually calculated as the ratio of the mean pixel value to the standard deviation of the pixel values over a given neighborhood.

Sometimes^{[further explanation needed]} SNR is defined as the square of the alternative definition above, in which case it is equivalent to the more common definition:

${displaystyle mathrm {SNR} ={frac {mu ^{2}}{sigma ^{2}}}}$

This definition is closely related to the sensitivity index or d‘, when assuming that the signal has two states separated by signal amplitude , and the noise standard deviation sigma does not change between the two states.

The Rose criterion (named after Albert Rose) states that an SNR of at least 5 is needed to be able to distinguish image features with certainty. An SNR less than 5 means less than 100% certainty in identifying image details.^[5]^[10]

Yet another alternative, very specific, and distinct definition of SNR is employed to characterize sensitivity of imaging systems; see Signal-to-noise ratio (imaging).

Related measures are the “contrast ratio” and the “contrast-to-noise ratio”.

Modulation system measurements[edit]

Amplitude modulation[edit]

Channel signal-to-noise ratio is given by

${mathrm {(SNR)_{{C,AM}}}}={frac {A_{C}^{2}(1+k_{a}^{2}P)}{2WN_{0}}}$

where W is the bandwidth and k_a is modulation index

Output signal-to-noise ratio (of AM receiver) is given by

$mathrm{(SNR)_{O,AM}} = frac{A_c^2 k_a^2 P} {2 W N_0}$

Frequency modulation[edit]

Channel signal-to-noise ratio is given by

$mathrm{(SNR)_{C,FM}} = frac{A_c^2} {2 W N_0}$

Output signal-to-noise ratio is given by

$mathrm{(SNR)_{O,FM}} = frac{A_c^2 k_f^2 P} {2 N_0 W^3}$

Noise reduction[edit]

Recording from a thermogravimetric analysis device with poor mechanical isolation; the middle of the plot shows lower noise due to reduced human activity at night.

All real measurements are disturbed by noise. This includes electronic noise, but can also include external events that affect the measured phenomenon — wind, vibrations, the gravitational attraction of the moon, variations of temperature, variations of humidity, etc., depending on what is measured and of the sensitivity of the device. It is often possible to reduce the noise by controlling the environment.

Internal electronic noise of measurement systems can be reduced through the use of low-noise amplifiers.

When the characteristics of the noise are known and are different from the signal, it is possible to use a filter to reduce the noise. For example, a lock-in amplifier can extract a narrow bandwidth signal from broadband noise a million times stronger.

When the signal is constant or periodic and the noise is random, it is possible to enhance the SNR by averaging the measurements. In this case the noise goes down as the square root of the number of averaged samples.

Digital signals[edit]

When a measurement is digitized, the number of bits used to represent the measurement determines the maximum possible signal-to-noise ratio. This is because the minimum possible noise level is the error caused by the quantization of the signal, sometimes called quantization noise. This noise level is non-linear and signal-dependent; different calculations exist for different signal models. Quantization noise is modeled as an analog error signal summed with the signal before quantization (“additive noise”).

This theoretical maximum SNR assumes a perfect input signal. If the input signal is already noisy (as is usually the case), the signal’s noise may be larger than the quantization noise. Real analog-to-digital converters also have other sources of noise that further decrease the SNR compared to the theoretical maximum from the idealized quantization noise, including the intentional addition of dither.

Although noise levels in a digital system can be expressed using SNR, it is more common to use E_b/N_o, the energy per bit per noise power spectral density.

The modulation error ratio (MER) is a measure of the SNR in a digitally modulated signal.

Fixed point[edit]

For n-bit integers with equal distance between quantization levels (uniform quantization) the dynamic range (DR) is also determined.

Assuming a uniform distribution of input signal values, the quantization noise is a uniformly distributed random signal with a peak-to-peak amplitude of one quantization level, making the amplitude ratio 2ⁿ/1. The formula is then:

$mathrm{DR_{dB}} = mathrm{SNR_{dB}} = 20 log_{10}(2^n) approx 6.02 cdot n$

This relationship is the origin of statements like “16-bit audio has a dynamic range of 96 dB”. Each extra quantization bit increases the dynamic range by roughly 6 dB.

Assuming a full-scale sine wave signal (that is, the quantizer is designed such that it has the same minimum and maximum values as the input signal), the quantization noise approximates a sawtooth wave with peak-to-peak amplitude of one quantization level^[11] and uniform distribution. In this case, the SNR is approximately

${displaystyle mathrm {SNR_{dB}} approx 20log _{10}(2^{n}{textstyle {sqrt {3/2}}})approx 6.02cdot n+1.761}$

Floating point[edit]

Floating-point numbers provide a way to trade off signal-to-noise ratio for an increase in dynamic range. For n bit floating-point numbers, with n-m bits in the mantissa and m bits in the exponent:

$mathrm{DR_{dB}} = 6.02 cdot 2^m$

$mathrm{SNR_{dB}} = 6.02 cdot (n-m)$

Note that the dynamic range is much larger than fixed-point, but at a cost of a worse signal-to-noise ratio. This makes floating-point preferable in situations where the dynamic range is large or unpredictable. Fixed-point’s simpler implementations can be used with no signal quality disadvantage in systems where dynamic range is less than 6.02m. The very large dynamic range of floating-point can be a disadvantage, since it requires more forethought in designing algorithms.^[12]^{[note 3]}^{[note 4]}

Optical signals[edit]

Optical signals have a carrier frequency (about 200 THz and more) that is much higher than the modulation frequency. This way the noise covers a bandwidth that is much wider than the signal itself. The resulting signal influence relies mainly on the filtering of the noise. To describe the signal quality without taking the receiver into account, the optical SNR (OSNR) is used. The OSNR is the ratio between the signal power and the noise power in a given bandwidth. Most commonly a reference bandwidth of 0.1 nm is used. This bandwidth is independent of the modulation format, the frequency and the receiver. For instance an OSNR of 20 dB/0.1 nm could be given, even the signal of 40 GBit DPSK would not fit in this bandwidth. OSNR is measured with an optical spectrum analyzer.

Types and abbreviations[edit]

Signal to noise ratio may be abbreviated as SNR and less commonly as S/N. PSNR stands for peak signal-to-noise ratio. GSNR stands for geometric signal-to-noise ratio.^{[citation needed]} SINR is the signal-to-interference-plus-noise ratio.

Other uses[edit]

While SNR is commonly quoted for electrical signals, it can be applied to any form of signal, for example isotope levels in an ice core, biochemical signaling between cells, or financial trading signals. The term is sometimes used metaphorically to refer to the ratio of useful information to false or irrelevant data in a conversation or exchange. For example, in online discussion forums and other online communities, off-topic posts and spam are regarded as noise that interferes with the signal of appropriate discussion.^[13]

Notes[edit]

^ The connection between optical power and voltage in an imaging system is linear. This usually means that the SNR of the electrical signal is calculated by the 10 log rule. With an interferometric system, however, where interest lies in the signal from one arm only, the field of the electromagnetic wave is proportional to the voltage (assuming that the intensity in the second, the reference arm is constant). Therefore the optical power of the measurement arm is directly proportional to the electrical power and electrical signals from optical interferometry are following the 20 log rule.^[2]
^ The exact methods may vary between fields. For example, if the signal data are known to be constant, then can be calculated using the standard deviation of the signal. If the signal data are not constant, then can be calculated from data where the signal is zero or relatively constant.
^ Often special filters are used to weight the noise: DIN-A, DIN-B, DIN-C, DIN-D, CCIR-601; for video, special filters such as comb filters may be used.
^ Maximum possible full scale signal can be charged as peak-to-peak or as RMS. Audio uses RMS, Video P-P, which gave +9 dB more SNR for video.

References[edit]

^ Charles Sherman; John Butler (2007). Transducers and Arrays for Underwater Sound. Springer Science & Business Media. p. 276. ISBN 9780387331393.
^ Michael A. Choma, Marinko V. Sarunic, Changhuei Yang, Joseph A. Izatt. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Optics Express, 11(18). Sept 2003.
^ Gabriel L. A. de Sousa; George C. Cardoso (18 June 2018). “A battery-resistor analogy for further insights on measurement uncertainties”. Physics Education. IOP Publishing. 53 (5): 055001. arXiv:1611.03425. Bibcode:2018PhyEd..53e5001D. doi:10.1088/1361-6552/aac84b. S2CID 125414987. Retrieved 5 May 2021.
^
D. J. Schroeder (1999). Astronomical optics (2nd ed.). Academic Press. p. 278. ISBN 978-0-12-629810-9., p.278
^ ^a ^b Bushberg, J. T., et al., The Essential Physics of Medical Imaging, (2e). Philadelphia: Lippincott Williams & Wilkins, 2006, p. 280.
^ Rafael C. González, Richard Eugene Woods (2008). Digital image processing. Prentice Hall. p. 354. ISBN 978-0-13-168728-8.
^ Tania Stathaki (2008). Image fusion: algorithms and applications. Academic Press. p. 471. ISBN 978-0-12-372529-5.
^ Jitendra R. Raol (2009). Multi-Sensor Data Fusion: Theory and Practice. CRC Press. ISBN 978-1-4398-0003-4.
^ John C. Russ (2007). The image processing handbook. CRC Press. ISBN 978-0-8493-7254-4.
^
Rose, Albert (1973). Vision – Human and Electronic. Plenum Press. p. 10. ISBN 9780306307324. […] to reduce the number of false alarms to below unity, we will need […] a signal whose amplitude is 4–5 times larger than the rms noise.
^ Defining and Testing Dynamic Parameters in High-Speed ADCs — Maxim Integrated Products Application note 728
^ Fixed-Point vs. Floating-Point DSP for Superior Audio — Rane Corporation technical library
^ Breeding, Andy (2004). The Music Internet Untangled: Using Online Services to Expand Your Musical Horizons. Giant Path. p. 128. ISBN 9781932340020.

External links[edit]

Walt Kester, Taking the Mystery out of the Infamous Formula,”SNR = 6.02N + 1.76dB,” and Why You Should Care (PDF), Analog Devices, archived (PDF) from the original on 2022-10-09, retrieved 2019-04-10
ADC and DAC Glossary – Maxim Integrated Products
Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so you don’t get lost in the noise floor – Analog Devices
The Relationship of dynamic range to data word size in digital audio processing
Calculation of signal-to-noise ratio, noise voltage, and noise level
Learning by simulations – a simulation showing the improvement of the SNR by time averaging
Dynamic Performance Testing of Digital Audio D/A Converters
Fundamental theorem of analog circuits: a minimum level of power must be dissipated to maintain a level of SNR
Interactive webdemo of visualization of SNR in a QAM constellation diagram Institute of Telecommunicatons, University of Stuttgart
Bernard Widrow,István Kollár (2008-07-03), Quantization Noise: Roundoff Error in Digital Computation, Signal Processing, Control, and Communications, Cambridge University Press, Cambridge, UK, 2008. 778 p., ISBN 9780521886710
Quantization Noise Widrow & Kollár Quantization book page with sample chapters and additional material
Signal-to-noise ratio online audio demonstrator – Virtual Communications Lab

Источник

Обратите
внимание, что у нас есть прямоугольный
сигнал, а поверх него — шум, то о чём мы
говорили раньше — это шестерёнки. Как
можно измерить его? По сути, это отношение
энергии сигнала к энергии шума в данном
диапазоне,
или иногда вводят понятия отношение
мощности сигнала к мощности шума, так
называемый параметр S/N.

Когда
мы говорим про сигнал, то имеем в виду
тот сигнал, который регистрируем, который
пришёл к приёмнику. Мощность
этого сигнала зависит от расстояния,
причём зависимость обратно пропорциональная
квадрату расстояния, то есть чем дальше
передатчик находится от приёмника, тем
меньше принимаемая мощность. Ещё мощность
принятого сигнала зависит от мощности
излучённого сигнала,
то есть чем больше излучим, тем больше
примем, но в первой степени.

Обратите
внимание на два интересных параметра,
которые обозначаются латинскими буквами
G, — это коэффициенты
усиления передающей и принимающей
антенны.
Они показывают во сколько раз в данном
направлении антенна, которую используем,
сильнее излучает сигнал по сравнению
с антенной, которая во все стороны
излучает равномерно — изотропной
антенной.

Фактически
антенна
фокусирует энергию радиоволны в каком-то
направлении,
а в остальных ослабляет. Соответственно
G — это коэффициент усиления антенны в
данном направлении. Но мы предполагаем,
что сейчас антенны смотрят друг на друга
так, что их коэффициент усиления
максимальный.

Вообще
говоря, антенны и теория антенн — это
довольно интересная вещь, которой можно
посвятить отдельный семинар или лекцию.

Обратите внимание на уравнение:

Формула 1

В выражении для мощности принятого сигнала (P_{пр.сигнала}) в числителе находится излучаемая мощность (P_пер), коэффициент усиления передающей (G₁) и приёмной (G₂) антенны, λ — это длина волны, в знаменателе r – расстояние между передающей и приемной антеннами. Это уравнение фактически определяет дальность связи, поскольку оно связывает между собой параметры передатчика и приёмника.

А где же шум?

Формула 2. Уравнение мощности шума

Это уравнение мощности шума, обратите внимание, что в нём только три множителя: k, T и Δf.

k — это постоянная Больцмана, знакомая с уроков термодинамики. Обратите внимание: в радиосигнале присутствует постоянная Больцмана, которая была введена на уроках физики, когда вы проходили термодинамику, она была необходима в тот момент, когда вы определяли температуру и энергию, и мощность.

T — это температура шумов в Кельвинах.

Δf — это та полоса частот, в которой мы работаем. Я уже говорил про эти 3000 Гц, вот это они.

Тогда, чтобы понять, что такое отношение сигнал/шум, нужно мощность принятого сигнала поделить на мощность шума, получим уравнение в следующем виде, где в знаменателе появился множитель kTΔf:

Формула 3 (уравнение отношения Сигнал/Шум)

Это то уравнение, которое определяет дальность радиосвязи. Когда у вас слабый сигнал, а шум сильный, то есть когда это отношение становится единицей и меньше, то разобрать то, что говорится в толпе, услышать другой голос или, стоя у водопада, услышать кого-то достаточно сложно.

Если соотношение сигнал/шум больше единицы, например, два, три, то уже с этим можно работать и какую-то связь обеспечивать. Когда отношение становится намного меньше единицы, то выделить сигнал на фоне шумов становиться очень не простой, но интересной задачей.

Например, давайте посмотрим такой вариант. В 1977 году, 43 года назад, 5 сентября был запущен в открытый космос Вояджер 1. Когда его запускали, на него установили трёхметровую антенну и передатчик 20 Ватт.

Чтобы вы понимали, мощность сотовой вышки тоже примерно 20 Ватт. Через ряд гравитационных манёвров Вояджер сумел набрать третью космическую скорость и вылететь за пределы Солнечной системы. В настоящее время расстояние между Землёй и Вояджером примерно двадцать два миллиарда километров (22 000 000 000 км).

Чтобы было понимание, расстояние между Землёй и Солнцем сто пятьдесят миллионов километров (150 000 000 км), одна астрономическая единица.

Обратите внимание на формулу 3, которую рассмотрели, что дальность (r) стоит не в первой степени, а во второй, то есть мощность сигнала падает обратно пропорционально второй степени от дальности. За счёт чего тогда мы слышим Вояджер?

За счёт того, что антенны остро направлены, то есть имеют высокий коэффициент усиления. Оценим длину волны, на которой работает Вояджер, вспомним скорость света равна 3·10⁸ м/с, частота, на которой Вояджер связывается с Землёй — 8 ГГц (8·10⁹ Гц), так называемый икс-диапазон, таким образом, несложно посчитать требуемую величину.

Коэффициент усиления передающей антенны на Вояджере на этой длине волны шестьдесят три тысячи (63 000), то есть он фокусирует всю энергию в очень узкий диапазон, около четверти градуса. А коэффициент усиления антенны, которая расположена на Земле, двадцать один с половиной миллион (21 500 000). Вот за счёт таких мощных коэффициентов усиления передающей и приёмной антенны и за счёт точного наведения одной на другую и возможно обеспечение устойчивой связи.

Например, если подставить все данные параметры в уравнение, мы получим отношение сигнал-шум примерно равное двум, что позволяет обеспечить связь.

К сожалению, Вояджер улетает от нас всё дальше и дальше, и, конечно, в какой-то момент это отношение уменьшится ещё больше, примерно лет через десять. Но есть предположение, что Вояджер ещё раньше потеряется, потому что он находится на таком большом расстоянии от Земли, что Солнце становится всё меньше и меньше, а он позиционируется как раз по изображению Солнца. Если он потеряет Солнце, то может переключиться на какую-то другую звезду и перенаправит свою приёмную антенну, и мы, к сожалению, потеряем с ним связь.

Для размышления

Попробуйте вычисления для радиоканала между Вояджером и Землёй выполнить самостоятельно!

Материалы

Английская статья о том, что такое отношение сигнал/шум и как его рассчитывают в реальных условиях

Источник

Отношение сигнал/шум

К счастью или несчастью, чаще всего случается так, что сигналы, которые нужно измерить, перемешаны с шумами или помехами настолько сильно, что их даже трудно увидеть на осциллографе. В тех случаях, когда шумы не создают проблем, обнаружение сигнала может быть затруднено его собственной статистической природой, например при наблюдении за распадом ядер в слабом источнике радиоактивности за минуту на счетчик поступает всего несколько импульсов. И наконец, в том случае, когда сигнал обнаруживается нормально, может возникнуть необходимость усилить его для того, чтобы выполнить более точные измерения.

Во всех перечисленных случаях необходимо принять меры для улучшения отношения сигнал/шум. Все дальнейшие приемы направлены на то, чтобы сузить ширину полосы пропускания при обнаружении и сохранить тем самым нужный сигнал, сократив одновременно общее количество принимаемых шумовых сигналов.

Первое, что приходит на ум при разговоре о сужении полосы пропускания, — это использование на выходе простого фильтр НЧ для усреднения шума. В некоторых случаях этот прием может оказаться полезным, но в большинстве случаев толку от него будет мало по двум причинам.

Во-первых, сам сигнал может включать в себя некоторые высокочастотные составляющие или его центральная частота может лежать в области высоких частот.

Во-вторых, даже если сигнал на самом деле изменяется медленно или является статичным, никуда не денешься от того, что плотность шумового сигнала определяется величиной 1/f. Значит, сужение полосы пропускания и исключение из нее высокочастотных составляющих большой пользы не принесут. Электронные и физические системы требуют к себе особого подхода.

Известно несколько методов сужения полосы пропускания, которые получили широкое распространение на практике. Эти методы имеют следующие названия:

— усреднение сигнала,
— переходное усреднение,
— метод интегрирования,
— многоканальное уплотнение,
— амплитудный анализ импульсов,
— детектирование с захватом,
— фазовое детектирование.

Все эти методы предполагают, что сигнал является периодическим. Это условие не создает трудностей, так как почти всегда сигнал можно сделать периодическим. Каким же образом производят сужение полосы пропускания?

Усреднение сигнала и многоканальное усреднение

Отношение сигнал/шум можно существенно улучшить, если просуммировать повторяющийся сигнал во времени. Этот процесс принято называть «усреднением сигнала» и его часто используют для аналоговых сигналов. Рассмотрим сначала ситуацию, которая, может быть, не очень похожа на реальную, а именно последовательность импульсов, скорость которых пропорциональна изменению амплитуды некоторого колебания во времени.

Начнем с этого примера, так как с ним связаны наиболее простые расчеты. На самом деле такие примеры встречаются и в жизни, они характерны, например, для электронных систем, предназначенных для подсчетов импульсов, — детекторы элементарных частиц или фотоумножители для низких уровней света.

Многоканальные счетчики (уплотнители)

Начнем с многоканального уплотнения, так как этот метод лежит в основе всех остальных и, кроме того, с ним связаны простые и понятные количественные соотношения. Многоканальный счетчик-уплотнитель — это аппаратное средство, которое включает в себя набор запоминающих регистров (обычно 1024 или больше), каждый из которых может хранить число, значение которого может достигать миллиона (20 двоичных разрядов или 24 разряда при двоично-десятичном представлении) или около того.

На вход многоканального уплотнителя поступают импульсы (или аналоговые напряжения, о которых речь пойдет позже). Дополнительно на него поступает сигнал (импульс) выборки канала и многоразрядный адрес канала в виде параллельного кода. Всякий раз, когда появляется входной импульс, уплотнитель увеличивает на единицу содержимое памяти канала, к которому в этот момент производится обращение. Дополнительные входы позволяют производить сброс адреса, очистку памяти и т.п.

Для того чтобы можно было использовать многоканальный уплотнитель, необходимо, чтобы сигнал повторялся через некоторый интервал времени. Предположим, что наблюдаемое явление само по себе периодично и период равен Т. Хотя в большинстве случаев периодичность приходится организовывать собственными усилиями, в жизни все-таки можно найти примеры строго периодических явлений, например излучение света пульсаром.

Допустим, что на вход поступают импульсы со скоростью, пропорциональной изменению сигнала во времени, и фоновые шумовые импульсы с высокой скоростью, т. е. импульсы, случайно распределенные во времени (это предположение снова вполне справедливо для пульсаров, сигналы от которых смешиваются со светом ночного неба).

Если посылать синхроимпульсы на входы выборки и сброса каналов, создается такой режим работы, при котором многоканальный уплотнитель подключается к каждому из 1024 каналов один раз за каждые Т секунд и при каждом обращении в память каналов добавляется новая величина (сигнал плюс шум). С течением времени сигнал будет увеличивать содержимое памяти по всем каналам, так как время прохода через весь набор каналов выбрано таким, что оно совпадает с периодом исследуемого сигнала. Следовательно, сигнал добавляется сам к себе и увеличивает накопленную сумму при каждом повторении.

Определение отношения сигнал/шум

Рассмотрим, что же происходит. Пусть скорость фоновых импульсов такова, что при каждом подключении к сумме в каждом канале добавляется величина n_ф, а сигнал добавляет величину n_с в тех каналах, на которые приходятся его пики:

Отношение сигнал/шум. Многоканальное усреднение сигнала

Многоканальное усреднение сигнала (импульсный вход). а – «сигнал» (если аналоговое измерение возможно), б – отчеты по сигналу (доказательство того, что число импульсов пропорционально амплитуде «сигнала»), в – фоновые отсчеты (доказательство того, что фоновые импульсы распределены случайно), г – за время одного прохода на интервале «всплеска» сигнала сигнал добавляет в среднем nс отсчетов, за время одного прохода на любом интервале фон добавляет в среднем nф отсчетов.

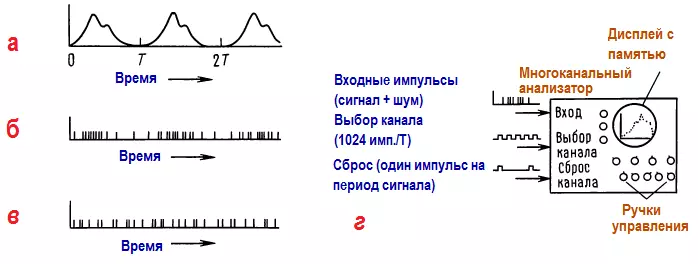
Допустим, что отношение сигнал/шум является плохим, т. е. n_с<<n_ф, а это значит, что большая часть накопленной суммы определяется шумом, а не сигналом. Если теперь изобразить содержимое памяти графически, то сигналу будут соответствовать «всплески» на фоне шума. Можно ли считать, что число импульсов в канале сигнала должно быть сравнимо с числом импульсов шума в этом же канале? Нет, это предположение неверно, так как средняя величина суммы, обусловленной шумом, совершенно случайна. Играет роль лишь величина флуктуаций этой суммы относительно среднего значения.

Следовательно, плохое отношение сигнал/шум на самом деле характеризуется соотношением n_с <<√ n_ф, которое означает, что в одном проходе по каналам сигнал нельзя отличить от шума, представленного на графике волнистой линией. Для простоты расчетов допустим, что n_с = 10 и n_ф = 1000. Тогда за один цикл работы предварительно сброшенный многоканальный уплотнитель накопит в каждом канале в среднем величину 1000, а в каналах, соответствующих пикам сигналов, будет присутствовать еще дополнительная величина 10.

В связи с тем, что флуктуации в канале оцениваются величиной 31 (корень квадратный из 1000), то после первого цикла «всплеск» сигнала будет потерян на фоне шума. После, например, 1000 циклов средняя сумма в канале составит примерно 1 000 000, а флуктуации будут оцениваться величиной 1000. В каналах, соответствующих пикам сигналов, дополнительная сумма будет равна 10000 (1000 циклов х 10 имп./цикл) для отношения сигнал/шум, равного 10. Отсюда видно, что сигнал будет выделяться на фоне шума.

Пример: резонанс Мессбауэра

Следующий рисунок иллюстрирует результаты как раз такого анализа для резонансного сигнала Мессбауэра. Сигнал состоит из шести отрицательных выбросов, которые возникают, когда на железную фольгу, обогащенную изотопом железа-57, воздействует гамма-излучение от радиоактивного кобальта-57.

Спектр поглощения Мессбауэра, иллюстрирующий эффект усреднения сигнала

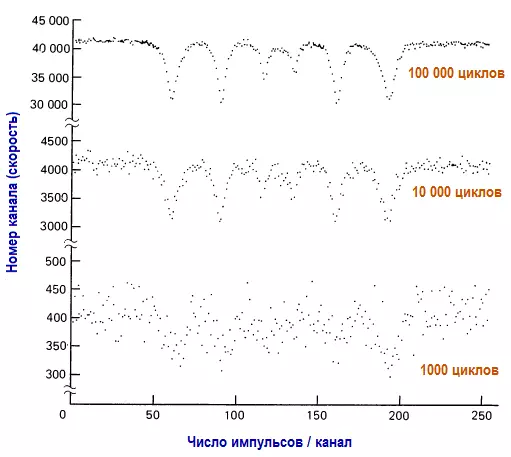
В данном случае приблизительно n_ф = 0,4 и n_с = 0,1, что соответствует плохому отношению сигнал/шум. Сигнал Мессбауэра полностью теряется на фоне шума после 10 или 100 циклов уплотнения. Он становится различимым лишь после примерно 1000 циклов. Приведенные результаты соответствуют 1000, 10000 и 100000 циклам, причем масштаб для каждого графика выбран так, чтобы величина сигнала сохранялась одинаковой. Обратите внимание, что «базовая ось» графика поднимается по мере того, как стабилизируется шум и одновременно заметно улучшается отношение сигнал/шум.

Нетрудно заметить, чем обусловлено увеличение отношения амплитуды сигнала к фоновым флуктуациям сигнала (шума) с течением времени. Амплитуда сигнала увеличивается пропорционально времени t. Среднее число фоновых импульсов (базовая ось) также увеличивается пропорционально времени t, но при этом флуктуации в количестве импульсов фона (шум) увеличиваются только пропорционально корню квадратному из t. Следовательно, отношение сигнала к флуктуациям фона увеличивается как отношение t к корню квадратному из t. Иными словами, увеличение отношения сигнал/шум пропорционально корню квадратному из времени.

Многоканальный анализ аналоговых сигналов (усреднение сигнала)

Тот же метод можно использовать и для анализа аналоговых сигналов, нужно всего лишь подключить на вход преобразователь напряжения в частоту. В коммерческих схемах многоканальных уплотнителей часто бывает предусмотрена возможность задания аналогового или импульсного режима работы. Такие устройства часто называют усреднителями сигнала или переходными усреднителями. Одна из фирм (ТМС) использовала для этих устройств название CAT (сокращение от английских слов computer of averged transients — вычислитель среднего значения поступающих сигналов), которое кое-где вошло в обиход.

Можно создать полностью аналоговый многоканальный уплотнитель, если для хранения накапливаемого сигнала использовать набор интеграторов. Наиболее простой интегратор представляет собой аналоговый усреднитель сигнала с единственным «скользящим каналом». Если учесть, что стоимость цифровой памяти в последнее десятилетие существенно уменьшилась, то оказывается, что нет смысла использовать аналоговые устройства для усреднения сигналов. За исключением, может быть, некоторых особых случаев.

Многоканальное уплотнение как средство сужения полосы пропускания.

В начале обсуждения предполагалось, что существует прямая связь между «магическими» методами улучшения отношения сигнал/шум и сужением полосы пропускания при измерениях. Эту связь нетрудно проследить. Представим себе, что на входе действует некоторый посторонний сигнал (помехи) с периодом Т’, который немного отличается от периода основного сигнала T.

После нескольких циклов этот сигнал также начинает накапливаться, угрожая неприятностями. Но немного терпения, и можно увидеть, что постепенно соответствующие ему всплески начинают «расползаться» и увеличивать содержимое счетчиков по всем каналам. Он распространится по всем каналам через время t=1/∆f, где ∆f — это разность частот 1/Т=1/Т’ основного и постороннего сигналов.

Иными словами, накапливая данные в течение времени t (определяемого согласно приведенному выше выражению), можно добиться, чтобы посторонний сигнал равномерно распределился по всем каналам. Если взглянуть на полученный результат с другой точки зрения, то можно сказать, что ширина полосы измеряемых частот уменьшилась приблизительно на величину ∆f = 1/t после накопления данных в течение времени t.

Итак, если проводить накопление, то ширина полосы пропускания уменьшится, а все посторонние сигналы будут исключены! На деле исключается также большая часть шума, так как он равномерно распределен по всем частотам. С этой точки зрения эффект многоканального уплотнения проявляется в сужении полосы принимаемых частот, при этом мощность принимаемого сигнала остается неизменной, а мощность шума заметно снижается.

А теперь выполним необходимые расчеты. Через время t ширина полосы пропускания уменьшается на величину ∆f = 1/t. Если плотность мощности шума p_ш составляет ватт на герц, а мощность сигнала P_с не изменяется в пределах измеряемой полосы частот, то через время t отношение сигнал/шум составит K_с/ш= 101og(P_ct/ p_ш) (амплитуда сигнала пропорциональна корню квадратному из t (3 дБ на каждое удвоение t).

Получение периодического сигнала

В самом начале было упомянуто, что для всех методов усреднения сигнала необходимо, чтобы сигнал повторялся многократно, только тогда можно будет уменьшить отношение сигнал/шум. Так как в большинстве случаев приходится измерять периодические по своей природе функции, то обычно повторение сигнала вызывают принудительным путем. Для этого известно немало приемов, которые зависят от конкретных случаев измерений. Проще всего привести несколько примеров, а не пытаться вывести правила для всех случаев жизни.

Измеряемую величину, которая зависит от некоторого внешнего параметра, очень просто сделать периодической — для этого нужно сделать изменяемым этот внешний параметр. Рассмотрим ядерный магнитный резонанс.

Резонансная частота изменяется по линейному закону под воздействием приложенного поля, поэтому используют следующий стандартный прием — модулируют ток в небольшой дополнительной обмотке. В случае резонанса Мессбауэра изменяется интенсивность источника. В случае квадропульного резонанса можно произвести развертку генератора.

В других случаях можно использовать собственный явно выраженный переходный процесс, а запуск производить внешним сигналом. Классическим примером служит импульс деполяризации в нервном волокне. Для того чтобы получить чистый импульс такого рода, нужно просто возбудить нерв внешним импульсом напряжения и одновременно запустить многоканальный уплотнитель (или произвести «упреждающий» запуск уплотнителя, а затем возбудить нерв задержанным импульсом). В этом случае период повторения устанавливается достаточно большим для того, чтобы перед приходом следующего импульса полностью завершилось восстановление нерва.

Последний пример дает наглядное представление о том, что источником информации для усреднения сигнала служит повторяющееся явление. Если подопытная лягушка отправилась на небеса, то чему бы ни было равно отношение сигнал/шум его уже не измерить!

Следует отметить, что те явления, в которых наблюдается явно выраженная собственная периодичность, на самом деле труднее всего измерить, так как нужно точно знать, чему равен период. В качестве примера рассмотрим «световую кривую» (зависимость яркости от времени), которая представлена на рисунке:

Зависимость яркости пульсара Крабовидной туманности от времени (световая кривая)

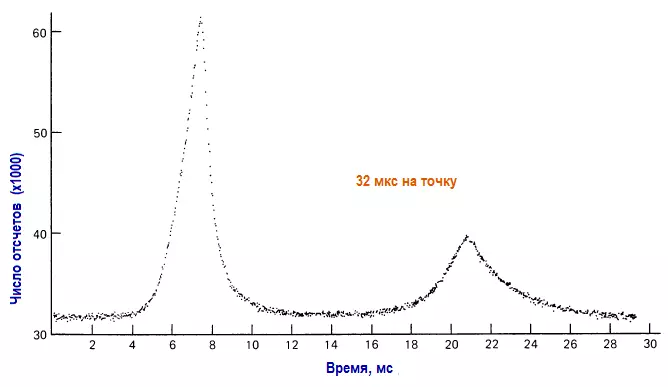
Эта кривая получена с помощью многоканального уплотнителя, подключенного к выходу фотоумножителя, установленного в фокусе 60-дюймового телескопа, и работающего совершенно синхронно с вращением пульсара. Даже при наличии телескопа такого размера требовалось в среднем около 5 млн. циклов для получения такой чистой кривой, так как среднее число фотонов для каждого полного импульса пульсара приблизительно равно 1. Такая малая величина периода предъявляет очень высокие требования к схеме переключения каналов уплотнителя, в данном случае требовалась стабильность порядка одной миллиардной доли и предусматривалась подстройка часов для компенсации неравномерности вращения Земли.

Стоит еще раз подчеркнуть, что суть метода усреднения сигналов состоит в сужении полосы пропускания, а для этого продолжительность эксперимента должна быть большой. По горизонтальной оси откладывается время эксперимента. Конкретная скорость сканирования или модуляции обычно большого значения не имеет, так как она достаточно далека от величины 1/f, характерной для шума вблизи частот постоянного тока.

Модуляцию можно представить себе как простой сдвиг сигнала, который необходимо измерить, из области частот постоянного тока в область модулирующей частоты. Эффект длительного накопления данных сводится в этом случае к концентрированию полосы шириной ∆f = 1/Т на частоте f_мод, а не к смещению ее в область частот постоянного тока.

Обнаружение путем захвата

Этот метод достаточно сложен для понимания. Для того чтобы разобраться с ним, необходимо уделить немного внимания фазовому детектору, рассмотренному ранее.

В рассмотренном ранее фазовом детекторе, выходное напряжение пропорционально разности фаз между двумя цифровыми сигналами (логическими уровнями). Для того чтобы перейти к обнаружению путем захвата, необходимо познакомиться с линейными фазовыми детекторами, так как почти всегда приходится иметь дело с аналоговыми уровнями напряжения.

Основная схема представлена на рисунке.

Фазовый детектор для линейных входных сигналов. Эта принципиальная схема использована в микросхеме AD630

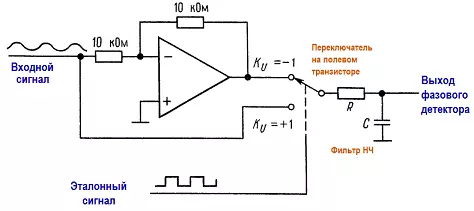
Аналоговый сигнал проходит через линейный усилитель, знак коэффициента усиления которого изменяется на противоположный под воздействием прямоугольного опорного сигнала, управляющего переключателем на полевом транзисторе. Выходной сигнал проходит через RС-фильтр низких частот. Вот и все, о чем можно здесь сказать. Посмотрим, что же это нам дает.

Выход фазового детектора

Для того чтобы проанализировать работу фазового детектора, допустим, что на вход подается сигнал Е_с cos (ωt + ϕ) и соответствующий ему опорный сигнал представляет собой прямоугольное колебание. В тех точках, где функция sin ωt проходит через нуль, происходит изменение полярности прямоугольного колебания, т. е. в точках t = 0, π/ω, 2π/ω и т. д. Предположим далее, что мы усредняем выходной сигнал U_вых, пропуская его через фильтр низких частот, постоянная времени которого превышает величину одного периода Ϯ= RС » Т= 2π/ω. Тогда выход фильтра низких частот описывается следующим выражением:

<E_ccos(ωt + ϕ)>|₀^π/ω — < E_ccos(ωt + ϕ)>|₀^2π/ω

где скобки <> использованы для представления среднего значения, а знак «минус» объясняется тем, что в двух половинах периода сигнала U_oп коэффициент усиления имеет противоположные знаки.

Полученный результат позволяет сделать следующий вывод:

для входного сигнала, имеющего такую же частоту, что и опорный сигнал, усредненный выходной сигнал пропорционален амплитуде E_c и синусу относительного сдвига фазы.

Прежде чем идти дальше, нужно получить еще один результат: каким будет выходное напряжение в случае, когда частота входного сигнала близка (но не равна) частоте опорного сигнала? Ответить на этот вопрос нетрудно, используя предыдущие выражения и приняв, что теперь величина ϕ есть медленно меняющаяся переменная. При частоте, слегка отличающейся от опорной (на ∆ω), имеем:

cos(ω + ∆ω)t = cos(ωt + ϕ); ϕ = t∆ω

Теперь выходной сигнал представляет собой медленно меняющуюся синусоиду:

U_вых = (2E_c/π)sin(∆ω)t,

которая проходит через фильтр НЧ почти без изменений при условии, что ∆ω <1/Ϯ = 1/RC, и значительно ослабляется при условии, что ω <1/Ϯ.

Метод захвата

Теперь для увеличения чувствительности введем так называемый усилитель захвата (фазочувствительный усилитель). Сначала искусственно создадим слабый периодический сигнал, как обсуждалось выше, взяв его частоту вблизи 100 Гц. Этот слабый сигнал, засоренный шумами, усилим и продетектируем по фазе относительно сигнала модуляции. Рассмотрим рис:

Обнаружение путем захвата

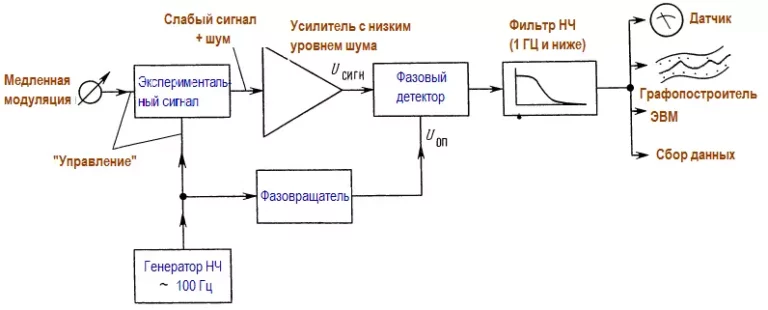
Будем проводить опыт при «двойном управлении» сигналом:

во-первых, должна быть быстрая модуляция, которая нужна для фазового детектирования,

во-вторых, медленная развертка по интересующим нас параметрам сигнала.

при ядерном магнитном резонансе, например, для быстрой модуляции можно использовать модуляцию магнитного поля небольшим сигналом с частотой 100 Гц, а для медленной -использовать 10-минутную развертку, охватывающую все резонансы.

Фазосдвигающая цепь отрегулирована так, чтобы выходной сигнал был максимальным, а постоянная времени фильтра низких частот имеет достаточно большое значение, которое выбирается с учетом отношения сигнал/шум. Спад характеристики фильтра низких частот определяет ширину полосы пропускания, например если сопрягающая частота равна 1 Гц, то схема будет пропускать посторонние сигналы и шум, частота которых лежит в пределе 1 Гц относительно частоты исследуемого сигнала (100 ± 1 Гц).

Ширину полосы пропускания ограничивает также скорость медленной модуляции, так как нет смысла устанавливать для развертки более короткое время, чем время отклика фильтра. Обычно величина постоянной времени лежит в пределах от долей секунды до десятков секунд, и часто для медленной модуляции используют часовой механизм, которым управляют с помощью выведенной куда-нибудь ручки.

Обратите внимание, что обнаружение путем захвата фазы сводится к сужению полосы пропускания, причем ширину полосы пропускания устанавливает оконечный фильтр НЧ. Как и в случае с усреднением сигнала, эффект модуляции заключается в центрировании сигнала на частоте быстрой модуляции, а не на частоте постоянного тока, при этом удается устранить шумы с фактором 1/ f (фликкер-шум, дрейф, дребезг и т.п.).

Два метода быстрой модуляции

Существуют два способа быстрой модуляции: в качестве модулирующего колебания можно использовать очень слабое синусоидальное колебание или очень сильное, по сравнению с искомым сигналом, прямоугольное колебание. Их иллюстрирует рисунок:

Методы модуляции при захвате. а – малый синусоидальный сигнал модуляции, б – большой прямоугольный сигнал модуляции.

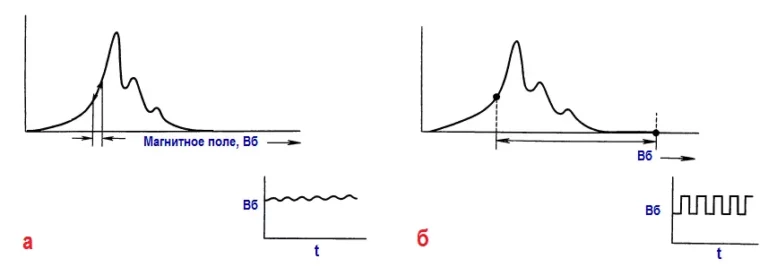
В первом случае выходной сигнал фазового детектора пропорционален наклону сигнала (т. е. его производной), а во втором случае — сигналу (при условии, что нет других спектральных линий, связанных с модулирующим колебанием). По этой причине все эти простые резонансные кривые, наблюдаемые при ядерном магнитном резонансе, выглядят как дисперсионные кривые:

Дифференцирование сигнала при обнаружении путем захвата

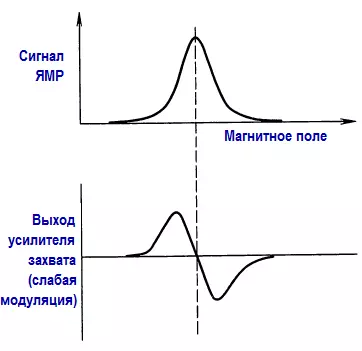
При модуляции прямоугольным колебанием с большим фазовым сдвигом существует хороший метод подавления сигнала прямого прохождения, применяемый в тех случаях, когда это явление создает трудности в работе. На следующем рисунке показано модулирующее колебание.

Схема модуляции для подавления сигнала прямого прохождения

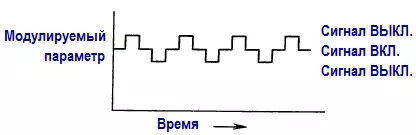
Сдвиги выше и ниже центрального значения уничтожают сигнал и создают модуляцию типа «включен/выключен» на удвоенной частоте по отношению к основной несущей. Этот метод предназначен для специальных случаев и не следует прибегать к нему ради красоты.

Модуляцию с прямоугольными колебаниями большой амплитуды очень часто используют в инфракрасной астрономии, где для переключения изображения инфракрасного источника приводят в движение вторичные зеркала телескопа. Этот метод популярен также в радиоастрономии и известен здесь под названием переключений Дикке.

Промышленные усилители с захватом имеют источники модулирующих колебаний с перестраиваемой частотой, следящий фильтр, оконечный фильтр с коммутируемой постоянной времени, высококачественный усилитель с низким уровнем шума и широким динамическим диапазоном, а также линейный фазовый детектор с хорошими характеристиками.

если бы шум не имел значения, то не нужно было бы и использовать обнаружение с захватом

Кроме того, они допускают возможность использования внешнего источника модуляции. С помощью ручки можно регулировать фазовый сдвиг, следовательно имеется возможность максимально увеличить обнаруженный сигнал. Весь прибор заключают в красивый корпус, на котором имеется шкала для считывания выходного сигнала.

Для того чтобы наглядно продемонстрировать возможности метода захвата фазы, существует следующий эксперимент. Используем захват фазы для выделения модулированного сигнала от небольшого светодиода, подобного тем, которые используют для индикации на панелях приборов. Частота модуляции имеет порядок несколько килогерц. Ток очень мал, и свечение диода при нормальном комнатном освещении можно заметить с трудом.

На расстоянии около 2 м установлен фототранзистор, направленный в сторону светодиода, а его выход подается на схему захвата фазы. Если свет в комнате выключить, то с фототранзистора на частоте модуляции будет сниматься очень слабый сигнал (смешанный с шумами). Сигнал легко обнаруживает схема захвата при условии, что постоянная времени равна нескольким секундам. Затем выключаем свет в комнате (флуоресцентное освещение), и в тот же момент фототранзистор начинает формировать колебания с частотой 120 Гц, амплитуда которых больше примерно на 50 дБ.

Теперь с помощью осциллографа обнаружить сигнал от светодиода невозможно, а схема захвата спокойно обнаруживает этот сигнал. Для того чтобы убедиться, что схема действительно работает, достаточно поместить руку между светодиодом и детектором. Впечатление огромное!

Амплитудный анализ импульсов

Работа анализатора амплитуды импульсов основана на простом расширении принципа работы многоканального уплотнителя. Этот прибор играет важную роль в ядерной и радиационной физике. Идея метода на редкость проста: импульсы, амплитуды которых лежат в некотором диапазоне, поступают на вход схемы пикового детектора с АЦП, которая преобразует относительную амплитуду импульса в адрес канала. Многоканальный уплотнитель затем наращивает выбранный адрес на единицу. В результате получаем график, который представляет собой гистограмму амплитуд импульсов. Вот и вся хитрость.

Широкое распространение анализаторов амплитуд импульсов обусловлено тем, что величина выходных импульсов многих датчиков заряженных частиц, рентгеновского и гамма-излучения пропорциональна энергии излучения, воспринятого датчиком.

примером могут служить пропорциональные счетчики, детекторы на твердом теле, детекторы с поверхностным барьером, сцинтилляторы, рассмотренные в детекторах элементарных частиц

Таким образом, анализатор амплитуды импульсов преобразует выход детектора в энергетический спектр.

Анализаторы амплитуды импульсов обычно разрабатывались как специальные приборы, в состав которых входили интегральные схемы и отдельные дискретные компоненты. В настоящее время все более широко стали использовать мини-компьютеры и быстродействующие АЦП с импульсным входом. При этом в нашем распоряжении оказываются разнообразные полезные для дела аппаратные и программные возможности ЭВМ, такие, как вычитание фоновых сигналов, энергетическая калибровка и идентификация линий, модули памяти, управление экспериментом в интерактивном режиме.

Это устройство заставляет микролуч потока протонов сканировать образец в двумерной плоскости, обнаруживает появившиеся рентгеновские лучи, сортирует их по химическим элементам и запоминает картину распределения по каждому элементу в образце. Одновременно есть возможность наблюдать рентгеновский спектр и само формирование картины распределения. Всем процессом управляет анализатор амплитуды импульсов, который и не подозревает, что на самом деле он представляет собой ЭВМ.

На входе анализатора амплитуды импульсов используется АЦП, с которым связана одна интересная особенность этой системы. Оказывается, что в данном случае нельзя использовать АЦП с последовательными приближениями, несмотря на его высокую скорость. Это связано с тем, что нельзя добиться точного равенства ширины каналов, плавная последовательность входных сигналов излучения даст волнистую базовую линию.

Во всех анализаторах амплитуды импульсов используют так называемый преобразователь Уилкинсона. Его принцип работы основан на преобразовании входного сигнала с единственным углом наклона — входной импульс заряжает конденсатор, который затем разряжается постоянным током, а во время разряда быстродействующий счетчик (обычно используется частота 200 МГц) подсчитывает адрес. Недостаток такого анализатора состоит в наличии «мертвой зоны», величина которой зависит от амплитуды последнего импульса, а его достоинство — в точном равенстве ширины каналов.

Входы многих анализаторов амплитуды импульсов позволяют использовать эти устройства в качестве многоканальных уплотнителей. А почему бы и нет? Все необходимые элементы здесь в наличии.

Преобразователи времени в амплитуду

В ядерной физике приходится определять распределение времени распада частиц с коротким временем жизни. Эту задачу помогает решить времяамплитудный преобразователь (ВАП), подключаемый на входе анализатора амплитуды импульсов. ВАП запускает генератор линейно изменяющегося сигнала, когда на один из его входов приходит импульс, и останавливает его, когда импульс появляется на другом входе. При этом происходит разряд конденсатора и формируется выходной импульс, пропорциональный интервалу времени между импульсами запуска и останова. Достигаемое при этом разрешение измеряется в пикосекундах. Рисунок иллюстрирует измерение продолжительности жизни мюона (неустойчивая элементарная частица с отрицательным электрическим зарядом и спином 1/2:

Отношение сигнал/шум. Измерение продолжительности жизни мюона на основе спектра временных интервалов

Измерение продолжительности жизни мюона на основе спектра временных интервалов (преобразователь времени в амплитуду + амплитудный анализатор импульсов)

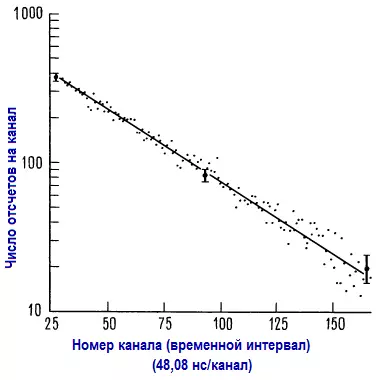
Измерение выполнено студентом путем определения времени задержки между захватом мюона космического излучения сцинтиллятором и его последующим распадом. Каждое обрабатываемое событие сопровождается вспышкой света, а ВАП используется для преобразования интервалов времени в импульсы. В приборе нашего студента распад космического мюона происходил в среднем один раз в 1 мин, поэтому для того, чтобы установить, что продолжительность жизни составляет 2,198 ±0,02 мкс, ему пришлось потратить 18 дней (более точным является значение 2,197134±0,00008 мкс).

Обратите внимание на использование логарифмического масштаба для построения графика и на систематическое уменьшение ошибки, пропорциональной n^1/2 (ошибки счета). Изображенный график соответствует распаду, который описывается выражением n(t)=n₀exp(— t/Ϯ).

Источник

Основы цифровой обработки сигналов: Виды шумов, отношение сигнал/шум, Статистическая обработка сигнала, Корреляционная функция

Рассмотрены 3 темы по основам цифровой обработки сигналов: виды шумов, отношение сигнал/шум, статистическая обработка сигнала, корреляционная функция.

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

Виды шумов, отношение сигнал/шум,
Статистическая обработка сигнала,
Корреляционная функция.

Виды шумов, отношение сигнал/шум.

В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.

Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.

Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.

Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением. Значение его – квадратный корень из дисперсии.

На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.

В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.

В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.

Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.

Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения. При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.

Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.

Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.

Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.

Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.

А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.

Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.

Слуйчайный процесс, у которого область частот заполнена равномерно, называется белым шумом.

Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности. В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.

Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.

Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления. К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.

Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.

У него равномерная спектральная плотность мощности, поэтому он белый.
Нормальное распределение, поэтому он Гауссовский.
С полезным сигналом он суммируется, поэтому он аддитивный.
И статистически он от сигнала независим.

На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.

Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных. Шум в подобных системах, конечно же, является нежелательным явлением.

Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.

Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.

Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.

Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.

Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.

Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума. Мы видим, то что распределение действительно равномерное, это белый шум.

Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному.

Теперь мы генерируем большое число зашумлённых сигналов. Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.

Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.

В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.

Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.

Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.

В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.

Наверх

Статистическая обработка сигнала.

В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.

У любого сигнала, непрерывного и дискретного, можно определить среднее значение. Оно может вычисляться по-разному.

Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.

Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.

То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.

Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.

Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.

Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».

При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.

Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.

Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего. Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.

Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.

Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.

Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми. В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.

Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего. Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.

Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.

А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах. Также можно построить Q-зубцы на том же самом графике.

Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.

Наверх

Корреляционная функция.

Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.

Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.

Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.

В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.

При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.

Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.

В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией.

Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.

Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный. В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.

Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.

Автокорреляционная функция прямоугольного импульса имеет форму треугольника.

Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.

Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов

А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.

Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.

А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.

Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти.

Область, которую мы выделили, обозначена на графике двумя пунктирными линиями. Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.

В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале.

Теперь давайте добавим шум к исходному сигналу и к фрагментам.

Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.

Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале. Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.

Источник

Основные причины плохих шумовых характеристик[править | править код]

Методы улучшения характеристик[править | править код]

Измерение[править | править код]

В звукотехнике[править | править код]

В видео[править | править код]

См. также[править | править код]

Примечания[править | править код]

Definition[edit]

Decibels[edit]

Dynamic range[edit]

Difference from conventional power[edit]

Alternative definition[edit]

Modulation system measurements[edit]

Amplitude modulation[edit]

Frequency modulation[edit]

Noise reduction[edit]

Digital signals[edit]

Fixed point[edit]

Floating point[edit]

Optical signals[edit]

Types and abbreviations[edit]

Other uses[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Для размышления

Материалы

Отношение сигнал/шум

Во-первых, сам сигнал может включать в себя некоторые высокочастотные составляющие или его центральная частота может лежать в области высоких частот.

Известно несколько методов сужения полосы пропускания, которые получили широкое распространение на практике. Эти методы имеют следующие названия:

Усреднение сигнала и многоканальное усреднение

Многоканальные счетчики (уплотнители)

Определение отношения сигнал/шум

Пример: резонанс Мессбауэра

Многоканальный анализ аналоговых сигналов (усреднение сигнала)

Многоканальное уплотнение как средство сужения полосы пропускания.

Получение периодического сигнала

Обнаружение путем захвата

Этот метод достаточно сложен для понимания. Для того чтобы разобраться с ним, необходимо уделить немного внимания фазовому детектору, рассмотренному ранее.

Основная схема представлена на рисунке.

Выход фазового детектора

<Eccos(ωt + ϕ)>|0π/ω — < Eccos(ωt + ϕ)>|02π/ω

Полученный результат позволяет сделать следующий вывод:

для входного сигнала, имеющего такую же частоту, что и опорный сигнал, усредненный выходной сигнал пропорционален амплитуде Ec и синусу относительного сдвига фазы.

cos(ω + ∆ω)t = cos(ωt + ϕ); ϕ = t∆ω

Теперь выходной сигнал представляет собой медленно меняющуюся синусоиду:

Uвых = (2Ec/π)sin(∆ω)t,

которая проходит через фильтр НЧ почти без изменений при условии, что ∆ω <1/Ϯ = 1/RC, и значительно ослабляется при условии, что ω <1/Ϯ.

Метод захвата

Будем проводить опыт при «двойном управлении» сигналом:

во-первых, должна быть быстрая модуляция, которая нужна для фазового детектирования,

во-вторых, медленная развертка по интересующим нас параметрам сигнала.

Два метода быстрой модуляции

если бы шум не имел значения, то не нужно было бы и использовать обнаружение с захватом

Амплитудный анализ импульсов

Таким образом, анализатор амплитуды импульсов преобразует выход детектора в энергетический спектр.

Преобразователи времени в амплитуду

Основы цифровой обработки сигналов: Виды шумов, отношение сигнал/шум, Статистическая обработка сигнала, Корреляционная функция

Виды шумов, отношение сигнал/шум.

Статистическая обработка сигнала.

Корреляционная функция.

Вам также может понравиться

Как найти срок по сложным процентам

Как найти частного юриста

Как найти адскую крепость через команду

Добавить комментарий Отменить ответ

<E_ccos(ωt + ϕ)>|₀^π/ω — < E_ccos(ωt + ϕ)>|₀^2π/ω

U_вых = (2E_c/π)sin(∆ω)t,