Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-

2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-

3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-

2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-

3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-

2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-

3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 144 126 раз.
Была ли эта статья полезной?
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами ![]() . Последний
. Последний ![]() элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные ![]()
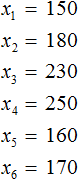
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
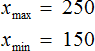
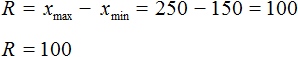
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
![]()
Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:
![]()
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
![]()
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
![]()
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
![]()
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:
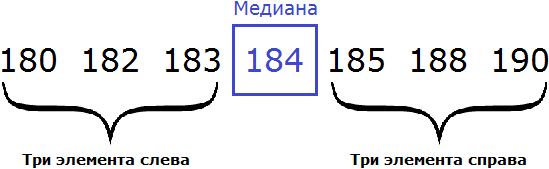
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186
![]()
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
![]()
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
![]()
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
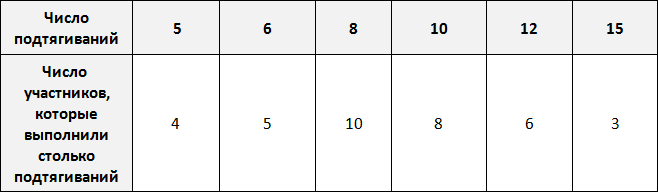
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Download Article
Preparing, calculating, and reporting your data
Download Article
Absolute frequency is a simple concept to grasp: it refers to the number of times a particular value appears in a specific data set (a collection of objects or values). However, relative frequency can be a little trickier. It refers to the proportion of times a particular value appears in a specific data set. In other words, relative frequency is, in essence, how many times a given event occurs divided by the total number of outcomes. If you organize your data, calculating and presenting relative frequency can become a simple task.
-

1
Collect your data. Unless you are just completing a math homework assignment, calculating relative frequency generally implies that you have some form of data. Conduct your experiment or study and collect the data. Decide how precisely you wish to report your results.[1]
- For example, suppose you are collecting data on the ages of people who attend a particular movie. You could decide to collect and report the exact age of everyone who attends. But this is likely to give you 60 or 70 different results, being every number from about 10 through 70 or 80. You may instead wish to collect data in groups, like “Under 20,” “20-29,” “30-39,” “40-49,” “50-59,” and “60 plus.” This would be a more manageable set of six data groups.
- As another example, a doctor might collect body temperatures of patients on a given day. In this case, just collecting whole numbers, like 97, 98, 99, might not be precise enough. It might be necessary to report data in decimals in this case.
-

2
Sort the data. After you complete your study or experiment, you are likely to have a collection of data values that could look like 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. In this form, the data appear almost meaningless and difficult to use. It is more helpful to sort the data in order from lowest to highest. This would result in the list 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.
- When you are sorting and rewriting your collection of data, be careful to include every point correctly. Count the data set to make sure you do not leave off any values.
Advertisement
-

3
Use a data table. You can summarize the results of your data collection by creating a simple data frequency table. This is a chart with three columns that you will use for your relative frequency calculations. Label the columns as follows:[2]
-
. This column will be filled with each value that appears in your data set. Do not repeat items. For example, if the value 4 appears several times in the list, just put
under the
column once.
-
,
or
. In statistics, the variable
is conventionally used to represent the count of a particular value. You may also write
, which is read as “n of x,” and means the count of each x-value. A final alternative is
, which means the “frequency of x.” In this column, you will put the number of times that the value appears. For example, if the number 4 appears three times, you will place a 3 next to the number 4.
- Relative Frequency or
. This final column is where you will record the relative frequency of each data item or grouping. The label
, which is read “P of x,” could mean the probability of x or the percentage of x. The calculation of relative frequency appears below. This column will be used after you complete that calculation for each value of x.
-
Advertisement
-

1
Count your full data set. Relative frequency is a measure of the number of times a particular value results, as a fraction of the full set. In order to calculate relative frequency, you need to know how many data points you have in your full data set. The will become the denominator in the fraction that you use for calculating.[3]
- In the sample data set provided above, counting each item results in 16 total data points.
-

2
Count each result. You need to determine the number of times that each data point appears in your results. You may want to calculate the relative frequency of one particular item, or you may be summarizing the overall data for the full data set.[4]
- For example, in the data set provided above, consider the value
. This value appears three times in the list.
- For example, in the data set provided above, consider the value
-

3
Divide each result by the total size of the set. This is the final calculation to determine the relative frequency of each item. You can set it up as a fraction or use a calculator or spreadsheet to perform the division.[5]
Advertisement
-

1
Present your results in a frequency table. The frequency table that you began above can be used to present the results in a format that is easy to review. As you perform each of the calculations, fill in the results in the corresponding places in the table. It is common to round your answers to two decimal places, although you will need to decide this for yourself based on the needs of your study. Because of rounding the end result may total something close to , but not exactly 1.0.[6]
- For example, using the data set above, the relative frequency table would appear as follows:
- x : n(x) : P(x)
- 1 : 3 : 0.19
- 2 : 1 : 0.06
- 3 : 2 : 0.13
- 4 : 3 : 0.19
- 5 : 4 : 0.25
- 6 : 2 : 0.13
- 7 : 1 : 0.06
- total : 16 : 1.01
-

2
Report items that do not appear. It may be just as meaningful to report items whose frequency is 0 as to report those items that do appear in your data set. Look at the kind of data you are collecting, and if you notice any gaps in your sorted data, you may need to report them as 0s.
- For example, the sample data set you have been working with includes all values from 1 to 7. But suppose that the number 3 never appeared. That could be important, and you would report the relative frequency of the value 3 as 0.
-

3
Show your results as percentages. You may wish to turn your decimal results into percentages. This is a common practice, as relative frequency is often used as a predictor of the percentage of times that some value will occur. To convert a decimal number to a percentage, simply shift the decimal point two spaces to the right, and add a percent symbol.[7]
- For example, the decimal result of 0.13 is equal to 13%.
- The decimal result of 0.06 is equal to 6%. (Don’t just skip over the 0.)
Advertisement
Add New Question
-
Question
What is frequency of the event?

It’s a measurement of how often the event occurs in a given time period.
-
Question
How can you calculate frequency from relative frequency?

The word “frequency” alone is not very clear. In statistics, there are absolute frequency (the number of times a data point appears), relative frequency (usually presented as a percentage), or cumulative frequency. Cumulative frequency begins at 0 and adds up the frequencies as you move through your list. If you are just asked for “frequency,” from the relative frequency, it probably means the absolute frequency. Take your relative frequency, and multiply it by the total number of items in the full data set, and you will have the absolute frequency.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Physically speaking, the relative frequency tells you the presence or occurrence of a particular event in a set of events.
-
If you add up the relative frequencies of all items in a data set, you should get a sum of 1. If you round off your values, the sum may not be exactly 1.0.
-
If your data set is too large for simple counting, you may need to use a software package like MS-Excel or MATLAB to avoid mistakes.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To stop face sweating, try applying an astringent containing tannic acid, like witch hazel, to your face twice a day using a cotton ball. Additionally, apply an antiperspirant spray to your scalp, temples, and upper forehead to temporarily block your sweat glands. Alternatively, try using a dry shampoo to manage scalp sweating by holding it 8 inches from your head, then spraying it in 2 inch sections of your hair at a time. After that, massage the dry shampoo into your scalp for even distribution. For more tips, like how to show your results as percentages, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 102,501 times.
Did this article help you?
Относительная частота и статистическая вероятность. Основные формулы и решения типовых задач
Относительная частота (частость) события А определяется равенством
где n – общее число проведенных испытаний; m – число испытаний, в которых событие А наступило (иначе – частота события А).
При статистическом определении за вероятность события принимают его относительную частоту, найденную по результатам большого числа испытаний.
Задача №1. При определении всхожести партии семян взяли пробу из 1000 единиц. Из отобранных семян не взошло 90. Какова относительная частота появления всхожего семени?
Решение. Обозначим событие: А – отобрано всхожее семя. Найдем относительную частоту события А, применив формулу (5). Общее число проведенных испытаний n = 1000. Число испытаний, в которых событие А наступило, равно m = 1000 – 90 = 910.
Относительная частота события А равна
Задача №2. Для проведения исследований на некотором поле взяли случайную выборку из 200 колосьев пшеницы. Относительная частота (частость) колосьев, имеющих по 12 колосков в колосе, оказалась равной 0,123, а по 18 колосков – 0,05. Найти для этой выборки частоты колосьев, имущих по 12 и по 18 колосков.
Решение. Рассмотрим события: A – взят колос, имеющий 12 колосков; В – взят колос, имеющий 18 колосков.
Найдем частоты и
событий А и В применив формулу (5).
Обозначим через относительную частоту события A, а через
относительную частоту события В. Так как число проведенных испытаний n = 200, то
Задача №3. Многолетними наблюдениями установлено, что в некоторой области ежегодно в среднем в тридцати хозяйствах из каждых ста среднегодовой удой молока от одной коровы составляет 4 100 – 4 300 кг. Какова вероятность того, что в текущем году в одном из хозяйств этой области, отобранном случайным образом, будет получен такой среднегодовой удой?
Решение. Обозначим событие: А – в текущем году в хозяйстве области, отобранном случайным образом, среднегодовой удой молока от одной коровы составит 4 100 – 4 300 кг.
Вероятность события А найдем, воспользовавшись ее статистическим определением.
Располагая статистическими данными, найдем, что относительная частота хозяйств области, в которых ежегодно имеют указанный средне-годовой удой молока от одной коровы, равна 0,3. Так как эти данные получены в результате проведения большого числа наблюдений, выполняемых в течение многих лет, то можно принять, что вероятность события А равна Р(А) = 0,3.
эмпирическая
функция распределения
Пусть исследуется произвольная случайная
величина
![]() и
и
относительно этой случайной величины
производится ряд независимых опытов
(испытаний) при наличии определённого
комплекса условий. Далее, пустьиз
генеральной совокупности извлечена
выборка, причем значение![]() наблюдалось
наблюдалось
![]()
раз,
![]() наблюдалось
наблюдалось![]() раз, и так далее
раз, и так далее
![]() наблюдалось
наблюдалось![]() раз, при этом натуральное число
раз, при этом натуральное число![]() и
и
![]() ,
,
выражает объём выборки,
значения![]() называютвариантами
называютвариантами
с.в.![]() .Вся совокупность
.Вся совокупность
значений с.в.![]() представляет
представляет
собой первичный статистический материал,
который подлежит дальнейшей обработке,
сначала подлежатьупорядочению.
Операцию по упорядочению значений
случайной величины (признака) по не
убыванию называют «ранжированием»
статистических данных. Полученная таким
способом последовательность значений![]() случайной
случайной
величины![]() ,
,
где![]() ;
;![]() ,
,![]() называетсявариационным рядом.
называетсявариационным рядом.
Числа
![]() ,
,
показывающие, сколько раз встречаются
варианты (числа)![]() в ряде наблюдений, называютсячастотами.
в ряде наблюдений, называютсячастотами.
А числа![]() равное отношение
равное отношение![]() к объёму выборки
к объёму выборки![]() ,
,
называютсяотносительными частотами,
т.е.
(1)
![]()
Перечень вариантов
и соответствующие им частость
или относительных
частот называют
статическим распределением
выборки или статическим рядом.
Статистическое распределение
записывается в виде таблицы, где в первой
строке пишут численные значения
вариантов, а вторая заполняется их
соответствующими частотами![]() .
.
Из
этой таблицы затем составляют
новую таблицу с указанием частотностей
(относительных
частот)
![]() ,
,
где должен выполняться «контроль»
![]()
Пример
2. Задано распределение
частот выборки объема
![]() ,
,
![]()
![]() .
.
Эта таблица означает, что
![]() принимается
принимается
три раза,![]() принимается 10 раз и
принимается 10 раз и![]() принимается 7 раз. В итоге:
принимается 7 раз. В итоге:![]() .
.
Написать таблицу распределение
относительных частот.
Решение.
Найдем относительные частоты, для чего
разделим частоты на объем выборки:
![]() .
.
Теперь, составим таблицу распределения
относительных частот:
![]()
![]() .
.
Контроль:
![]()
Пример 3. В
результате тестирования группы из 10
человек для приёма на работу претенденты
набрали баллы:
![]() Составить
Составить
а) вариационный ряд;
б) статический ряд;
в) таблицу частот и относительных
частот.
Решение. а)
Упорядочив статические данные, получим
вариационный ряд:
![]()
![]() ;
;
б) Подсчитав частоту
и относительную частотность
вариантов: ![]()
![]() получим статическое распределение
получим статическое распределение
выборки (так называемый дискретный
ряд).
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
2 |
1 |
1 |
2 |
3 |
где
![]() .
.
Контроль.
Построим таблицу относительную частоту
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
где
![]() .
.
Контроль.
Статистическое распределение выборки
является оценкой неизвестного
распределения.
По теореме Бернулли, относительные
частоты
![]() сходятся при
сходятся при![]() к соответствующим вероятностям,
к соответствующим вероятностям,![]() т.е.
т.е.![]() .
.
Поэтому, при больших значениях![]() статическое распределение мало отличается
статическое распределение мало отличается
от истинного распределения.
В случаях, когда количество значений
признака (с.в.![]() )
)
достаточно велико или когда случайная
величина![]() является непрерывной (т.е. её значение
является непрерывной (т.е. её значение
заполняет некоторый отрезок числовой
прямой),составляют интервальный
статистический ряд.
В первую очередь образуют частичные
промежутки,
![]() которые берут обычно с одинаковыми
которые берут обычно с одинаковыми
длинами, равными![]() .
.
|
Интервалы |
|
|
|
|
|
|
Частота |
|
|
|
|
|
|
Частость |
|
|
|
|
|
Эта таблица означает, что весь диапазон
изменения величины![]() разбит на интервалы
разбит на интервалы
(границами
![]() го
го
интервала являются,![]() и
и![]() );
);
число![]() есть частота попадания в
есть частота попадания в![]() й
й
интервал,![]() ,
,
где![]() количество
количество
чисел в исходном ряде (выборке),
приходящихся в![]() –
–
й интервал. На практике число интервалов
выбирается обычно в пределах одного-двух
десятков. Также следует отметить, что
в общем случае длины интервалов не
обязаны быть одинаковыми.
Для определения величины интервала
![]() существуют разные подходы, в качестве
существуют разные подходы, в качестве
одного из таких способов разбиения,
может быть использована формула
Стерджесса:
![]()
где
![]() выражает
выражает
разность между наибольшим и наименьшим
значениями признака,
числа интервалов
![]() ;
;![]() .
.
За начало первого интервала рекомендуется
брать величину![]() ,
,
и если конец последнего промежутка
входит во множестве с.в.![]() ,
,
то оно также включается в число элементов,
входящих в последний промежуток. После
завершения «разбиения» первую строку
таблицы статического распределения
заполняют полученными частичными
промежутками. Во второй строчке
статистического ряда вписывают числа![]() –
–
количество наблюдений, попавших в каждый
интервал, а затем составляют вторую
таблицу относительных частот по выше
указанному принципу, где мы для удобства
объединили обе таблицы.
Заметим, что в теории вероятностей под
распределением понимают соответствие
между возможными значениями случайной
величины и их вероятностями, а в
математической статистике —
соответствие между наблюдаемыми
вариантами и их частотами, иличастость
(относительные частоты).
Пример 4. Измерили рост (с некоторой
точностью скажем до 1 см.) 30 наудачу
отобранных студентов. Результаты
измерения показали:
![]()
![]()
![]()
Построить интервальный статистический
ряд.
Решение.Сначала упорядочим полученные
данные.
![]()
![]()
Следует, что
![]() рост
рост
студентов является непрерывной с.в. При
более точном измерении роста значения
с.в.![]() обычно
обычно
не повторяется и может отличиться друг
от друга на несколько миллиметров.
Вероятность наличия на Земле двух
человека с одинаковым ростом, например,
![]() метров, равна нулю.
метров, равна нулю.
Отсюда следует, что
![]() ;
;
в соответствии с формулой Стерджесса,
при![]() ,
,
находим длину частичного интервала
разбиения:
![]()
Если примем за
![]() ,
,
тогда![]() Все исходные данные разбиваем на
Все исходные данные разбиваем на![]() интервалов (при
интервалов (при![]() ):
):![]()
Подсчитав общее число студентов
![]() ,
,
попавших в каждый из полученных
промежутков, получим интервальный
статистический ряд:
|
Рост |
[150-156) |
[156-162) |
[162-168) |
[168-174) |
[174-180) |
[180-186) |
|
Частота |
4 |
5 |
6 |
7 |
5 |
3 |
|
Частость |
0,13 |
0,17 |
0,20 |
0,23 |
0,17 |
0,10 |
Одним из способов статистической
обработки вариационного ряда является
построение
эмпирической функции распределения.
Пусть известно статистическое
распределение частот количественного
признака
![]()
![]() число наблюдений, при которых наблюдалось
число наблюдений, при которых наблюдалось
значение признака![]() ,
,
а
![]() общее
общее
число наблюдений (объем выборки).
Эмпирической (статистической) функцией
распределения называется функция,![]() определяющая для каждого значения
определяющая для каждого значения![]() частость события
частость события![]() :
:
(2)
![]() .
.
В отличие от эмпирической функции
распределения выборки, интегральную
функцию
![]() распределения генеральной совокупности
распределения генеральной совокупности
называюттеоретической функцией
распределения. Различие
между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция
(3)
![]()
– определяет вероятность
события![]() ,
,
а эмпирическая функция
![]() определяет
определяет
относительную частоту этого же события.
Очевидно, что функция
![]() удовлетворяет
удовлетворяет
тем же условиям, что и истинная функция![]() (см.Т.3).Другими словами,
(см.Т.3).Другими словами,
числа ![]()
и ![]() мало отличаются одно от
мало отличаются одно от
другого. Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции ![]()
-распределения генеральной
совокупности. Такое заключение
подтверждается и тем, что ![]()
обладает всеми
свойствами ![]() .
.
Действительно, из
определения функции ![]() вытекают следующие ее
вытекают следующие ее
свойства:
1. Значения эмпирической функции
принадлежат отрезку [0,1];
2. ![]()
неубывающая функция;
3. Если
![]() наименьшая
наименьшая
варианта, то![]()
при
![]() ;
;
и если
![]()
наибольшая варианта, то при
![]() ,
,![]() .
.
На основании теорем ЗБЧ при увеличении
числа
![]() наблюдений (опытов) относительная
наблюдений (опытов) относительная
частота события![]() приближается к истинной вероятности
приближается к истинной вероятности
этого события.
Эмпирическая функция распределения
![]() является
является
как бы «оценкой» вероятности события![]() ,
,
т.е. оценкой теоретической функции
распределения![]() с.в.
с.в.![]() .
.
Таким образом, можно заключить, что
имеет место утверждение,
Пусть
![]() является теоретическая функция
является теоретическая функция
распределения случайной величины![]() ,
,
а![]() её эмпирической функцией распределения.
её эмпирической функцией распределения.
Тогда для любого![]() справедливо предельное соотношение
справедливо предельное соотношение
(4)
![]()
Пример 5.В условиях примера 3, и
используя полученные результаты,
построим эмпирическую функцию![]() .
.
Решение. В нашем случае по условию![]() .
.
В целях наглядности решения примера
приведём ещё раз полученную таблицу
относительных частот
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
где
![]() .
.
Контроль.
Поэтому
![]() при
при![]() (наблюдений меньше
(наблюдений меньше![]() отсутствует);
отсутствует);![]() при
при![]() (здесь
(здесь
по таблице![]() ).
).![]() при
при![]() (здесь
(здесь![]() )
)
и т.д. Таким образом, получаем![]()
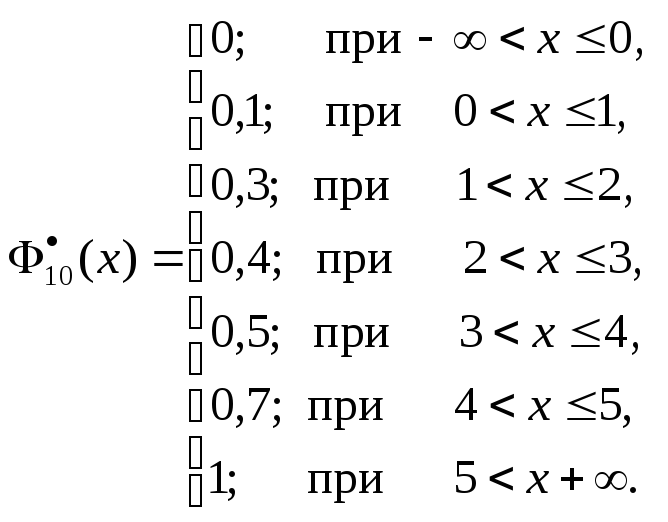
![]()
График эмпирической функции распределения
имеет вид: (Рис. 72.)
Рисунок 72 из Письменного
Соседние файлы в папке Теория вероятностей от исмоилова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.02.20162.36 Mб71~WRL0002.tmp
- #
06.02.20161.87 Mб67~WRL0005.tmp
