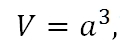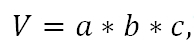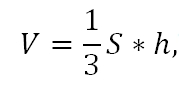Объёмы многогранников
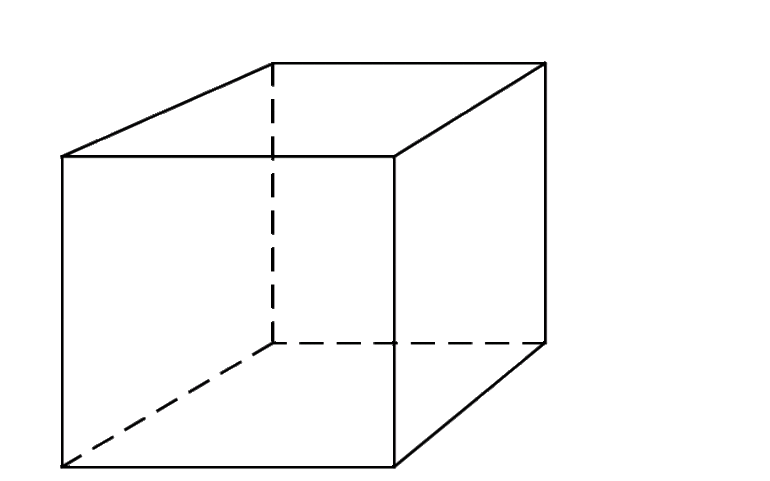
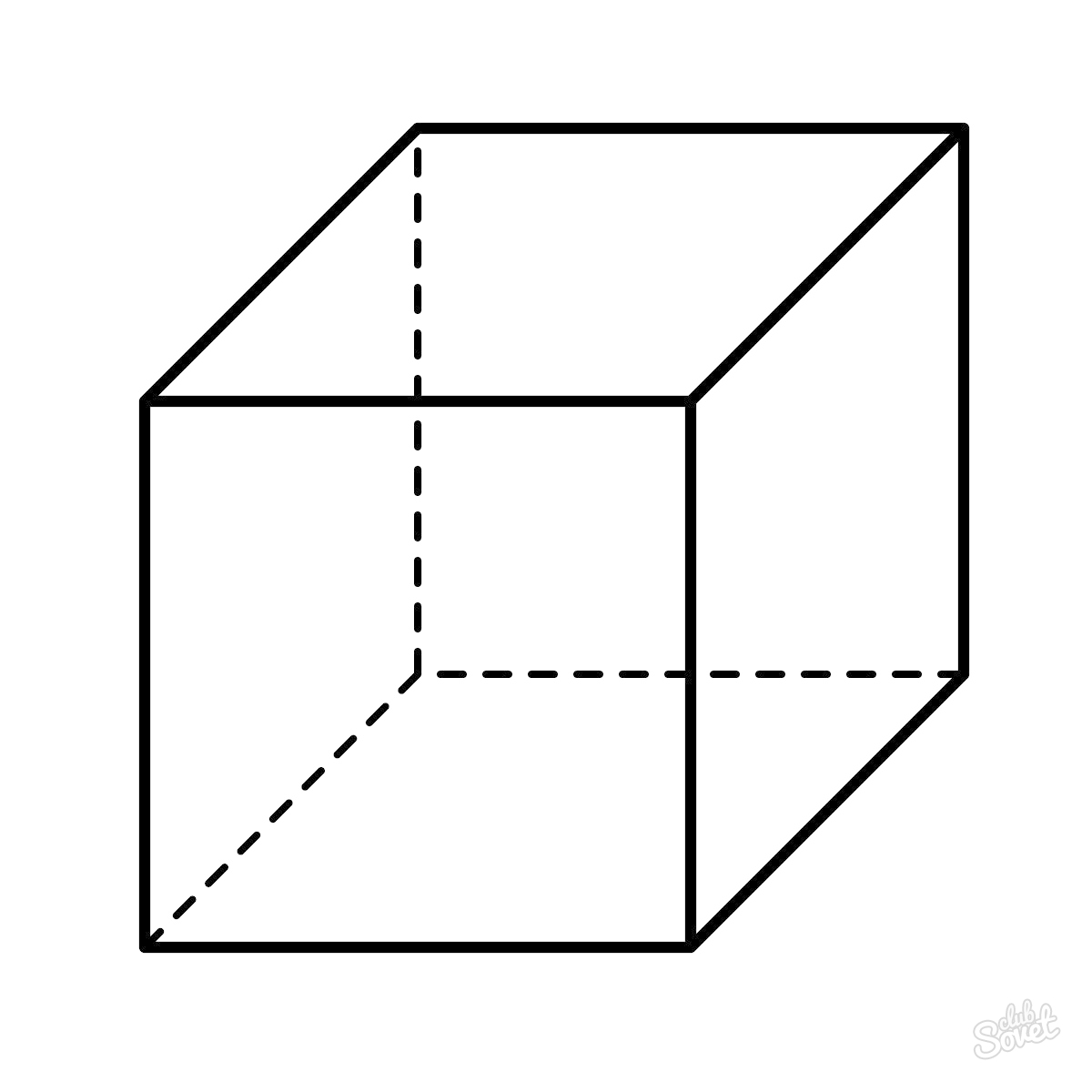
Куб
V = a3 , где а — ребро куба
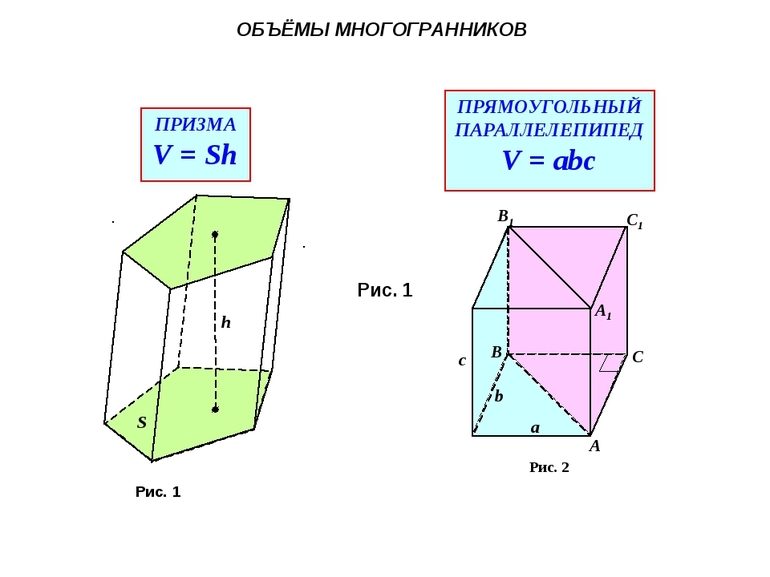
Прямоугольный параллелепипед
V = a * b * c, где a, b, c — рёбра фигуры: высота, ширина и длина
Параллелепипед
V = Sоснования * h, где h — высота параллепипеда.
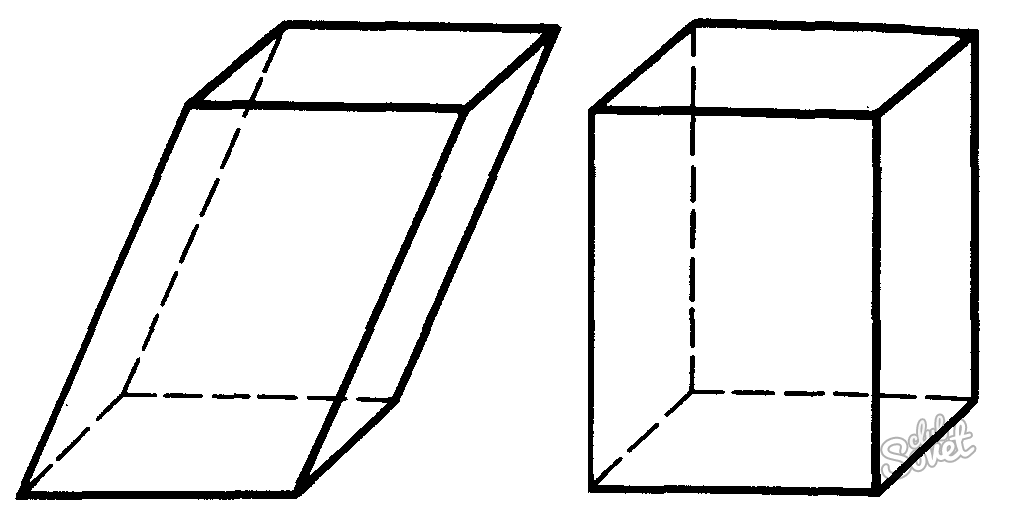
Призма
V = Sоснования * h, где h — высота призмы
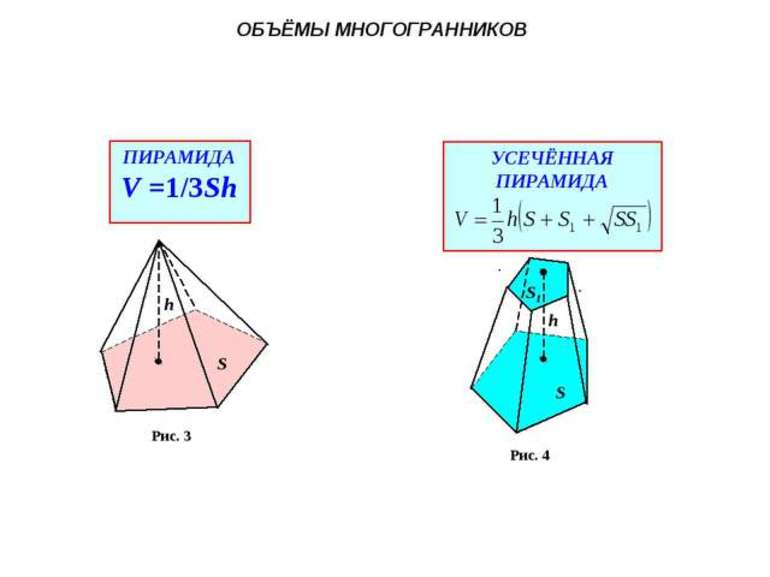
Пирамида
V = 1/3 Sоснования * h, где h — высота пирамиды
Объёмы тел вращения
Цилиндр
V = πR2h, где R — радиус основания, h — высота
Конус
V = 13 Sоснования * h
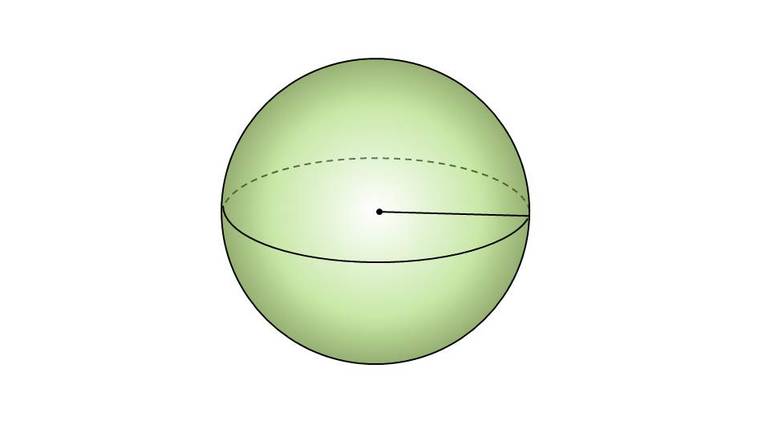
Шар
V = 43πR3 , где R — радиус шара
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Многогранники
Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.
В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).
Объемы различных многогранников:
- Призма $V=S_{осн}·h$
- Пирамида $V={1}/{3}S_{осн}·h$
- Параллелепипед $V=a·b·c$, где $a, b$ и $c$ – длина, ширина и высота.
- Куб $V=а^3$, где $а$ – сторона куба
Задачи на нахождение объема составного многогранника:
- Первый способ.
- Составной многогранник надо достроить до полного параллелепипеда или куба.
- Найти объем параллелепипеда.
- Найти объем лишней части фигуры.
- Вычесть из объема параллелепипеда объем лишней части.
Пример:
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение:
1. Достроим составной многогранник до параллелепипеда.
Найдем его объем. Для этого перемножим все три измерения параллелепипеда:
$V=10·9·4=360$
2. Найдем объем лишнего маленького параллелепипеда:
Его длина равна $9-4=5$
Ширина равна $4$
Высота равна $7$
$V=7·4·5=140$
3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
$V=360-140=220$
Ответ: $220$
- Второй способ
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
– Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
Пример:
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
– Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Задачи на рассмотрение подобия фигур.
При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.
В стереометрии изучаются свойства самых разнообразных объемных тел, в том числе приводятся доказательства формул объемов многогранников от самого простого — куба — до сложных геометрических тел с n-м количеством граней.
Определение геометрических тел
Один из разделов геометрии — стереометрия — изучает самые разнообразные пространственные фигуры и их свойства. В общем случае геометрическое тело — это часть пространства, имеющая наружные границы в виде замкнутой поверхности. Сугубо геометрическое определение описывает любую пространственную форму как компактную совокупность множества точек, каждые две из которых можно соединить отрезком и он будет полностью находиться внутри заданного ограниченного контура.
Совокупность всех точек, которые находятся на границе тела, составляет его поверхность. Кроме того, можно сказать, что любое геометрическое тело образовано множеством внутренних точек. В
иды пространственных фигур:
- многогранники;
- тела вращения.
Конечное число плоских многоугольников, ограничивающих пространственное тело, называется многогранником. При этом должны соблюдаться два свойства:
- Любая сторона каждого из многоугольников одновременно является стороной другого многоугольника и только их двоих. Соприкасающиеся стороны называются смежными.
- Все многоугольники связаны между собой — от каждого из них можно проложить путь до любого другого через смежные стороны.
В геометрии многоугольники, образующие сложный пространственный многогранник, называют гранями, отрезки, образованные местом соединения двух смежных граней — ребрами, а углы, образованные соединенными в одной точке гранями — вершинами.
Общий принцип названий таких геометрических тел заключается в указании количества их сторон.
Таким образом, если число граней обозначить n, то название образуется как n-гранник:
- 4 грани — четырехгранник;
- 5 граней — пятигранник;
- 6 граней — шестигранник;
- 8 граней — восьмигранник.
Если весь многогранник находится только с одной стороны каждой своей грани, то его называют выпуклым, в противном случае — вогнутым или невыпуклым. Звездчатые многогранники, состоящие из множества правильных пространственных фигур, относятся к невыпуклым.
Отрезок, проложенный между двумя вершинами, принадлежащими разным граням и соединяющий их — диагональ многогранника.
Понятие объема
У людей давно возникла необходимость подсчитывать или отмерять необходимое количество разных веществ.
При измерении жидких и сыпучих материалов это было сделать легко, поместив их в сосуд известного объема. Для определения вместимости любых пространственных форм в стереометрии было введено понятие объема. Величина, описывающая размер части пространства, которую занимает геометрическое тело, называется его объемом и обозначается латинской буквой V. Для величины объема верны две аксиомы:
- Полный объем любого многогранника равен сумме объемов всех его простых частей. Это свойство используется при вычислении объемов составных пространственных фигур.
- У равных тел и объемы равные, что доказывается принципом наложения, и при параллельном переносе их объем не изменяется.
На величину объема никак не влияет ни пространственное местонахождение тела, ни то, каким образом оно делится на части. Как физическая величина объем выражается через массу и плотность вещества.
Чтобы понять, какая из емкостей более вместительная, можно заполнить одну жидкостью, а потом перелить в другую и увидеть, сколько жидкости останется или не хватит. Но это очень неудобно, и при решении геометрических задач пользуются понятием единицы измерения объема. Она равна объему куба, длина ребра которого — это единица длины.
Исторически известны разные меры емкостей — бушель, галлон, ведро, бочка и т. п. , объем нефти и сейчас измеряется в баррелях. В СИ за единицу объема принят 1 кубический метр, равный количеству вещества, вмещаемого кубом с длиной грани 1 м. В стереометрии обычно используются кубические сантиметры.
Виды многогранников
Различают несколько условных классов пространственных фигур.
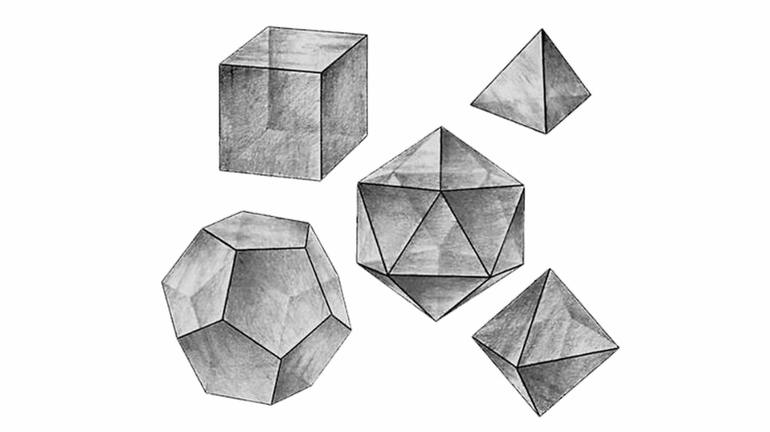
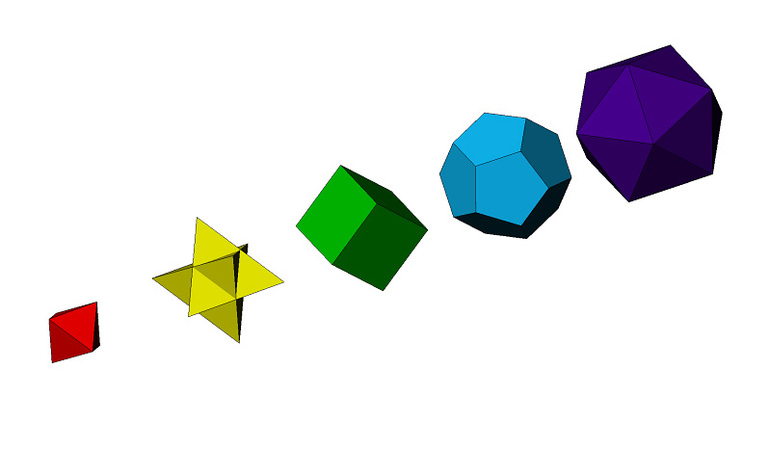
К обычным или классическим относятся параллелепипеды всех разновидностей, пирамиды и призмы. Правильными или Платоновыми телами называют отдельную группу из пяти многогранников, состоящих только из правильных многоугольников. Полуправильными или Архимедовыми телами называют усеченные Платоновы тела.
Отдельно рассматриваются сложные многогранники, такие как звездчатые, криволинейные или составленные из классических геометрических тел. Следует отметить, что одно и то же геометрическое тело может относиться к разным классам или являться частным случаем другого. Например, параллелепипед — частный случай призмы, а куб — правильный многогранник и частный случай параллелепипеда. Объем произвольных многогранников определяется как сумма объемов его простых частей.
Призма и параллелепипед
Такие многогранники всегда образованы двумя конгруэнтными основаниями, принадлежащими параллельным плоскостям, и n-м числом параллелограммов, являющихся их боковыми гранями. Если все ребра перпендикулярны основаниям призмы, то она называется прямой. У наклонной призмы величина углов между ребрами и основаниями отличается от 90º. Для правильной призмы обязательно выполнение условия — ее основание должно быть правильным многоугольником.
Высота — важная характеристика этого многогранника, она обозначается как h и в численном выражении представляет собой длину перпендикулярного отрезка между его основаниями. У прямой призмы высота равна длине ее ребра.
Формула для призмы: V = Sо·h, где Sо — площадь основания.
Параллелепипед является частным случаем призмы с основанием в виде четырехугольного многоугольника — параллелограмма. Тела такой формы тоже могут быть прямыми или наклонными и имеют две пары противоположных граней и четыре смежных. Если в основании параллелепипеда лежит прямоугольник, а его грани перпендикулярны основаниям, то он называется прямоугольным.
Формула объема многогранника прямоугольного параллелепипеда: V = a·b·c, где a и b — длина и ширина основания, а c — высота ребра.
К другой разновидности призм относится призматоид, если его изобразить на рисунке, то легко заметить, что грани такого тела — треугольники, одна сторона которых совпадает со стороной верхнего или нижнего основания, или трапеции, основания которых совпадают со сторонами оснований призматоида. Формула Симпсона: V = h/6 x (Sо + 4S + S1), где Sо и S1 — обозначения площадей оснований, а S — площадь параллельного и равноудаленного от оснований сечения.
Разновидности пирамиды
Пирамида представляет собой многогранник, строение которого включает в себя одно основание и n-е число треугольных граней, сходящихся в одной точке — вершине. К пирамидам относится простейший многогранник — четырехгранная пирамида, сторонами которой являются треугольники. В зависимости от того, какой многоугольник является основанием пирамиды, она может быть треугольной, четырехугольной, пятиугольной и т. д. Если при этом основания — правильные фигуры
Формула расчета для пирамиды: V = 1/3 x So·h, где So — площадь основания, h — высота пирамиды, соединяющая ее вершину и центр основания.
Усеченная пирамида получается, если часть полной пирамиды отсекается параллельной основанию плоскостью. Получившееся сечение образует второе основание пирамиды.
Для усеченной пирамиды: V = 1/3 x h x (S1 + √(S1·S2) +S2), где S1 — площадь нижнего, а S2 — площадь верхнего оснований.
Правильные многогранники
Платоновы тела относятся к выпуклым многогранникам, обладают пространственной симметрией и состоят из одинаковых правильных многоугольников. Тетраэдр имеет форму пирамиды и состоит из четырех равносторонних треугольников. Его объем можно вычислить по стандартной формуле для пирамиды или так: V = √2/12 x a³, где a — длина ребра.
Следующий правильный многоугольник — это гексаэдр, который обычно называется кубом, у него шесть квадратных граней, следовательно, длины всех ребер равны между собой.
Формула объема куба: V = a³, где a — длина ребра.
Октаэдр имеет восемь треугольных граней. Формула объема этого правильного многогранника: V = (a³√2)/3.
Икосаэдр состоит из двадцати треугольных граней. Формула: V = (5a³(3 + √5))/12. Додекаэдр имеет 12 пятиугольных граней, а его объем вычисляется так: V = (a³(15 + 7√5))/4.
Тела вращения
Если какую-либо плоскую геометрическую фигуру вращать вокруг оси, расположенной в той же плоскости, то получится объемное тело вращения.
Шар образуется при вращении круга вокруг своей оси. Если сделать оборот прямоугольника вокруг одной из его сторон, то получится цилиндр. Конус образуется вращением треугольника по линии одного из его катетов. Окружность, вращающаяся вокруг прямой, ее не пересекающей, образует тор. Объемы сложных криволинейных тел определяются по специальной формуле с помощью интеграла.
Формулы для определения объема тел вращения приведены в таблице.
| Тело | Формула объема |
| Цилиндр | V = π R² h, R — радиус основания цилиндра, h — высота |
| Конус | V = 1/3 x π R² h, R — радиус основания конуса, h — высота |
| Шар | V = 4/3 x π R³, R — радиус, π — число пи, равное 3,14 |
Объемы деталей, представляющих собой составные многогранники можно вычислить с помощью онлайн-калькулятора.
Как найти объем многогранника
Прежде всего определимся, что же такое многогранник. Это трехмерная геометрическая фигура, грани которой представлены в виде плоских многоугольников. Единой формулы поиска объема многогранника не существует, так как многогранники бывают разной формы. Для того чтобы найти объем сложного многогранника, его условно делят на несколько простых, таких как параллелепипед, призма, пирамида, а затем складывают объемы простых многогранников и получают в результате искомый объем фигуры.
1
Как найти объем многогранника – параллелепипеда
Для начала найдем площадь прямоугольного параллелепипеда. У такой геометрической фигуры все грани представлены в виде плоских прямоугольных фигур.
- Самый простой прямоугольный параллелепипед – это куб. Все ребра куба равны между собой. Всего у такого параллелепипеда 6 граней, то есть 6 одинаковых квадратов. Объем такой фигуры рассчитывается таким образом:
где a – длина любого ребра куба.
- Объем прямоугольного параллелепипеда, стороны которого имеют различные измерения, рассчитывается по следующей формуле:
где a, b и с – длины ребер.
2
Как найти объем многогранника – наклонного параллелепипеда
У наклонного параллелепипеда так же 6 граней, 2 их них – основания фигуры, еще 4 – боковые грани. Наклонный параллелепипед отличается от прямого тем, что его боковые грани по отношению к основанию расположены не под прямым углом. Объем такой фигуры рассчитывается как произведение между площадью основания и высотой:
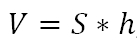
где S – это площадь четырехугольника, лежащего в основании, h – высота искомой фигуры.
3
Как найти объем многогранника – призмы
Объемная геометрическая фигура, основание которой представлено многоугольником любой формы, а боковые грани – параллелограммами, имеющими общие стороны с основанием – называется призмой. У призмы два основания, а боковых граней столько, сколько сторон у фигуры, являющейся основанием.
Для нахождения объема любой призмы, как прямой, так и наклонной, умножают площадь основания на высоту:
где S – площадь многоугольника в основании фигуры, а h – высота призмы.
4
Как найти объем многогранника – пирамиды
Если в основании фигуры расположен многоугольник, а боковые грани представлены в виде треугольников, смыкающихся в общей вершине, то такую фигуру называют пирамидой. Она отличается от вышеперечисленных фигур тем, что у нее имеется только одно основание, кроме этого, у нее есть вершина. Чтобы найти объем пирамиды, ее основание умножают на высоту, и делят результат на 3:
здесь S – площадь основания искомой геометрической фигуры, а h – высота.
Площадь простого многогранника найти достаточно просто, гораздо сложнее найти площадь фигуры, состоящей из множества многогранников. Особое внимание придется уделить правильному разделению сложного многогранника на простые.
Правильный выпуклый многогранник образован из одинаковых правильных многоугольников и обладает пространственной симметрией. Как это ни странно, но существует только 5 правильных многогранников: тетраэдр, октаэдр, икосаэдр, гексаэдр или куб и додекаэдр. Тетраэдр это правильная треугольная пирамида, число граней 4 и ребер 6. Октаэдр соответственно 8 и 12. Икосаэдр 20 и 30 – здорово! Куб нам знаком 6 и 12. Додекаэдр 20 и 30. Эйлер дает такую формулу, которая связывает число граней (Г), ребер (Р) и вершин (В) любого выпуклого многогранника В + Г = Р + 2. Обозначим р – число сторон каждой грани и q – число ребер, сходящихся в каждой вершине. При этом выполняются соотношения: рГ = 2Р = qВ.
Внутри каждого правильного многогранника можно поместить так называемую вписанную сферу радиусом r (которая касается каждой грани в ее центре), а снаружи любого такого многогранника можно построить описанную сферу радиусом R (которая проходит через вершины многогранника). Эти радиусы вычисляются по формулам
R = (a/2)∙tg(π/q)∙tg(θ/2) (1)
r = (a/2)∙ctg(π/p)∙tg(θ/2) (2)
где θ – двугранный угол между смежными гранями
sin(θ/2) = cos(π/q)/sin(π/p) (3)
и а – длина ребра для всех рассмотренных многогранников. Площадь поверхности многогранника S это есть площадь правильного р-угольника, умноженное на число граней Г
S = (a/2)^2∙p∙ctg(π/p) (4)
Вот мы и дошли до объема правильного многогранника V
V = (1/3)rS (5)
Объем вычисляется как объем правильной пирамиды (основанием пирамиды является правильный р-угольник, а высотой – радиус вписанной сферы r) на число этих пирамид. А число пирамид равно числу граней Г. Михаил Белодедов так и предложил вычислять объем многогранника.
Если принять, что длины ребер любого многогранника а = 2, то получим для куба радиус вписанной сферы r = 1, радиус описанной сферы R = √3, площадь поверхности r = 24 и объем куба V = 8. Можете это проверить, так как куб очень простая фигура и его можно просчитать и без приведенных формул. Попробуйте.