P anb как найти

Asked by: Leonard Bauch

Score: 4.7/5
(15 votes)

Formula for the probability of A and B (independent events): p(A and B) = p(A) * p(B). If the probability of one event doesn’t affect the other, you have an independent event. All you do is multiply the probability of one by the probability of another.

What is ANB formula?

We apply P(A ∩ B) formula to calculate the probability of two independent events A and B occurring together. It is given as, P(A∩B) = P(A) × P(B), where, P(A) is Probability of an event “A” and P(B) = Probability of an event “B”.

What does a ∩ B represent in P a ∩ B?

P(A∩B) is the probability that events A and B both happen. Basically ∩ means ‘and’. U is the union, so P(A U B) means the probability that either A or B occurs, or both; it’s the probability that at least one of the events happens.

What is the formula of P AUB?

P(AUB) = P(A) + P(B) – P(AB).

How do you calculate PA?

P(A/B) Formula is given as, P(A/B) = P(A∩B) / P(B), where, P(A) is probability of event A happening, P(B) is the probability of event B happening and P(A∩B) is the probability of happening of both A and B.

41 related questions found

Теорема сложения

P(AuB)=P(A)+P(B)-P(AnB)

Док-во: воспользуемся
геометрической трактовкой вероятности

Пл.A+пл.B-пл.(AnB),

а т.к. площадь совпадает
с вероятностью то мы доказали

В частности, если
AnB=
,
то теорема совпадает с аксиомой
вероятностей: P(AuB)=P(A)+P(B)

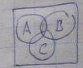
P(AuBuC)=P(A)+P(B)+P(C)-P(AnB)-P(AnC)-P(BnC)+P(AnBnC)

Условная вероятность

Для формулировки т.
умножения вероятности т.е. P(AnB)
нам потребуется условная вероятность
события B

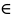
S

Из понятия частоты
мы дадим определение:

Условной вероятностью
события A при условии, что
событие B наступило, т.е.
P(B)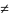
0
назыв. величина :

P(A/B)=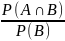

P(B)
0

Т.к. события
A и B
равноправные относительно рассуждения

P(B/A)=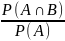

P(A)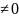

Теорема умножения
вероятностей

При условии P(A)
0
и P(B)
0,
то P(AnB)=P(A)P(B/A)=P(B)P(A/B)

Док-во следует из опр.
Условной вероятности

Если условная
вероятность события совпадает с
безусловной, т.е. P(A/B)=P(A)
(*), то

говорят, что событие
A не зависит от B,
в этом случае теорема об умножении
принимает вид:

P(AnB)=P(A)P(B)
(**)

Выражения (*) и (**)
эквивалентны и тогда события A
и B назыв. независимыми

Сл. из т. умножения

P(AnBnC)=P(A)P(B/A)P(C/AnB)

6. п.1 Пусть Mi(i=1,2…n)
попарно несовместные события образующие
полную группу (P(Mi)=0).
Пусть событие А может наступить только
вместе с одним из них с некоторой условной
вероятностью (P(A|Mi).
Тогда справедлива так называемая ф-ла
полной вероятности P(A)=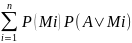

(1)

События Mi
по отношению к событию А являются
гипотезами

Доказательство

А=(А
M1)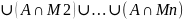

(события в скобках несовместные)

Тогда P(A)=P[(A
M1)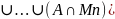
=
применим т. о сложении несовм событий
=
=

ч.т.д.

п.2. теорема байеса

пусть выполнены
условия п.1 и стало известно что событие
А произошло . тогда справедлива формула
P(Mi|A)=(P(Mi)P(A|Mi))/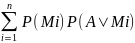

(2)

Док–во

P(A
Mi)=P(A)P(Mi|A)=P(Mi)P(A|Mi)

P(Mi|A)=(P(Mi)P(A|Mi))/P(A)=
(P(Mi)P(A|Mi))/

ч.т.д.

Рассмотрим содержательную
часть ф-лы (1) и (2).Пусть событие А происходит
при различных условиях по поводу
некоторых можно высказать условие Mi.
Допустим что известны вероятности
Mi(априорные) ф-ла (2) дает
значение вероятности если же известно
какая из нипотез в действительности
произошла.Пусть теперь событие А
произошло, тогда можно пересчитать т.е.
вычислить условные вероятности P(Mi)
по формуле (2) эти уточненные обстоятельства
назыв. Апостериорными

7. схема бернули

Испытание наз.
независимыми если исход каждого из них
не зависит от исхода всех предшествующих.
В схеме Бернули рассм. серия n
независимых испытаний, каждое из которых
имеет лиша 2 исхода, наступление какого
либо события А(успех) или его не наступление
причем вероятность успеха при одном
испытании P(A)=P(0<p<1)
вероятность постоянна и не зависит от
номера испытания, числа Р и n
наз. Параметрами схемы Бернули.

В этих усл. Нам надо
найти вероятность того что событие А в
данной серии из n испытаний
наступит не раз(0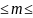
n).
Это определяется по ф-ле Бернули P_n(m)=C^m_n
p^mp^n–m
q=1-p

8.Определение функции
распределения и её свойства

Случайной величиной
наз. величина которая в ряде эксперимента
может принимать то или иное значение
причем заранее не известно какое именно.
Функцией распределения случ. вел. X
наз функция F(x)
определяемая равенством F(x)=P(X<x)
эта ф-ия наз. так же интегральной функцией
или законом распределения слу. Вел. Это
самая универсальная характеристика.
Она справедлива как для дисперсных так
и непрерывных случ. вел. И полностью
характеризует слу. Вел. с вероятнотностной
точкой зрения т.е. одной из форм законов
распределения.

Общие свойства ффункции
распределения

1)для любого вещественного
x

2) F(x)
неубывающая функция т.е. x_1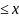
2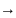
F(x₁₎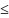

F(x₂₎

3)вероятность попадания
x в X в [a,b]
равна приращению функции на этот
промежуток x_1<x₂
P(x₁
X<x₂)=
F(x₂₎–
F(x₎

4)
=0

=1

5)непрерывна слева
т.е.

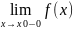
=f(x₀)
– по письменному

В тетради f(x)-
непрерывна справа F(x-0)=F(x)

9. Мат ожидание случ.
вел-ны и его св-ва

Мат. Ожиданием или
средним значением случ. вел-ны X
заданной на дискретном множестве
элементарных исходов наз. MX=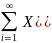
_k)P(w_k)
суммой ряда, при условии что ряд сх.
Абсолютно.

Если ряд не абсолютно
сходящийся то говорят что случю вел-на
X математич. ожид. Не имеет.

Св-ва мат. ожидания :

1)MC=C
где С-const математич.
ожидание постоянной равно самой
постоянной

2)М(СХ)=CMX
, c=const

3)пусть X
и Y две случ. величины
заданные на одном и том же множестве
исх. Тогда если сущ. MX и
MY то сущ. и M(x+y)
причем M(x+y)=MX+MY

4)M(C₁X+C₂Y)=C₁X+C₂Y

5) пусть X
имеет ряд распределения

x	x1	x2	…
p	p1	p2	…

Тогда если MX
сущ. то MX=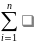
x_ip_i

6)пусть X
и Y независимые случ. вел.
тогда если сущ. MX и MY
то сущ. M(XY)
причем M(XY)=MX*MY

Пусть X
и Y независимы случ. вел-ны
заданные на одном и том же множестве
элементарных исходов, говорят что X
и Y независимы

P(X=Xi,Y=Yi)=P(X=Xi)*P(Y=Yi)
для любых Xi Yi

10. Дисперсия случ.
вел. на дискретном множестве событий и
её свойства

Пусть X
имеющая мат. ожидание . Дисперсией случ.
вел. X наз. мат. ожидание
квадрата её отклонения от своего мат.
ожидания DX=M(X-MX)²

Свойства дисперсии

1)DC=0
с=const

2)DX

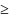
0

3) D(CX)=C²DX

4)Если X и Y
две независимые случ. вел. Имеющие
диспресию то D(X+Y)=DX+DY

5)DX=M(X²)-(MX)²

Док-во (3)

DX=M(x²-2X*MX+(MX)²)=MX²-M(2X*MX)+M(MX)²=MX²-2MX*MX+(MX)²=MX²-(MX)²

Док–во
(4)

D(X+Y)=M(X+Y)²-(M(X+Y))²=
MX²+2MXY+MY²-(MX)²-2MX*MY-(MY)²=MX²-(MX)²-MY²-(MY)²+2(MXY-MX*MY)=DX+DY+2(MX*MY+MX*

11

Биноминальная
случайная величина, ее мат. ожидание и
дисперсия. Случаи применения этой
случайной величины.

Если случ. вел Х
принимает целочисленные значения 0, 1,
2… n, а вероятность этих значений опр-ся
по формуле Р(Х=m)=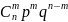
,
q=1-p

MX=np

DX=npq

np-q
k
np+q

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Алгебра,


вопрос задал vadikrozzin,


8 месяцев назад

Ответы на вопрос

Ответил GluV

0

Ответ:

22/45

Объяснение:

P(a)+P(B)-P(AnB)=P(AuB)

Тогда P(AnB)=P(a)+P(B)-P(AuB)=3/5+1/3-4/9=22/45

Новые вопросы

Математика,
1 месяц назад

запиши разность числа 2 и а. Найди ее значение при а=0; а=1; а=2.

Геометрия,
1 месяц назад

Выразить вектор АВ через векторы Со и ДО Дано:Вектор р=(1;-2) q=(3;-1) М=3р-2q найти Модуль Вектора М…

Обществознание,
8 месяцев назад

Как взаимосвязаны глобальные проблемы? Почему невозможно решить какую то одну проблему обособленно?

Физика,
8 месяцев назад

Средняя скорость автомобиля на второй половине пути в 1,5 раза больше средней скорости на первой половине. Во сколько раз средняя скорость автомобиля на всем пути превышает среднюю скорость на первой…

Математика,
6 лет назад

помогите пж заранее спасибо!!))…

Музыка,
6 лет назад

пожалуйста помогите сделать задание по музыке…

In compound probability of 2 events A and B, we may face the following situation.

That is, if the occurrence of one event, say B, is influenced by the occurrence of another event A, then the two events A and B are known as dependent events.

Joint Probability of the events A and B is denoted by P(AnB).

The formula to find P(AnB) is given by

P(AnB) = P(A) x P(B/A)

The above formula has been clearly illustrated in the picture given below.

We use the notation P(B/A), to be read as ‘probability of the event B given that the event A has already occurred (or ‘the conditional probability of B given A) to suggest that another event B will happen if and only if the first event A has already happened.

This is given by

Provided P(A) > 0 i.e. A is not an impossible event.

Similarly,P(A/B) = P(AnB)/P(B).

Let A, B and C be the three events in the following order of occurrence.

A – 1 st event (Independent)

B – 2 nd event (Influenced by A)

C – 3 rd event (Influenced by both A and B)

Then, the formula to find P(AnBnC) is given by

Example :

If a box contains 5 red and 8 white balls and two successive draws of 2 balls are made from it without replacement, then the probability of the event ‘the second draw would result in 2 white balls given that the first draw has resulted in 2 Red balls’ is an example of conditional probability.

Since the drawings are made without replacement, the composition of the balls in the box changes and the occurrence of 2 white balls (W₂)  in the second draw is dependent on the outcome of the first draw (R₂).

This event may b denoted by

P(W₂/R₂)

Solved Problems

Problem 1 :

A pair of dice is thrown together and the sum of points of the two dice is noted to be 10. What is the probability that one of the two dice has shown the point 4?

Solution :

Here, the condition is “The sum of points of the two dice is noted to be 10″.

When a pair of dice is thrown together, n(S) = 36.

Let A be the event of getting sum of the points to be 10.

Then, A = {(4, 6), (5, 5), (6, 4)}.

n(A) = 3

P(A) = n(A)/n(S)

= 3/36

= 1/12

Let B be the event of getting 4 on one of the dice.

Then,

B = {(1, 4), (2, 4), (3, 4), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 4), (6, 4)}

AnB = {(4, 6), (6, 4)} —-> n(AnB) = 2

P(AnB) = n(AnB)/n(S)

= 2/36

= 1/18

Probability that one of the two dice has shown the point 4 with the condition “sum of points of the two dice to be 10″ is

P(B/A) = P(AnB)/P(A)

= (1/18)/(1/12)

= (1/18) x (12/1)

= (1×12)/(18×1)

= 12/18

= 2/3

Problem 2 :

In a group of 20 males and 15 females, 12 males and 8 females are service holders. What is the probability that a person selected at random from the group is a service holder given that the selected person is a male?

Solution :

Here, the condition is “The selected person is a male“.

From, the given information, n(S) = 35.

Let A be the event of selecting a male person.

Then, n(A) = 20.

P(A) = n(A)/n(S)

= 20/35

= 4/7

Let B be the event of selecting a service holder.

Then, n(AnB) = 12.

P(AnB) = n(AnB)/n(S)

= 12/35

(Because, there are 12 male service holders)

The probability that a person selected at random from the group is a service holder given that the selected person is a male is

P(B/A)  =  P(AnB)/P(A)

= (12/35) / (20/35)

= (12/35) x (35/20)

= (12×35)/(35×20)

= 3/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

©All rights reserved. onlinemath4all.com