Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
– Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

– Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

– Аналогично с (a<-1), только график вытянут вниз.

– Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

– Аналогично (a∈(-1;0)), только ветви направлены вниз.

-
Парабола пересекает ось y в точке (c).

-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
-
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа – вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
-
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
-
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
Как найти k и b по графику линейной функции?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 декабря 2022 года; проверки требует 1 правка.
| Парабола | |
|---|---|
|
Парабола как коническое сечение |
|
 Парабола, её фокус и директриса |
|
| Эксцентриситет |
 |
| Уравнения | |
 |
|
| Другие конические сечения | |
|
Пара́бола (греч. παραβολή — приближение[1]) — плоская кривая, один из типов конических сечений.
Определение[править | править код]
Античные математики определяли параболу как результат пересечения кругового конуса с плоскостью, которая не проходит через вершину конуса и параллельна его образующей (см. рисунок). В аналитической геометрии удобнее эквивалентное определение: парабола есть геометрическое место точек на плоскости, для которых расстояние до заданной точки (фокуса) равно расстоянию до заданной прямой (директрисы) (см. рисунок)[2].
Если фокус лежит на директрисе, то парабола вырождается в ломаную.
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Парабола в семействе конических сечений
Вершина[править | править код]
Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.
Уравнения[править | править код]
Каноническое уравнение параболы в прямоугольной системе координат:
(или
, если поменять местами оси координат).
Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы[3]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии 
| Вывод |
|---|
|
Уравнение директрисы PQ: После возведения в квадрат и некоторых преобразований получается равносильное уравнение |
Парабола, заданная квадратичной функцией[править | править код]
Квадратичная функция 


где
— дискриминант квадратного трёхчлена.
Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При a > 0 (a < 0) фокус лежит на этой оси над (под) вершиной на расстоянии 1/4a, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение 


Общее уравнение параболы[править | править код]
В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:
Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант 
Уравнение в полярной системе[править | править код]
Парабола в полярной системе координат 
где p — фокальный параметр (расстояние от фокуса до директрисы или удвоенное расстояние от фокуса до вершины)
Расчёт коэффициентов квадратичной функции[править | править код]
Если для уравнения параболы с осью, параллельной оси ординат, 

Если же заданы вершина 

Свойства[править | править код]

Отражательное свойство параболы (оптика)

Расстояние от
Pn до фокуса
F такое же, как и от
Pn до
Qn (на директрисе L)

Длина линий
FPnQn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)
- Парабола — кривая второго порядка.
- Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
- Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. Сигнал также придет в одной фазе, что важно для антенн.
- Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
- Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
- Парабола является антиподерой прямой.
- Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
- Траектория фокуса параболы, катящейся по прямой, есть Цепная линия[4].
- Описанная окружность треугольника, описанного около параболы, проходит через её фокус, а точка пересечения высот лежит на её директрисе
Связанные определения[править | править код]
- При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
Вариации и обобщения[править | править код]
Графики степенной функции 



Парабола также представляет собой синусоидальную спираль при 
Параболы в физическом пространстве[править | править код]
Параболический компас Леонардо да Винчи
Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).
Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.
При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.
Также параболические зеркала используются в любительских переносных телескопах систем Кассегрена, Шмидта — Кассегрена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.
При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.
Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.
Форма параболы иногда используется в архитектуре для строительства крыш и куполов.
-
Параболическая орбита и движение спутника по ней (анимация)
-

-

-

Параболические траектории струй воды
-

Вращающийся сосуд с жидкостью
Примечания[править | править код]
- ↑ Парабола. Словарь иностранных слов. Дата обращения: 19 июня 2021. Архивировано 14 января 2020 года.
- ↑ Математическая энциклопедия, 1984.
- ↑ Александров П. С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
- ↑ Савелов А. А. Плоские кривые. Систематика, свойства, применения (Справочное руководство)/ Под ред. А. П. Нордена. М.: Физматлит, 1960. С. 250.
- ↑ Битюцков В. И. Степенная функция // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 208—209. — 1248 с.
- ↑ Степенная функция // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 564—565. — 847 с.
Литература[править | править код]
- Акопян А. А., Заславский А. В. Геометрические свойства кривых второго порядка. — М.: МЦНМО, 2007. — 136 с.
- Бронштейн И. Парабола // Квант. — 1975. — № 4. — С. 9—16.
- Маркушевич А. И. Замечательные кривые. — Гостехиздат, 1952. — 32 с. — (Популярные лекции по математике, выпуск 4).
- Парабола // Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 191—192. — 1216 с.
Ссылки[править | править код]
- Статья в справочнике «Прикладная математика».
- Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
- Информация (англ.) о связи параболы с физикой.
- Учебный фильм о параболе
Описание презентации по отдельным слайдам:
-

1 слайд
Алгоритм
нахождения значения коэффициентов a, b, c
по графику квадратичной функции
y= ax2 +bx+c. -

2 слайд
Нахождение коэффициента a
1) по графику параболы определяем координаты вершины (m,n)
2) по графику параболы определяем координаты любой точки А (х1;у1)
3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
4) решаем полученное уравнение. -

3 слайд
Нахождение коэффициента b
1) Сначала находим значение коэффициента a
(шаг I, смотри выше)2)В формулу для абсциссы параболы m= -b/2a подставляем значения
m и a3) Вычисляем значение коэффициента b.
-

4 слайд
Нахождение коэффициента с:
1)Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с)-точка пересечения графика параболы с осью Оу.
2)Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a,b)
3)Подставляем найденные значения a, b , А(х1 ;у1) в уравнение
у=ax2 +bx+c и находим с. -

5 слайд
По графику функции найдите значения коэффициентов a, b, c
-

-

-

Нахождение коэффициентов квадратичной функции y=ax2 + bx +c
I Нахождение коэффициента а :
-
по графику параболы определяем координаты вершины (m,n)
-
по графику параболы определяем координаты любой точки A (x;y)
-
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
y=а(х-m)2+n
-
решаем полученное уравнение.
II. нахождение коэффициента b: b= – (х1 + х2) это для приведённого уравнения
-
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 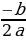 подставляем значения m и а
подставляем значения m и а
-
Вычисляем значение коэффициента b.
III. нахождение коэффициента с: с = х1 ∙ х2 это для приведённого уравнения
-
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
-
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)
-
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах2 +bх+с и находим с.
I Нахождение коэффициента а :
-
по графику параболы определяем координаты вершины (m,n)
-
по графику параболы определяем координаты любой точки A (x;y)
-
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
y=а(х-m)2+n
-
решаем полученное уравнение.
II. нахождение коэффициента b:
-
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 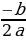 подставляем значения m и а
подставляем значения m и а
-
Вычисляем значение коэффициента b.
III. нахождение коэффициента с:
-
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
-
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)
-
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах2 +bх+с и находим с.
Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:
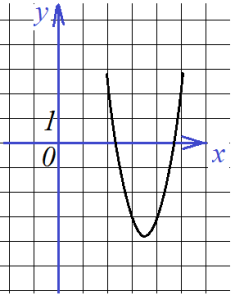
Найти все коэффициенты по графику функции
Подставляем в уравнение:![]() координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:
координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:
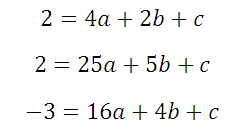
Последние два уравнения вычтем:
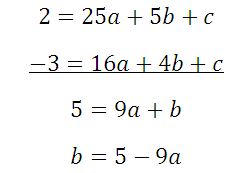
Данное выражение подставим в первое и второе уравнения:
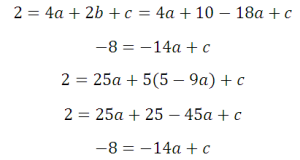
Вычтем два получившихся уравнения:
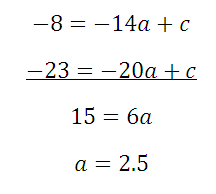 Зная а, можем найти и остальные коэффициенты:
Зная а, можем найти и остальные коэффициенты:
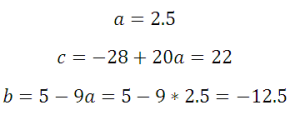
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:
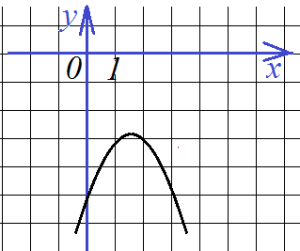
Найти все коэффициенты по графику функции
Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):
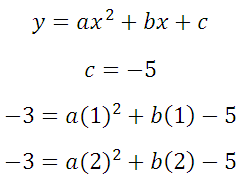
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:
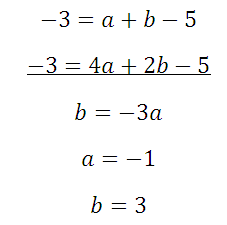
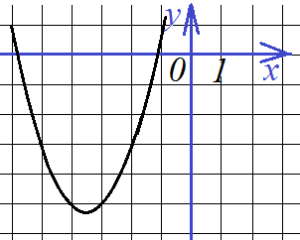
Найти все коэффициенты по графику функции
Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:
Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.
Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:
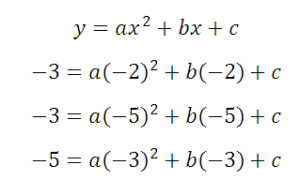
Из первого уравнения вычитаем второе:
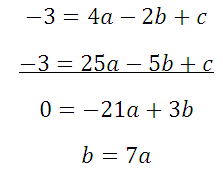
Полученное подставим в первое и третье:
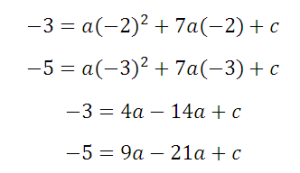
Полученные уравнения вычтем вновь, и найдем искомое:
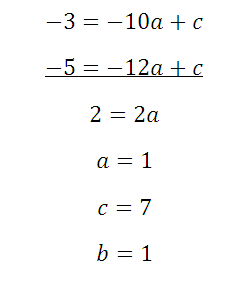
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0. 
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
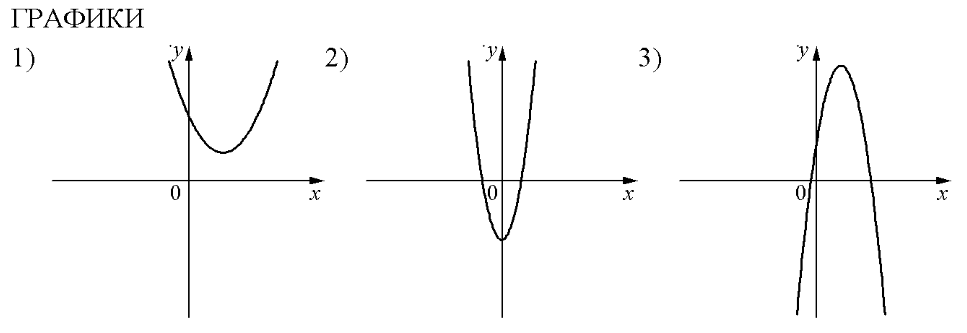
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
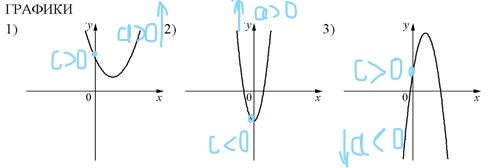
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
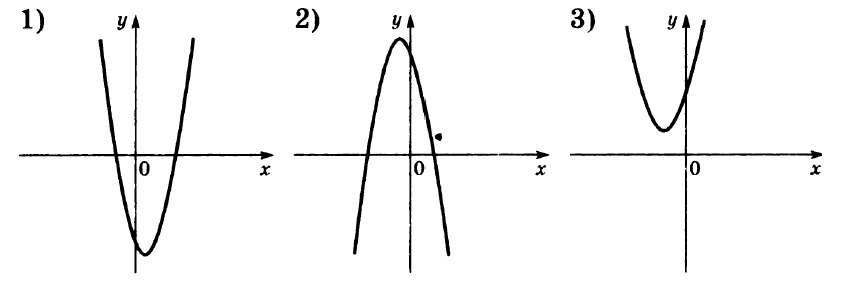
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.5k
















