Четырехугольная призма, в основании которой находится параллелограмм, является параллелепипедом. В параллелепипеде 6 граней: 4 — боковые и 2 — его основание. Грани, как правило, представляют собой параллелограмм. Противолежащие грани параллельны и равны. Параллелепипеды бывают прямыми и наклонными. У прямого параллелепипеда боковые грани являются прямоугольниками. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным. У него все шесть граней — прямоугольники, противоположные стороны которых параллельны и равны, а все углы — прямые. Прямоугольный параллелепипед строится на трех ребрах, расположенных друг к другу под прямым углом. Длины этих ребер, обладающих общим концом, называются его измерениями.
Боковое ребро прямоугольного параллелепипеда можно рассчитать несколькими способами, в зависимости от исходных данных.
Если известны объем (V) и два ребра (b, c) правильного параллелепипеда, третье ребро (а) будет равно частному от деления объема на произведение двух ребер (b×c):
a = V / bc
Если известна площадь боковой поверхности и два ребра (b, c), находим неизвестное ребро (а) путем деления площади боковой поверхности (S) на удвоенную сумму двух известных ребер 2 (b+c).
a = Sб.п. / 2 (a+c)
Если известны два ребра (b, c) и полная площадь поверхности (S п.п.), неизвестное ребро (а) находим по формуле:
a = (Sп.п. — 2bc) / 2 (b+c)
Проведенный внутри параллелепипеда отрезок, соединяющий противоположные вершины двух его оснований, является диагональю параллелепипеда (D). Отрезок, соединяющий противоположные вершины одного из оснований, является диагональю основания (d). Внутри прямоугольного параллелепипеда можно построить прямоугольный треугольник, у которого гипотенузой будет диагональ параллелепипеда D, одним из катетов — диагональ основания d, другим — боковое ребро параллелепипеда (а). Используя теорему Пифагора, выразим квадрат диагонали основания d (гипотенузу) как сумму квадратов его сторон (катетов) b, с. Отсюда, квадрат длины диагонали прямоугольного параллелепипеда (D) равен сумме квадратов трёх его измерений (а,b,с). Зная ребра и диагональ параллелепипеда, находим боковое ребро по формуле:
a = √D2 + d2 = √D2 + b2 + c2
![]()
где b, c — ребра параллелепипеда, a — боковое ребро параллелепипеда, D — диагональ параллелепипеда, d — диагональ основания.
Калькулятор расчета длины бокового ребра правильного параллелепипеда
Прямоугольный параллелепипед является прямой призмой, в основании которой лежит квадрат или прямоугольник, таким образом, совокупность ребер прямоугольного параллелепипеда может представлять собой два или три разных параметра. Если же они все равны между собой, то можно с уверенностью сказать, что такой параллелепипед является кубом, и его ребро можно найти по формулам, приведенным в разделе «Ребро куба».
Ребро прямоугольного параллелепипеда можно найти, зная объем тела и другие ребра:

Также можно рассчитать ребро прямоугольного параллелепипеда через площадь боковой или полной поверхности, тоже зная остальные два ребра:


Как и в случае с кубом, внутри прямоугольного параллелепипеда можно провести диагональ, которая соединит противоположные вершины оснований. В прямоугольном треугольнике диагональ параллелепипеда D будет гипотенузой, а диагональ основания d и ребро a – катетами. Тогда боковое ребро параллелепипеда можно будет найти через теорему Пифагора.


Если дана диагональ параллелепипеда, но нужно найти ребро, не входящее во внутренний прямоугольный треугольник, а являющееся стороной основания, то формула придет к точно такому же виду.
Содержание материала
- Калькулятор расчёта диагонали прямоугольного параллелепипеда зная длину его рёбер, онлайн
- Видео
- Теорема Пифагора
- Прямоугольный параллелепипед
- Объем и площадь поверхности
- Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
- Косоугольная фигура
- Диагонали прямоугольного параллелепипеда: теорема
- Что мы узнали?
Калькулятор расчёта диагонали прямоугольного параллелепипеда зная длину его рёбер, онлайн
| Длина ребра параллелепипеда (a) | |
| Длина ребра параллелепипеда (b) | |
| Длина ребра параллелепипеда (c) |
Площадь параллелепипеда (призмы)Объем параллелепипедаНайти боковое ребро правильного параллелепипеда зная длину ребра и диагональ
Видео
Теорема Пифагора
Теорема справедлива для любого треугольника с прямым углом. Данные исторических архивов свидетельствуют, что греческий философ Пифагор впервые доказал, что при складывании квадратов катетов всегда получается квадрат гипотенузы, то есть стороны, которая лежит против прямого угла.

Теорема Пифагора — полезный геометрический инструмент при расчетах параметров не только треугольников, но и прямоугольников. Если 2 противоположные (несмежные) вершины четырехугольника соединить, получится отрезок, который называется диагональю. Она делит фигуру ровно на 2 половинки, каждая представляет собой треугольник с углом 90 градусов, если исходный четырехугольник является прямоугольным.
Исходя из геометрических построений можно понять, что прямоугольник имеет 2 одинаковые диагонали. Если предположить, что стороны фигуры равны a и b, диагональ c легко рассчитывается по теореме Пифагора: c = (a 2 + b 2 )^0,5.
В случае квадрата получается еще более простая формула: c = a*(2)^0,5.
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
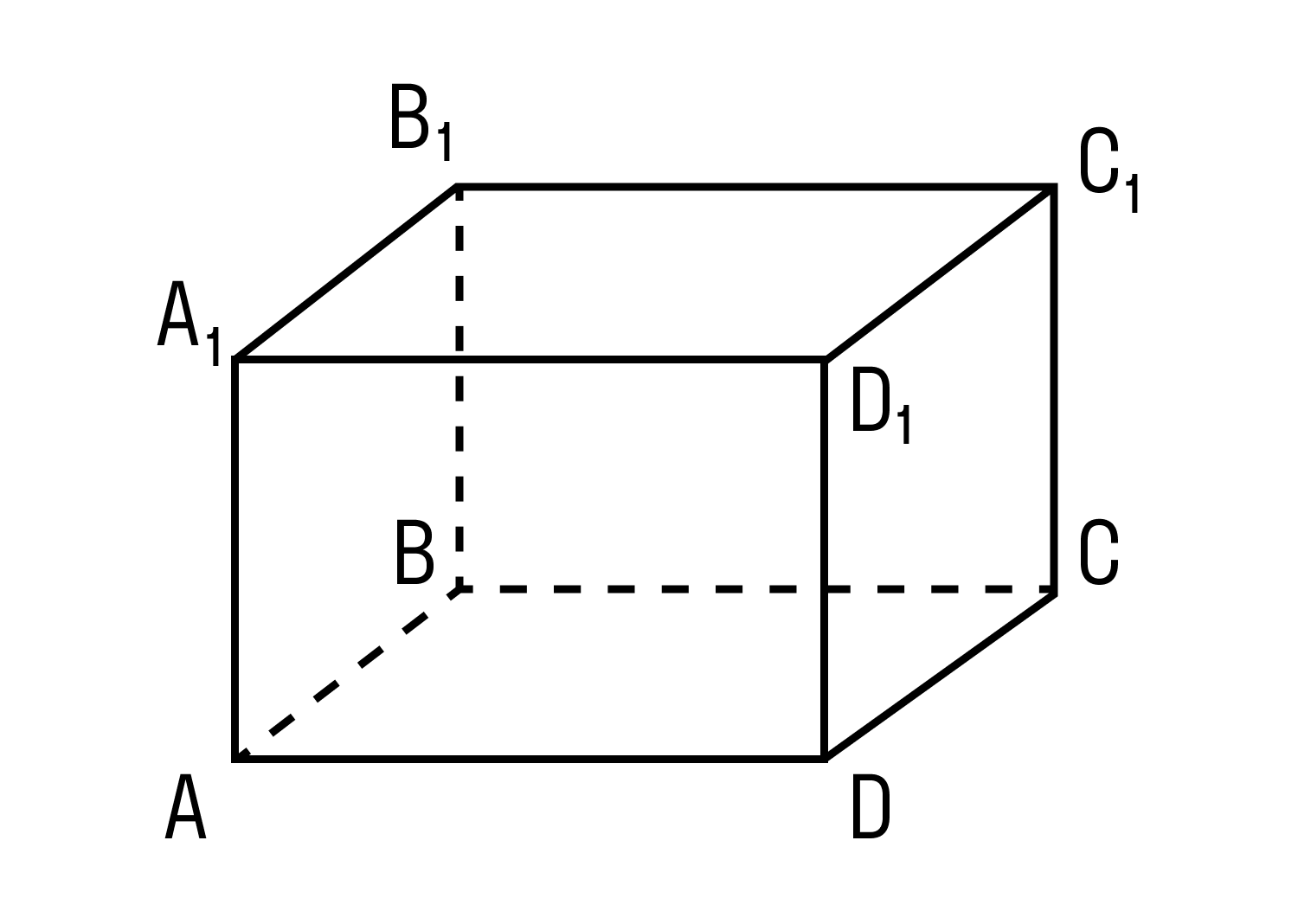
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Объем и площадь поверхности
Полученная формула для диагонали не является исключительно теоретической. Ее можно применять для расчета важных для практики величин, например, объема фигуры и площади ее поверхности.
Объем V и площадь поверхности S вычисляются по таким формулам:
- V = a*b*h;
- S = 2*(a*b + a*h + b*h).
V и S однозначно определяются, если знать 3 линейных параметра фигуры. Одним из них может являться длина объемной диагонали, которая зависит от тех же величин, что V и S.
При решении задач, в которых необходимо найти какой-либо объемный параметр или характеристику площади через известные диагонали, потребуется выполнять вычисления с квадратными и кубическими уравнениями.
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Определение
Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.
(V=acdot bcdot h,)
где V — объем, a — длина, b — ширина, h — высота.
Примечание
Площадь боковой поверхности равна сумме площадей боковых граней.
(S_{бп}=2(ab+ac))
Примечание
Площадь полной поверхности равна сумме площадей боковых граней и оснований.
(S_{пп}=2(ab+bc+ac))
Косоугольная фигура
Параллелепипед бывает не только прямоугольным, но и наклонным или косоугольным. Основной его отличительной чертой является, что боковое ребро наклонено к плоскости прямоугольного основания под некоторым углом, который отличается от 90 градусов. В таком случае высота фигуры оказывается меньше длины этого ребра.
Наклонный параллелепипед также имеет 4 диагонали в объеме, однако они не всегда имеют одинаковую длину. В этом случае не существует какой-либо конкретной формулы для расчета длины. Для решения подобных сложных задач можно воспользоваться двумя методами:

Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
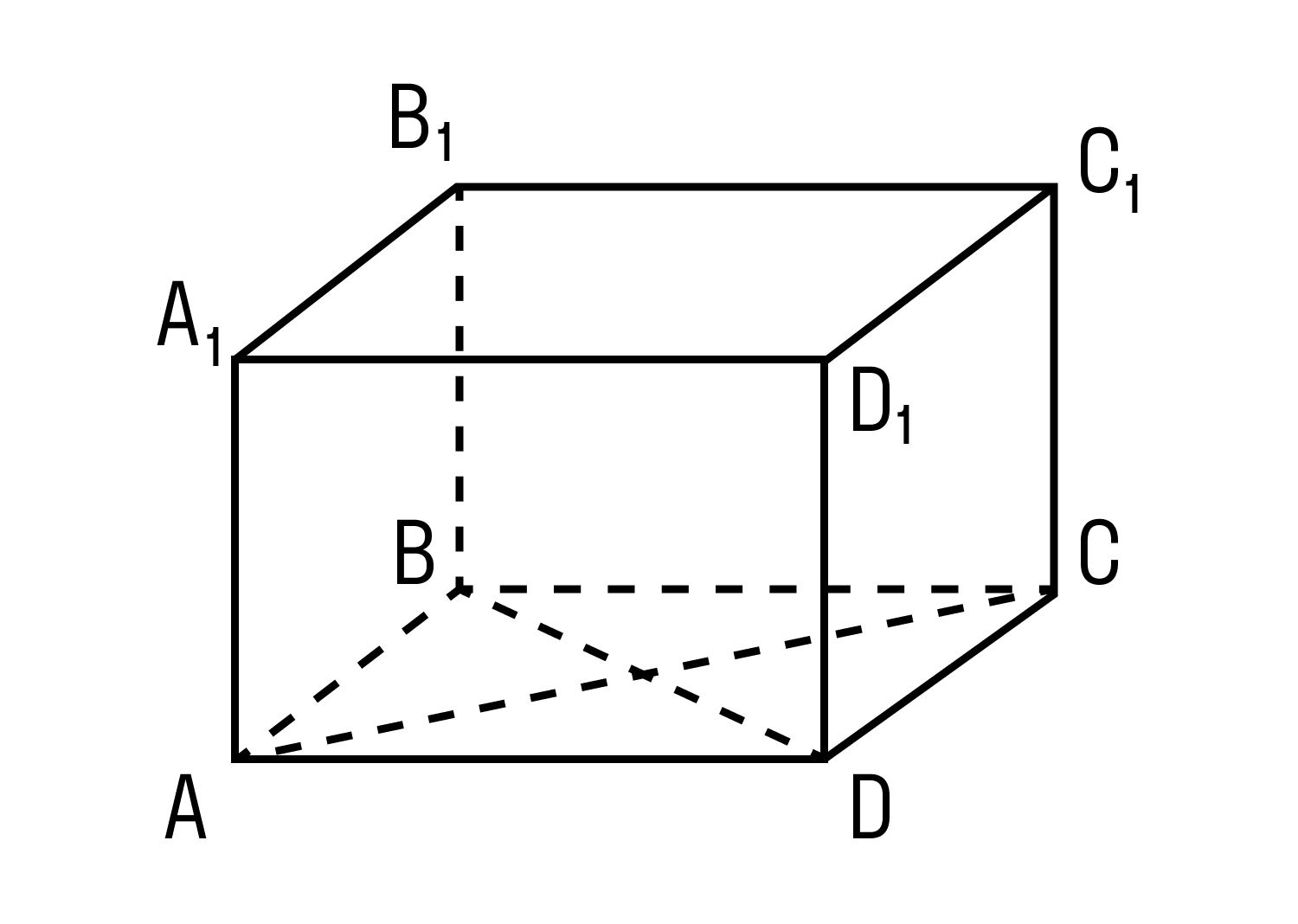
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.

Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Применяем формулу:
d² = a² + b² + c²
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
d₁² = a² + b²
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Что мы узнали?
Мы поговорили о диагоналях прямоугольного параллелепипеда. Узнали, что, используя свойства диагоналей параллелепипеда, можно найти ширину, длину и высоту параллелепипеда. Поговорили о том, как найти центр симметрии, и определить длину диагоналей прямоугольного параллелепипеда.
Теги
Вновь поступил вопрос про прямоугольный параллелепипед. И вопрос этот не простой, смотрите сами:
Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Подскажите, как это переварить?
Вопрос, конечно, не простой — что такое прямоугольный параллелепипед, как и с чем его едят? В частности, как найти рецепт приготовления площади поверхности этого то ли фрукта, то ли овоща? Так, для начала давайте посмотрим, что это вообще такое — прямоугольный параллелепипед? Вот картинка прямоугольного параллелепипеда.
Как видите, прямоугольный параллелепипед — это, собственно, обыкновенный кирпич. Кстати, если бы Ньютону на голову упала не сфера в виде яблока, а прямоугольный параллелепипед в виде кирпича, то в школе мы вряд ли бы учили его законы. Прямоугольная комната — это тоже прямоугольный параллелепипед, который позволяет вам совершить обзорную экскурсию по его достопримечательностям прямо изнутри. Если вы хотите произвести внешний осмотр достопримечательностей сего математического чуда, тогда возьмите в руки коробку из-под обуви и можете вертеть её, сколько душе угодно.
И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать. Нам сейчас диагональ не нужна. Закон движения учеников в классе знаете? Если леди-учитель покидает класс, класс движется быстрее. Закон решения задач очень похож: чем меньше всякой ерунды нам нужно искать, тем проще задача.
Первая проблема, с которой мы сталкиваемся в задаче, это проблема сленга. Задача сформулирована на бытовом сленге, а все формулы и определения в математике формулируются на математическом сленге. Поэтому нам самим предстоит выполнить перевод. Приступаем к поэтапному переводу, по фразам.
«Рёбра прямоугольного параллелепипеда, выходящие из одной вершины …» — собственно, здесь говорится о тех ребрах, которые позволяют нам определить размеры прямоугольного параллелепипеда и на основании этих размеров выполнить все необходимые вычисления. На картинке это ребра a, b и c. Кто бы сомневался, что именно эти три ребра нам дадут по условию, но только не я. Ни один математик вам этого не скажет (не потому, что они этого не знают, а из боязни нарваться на очень неудобные вопросы), но если в условии задачи дать две длины параллельных ребер и одного перпендикулярного им, то нашу задачу в принципе решить будет невозможно. В прямоугольном параллелепипеде из любой вершины всегда выходит три взаимно перпендикулярных ребра. Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества.
Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил (или выдумал эти размеры, что в данном случае принципиального значения не имеет). Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся.
Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются. Вот два способа получения результата в математике.
разные числа + одинаковые единицы измерения = разный результат
одинаковые числа + разные единицы измерения = разный результат
Приблизительно, как в этом счетчике. Крутим одно колесико — меняются числа. Крутим другое колесико — меняются единицы измерения. Так устроена настоящая математика, маленький кусочек которой мы сейчас рассматриваем.
Это уже не детская математика, придуманная специально для того, чтобы мучить нас задачками. Это взрослая математика, одинаковая для всех.
В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.
Теперь нам осталось только достать из глубокого кармана шпаргалку с формулами для прямоугольного параллелепипеда и посмотреть, чего полезного для нас там имеется.
Что вообще есть в этой шпаргалке? Формула диагонали прямоугольного параллелепипеда, формула объема. Есть несколько формул для площади поверхности: полная, основания, боковая. Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания — это площадь донышка или крышки коробки. Площадь боковой поверхности — это боковые стеночки коробки без донышка и крышки. Полная площадь — это боковые стеночки вместе с донышком и крышкой.
Теперь смотрим в условие задачи и определяем, «чё тебе надобно, старче?». А надобно ему (ей, им) «площадь поверхности». Если уточнений типа «боковой» или «основания» нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Заморачиваться с основаниями и боками нам нет смысла.
Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате. Какие именно единицы? А какие вам не жалко или какие вы больше всего любите.
По просьбе учащихся добавляю картинку про сумму длин ребер прямоугольного параллелепипеда.
 |
| Сумма ребер прямоугольного параллелепипеда |
Сумму длин всех ребер параллелепипеда я обозначил через букву «P», поскольку она очень похожа на периметр прямоугольника. Кстати, в формуле длин всех ребер я этого не записал, но если мы возьмем три фигурообразующие грани прямоугольного параллелепипеда, которыми являются прямоугольники, то сумма длин всех ребер параллелепипеда будет равна сумме периметров этих прямоугольников.
Содержание
- Объем параллелепипеда
- Понятие объема
- Объем прямоугольного параллелепипеда
- Как найти ребро куба через объем параллелепипеда
- Как написать хороший ответ?
- Как найти ребро куба через объем параллелепипеда
- Свойства куба:
- Прямоугольный параллелепипед
- Пирамида
- Объем параллелепипеда
- Понятие объема
- Объем прямоугольного параллелепипеда
- Формулы объема геометрических фигур, параллелепипеда
- Определения:
- Типы параллелепипеда.
- Формулы прямоугольного параллелепипеда.
- Геометрические фигуры. Прямой параллелепипед.
- Объем куба
- Как сделать прямоугольный параллелепипед?
- Объем параллелепипеда через стороны
- Параллелепипед: определение, виды и свойства
Объем параллелепипеда

Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
- У равных тел равные объёмы. Например, у двух одинаковых пакетов сока равные объемы.
- Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда
Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
Источник
Как найти ребро куба через объем параллелепипеда
Измерения прямоугольного параллелепипеда равны 4см, 6см, 9см. Найти ребро куба, объём которого равен объёму этого параллелепипеда
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 2
Найдем объем параллелепипеда, он равен произведению трех его измерений: 4*6*9 = 216 см³. Так как объем куба равен кубу его ребра, то ребро искомого куба равно: ∛216 = 6 см
Так как дан прямоугольный параллелепипед, то, по определению, основанием служит прямоугольник
a=4, b=6, c=9
V=S*h
S=a*b
S=4*6=24
h=9
V=24*9
V=216 ( см³)
Vк=Vп
Vк=a³, a — ребро куба
a³=216
a=6 см
Ответ: 6 см
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Источник
Как найти ребро куба через объем параллелепипеда
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
Свойства куба:
1. В кубе $6$ граней и все они являются квадратами.
2. Противоположные грани попарно параллельны.
3. Все двугранные углы куба – прямые.
5. Куб имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Диагональ куба в $√3$ раз больше его ребра
7. Диагональ грани куба в $√2$ раза больше длины ребра.
Пусть $а-$длина ребра куба, $d-$диагональ куба, тогда справедливы формулы:
Площадь полной поверхности: $S_<п.п>=6а^2=2d^2$
Радиус сферы, описанной около куба: $R=/<2>$
Радиус сферы, вписанной в куб: $r=/<2>$
При увеличении всех линейных размеров куба в $k$ раз, его объём увеличится в $k^3$ раз.
При увеличении всех линейных размеров куба в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$-высота(она же боковое ребро);
$S_<п.п>$-площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Формулы вычисления объема и площади поверхности правильной пирамиды.
$h_a$ — высота боковой грани (апофема)
В основании лежат правильные многоугольники, рассмотрим их площади:
- Для равностороннего треугольника $S=√3>/<4>$, где $а$ — длина стороны.
- Квадрат $S=a^2$, где $а$ — сторона квадрата.
Задачи на нахождение объема составного многогранника:
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Источник
Объем параллелепипеда

Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
- У равных тел равные объёмы. Например, у двух одинаковых пакетов сока равные объемы.
- Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.

Формула объема прямоугольного параллелепипеда
Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
Источник
Формулы объема геометрических фигур, параллелепипеда
Определения:
Параллелепипедом называется многогранник, имеющий шесть сторон, каждая из которых представляет из себя параллелограмм.
- Параллелепипеды могут быть наклонными или прямыми.
- Наклонный параллелепипед – это такой параллелепипед, в котором грани не перпендикулярны основанию.
- Прямоугольный параллелепипед – это частный случай, где все грани фигуры являются не просто параллелограммами, а прямоугольниками, и они перпендикулярны основанию.
- Высота параллелепипеда – это расстояние между двумя его противоположными плоскостями (отрезок, перпендикулярный основаниям).
Рассмотрим разные способы, как находить высоту параллелепипеда.
Типы параллелепипеда.
Существует несколько видов параллелепипедов:
Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.
Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов .

Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом . Каждая из граней куба – это равные квадраты .
Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения .
Формулы прямоугольного параллелепипеда.
Прямоугольный параллелепипед с одинаковыми измерениями является кубом . Все 6 граней куба являются равными квадратами .
Обозначим длину ребра куба как n, тогда площадь 1-ой грани:
У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).
Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.
Прямоугольный параллелепипед определяют 3-мя измерениями:
Высота (обозначают как h) равняется длине ребра № 1.
Длина (обозначают как m) равняется длине ребра № 2.
Ширина (обозначают как n) равняется длине ребра № 3.
Площадь всей поверхности параллелепипеда обозначают как S:
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
Площадь боковой поверхности:
где a, b — стороны основания,
c — боковое ребро прямоугольного параллелепипеда.
Площадь полной поверхности:
Геометрические фигуры. Прямой параллелепипед.
Объем куба

Объем куба равен кубу длины его грани.
Как сделать прямоугольный параллелепипед?


Для сборки параллелепипеда потребуется распечатать развёртку на обычном листе формата А4.
Объем параллелепипеда через стороны

Формула для нахождения объема параллелепипеда через стороны: , где a, b, c — стороны параллелепипеда.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.

У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.

Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Источник
Adblock
detector
| Прямой параллелепипед – это параллелепипед с ребром, перпендикулярным плоскости основания. |
| Геометрические фигуры. Прямой параллелепипед. |





