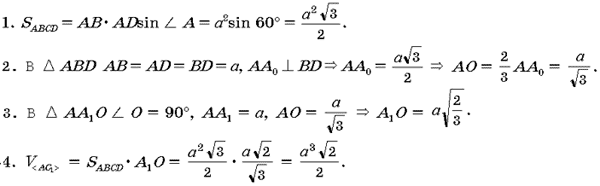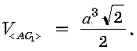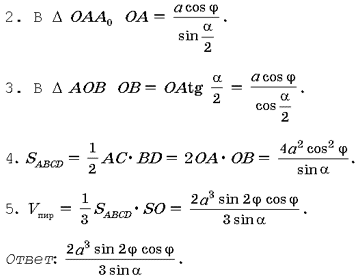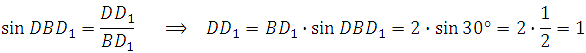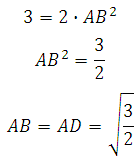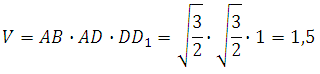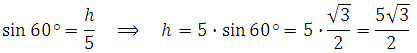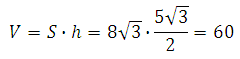Геометрические фигуры. Наклонный параллелепипед. Объем наклонного параллелепипеда.
Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, относительно оснований, под не прямым углом.
Наклонная призма эквивалентна такой прямой призме, у которой основание равняется перпендикулярному сечению наклонной призмы, а высота — ее боковому ребру.
Свойства наклонного параллелепипеда.
1) Каждая его грань – параллелограмм, а противолежащие грани — одинаковые параллелограммы.
2) Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точкой на две равные части.
3) Все параллелепипеды состоят из 6-ти одинаковых по объему треугольных пирамид.
Объем наклонного параллелепипеда.
где Sосн — площадь основания, h – высота.
Объем параллелепипеда можно найти как произведение площади поперечного сечения на боковое ребро:
Кроме того, объем параллелепипеда определяют как произведение площади основания на высоту. Доказывается так, что объем наклонного параллелепипеда равняется объему прямоугольного параллелепипеда с такой же площадью основания и высотой, как и у наклонного параллелепипеда.
Что такое параллелепипед: определение, элементы, виды, свойства
В данной публикации мы рассмотрим определение, элементы, виды и основные свойства параллелепипеда, в т.ч. прямоугольного. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение параллелепипеда
Параллелепипед – это геометрическая фигура в пространстве; шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.
Параллелепипед – это разновидность призмы с параллелограммом в качестве оснований. Основные элементы фигуры те же, что и у призмы.
Примечание: Формулы для расчета площади поверхности (для прямоугольной фигуры) и объема параллелепипеда представлены в отдельных публикациях.
Виды параллелепипедов
- Прямой параллелепипед – боковые грани фигуры перпендикулярны ее основаниям и являются прямоугольниками.
- Прямой параллелепипед может быть прямоугольным – основаниями являются прямоугольники.
- Наклонный параллелепипед – боковые грани не перпендикулярны основаниям.
- Куб – все грани фигуры являются равными квадратами.
- Если все грани параллелепипеда – это одинаковые ромбы, он называется ромбоэдром.
Свойства параллелепипеда
1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами.
2. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам.
3. Квадрат диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины (a), ширины (b) и высоты (c).
d 2 = a 2 + b 2 + c 2
Примечание: к параллелепипеду, также, применимы свойства призмы.
Прямоугольный параллелепипед. Что это такое?
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
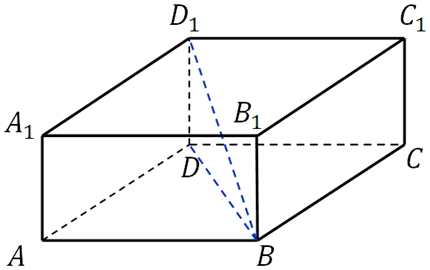
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a – длина, b – ширина, c – высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) – сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) – сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) – сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X – сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°.
По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 – AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB = 1.
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/pryamougolnyj-parallelepiped
[/spoiler]
Основание прямого параллелепипеда – ромб.
Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений P и Q.
На странице вопроса Основание прямого параллелепипеда – ромб? из категории Геометрия вы найдете
ответ для уровня учащихся 10 – 11 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.
Э. Капленко,
г. Воронеж
Чертеж в
стереометрических задачах
Пособие для учителей
11 класс
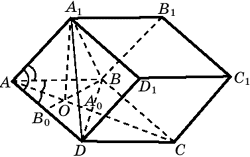
Задача № 7. Грани параллелепипеда – равные
ромбы со стороной a и острым углом 60°.
Найдите объем параллелепипеда.
Нужно обосновать построение изображения
высоты параллелепипеда.
1. Обоснование чертежа
Предположим, что ABCDA1B1C1D1
– параллелепипед с нижним основанием ABCD, все
грани которого являются ромбами со стороной a и
острым углом 60°. Очевидно, что при одной вершине
параллелепипеда, каждая из которых является
также вершиной трехгранного угла, могут
сочетаться лишь плоские углы с градусными мерами
{60°; 60°; 60°} или {60°; 120°; 120°} (это следует из свойств
многогранных углов; сумма всех плоских углов
меньше 360°; каждый из плоских углов меньше суммы
всех остальных). Будем считать, что в вершине A
сходятся три плоских угла по 60°.
Предполагая, что O – проекция вершины A1 на
плоскость нижнего основания (т. е. что A1O
– одна из высот параллелепипеда), можно
заключить, что O принадлежит диагонали AC ромба ABCD
(рис. 8).
Рис. 8
Учитывая величины внутренних углов
ромбов-граней, нетрудно установить, что пирамида
A1ABD является правильным тетраэдром, и
потому основанием высоты A1O этого тетраэдра
является центр правильного треугольника ABD (на
чертеже это точка пересечения медиан). Ввиду
полученных результатов можно установить
наиболее рациональную последовательность
конструирования чертежа: его следует начать с
построения правильного тетраэдра A1ABD,
который затем достроить до параллелепипеда.
2. Вычислительная часть
Дано: ABCDA1B1C1D1 –
параллелепипед с высотой A1O (OОAC)
и нижним основанием ABCD; AB=AD=AA1 = a, РA1AB=РBAD=РA1AD = 60°.
Найти .
Решение.
Ответ:
Задача № 8. Дан куб ABCDA1B1C1D1
(ABCD – нижнее основание). Найдите величину угла
между плоскостью грани ABB1A1 куба и
плоскостью, проходящей через диагональ AB1
этой грани и середину M ребра DC куба.
Необходимо обосновать:
а) построение сечения куба плоскостью AB1M;
б) построение линейного угла двугранного угла
между плоскостью ABB1 и секущей плоскостью AB1M.
1. Обоснование чертежа
а) Для построения сечения данного куба
плоскостью AB1M найдем K = AMЗBC,
соединим K с вершиной B1 и найдем N = BKЗCC1.
Соединив точки M и N, получим четырехугольник AB1NM,
который и является сечением.
Из равенства треугольников ADM и KCM следует, что KC
= AD, а из равенства DCKN и DC1B1N
следует, что CN = C1N, т. е. что N – середина
ребра CC1. Легко видеть, что DAB1K
равнобедренный, а сечение AB1NM является
равнобочной трапецией (AB1пкMN,
так как это линии пересечения параллельных
плоскостей плоскостью AB1M) (рис. 9).
Рис. 9
б) Рассмотрим двугранный угол с ребром AB1
(т. е. угол, образованный полуплоскостями AB1B
и AB1K). Для плоскости ABB1 прямая KB
является перпендикуляром (KB^BA, KB^BB1 Ю KB^(ABB1)),
а прямая KO – наклонной (O = AB1ЗA1B),
поэтому OB – проекция OK на плоскость ABB1. На
основании определения угла между прямой и
плоскостью как угла между прямой и ее проекцией
на эту плоскость можно заключить, что Р BOK
– угол между плоскостью грани ABB1A1
куба и секущей плоскостью AB1M.
2. Вычислительная часть
Дано: ABCDA1B1C1D1 – куб; M –
середина DC, AMЗBC = K, BKЗCC1
= N – середина CC1; РBOK –
линейный угол двугранного угла при ребре AB1.
Найти РBOK.
Решение. Пусть a – длина ребра куба.
Ответ:
Задача № 9. В правильной четырехугольной
призме через середины двух смежных сторон
основания проведена плоскость, пересекающая три
боковых ребра и наклоненная к плоскости
основания под углом j. Сторона
основания равна a. Найдите площадь полученного
сечения.
Необходимо обосновать:
а) построение сечения куба заданной плоскостью;
б) построение линейного угла двугранного угла
между секущей плоскостью и плоскостью основания
куба.
1. Обоснование чертежа
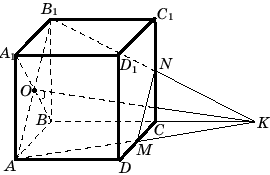
Пусть ABCDA1B1C1D1 – данная
призма. Так как она правильная, то ее основания –
квадраты, а боковые ребра перпендикулярны
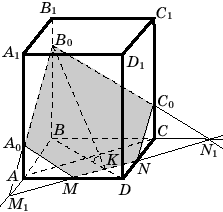
плоскостям оснований. Пусть M – середина AD, N –
середина DC. Возьмем произвольную точку B0 на ребре
BB1 и будем считать (B0MN) секущей
плоскостью.
а) Построение сечения начнем с построения
точек M1=MNЗAB и N1=MNЗBC. Точки M1 и B0 лежат в
плоскости грани ABB1A1, а N1 и B0
– в плоскости грани BCC1B1. Проводя
через них прямые, получим вершины сечения на
ребрах AA1 и CC1, A0=M1B0ЗAA1, C0=N1B0ЗCC1. Искомым сечением является
пятиугольник MA0B0C0N (рис. 10).
Рис. 10
Легко видеть, что пятиугольник MA0B0C0N
симметричен относительно прямой B0K (это
следует из того, что диагональная плоскость BDD1B1
является плоскостью симметрии для данной призмы,
ввиду чего пары точек M®N, A0®C0 симметричны относительно
нее).
б) Для построения линейного угла двугранного
угла с ребром MN между плоскостями B0MN и ABC
нужно пересечь его плоскостью, перпендикулярной
ребру. На чертеже такой плоскостью является (BB0K).
В самом деле, BK^MN, так как BK^AC (диагонали квадрата
перпендикулярны) и MNпкAC (MN –
средняя линия DACD); B0K^MN
– по теореме о трех перпендикулярах; таким
образом, прямая MN оказывается перпендикулярной
двум пересекающимся прямым BK и B0K плоскости
BB0K, поэтому на основании признака
перпендикулярности прямой и плоскости MN^(BB0K). Теперь можно применить
определение линейного угла двугранного угла, из
которого следует, что РB0KB –
линейный угол двугранного угла между секущей
плоскостью и плоскостью основания призмы. По
условию РB0KB=j.
2. Вычислительная часть
Дано: ABCDA1B1C1D1 –
правильная призма, ABCD и A1B1C1D1
– квадраты, AB = a; M – середина AD, N – середина
DC, B0ОBB1; MA0B0C0N
– сечение куба (A0ОAA1, C0ОCC1); РB0KB=j (K=MNЗBD).
Найти
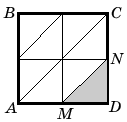
Решение. 1. SABCD = a2.
2. (это
легко видеть из разбиения квадрата на
треугольники его средними линиями, одной
диагональю и средними линиями треугольников, на
которые диагональ разбивает этот квадрат) (рис. 11).
Рис. 11
3. Пятиугольник MABCN является ортогональной
проекцией пятиугольника MA0B0C0N.
Так как угол между плоскостями этих
пятиугольников известен (j), то
можно воспользоваться известной теоремой об
ортогональной проекции многоугольника, SF’ =
SFcos j, где F –
многоугольник, а F’ – его ортогональная проекция
на плоскость, которая образует с плоскостью
многоугольника F угол j.
Ответ:
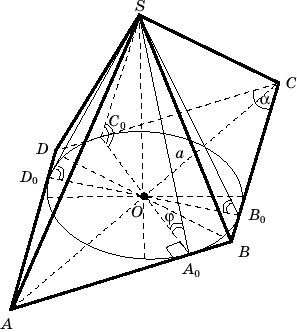
Задача № 10. Образующая прямого кругового
конуса равна a и составляет с плоскостью
основания угол j. Найдите объем
описанной около конуса пирамиды, основанием
которой служит ромб с острым углом a.
Необходимо обосновать:
а) построение изображения пирамиды с
ромбическим основанием, описанной около конуса;
б) построение изображения угла между
какой-нибудь образующей конуса и плоскостью
основания.
1. Обоснование чертежа
а) Будем считать, что изображение прямого
кругового конуса дано. Тогда построение
описанной около него пирамиды с ромбическим
основанием сведется к построению изображения
ромба, описанного около данной окружности (а это
одно из базовых построений на изображениях
плоских фигур); сначала проводится анализ
оригинала основания, затем строится изображение
основания, которое затем достраивается до
изображения полной фигуры.
Анализ оригинала основания. – два произвольных
диаметра окружности; стороны ромба –
касательные к окружности в концах этих диаметров
(рис. 12).
Рис. 12
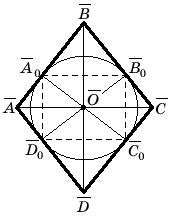
Построение изображения основания. A0C0
и B0D0 – два произвольных (не
сопряженных) диаметра эллипса; AB, BC, CD, AD –
касательные к эллипсу в точках A0, B0, C0,
D0 (рис. 13).
Рис. 13
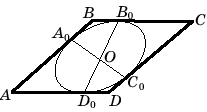
Итак, пусть SABCD – пирамида, описанная около
конуса. Это означает, что пирамида и конус имеют
общую высоту SO, где O = ACЗBD – центр
окружности, лежащий в основании конуса. Если при
этом A0, B0, C0, D0 – точки
касания сторон AB, BC, CD, DA ромба ABCD и окружности
основания конуса, то SA0, SB0, SC0, SD0
– образующие конуса, которые являются линиями
прикосновения боковой поверхности конуса с
боковыми гранями пирамиды, рис. 14.
Рис. 14
б) Возьмем образующую SA0, она является
наклонной к плоскости основания. Тогда OA0 –
проекция этой образующей на плоскость основания.
По определению угла между прямой и плоскостью, РSA0O – это угол, который
составляет с плоскостью основания образующая SA0.
По условию РSA0O=j.
2. Вычислительная часть
Дано: F – конус с высотой SO; SA0 –
образующая, SA0=a, РSA0O=j; SABCD – пирамида, описанная около
конуса F: SA0, SB0, SC0, SD0 –
линии прикосновения конуса и пирамиды; ABCD – ромб,
РA=РC=a<
90°.
Найти VSABCD.
Решение.
1. В D SOA0 SO = asin j, OA0=acos j.
Задачи для самостоятельного
решения (с указаниями)
1. В основании пирамиды лежит треугольник с
внутренними углами a и b
и радиусом описанной окружности R. Все боковые
ребра пирамиды наклонены к плоскости основания
под углом g. Найдите объем
пирамиды.
Указание. Нужно обосновать:
а) построение изображения основания высоты
пирамиды;
б) построение углов между боковыми ребрами
пирамиды и плоскостью ее основания.
Ответ:
2. В прямоугольном параллелепипеде стороны
основания равны a и b, а его диагональ
составляет с боковой гранью, содержащей сторону a,
угол 30°. Найдите объем параллелепипеда.
Указание. Нужно обосновать построение угла
между диагональю параллелепипеда и его боковой
гранью.
Ответ:
3. Чему равен объем прямоугольного
параллелепипеда, диагональ которого длины a
составляет с плоскостью основания угол a, а с боковой гранью – угол b?
Указание. Нужно обосновать:
а) построение угла между диагональю
параллелепипеда и плоскостью основания;
б) построение угла между диагональю и плоскостью
боковой грани.
Ответ:
4. В прямом параллелепипеде стороны
основания равны 3 см и 5 см, а одна из
диагоналей основания равна 4 см. Найдите длину
большей диагонали параллелепипеда, зная, что
меньшая образует с плоскостью основания угол 60°.
Указание. Установить, какая из диагоналей
параллелепипеда является меньшей (использовать
свойства наклонных к плоскости и их проекций на
эту плоскость). Обосновать построение угла между
меньшей диагональю и плоскостью нижнего
основания параллелепипеда.
Ответ: 10 см.
5. Основанием прямого параллелепипеда служит
ромб со стороной 4 см и углом 60°. Большая
диагональ параллелепипеда образует с плоскостью
основания угол 45°. Найдите боковую поверхность
параллелепипеда.
Указание. Установить, какая из диагоналей
параллелепипеда является большей. Обосновать
построение угла между этой диагональю и
плоскостью нижнего основания.
Ответ: .
6. Одно ребро тетраэдра равно 4 см, а каждое
из остальных 3 см. Найдите объем тетраэдра.
Указание. Обосновать построение изображения
основания высоты пирамиды. В качестве основания
тетраэдра можно брать равнобедренный
треугольник (тогда все боковые ребра равны) или
равносторонний треугольник; в первом случае
обоснование чертежа является более простым.
Ответ:
7. Высота правильной четырехугольной
пирамиды равна см,
а ее боковое ребро см. Найдите величину двугранного угла
при основании пирамиды.
Указание. Нужно обосновать:
а) в какую точку плоскости основания
проецируется вершина пирамиды;
б) построение на чертеже линейного угла
двугранного угла при основании пирамиды.
Ответ: 60°.
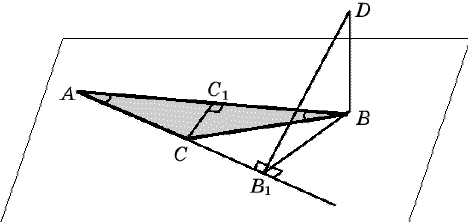
8. В треугольнике ABC AC=BC=10 см, РA=РB=30°. Прямая BD перпендикулярна
плоскости данного треугольника и BD=5 см.
Найдите расстояние от точки D до прямой AC.
Указание. Нужно обосновать построение
изображения перпендикуляра из точки D на прямую
AC. При этом следует учесть, что РACB
тупой, и потому основание этого перпендикуляра
будет внешней точкой по отношению к отрезку AC
(рис. 15).
Рис. 15
Ответ: 10.
9. Точка M, лежащая вне плоскости данного
прямого угла, удалена от вершины угла на
расстояние a, а от его сторон на расстояние b.
Найдите расстояние от точки M до плоскости угла.
Указание. Обосновать построение проекций точки
M на плоскость, в которой лежит данный угол, и на
его обе стороны.
Ответ:
10. В равнобедренном треугольнике основание и
высота равны 4 см. Данная точка находится на
расстоянии 6 см от плоскости треугольника и на
равных расстояниях от его вершин. Найдите это
расстояние.
Указание. Необходимо обосновать построение
изображения основания перпендикуляра из данной
точки на плоскость данного треугольника.
Ответ: 6,5.
11. Основанием пирамиды является
прямоугольный треугольник с катетами 6 см и
8 см. Все двугранные углы при основании
пирамиды равны 60°. Найдите высоту пирамиды.
Указание. Нужно обосновать:
а) построение точки, являющейся основанием
высоты пирамиды;
б) построение линейных углов двугранных углов
при основании пирамиды.
Ответ:
12. Вычислите объем четырехугольной пирамиды,
в основании которой лежит равнобедренная
трапеция с нижним основанием 2 см, боковой
стороной 1 см и острым углом 60°, если известно,
что все боковые ребра пирамиды равны 2 см.
Указание. Обосновать построение изображения
высоты (доказать при проведении обоснования
чертежа, что основанием высоты пирамиды будет
являться середина нижнего основания трапеции).
Ответ:
13. Дан куб ABCDA1B1C1D1 с ребром a.
Вычислите площадь сечения этого куба плоскостью,
проходящей через диагональ AB1 боковой
грани и середину M ребра CD.
Ответ: .
14. Найдите площадь сечения куба ABCDA1B1C1D1
плоскостью, проходящей через вершину D и середины
M и N ребер A1B1 и B1C1, если
ребро куба равно 1.
Ответ:
15. Высота цилиндра 8 см, радиус основания
5 см. Цилиндр пересечен плоскостью так, что в
сечении получается квадрат. Найдите расстояние
от плоскости сечения до оси цилиндра.
Указание. Доказать, что в сечении цилиндра
плоскостью может получиться квадрат лишь в том
случае, когда секущая плоскость параллельна оси
цилиндра, причем высота цилиндра не должна
превышать диаметра основания. Обосновать
построение отрезка, выражающего расстояние от
прямой (оси цилиндра) до параллельной ей
плоскости (секущей).
Ответ: 3.
16. Образующая конуса равна 6 см и образует
с его основанием угол 45°. Найдите площадь сечения
конуса плоскостью, проведенной через две его
образующие, угол между которыми равен 60°.
Указание. Необходимо обосновать:
а) построение угла между образующей конуса и
плоскостью его основания;
б) существование сечения, проходящего через две
образующие, угол между которыми равен 60°
(найдутся ли среди множества образующих конуса
две такие, угол между которыми 60°?).
Ответ:
17. Высота конуса равна 6. Образующая конуса
составляет с плоскостью основания угол 60°. В
конус помещена пирамида, основанием которой
служит равнобедренный прямоугольный
треугольник, вписанный в основание конуса, а
вершиной – середина одной из образующих конуса.
Найдите объем пирамиды.
Ответ: 12.
18. В тетраэдре ABCD все ребра, кроме AB, имеют
равные длины. Угол ACB – прямой. Найдите величину
двугранного угла при ребре BC.
Указание. Нужно обосновать:
а) построение изображения высоты пирамиды;
б) построение изображения линейного угла
двугранного угла при ребре BC.
Ответ:
Окончание. См. № 27–28/2002.
.
Предлагаю вашему вниманию ещё две задачи с параллелепипедами. На данный момент рассмотрены почти все задачи с кубами и параллелепипедами, которые присутствуют в открытом банке заданий ЕГЭ по математике. С ними вы можете ознакомиться, посмотрев предыдущие статьи. В представленных ниже задачах есть некоторые особенности. Что ж, приступим:
Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна 2 и образует с плоскостью этой грани угол 300. Найдите объем параллелепипеда.
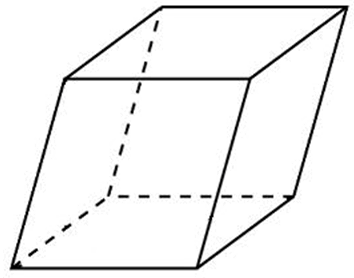
Построим данный параллелепипед. Сказано, что диагональ образует с гранью, являющейся квадратом угол в 300, поэтому выполним построение следующим образом – грань в основании у нас будет являться квадратом, далее на этом основании строим сам параллелепипед, затем строим диагональ и обозначаем вершины:
Угол между диагональю и основанием это угол DBD1 в прямоугольном треугольнике BD1D, так как плоскость проходящая через точки D, B и D1 в данном параллелепипеде перпендикулярна плоскости основания.
Для того, чтобы найти объём параллелепипеда нам нужно знать три его рёбра.
В прямоугольном треугольнике BD1D мы можем найти DD1, так как нам известна его гипотенуза и острый угол:
Для того, чтобы найти рёбра AB и AD, достаточно знать чему равна диагональ BD квадрата ABCD.
Отрезок BD мы также можем найти из рассмотренного нами прямоугольного треугольника. По теореме Пифагора:
Теперь найдём АВ. По теореме Пифагора:
Так как AB = AD, то
Значит
Теперь можем найти объём параллелепипеда:
Ответ: 1,5
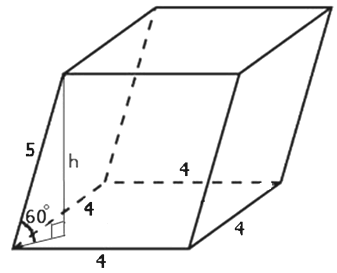
Гранью параллелепипеда является ромб со стороной 4 и острым углом 600. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 600 и равно 5. Найдите объем параллелепипеда.
*Условие данной задачи может некоторых немного «запутать», тем более, если не будет дан рисунок. Вроде как речь идёт об одной какой-то грани, которая является ромбом…
У кого-то может возникнуть вопрос: а что с остальными гранями, чем они являются и как расположены?
Так же сказано, что одно из рёбер с плоскостью этой грани составляет угол 600. Об остальных рёбрах вроде как и нет речи.
Здесь всё просто. Нужно помнить что представляет из себя параллелепипед – это тело, гранями которого являются параллелограммы.
Вернёмся к условию. Так как сказано, что одна из граней это ромб и одно из рёбер с данной гранью составляет угол 600, то смело можете сразу эту грань принять как основание параллелепипеда, при чём все остальные рёбра будут расположены под тем же углом к основанию, что оговоренное в условии.
Условие задачи могло бы звучать так:
Основанием параллелепипеда является ромб со стороной 4 и острым углом 600. Боковые рёбра параллелепипеда составляют с плоскостью этой грани угол 600 и равны 5. Найдите объем параллелепипеда.
Строим сам параллелепипед:
Покажем на эскизе заданные размеры:
Объём параллелепипеда равен произведению площади его основания и высоты:
S – площадь основания параллелепипеда
h – высота параллелепипеда
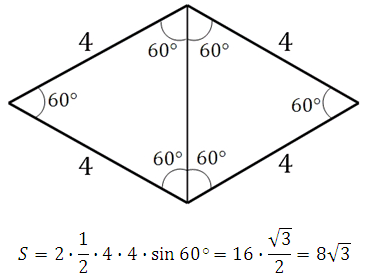
Площадь ромба (основание параллелепипеда) с острым углом в 60° равна двум площадям равносторонних треугольников:
*Использовали формулу: площадь треугольника равна половине произведения соседних сторон на синус угла межу ними.
Высоту можем найти из прямоугольного треугольника, в котором нам известна гипотенуза равная пяти и острый угол 600. По определению синуса в прямоугольном треугольнике:
Вычисляем объем:
Ответ: 60
27103. Диагональ прямоугольного параллелепипеда равна корню из восьми и образует углы 300, 300 и 450 с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Посмотреть решение
27104. Гранью параллелепипеда является ромб со стороной 1 и острым углом 600. Одно из ребер параллелепипеда составляет с этой гранью угол в 600 и равно 2. Найдите объем параллелепипеда.
Посмотреть решение
В будущем продолжим рассматривать задачи по стереометрии, не пропустите!
На этом всё! Успеха вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задание. В основании прямого
параллелепипеда лежит ромб. Найдите значение выражения S2, где S – площадь боковой
поверхности прямого параллелепипеда, если площади его диагональных сечений
равны 3 и √7.
Решение.
Прямой
параллелепипед – это такой параллелепипед, в основании которого лежит
параллелограмм (по условию – ромб), а боковые грани являются прямоугольниками. Sбок=Pосн∙h,
где h –
высота параллелепипеда. Диагональными сечениями являются прямоугольники, одна
сторона которых является диагональю основания, а другая – высотой (h).
Рассмотрим рисунок основания. ABCD – ромб, лежащий в основании
параллелепипеда. AC = √7/h;
BD
= 3/h. (следует из площадей диагональных
сечений). Пусть диагонали пересекаются в точке O, тогда рассмотрим треугольник BOC, у него BO=BD/2=3/2h;
CO=AC/2=√7/2h,
по теореме Пифагора находим гипотенузу:BC
= √(9/4h2+7/4h2)=√4/h2=2/h. Значит, периметр основания 4∙2/h =8/h. Тогда Sбок=Pосн∙h=8/h∙h=8
S2=64
Ответ. 64