Параметрические уравнения сторон треугольника как найти

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 ( x 1 , y 1 ) и направляющий вектор заданной прямой a → = ( a x , a y ) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М ( x , y ) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = ( x – x 1 , y – y 1 ) . Опишем полученное: прямая задана множеством точек М ( x , y ) , проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) являются коллинеарными.

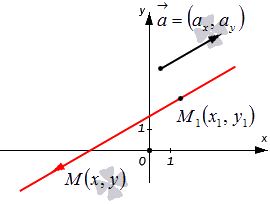
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = ( x – x 1 , y – y 1 ) и a → = ( a x , a y ) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x – x 1 = λ · a x y – y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 ( x 1 , y 1 ) и имеет направляющий вектор a → = ( a x , a y ) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 ( 2 , 3 ) и ее направляющий вектор a → = ( 3 , 1 ) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

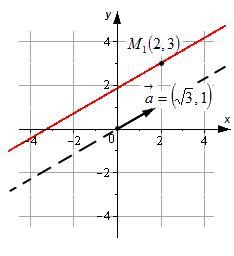
Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = ( a x , a y ) служит направляющим вектором прямой а, а точки М 1 ( x 1 , y 1 ) и М 2 ( x 2 , y 2 ) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = ( 2 , – 1 ) , а также точки М 1 ( 1 , – 2 ) и М 2 ( 3 , – 3 ) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = – 2 – λ или x = 3 + 2 · λ y = – 3 – λ .

Следует обратить внимание и на такой факт: если a → = ( a x , a y ) – направляющий вектор прямой a , то ее направляющим вектором будет и любой из векторов μ · a → = ( μ · a x , μ · a y ) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = – 2 – 5 · λ . Тогда a → = ( 2 , – 5 ) – направляющий вектор этой прямой. А также любой из векторов μ · a → = ( μ · 2 , μ · – 5 ) = 2 μ , – 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор – 2 · a → = ( – 4 , 10 ) , ему соответствует значение μ = – 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 – 4 · λ y = – 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x – x 1 a x = y – y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = – 2 – 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = – 2 – 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = – 2 – 4 · λ ⇔ λ = x – 3 0 λ = y + 2 – 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x – 3 0 = y + 2 – 4

Ответ: x – 3 0 = y + 2 – 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y ⇔ x – x 1 a x = y – y 1 a y ⇔ ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ A x + B y + C = 0

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = – 1 + 2 · λ y = – 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = – 1 + 2 · λ y = – 3 · λ ⇔ λ = x + 1 2 λ = y – 3 ⇔ x + 1 2 = y – 3

Полученная пропорция идентична равенству – 3 · ( x + 1 ) = 2 · y . Раскроем скобки и получим общее уравнение прямой: – 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x – x 1 a x = y – y 1 a y . Каждое из отношений этого равенства примем равным параметру λ :

x – x 1 a x = y – y 1 a y = λ ⇔ λ = x – x 1 a x λ = y – y 1 a y

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x – 2 5 = y – 2 2

Решение

Приравняем части известного уравнения к параметру λ : x – 2 5 = y – 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x – 2 5 = y – 2 2 = λ ⇔ λ = x – 2 5 λ = y – 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x – 3 y – 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x – 3 y – 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = – 1 3 + 4 · λ

Ответ: x = 3 · λ y = – 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа ( x , y ) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 – 1 6 · λ y = – 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 – 1 6 · 3 y = – 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 ( x 0 , y 0 ) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки М 0 ( 4 , – 2 ) и N 0 ( – 2 , 1 ) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = – 1 – 1 2 · λ .

Решение

Подставим координаты точки М 0 ( 4 , – 2 ) в заданные параметрические уравнения:

4 = 2 · λ – 2 = – 1 – 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

Далее по аналогии проверим заданную точку N 0 ( – 2 , 1 ) , подставив ее координаты в заданные параметрические уравнения:

– 2 = 2 · λ 1 = – 1 – 1 2 · λ ⇔ λ = – 1 λ = – 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 ( – 2 , 1 ) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Пример 8

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y – 3 – 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y – 3 – 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y – 3 – 1 , который запишем в виде: a → = ( 2 , – 1 ) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + ( – 1 ) · λ ⇔ x = 1 2 + x · λ y = 2 3 – λ

Ответ: x = 1 2 + x · λ y = 2 3 – λ .

Задана точка М 1 ( 0 , – 7 ) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты ( 3 , – 2 ) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = – 7 + ( – 2 ) · λ ⇔ x = 3 · λ y = – 7 – 2 · λ

Ответ: x = 3 · λ y = – 7 – 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Пример 10

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 – 3 4 · λ y = – 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 – 3 4 · λ y = – 1 + λ ⇔ λ = x – 1 – 3 4 λ = y + 1 1 ⇔ x – 1 – 3 4 = y + 1 1 ⇔ ⇔ 1 · x – 1 = – 3 4 · y + 1 ⇔ x + 3 4 y – 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 – 3 4 · λ y = – 1 + λ имеет координаты 1 , 3 4 .

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parametricheskie-uravnenija-prjamoj-na-ploskosti/

[/spoiler]

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

210

Определить,
какие из точек M₁(3;
1), M₂(2;
3), M₃(6;
3), M₄(-3;
-3), M₅(3;
-1), M₆(-2;
1) лежат на прямой
и
какие на ней не лежат.

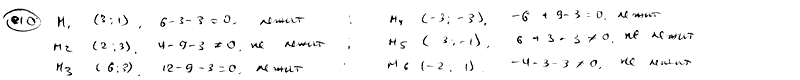
211

Точки
P₁,
P₂,
P₃,
P₄,
P₅
расположены на прямой
;
их абсциссы соответственно равны
числам 4; 0; 2; -2; -6. Определить ординаты
этих точек.

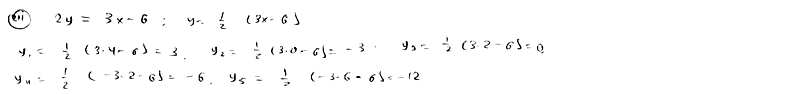
212

Точки
Q₁,
Q₂,
Q₃,
Q₄,
Q₅
расположены на прямой
;
их ординаты соответственно равны
числам 1; 0; 2; -1, 3. Определить абсциссы
этих точек.

213

Определить
точки пересечения прямой
с
координатными осями и построить эту
прямую на чертеже.

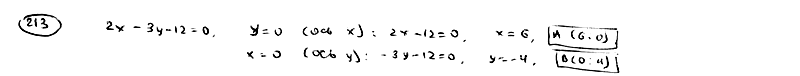
214

Найти
точку пересечения двух прямых
,.

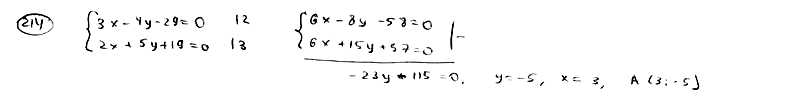
215

Стороны
АВ, ВС и АС треугольника АВС даны
соответственно уравнениями
,,.
Определить координаты его вершин.

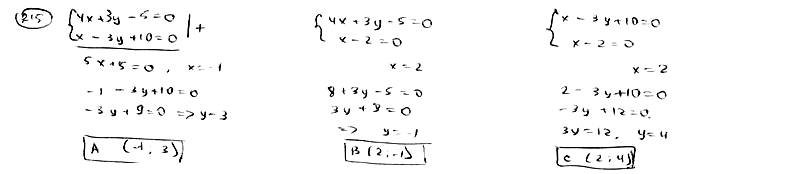
216

Даны
уравнения двух сторон параллелограмма
,и
уравнение одной из его диагоналей.
Определить координаты вершин этого
параллелограмма.

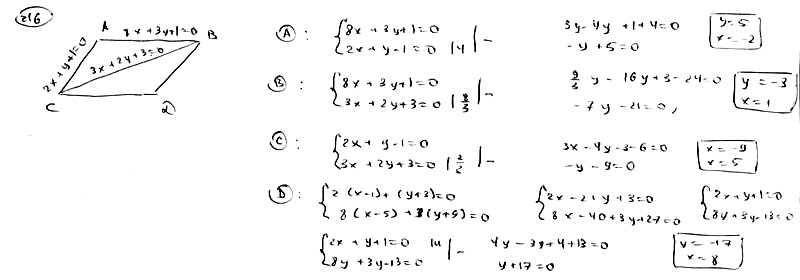
217

Стороны
треугольника лежат на прямых
,,.
Вычислить его площадь S.

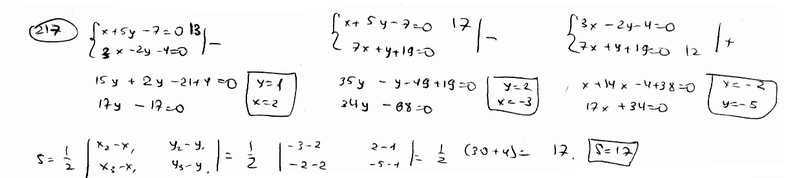
218

Площадь
треугольника S=8, две его вершины суть
точки А(1; -2), В(2; 3), а третья вершина С
лежит на прямой
.
Определить координаты вершины С.

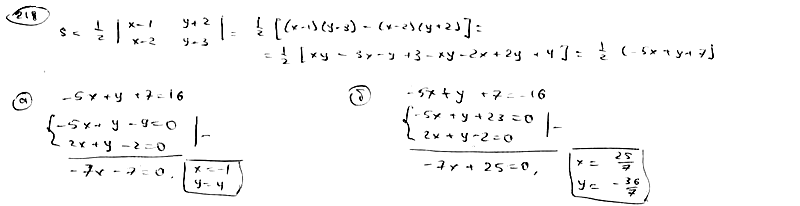
219

Площадь
треугольника S=1,5, две его вершины суть
точки А(2; -3), В(3; -2), центр масс этого
треугольника лежит на прямой
.
Определить координаты третьей вершины
С.

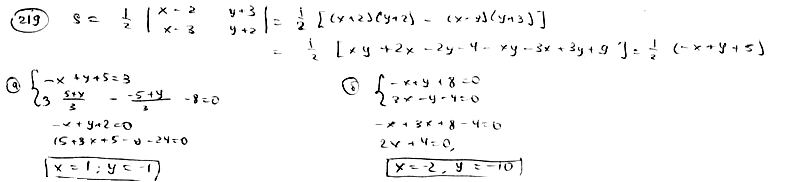
220

Составить
уравнение прямой и построить прямую
на чертеже, зная ее угловой коэффициент
k и отрезок b, отсекаемый ею на оси Oy:

220.1

k=2/3,
b=3;

220.2

k=3,
b=0;

220.3

k=0,
b=-2;

220.4

k=-3/4,
b=3;

220.5

k=-2,
b=-5;

220.6

k=-1/3,
b=2/3.

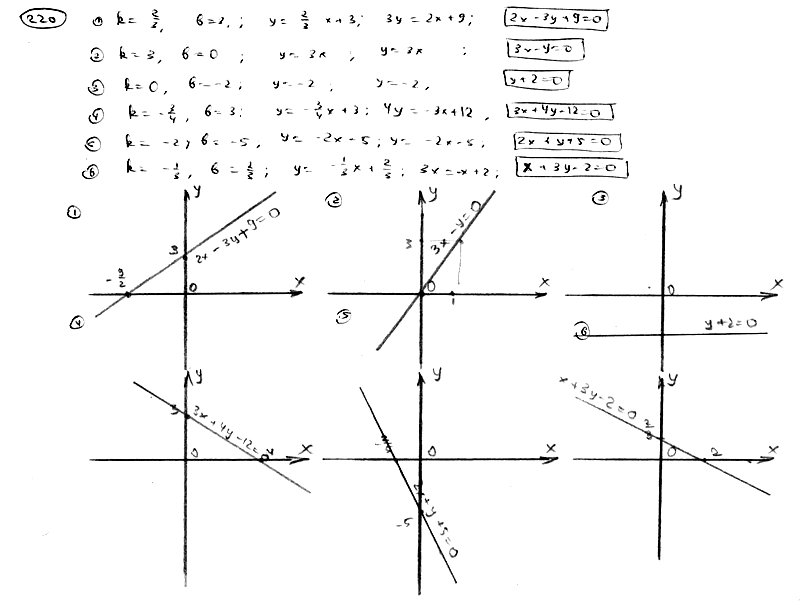
221

Определить
угловой коэффициент k и отрезок b,
отсекаемый на оси Oy, для каждой из
прямых:

221.1

;

221.2

;

221.3

;

221.4

;

221.5

.

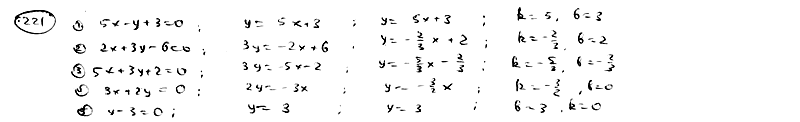
222

Дана
прямая
.
Определить угловой коэффициент k
прямой:

222.1

Параллельной
данной прямой;

222.2

Перпендикулярно
к данной прямой.

223

Дана
прямая
.
Составить уравнение прямой, проходящей
через точку М₀(2;
1):

223.1

Параллельно
данной прямой;

223.2

Перпендикулярно
данной прямой.

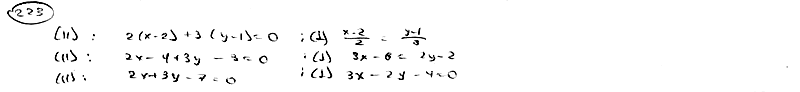
224

Даны
уравнения двух сторон прямоугольника
,и
одна из его вершин А(2; -3). Составить
уравнения двух других сторон этого
прямоугольника.

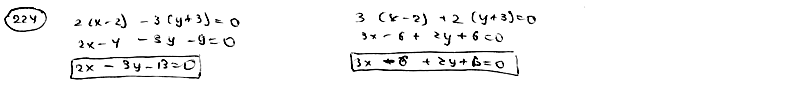
225

Даны
уравнения двух сторон прямоугольника
,и
уравнение одной из его диагоналей.
Найти вершины прямоугольника.

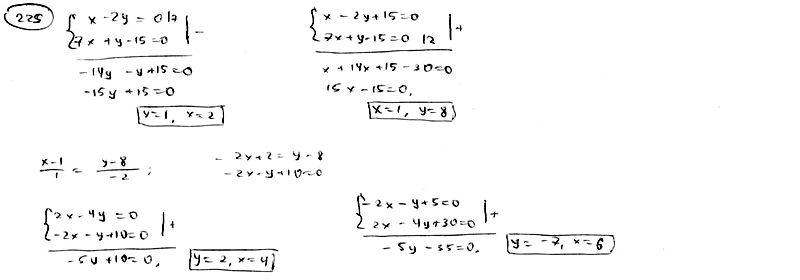
226

Найти
проекцию точке Р(-5; 13) относительно
прямой
.

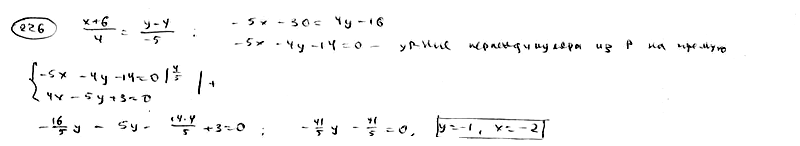
227

Найти
точку Q, симметричную точке Р(-5; 13)
относительно прямой
.

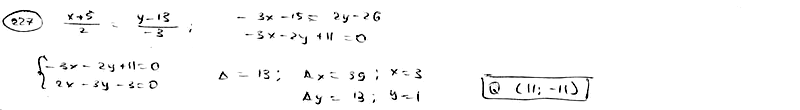
228

В
каждом из следующих случаев составить
уравнение прямой, параллельной двум
данным прямым и проходящей посередине
между ними:

228.1

,
;

228.2

,
;

228.3

,
;

228.4

,
;

228.5

,
.

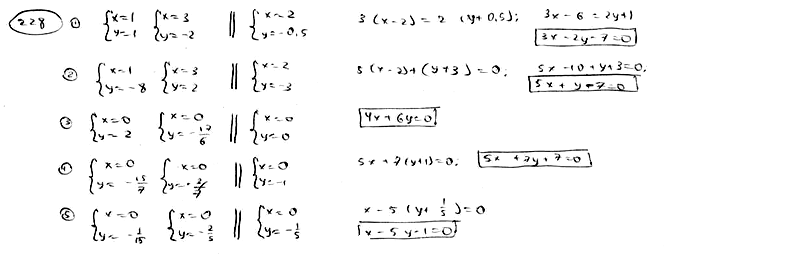
229

Вычислить
угловой коэффициент k прямой, проходящей
через две данные точки:

229.1

M₁(2;
-5), M₂(3;
2);

229.2

P(-3,
1), Q(7; 8);

229.3

A(5;
-3), B(-1; 6).

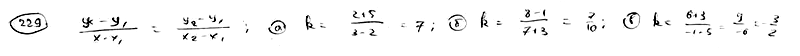
230

Составить
уравнения прямых, проходящих через
вершины треугольника A(5; -4), B(-1; 3), C(-3;
-2) параллельно противоположным
сторонам.

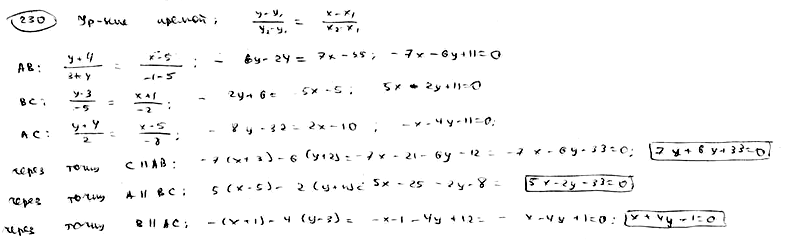
231

Даны
середины сторон треугольника M₁(2;
1), M₂(5;
3), M₃(3;
-4). Составить уравнение его сторон.

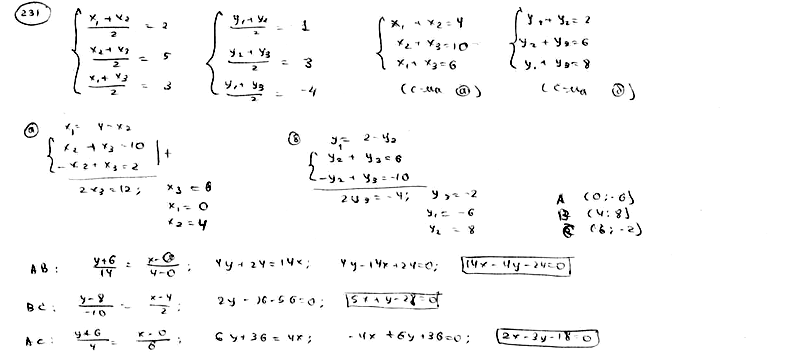
232

Даны
две точки P(2; 3), Q(-1; 0). Составить уравнение
прямой, проходящей через точку Q
перпендикулярно к отрезку
.

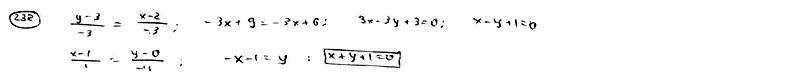
233

Составить
уравнение прямой, если точка P(2; 3)
служит основанием перпендикуляра,
опущенного из начала координат на эту
прямую.

234

Даны
вершины треугольника M₁(2;
1), M₂(-1;
-1), M₃(3;
2). Составить уравнения его высот.

235

Стороны
треугольника даны уравнениями
,,.
Определить точку пересечения его
высот.

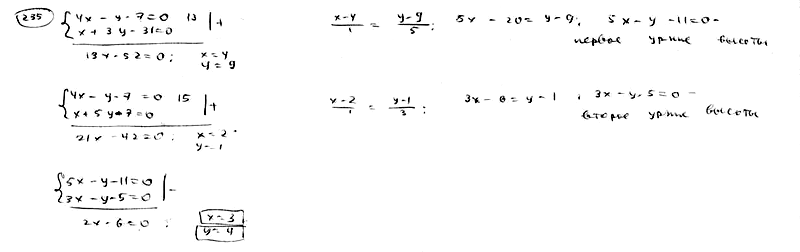
236

Даны
вершины треугольника A(1; -1), B(-2; 1), C(3;
5). Составить уравнение перпендикуляра,
опущенного из вершины А на медиану,
проведенную из вершины В.

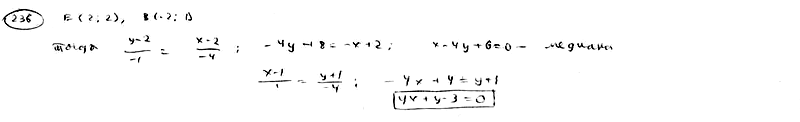
237

Даны
вершины треугольника A(2; -2), B(3; -5), C(5;
7). Составить уравнение перпендикуляра,
опущенного из вершины С на биссектрису
внутреннего угла при вершине А.

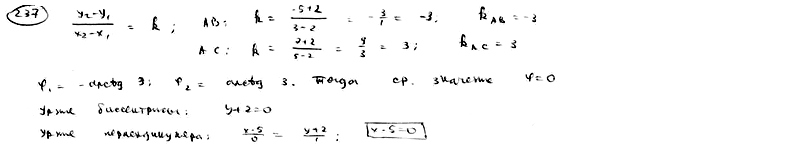
238

Составить
уравнения сторон и медиан треугольника
с вершинами A(3; 2), B(5; -2), C(1; 0).

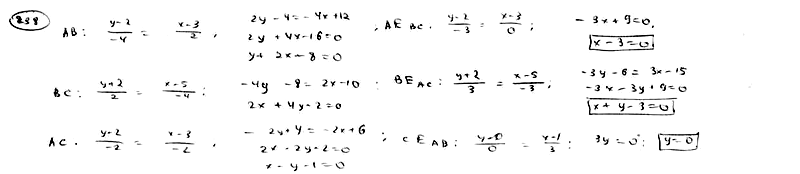
239

Через
точки M₁(-1;
2), M₂(2;
3) проведена прямая. Определить точки
пересечения этой прямой с осями
координат.

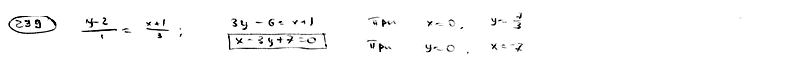
240

Доказать,
что условие, при котором три точки
M₁(x₁,
y₁),
M₂(x₂,
y₂),
M₃(x₃,
y₃)
лежат на одной прямой, может быть
записано в следующем виде:

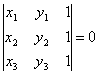
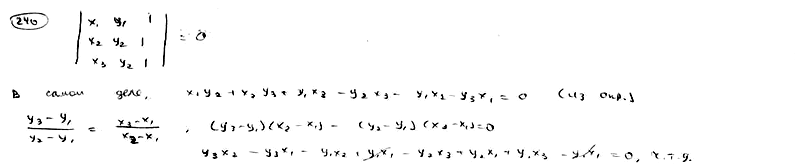
241

Доказать,
что уравнение прямой, проходящей через
две данные точки M₁(x₁,
y₁),
M₂(x₂,
y₂),
может быть записано в следующем виде:

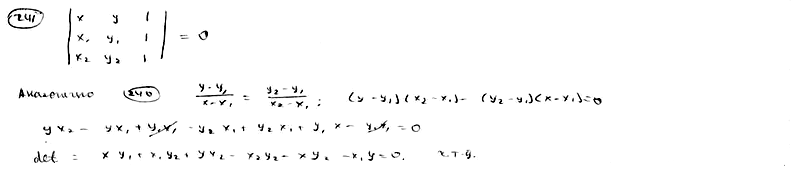
242

Даны
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2;
-6). Определить точку пересечения его
диагоналей.

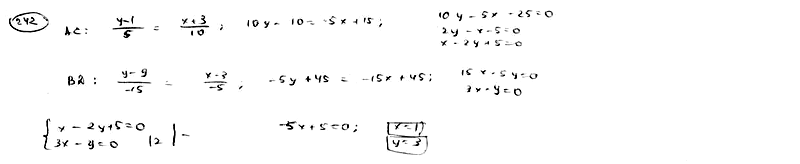
243

Даны
две смежные вершины A(-3; -1), B(2; 2)
параллелограмма ABCD и точка Q(3; 0)
пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма.

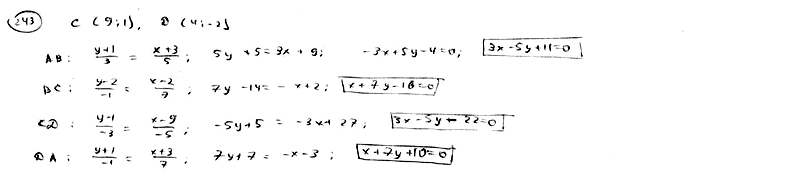
244

Даны
уравнения двух сторон прямоугольника
,и
уравнение его диагонали.
Составить уравнения остальных сторон
и второй диагонали этого прямоугольника.

245

Даны
вершины треугольника A(1; -2), B(5; 4), C(-2;
0). Составить уравнения биссектрис его
внутреннего и внешнего углов при
вершине А.

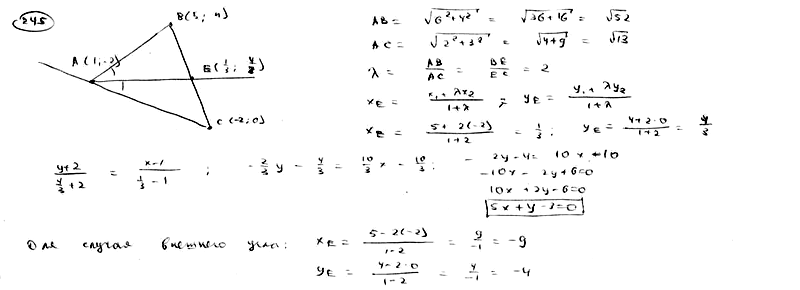
246

Составить
уравнение прямой, проходящей через
точку P(3; 5) на одинаковых расстояниях
от точек A(-7; 3) и B(11; -15).

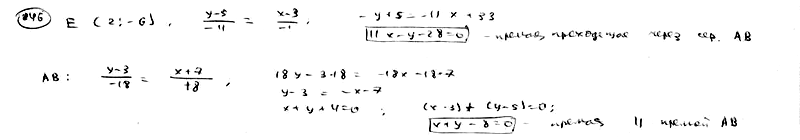
247

Найти
проекцию точки P(-8; 12) на прямую,
проходящую через точки A(2; -3), B(-5; 1).

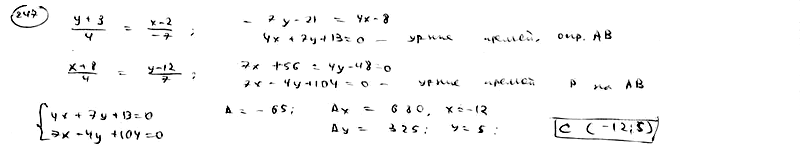
248

Найти
точку M₁,
симметричную точке М₂(8;
-9) относительно прямой, проходящей
через точки А(3; -4), B(-1; -2).

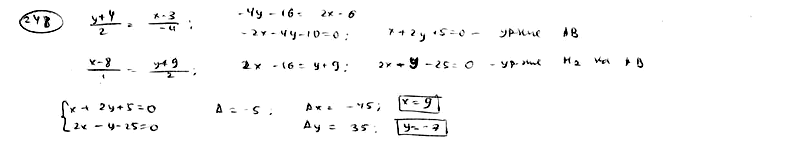
249

На
оси абсцисс найти такую точку P, чтобы
сумма ее расстояний до точек M(1; 2), N(3;
4) была наименьшей.

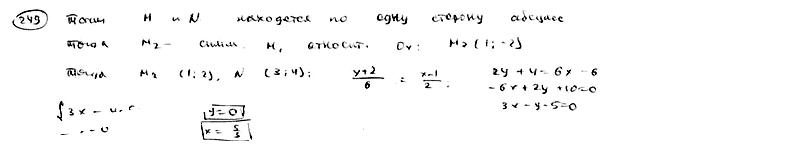
250

На
оси ординат найти такую точку P, чтобы
сумма ее расстояний до точек M(-3; 2),
N(2; 5) была наибольшей.

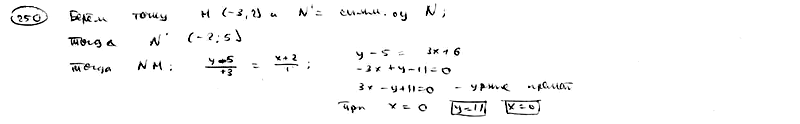
251

На
прямой
найти
такую точку Р, сумма расстояний которой
до точек A(-7; 1), B(-5; 5) была бы наименьшей.

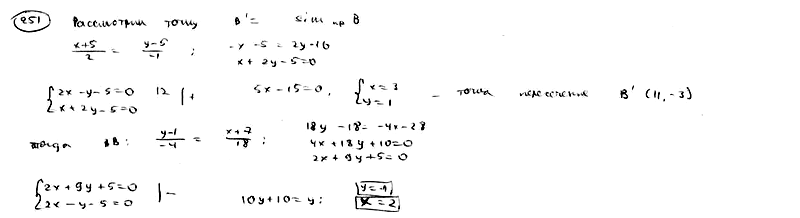
252

На
прямой
найти
такую точку Р, разность расстояний
которой до точек A(4; 1), B(0; 4) была бы
наибольшей.

253

Определить
угол
между
двумя прямыми:

253.1

,
;

253.2

,
;

253.3

,
;

253.4

,
.

254

Дана
прямая
.
Составить уравнение прямой, проходящей
через точку M₀(2;
1) под углом 45⁰
к данной прямой.

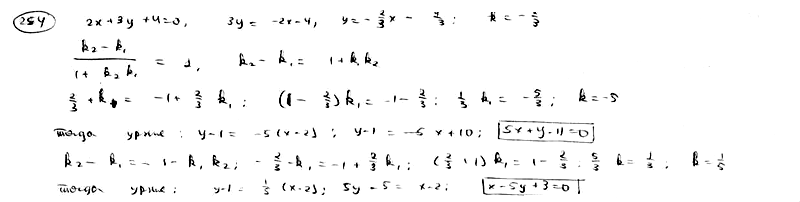
255

Точка
А(-4; 5) является вершиной квадрата,
диагональ которого лежит на прямой
.
Составить уравнения сторон и второй
диагонали этого квадрата.

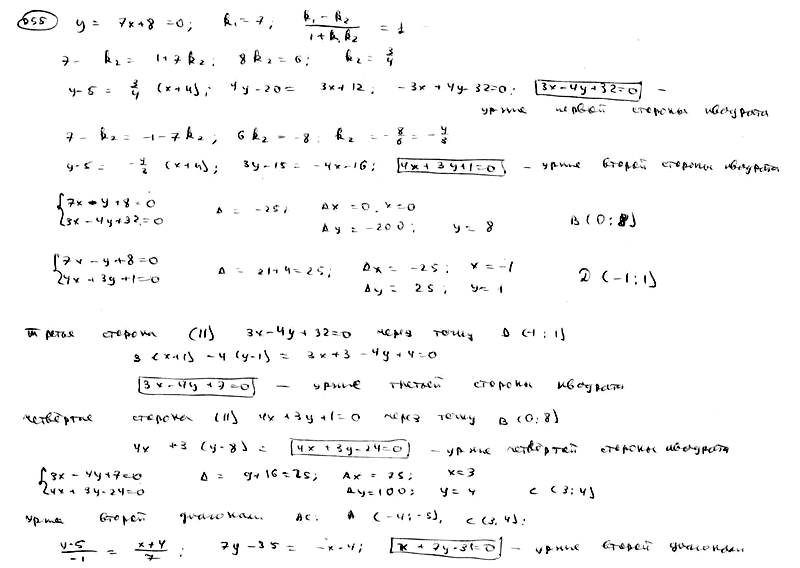
256

Даны
две противоположные вершины квадрата
A(-1; 3), C(6; 2). Составить уравнения его
сторон.

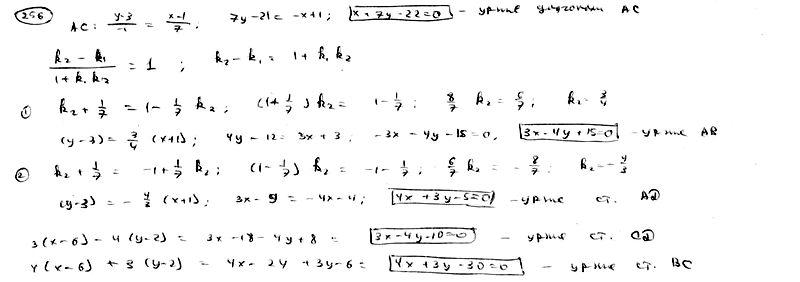
257

Точка
E(1; -1) является центром квадрата, одна
из сторон которого лежит на прямой
.
Составить уравнения прямых, на которых
лежат остальные стороны этого квадрата.

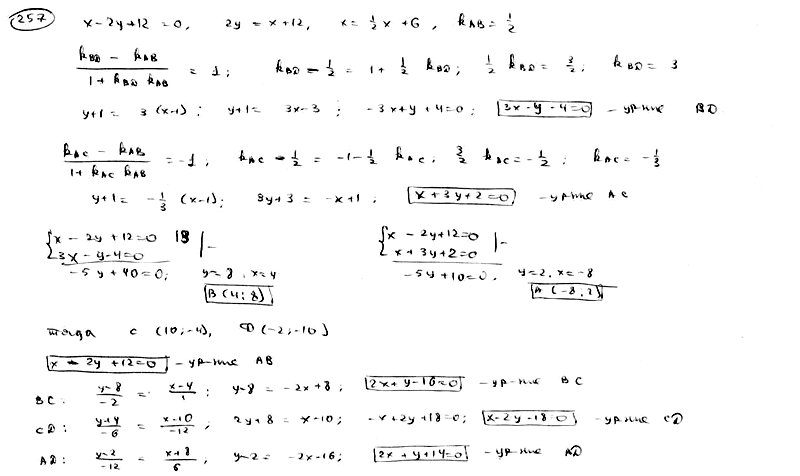
258

Из
точки M₀(-2;
3) под углом
к
оси Ox направлен луч света. Известно,
что.
Дойдя до оси Ox, луч от нее отразился.
Составить уравнения прямых, на которых
лежат падающий и отраженный лучи.

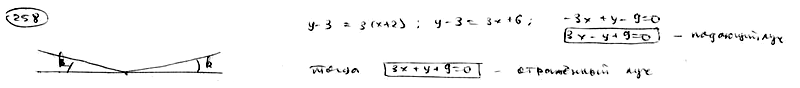
259

Луч
света направлен по прямой
,
луч от нее отразился. Составить
уравнение прямой, на которой лежит
отраженный луч.

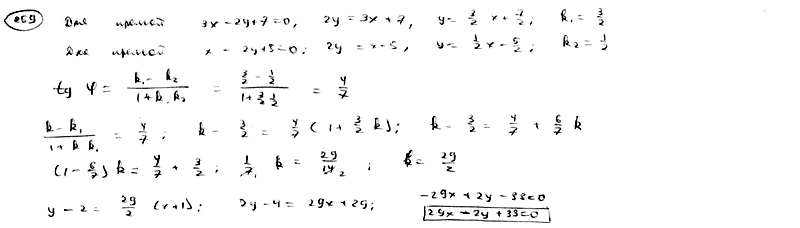
260

Даны
уравнения сторон треугольника
,,.
Доказать, что этот треугольник
равнобедренный. Решить задачу при
помощи сравнения углов треугольника.

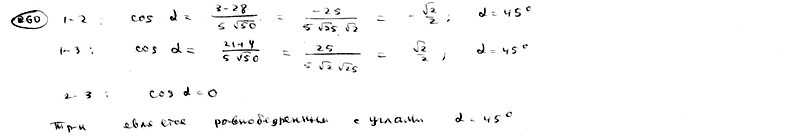
261

Доказатть,
что уравнение прямой, проходящей через
точку M₁(x₁;
y₁)
параллельно прямой
,
может быть записано в виде.

262

Составить
уравнение прямой, проходящей через
точку М₁(2:
-3) параллельно прямой:

262.1

;

262.2

;

262.3

;

262.4

;

262.5

.

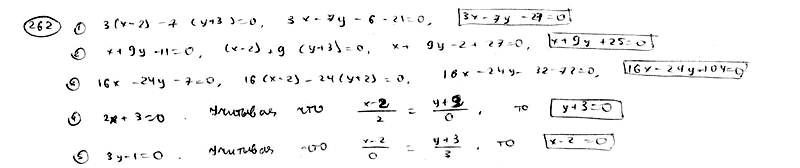
263

Доказать,
что условие перпендикулярности прямых
;может
быть записано в следующем виде:.

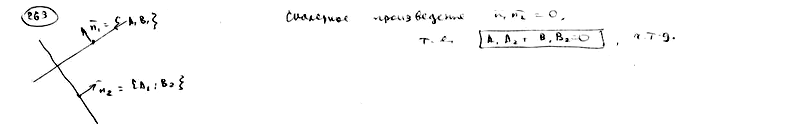
264

Установить,
какие из следующих пар прямых
перпендикулярны. Решить задачу, не
вычисляя угловых коэффициентов данных
прямых.

264.1

 ,
;

264.2

,
;

264.3

,
;

264.4

,
;

264.5

,
;

264.6

,
.

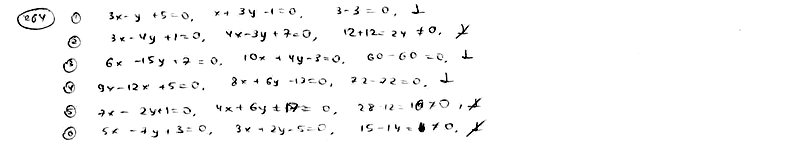
265

Доказать,
что формула для определения угла
между
прямыми,может
быть записана в следующей форме:

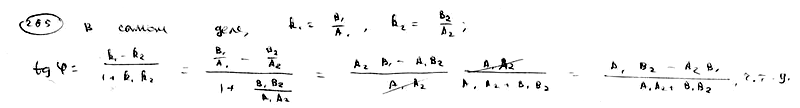
266

Определить
угол
,
образованный двумя прямыми. Решить
задачу, не вычисляя угловых коэффициентов
данных прямых.

266.1

,
;

266.2

 ,
;

266.3

 ,
.

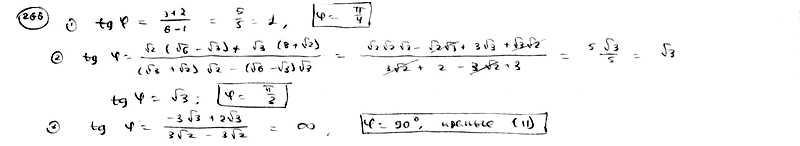
267

Даны
две вершины треугольника M₁(-10;
2), M₂(6;
4); его высоты пересекаются в точке
N(5; 2). Определить координаты третьей
вершины M₃.

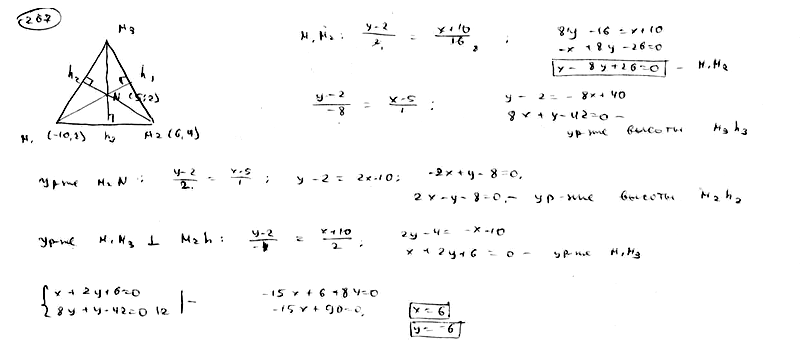
268

Даны
две вершины A(3; -1), B(5; 7) треугольника
ABC и точка N(4; -1) пересечения его высот.
Составить уравнения сторон этого
треугольника.

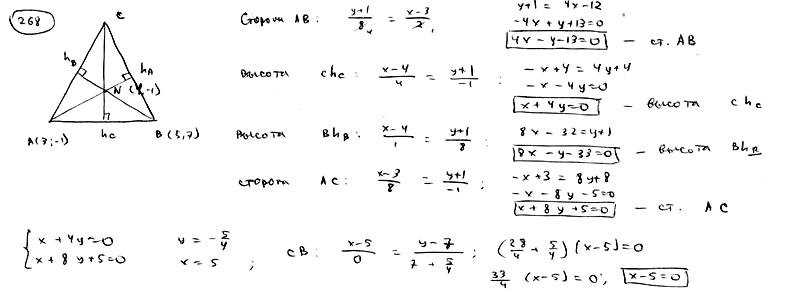
269

В
треугольнике АВС даны: уравнение
стороны АВ:
,
уравнения высот АМ:и
BN:.
Составить уравнения двух других сторон
и третьей высоты этого треугольника.

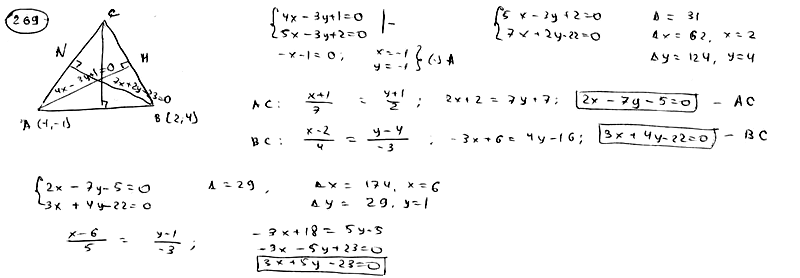
270

Составить
уравнения сторон треугольника АВС,
если даны одна из его вершина А(1; 3) и
уравнения двух медиан
,.

271

Составить
уравнения сторон треугольника, сли
даны одна из его вершин B(-4; -5) и уравнения
двух высот
,.

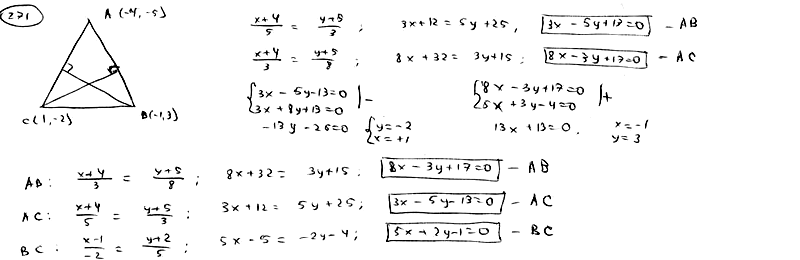
272

Составить
уравнения сторон треугольника, зная
одну из его вершин A(4; -1) и уравнения
двух биссектрис
,.

273

Составить
уравнения сторон треугольника, зная
одну из его вершин B(2; 6), а также уравнения
высоты
и
биссектрисы,
проведенных из одной вершины.

274

Составить
уравнения сторон треугольника, зная
одну его вершину B(2; -1), а также уравнения
высоты
и
биссектрисы,
проведенных из различных вершин.

275

Составить
уравнения сторон треугольника, зная
одну его вершину C(4; -1), а также уравнения
высоты
и
медианы,
проведенной из одной вершины.

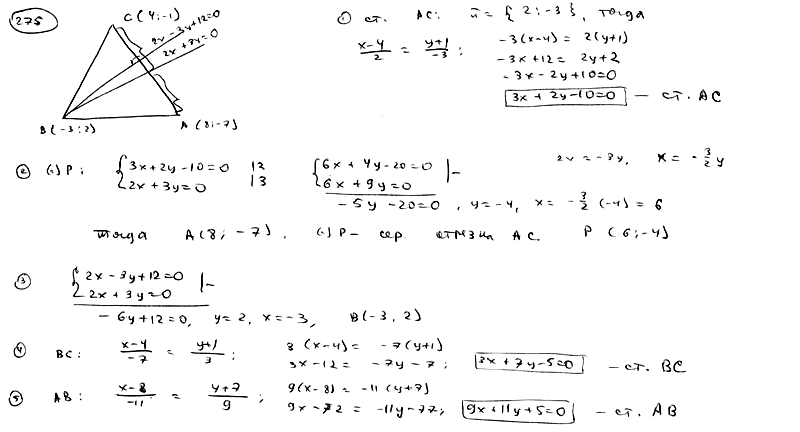
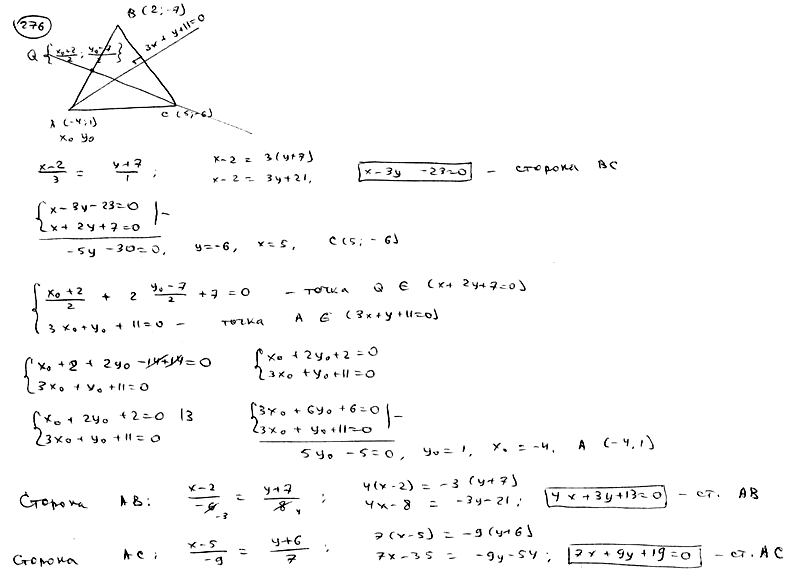
276

Составить
уравнения сторон треугольника, зная
одну его вершину B(2; -7), а также уравнения
высоты
и
медианы,
проведенных из различных вершин.

277

Составить
уравнения сторон треугольника, зная
одну его вершину C(4; 3), а также уравнения
биссектрисы
и
медианы,
проведенных из одной вершины.

278

Составить
уравнения сторон треугольника, зная
одну его вершину A(3; -1), а также уравнения
биссектрисы
и
медианы,
проведенных из различных вершин.

279

Составить
уравнение прямой, которая проходит
черезначало координат и вместе с
прямыми
,образует
треугольник с площадью, равной 1,5.

280

Среди
прямых, проходящих через точку P(3; 0),
найти такую, отрезок которой, заключенный
между прямыми
,,
делится в точке Р пополам.

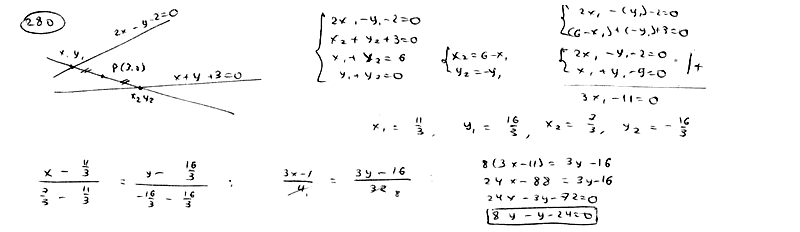
281

Через
точку Р(-3; -1) проведены всевозможные
прямые. Доказать, что отрезок каждой
из них, заключенный между прямыми
,,
делится в точке Р пополам.

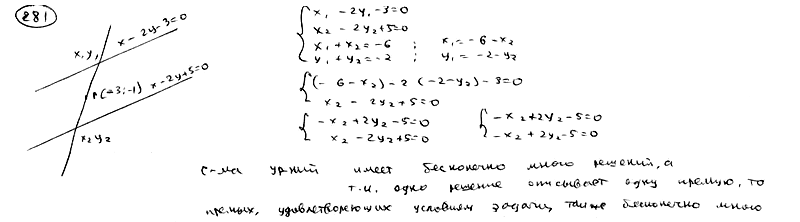
282

Через
точку Р(0; 1) проведены всевозможные
прямые. Доказать, что среди них нет
прямой, отрезок которой, заключенный
между прямыми
,,
делился бы в точке Р пополам.

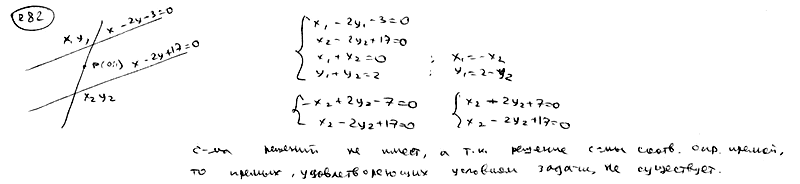
283

Составить
уравнение прямой, проходящей через
начало координат, зная, что длина ее
отрезка, заключенного между прямыми
,,
равна.

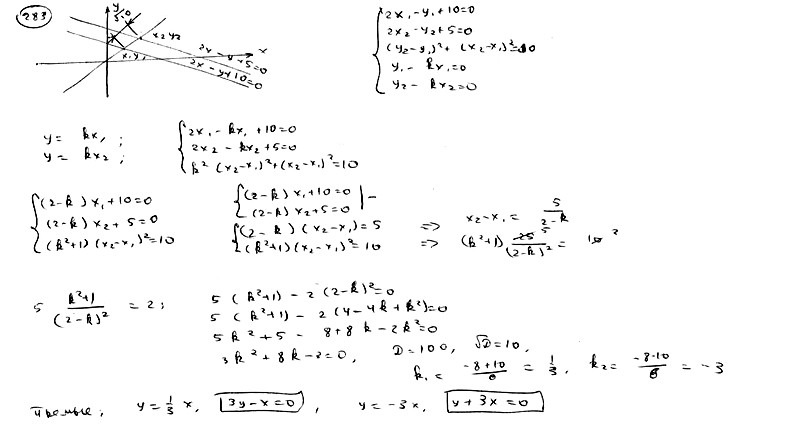
284

Составить
уравнение прямой, проходящей через
точку С(-5; 4), зная, что длина ее отрезка,
заключенного между прямыми
,,
равна 5.