Среди геометрических фигур очень большую часть составляют многоугольники. Это квадрат, прямоугольник, параллелограмм, ромб, треугольник, трапеция и другие n-угольники (n — количество сторон многоугольника).
Периметр любого многоугольника – это сумма длин всех его сторон.
Онлайн-калькулятор периметра многоугольника
Формула периметра многоугольника
P=a+b+c+d+e+…P=a+b+c+d+e+…,
где a,b,c,d,e,…a, b, c, d, e,… — длины сторон многоугольника.
Частным случаем многоугольника является так называемый правильный многоугольник.
Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.
Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.
P=n⋅aP=ncdot a
aa — длина стороны многоугольника;
nn — количество сторон многоугольника.
Разберем задачи на нахождение периметра правильного и неправильного многоугольников.
Найти периметр правильного шестиугольника со стороной 10 см.
Решение
a=10a=10
n=6n=6
Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aa численное значение:
P=n⋅a=6⋅10=60P=ncdot a=6cdot 10=60 см.
Ответ: P=60P=60 см.
Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.
Решение
a=6a=6
b=5b=5
c=2c=2
d=3d=3
e=1e=1
В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:
P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.
Ответ: P=17P=17 см.
Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!
Тест по теме “Периметр многоугольника”
Периметром фигур является длина их пограничных линий. Знание периметра требуется в различных практических ситуациях. Периметр фигур тесно связан с определением их площади.
Общей формулы для вычисления периметров различных фигур не существует, по этой причине на странице предлагается набор онлайн калькуляторов, позволяющий вычислять данный параметр для основных геометрических фигур. Наличествуют программы вычисления длин окружности и дуги.
Пользоваться калькуляторами очень легко, в соответствующих полях нужно задать координаты точек фигуры, значения длин сторон, радиусов или углов. При нажатии на кнопку «Вычислить» в соответствующем поле можно прочитать результат.
Программные скрипты используют при вычислении следующие формулы расчета периметров:
|
– P = 2 х π х r; – P = a + b +c; |
– P = 4 х a; – P = 2 х (a + b); |
– P = a + b + c + d; – P = n х a и др. |
В обыденной жизни чаще всего расчет периметра необходим для определения количества стройматериалов при устройстве ограждения придомового или производственного участка, площадки для автостоянки, выпаса скота и пр.
Вычислить, найти периметр геометрических фигур
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Периметр многоугольника
Любой многоугольник – это замкнутая ломаная линия.
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
Значит, периметр многоугольника – это сумма длин всех его сторон.
В математике периметр обозначают буквой P (пэ).
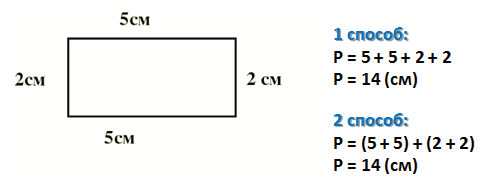
Периметр прямоугольника
Например, найдём периметр данного прямоугольника.
1 способ:
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
2 способ:
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
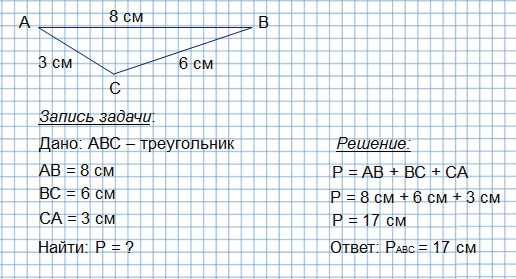
Периметр треугольника
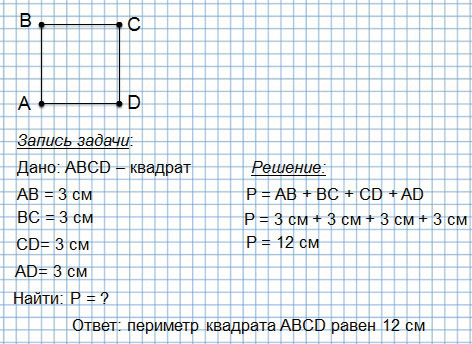
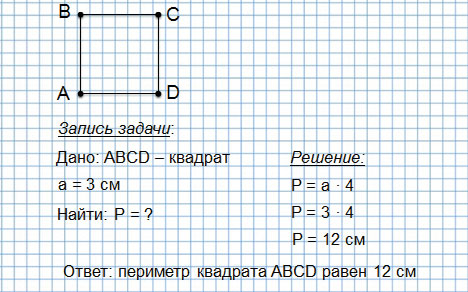
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
1 класс
Страница 4. Урок 3,
Петерсон, Учебник, часть 3
Страница 5. Урок 3,
Петерсон, Учебник, часть 3
Страница 87. Урок 44,
Петерсон, Учебник, часть 3
2 класс
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 66. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 43. Урок 22,
Петерсон, Учебник, часть 1
3 класс
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 80. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 111,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 70,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 84. Урок 30,
Петерсон, Учебник, часть 1
Страница 95. Урок 42,
Петерсон, Учебник, часть 2
4 класс
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 80,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 8,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 54,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 207,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 208,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 210,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Задание 389,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
1) Измерь стороны многоугольников и найди периметр каждого из них в сантиметрах.
2) Вспомни, как, используя циркуль, находили длину ломаной. Расскажи, как можно найти периметр многоугольника, не узнавая длину каждой из его сторон. Найди этим способом периметр треугольника.
reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 1. Страница 42. Номер №1
Решение 1
Первая фигура:
3 + 4 + 1 + 4 = 7 + 1 + 4 = 8 + 4 = 12 (см) − периметр первой фигуры.
Вторая фигура:
4 + 3 + 3 = 7 + 3 = 10 (см) − периметр второй фигуры.
Третья фигура:
2 + 3 + 5 + 5 = 5 + 5 + 5 = 10 + 5 = 15 (см) − периметр третьей фигуры.
Решение 2
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 1, и узнаем длину всего получившегося отрезка (12 см).
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 2, и узнаем длину всего получившегося отрезка (10 см).
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 3, и узнаем длину всего получившегося отрезка (15 см).
|
прямоугольник с таким же периметром? Ну,раз периметр равен 22 сантиметра то возможны в целых сантиметрах следующие варианты прямоугольников:(1+10+1+10) ; (2+9+2+9) ; (3+8+3+8) (4+7+4+7) ; (5+6+5+6).Ну а в дробных сантиметрах будем много вариантов.( даже сколько-угодно) автор вопроса выбрал этот ответ лучшим RIOLIt 4 года назад Периметр ломаной фигуры- 22см., один из вариантов прямоугольника- ширина 3 сантиметра, длина 8 сантиметров. Квадрат не получается, так как двадцать два число- не “високосное”, разве что со стороной пять с половиной сантиметра. Знаете ответ? |