Периметр восьмиугольника формула 5 класс как найти

Как найти периметр восьмиугольника

Периметром восьмиугольника, как и любой другой плоской геометрической фигуры, называют сумму длин его сторон. Решать задачу определения этого параметра многоугольника иногда приходится только с использованием математических формул, а иногда – измерять их какими-либо подручными средствами. В любом случае способов решения задачи существует несколько и каждый из них будет оптимален применительно к определенному набору исходных условий.

Инструкция

Если вычислить периметр (P) восьмиугольника надо в теории, а в исходных условиях даны длины всех сторон этой фигуры (a, b, c, d, e, f, g, h), то сложите эти величины: P = a+b+c+d+e+f+g+h. Знать длины всех сторон необходимо только в случае неправильного многоугольника, а если из условий задачи известно, что фигура является правильной, то будет достаточно длины одной стороны – просто увеличьте ее в восемь раз: P = 8*a.

Если в исходных данных ничего не говорится о длине стороны правильного восьмиугольника, но приведен радиус описанной около этой фигуры окружности (R), то перед применением формулы из предыдущего шага придется вычислить недостающую переменную. Каждую из сторон в таком восьмиугольнике можно считать основанием равнобедренного треугольника, боковыми сторонами которого являются радиусы описанной окружности. Поскольку всего таких одинаковых треугольников будет восемь, то величина угла между радиусами каждого из них составит одну восьмую часть от полного оборота: 360°/8 = 45°. Зная длины двух сторон треугольника и величину угла между ними, определите величину основания – косинус половины угла умножьте на удвоенную длину боковой стороны: 2*R*cos(22,5°) ≈ 2*R* 0,924 ≈ R* 1,848. Полученное значение подставьте в формулу из первого шага: P ≈ 8*R*1,848 ≈ R*14,782.

Если в условиях задачи дан лишь радиус (r) вписанной в правильный восьмиугольник окружности, то надо произвести вычисления, аналогичные описанным выше. В этом случае радиус можно представить в качестве одного из катетов прямоугольного треугольника, другим катетом которого будет половина от нужной вам стороны восьмиугольника. Острый угол, примыкающий к радиусу, будет в два раза меньшее вычисленного в предыдущем шаге: 360°/16 = 22,5°. Длину нужного катета вычислите умножением тангенса этого угла на другой катет (радиус), а для определения величины стороны восьмиугольника полученное значение удвойте: 2*r*tg(22,5°) ≈ 2*r*0,414 ≈ r*0,828. Подставьте это выражение в формулу из первого шага: P ≈ 8*r*0,828 ≈ r*6,627.

Если вычислять радиус требуется методом практических измерений, то, в зависимости от размера фигуры, воспользуйтесь, например, линейкой, курвиметром («роликовым дальномером») или шагомером. Полученные значения длин сторон подставьте в одну из двух формул, приведенных в одном из шагов.

Источники:

• найдите периметр восьмиугольника
• Определения положения объектов на местности при помощи

Как рассчитать периметр и площадь восьмиугольника

Геометрическая фигура восьми сторон, называемая восьмиугольником или восьмиугольником, обычно представляется в двух измерениях в виде чертежа или плоского объекта, распространенным примером которого является сигнал светофора. Площадь восьмиугольной фигуры легко рассчитывается с помощью базовой математики. Вычисление стороны, сторон или периметра восьмиугольника, это простой вопрос сложения длин сторон. Хотя это редко, трехмерные объекты также могут быть сформированы с восемью сторонами, и боковая площадь вычисляется по той же формуле, что и квадрат или прямоугольник. Мы хотим облегчить вам задачу и объясним, как рассчитать периметр и площадь восьмиугольника.

Вам понадобится:

• правило
• калькулятор

Шаги, чтобы следовать:

1

Первое, что вам нужно сделать, это измерить длину каждой стороны восьмиугольника ; Следует отметить, что этот многоугольник может быть регулярным, то есть все его стороны идентичны и иметь одинаковые размеры, или нерегулярными в случае, если стороны разные.

2

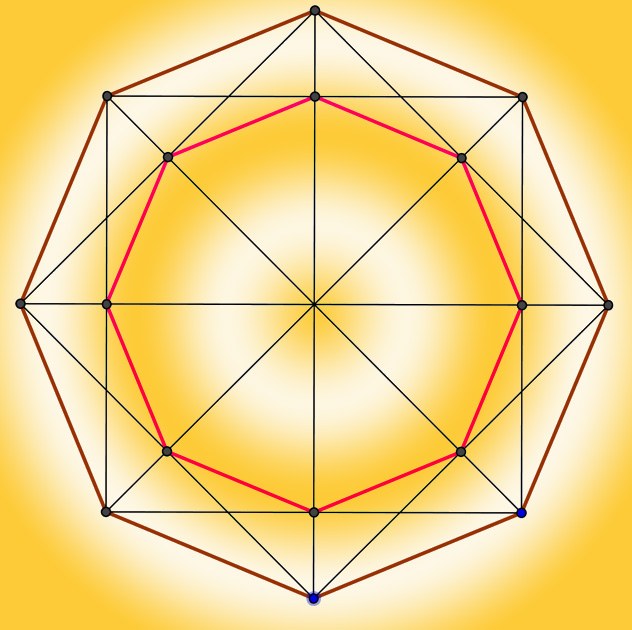
Чтобы узнать периметр правильного восьмиугольника, подобного тому, который вы видите на рисунке ниже, вы должны умножить длину одной стороны восьмиугольника на количество сторон в восьмиугольнике, равное 8. Таким образом, математическая формула говорит, что P = l · 8

Например, если восемь сторон восьмиугольника имеют одинаковую длину в пять сантиметров, периметр восьмиугольника рассчитывается:

5 см х 8 сторон = 40 см по периметру

3

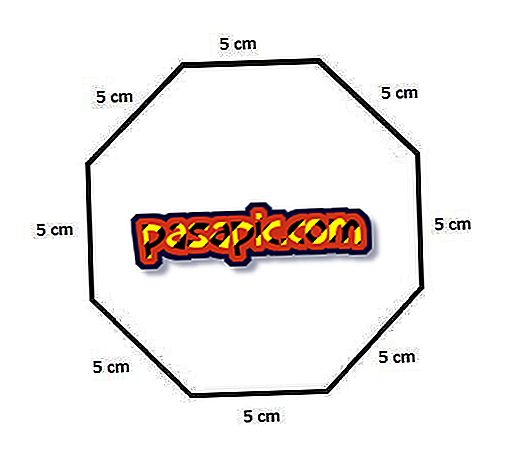
В случае неправильных восьмиугольников вы должны определить периметр, рассчитав каждую сторону отдельно и сумму этих цифр .

Например: если первая сторона 5 сантиметров, вторая сторона 4 сантиметра, третья сторона 7 сантиметров, четвертая сторона 3 сантиметра, а стороны пять, шесть, семь и восемь равны 10 сантиметрам, периметр восьмиугольник будет равен 60 сантиметрам

Периметр = 5 + 4 + 7 + 3 + 10 + 10 + 10 + 10 = 60 см.

4

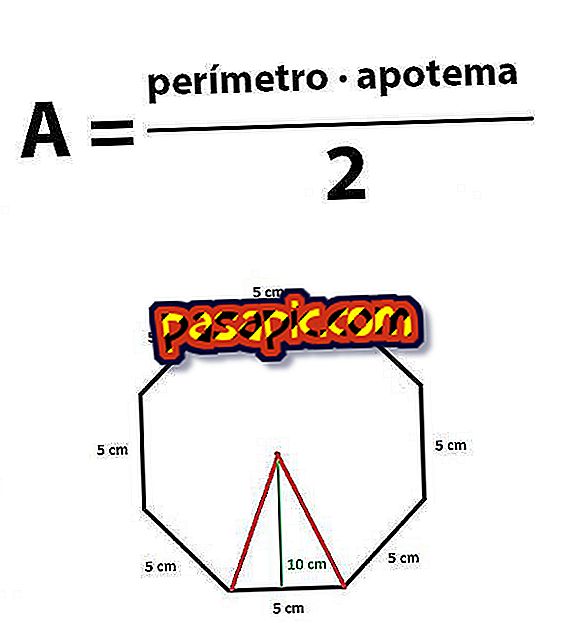
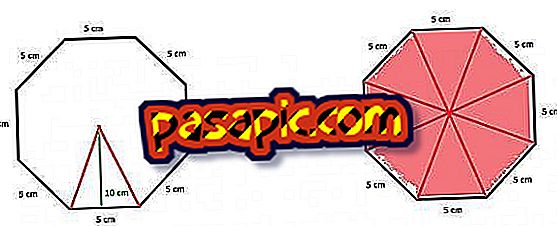
Если мы хотим вычислить поверхность или площадь правильного восьмиугольника, мы должны применить математическую формулу, которая гласит, что площадь равна умножению периметра на апотем, деленный на два.

Итак, мы уже знаем, как рассчитать периметр восьмиугольника, но что такое апофем ? Это расстояние, которое отделяет центр многоугольника от центральной точки каждой стороны восьмиугольника; Если вы посмотрите на изображение, мы указали его зеленым цветом.

Следуя примеру, если каждая сторона равна 5 см, а апотема равна 10 см, мы вычисляем поверхность восьмиугольника, умножая сторону на 8 и на апотему и деля результат на два:

S = (5 см · 8 см) · 10/2 = 40 · 10/2 = 200 см²

5

Другой не менее действительный вариант для вычисления поверхности правильного восьмиугольника – это разделить многоугольник на восемь равных треугольников, вычислить его площадь и затем умножить на восемь. Таким образом, апофема правильного восьмиугольника будет равна высоте каждого из этих треугольников и стороне, равной основанию, которые являются двумя элементами, которые нам нужны для вычисления площади треугольника.

Таким образом, поверхность треугольника получается путем применения формулы, которая говорит, что она равна умножению основания на высоту и делению его результата на два:

S = (5 · 10) / 2 = 50/2 = 25 см²

Как только это будет сделано, нам нужно будет только умножить поверхность или площадь треугольника на 8, то есть количество правильных треугольников, составляющих многоугольник с восемью сторонами:

S = 25 · 8 = = 200 см²

Как видим, результат один и тот же, несмотря на применение двух разных методов.

6

Эти другие статьи:

• Как найти периметр четырехугольника
• Как найти периметр квадрата
• Как определить площадь овала
• Как найти высоту косого треугольника с площадью

чаевые

• Помните, что всякий раз, когда вы вычисляете расстояния, поверхности, углы и т. Д., Вы должны указывать единицы измерения в результате.

Восьмиугольник, виды, свойства и формулы.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник, выпуклый и невыпуклый восьмиугольник

Правильный восьмиугольник (понятие и определение)

Свойства правильного восьмиугольника

Формулы правильного восьмиугольника

Правильный восьмиугольник в природе, технике и культуре

Шестиугольник

Восьмиугольник, выпуклый и невыпуклый восьмиугольник:

Восьмиугольник – это многоугольник с восемью углами.

Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.

Восьмиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый восьмиугольник

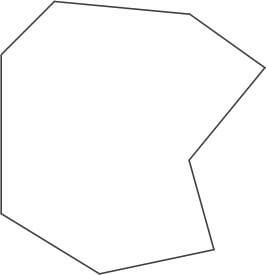
Рис. 2. Невыпуклый восьмиугольник

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.

Правильный восьмиугольник (понятие и определение):

Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.

Рис. 3. Правильный восьмиугольник

Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.

Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.

Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.

Свойства правильного восьмиугольника:

1. Все стороны правильного восьмиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇ = a₈. 

2. Все углы равны между собой и составляют 135°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = α₈ = 135°.

Рис. 4. Правильный восьмиугольник

3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.

Рис. 5. Правильный восьмиугольник

5. Количество диагоналей правильного восьмиугольника равно 20.

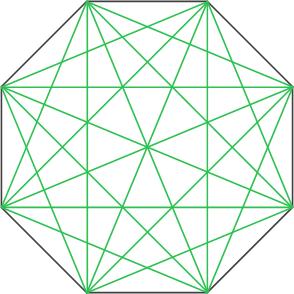
Рис. 6. Правильный восьмиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

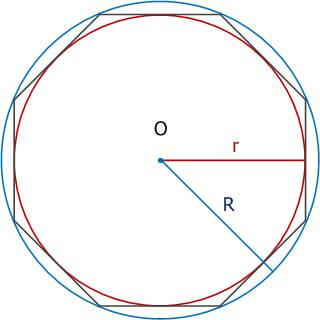
Рис. 7. Правильный восьмиугольник

Формулы правильного восьмиугольника:

Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.

Формула константы правильного восьмиугольника:

Формула периметра правильного восьмиугольника:

Формулы площади правильного восьмиугольника:

Формулы радиуса окружности, вписанной в правильный восьмиугольник:

Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:

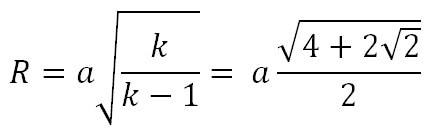
Формулы стороны правильного восьмиугольника:

Правильный восьмиугольник в природе, технике и культуре:

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.

Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
7 123

Geometry is a mathematical branch that is about the study of shapes. The category of shapes is divided into two viz. flat shapes and solid shapes. Geometry deals with the study of the area, perimeter, volume, and other parameters of these shapes by giving standard formulas.

The article explains the octagon formula which gives the formula of area and perimeter of an octagon. It also comprises sample numerical problems for better understanding.

Octagon

Octagon is a plane shape having eight sides and eight angles. It is a regular polygon of eight sides. Each interior angle of the octagon measures 135° and the sum of all the interior angles of an octagon equals 108°. Similarly, the exterior angle of an octagon is 45 degrees and the sum of all the exterior angles equals 360°.

Octagon consists of 20 diagonals that meet at the center of the figure. All these diagonals have the same length.

Octagon Formula 

The geometry provides separately derived formulas for the calculation of perimeter, area, and diagonals of a regular octagon. The perimeter, area, and diagonal formula of an octagon is collectively known as the Octagon Formula.

To find the number of diagonals of an octagon we use the given formula.

Number of Diagonals = n(n – 3)/2 

8(8 – 3)/2 

20

Where s denotes  side length

And, n denotes the number of sides

A regular polygon generally consists of 20 diagonals. So, the octagon formula is mostly used to calculate the area and perimeter of an octagon. These calculations are carried out by using the length of a side of the octagon.

The area formula of  an octagon is given by

Area of octagon(A) = 2s²(1 + √2)

Where s is the length of a side

The perimeter formula of an octagon is given by,

The perimeter of the octagon(P) = 8s

Where s is the length of a side.

Sample Problems

Question 1: Find the area and perimeter of an octagon having a side 2cm using the octagon formula.

Solution:

Given:

length of a side of the octagon is 2cm

By using the octagon formula for the area

Area of octagon(A) = 2s²(1 + √2)

A = 2(2)²(1 + √2)

A = 19.31cm²

By using the octagon formula for the perimeter,

Perimeter of the octagon (P) = 8s

P = 8 × 2

P = 16cm

Hence, the area and perimeter of the given octagon are 19.31cm² and 16cm respectively.

Question 2: Find the area and perimeter of an octagon having a side of 4cm using the octagon formula.

Solution:

Given:

length of a side of the octagon is 4cm

By using the octagon formula for the area

Area of octagon(A) = 2s²(1 + √2)

A = 2(4)²(1 + √2)

A = 77.25cm²

By using the octagon formula for the perimeter

The perimeter of the octagon (P) = 8s

P = 8 × 4

P = 32cm

Hence, the area and perimeter of the given octagon are 77.25cm² and 32cm respectively.

Question 3: Find the area and perimeter of an octagon having a side of 2.5cm using the octagon formula.

Solution:

Given:

length of a side of the octagon is 2.5cm

By using the octagon formula for the area

Area of octagon(A) = 2s²(1 + √2)

A = 2(2.5)²(1 + √2)

A = 30.17cm²

By using the octagon formula for the perimeter

The perimeter of the octagon (P)=8s

P = 8 × 2.5

P = 20cm

Hence, the area and perimeter of the given octagon are 30.17cm² and 20cm respectively.

Question 4: A regular octagon is given which has a perimeter equal to 32cm. Find its area using the octagon formula.

Solution:

Given:

The perimeter of the octagon is 32cm.

The perimeter of the octagon(P) = 8s

32 = 8s

s = 4cm

By using the octagon formula for the area

Area of octagon(A) = 2s²(1 + √2)

A = 2(4)²(1 + √2)

A = 77.25cm²

Question 5: A regular octagon is given which has a perimeter of 48cm. Find its area using the octagon formula.

Solution:

Given:

The perimeter of the octagon is 48cm.

The perimeter of the octagon(P) = 8s

48 = 8s

s = 6cm

By using the octagon formula for the area

Area of octagon(A) = 2s²(1 + √2)

A = 2(6)²(1 + √2)

A = 173.82cm²

Question 6: If the perimeter of an octagon is given which is equal to 40cm. Calculate the area of the given octagon.

Solution:

Given:

The perimeter of the octagon is 40cm.

The perimeter of the octagon(P) = 8s

40 = 8s

s = 5cm

By using the octagon formula for the area 

Area of octagon(A) = 2s²(1 + √2)

A = 2(5)²(1 + √2)

A = 120.71cm²

Question 7: If an octagon is given having length of 3cm, its area and perimeter be, calculated using the octagon formula?

Solution:

Given:

The side of the octagon is 3cm

By using the octagon formula for the area 

Area of octagon(A) = 2s²(1 + √2)

A = 2(3)²(1 + √2)

A = 43.45cm²

By using the octagon formula for the perimeter

The perimeter of the octagon (P) = 8s

P = 8 × 3

P = 24cm

Hence, the area and perimeter of the given octagon are 43.45cm² and 24cm respectively.

Last Updated :
01 Feb, 2022

Like Article

Save Article