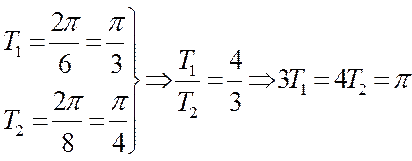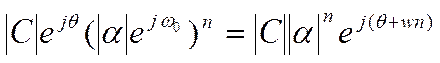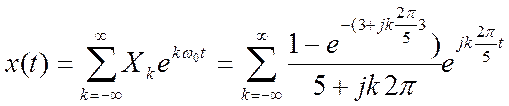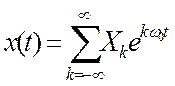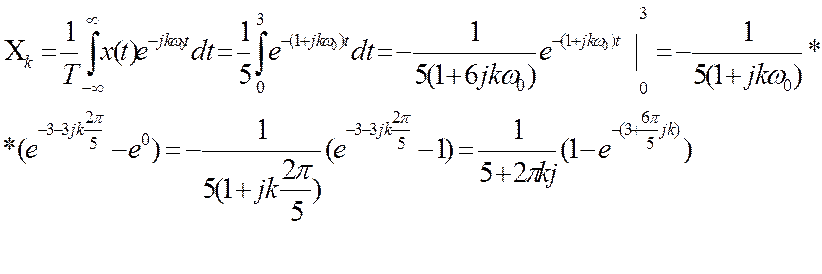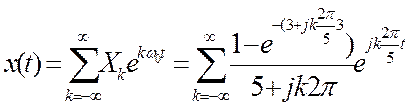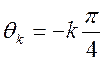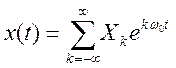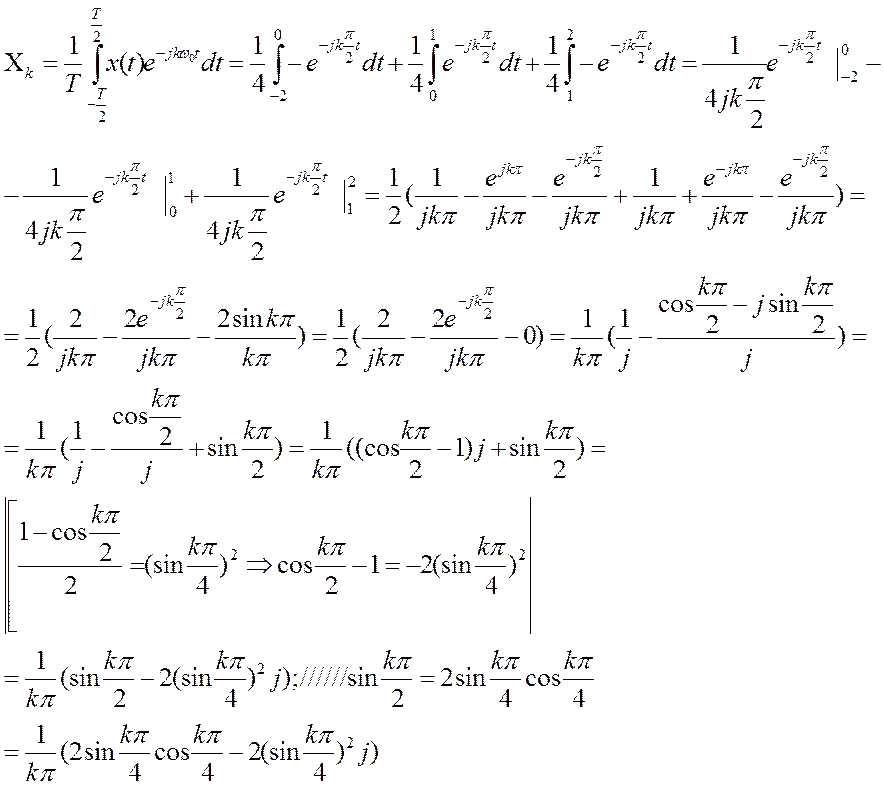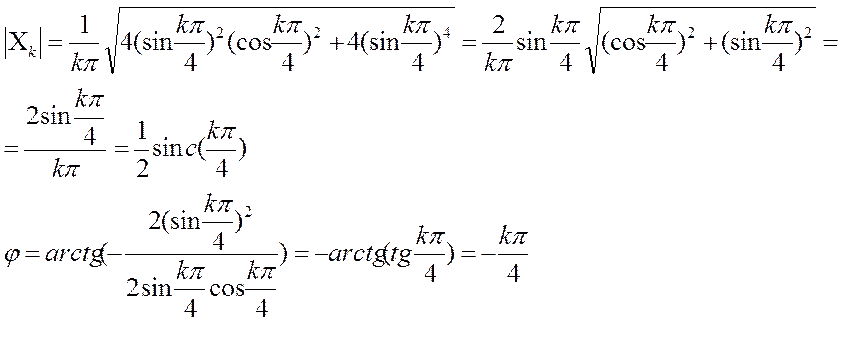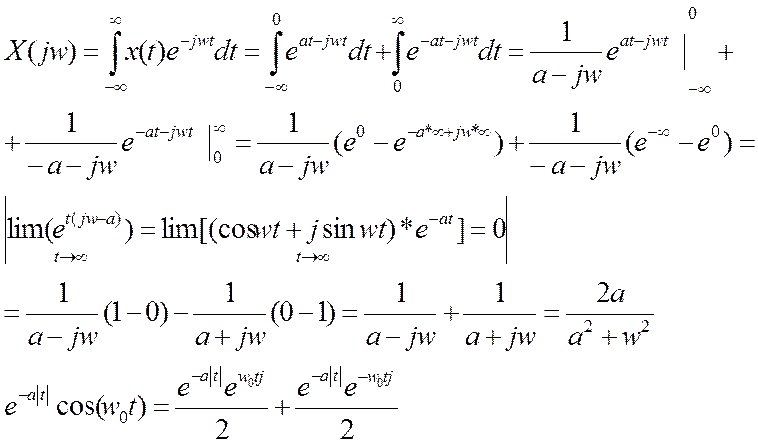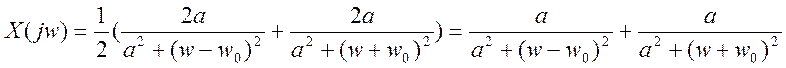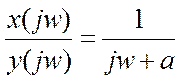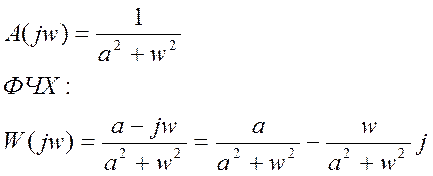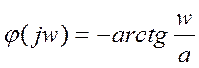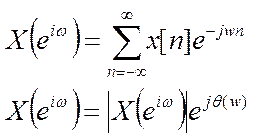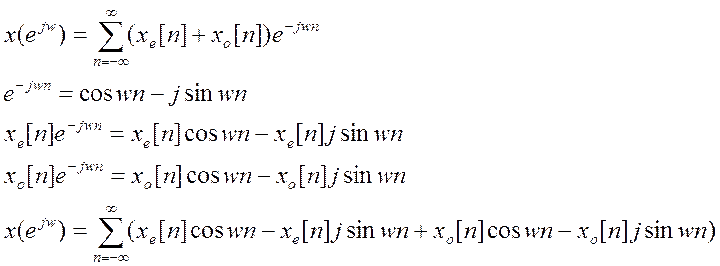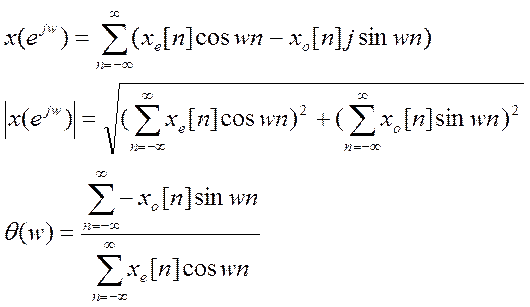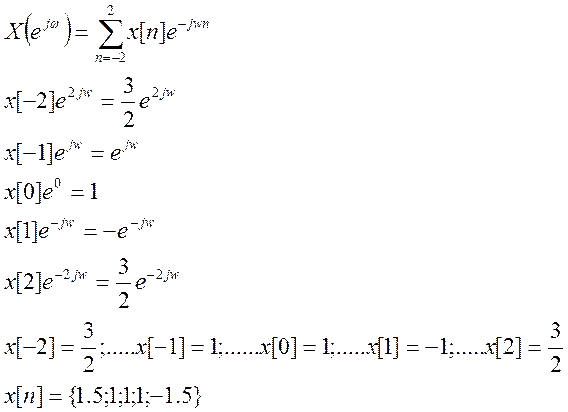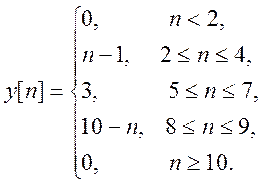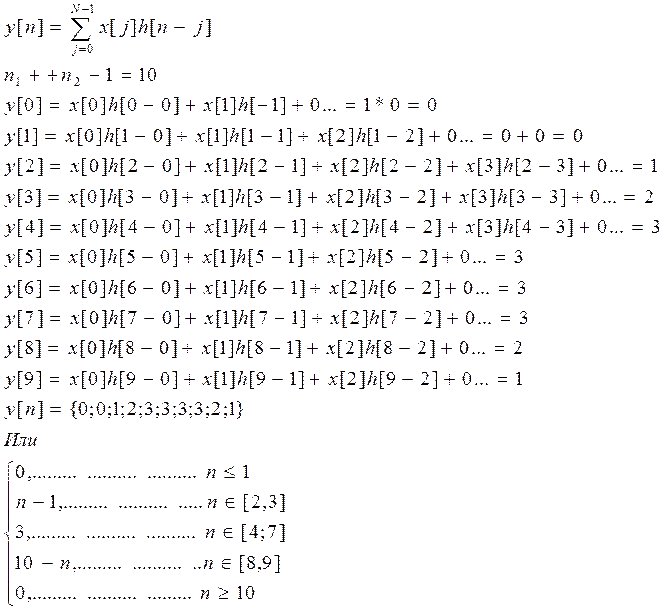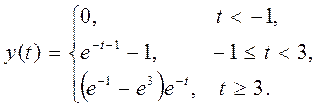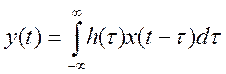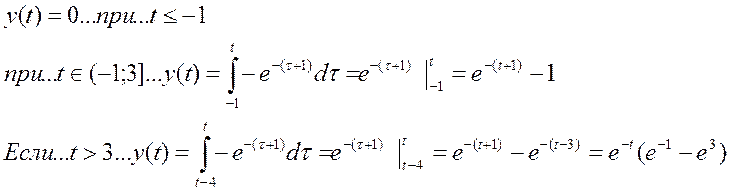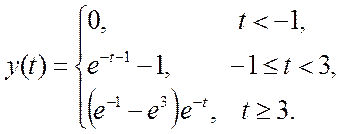Период спектра как найти

Условие задачи:

Найти период решетки, если дифракционный максимум 1-го порядка для волны 486 нм находится в 2,43 см от центрального, а расстояние от решетки до экрана 1 м.

Задача №10.7.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(k=1), (lambda=486) нм, (l=2,43) см, (L=1) м, (d-?)

Решение задачи:

Запишем формулу дифракционной решетки:

[dsin varphi = klambda;;;;(1)]

В этой формуле (d) – период решетки (также называют постоянной решетки), (varphi) – угол дифракции, (k) – порядок максимума (в данной задаче (k=1)), (lambda) – длина волны, падающей нормально на решетку.

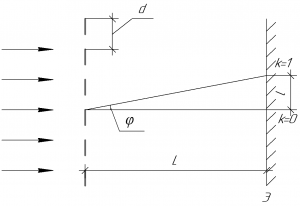
Если расписать синус угла дифракции (см. рисунок к задаче), то имеем:

[dfrac{l}{{sqrt {{L^2} + {l^2}} }} = klambda ]

Осталось из полученной формулы выразить искомый период дифракционной решетки (d):

[d = frac{{klambda sqrt {{L^2} + {l^2}} }}{l}]

Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:

[d = frac{{1 cdot 486 cdot {{10}^{ – 9}} cdot sqrt {{1^2} + {{0,0243}^2}} }}{{0,0243}} = 20 cdot {10^{ – 6}};м = 20;мкм]

Ответ: 20 мкм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.7.31 Определить длину волны, падающей на дифракционную решетку, имеющую 400 штрихов
10.7.33 Найдите наибольший порядок спектра для длины волны, равной 600 нм, если период
10.7.34 На дифракционную решетку с периодом 1 мкм падает нормально монохроматический свет

Источник

Расчёт периода сигнала. Определение амплитудного и фазового спектра периодического сигнала и построение их графиков

Страницы работы

Содержание работы

НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ
АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра Систем Сбора и Обработки Данных

Расчетно-графическая работа по курсу

«Теория обработки сигналов»

5 – й семестр

Вариант – 6,7.

Cтудентка: Березикова Н.
Преподаватель:

Факультет:
АВТ Еленычев С.В.

Группа
АО-31

Новосибирск

2005

Раздел1.

1.6.
Найдите период сигнала

Ответ. Период T = π.

То есть период x(t)=π.

1.7.
Исследуйте характер поведения экспоненциального сигнала дискретного времени при комплексных значениях .

X[n]=

Используя формулу Эйлера ,
функцию x[n] можно
выразить в виде

Если а по модулю меньше единицы, то в области положительных
значений n амплитуда функции
будет затухающей. В области отрицательных значений n,
наоборот – возрастающей. Если а по модулю больше единицы, то функция затухает в
области отрицательных значений n, возрастает в
положительной области. И действительная, и мнимая части являются затухающими
(возрастающими) гармониками.

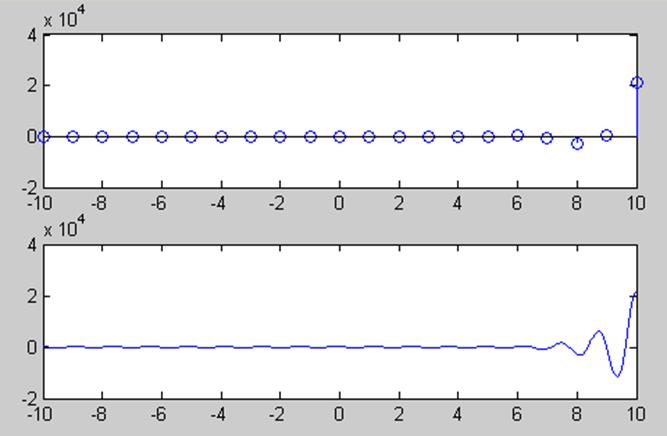
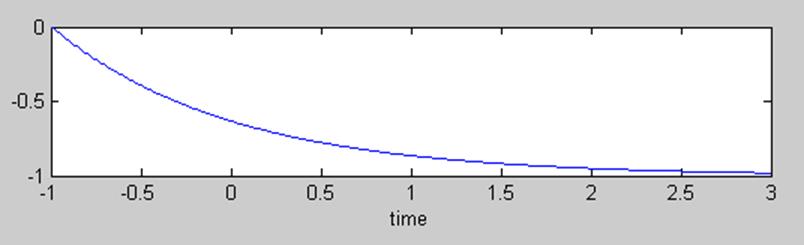
Изобразим график действительной части для а=e, что >1; =π/6; w=5; С=1:

n=-10:1:10;

x=exp(n).*cos((pi./6)+5*n);

subplot(211);

stem(n,x);

n1=-10:0.05:10;

x1=exp(n1).*cos((pi./6)+5*n1);

subplot(212);

plot(n1,x1);

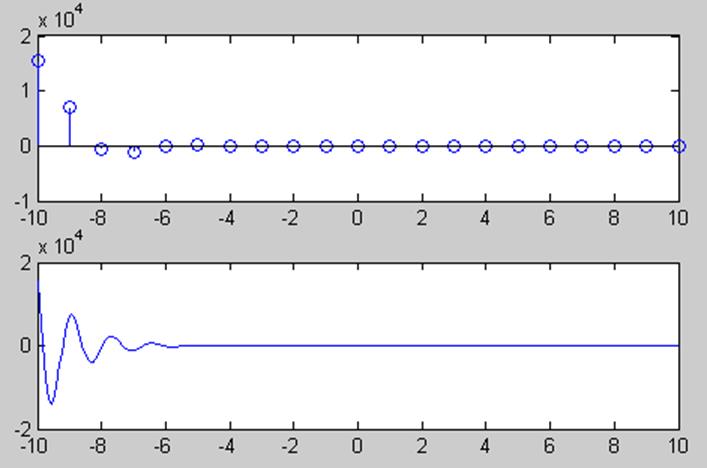
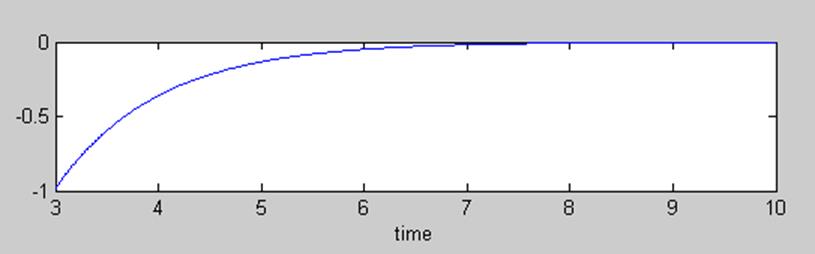
Теперь построим график для а<1, возьмем e^-1,
остальные данные такие же.

n=-10:1:10;

x=exp(-n).*cos((pi./6)+5*n);

subplot(211);

stem(n,x);

n1=-10:0.05:10;

x1=exp(-n1).*cos((pi./6)+5*n1);

subplot(212);

plot(n1,x1);

Для каждого случая выведены 2 графика, один из которых
является графиком для дискретного времени, а второй выводится для большей
наглядности того, что сигнал состоит из возрастающих (затухающих) гармоник
действительной и мнимой части (для мнимой гармоникой будет являться синус).

Раздел2.

2.6. Определите коэффициенты и
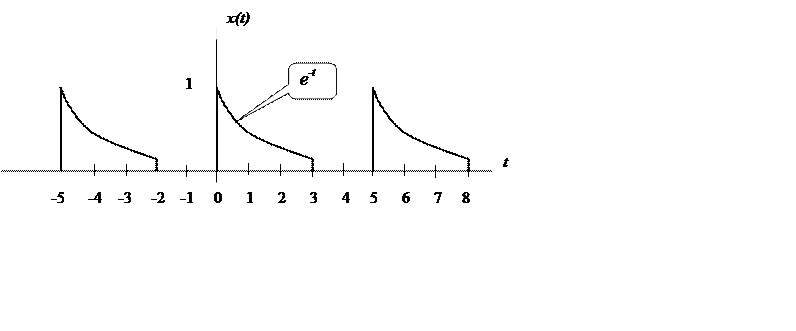
ряд Фурье сигнала

Ответ.

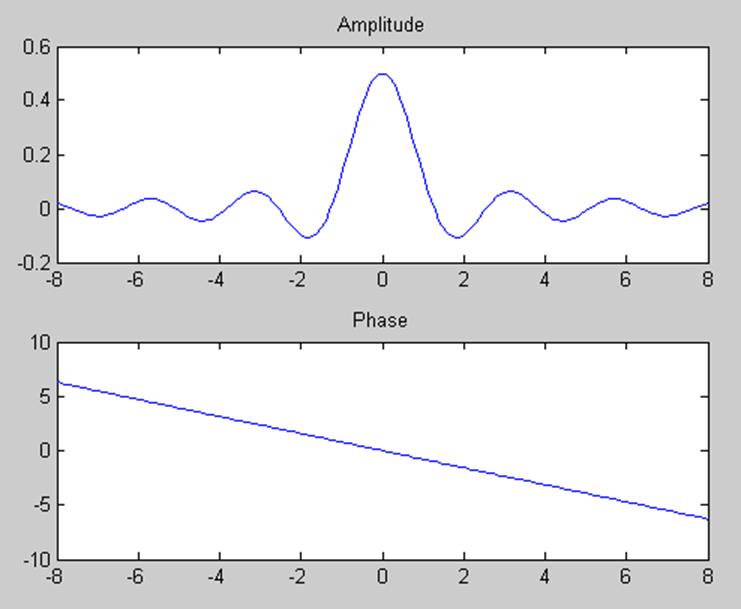
2.7. Определите амплитудный и фазовый спектры периодического
сигнала и постройте их графики.

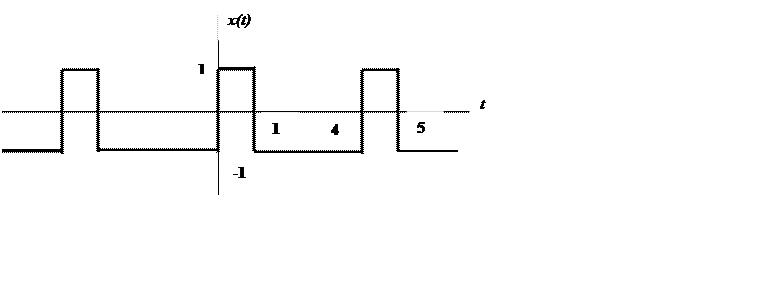Ответ. ,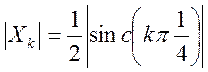

Модуль этого коэффициента равен:

k=-8:0.1:8;

subplot(211);

y=sinc(k*pi./4)./2;

plot(k,y);

title(‘Amplitude’);

f=-k*pi./4;

subplot(212);

plot(k,f);

title(‘Phase’)

Графики для амплитудного и фазового спектров.

Раздел3.

3.6. Найдите преобразование Фурье и постройте график
амплитудного спектра сигнала

Ответ: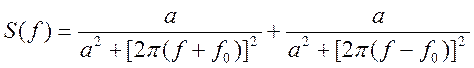

Умножение сигнала на экспоненту, где в степени есть
зависимость от времени и мнимого числа во временной области, приведет к сдвигу
на w₀ в частотной области. Это свойство
преобразования Фурье можно применить и в данном примере.

То есть в частотной области преобразование Фурье заданного
сигнала будет равно:

Так как функция является действительной, то она сама будет
определять амплитудный спектр, поэтому можно написать такую программу, если
присвоить a и w0
какие-то определенные значения, например а=2, w0=1.5:

w=-4*pi:0.01*pi:4*pi;

a=2;

w0=1.5;

x=a./(a.^2+(w-w0).^2);

y=a./(a.^2+(w+w0).^2);

z=x+y;

plot(w,z);

title(‘Amplitude’);

xlabel(‘Chastota,rad/sec’);

ylabel(‘abs[x(jw)]’);

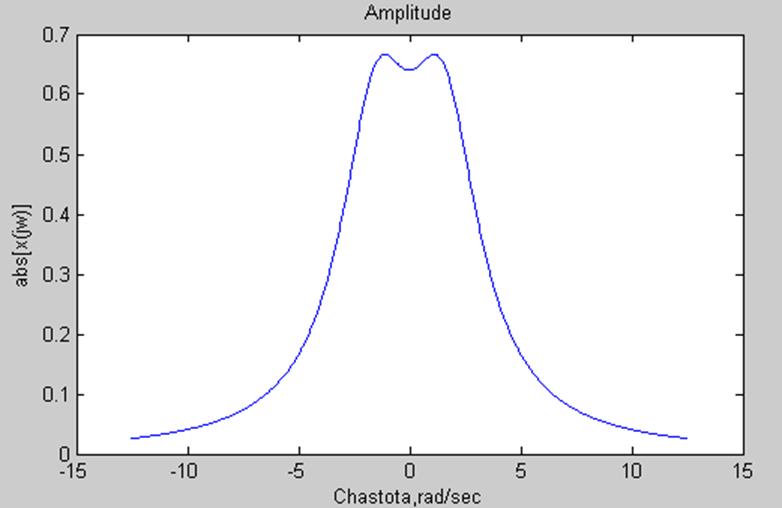
Построим график
амплитудного спектра для данных значений а и w0.

3.7. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы
.
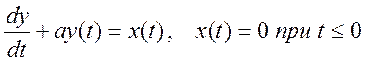
Найдите преобразование Фурье этого уравнения. Определите отношение
преобразований Фурье левой и правой части, т.е. .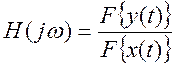
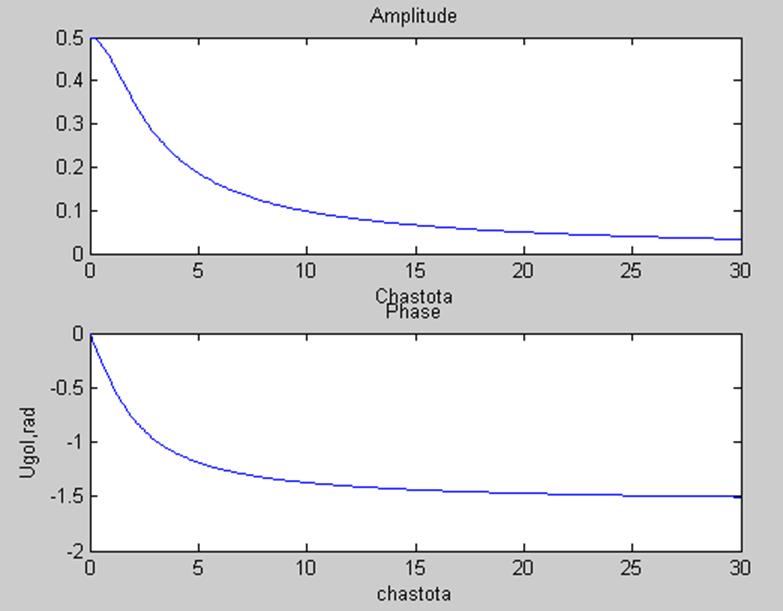
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.

Ответ. .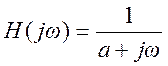

Преобразование Фурье для y:

Преобразование Фурье для x:

АЧХ:

Вещественная часть для a>0 всегда
положительна, поэтому:

Пусть а=2

w=0:0.1:30;

a=2;

W=(a-w*j)./(a.^2+w.^2);

y=abs(W);

subplot(211);

plot(w,y);

title(‘Amplitude’)

xlabel(‘Chastota’)

subplot(212);

f=angle(W);

plot(w,f);

title(‘Phase’)

xlabel(‘chastota’)

ylabel(‘Ugol,rad’)

На графиках изображены амплитудный и фазовый спектры.
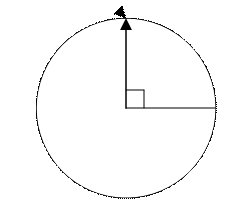
Интерпретацию смысла функций можно показать с помощью рисунка:

На рисунке показана окружность и стрелка, которая имея
какую-либо угловую скорость w может вращаться на угол φ,
который определяет фазовый спектр, а ее длину определяет амплитудный спектр.
График, который получается в результате «совмещения» двух спектров называется
годографом.

Раздел4.

4.6. Докажите, что для
действительной последовательности x[n] амплитудный спектр 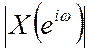является
четной функцией от ω, а фазовый спектр

– нечетной функцией от ω.

Сигнал x[n]
можно представить в виде суммы четной и нечетной составляющей:

X[n]=x_e[n]+x_o[n], где первая – это четная составляющая, а вторая –
нечетная.

Подставим это выражение в первую формулу:

Так как бесконечная сумма нечетной функции равна 0, запишем
это равенство в следующем виде:

Для амплитудного спектра видно, что под корнем получается
четная функция, а значит и сам корень является четной функцией.

Для фазового спектра – так как в сумму числителя входит sin, то функция является нечет.

4.7. Найдите вид сигнала x[n], ДВПФ которого

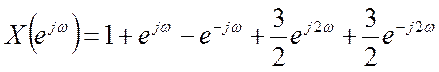
Ответ. x[-2]=1,5, x[-1]=1, x[0]=1, x[1]= -1, x[2]=1,5.

Раздел5.

5.6. Вычислите свертку сигналов

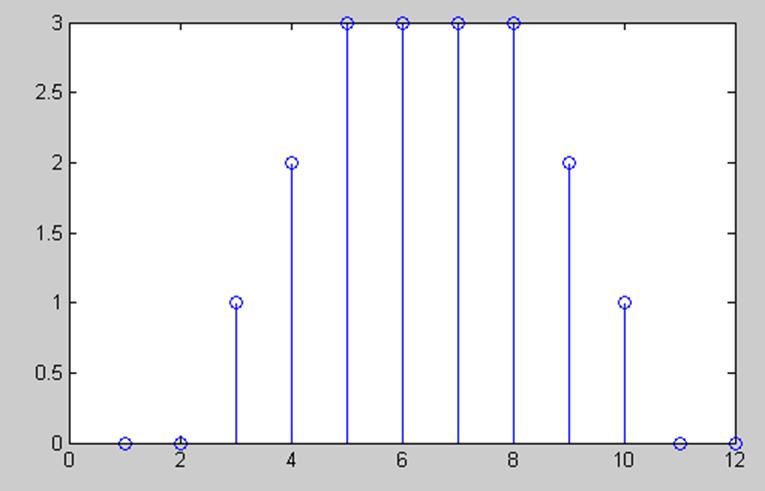
Изобразите график свертки.

Ответ.

x1=[1 1 1 0 0];

x2=[0 0 1 1 1 1 1 1];

n1=length(x1);

n2=length(x2);

y=conv(x1,x2);

k=1:1:n1+n2-1;

stem(k,y);

Свертка.

5.7. Вычислите свертку двух
непрерывных сигналов и изобразите её график

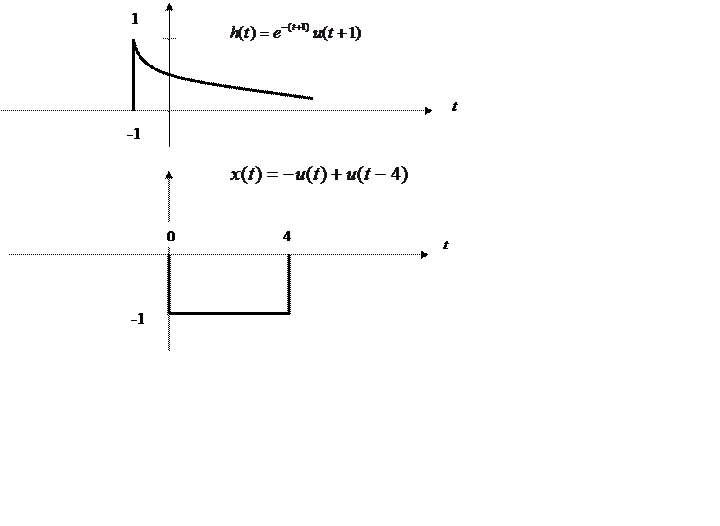Ответ.

Для данных функций, при зеркальном отображении сигнала x относительно оси ординат, пересечение происходит при
значении t=-1. Затем отрезок, на котором происходит
пересечение начинает увеличиваться, поэтому пределы интеграла стоит выбрать от
-1 и до t. Но с того момента, как t
станет равным 3 отрезок пересечения будет постоянным и при t=3
уже стоит брать границы интегрирования такие: от (t-4) и
до (t).

То есть

Информация о работе

Тип:

Расчетно-графические работы

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Источник

Спектр периодической последовательности прямоугольных импульсов

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Вводные замечания

В предыдущих разделах мы рассмотрели

разложение периодических сигналов в ряд Фурье,

а также изучили

некоторые свойства
представления периодических сигналов рядом Фурье.

Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент,
отстоящих друг от друга на частоту $Delta omega = frac{2pi}{T}$ рад/c,
где — период повторения сигнала.
В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала.
Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.

В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов,
как одного из важнейших сигналов, используемого в практических приложениях.

Спектр периодической последовательности прямоугольных импульсов

Пусть входной сигнал s(t) представляет собой периодическую последовательность
прямоугольных импульсов амплитуды , длительности tau секунд следующих с
периодом секунд, как это показано на рисунке 1

Рисунок 1. Периодическая последовательность прямоугольных импульсов

Единица измерения амплитуды сигнала зависит от
физического процесса, который описывает сигнал s(t) .
Это может быть напряжение, или, сила тока,
или любая другая физическая величина со своей единицей измерения,
которая меняется во времени как s(t) .
При этом, единицы измерения амплитуд спектра
, $omega_n = frac{2 pi}{T} n$ ,
будут совпадать с единицами
измерения амплитуды исходного сигнала.

Тогда спектр , $omega_n = frac{2 pi}{T} n$ ,
данного сигнала может быть представлен как:

(1)

Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида
$S(omega) = A , frac{sin left(omega tau/2 right) }{omega T/2}$ .

Свойства спектра периодической последовательности прямоугольных импульсов

Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.

Постоянная составляющая огибающей S(0) может быть получена как предел:

(2)

Для раскрытия неопределенности воспользуемся правилом Лопиталя [1, стр. 257]:

(3)

где $Q = frac{T}{tau} > 1$ называется скважностью импульсов и задает отношение
периода повторения импульсов к длительности одиночного импульса.

Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность.
При увеличении скважности (т.е. при уменьшении длительности импульса при
фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.

Используя скважность импульсов выражение (1) можно переписать в виде:

(4)

где .

Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:

(5)

Знаменатель обращается в ноль только при , однако, как мы выяснили выше
$S(0) = frac{A}{Q} neq 0$ , тогда решением уравнения будет

(6)

Тогда огибающая обращается в ноль если

(7)

На рисунке 2 показана огибающая спектра периодической последовательности
прямоугольных импульсов (пунктирная линия) и частотные
соотношения огибающей и дискретного спектра .

Рисунок 2. Cпектр периодической последовательности
прямоугольных импульсов

Также показаны амплитудная огибающая , амплитудный спектр , а также фазовая огибающая и фазовый спектр
.

Из рисунка 2 можно заметить, что фазовый спектр принимает значения pm pi
когда огибающая имеет отрицательные значения.
Заметим, что и соответствуют одной и
той же точке комплексной плоскости равной .

Пример спектра периодической последовательности прямоугольных импульсов

Пусть входной сигнал s(t) представляет собой периодическую последовательность
прямоугольных импульсов амплитуды A = 2 , следующих с периодом T = 4 секунды
и различной скважностью .
На рисунке 3а показаны временные осциллограммы указанных сигналов,
их амплитудные спектры (рисунок 3б),
а также непрерывные огибающие спектров (пунктирная линия).

Рисунок 3. Cпектр периодической последовательности
прямоугольных импульсов при различном значении скважности
а — временные осциллограммы; б — амплитудный спектр

Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов s(t) уменьшается,
огибающая спектра расширяется и уменьшается по амплитуде (пунктирная линия).
В результате, в пределах главного лепестка увеличивается количество гармоник спектра .

Спектр смещенной во времени периодической последовательности прямоугольных импульсов

Выше мы подробно изучили спектр периодической последовательности прямоугольных
импульсов для случая, когда исходный сигнал s(t) являлся симметричным относительно t = 0 .
В результате спектр такого сигнала является вещественным и задается выражением (1).
Теперь мы рассмотрим, что произойдет со спектром сигнала $s_{textrm{sh}}(t)$
если мы сместим сигнал s(t) во времени,как это показано на рисунке 4 .

Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов

Смещенный сигнал $s_{textrm{sh}}(t)$ можно представить как сигнал s(t) ,
задержанный на половину длительности импульса
$s_{textrm{sh}}(t) = s left( t - frac{tau}{2}right)$ .
Спектр $S_{textrm{sh}}(omega_n)$ смещенного сигнала $s_{textrm{sh}}(t)$ можно представить
согласно свойству

циклического временного сдвига

как:

(8)

Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не
является чисто вещественной функцией, а приобретает дополнительный фазовый множитель
$expleft( -j omega_n frac{tau}{2}right)$ .
Амплитудный $left|S_{textrm{sh}}(omega_n) right|$ и фазовый $Phi_{textrm{sh}}(omega)$
спектры показаны на рисунке 5.

Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической
последовательности прямоугольных импульсов

Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала,
но добавляет линейную составляющую к фазовому спектру сигнала.

Выводы

В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.

Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры
спектров при различном значении скважности.

Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано,
что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.

Программная реализация в библиотеке DSPL

Данные для построения рисунков данного раздела были просчитаны при использовании

библиотеки DSPL-2.0

Ниже приведён исходный код программы расчета данных для построения рисунка 3:

fourier_series_pimp_q.c


#include <stdio.h>
#include <string.h>
#include "dspl.h"

/* Размер векторов входных сигналов и огибающей спетра */
#define N  1000 

/* Период повторения импульса. Для изменения скважности мы будем менять 
 * длительность импульса при фиксированном периоде повторения */
#define T  4.0

/* Амплитуда */
#define A  2.0

/* Количество спектральных гармоник разложения в ряд Фурье  */
#define M  41


/* длина команды Gnuplot */
#define PLOTCMD_LEN 256


int main(int argc, char* argv[])
{

  double    t1[N];   /* время (сек) на одном периоде повторения      */
  double    t4[N];   /* время (сек) на четырех периодах повторения   */
  double    s[N];    /* входной сигнал                               */
  complex_t S[M];    /* комплексный спектр периодического сигнала    */
  double    Smag[M]; /* амплитудный спектр периодического сигнала    */
  double    w[M];    /* частота (рад/c) дискретного спектра          */
  double    wc[N];   /* частота (рад/с) огибающей спектра            */
  double    Sc[N];   /* огибающая спектра                            */
  double    tau;     /* длительность импульса                        */

  /* скважность */
  double    Q[3] = {5.0, 2.0, 1.25};

  int q, m, n;
  
  char fname[64];            /* имя файла данных */
  char plotcmd[PLOTCMD_LEN]; /* Команда Gnuplot  */ 
  
  void* hdspl;  /* DSPL handle        */
  void* hplot;  /* GNUPLOT handle     */
  
  hdspl = dspl_load();
  if(!hdspl)
  {
    printf("Cannot to load libdspl!n");
    return 0;
  }
  
  /* Вектор частот непрерывной огибаюхей вида sin(w/2*tau) / (w/2*T) */
  linspace(-M_PI*(double)M/(double)T, M_PI*(double)M/(double)T,  N, DSPL_SYMMETRIC, wc);
  
  /* заполнение массива временных отсчетов  */
  /* на одном периоде повторения сигнала    */
  linspace(-T/2.0, T/2.0,  N, DSPL_PERIODIC, t1);
  
  /* заполнение массива временных отсчетов
   * на 4-x периодах повторения сигнала
   * для отображения на осциллограмме */
  linspace(-T*2.0, T*2.0,  N, DSPL_PERIODIC, t4);
  
  
  /* Построение графиков пакетом GNUPLOT */
  gnuplot_create(argc, argv, 800, 640,  "img/fourier_series_rec.png", &hplot);
  gnuplot_cmd(hplot, "unset key");
  gnuplot_cmd(hplot, "set multiplot layout 3,2 rowsfirst");
  gnuplot_cmd(hplot, "set yrange [0:2.2]");
  
  for(q = 0; q < 3; q++)
  {
    tau = T/Q[q];

    /* 4 периода повторения п-импульса скважности Q[q] */
    signal_pimp(t4, N, A, tau, 0.0, T, s);

    /* сохранение в текстовый файл временных осциллограмм */
    sprintf(fname, "dat/pimp_time_%.2lf.csv", Q[q]);
    writetxt(t4, s, N, fname);

    /* Построение временнОй осциллограммы */
    sprintf(plotcmd, "plot '%s' with lines", fname);
    gnuplot_cmd(hplot, plotcmd);

    /* один период повторения п-импульса скважности Q[q] */
    signal_pimp(t1, N, A, tau, 0.0, T, s);

    /* разложение в ряд Фурье */
    fourier_series_dec(t1, s, N, T, M, w, S);

    /* Рассчет амплитудного спектра */
    for(m = 0; m < M; m++)
    {
      /*printf("S[%d] = %f     %fn", m, RE(S[m]), IM(S[m]));*/
      Smag[m] = ABS(S[m]);
    }

    /* Сохранение в файл амплитудного спетра для скважности Q[q] */
    sprintf(fname, "dat/pimp_freq_discrete_%.2lf.csv", Q[q]);
    writetxt(w, Smag, M, fname);

    /* Построение на график амплитудного спектра для заданной скважности */
    sprintf(plotcmd, "plot '%s' with  impulses lt 1 ,\", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);

    sprintf(plotcmd, "'%s'  with points pt 7 ps 0.5 lt 1 ,\", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);

    /* Расчет огибающей */
    for(n = 0; n < N; n++)
      Sc[n] = (wc[n] == 0.0) ? A/Q[q] : fabs( A * sin(0.5*wc[n]*tau) / (0.5*wc[n] * T));

    /* сохранение огибающей в файл для скважности Q[q] */
    sprintf(fname, "dat/pimp_freq_cont_%.2lf.csv", Q[q]);
    writetxt(wc, Sc, N, fname);
    
    /* Построение на график непрерывной огибающей 
    амплитудного спектра для заданной скважности */
    sprintf(plotcmd, "'%s'  with lines", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);
  }

  gnuplot_cmd(hplot, "unset multiplot");
  gnuplot_close(hplot);
  
  /* remember to free the resource */
  dspl_free(hdspl);
  return 0;
}

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье

Список литературы

[1]

Основы математического анализа.
Москва, Наука, 1965, 572 c.

[2]

Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[4]

Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.

[5]

Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:36)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

Дифракция на дифракционной решетке

Рассмотрим
дифракцию на одномерной дифракционной
решетке, так как этот вид дифракции
находит широкое применение во многих
методах спектрального анализа.

Дифракционная
решетка представляет собой систему
большого числа одинаковых по ширине и
параллельных друг другу щелей, лежащих
в одной плоскости и разделенных
непрозрачными промежутками, равными
по ширине. Изготавливается путем
нанесения параллельных штрихов на
поверхность стекла с помощью делительных
машин. Эти места являются, таким образом,
практически непрозрачными промежутками
между неповрежденными частями
пластинки, которые играют роль щелей.
Число штрихов на
1 мм
определяется областью спектра исследуемого
излучения –
от
300 мкм
в инфракрасной области до
1200 мкм –
в ультрафиолетовой).

Итак,
имеется система из N
параллельных щелей с шириной каждой
цели a
и расстоянием между соседними щелями
b
(рис.
2.6). Сумма
a
+ b
= d
называется периодом, или постоянной
дифракционной решетки. На решетку
нормально падает плоская монохроматическая
волна. Требуется исследовать интенсивность
света, распространяющегося в
направлении, составляющем угол
φ с нормалью
к плоскости решетки.

Кроме распределения
интенсивности света вследствие
дифракции на каждой щели, нужно учесть
интерференцию между
N
пучками (перераспределение световой
энергии за счет интерференции волн
от N
щелей 
когерентных источников).
Очевидно, минимумы
будут на прежних местах, ибо условие
минимума дифракции для
всех щелей одинаково. Эти минимумы
называются главными
минимумами.
Они соответствуют таким углам φ
, для которых А_φ
= 0, т.е. свет от разных
частей каждой щели полностью гасится.
В этом направлении ни одна щель не
дает света. Условие главных
минимумов
совпадает с условием
(2.6).

К
главным минимумам, создаваемым каждой
щелью в отдельности, добавляются
минимумы, возникающие в результате
интерференции света, прошедшего
через различные щели. Появляются
добавочные минимумы в областях
дифракционных максимумов. Внешне это
проявляется в том, что широкие полосы,
создаваемые одной узкой щелью, покрываются
рядом более тонких полос, вызванных
интерференцией лучей, исходящих от
разных щелей: первой и второй, первой и
третьей и т.д. Чем больше щелей, тем
больше добавочных минимумов может
возникнуть. Так как общий световой поток
остается неизменным, происходит
усиление световых потоков около
направлений, удовлетворявших условиям
максимумов при интерференции от разных
щелей за счет уменьшения световой
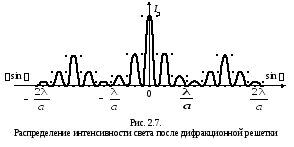
энергии в других направлениях. На рис.
2.7 для примера показано распределение
интенсивности света и расположение
максимумов иминимумов
в случае двух щелей.

Воспользуемся
методом Френеля. В одном и том же
направлении все щели излучают свет
совершенно одинаково. Результат
интерференции зависит от оптической
разности хода в сходственных точках
двух соседних щелей до точки С_–_φ,
на экране.
Для всех сходственных точек
эта разность
хода одинакова и равна
d sin
φ. Если

(2.7)

колебания
от соседних щелей взаимно усиливают
друг друга, и в точке С_–_φ
наблюдается
максимум
дифракции. Амплитуда суммарного
колебания в этих точках экрана максимальна:

А_max≈
NA_φ,

где
A_φ

амплитуда колебания, посылаемого одной
щелью под углом φ.

Интенсивность
главного максимума

,
(2.8)

поэтому
формула
(2.7) определяет
положение главных максимумов
интенсивности. Число k
дает порядок главного максимума. Максимум
нулевого порядка один и расположен
в точке С₀;
максимумов первого, второго и т.д.
порядков по два и расположены они
симметрично относительно С₀
, на что
указывает знак
“±”.

Кроме
главных максимумов, имеется большое
число более слабых побочных максимумов,
разделенных добавочными
минимумами.
Побочные максимумы значительно слабее
главных
максимумов.
Расчет показывает, что интенсивность
побочных максимумов не превышает
1/23
интенсивности ближайшего главного
максимума. В главных максимумах амплитуда
суммарного колебания в
N
раз, а
интенсивность в
N²
раз больше, чем в соответствующем месте
дает одна щель. Увеличение максимумов
происходит также за счет того, что в
случае решетки отдельные яркие главные
максимумы разделены темными областями
добавочных минимумов и очень слабых
побочных максимумов. В итоге происходит
резкое сужение, дифракционных
максимумов (пропорционально ~
1/N),
которые становятся тонкими и яркими.
Такие яркие линии, четко локализованные
в пространстве, легко обнаруживаются
и могут быть использованы
для
спектроскопических исследований.

По
мере удаления от центра экрана
интенсивность дифракционных максимумов
убывает (увеличивается расстояние от
источников). Поэтому не удается наблюдать
все возможные дифракционные максимумы.

Заметим,
что количество дифракционных максимумов,
даваемых решеткой по одну сторону от
центра экрана, определяется условием
φ = π/2 
максимальный
угол дифракции; sin
φ
< 1, откуда с учетом
(2.8)

.
(2.9)

При
этом не следует забывать, что k

целое число.

Положение
главных максимумов зависит от длины
волны λ.
Поэтому при освещении дифракционной
решетки белым светом все максимумы,
кроме центрального
(k
= 0), разложатся
в спектр, обращенный фиолетовым концом
к центру дифракционной картины. Таким
образом, дифракционная решетка может
служить для исследования спектрального
состава света, т.е. для определения
частот (или длин волн) и интенсивности
всех его монохроматических компонент.
Применяемые для этих целей приборы
называются дифракционными спектрографами,
если исследуемый спектр регистрируется
с помощью фотопластинки, и дифракционными
спектроскопами, если спектр наблюдается
визуально.

Угловая дисперсия
дифракционной решетки

Качество дифракционной решетки
определяется двумя характеристиками:
угловой дисперсией (D)
и разрешающей силой (разрешающей
способностьюR).

Основное
назначение дифракционной решетки

установление длины волны исследуемого
излучения. Так как положение спектральных
линий задается углом, определяющим
направление лучей (см. уравнение
(2.7)),
целесообразно ввести угловую дисперсию
D:

,
(2.10)

где
∆φ

угловое расстояние между спектральными
линиями, отличающимися по длине волны
на ∆λ
(рис.2.8); D

угловое расстояние между двумя линиями,
отличающимися по длине волны на
1
(1=10^-10
м).

Дифференцируя
(2.7)
слева по
φ,
а справа по λ,
находим, что ,
откуда

Чем
меньше период решетки d
и чем выше порядок спектра k
, тем больше
угловая дисперсия. В пределах небольших
углов
(cos
φ
~1 )
можно положить

.
(2.11)

Из
выражения
(2.11) следует,
что угловая дисперсия прямо пропорциональна
порядку дифракции k
и обратно
пропорциональна расстоянию между
соседними штрихами (периодом решетки)
d
.
Следовательно, для увеличения дисперсии
необходимо увеличивать число штрихов
на единицу длины. Этим объясняется
необходимость изготавливать дифракционные
решетки с возможно большим числом
штрихов на
1 мм
ее ширины.

Разрешающая
сила дифракционной решетки

Большая дисперсия
оптических приборов (в том числе
дифракционной решетки) является
необходимым, но не достаточным условием
для раздельного наблюдения двух
близлежащих линий. В зависимости от
крутизны кривой интенсивности соседние
максимумы длин волн λ₁
и λ₂
могут наблюдаться как два самостоятельных
или как один максимум. Как видно из рис.
2.9, при одинаковой угловой дисперсии
линий λ₁
и λ₂
возможность их
разрешения (раздельного восприятия)
различна. Так, на рис. 2.9 слева минимум
между линиями λ₁
и λ₂
, отсутствует, и эти линии не различаются
как самостоятельные, а на рис. 2.9
справа имеются наблюдаемые
минимумы между линиями λ₁
и λ₂.

Чтобы
охарактеризовать способность прибора
при данной дисперсии различать две
близлежащие линии, вводится понятие
разрешающей силы R.
Для количественной характеристики
этого понятия нужно ввести критерий
разрешения. Согласно Рэлею, две близлежащие
спектральные линии с равными интенсивностями
и симметричными одинаковыми контурами
разрешимы, если максимум одной длины
волны λ₁,
совпадает с минимумом другой и
наоборот. При удовлетворении этого
условия интенсивность «провала»
между максимумами составляет
80 %
интенсивности
каждой линии, что является достаточным
для раздельного наблюдения линий
λ₁
и λ₂.
Нарушение критерия Рэлея приводит
к наблюдению одной линии вместо двух.

Если
разность длин волн | λ₂
– λ₁
| между двумя соседними максимумами,
для которых выполняется критерий Рэлея,
обозначить через ∆λ
, а среднюю
длину волны, соответствующую центру
провала между максимумами,
– через
λ,
то в качестве количественной характеристики
разрешающей силы можно взять величину

.
(2.12)

Таким
образом, разрешающей силой R
дифракционной
решетки называется величина, обратная
минимальной разности длин волн ∆λ
(взятой около некоторой длины волны λ),
которые разделены (разрешены) данной
решеткой. Согласно условию Рэлея, а
также (2.7) разрешение линий имеет
место при

R
= k
N,

(2.12)

где
k

порядок дифракционного максимума;
N

общее число щелей решетки.

Из
выражения
(2.12) видно,
что чем больше число щелей решетки N
, тем больше
её разрешающая сила (разрешающая
способность). При заданном числе щелей
R
увеличивается при переходе к спектрам
высших порядков. Современные дифракционные
решетки обладают довольно высокой
разрешающей способностью (до
210⁵
).

Дифракция на
пространственной решетке

Дифракция
света наблюдается не только на плоской
одномерной решетке, но и на двумерной
решетке (штрихи нанесены во взаимно
перпендикулярных направлениях) в одной
и той же плоскости. Но наибольший
практический интерес представляет
дифракция на пространственных
(трехмерных) решетках. В качестве
пространственных дифракционных решеток
могут быть использованы кристаллические
тела (например, монокристаллы), так как
в них неоднородности (атомы, ионы)
регулярно повторяются в трех направлениях
(рис. 2.10). Этот случай дифракции привел
Лауэ
(1912 г.) к
открытию метода исследования кристаллов
при помощи дифракции рентгеновских
лучей.

Действительно,
для того, чтобы решетка могла эффективно
разложить излучение в спектр, её
постоянная d
должна быть по порядку величины
примерно такой же, как и длина волны λ.
Для оптической области излучения

это решетка c
периодом d

10^-6м.
В природе существуют естественные
пространственные структуры с периодом

10^-10м.
Это
кристаллы,
у которых атомы, ионы или молекулы
расположены упорядоченно и образуют
пространственную периодическую
структуру, напоминающую дифракционную
решетку. Период кристаллической решетки
соизмерим с длинами волн рентгеновской
области спектра. Просвечивая кристаллы
рентгеновскими лучами, можно определить
период кристаллической решетки
с помощью явления дифракции на
пространственной структуре. Таким
образом, был разработан структурный
анализ кристаллических образований.
С другой стороны, метод Лауэ дал
возможность определять длину волны
рентгеновских лучей, если известна
кристаллическая структура той решетки,
которая служит дифракционной. Метод
явился основой спектроскопии
рентгеновских лучей, позволяющей
установить важнейшие особенности
строения атома.

В
1913 году русский физик
Г.В. Вульф и англичанин У.Л. Брэгг
предложили простой метод расчета
дифракции рентгеновских лучей в
кристаллах. Направления, в которых
получаются дифракционные максимумы,
определяются условием:

,
(2.13)

где
d
– период
структуры, 
– угол скольжения падающих лучей.

Метод позволяет исследовать спектральный
состав рентгеновского излучения,
если известны расстояния между
отражающими плоскостями ААиВВкристалла
(рентгеновская спектроскопия). И,
наоборот, изучать структуру кристаллов
(определять расстояние между плоскостями,
тип кристаллической решетки и т.д.), если
известна длина волны монохроматического
рентгеновского излучения (рентгеноструктурный
анализ).

ВОПРОСЫ ДЛЯ
САМОКОНТРОЛЯ

В чем заключается
явление дифракции света?
При каких условиях
наблюдается дифракция света?
Сущность
принципа Гюйгенса
– Френеля.
Сущность метода
зон Френеля. Что такое зона Френеля?
Как
c помощью метода зон Френеля объясняется
прямолинейное распространение света?
При каких условиях
возникает дифракция Френеля?
При каких условиях
возникает дифракция Фраунгофера?
Условия
образования максимумов и минимумов
при дифракции от одной щели. Что означает
величина k
в формулах максимумов и минимумов
дифракции?
Изобразите
графически распределение интенсивности
света на экране при дифракции на одной
щели. Дайте пояснения.
Какой
вид имеют дифракционные максимумы при
освещении щели: а) монохроматическим
светом, б) белым светом? Дайте пояснения.
Какое
устройство называется дифракционной
решеткой?
Перечислите
характеристики дифракционной решетки.
Что
называют периодом (постоянной)
дифракционной решетки? Как вычислить
период дифракционной решетки, зная
число штрихов на единицу длины?
Какую
величину называют угловой дисперсией
дифракционной решетки? Как увеличить
угловую дисперсию дифракционной
решетки?
Какую
величину называют разрешающей силой
(разрешающей способностью) дифракционной
решетки? Как увеличить разрешающую
способность дифракционной решетки?
Напишите
условия образования главных максимумов
и главных минимумов при дифракции на
дифракционной решетке.

17.
В чем преимущества дифракционной решетки
перед щелью?

18.
От каких параметров зависит яркость и
ширина дифракционного максимума при
дифракции на решетке? От чего зависит
общее число дифракционных максимумов,
полученных на экране за решеткой?

19.
Сущность
спектрального анализа. Какие характеристики
определяются с его помощью?

20.Где применяется явление
дифракции рентгеновских лучей? Какие
физические характеристики определяются
с помощью этого явления?

Соседние файлы в папке Уч_Пособие_Часть_3

Источник

Как определить наибольший порядок спектра дифракционной решетки

Проходя через дифракционную решетку луч света отклоняется от своего направления под несколькими разными углами. В результате по другую сторону решетки получается картина распределения яркости, в которой яркие участки чередуются с темными. Вся эта картина называется дифракционным спектром, а число ярких участков в ней определяет порядок спектра.

Инструкция

В расчетах исходите из формулы, которая связывает между собой угол падения света (α) на дифракционную решетку, длину его волны (λ), период решетки (d), угол дифракции (φ) и порядок спектра (k). В этой формуле произведение периода решетки на разницу между синусами углов дифракции и падения приравнивается к произведению порядка спектра на длину волны монохроматического света: d*(sin(φ)-sin(α)) = k*λ.

Выразите из приведенной в первом шаге формулы порядок спектра. В результате у вас должно получиться равенство, в левой части которого останется искомая величина, а в правой будет отношение произведения периода решетки на разность синусов двух известных углов к длине волны света: k = d*(sin(φ)-sin(α))/λ.

Так как период решетки, длина волны и угол падения в полученной формуле являются величинами постоянными, порядок спектра зависит только от угла дифракции. В формуле он выражен через синус и стоит в числителе формулы. Из этого вытекает, что чем больше синус этого угла, тем выше порядок спектра. Максимальное значение, которое может принимать синус, равно единице, поэтому просто замените в формуле sin(φ) на единичку: k = d*(1-sin(α))/λ. Это и есть окончательная формула вычисления максимального значения порядка дифракционного спектра.

Подставьте численные величины из условий задачи и рассчитайте конкретное значение искомой характеристики дифракционного спектра. В исходных условиях может быть сказано, что падающий на дифракционную решетку свет составлен из нескольких оттенков с разными длинами волн. В этом случае используйте в расчетах ту из них, которая имеет меньшее значение. Эта величина стоит в числителе формулы, поэтому наибольшее значение периода спектра будет получено при наименьшем значении длины волны.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 20 мкм.

Смотрите также задачи:

Расчёт периода сигнала. Определение амплитудного и фазового спектра периодического сигнала и построение их графиков

Страницы работы

Содержание работы

Похожие материалы

Информация о работе

Спектр периодической последовательности прямоугольных импульсов

Дифракция на дифракционной решетке

Как определить наибольший порядок спектра дифракционной решетки

Добавить комментарий Отменить ответ

Условие задачи:

Дано:

Решение задачи:

Ответ: 20 мкм.

Смотрите также задачи:

Расчёт периода сигнала. Определение амплитудного и фазового спектра периодического сигнала и построение их графиков

Страницы работы

Содержание работы

Похожие материалы

Информация о работе

Спектр периодической последовательности прямоугольных импульсов

Дифракция на дифракционной решетке

Как определить наибольший порядок спектра дифракционной решетки

Вам также может понравиться

Как составить акт ревизии кассы предприятия

Как найти сердце контролера тт2

Как найти атмосферное давление по карте

Добавить комментарий Отменить ответ