
Теорема Пифагора: a2 + b2 = c2

Анимация простейшей пифагоровой тройки: 32 + 42 = 52
Пифаго́рова тро́йка — упорядоченный набор из трёх натуральных чисел 
При этом числа, образующие пифагорову тройку, называются пифагоровыми числами. Названы в честь Пифагора Самосского, хотя открыты задолго до него.
Треугольник, длины сторон которого образуют пифагорову тройку, является прямоугольным и называется пифагоровым треугольником.
Примитивные тройки[править | править код]
Поскольку уравнение 






В примитивной тройке 



Любая примитивная пифагорова тройка 




Эти числа можно вычислить по формулам
Наоборот, любая такая пара чисел 

Примеры[править | править код]
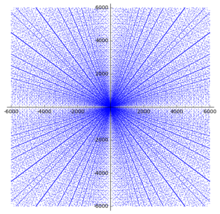
Диаграмма рассеяния катетов 
Имеется 16 примитивных пифагоровых троек с 
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Не все тройки с 
Примитивные тройки с 
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Возможные значения 
- 5, 10, 13, 15, 17, 20, 25, 26, 29, 30, 34, 35, 37, 39, 40, 41, 45, 50, …
Основываясь на свойствах чисел Фибоначчи, можно образовывать из этих чисел, например, такие пифагоровы тройки:
История[править | править код]

Наиболее известной в развитых древних культурах была тройка (3, 4, 5), которая позволяла древним строить прямые углы. Витрувий считал эту тройку высшим достижением математики, а Платон — символом супружества, что говорит о большом значении, которое придавали древние тройке (3, 4, 5).
В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.
Вавилонские математики умели вычислять пифагоровы тройки.
Вавилонская глиняная табличка, названная Plimpton 322, содержит пятнадцать пифагоровых троек (точнее пятнадцать пар чисел 

Считается, что эта табличка была создана около 1800 года до н. э.[2]
Генерация троек[править | править код]

Примитивные пифагоровы тройки. Нечётный катет 




Диаграмма треугольников, полученных из формулы Евклида, показывающая часть конуса 


Формула Евклида[3] является основным средством построения пифагоровых троек. Согласно ей для любой пары натуральных чисел 


образуют пифагорову тройку. Тройки, образованные по формуле Евклида, примитивны тогда и только тогда, когда 












Любая примитивная тройка получается из единственной пары взаимно простых чисел 

Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. При добавлении дополнительного параметра 
где 






То, что эти формулы образуют пифагоровы тройки, можно проверить путём подстановок в 





Со времён Евклида было найдено множество формул для генерации троек.
Доказательство формул Евклида[править | править код]
Тот факт, что числа 








Обратное утверждение, что 






















относительно 

Поскольку 















Более длинное, но и более общепринятое доказательство приведено в книгах Маора (Maor, 2007)[6] и Серпинского[7].
Интерпретация параметров в формуле Евклида[править | править код]
Пусть стороны пифагорова треугольника равны 





Элементарные свойства примитивных пифагоровых троек[править | править код]
Свойства примитивной пифагоровой тройки (a, b, c), где a < b < c (без указания чётности чисел a или b):
всегда является полным квадратом[9]. Это особенно полезно для проверки, является ли заданная тройка чисел пифагоровой, хотя это и не является достаточным условием. Тройка (6, 12, 18) проходит этот тест, поскольку (c − a)(c − b)/2 является полным квадратом, но эта тройка не является пифагоровой. Если тройка чисел a, b и c образует пифагорову тройку, то число (c минус чётный катет) и половина числа (c минус нечётный катет) являются полными квадратами, однако это не является достаточным условием, и тройка (1, 8, 9) является контрпримером, поскольку 12 + 82 ≠ 92.
- Максимум одно из чисел a, b и c является квадратом[10].
- Площадь пифагорова треугольника не может быть квадратом[11] или удвоенным квадратом[12] натурального числа.
- В точности одно из чисел a и b нечётно, c всегда нечётно[13].
- В точности одно из чисел a и b делится на 3.[14]
- В точности одно из чисел a и b делится на 4.[7]
- В точности одно из чисел a, b и c делится на 5.[7]
- Максимальное число, которое всегда делит произведение abc, равно 60.[15]
- Все простые множители c являются простыми вида 4n + 1[16]. Таким образом, c имеет вид 4n + 1.
- Число (b − a) является произведением простых чисел вида 8n ± 1, то есть не имеет таких сомножителей, как 2, 3, 5, 11, 13, 19, 29, 37, 43, 53, 59, 61, 67, 83, 101, …
- Площадь (K = ab/2) является чётным конгруэнтным числом[17].
- В любой пифагоровой тройке радиус вписанной окружности и радиусы трёх вневписанных окружностей являются натуральными числами. В частности, для примитивной тройки радиус вписанной окружности равен r = n(m − n), а радиусы вневписанных окружностей, касающихся катетов m2 − n2, 2mn, и гипотенузы m2 + n2 равны соответственно m(m − n), n(m + n) и m(m + n)[18].
- Как и для любого прямоугольного треугольника, обратное утверждение к теореме Фалеса гласит, что диаметр описанной окружности равен гипотенузе. Поскольку для примитивных троек диаметр равен √m2 + n2, радиус описанной окружности является половиной этого числа и это число рациональное, но не целое (поскольку m и n имеют разную чётность).
- Если площадь пифагорова треугольника умножить на кривизны вписанной окружности и трёх вневписанных, в результате получим четыре положительных целых w > x > y > z соответственно. Эти числа w, x, y, z удовлетворяют уравнению декартовых окружностей[19]. Эквивалентно, радиус внешней окружности Содди[en] любого прямоугольного треугольника равен его полупериметру. Внешний центр Содди расположен в точке D, где ACBD — прямоугольник, ACB — прямоугольный треугольник, а AB — его гипотенуза.[20]
- Не существует пифагоровых троек, для которых гипотенуза и один из катетов являются катетами другой пифагоровой тройки. Это одна из формулировок теоремы Ферма о прямоугольном треугольнике[21].
- Каждый примитивный пифагоров треугольник имеет уникальное отношение площади к квадрату полупериметра (то есть отношения для различных примитивных треугольников различны), и это отношение равно[22]
- Ни в каком примитивном пифагоровом треугольнике высота, опирающаяся на гипотенузу, не выражается целым числом, а потому он не может быть разбит на два пифагоровых треугольника.[23]
Кроме того, могут существовать специальные пифагоровы тройки с некоторыми дополнительными свойствами:
- Любое целое, большее 2, которое не сравнимо с 2 по модулю 4[en] (другими словами, если оно больше 2 и не имеет вид 4n + 2) является частью примитивной пифагоровой тройки.
- Любое целое число, большее 2, входит в примитивную или непримитивную пифагорову тройку. Например, числа 6, 10, 14 и 18 не содержатся ни в какой примитивной тройке, но входят в тройки 6, 8, 10; 14, 48, 50 и 18, 80, 82.
- Существует бесконечно много пифагоровых троек, в которых гипотенуза и больший из катетов отличаются ровно на единицу (такие тройки заведомо примитивны). Один из способов получения таких троек — равенство (2n + 1)2 + [2n(n + 1)]2 = [2n(n + 1) + 1]2, приводящее к тройкам (3, 4, 5), (5, 12, 13), (7, 24, 25), и т. д. Более общее утверждение: для любого нечётного целого j существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и чётный катет отличаются на j2.
- Существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и больший по длине катет отличается ровно на два. Обобщение: Для любого целого k > 0, существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и нечётный катет отличаются на 2k2.
- Существует бесконечно много пифагоровых троек, в которых два катета отличаются ровно на единицу. Например, 202 + 212 = 292.
- Для любого натурального n существует n пифагоровых троек с различными гипотенузами и одной и той же площадью.
- Для любого натурального n существует по меньшей мере n различных пифагоровых троек с одним и тем же катетом a, где a — некоторое натуральное число
- Для любого натурального n существует по меньшей мере n различных пифагоровых троек с одной и той же гипотенузой.[24]
- Существует бесконечно много пифагоровых троек, у которых квадратами являются гипотенуза c и сумма катетов a + b. В наименьшей такой тройке[25] a = 4 565 486 027 761; b = 1 061 652 293 520; c = 4 687 298 610 289. Здесь a + b = 2 372 1592 и c = 2 165 0172. В формуле Евклида эти значения соответствуют m = 2 150 905 и n = 246 792.
- Существуют пифагоровы треугольники с целой высотой, опирающейся на гипотенузу. Такие треугольники известны как разбиваемые, поскольку их можно разбить этой высотой на два меньших пифагоровых треугольника. Ни один из разбиваемых треугольников не образован примитивной тройкой[26].
- Множество всех примитивных пифагоровых треугольников образует корневое тернарное дерево[en] естественным способом, см. Дерево примитивных пифагоровых троек.
Неизвестно, существуют ли две различные пифагоровы тройки с одинаковым произведением входящих в них чисел[27].
Геометрия формулы Евклида[править | править код]

3, 4, 5 отображается в точку (4/5, 3/5) единичной окружности

Формулу Евклида для пифагоровой тройки
можно понять в терминах геометрии рациональных точек на единичной окружности [28]. Пусть имеется треугольник с катетами a и b и гипотенузой c, где a, b и c — положительные целые. По теореме Пифагора a2 + b2 = c2, а после деления обеих сторон на c2
Геометрически, точка на декартовой плоскости с координатами
лежит на единичной окружности x2 + y2 = 1.
В этом уравнении координаты x и y задаются рациональными числами. И обратно, любая точка на окружности с рациональными координатами x и y даёт примитивную пифагорову тройку. В самом деле, запишем x и y как несократимые дроби:
где наибольший общий делитель чисел a, b и c равен 1. Поскольку точка с координатами x и y лежит на единичной окружности, то
что и требовалось доказать.

Стереографическая проекция единичной окружности на ось
x. Если задана точка
P на единичной окружности, проведём прямую из точки
P в точку N = (0, 1) (северный полюс). Прямая пересекает ось
x в точке
P′, которая является стереографической проекцией точки
P. И наоборот, начав с точки
P′ на оси
x, проводим прямую, проходящую через
P′ и
N, и обратная стереографическая проекция — это точка
P, в которой прямая пересекает окружность
Таким образом, существует соответствие между точками с рациональными координатами на единичной окружности[en] и примитивными пифагоровыми треугольниками. Исходя из этого, формулы Евклида можно получить методами тригонометрии или с использованием стереографической проекции.
Для применения стереографического подхода предположим, что P′ является точкой на оси x с рациональными координатами
Тогда с помощью алгебраических вычислений можно показать, что точка P имеет координаты
Таким образом, получаем, что любая рациональная точка[en] оси x соответствует рациональной точке единичной окружности. И обратно, пусть P(x, y) — точка единичной окружности с рациональными координатами x и y. Тогда стереографическая проекция P′ на ось x имеет рациональные координаты
В терминах алгебраической геометрии алгебраическое многообразие рациональных точек единичной окружности является бирациональным к аффинной прямой над рациональными числами. Единичная окружность тогда называется рациональной кривой. Соответствие рациональных точек прямой и окружности даёт возможность дать явную параметризацию (рациональных) точек на окружности с помощью рациональных функций.
Группа пифагоровых троек[править | править код]
Любая рациональная точка на единичной окружности соответствует пифагоровой тройке (a, b, c), точнее — обобщённой пифагоровой тройке, так как a и b могут быть нулевыми и отрицательными.
Пусть даны два пифагоровых треугольников (a1, b1, c1) и (a2, b2, c2) с углами α и β.
Можно построить треугольники с углами α ± β, используя формулы сложения углов:
Эти прямоугольные треугольники тоже будут целочисленными, то есть пифагоровыми. Можно ввести операцию над тройками, используя вышеприведённые формулы. Эта операция будет коммутативной и ассоциативной, то есть обобщённые пифагоровы тройки образуют абелеву группу[29].
Пифагоровы тройки на двумерной решётке[править | править код]
Двумерная решётка — это набор изолированных точек, в котором, если выбрать одну точку в качестве начала координат (0, 0), все другие точки имеют координаты (x, y), где x и y пробегают все положительные и отрицательные целые числа. Любую пифагорову тройку (a, b, c) можно нарисовать на двумерной решётке как точки с координатами (a, 0) и (0, b). По теореме Пика число точек решётки, лежащих строго внутри треугольника, задаётся формулой ![{displaystyle [(a-1)(b-1)-gcd(a,b)+1]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf82ec50d495b3453d2df1b107e026a5f88670e)


Интересно, что первый случай совпадения площадей примитивных пифагоровых троек появляется на тройках (20, 21, 29), (12, 35, 37) с площадью 210[31]. Первое же появление примитивных пифагоровых троек с одинаковым числом точек решётки появляется лишь на (18 108, 252 685, 253 333), (28 077, 162 964, 165 365) с числом точек 2 287 674 594[32]. Найдены три примитивные пифагоровы тройки с одинаковыми площадями (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19 019, 19 069) и площадью 13 123 110. Тем не менее ни одной тройки примитивных пифагоровых троек с одинаковым числом точек решётки пока не найдено.
Спиноры и модулярная группа[править | править код]
Пифагоровы тройки можно представить в виде матриц вида
Матрица этого вида симметрична. Кроме того, её определитель
равен нулю в точности тогда, когда (a, b, c) является пифагоровой тройкой. Если X соответствует пифагоровой тройке, то она должна иметь ранг 1.
Поскольку X симметрична, из линейной алгебры известно, что существует вектор ξ = [m n]T, такой, что для внешнего произведения выполняется
(1)
где T означает транспонирование. Вектор ξ называется спинором (для группы Лоренца SO(1, 2). В абстрактных терминах формула Евклида означает, что каждая примитивная пифагорова тройка может быть записана как внешнее произведение на себя спинора с целыми элементами, как в формуле (1).
Модулярная группа Γ — это множество матриц 2 × 2 с целыми элементами
и определителем, равным единице: αδ − βγ = 1. Это множество образует группу, поскольку обратная к матрице из Γ является снова матрицей из Γ, как и произведение двух матриц из Γ. Модулярная группа действует на множество всех целых спиноров. Более того, группа транзитивна на множестве целых спиноров со взаимно простыми элементами. Если [m n]T содержит взаимно простые элементы, то
где u и v выбраны (с помощью алгоритма Евклида) так, что mu + nv = 1.
Действуя на спинор ξ в (1), действие в Γ переходит в действие над пифагоровыми тройками, позволяя при этом тройки с отрицательными значениями. Если A — матрица в Γ, то
(2)
даёт начало действиям на матрицу X в (1). Это не даёт хорошо определённое действие на примитивные тройки, поскольку оно может переводить примитивную тройку в непримитивную. В этом месте принято (следуя Траутману[28]) называть тройку (a, b, c) стандартной, если c > 0 и либо (a, b, c) взаимно просты, либо (a/2, b/2, c/2) взаимно просты и a/2 нечётно. Если спинор [m n]T имеет взаимно простые элементы, то связанная тройка (a, b, c), задаваемая формулой (1), является стандартной тройкой. Отсюда следует, что действие модулярной группы транзитивно на множестве стандартных троек.
Альтернативно, ограничимся теми значениями m и n, для которых m нечётно, а n чётно. Пусть подгруппа Γ(2) группы Γ — ядро гомоморфизма
где SL(2, Z2) — специальная линейная группа над конечным полем Z2 целых по модулю 2. Тогда Γ(2) является группой унимодулярных преобразований, которая сохраняет чётность каждого элемента. Таким образом, если элемент вектора ξ нечётный, а второй чётный, то то же самое верно для Aξ для всех A ∈ Γ(2). Фактически под действием (2) группа Γ(2) действует транзитивно на множество примитивных пифагоровых троек[33].
Группа Γ(2) является свободной группой, генераторами которой являются матрицы
Поэтому любая примитивная пифагорова тройка может быть получена единственным образом как произведение копий матриц U и L.
Отношения «родитель — потомок»[править | править код]
Как показал Берггрен[34], все примитивные пифагоровы тройки могут быть получены из треугольника (3, 4, 5) с использованием трёх линейных преобразований T1, T2, T3, где a, b, c являются сторонами тройки:
| новая сторона a | новая сторона b | новая сторона c | |
| T1: | a − 2b + 2c | 2a − b + 2c | 2a − 2b + 3c |
| T2: | a + 2b + 2c | 2a + b + 2c | 2a + 2b + 3c |
| T3: | −a + 2b + 2c | −2a + b + 2c | −2a + 2b + 3c |
Если начать с 3, 4, 5, то все другие примитивные тройки, в конечном счёте, будут получены. Другими словами, любая примитивная тройка будет «родителем» 3 дополнительным примитивным тройкам.
Если начать с a = 3, b = 4 и c = 5, то следующим поколением троек будет
| новая сторона a | новая сторона b | новая сторона c |
| 3 − (2×4) + (2×5) = 5 | (2×3) − 4 + (2×5) = 12 | (2×3) − (2×4) + (3×5) = 13 |
| 3 + (2×4) + (2×5) = 21 | (2×3) + 4 + (2×5) = 20 | (2×3) + (2×4) + (3×5) = 29 |
| −3 + (2×4) + (2×5) = 15 | −(2×3) + 4 + (2×5) = 8 | −(2×3) + (2×4) + (3×5) = 17 |
Линейные преобразования T1, T2 и T3 имеют геометрическую интерпретацию на языке квадратичных форм. Они тесно связаны (но не эквивалентны) с отражениями, генерируемыми ортогональной группой x2 + y2 − z2 над целыми числами. Другое множество трёх линейных преобразований обсуждается в статье Генерация пифагоровых троек с помощью матриц и линейных преобразований[en][35].
Связь с гауссовыми целыми числами[править | править код]
Формулы Евклида могут быть проанализированы и доказаны с помощью гауссовых целых чисел[36]. Гауссовы целые — это комплексные числа вида α = u + vi, где u и v обычные целые числа, а i — корень из минус единицы. Единицы гауссовых целых — это ±1 и ±i. Обычные целые называются целыми и обозначаются Z. Гауссовы целые обозначаются Z[i]. Правая часть теоремы Пифагора можно разложить на гауссовы целые:
Примитивная пифагорова тройка — это тройка, в которой a и b взаимно просты, то есть не имеют общих простых делителей. Для таких троек либо a, либо b чётно, а второе нечётно. Отсюда следует, что c также нечётно.
Каждое из двух множителей z = a + bi и z* = a — bi примитивной пифагоровой тройки равно квадрату гауссового целого. Это можно доказать с помощью свойства, что любое гауссово целое можно единственным образом разложить на гауссовы простые с точностью до единицы[37]. (Единственность разложения, грубо говоря, следует из того, что для них можно определить версию алгоритма Евклида) Доказательство имеет три шага. Сначала доказывается, что если a и b не имеют простых чисел в целых числах, то они не имеют простых общих множителей в гауссовых целых. Отсюда следует, что z и z* не имеют общих простых множителей в гауссовых целых. И наконец, поскольку c2 является квадратом, любое гауссово простое в разложении повторяется дважды. Поскольку z и z* не имеют общих простых множителей, это удвоение верно и для них. Следовательно, z и z* являются квадратами.
Таким образом, первый множитель можно записать в виде
Вещественные и мнимые части этого уравнения дают две формулы:
Для любой примитивной пифагоровой тройки должны существовать целые m и n, такие что эти два равенства выполняются. Отсюда, любая пифагорова тройка может быть получена путём выбора этих целых.
Как полный квадрат гауссовых целых[править | править код]
Если взять квадрат гауссового целого, мы получим следующую интерпретацию формул Евклида как представление полного квадрата гауссовых целых.
Если использовать факт, что гауссовы целые являются евклидовой областью и то, что для гауссовых целых p квадрат модуля 
Распределение троек[править | править код]
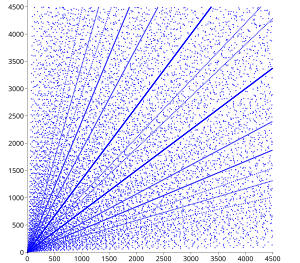
Имеется множество результатов относительно распределения пифагоровых троек. В диаграмме рассеяния проявляются некоторые очевидные закономерности. Если катеты (a, b) примитивной тройки появляются на диаграмме, то и все произведения на целое число этих катетов должны также быть на диаграмме, и это свойство объясняет появление на диаграмме радиальных прямых из начала координат.
На диаграмме наблюдаются множества парабол с высокой плотностью точек, имеющих фокусы в начале координат. Параболы отражаются от осей с углом 45 градусов, и в той же точке третья парабола подходит к оси перпендикулярно.
Эти узоры можно объяснить следующим образом. Если 




Угловые свойства, описанные выше следуют немедленно из функционального вида парабол. Параболы отражаются от оси a в точке a = 2n и производная b по a в этой точке равна −1. Таким образом, угол наклона равен 45°.
Поскольку кластеры, как и треугольники, повторяются при умножении на целую константу, значение 2n тоже принадлежит кластеру. Соответствующая парабола пересекает ось b под прямым углом в точке b = 2n, а потому является симметричным отражением параболы, которая получается обменом переменных a и b и которая пересекает ось a под прямым углом в точке a = 2n.
Альберт Фесслер (Albert Fässler) и др. показали значимость этих парабол в контексте конформных отображений[38][39].
Специальные случаи[править | править код]
Последовательность Платона[править | править код]
Случай n = 1 общей конструкции пифагоровых троек известен давно. Прокл, в своём комментарии к 47-му утверждению в первой книге Начал Евклида, описывает это следующим образом:
Некоторые методы получения таких треугольников этого вида легко получить, один из них принадлежит Платону, другой — Пифагору. (Последний) начал с нечётных чисел. Для этого он выбрал нечётное число в качестве меньшего из катетов. Затем он возвёл его в квадрат, вычел единицу и половину этой разницы использовал как второй катет. Наконец, он добавил единицу к этому катету и получил гипотенузу.
…Метод Платона работает с чётными числами. Он использует заданное чётное число в качестве одного из катетов. Половина этого числа возводится в квадрат и добавляется единица, что даёт гипотенузу, а вычитание единицы даёт второй катет. … И это даёт тот же треугольник, что и другой метод.
В виде уравнений:
Можно показать, что все пифагоровы тройки получаются из последовательности Платона (x, y, z) = p, (p2 − 1)/2 и (p2 + 1)/2, если позволить p принимать нецелые (рациональные) значения. Если в этой последовательности p заменить рациональной дробью m/n, получим ‘стандартный’ генератор троек 2mn, m2 − n2 и m2 + n2. Отсюда следует, что любой тройке соответствует рациональное значение p, которое можно использовать для получения подобного треугольника с рациональными сторонами, пропорциональными сторонам исходного треугольника. Например, платоновым эквивалентом тройке (6, 8, 10) будет (3/2; 2, 5/2).
Уравнение Якоби — Маддена[править | править код]
Уравнение
эквивалентно специальной диофантовой тройке
Существует бесконечное число решений этого уравнения, которые можно получить используя эллиптическую кривую. Два из этих решений:
Равные суммы двух квадратов[править | править код]
Один из способов генерации решений для 
Равные суммы двух четвёртых степеней[править | править код]
Если даны два набора пифагоровых троек:
то задача поиска равных произведений катета и гипотенузы
как легко видеть, эквивалентна уравнению
то есть
для которого Эйлер получил решение 
Теорема Декарта об окружностях[править | править код]
В случае теоремы Декарта[en], когда все переменные являются квадратами,
Эйлер показал, что это эквивалентно трём пифагоровым тройкам:
Здесь тоже существует бесконечное число решений, а для специального случая 
которое имеет решение с небольшими числами 
Почти равнобедренные пифагоровы тройки[править | править код]
Имеются прямоугольные треугольники[en] с целыми сторонами, у которых длины катетов отличаются на единицу, например:
и бесконечное число других. Для них можно вывести общую формулу
где (x, y) являются решениями уравнения Пелля 
В случае, когда катет и гипотенуза отличаются на единицу, как в случаях
общим решением будет
откуда видно, что все нечётные числа (большие 1) появляются в примитивных пифагоровых тройках.
Обобщения[править | править код]
Имеется несколько вариантов обобщения концепции пифагоровых троек.
Пифагоровы четвёрки[править | править код]
Множество из четырёх натуральных чисел a, b, c и d, таких, что a2 + b2+ c2 = d2 называется пифагоровой четвёркой. Простейший пример — (1, 2, 2, 3), поскольку 12 + 22 + 22 = 32.
Следующий (примитивный) простейший пример — (2, 3, 6, 7), поскольку 22 + 32 + 62 = 72.
Все четвёрки задаются формулой
Пифагоровы n-наборы[править | править код]
Используя простое алгебраическое тождество
для произвольных x0, x1, просто доказать, что квадрат суммы n квадратов сам является суммой n квадратов, для чего положим x0 = x22 + x32 + … + xn2 и раскроем скобки[41]. Можно легко видеть, что пифагоровы тройки и четвёрки являются просто частными случаями x0 = x22 и x0 = x22 + x32 соответственно, что можно продолжать для других n, используя формулу для пятёрки квадратов
Поскольку сумма F(k,m) k последовательных квадратов, начиная с m2, задаётся формулой[42]
можно найти значения (k, m) такие, что F(k,m) является квадратом. Так, Хиршхорн нашёл формулу для последовательностей, в которых число членов само является квадратом[43],
и v ⩾ 5 есть любое натуральное число, не делящееся на 2 или 3. Наименьшее значение v = 5, откуда k = 25, что даёт хорошо известное значение из задачи Люка складирования пушечных ядер:
факт, который связан с решёткой Лича.
Кроме того, если в пифагоровом n-наборе (n ⩾ 4) все слагаемые являются последовательными натуральными числами, за исключением последнего, можно использовать равенство[44]
Поскольку вторая степень p сокращается, остаётся линейное уравнение, которое легко решается 
Таким образом, получаем метод генерации пифагоровых n-наборов путём подбора x[45]:
где q = n − 2 и
Великая теорема Ферма[править | править код]
Обобщением концепции пифагоровых троек служит поиск троек натуральных чисел a, b и c, таких, что an + bn = cn для некоторого n, большего 2. Пьер Ферма в 1637 году высказал утверждение, что таких троек не существует, и это утверждение стало известно как Великая теорема Ферма, поскольку её доказательство или опровержение отняло много больше времени, чем любая другая гипотеза Ферма. Первое доказательство было дано Уайлсом в 1994 году.
n — 1 или n n-х степеней как n-я степень[править | править код]
Другим обобщением является поиск последовательностей из n + 1 натуральных чисел, для которых n-я степень последнего члена последовательности равна сумме n-х степеней предыдущих членов. Наименьшие последовательности для известных значений n:
- n = 3: {3, 4, 5; 6}.
- n = 4: {30, 120, 272, 315; 353}
- n = 5: {19, 43, 46, 47, 67; 72}
- n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
- n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}
В слегка отличном обобщении сумма (k + 1) n-х степеней приравнивается сумме (n − k) n-х степеней. Например:
- (n = 3): 13 + 123 = 93 + 103. Пример стал известным после воспоминаний Харди о разговоре с Рамануджаном о числе 1729, которое является наименьшим числом, которое можно представить в виде суммы двух кубов двумя различными способами.
Может существовать также n − 1 n-х степеней натуральных чисел, дающих в сумме n-ю степень натурального числа (хотя, согласно великой теореме Ферма, не для n = 3). Эти последовательности являются контрпримерами гипотезе Эйлера. Наименьшие известные контрпримеры[46][47]
- n = 4: (95800, 217519, 414560; 422481)
- n = 5: (27, 84, 110, 133; 144)
Тройки треугольника Герона[править | править код]
Треугольник Герона обычно определяется как треугольник с целыми сторонами, площадь которого тоже целое число, и мы будем полагать, что стороны треугольника различны. Длины сторон такого треугольника образуют тройку Герона (a, b, c), где a < b < c.
Ясно, что пифагоровы тройки являются тройками Герона, поскольку в пифагоровой тройке по меньшей мере один из катетов a и b является чётным числом, так что площадь треугольника ab/2 будет целым числом. Не всякая тройка Герона является пифагоровой, поскольку, например, тройка (4, 13, 15) с площадью 24 не пифагорова.
Если (a, b, c) является тройкой Герона, то таковой будет и (ma, mb, mc) при любом натуральном m, большим единицы.
Тройка Герона (a, b, c) примитивна, если a, b и c попарно взаимно просты (как и в случае пифагоровых троек). Ниже приведено несколько троек Герона, не являющихся пифагоровыми:
- (4, 13, 15) с площадью 24,
- (3, 25, 26) с площадью 36,
- (7, 15, 20) с площадью 42,
- (6, 25, 29) с площадью 60,
- (11, 13, 20) с площадью 66,
- (13, 14, 15) с площадью 84,
- (13, 20, 21) с площадью 126.
По формуле Герона, чтобы тройка натуральных чисел (a, b, c) с a < b < c была тройкой Герона, необходимо, чтобы
- (a2 + b2 + c2)2 − 2 (a4 + b4 + c4)
или, что то же самое,
- 2 (a2b2 + a2c2 + b2c2) − (a4 + b4 + c4)
было ненулевым полным квадратом, делящимся на 16.
Использование[править | править код]
Примитивные пифагоровы тройки используются в криптографии в качестве случайных последовательностей и для генерации ключей[48].
См. также[править | править код]
- Геронов треугольник
- Диофант II.VIII[en]
- Египетский треугольник
- Негипотенузное число
- Пифагорова четвёрка
- Простое число Пифагора
- Прямоугольный треугольник
- Сравнение по модулю
- Совершенный кубоид
- Теорема Пифагора
- Теорема Гильберта 90
- Теорема Ферма о прямоугольном треугольнике
- Тригонометрические тождества
- Тройка Эйзенштейна
- Формула тангенса половинного угла
- Целочисленный треугольник
Примечания[править | править код]
- ↑ В. Серпинский. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
- ↑ Robson, Eleanor (February 2002), Words and pictures: new light on Plimpton 322, American Mathematical Monthly (Mathematical Association of America) . — Т. 109 (2): 105–120, doi:10.2307/2695324, <http://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Robson105-120.pdf> Архивная копия от 10 августа 2017 на Wayback Machine
- ↑ D. E. Joyce. Euclid’s Elements. — Clark University, June 1997. — С. Book X, Proposition XXIX.
- ↑ Douglas W. Mitchell. An Alternative Characterisation of All Primitive Pythagorean Triples // The Mathematical Gazette. — July 2001. — Т. 85, вып. 503. — С. 273–5. — JSTOR 3622017.
- ↑ Raymond A. Beauregard, E. R. Suryanarayan. Proofs Without Words: More Exercises in Visual Thinking / Roger B. Nelsen. — Mathematical Association of America, 2000. — Т. II. — С. 120. — ISBN 978-0-88385-721-2.
- ↑ Eli Maor. The Pythagorean Theorem. — Princeton University Press, 2007. — С. Appendix B.
- ↑ 1 2 3 Sierpinski, 2003.
- ↑ Houston, 1993, с. 141.
- ↑ Posamentier, 2010, с. 156.
- ↑ Несуществование решения, в котором и a, и b являются квадратами, первоначально доказано Пьером Ферма. Для других случаев, в которых c является одним из квадратов, см. в книге Стиллвела.
- ↑ Carmichael, 1959, с. 17.
- ↑ Carmichael, 1959, с. 21.
- ↑ Sierpinski, 2003, с. 4—6.
- ↑ Sierpinski, 2003, с. 23—25.
- ↑ MacHale, Bosch, 2012, с. 91—96.
- ↑ Sally, 2007, с. 74—75.
- ↑ Это следует из факта, что одно из чисел a или b делится на четыре, и из определения конгруэнтных чисел как площадей прямоугольных треугольников с рациональными сторонами
- ↑ Baragar, 2001, с. 301, упражнение 15.3.
- ↑ Bernhart, Price, 2005.
- ↑ Bernhart, Price, 2005, с. 6.
- ↑ Carmichael, 1959, с. 14.
- ↑ Rosenberg, Spillane, Wulf, May 2008, с. 656—663.
- ↑ Paul Yiu, 2008.
- ↑ Sierpinski, 2003, с. 31.
- ↑ Pickover, 2009, с. 40.
- ↑ Paul Yiu, 2008, с. 17.
- ↑ Weisstein, Eric W. Пифагорова тройка (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Trautman, 1998.
- ↑ Eckert, 1984.
- ↑ Paul Yiu, 2003.
- ↑ Последовательность A093536 в OEIS.
- ↑ Последовательность A225760 в OEIS.
- ↑ Alperin, 2005.
- ↑ Berggren, 1934.
- ↑ Дальнейшее обсуждение отношения «родитель — потомок» — Pythagorean triple (Wolfram) Архивная копия от 17 марта 2015 на Wayback Machine, Alperin, 2005.
- ↑ Stillwell, 2002, с. 110–2 Глава 6.6 Pythagorean Triples.
- ↑ Gauss, 1832 См. также Werke, 2:67-148.
- ↑ 1988 Preprint Архивная копия от 9 августа 2011 на Wayback Machine См. рисунок 2 на с. 3. Позднее это было напечатано в (Fässler 1991)
- ↑ Benito, Varona, 2002, с. 117–126.
- ↑ Nahin, Paul. An Imaginary Tale: The Story of
p. 25—26.
- ↑ A Collection of Algebraic Identities: Sums of n Squares. Дата обращения: 15 марта 2015. Архивировано 6 марта 2012 года.
- ↑ Sum of consecutive cubes equal a cube. Архивировано из оригинала 15 мая 2008 года.
- ↑ Michael Hirschhorn. When is the sum of consecutive squares a square? // The Mathematical Gazette. — November 2011. — Т. 95. — С. 511–2. — ISSN 0025-5572.
- ↑ John F. Jr. Goehl. Reader reflections // Mathematics Teacher. — May 2005. — Т. 98, вып. 9. — С. 580.
- ↑ John F. Goehl, Jr. Triples, quartets, pentads // Mathematics Teacher. — May 2005. — Т. 98. — С. 580.
- ↑ Scott Kim. Bogglers // Discover. — May 2002. — С. 82.
Уравнениесложнее, лишь в 1988 году после 200 лет безуспешных попыток математиков доказать невозможность решить уравнение Ноам Элкис из Гарварда нашёл контрпример — 2.682.4404 + 15.365.6394 + 18.796.7604 = 20.615.6734:
- Noam Elkies. On A4 + B4 + C4 = D4 // Mathematics of Computation. — 1988. — Т. 51. — С. 825–835.
- ↑ MacHale, Bosch, 2012, с. 91-96.
- ↑ S. Kak, M. Prabhu. Cryptographic applications of primitive Pythagorean triples // Cryptologia. — 2014. — Т. 38, вып. 3. — С. 215-222.
Литература[править | править код]
- R. D. Carmichael. The Theory of Numbers and Diophantine Analysis. — Dover Publ, 1959. — С. Diophantine analysis.
- Waclaw Sierpinski. Pythagorean Triangles. — Dover, 2003. — ISBN 978-0-486-43278-6.
- John Stillwell. Numbers and Geometry. — Springer, 1998. — С. 133. — (Undergraduate Texts in Mathematics). — ISBN 9780387982892.
- Thomas Koshy. Elementary Number Theory with Applications. — Academic Press, 2002. — С. 545. — ISBN 9780124211711.
- David Houston. Proofs Without Words: Exercises in Visual Thinking / Roger B. Nelsen. — Mathematical Association of America, 1993. — С. 141. — ISBN 978-0-88385-700-7.
- Alfred S. Posamentier. The Pythagorean Theorem: The Story of Its Power and Beauty. — Prometheus Books, 2010. — ISBN 9781616141813.
- Des MacHale, Christian van den Bosch. Generalising a result about Pythagorean triples // Mathematical Gazette. — 2012. — Т. 96.
- Judith D. Sally. Roots to Research: A Vertical Development of Mathematical Problems. — American Mathematical Society, 2007. — ISBN 9780821872673..
- Neal Koblitz. Introduction to Elliptic Curves and Modular Forms. — Springer, 1993. — Т. 97. — (Graduate Texts in Mathematics). — ISBN 9780387979663.
- Arthur Baragar. A Survey of Classical and Modern Geometries: With Computer Activities. — Prentice Hall, 2001. — ISBN 9780130143181.
- Paul Yiu. Heron triangles which cannot be decomposed into two integer right triangles. — 41st Meeting of Florida Section of Mathematical Association of America, 2008.
- Clifford A. Pickover. The Math Book. — Sterling, 2009. — С. Глава «Pythagorean Theorem and Triangles». — ISBN 1402757964.
- John Stillwell. Elements of Number Theory. — Springer, 2002. — ISBN 978-0-387-95587-2.
- Pythagorean Triples and the Unit Circle Архивная копия от 15 декабря 2011 на Wayback Machine, chap. 2-3, in «A Friendly Introduction to Number Theory Архивная копия от 6 марта 2015 на Wayback Machine» by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
- Дмитрий Викторович Аносов. Взгляд на математику и нечто из неё. — 2-е изд. — М.: МЦНМО, 2003. — Т. 3. — 32 с. — (Библиотека «Математическое просвещение»). — 3000+1500 экз. — ISBN 5-94057-111-5. Архивная копия от 12 января 2014 на Wayback Machine
Ссылки[править | править код]
- Paul Yiu. Recreational Mathematics // Course Notes, Dept. of Mathematical Sciences, Florida Atlantic University. — 2003.
- Frank R. Bernhart, H. Lee Price. Heron’s formula, Descartes circles, and Pythagorean triangles. — 2005. arXiv
- Steven Rosenberg, Michael Spillane, Daniel B. Wulf. Heron triangles and moduli spaces // Mathematics Teacher. — May 2008. — Т. 101.
- Gauss C. F. Theoria residuorum biquadraticorum // Comm. Soc. Reg. Sci. Gött. Rec.. — 1832. — Т. 4.
- Albert Fässler. Multiple Pythagorean number triples // American Mathematical Monthly. — 1991. — Т. 98, вып. 6. — JSTOR 2324870.
- Manuel Benito, Juan L. Varona. Pythagorean triangles with legs less than n. — 2002. — Т. 143. — doi:10.1016/S0377-0427(01)00496-4.
- Roger C. Alperin. The modular tree of Pythagoras // American Mathematical Monthly. — Mathematical Association of America, 2005. — Т. 112, вып. 9. — С. 807–816. — JSTOR 30037602.
- B. Berggren. Pytagoreiska trianglar (швед.) // Tidskrift för elementär matematik, fysik och kemi. — 1934. — Т. 17. — С. 129–139.
- Ernest Eckert. Primitive Pythagorean triples // The College Mathematics Journal. — Mathematical Association of America, 1992. — Т. 23, вып. 5. — С. 413–417. — JSTOR 2686417.
- Ernest J. Eckert, Preben Dahl Vesrergaard. Groups of integral triangles // The Fibonacci Quarterly. — 1989. — Т. 27, вып. 5. — С. 458—464.
- Ernest J. Eckert. The Group of Primitive Pythagorean Triangles // Mathematics Magazine. — 1984. — Т. 57.
- Noam Elkies. Pythagorean triples and Hilbert’s theorem 90.
- Artemas Martin. Rational right angled triangles nearly isosceles // The Analyst. — Annals of Mathematics, 1875. — Т. 3, вып. 2. — С. 47–50. — doi:10.2307/2635906. — JSTOR 2635906.
- Andrzej Trautman. Geometric universe / S. A. Hugget, L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse. — 1998.
- Weisstein, Eric W. Pythagorean Triple (англ.) на сайте Wolfram MathWorld.
Pythagorean triples concept was used since ancient times by many greeks, Chinese and Indian philosophers. It is used to explain the relationship between the three sides (i.e., a, b, and c) of the right triangle. It states that in any right triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides of the triangle. In this article, we will learn about the Pythagorean triples formula in detail, along with examples.
What are Pythagorean Triples?
Pythagorean triples are used to find the three positive integers or terms that satisfy the Pythagorean theorem. Generally, these three terms can be written in the form (a, b, c), and the triangle formed by these terms is known as the Pythagorean triangle. Let us consider a right-angled triangle in which b is the base, a is the perpendicular, and c is the hypotenuse. So, according to the Pythagorean triples theorem: the sum of squares of any two sides is equal to the square of the third side.
a2 + b2 = c2
Here, a, b, and c are base, perpendicular, and hypotenuse.
Examples of Pythagorean Triples
There is n number of Pythagorean triples. Take any Pythagoras triangle as an example. Let’s say the perpendicular of the triangle is 4 units, and the base is 3 units, then the hypotenuse will be:
a2 + b2 = c2
32 + 42 = c2
c2 = 9 + 16
c = √25 = 5 units.

So, the Pythagorean triples are (3, 4, and 5). Many other Pythagorean triples can be generated with the help of these basic Pythagorean triples. The best way to obtain more triples is to scale them up, that is (3n, 4n, and 5n). Here, n is the positive integer value.
| n | (3n, 4n, 5n) |
| 2 | (6, 8, 10) |
| 3 | (9, 12, 15) |
| 4 | (12, 16, 20) |
| 5 | (15, 20, 25) |
Pythagorean Triples Formula
If the triangle given is a right-angled triangle, then the set of the sides of the triangle gives Pythagorean triples. Pythagorean triples are obtained from the Pythagoras theorem. The pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of base and perpendicular. Let’s say the perpendicular is denoted by ‘a’, the base is denoted by ‘b’, and the hypotenuse is denoted by ‘c’, then the Pythagorean triples formula will be:
c2 = a2 + b2
Pythagorean Triples Proof
We can prove the Pythagorean triples Formula in many ways, but here we use the algebraic method. In this method, we use the terms shown in the below figure.

Step 1: We have four right-angled triangles with base m, perpendicular n, and hypotenuse p. Now arrange these triangles so that they make two squares one is outer square ABCD, whose side is m+n, and another one is inner square WZXY, whose side is c.
Step 2: Now we find the area of the inner, outer square, and triangles:
Area of outer square ABCD = (m + n)2
Area of inner square WXYZ = (p)2
Area of one triangle = 1/2(m × n)2
Area of four triangles = 4 × 1/2(m × n)2 = 2(m × n)2
Step 3: As we know that the area of square ABCD = Area of square WXYZ + Area of four triangles
So (m + n)2 = 2(m × n)2 + p2
m2 + 2 × m × n + n2 = 2 × m × n + p2
m2 + n2 = p2
Hence Pythagorean triples Formula is proved.
How to Form Pythagorean Triples?
Pythagorean triples can be positive integers. We can say there are two cases that can be generated. The numbers can either be odd or even. Below are the cases explained in detail:
If the Number is Odd
The below formula can be used to find the triples. If we have an odd number (1, 3, 5, 7, 9, etc.) that can be taken as m, then the two numbers can be found by putting m in the formula.
(m, (m2 – 1)/2 , (m2 + 1)/2)
Here m should be greater than 1.
Example: If m = 3, find the rest of the Pythagorean triples.
Solution:
(m2 -1)/2 = (32 – 1)/2 = 8/2 = 4.
(m2 + 1)/2 = (32 + 1)/2 = 10/2 = 5
Therefore, the Pythagorean triples are (2, 4, 5).
If the Number is Even
The below formula can be used to find the triples. If we have an even number (2, 4, 6, 8,10, etc.) that can be taken as m, then the other two numbers can be found by putting m in the formula.
(m, (m2 – 4)/4, (m2 + 4)/4)
Here m should be greater than 2.
Example: Find the rest of the Pythagorean triples if m = 4.
Solution:
(m2 – 4)/4 = (44 – 4)/4 = 252/4 = 63.
(m2 + 4)/4 = (44 + 4)/4 = 260/4 = 230/2 = 115.
Therefore, the Pythagorean triples are (4, 63, 115).
Note: Even if the method helps solve and find infinitely many Pythagorean triples, it still cannot find them all. Fir instance, the Pythagorean triples (20, 21, 29) cannot be formed using this technique.
How to Generate Pythagorean Triples?
In order to generate Pythagorean triples, the Pythagorean triplet checker is used. Pythagorean triplet checker is the formula that is defined specifically to find out the values of Pythagorean triples. Assume the sides of the right-angled triangle are a, b and c. Now, m and n are the two integers that will be used in order to find the values of a, b, and c.
- a, b, and c are the sides of the right-angled triangle.
- m and n are the co-prime numbers that are positive numbers. Here, m>n.

In the above figure, it can be easily seen that the values of a, b and c are dependent upon m and n. The sides in terms of m and n are defined as:
- a is the perpendicular of the triangle here, and a = 2mn.
- b is the base of the triangle, and b = m2 – n2.
- c is the hypotenuse of the triangle, and c = m2 + n2.
Now simply assume co-prime natural numbers in order to find the values of Pythagorean triples. It is important to note that m must be greater than n.
Example: Find the Pythagorean triples when the values of m and n are 3 and 2, respectively.
Solution:
Pythagorean triples checker is,
- a = 2mn
- b = m2 – n2
- c = m2 + n2
Therefore, putting m = 3 and n = 2.
a = 2 × 3 × 2 = 12 units.
b = 32 – 22 = 9 – 4 = 5 units
c = 33 + 22 = 9 + 4 = 13 units.
Therefore, the Pythagorean triples are (12, 5, 13).
List of Pythagorean Triples
Below is the Pythagorean triples list where the value of c is greater than 100:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
These values verify the formula a2 + b2 = c2.
Types of Pythagorean Triples
Primitive Pythagorean Triples
Primitive Pythagoras triples are also known as Reduced triples. The greatest common factor of these triples are 1. Or we can say that primitive Pythagorean triples are those triples in which the three numbers do not have any common divisor other than one. Such type of triples only contains one even positive number among the three given three numbers.
Example: 3, 4, 5
3, 4, 5 are Pythagorean triples as they satisfy the Pythagorean triples formula also the greatest common factor of 3, 4, 5 is 1.
Non-Primitive Pythagorean Triples
Non-primitive Pythagoras triples are also known as imprimitive Pythagorean triples. Non-primitive Pythagorean triples are those triples in which the three numbers have a common divisor. Such types of triples can contain more than one even positive number among the three given three numbers.
Example: 6, 8, 10
6, 8, 10 are Pythagorean triples as they satisfy the Pythagorean triples formula but the greatest common factor of 6, 8, 10 is not equal to 1 so these are non – primitive Pythagorean triples.
Properties of Pythagorean Triples
- Pythagorean triples are the sides of a right-angled triangle, represented as m, n, p.
- These numbers satisfy the Pythagorean triples formula m2 + n2 = p2.
- The sides m and n are the sides of a right triangle, which represent perpendicular and base, while p is the hypotenuse.
- Pythagorean Triplet consists of all even numbers, or two odd numbers and one even number.
- All three numbers of a Pythagorean Triplet can never be odd.
Solved Examples on Pythagoras Triples
Example 1: Find Pythagorean triples if m = 8.
Solution:
This is the case when the number is even:
Given m = 8,
So, (m2 – 4)/4 = (64 – 4)/4 = 15
(m2 + 4)/4 = (64 + 4)/4 = 17
Hence Pythagorean triples are 8, 15, 17.
Example 2: Find Pythagorean triples if m = 9.
Solution:
This is the case when the number is odd:
Given m = 9,
So, (m2 – 1)/2 = (81 – 1)/2 = 40
(m2 + 1)/2 = (81 + 1)/2 = 41
Hence Pythagorean triples are 9, 40, 41.
Example 3: Find Pythagorean triples, one of whose members is 13.
Solution:
Take m = 13,
So, (m2 – 1)/2 = (169 – 1)/2 = 84
(m2 + 1)/2 =(169 + 1)/2 = 85
Hence Pythagorean triples are 13, 84, 85.
Example 4: Checking if (6, 8, 10) is a Pythagorean triplet or not.
Solution:
Let us take m = 6, n = 8, and p = 10
According to the formula
m2 + n2 = p2
We get
(6)2 + (8)2 = (10)2
36 + 64 = 100
100 = 100
Here L.H.S = R.H.S
Hence proved that (6, 8, 10) is a Pythagorean triplet.
Example 5: If (y, 84, 85) is a Pythagorean triplet, then find the value of y.
Solution:
Let us take m = y, n = 84, and p = 85
According to the formula
m2 + n2 = p2
We get
(y)2 + (84)2 = (85)2
y2 + 7056 = 7225
y2 = 169
y = 13
FAQs on Pythagorean Triples
Question 1: What are Pythagorean triples?
Answer:
Pythagorean triples are the natural numbers that satisfy the pythagoras theorem. Therefore, the Pythagorean triples satisfy the formula c2 = a2 + b2, here, c is the hypotenuse of the right-angled triangle, a and b are the legs of the triangle.
Question 2: What are the five most common Pythagorean triples?
Answer:
The five most common Pythagorean triples are: (3, 4, 5), (5, 12, 13), (6, 8, 10), (9, 12, 15), (15, 20, 25).
Question 3: How to find Pythagorean triples?
Answer:
The Pythagorean triples can be easily obtained by the help of pythagoras theorem, if two triples are already given, the third triplet can be found:
a2 + b2 = c2
Where, a and b are the legs of the triangle and c is the hypotenuse of the triangle.
There are times when only one Pythagorean triplet is given, two cases arise in this situation, if the value of m given is odd, the formula used for the Pythagorean triples are (m, (m2 – 1)/2, (m2 + 1)/2). If the value of m given is even, the formula becomes (m, (m2 – 4)/4, (m2 + 4)/4).
Question 4: Can Pythagorean triples be decimals?
Answer:
Pythagorean triples are the positive integers, that is, natural numbers that satisfy the pythagoras theorem, Therefore, they can not be in decimal form.
Question 5: What is the scaling of triples?
Answer:
The scaling of the pythagoras triples is multiplying the given triples with some natural numbers and observing that the new set generated satisfies the Pythagorean triples condition too. For example, a Pythagorean triplet (3, 4, 5) is given to us, if we multiply the triples with 3, it will give (9, 12, 15).
Пифагорово число (пифагорова тройка) — комбинация из трёх целых чисел 

Свойства
Поскольку уравнение 




Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, т. е. таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 (
Пифагорова тройка 


Любая примитивная пифагорова тройка однозначно представляется в виде 


Примеры
Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):
(3, 4, 5),
(6, 8, 10),
(5, 12, 13),
(9, 12, 15),
(8, 15, 17),
(12, 16, 20),
(15, 20, 25),
(7, 24, 25),
(10, 24, 26),
(20, 21, 29),
(18, 24, 30),
(16, 30, 34),
(21, 28, 35),
(12, 35, 37),
(15, 36, 39),
(24, 32, 40),
(9, 40, 41),
(14, 48, 50),
(30, 40, 50)…
См. также
- Великая теорема Ферма
- Теорема Пифагора
be-x-old:Піфагорава тройка
bg:Питагоров триъгълник
da:Pythagoræiske tal
eo:Pitagora triopo
he:שלשה פיתגורית
hu:Pitagoraszi számhármasok
is:Pýþagórískur þríhyrningur
nl:Pythagorese drietallen
pl:Trójki pitagorejskie
scn:Terna pitagòrica
sl:Pitagorejska trojica
sv:Pythagoreisk trippel
Ещё примеры пифагоровых троек (где катеты меньше 1000, их 179):
3 4 5 9+16=25 5 12 13 25+144=169 7 24 25 49+576=625 8 15 17 64+225=289 9 40 41 81+1600=1681 11 60 61 121+3600=3721 12 35 37 144+1225=1369 13 84 85 169+7056=7225 15 112 113 225+12544=12769 16 63 65 256+3969=4225 17 144 145 289+20736=21025 19 180 181 361+32400=32761 20 21 29 400+441=841 20 99 101 400+9801=10201 21 220 221 441+48400=48841 23 264 265 529+69696=70225 24 143 145 576+20449=21025 25 312 313 625+97344=97969 27 364 365 729+132496=133225 28 45 53 784+2025=2809 28 195 197 784+38025=38809 29 420 421 841+176400=177241 31 480 481 961+230400=231361 32 255 257 1024+65025=66049 33 56 65 1089+3136=4225 33 544 545 1089+295936=297025 35 612 613 1225+374544=375769 36 77 85 1296+5929=7225 36 323 325 1296+104329=105625 37 684 685 1369+467856=469225 39 80 89 1521+6400=7921 39 760 761 1521+577600=579121 40 399 401 1600+159201=160801 41 840 841 1681+705600=707281 43 924 925 1849+853776=855625 44 117 125 1936+13689=15625 44 483 485 1936+233289=235225 48 55 73 2304+3025=5329 48 575 577 2304+330625=332929 51 140 149 2601+19600=22201 52 165 173 2704+27225=29929 52 675 677 2704+455625=458329 56 783 785 3136+613089=616225 57 176 185 3249+30976=34225 60 91 109 3600+8281=11881 60 221 229 3600+48841=52441 60 899 901 3600+808201=811801 65 72 97 4225+5184=9409 68 285 293 4624+81225=85849 69 260 269 4761+67600=72361 75 308 317 5625+94864=100489 76 357 365 5776+127449=133225 84 187 205 7056+34969=42025 84 437 445 7056+190969=198025 85 132 157 7225+17424=24649 87 416 425 7569+173056=180625 88 105 137 7744+11025=18769 92 525 533 8464+275625=284089 93 476 485 8649+226576=235225 95 168 193 9025+28224=37249 96 247 265 9216+61009=70225 100 621 629 10000+385641=395641 104 153 185 10816+23409=34225 105 208 233 11025+43264=54289 105 608 617 11025+369664=380689 108 725 733 11664+525625=537289 111 680 689 12321+462400=474721 115 252 277 13225+63504=76729 116 837 845 13456+700569=714025 119 120 169 14161+14400=28561 120 209 241 14400+43681=58081 120 391 409 14400+152881=167281 123 836 845 15129+698896=714025 124 957 965 15376+915849=931225 129 920 929 16641+846400=863041 132 475 493 17424+225625=243049 133 156 205 17689+24336=42025 135 352 377 18225+123904=142129 136 273 305 18496+74529=93025 140 171 221 19600+29241=48841 145 408 433 21025+166464=187489 152 345 377 23104+119025=142129 155 468 493 24025+219024=243049 156 667 685 24336+444889=469225 160 231 281 25600+53361=78961 161 240 289 25921+57600=83521 165 532 557 27225+283024=310249 168 425 457 28224+180625=208849 168 775 793 28224+600625=628849 175 288 337 30625+82944=113569 180 299 349 32400+89401=121801 184 513 545 33856+263169=297025 185 672 697 34225+451584=485809 189 340 389 35721+115600=151321 195 748 773 38025+559504=597529 200 609 641 40000+370881=410881 203 396 445 41209+156816=198025 204 253 325 41616+64009=105625 205 828 853 42025+685584=727609 207 224 305 42849+50176=93025 215 912 937 46225+831744=877969 216 713 745 46656+508369=555025 217 456 505 47089+207936=255025 220 459 509 48400+210681=259081 225 272 353 50625+73984=124609 228 325 397 51984+105625=157609 231 520 569 53361+270400=323761 232 825 857 53824+680625=734449 240 551 601 57600+303601=361201 248 945 977 61504+893025=954529 252 275 373 63504+75625=139129 259 660 709 67081+435600=502681 260 651 701 67600+423801=491401 261 380 461 68121+144400=212521 273 736 785 74529+541696=616225 276 493 565 76176+243049=319225 279 440 521 77841+193600=271441 280 351 449 78400+123201=201601 280 759 809 78400+576081=654481 287 816 865 82369+665856=748225 297 304 425 88209+92416=180625 300 589 661 90000+346921=436921 301 900 949 90601+810000=900601 308 435 533 94864+189225=284089 315 572 653 99225+327184=426409 315 988 1037 99225+976144=1075369 319 360 481 101761+129600=231361 320 999 1049 102400+998001=1100401 333 644 725 110889+414736=525625 336 377 505 112896+142129=255025 336 527 625 112896+277729=390625 341 420 541 116281+176400=292681 348 805 877 121104+648025=769129 364 627 725 132496+393129=525625 368 465 593 135424+216225=351649 369 800 881 136161+640000=776161 372 925 997 138384+855625=994009 385 552 673 148225+304704=452929 387 884 965 149769+781456=931225 396 403 565 156816+162409=319225 400 561 689 160000+314721=474721 407 624 745 165649+389376=555025 420 851 949 176400+724201=900601 429 460 629 184041+211600=395641 429 700 821 184041+490000=674041 432 665 793 186624+442225=628849 448 975 1073 200704+950625=1151329 451 780 901 203401+608400=811801 455 528 697 207025+278784=485809 464 777 905 215296+603729=819025 468 595 757 219024+354025=573049 473 864 985 223729+746496=970225 481 600 769 231361+360000=591361 495 952 1073 245025+906304=1151329 496 897 1025 246016+804609=1050625 504 703 865 254016+494209=748225 533 756 925 284089+571536=855625 540 629 829 291600+395641=687241 555 572 797 308025+327184=635209 559 840 1009 312481+705600=1018081 576 943 1105 331776+889249=1221025 580 741 941 336400+549081=885481 585 928 1097 342225+861184=1203409 615 728 953 378225+529984=908209 616 663 905 379456+439569=819025 620 861 1061 384400+741321=1125721 645 812 1037 416025+659344=1075369 660 779 1021 435600+606841=1042441 660 989 1189 435600+978121=1413721 696 697 985 484416+485809=970225 704 903 1145 495616+815409=1311025 705 992 1217 497025+984064=1481089 731 780 1069 534361+608400=1142761 744 817 1105 553536+667489=1221025 765 868 1157 585225+753424=1338649 799 960 1249 638401+921600=1560001 832 855 1193 692224+731025=1423249 884 987 1325 781456+974169=1755625 893 924 1285 797449+853776=1651225
Ссылки
Пифагоровы тройки чисел – Yaptro
Тема:
Пифагоровы тройки
Оглавление
Введение
Глава
1. История возникновения Пифагоровых троек
1.1. История открытия
Пифагоровых троек и их понятие
1.2. Способы получения
Пифагоровых троек
Глава
2. Применение Пифагоровых трок для решения геометрических задач
2.1. Анализ
геометрических задач в 8-9 классе
2.2. Эффективность
применения Пифагоровых троек при решении задач
Заключение
Список
литературы
Введение
Актуальность темы: можно быстро изучить теорему Пифагора с помощью Пифагоровых троек.
Она помогает при решении геометрических задач практического
применения в современной жизни.
Цель: заключается в изучении пифагоровых троек и их применения для
решения задач курса геометрии.
Из этого выведем задачи:
1. Проанализировать литературу по теме исследования;
2. Показать уникальные открытия Пифагора и дать определение
понятия пифагоровым тройкам;
3. Описать способы
формирования Пифагоровых трок;
4. Проанализировать
возможные применения пифагоровых троек для решения геометрических задач.
Проблема: Пифагоровы тройки
изучаются в контексте теоремы Пифагора и являются ее устно вычисленными
решениями, однако пифагоровы тройки нужно изучать как самостоятельную тему
математики, т.к. она помогает эффективнее решать геометрические задачи.
Предмет исследования: математика.
Объект исследования:
Пифагоровы тройки.
Метод исследования: теоретический.
Глава 1. История возникновения Пифагоровых троек
1.1. История открытия Пифагоровых троек и их понятие
Начнем с того, что же такое геометрия, ведь благодаря ей мы знакомимся с Пифагоровыми тройками.
• Геометрия - раздел математики, изучающий пространственные формы и отношения тел.
Геометрия была открыта древними египтянами, она возникла при измерении земельных участков и при астрономических наблюдениях. Долгое время она оставалась важнейшим средством познания Вселенной. Наибольший вклад в ее становление и развитие как науки внесли древнегреческие математики: Пифагор, Евклид, Архимед. На протяжении веков геометрия занимала видное место в начальном и университетском образовании, она входила в плоть и кровь образованных людей любых специальностей. Ее изучение требовало больших умственных усилий. [3.41]
Применение пифагоровых троек в решении задач позволяет экономить время, избегать вычислительных ошибок. Знание этих троек подталкивает к иному решению задачи. Проведенные исследования показывают эффективность применения пифагоровых троек при решении геометрических задач. В целях экономии времени и избежание вычислительных ошибок рекомендуем объяснять на уроках способы формирования пифагоровых троек и стремиться к их применению на практике. Они так же могут помочь на ОГЭ и ЕГЭ, поэтому нам стоит знать, как они применяются на практике.
А теперь и сама теорема. Пифагоровы тройки - упорядоченный набор из трёх натуральных чисел. Удовлетворяющих следующему однородному квадратному уравнению:. Теорема Пифагора – одна из главных и, можно даже сказать, самая главная теорема геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна ещё и тем, что сама по себе она вовсе не очевидна.
Например, свойства прямоугольного треугольника можно видеть непосредственно на чертеже.

Но сколько ни гляди на прямоугольный треугольник, никак не увидишь, что между его сторонами есть такое простое соотношение:.
Давайте рассмотрим пару теорий возникновения Пифагоровых троек. Прочитав литературу, мы узнаем о двух теориях возникновения.
Первая теория возникновения: Пифагоровы тройки представляют собой когорту из трех целых чисел, удовлетворяющих соотношению Пифагора.
Вообще, это частный случай Диофантовых уравнений, а именно, системы уравнений, в которых число неизвестных больше, чем число уравнений. Известны они давно, еще со времён Вавилона, то есть, задолго до Пифагора. А название они приобрели после того, как Пифагор на их основе доказал свою знаменитую теорему. Однако, как следует из анализа многочисленных источников, в которых вопрос о пифагоровых тройках, существующих классах этих троек и о возможных способах их формирования, до сих пор не раскрыт в полной мере.
Вторая теория возникновения: Все мы знаем, что Пифагоровы тройки открыл сам Пифагор, в честь его и назвали эти числа.
Пифагор Самосский - древнегреческий философ из города Регия, математик и мистик. В Кротоне основал религиозно-философскую школу пифагорейцев. Итак, Пифагоровы тройки известны очень давно. В архитектуре древне-месопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей (Локоть – это древнейшая мера длины, которой пользовались многие народы мира. Локоть составляет расстояние от конца вытянутого среднего пальца руки до локтевого сгиба. Обычно от 38 см. до 46 см.).
Пифагор и его ученики описали все тройки целых чисел, которые могут быть длинами сторон прямоугольного треугольника. На практике мы сможем понаблюдать за тем, как взаимообратные числа, и какое их множество. [1.186]
Пифагоровы числа обладают рядом свойств:
· Один из катетов должен быть кратным трём,
· Один из катетов должен быть кратным четырём,
· Одно из пифагоровых чисел должно быть кратным пяти.
Пифагоровы тройки могут быть:
· Примитивными (все три числа-взаимно простые),
· Не примитивными (если каждое число тройки умножить на одно и то же число, получится новая тройка, которая не является примитивной).
Итак, пифагоровы тройки - это тройки натуральных чисел (a, b, c) прямоугольного треугольника, для которых выполняется неравенство:

Это уравнение звучит так: сумма квадратов катетов, равна квадрату гипотенузы. Это и есть сама теорема Пифагора, которую изучают еще в 8 классе и применяют в различных видах задач и уравнений.
Но в простейшей пифагоровой тройке только одно число может быть чётным, а так же, в простейшей пифагоровой тройке числа а и b не могут быть одновременно нечётными.
1.2. Способы получения Пифагоровых троек
Итак, возникает вопрос: какие способы существуют для нахождения
пифагоровых троек, которые являются решением уравнения.
Способ 1. Проанализировав литературу и прочтя учебники 8-9 классов
можно сделать вывод в виде небольшой таблицы, где будет видно, что при сложении
двух квадратов чисел (первых двух в строке) мы получим квадрат третьего числа,
которое потом выносим из под корня. (третье число в строке).[3.42-52]
3, 4, 5
|
6, 8, 10
|
5, 12, 13
|
10, 24, 26
|
9, 12, 15
|
18, 24, 30
|
8, 15, 17
|
16, 30, 34
|
Давайте проверим эту таблицу на одном из примеров.
Итак, возьмем числа: 18, 24, 30.
1) По формуле Пифагора - сложим квадрат первых двух чисел:

2) Теперь сравним ответ первого действия и квадрат третьего числа:


3) Сделаем вывод, что эта таблица правильная и можно ей пользоваться.
Способ 2. Эти формулы были известны уже две с половиной тысячи лет назад.
Пусть (a, b, c,) – пифагорова тройка и a –нечетное число. Тогдаи
. По этому правилу можно получить уже известные нам тройки:
Если a = 3, то; b=4;
; c=5; получилась первая тройка (3, 4, 5).
Если a = 5, то; b=12;
; c=13; вторая тройка (5, 12, 13).
Если a = 7, то; b=24;
; c=25; третья тройка (7, 24, 25) и так далее.
Способ 3. Вам, так же, возможно, известны формулы для вычисления новых Пифагоровых троек.
, где
2)
3)
Сначала вычислим по формулам Пифагоровы тройки, а затем проверим, получилось ли найти эти тройки.
Для этого возьмем числа:.
1) Вычислим первую формулу тройки:


2) Вычислим вторую формулу тройки:


3) Вычислим третью формулу тройки:


4) Теперь можем проверить их по формуле Пифагора:


Из этого сделаем вывод: эти формулы можно использовать для нахождения трех чисел, которые подойдут к теореме Пифагора.
Так же в этих трех формулах может быть дополнительный множитель - k. Тогда из уравненияполучаем
[2.91-95]
Глава 2. Применение Пифагоровых трок для решения геометрических задач
2.1. Анализ геометрических задач в 8-9 классе
Давайте, начнем с советов. Что бы мы могли быстрее решать задачи по геометрии, есть некоторые советы, в решении задач с теоремой Пифагора.
· Гипотенуза всегда:
o лежит напротив прямого угла;
o является самой длинной стороной прямоугольного треугольника;
o обозначается как «с» в теореме Пифагора;
· Не забывайте проверять ответ. Если ответ кажется неправильным, проделайте вычисления снова.
· Еще один момент - самая длинная сторона лежит напротив наибольшего угла, а самая короткая сторона - напротив наименьшего угла.
· Выучите числа пифагоровой тройки, образующие стороны прямоугольного треугольника. Самая примитивная пифагорова тройка - это 3, 4, 5 (это так же Египетский треугольник). Так, зная длину двух сторон, третью искать не придется.
· Если дан обычный треугольник, а не прямоугольный, то требуется больше информации, чем просто длины двух сторон.
· Графики являются наглядным способом нанесения обозначений а, b и с.
· Если дана длина только одной стороны, то теорему Пифагора применять нельзя. Попробуйте использовать тригонометрию (sin, cos, tg).
· Если речь идет о задаче из некого сюжета, можно смело предположить, что деревья, столбы, стены и так далее образуют прямой угол с землей, если не указано иное.
· Когда число выносится из под корня, то сразу можно отбрасывать отрицательное число, т.к. сторона не может быть отрицательной.
Решим немного задач по геометрии с применением Пифагоровых троек.
Задача №1.
Дан прямоугольный треугольник ABC, C=90∘, AC=3, BC=4. Найдите длину AB.
Решение:
Согласно теореме Пифагора:






Ответ: АВ=5.
Задача №2.
Центр окружности, описанный около тр. АВС, лежит на стороне АВ. Радиус окружности равен 8,5. Найдите ВС, если АС равно 8?
Решение:

Если центр окружности лежит на стороне АВ, значит АВ - диаметр. Угол С=90, т. к. опирается на диаметр, т. е. треугольник АВС - прямоугольный.
1)
2) По теореме Пифагора




Ответ: ВС=15.
Задача №3.
В прямоугольном треугольнике АВС, катеты СА и СВ равны 9 и 12, соответственно. Найдите гипотенузу ВА,,
,
.
Дано: АВС-прямоугольный треугольник; СА=, ВС=12.
Найти: ВА=?,,
,
Решение:

По теореме Пифагора:
.



Ответ: АВ=15, sin A=, cos A=
,tg A=
.
Задача №4.
В прямоугольнике ABCD найдите ВС, если CD=1,5; AC=2,5.
Решение:

1) Т.к. это прямоугольник то, по его свойствам мы знаем, что его параллельные стороны равны, т.е. AB=CD и BC=AD.
2) Далее, рассмотрим треугольник ADC, угол D прямой, а значит, мы можем применить формулу Пифагора.
3)




BC=AD=2
Сейчас решим одно задание ОГЭ. Она так же может присутствовать и в жизни.
Задача №5.
Лестницу поставили к окну, расположенному на высоте 12м от земли. Нижний конец лестницы отстоит от стены на 5м. Какова длина лестницы?
Решение:

Можно решать сразу через т. Пифагора, т.к. дом и земля перпендикулярны друг другу, и поэтому они образуют прямой угол. Пусть 5м - «у», 12м - «z», а за «х» возьмем длину лестницы.
По т. Пифагора:




Ответ: Длина лестницы равна 13 метрам.
Такое применение Пифагоровых троек поможет нам в жизни.
Особенно, если у Вас есть дачи.
2.2.
Эффективность применения Пифагоровых троек при решении задач
В наши дни теорема Пифагора очень важна и актуальна. Она была известна еще за долго до Пифагора. Пифагор внес и дополнил ее своими исследованиями, повысив значимость в мире математических открытий. Теорема меняется в геометрии на каждом шагу. Она имеет неослабевающий интерес со стороны широкой математической общественности. Можно увидеть применение Пифагоровых троек и в наши дни.
В ходе исследования, мы узнали, что теорема Пифагора так же
применялась в архитектуре. Взгляните на эти здания, которые украшают
зарубежные города:
Административное здание Kuggen, Гётеборг, Швеция.

Если Вы заметили, то окна в этом здании имеют вид прямоугольного
треугольника.
Скульптурный павильон в одном из садов в Англии.

Музей в Милуоки, США.

Еще в 12 веке были использованы Пифагоровы тройки в зданиях
готического и романского стиля.
Романский стиль: Готический
стиль:


Верхние части окон расчленяются каменными ребрами, которые не
только играют роль орнамента, но и способствуют прочности окон.
На рисунке представлен простой пример такого окна в готическом
стиле.

Способ построения его очень прост: из рисунка легко найти центры
шести дуг окружностей, радиусы которых равны
ширине окна (b) для наружных дуг
половине ширины, ![]() для
для
внутренних дуг.
Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена
между двумя концентрическими окружностями, то ее диаметр равен расстоянию между
этими окружностями, т. е.![]() и,
и,
следовательно, радиус равен![]() .А тогда
.А тогда
становится ясным и
положение её центра.
В романской архитектуре часто встречается мотив, представленный на рисунке.
Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут
равны ![]() и
и ![]() . Радиус – p
. Радиус – p
внутренней окружности можно вычислить из прямоугольного треугольника.
Гипотенуза этого треугольника, проходящая через точку касания окружностей,
равна![]() , один катет
, один катет
равен ![]() , а другой
, а другой![]() . По теореме
. По теореме
Пифагора имеем:
![]() Из этого:
Из этого:
![]()
Разделив на b и приводя подобные члены, получим:
![]()
![]()
Заключение
Пифагоровы тройки представляют собой очень важный и интересный предмет изучения. Запомнив простые правила их нахождения, можно с легкостью решать задачи разного уровня, а также находить им хорошее применение в архитектуре и строительстве. Знание этих троек подталкивает к иному решению задачи. Проведенные исследования показывают эффективность применения пифагоровых троек при решении геометрических задач. В целях экономии времени и избежание вычислительных ошибок рекомендуем объяснять на уроках способы формирования пифагоровых троек и стремиться к их применению на практике. Они так же могут помочь на ОГЭ и ЕГЭ, поэтому нам стоит знать, как они применяются на практике.
Список
литературы
1.
Книга “О Пифагоровой
жизни”-Ямвлих; перевод И.Ю. Мельникова. — Москва: Новый Акрополь, 2014г. —
186 cтр.
http://www.iprbookshop.ru/26960.html
2. Учебник по геометрии 7-9 класс, Погорелов А.В. 7.Теорема Пифагора(п.62-70), изд.9-е., 2009г.
https://gdzputina.ru/po-geometrii/7-klass/pogorelov
3.
Учебник и практикум для среднего профессионального образования,
Ю. В. Павлюченко, Н. Ш. Хассан; под общей редакцией
Ю. В. Павлюченко. – 4-е изд., перераб. и доп. — Москва:
Издательство Юрайт, 2020. -238 с. – Профессиональное
образование). – ISBN 978-5-534-01261-3. -Текст: электронный // ЭБС
Юрайт [сайт].с. 41 — URL: https://urait.ru/viewer/matematika-449041#page/
В математике пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел 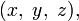 удовлетворяющих соотношению Пифагора:
удовлетворяющих соотношению Пифагора:
- x2 + y2 = z2.
Содержание
- 1 Свойства
- 2 Примеры
- 3 История
- 4 См. также
- 5 Ссылки
Свойства
Поскольку уравнение x2 + y2 = z2 однородно, при домножении x, y и z на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть 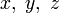 — взаимно простые числа.
— взаимно простые числа.
Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 (32 + 42 = 52).
Пифагорова тройка 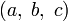 задаёт точку с рациональными координатами
задаёт точку с рациональными координатами 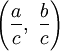 на единичной окружности x2 + y2 = 1.
на единичной окружности x2 + y2 = 1.
Нетрудно видеть, что в примитивной тройке (x,y,z) числа x и y имеют разную чётность. Любая примитивная пифагорова тройка (x,y,z), где x – нечётно, а y – чётно, однозначно представляется в виде 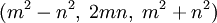 для некоторых натуральных взаимно простых чисел m > n разной чётности. Наоборот, любая такая пара
для некоторых натуральных взаимно простых чисел m > n разной чётности. Наоборот, любая такая пара 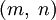 задаёт примитивную пифагорову тройку
задаёт примитивную пифагорову тройку 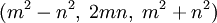 . [1]
. [1]
Примеры
Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (14, 48, 50), (30, 40, 50)…
История
Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.
X Всероссийский симпозиум по прикладной и промышленной математике. Санкт – Петербург, 19 мая 2009г.
Доклад: Алгоритм решения Диофантовых уравнений.
В работе рассмотрен метод исследования Диофантовых уравнений и представлены решенные этим методом: – великая теорема Ферма; – поиск Пифагоровых троек и тд. http://referats.protoplex.ru/referats_show/6954.html
См. также
- Великая теорема Ферма
- Теорема Пифагора
Ссылки
- ↑ В. Н. Серпинский Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
- Е. А. Горин Степени простых чисел в составе пифагоровых троек // Математическое просвещение. — 2008. — В. 12. — С. 105-125.
Wikimedia Foundation.
2010.





























































