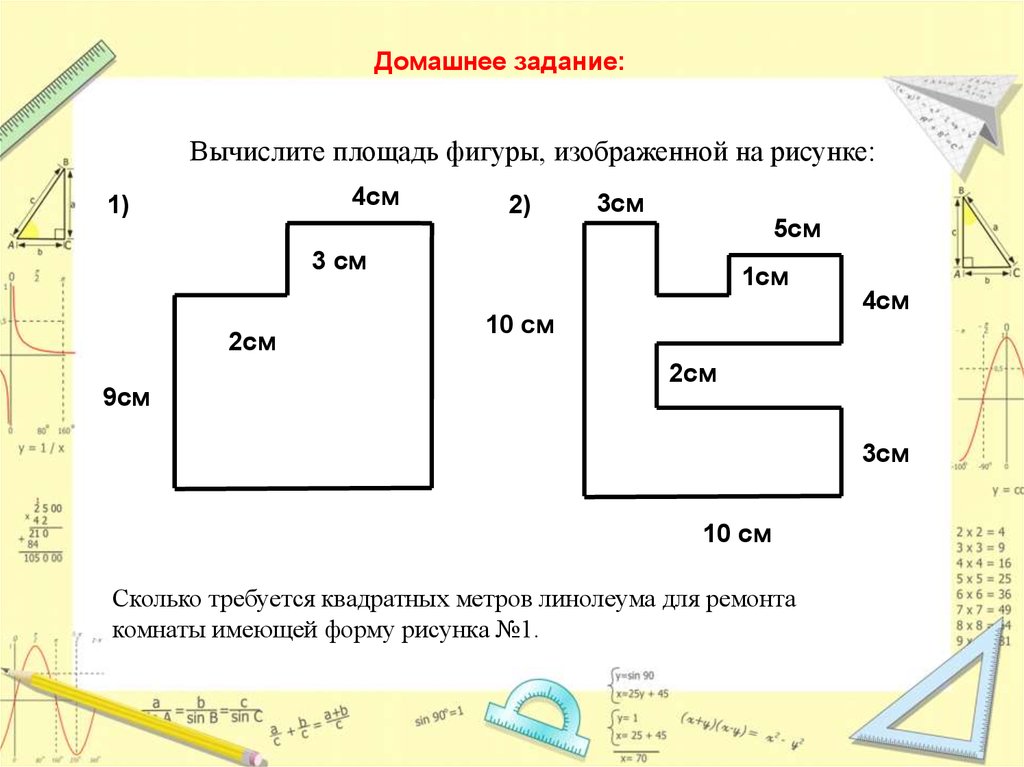
Определение площади различных геометрических фигур является важным элементом понимания и применения основ математики. Точность расчетов и алгоритмов являются ключом к недостижимому знанию о пространстве вокруг нас. В освоении этой области на ее месте уникальное значение стоит возможно doback размышлять на тему: “Площадь фигуры как найти”. В нашей статье мы обзорным образом рассмотрим ключевые понятия и приемы, помогающие в определении площади знакомых и нечасто встречаемых в повседневной жизни фигур.
В процессе образования теория начертательной геометрии является необходимым предметом рационального мировосприятия. Ученикам занимается площадь прямоугольников, треугольников и кругов, что иллюстрирует фрагменты сложнейшего мира геометрических форм окружающего пространства. Однако бывают случаи, когда опытные рисовальщики должны подобрать справедливую площадь менее очевидных и уникальных фигур, вроде сегментов круга, повёрнутых трапеций, изоседральных треугольников. В таких затруднительных местах умение вычислять площадь фигуры бывает немаловажным ресурсом продуктивности.
Чтобы превратить площадь фигуры из камня преткновения в полезный сопротивитель, рассмотрим основные приемы вычисления площади различных известных геометрических фигур. Восприимчивым к математическому мышлению умы учит экспрессивные видеоуроки, философизированные методические разработки и современные обучающие сайтов, предлагающие наглядные примеры и модели.
Площадь геометрических фигур
В геометрии площадью называется соотношение величины поверхности фигуры к квадрату ее линейной меры. Таким образом, площадь показывает то, сколько единиц квадрата можно вместить внутри данной фигуры. В данном разделе мы рассмотрим основные типы геометрических фигур и методы их площади измерения.
Площадь прямоугольника
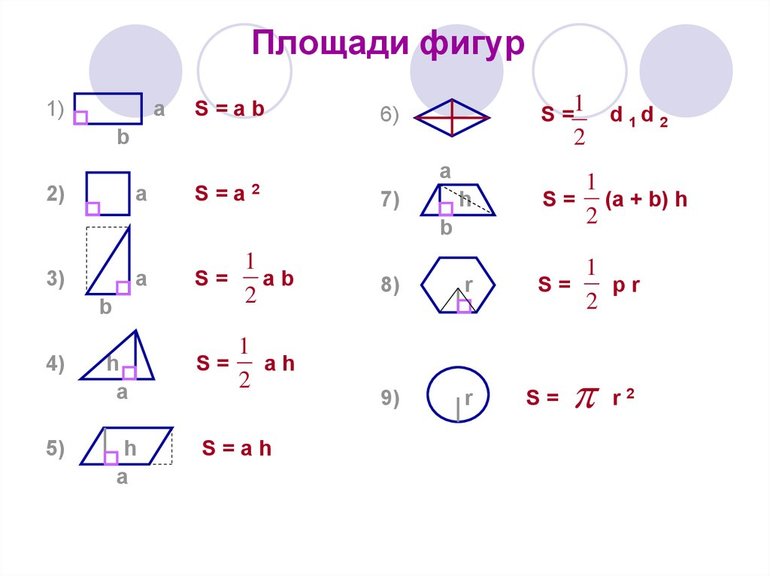
Площадь прямоугольника рассчитывается как произведение длины и ширины. Этот геометрический параметр в математике является важным, поскольку прямоугольники часто встречаются в реальной жизни.
Формула для площади прямоугольника: А = ab
Где:
- a – длина прямоугольника
- b – ширина прямоугольника
- А – площадь прямоугольника
Площадь круга
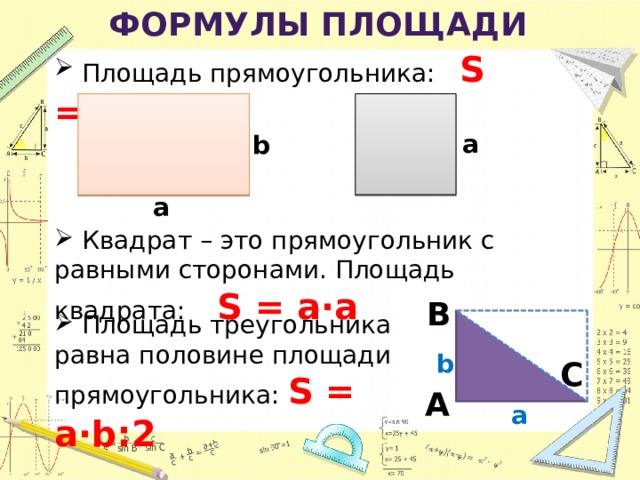
Площадь круга считается на основе его радиуса. Для расчета площади круга используется математический термин pi (π), который равняется приблизительно 3,14. Он представляет собой отношение окружности круга к его диаметру.
Формула для площади круга: A = π * r^2
Где:
- π – математическая константа pi, близкая к 3,14159
- r – радиус круга
- А – площадь круга
Внимание: в пункте “Площадь круга”, фигура “круг” идентифицируется как кривые геометрические фигуры, являющиеся частью аналитической геометрии, в то время как предыдущий пункт “Площадь прямоугольника” относится к геометрическим фигурам, сформированным с помощью прямых линий и является частью Евклидовой геометрии.
Площадь треугольника
Площадь треугольника принято находить исходя из формулы, которая называется формулой Герона. Эта формула дает возможность найти площадь треугольника, зная длины его сторон.
Формула для площади треугольника: A = √[s * (s – a) * (s – b) * (s – c)], где s = (a + b + c) / 2
- a, b, c – стороны треугольника
- s – полупериметр треугольника
- A – площадь треугольника
Обратите внимание, что эта формула для площади треугольника известна как формула Герона и использует евклидову геометрию для вычисления площади треугольника по его сторонам. Оптимальный способ определения площади треугольника – вычисление по формуле Герона, даже если треугольник неравносторонний. Это способствует точности и упрощенности вычислений, так как требует известное требование для вычисления – длины трех его сторон.
Тем не менее, существует и другие методы расчета площади треугольника, такие как использование медиан, высот, базисов и т. д., важно понимать основную теорию Эвклида и его геометрию. У каждого используемого метода есть свои объяснения и сопутствующие теории, однако Гиперболическая геометрия используется редко, тем более такой вариант ее как теория Элипсовых аномалий.
Теория: основные понятия и принципы

В теории фигуры представляют собой множество точек в пространстве, ограниченное определенными границами. Площадь фигуры определяется как количество единиц поверхности, занимаемое фигурой.
Основные понятия
Площадь: размер пространства ограниченного фигуры. Формула площади определяет математическую модель, которая помогает нам найти площадь любой фигуры.
Принципы расчета площади фигур
Обозначим через S – площадь фигуры, а буквы A, B, C и т.д. – длину сторон или другие необходимые величины. Значения для данной фигуры входят в формулу площади.
Чтобы найти площадь, необходимо использовать формулу и ввести значения для разных типов фигур.
– Квадрат: S = A², где A – сторона квадрата.
– Прямоугольник: S = AB, где A и B – стороны прямоугольника.
– Треугольник: S = 1/2 * AB * sin C, где А, B и С – стороны треугольника, C – угол между сторонами A и B.
– Круг: S = π * R², где R – радиус круга.
Для более сложных фигур площадь всегда вычисляется по специальным формулам, которые включают в себя основные понятия геометрии.
Если формулы не помогают найти площадь фигуры, можно прибегнуть к другому принципу – разбиению фигуры на известные части.
Важно: Систематические тренировки с расчетами площади разнообразных фигур помогут совершенствовать навыки и освоить методы нахождения площади весьма скоро.
Умножение площадей прямоугольников
Площадь прямоугольника
Перед тем, как перейти к умножению площадей прямоугольников, давайте рассмотрим, как найти площадь одного прямоугольника. Площадь прямоугольника находится путем умножения длины одной из его сторон на длину другой противоположной стороны. Если мы обозначим длины сторон прямоугольника как a и b, то площадь прямоугольника S будет равна a * b.
Умножение площадей прямоугольников
Пусть имеется два прямоугольника с известными площадями S1 и S2 соответственно. Вам необходимо найти площадь прямоугольника с площадью S1 * S2. Это можно сделать путём умножения площадей S1 и S2.
Заметьте: это предполагает, что площади умножаемых прямоугольников не связаны и являются независимыми, предполагается, что результирующий прямоугольник размещается в пространстве без ограничений.
Например, если S1 = 5 и S2 = 6, площадь результирующего прямоугольника будет равна площади прямоугольника с длинными сторонами, равными 5 и 6, то есть S1 * S2 = 5 * 6 = 30.
Однако стоит отметить, что единственным случаем, когда допустимо простое умножение площадей двух прямоугольников для получения площади их произведения, является случай, когда они не ограничены объединенной геометрической конструкцией или не сильно взаимодействуют между собой.
Следите за тем, чтобы понимать условия задачи перед переходом к умножению площадей прямоугольников, чтобы избежать потенциальных недоразумений и получить корректный результат.
Способы вычисления площадей в нижних измерениях
Площадь в двумерном пространстве
Двумерные фигуры, такие как прямоугольник, треугольник и круг являются основной темой для изучения вычисления площадей. Площадь вычисляется как количество ячеек квадратного пикселя на горизонтальной плоскости.
Для прямоугольника: вычислительная формула состоит из произведения длины и ширины (Площадь = длина * ширина).
Для треугольника: формула площади вычисляется как половина произведения основания и высоты (Площадь = 1/2 * основание * высота).
Для круга: площадь круговой фигуры вычисляется с использованием радиуса и числа Пи: площь = числу Пи * радиус2 (Площадь = П * r2).
Площадь в одномерном пространстве
В связи с одномерными объектами, такими как линия или отрезок, имеется только один измерение длины, и не имеет смысла говорить о площади. В некоторых контекстах может быть полезно определять площадь только для нахождения функций в более высоких размерностях. В таком контексте площадь одномерного объекта, такого как отрезок длины l, может быть вычислена как единица площади, заключающаяся в ареале пространство, соответствующего отрезку, вращённому на 360 градусов вокруг точки или направления, образующего отрезок.
Поскольку обычный отрезок имеет одно измерение длины, а не площадь, высокая концепция площади одномерного отрезка может использоваться для поддержки более сложных вычислений в трёхмерных пространствах.
Системы координат и приложения в географии
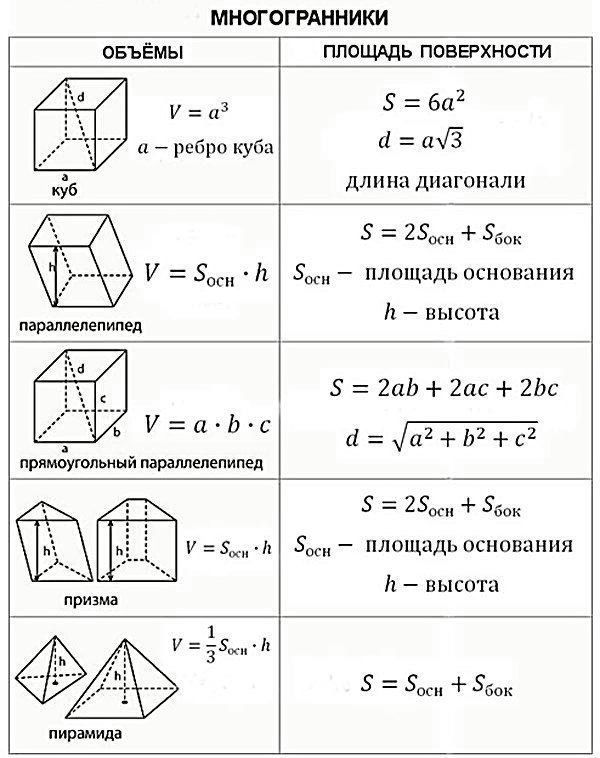
Типы систем координат
Существует несколько типов систем координат, которые используются в географии. Они включают:
- Декартова система координат (вертикально-горизонтальные координаты)
- Полярная система координат
- Гибридная система координат (гибрид декартовой и полярной систем)
- Географическая система координат (локальная, прямоугольная или проекция Меркатора)
Применение систем координат в географии
Системы координат используются для определения и анализа расположения людей, мест, объектов и других событий на Земле. Они имеют важное значение в таких областях, как:
- Картография: Системы координат позволяют создавать точные карты, на которых изображены географические, политические и экономические объекты. Эти карты могут быть использованы для изучения и объяснения реальных и исторических явлений.
- Геодезия: Системы координат имеют важное значение для измерения отдельных элементов, таких как меридианы, параллели, линии долготы и широты. Эти измерения могут быть основаны на гравитации, аномалиях, магнитных полях и других земных явлениях.
- Навигация: Системы координат очень важны для определения где на картах корабли, самолеты, автомобили и другие транспортные средства движутся. Географические системы координат являются основой для спутниковой навигационной системы (GPS).
- Архивы: Системы координат могут быть использованы для сохранения и предоставления информации, такой как геологическая история или археологические находки, которые могут влиять на озелененные территории. Например, во второй половине 20 века системы координат использовались для наблюдения за изменениями в ландшафте.
Итак, системы координат имеют очень значительное значение в математическом определении и анализе физических природных явлений. Они также имеют большое влияние на многие отрасли географии, от картографии до геодезии.
Инструменты и технологии измерения площадей

Для измерения площадей используются разные инструменты и технологии, обеспечивающие точность результатов независимо от размера или формы исследуемых фигур. Ниже приведены некоторые из основных методов измерения площадей.
Классические методы измерения площадей
Некоторые из самых простых и компактных инструментов полезны в быту и строительстве:
- Треугольник Якоби – инструмент для плоских мероприятий, позволяющий выполнить прямые, углые или кривые отсечения. Треугольник Якоби используется в паре с шестиметровыми нитками и линейная измерительная лента, и позволяет быстро и задавать проект строительных работ.
- Линейка с КМ или клетчатый лист плоскости – пригодны для измерения площадей, заполненных нецентральными отделанными орнаментами, в том числе полупроизводными, с ошибкой 5% – 10%. Вершины пользователей такие инструменты на платформе метр.
Современные технологии измерения площадей

Современные технологии измерения площадей на основе компьютерного моделирования и визуализации, особенно удобны при работе с сложными формулами и углами:
- Автономная GPS – система определения координаты точки на поверхности земли, которая может использоваться для беспилотных сетей (внешних), передвигающихся на автомашинах, короткого и воздушного наблюдения (в основном в военных целях).
- Лазерное сканирование – методика трехмерного цифрового моделирования объектов, основанная на регистрации времени возврата отдаленных объектов микроволновым сигналом из электрофотографии.
- Краевые радари – способ измерения скоростей и местоположений объектов, основанная на определении разности в амплитуде отраженных радиоволн от двух мест разных объектов – сферы.
С помощью матрично-многошагового программного обеспечения вы можете легко создавать настраиваемые графики, высчитывать площади и проводить детальный анализ геометрии своих строительных проектов.
Примеры плотности: измерение площадей в биометрии
Чтобы понять, как пространство может быть разделено в биометрии, рассмотрим примеры разных возникающих из измерения плотность:
Площадь кожи человека:
Влияние накона производит важно для оценки обменных процессов и передачи тепла у человека. Чтобы измерить площадь кожи, используют различные методы, в том числе сканеры 3D. С помощью этого устройства кожа человека сканируется, и генерируется чёрно-белый изображения с различными градациями, после чего реализация оценки помощи администратора или специального программного обеспечение.
Как только площадь кожи человека определенна, можно правильнее оценить потребление энергии, количество тепла и других имеющих значение параметрических пределов. Например, площадь кожи молодых людей обычно выше за счёт более тонкой и эластичной кожи, в то время как у пожилых людей она часто уменьшена, вследствие разрушения кожи со временем.
Площадь крыльев насекомых:
Площадь крыльев насекомых имеет влияние на их полетные характеристики и способности к быстрому передвижению. Узнав площадь крыльев за счёт измерения миллиметров по длине, а затем ширине крыла и умножая эти числа, можно определить площадь крыла. Наличие данных о площади крыльев позволяет лучше аспекты эволюции и адаптации различных видов насекомых к окружающей среде.
Например, для летучих насекомых, выполняющих большое разнообразие процессов передвижения, как космическое, насыщенность смеритых большие потребности в размерах крыльев для лучшего контроля и маневренности. Другими словами, более хорошее понимание биометрии, площадия является необходимым для информирования свойства и характеристики различных видов насекомых.
Площадь листьев растений:
Оценка площади листьев растений является важным аспектом изучения их энергетических потребностей, процессов роста и развития. Площадь листьев растений может быть измерена с помощью специальных приборов или метода вручную треугольников, когда листья растений бывают отделены и размерами, в длину и ширину и затем умножаются цифры, чтобы получить площадь. Краткая площадь листьев указывает на высокий темп роста растений и развитие их корневой системы.
К примеру, площадь листьев растений может меняться в зависимости от факторов окружающей среды, таких как количество света, влажность воздуха, здоровье и наличие удобрения. Обладая данными о площади листьев растения, можно сделать более информированные решению, регулировать условия выращивания, улучшать урожай и обеспечивать здоровье культивация процессов.
В общем, измерение площади является основным примером плотности исследования в биометрии, поскольку оно позволяет лучше определить качественные параметры и характеристики организмов. Используя информацию про их плотность, научные исследования могут принимать интеллектуальные решения, улучшать безопасность и здоровье, а также делать преемственности глобальный и социумом на благо.
Примечание: В тексте упомянуты отдельные примеры из области биометрии, связанные с измерением площади на различных организмах. Это должно дать представление о важности этой области в научных исследованиях и применении интеллектуальных решений для продвижения научного понимания и рационализации процессов, связанных с организмами природы.
Вопрос-ответ:
Каким образом можно найти площадь прямоугольника, зная только две стороны?
Чтобы найти площадь прямоугольника, достаточно умножить длину и ширину этой фигуры. Например, если у вас есть прямоугольник размером 5×3, то его площадь будет 5*3=15 квадратных единиц. Это происходит потому, что площадь геометрической фигуры есть количество единичных квадратиков (например, квадратиков размером 1×1), которые умещаются внутри этой фигуры без перекрытия или пропусков. В данном случае, мы накладываем квадратики на прямоугольник, по одному на каждую пару соседних сторон, их количество будет равно произведению длины и ширины.
Можно ли найти площадь треугольника, зная только его основание и двух сторон?
Если у вас есть треугольник со всеми сторонами разных величин, и вы знаете только основание и две другие стороны, площадь свойственно найти с ошибкой. В этом случае используется формула Герона (известная также как формула полупериметра), где она учитывает длину трех сторон треугольника: a, b и c. Сначала вычисляется полупериметр (p = (a+b+c)/2), потом площадь вычисляется по формуле: S = √(p(p-a)(p-b)(p-c)), где “√” обозначает квадратный корень. Но если ваш треугольник является прямоугольным, то, зная основание и высоту, площадь можно найти, поделив пересечение основания и высоты на основание.