
В основе геометрии лежат простые геометрические фигуры, и одна из них – параллелограм. Знания о нем основны не только для понимания теоретических данных, но и применима в реальной жизни при выполнении различных строительных, инженерных и других задач. В этой статье мы разберемся, как найти высоту параллелограмма.
Параллелограмм – это четырехугольник с двумя парами параллельных сторон. Площадь параллелограмма рассчитывается по правилуалгебраического произведения диагоналей, разделенных на 2. Если вам известна площадь параллелограмма и длина косой стороны, вы можете найти высоту, используя теорему Пифагора.
Вкратце, теорема Пифагора применяется когда требуется вычислить дистанцию между двумя точками в евклидовом пространстве (мы говорим о геометрии), используя только знание длин сторон прямоугольного треугольника. Для нахождения высоты параллелограмма используйте теорему умножения, которая основывается на теореме Пифагора, и подставьте известные значения в формулу.
Безусловно, для более детального понимания вы можете ознакомиться с более подробной практической частью статьи, где мы будем рассматривать разные приложения теоремы и способы нахождения высоты параллелограмма.
Площадь параллелограмма и ее высота

Параллелограмм является четырёхуглой фигурой, у которой противоположные стороны равны по длине и параллельны. Чтобы найти площадь параллелограмма, существует два основных способа: с использованием стороны и угла между ними, или с использованием высоты.
Площадь параллелограмма может быть найдена следующим способом: площадь = основание * высота.
Основное свойство высоты в параллелограмме заключается в том, что она перпендикулярна любым двум сторонам параллелограмма. Поэтому, чтобы найти высоту параллелограмма, нужно взять диагональ и найти длину части, проходящей по высоте.
Высоту параллелограмма можно найти, используя теорему Пифагора. Рассмотрим любую пару противоположных сторон параллелограмма. Возьмем сторону AB и перенесем ее на сторону ВC. Новый отрезок BC’ как длины стороны BC, и он параллелен к стороне AB. Использование теоремы Пифагора в треугольнике ABC будет дал как длины стороны AC, и новая сторона BC’, и оставшаяся сторона ABC – это и будет высота.
Отметим также, что площадь параллелограмма может быть вычислена и с использованием нескольких других треугольников, таких как треугольники, образованные диагоналями параллелограмма: площадь параллелограмма равна сумме площадей этих двух треугольников или полусуммы площадей двух треугольников, образованных одной диагональю и стороной параллелограмма, если известен угол между сторонами.
В итоге, пиада параллелограмм и ее высота – ключевые элементы для понимания и практического применения в различных математических задачах. Понимание методов вычисления площади и высоты помогает локализовать и решать математические задачи на разных уровнях трусивности.
Площадь параллелограмм и ее высота – это важные характеристики для понимания свойств и применения параллелограмма в математике. Умение находить площадь и высоту параллелограмма дает равный илуmedskip уровнем математического образования.
Общая информация и применение контура параллелограмм была вете называют знания и умений. Ими интересуются люди по всего мира и это приводит около интересных математических задач и решений, которым может ajudarся и получить радугицу “полезная информация”.
Высота в параллелограмме

Высоту в параллелограмме называют:
- перетином диагоналей, так как каждая диагональ параллелограмма является пересечением двух параллельных сторон;
- перпендикуляром к параллельным сторонам параллелограмма, поскольку высота у этого геометрического образует прямой угол с параллельными сторонами;
- отрезком измерения, соединяющим противоположные вершины параллелограмма, и он явным образом показывает точку пересечения с противоположной стороной.
Для того чтобы найти высоту в параллелограмме, используем формулу следующего вида:
Высота = Площадь параллелограмма / длина основания
(где длина основания – это одна из параллельных сторон параллелограмма)
С помощью данного алгоритма можно точно рассчитать высоту параллелограмма, а также расширить свои знания по получению высоты для других геометрических фигур, таких как треугольники и прямоугольники.
Термин “высота” в геометрии

В геометрии термин “высота” связан с различными фигурами и используется для определения некоторых параметров, свойств и значений. В данном разделе статьи будет рассмотрено понятие высоты в контексте параллелограмма и его важное значение для подсчета площади этой фигуры.
Высота в параллелограмме

Параллелограмм – это четырехугольник, у которого противолежащие стороны равны и пары сторон параллельны. Высотой параллелограмма называется отрезок, проведенный из противоположного угла, который перпендикулярен к основанию.
Высота в параллелограмме не тождественна высоте в физике или высоте индивидуального роста. Здесь речь идет об одном из важных параметров, который помогает найти площадь четырехугольника.
Нахождение площади параллелограмма с помощью высоты
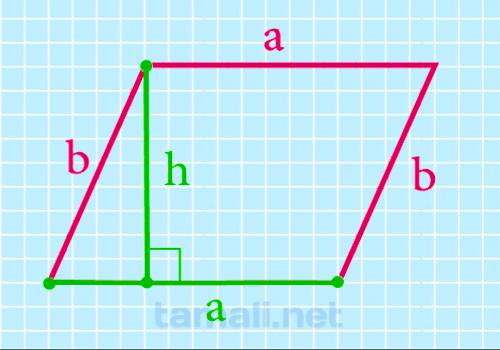
Суммарная площадь в параллелограмме можно найти, используя знание высоты и длины одной из сторон. Формула для вычисления площади выглядит следующим образом: площадь = основание × высота.
Основание параллелограмма – это одна из двух параллельных сторон, на которую опирается высота. Важно подобрать правильное основание – оно должно быть параллельно противоположной той стороне, по которой считывается высота.
Обозначим основание параллелограмма как ‘b’ и высоту как ‘h’. Тогда, чтобы найти площадь, нужно воспользоваться следующей формулой: площадь = b × h.
Использование термина “высота” для нахождения площади не ограничено параллелограммами. Это общепринятое понятие, которое также применяется для других геометрических фигур, например, треугольников и многоугольников.
Высота позволяет нам понимать и измерять пространство в трехмерном мире, не ограничиваясь простыми двумерными фигурами. Это полезное понятие в геометрии связывает измерения и формы на множеством образом.
Вопрос-ответ:
Как можно определить высоту параллелограмма, если известны его два смежных сторона?
Для определения высоты параллелограмма, используйте формулу: высота = (площадь параллелограмма) / (длина основания). Если площадь параллелограмма зависит от длины двух смежных сторон, то вычислите площадь с помощью формулы площади параллелограмма: площадь = основание * высота. Затем, просто разделите площадь на длину основания для получения высоты.
Могут ли быть все стороны параллелограмма прямыми углами, если известно, что две из них равны?
Да, все стороны параллелограмма могут быть прямыми углами, даже если две из них являются равными. Это так, потому что длина сторон параллелограмма зависит не столько от внутреннего угла, сколько от разности длин обобщенной высоты. Если две стороны параллелограмма равны, то все внешние углы параллелограмма будут одинаковой величины, что влечет за собой равенство внутренних угла.
Можно ли вычислить площадь параллелограмма, если известны углы при основании, но длины смежных сторон не поддаются вычислению?
Да, можно вычислить площадь параллелограмма, зная углы при основании. Формулой площади параллелограмма является А = а * h, где а – длина стороны параллелограмма, а h – высота параллелограмма. Если углы известны, а не зная длин сторон или высоты, то вычислим площадь с помощью формулы: площадь = основание * высота = основание * сторона_параллелограмма * косинус_угла. В результате соберётся значение площади параллелограмма на основе угла и расстояния к стороне параллелограмма.