Площадь параллелограмма внутри параллелограмма как найти

Как найти площадь параллелограмма — три основных формулы

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.

Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.

Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.

Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».

Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.

Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.

Формулы для расчета площади параллелограмма

Есть три основных формулы для вычисления площади параллелограмма:

1. если известна длина стороны и высота, проведенная к ней;
2. если известны длины сторон и углы между ними;
3. если известны длины диагоналей и угол между ними.

Теперь о каждом из этих способов подробнее.

Как найти площадь параллелограмма, если известны сторона и высота

Возьмем для примера такой параллелограмм:

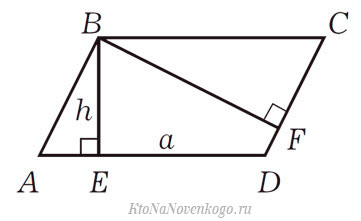
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.

В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.

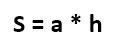
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.

Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:

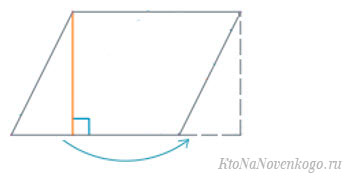
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.

Формула площади параллелограмма, если известны стороны и угол

Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.

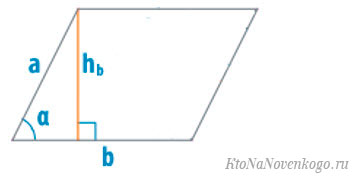
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.

Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:

Соответственно, чтобы посчитать значение высоты надо:

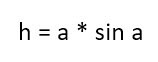
И наша конечная формула для расчета площади будет выглядеть следующим образом:

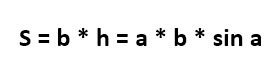
Как найти площадь параллелограмма через диагонали

Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.

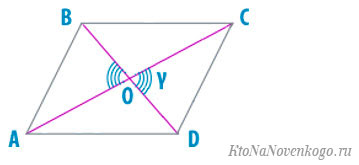
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:

Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.

Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.

Area of a parallelogram is the space or the region enclosed by the boundary of the parallelogram in a two-dimensional space. It is defined as the area covered inside the perimeter of the parallelogram. It is calculated by multiplying the base of the parallelogram by its height. It is calculated in unit square and the standard unit for the measurement of the area of the parallelogram is m².

Let’s learn more about its area, and others in this article. 

What is the Area of a Parallelogram?

The total surface occupies by the parallelogram on a two-dimensional plane surface is the area of a parallelogram. The area of a parallelogram can be determined by using its height, length of sides, or diagonals. As the area of the parallelogram is nothing but the area it is measured in the unit square, i.e. m², cm² 

Area of a Parallelogram Formula

The area of a parallelogram can be determined by multiplying its base by its altitude. As seen in the following diagram, a parallelogram’s base and height are perpendicular to one another. Thus, the following formula can be used to determine a parallelogram’s area,

Area of Parallelogram = Base × Height 

A = b × h

where,
b is the base of Parallelogram
h is the height of Parallelogram

How to Find the Area of a Parallelogram?

Generally, the area of a parallelogram can be calculated using its base and height. In addition to that, the area of a parallelogram can also be determined if the lengths of its parallel sides and any angles between them are known, as well as the angles at which its two diagonals intersect. As a result, there are three ways to calculate the parallelogram’s area:

• When the Base and Height of the parallelogram are known.
• When the lengths of the sides of the parallelogram are known.
• When the lengths of the diagonals of the parallelogram are known.

Area of a Parallelogram using Base and Height

The area of a parallelogram using the height is given by the product of its base and height.

Mathematically it is written as

Area of parallelogram = b × h

where,
b is the base of Parallelogram
h is the height of Parallelogram

Example: Find the area of a parallelogram whose base is 12 cm and height is 8 cm. 

Solution:

 Given that, 

 Base (b) = 12 cm

 Height (h) = 8 cm

The formula to calculate the area of a parallelogram is,

A = b × h 

A = 12 × 8 

A = 96 cm²

Area of a Parallelogram using Side Lengths

The area of a parallelogram can be calculated by using the length of sides and adjacent angles if the height is not given.

Mathematically it is written as,

Area of Parallelogram = ab sin (θ)

where, 
a and b are the lengths of parallel sides
θ is the angle between the sides

Example: If the angle between two sides of a parallelogram is 30 degrees and the length of its adjacent sides are 5 cm and 6 cm. Determine the area of the parallelogram.

Solution:

Given that, 

Length of one side (a) = 5 cm,

Length of the other side (b) = 4 cm,

Angle between the two adjacent sides (θ) = 30 degrees

The formula to calculate the area of a parallelogram is,

A = ab sin (θ)

A = 5 × 4 × sin (30)

A = 10 cm²

Area of a Parallelogram using Diagonals

A parallelogram consists of two diagonals that intersect each other at a certain angle meeting at a particular point. The area of a parallelogram can be calculated by using the length of its diagonals.

The formula for the area of a parallelogram by using the length of diagonals is given by,

Area of parallelogram = 1/2 × d₁ × d₂ sin (x)

where,
d₁ and d₂ are the lengths of the diagonals
x is the angle between the diagonals

Example: Determine the area of the parallelogram, when the angle between two intersecting diagonals of a parallelogram is 90 degrees and the length of its diagonals are 2 cm and 6 cm.

Solution:

Given that, 

Length of one diagonal (d₁) = 2 cm,

Length of the other diagonal (d₂) = 6 cm,

Angle between the two intersecting diagonals (x) = 90 degrees

The formula to calculate the area of a parallelogram is,

A = 1/2 × d₁ × d₂ sin (x)

A = 1/2 × 2 × 6 × sin (90)

A = 6 cm²

Area of Parallelogram Vector

The area of a parallelogram can be calculated even when the sides and the diagonals of the parallelogram are given in vector form. Considering a parallelogram PQRS, with adjacent sides   and   respectively. And the diagonals are    and   .

Now, the area of the parallelogram in vector form is given by using the adjacent sides  and  as, 

Using the Parallelogram Law of Vector Addition

Now, 

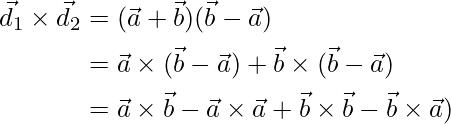
But, ,  and 

Therefore, 

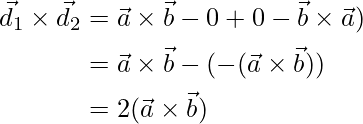
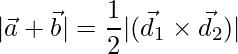
Thus from equation (1), the area of the parallelogram in vector form is stated as:

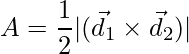
Summary

• Area of a parallelogram using Base and Height,

A = b × h

• Area of a parallelogram using the side lengths,

A = ab sin (θ)

• Area of parallelogram using diagonals,

A = 1/2 × d₁ × d₂ sin (x)

Read, More

• Area of Trapezium
• Area of a Square
• Area of a Circle

Solved Examples on Area of a Parallelogram

Example 1: Find the area of a parallelogram whose base is 10 cm and height is 8 cm.

Solution:

Given,

Base (b) = 10 cm

Height (h) = 8 cm

We have,

A = b × h

   = 10 × 8

   = 80 cm²

Example 2: Find the area of a parallelogram whose base is 5 cm and height is 4 cm. 

Solution:

Given,

Base (b) = 5cm 

Height (h) = 4cm

Area(A) = b × h 

A = 5 × 4 

   = 20 cm²

Example 3: Determine the area of the parallelogram, when the angle between two intersecting diagonals of a parallelogram is 90 degrees and the length of its adjacent sides are 4 cm and 8 cm.

Solution:

Given that, 

Length of one diagonal (d₁) = 4 cm,

Length of the other diagonal (d₂) = 8 cm,

Angle between the two intersecting diagonals (x) = 90 degrees

The formula to calculate the area of a parallelogram is,

A = 1/2 × d₁ × d₂ sin (x)

A = 1/2 × 4 × 8 × sin (90)

A = 16 cm²

Example 4: If the angle between two sides of a parallelogram is 60 degrees and the length of its adjacent sides is 3 cm and 6 cm. Determine the area of the parallelogram.

Solution:

Given that,

Length of one side (a) = 3 cm,

Length of the other side (b) = 6 cm,

Angle between the two adjacent sides (θ) = 60 degrees

The formula to calculate the area of a parallelogram is,

A = ab sin (θ)

A = 3 × 6 × sin (60)

A = 15.6 cm²

Example 5: Find the area of a parallelogram whose parallel sides are 4 cm and 3 cm and the angle between these sides is 90°.

Solution:

Given,

Let the lengths of the sides by a and b with values 4 cm and 3 cm respectively.

Angle between the sides 90°

Area = ab sinθ

A = 4 × 3 sin 90°

A = 12 cm²

FAQs on Area of a Parallelogram

Q1: What is the Area of a Parallelogram?

Answer:

Area of parallelogram is the area inclosed by the  boundary of the parallelogram it can be defined as the 2-D space inside the perimeter of the parallelogram. 

Q2: What is the Perimeter of a Parallelogram?

Answer:

Perimeter of a parallelogram is defined as the sum of its all four sides, so is given as,

P = 2 (a + b)

where
a and b are the length of the opposite sides of a parallelogram

Q3: What are the Properties of a Parallelogram?

Answer:

The Properties of Parallelogram are,

• Opposite sides of a parallelogram are equal and parallel to each other.
• Opposite angles of a parallelogram are equal.
• Sum of interior angles of a parallelogram is equal to 360°.
• Adjacent angles of a parallelogram must be supplementary i.e. equal to 180°.

Q4: What is the formula for finding the height of a parallelogram?

Answer:

The formula for the height of a parallelogram, when the area and the base of a parallelogram are known then:

h = A/b

where,
h is the height
b is the base
A is the area of the parallelogram

Q5: How to calculate the area of a parallelogram?

Answer:

Area of paralleogram is calculated using the formula,

Area = B × H

where,
B is the base of the parallelogram
H is the height of the parallelogram

Q6: How to find the area of a parallelogram without height?

Answer:

The area of a parallelogram when height is not given is calculated using the formula,

Area = ab sin (θ)

where, 
a and b are the lengths of parallel sides
θ is the angle between the sides.

Q7: How to find the area of parallelogram when diagonals are given?

Answer:

The area of a parallelogram when diagonals are given is calculated using the formula,

Area = 1/2 × d₁ × d₂ sin (x)

where,
d₁ and d₂ are the lengths of the diagonals
x is the angle between the diagonals

Q8: How to find the area of parallelogram in coordinate geometry?

Answer:

If the coordinate of the vertices of the paralleogram A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), and D(x₄, y₄) are given then it can be divided into two triangles, triangle ABC and triangle BCD and its area can be calculated using the area of triangle with given coordinate. 

Определение параллелограмма

Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.

Онлайн-калькулятор площади параллелограмма

Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.

Рассмотрим несколько способов и формул с последующим решением простых примеров.

Формула площади параллелограмма по основанию и высоте

Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.

Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:

S=a⋅hS=acdot h

aa — основание;
hh — высота.

Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.

Пример

Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).

Решение

a=10a=10
h=5h=5

Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)

Ответ: 50 (см. кв)

Формула площади параллелограмма по двум сторонам и углу между ними

В этом случае искомая величина находится так:

S=a⋅b⋅sin⁡(α)S=acdot bcdotsin(alpha)

a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.

Теперь решим другой пример и воспользуемся вышеописанной формулой.

Пример

Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.

Решение

a=20a=20
p=100p=100
α=30∘alpha=30^{circ}

Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30

Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin⁡(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)

Ответ: 300 (см. кв.)

Формула площади параллелограмма по диагоналям и углу между ними

S=12⋅D⋅d⋅sin⁡(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)

DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.

Пример

Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.

Решение

D=10D=10
d=5d=5
α=30∘alpha=30^{circ}

S=12⋅10⋅5⋅sin⁡(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)

Ответ: 12.5 (см. кв.)

Решение контрольной работы по геометрии онлайн – от профильных экспертов Студворк!

Тест по теме «Площадь параллелограмма»

Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье площадь параллелограмма. Площадь будет равняться произведению модулей на синус угла между ними:

Рассмотрим пример расчета площади параллелограмма построенного на векторах.

Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами

Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a(x1;y1;z1), а вектора b(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:


Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.

Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.