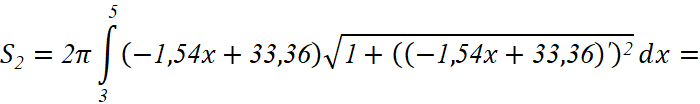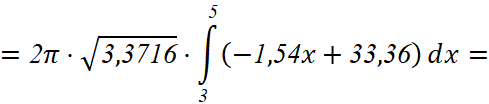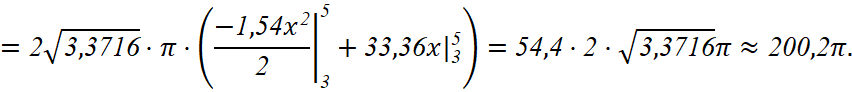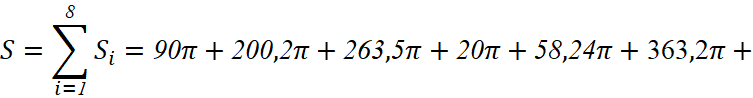Как рассчитать общую площадь поверхности, чтобы узнать, какое количество лакокрасочных материалов требуется приобрести для покраски основания? Перед окрашиванием помещений, металлоконструкций, в том числе профилей нужно учесть сумму расхода на материалы, а для этого важно определить, сколько квадратных метров (м2) требуется обработать.
Как рассчитать площадь комнаты
Чтобы наиболее точно определить, как рассчитать общую площадь комнаты, изначально рекомендуется подготовить ручку, рулетку, блокнот. Последовательность выполнения задачи:
- Производится измерение длины и ширины стен, а после вычисление периметра.
- Высота помещения замеряется таким же способом.
- Полученное значение периметра перемножается на высоту и получается общая площадь поверхности.
Посчитать общую площадь можно, используя простые действия: а – это длина одной стены, равная 3 м, в – это длина другой стены, она равна 4 м. Можно найти периметр по формуле: Р = 2х (а+в) = 2х(3+4) = 14 м. Теперь требуется замерить высоту потолка (Н). Допустим, она равна 2 м. Для определения площади S достаточно выполнить умножение или S = РхН = 14х2= 28 м2.
На видео: как рассчитать площадь стен в комнате.
Определяем нужное количество краски
Теперь требуется рассчитать количество краски для обработки поверхности площадью 28 м2. На банке с краской указывается расход материала на 1 м2. К примеру, для данного случая – 120 г/м2. Вычислением 28х120 определяем расход. Получается 3 кг 360 граммов.
Выше мы получили показатели при условии покраски в один слой, обычно поверхность покрывают в 2 слоя, то есть расход увеличивается вдвое.
Не нужно забывать и о наличии оконных, дверных проемов. Для этого достаточно замерить их высоту и ширину каждого по отдельности. После подсчета площадей каждого проема, согласно геометрическим формулам, полученный результат следует суммировать. Теперь остается вычесть из значения общей площади суммированный показатель площадей дверных и оконных блоков. Расчёт площади помещения, подлежащего окрашиванию, выполнен.
Перед окрашиванием поверхностей, в том числе уголков и труб, следует также учитывать качественную составляющую их обработки, свойства и расход материала на квадратный метр. Последнее указывается непосредственно на банке с краской.
Далее можно приобретать требуемое количество материала и приступать к окрашиванию. Если в процессе работы требуется выкрасить иные конструкции, например, дверные ручки, уголки, шпингалеты и другие декорации, то и расчеты соответственно будут сложнее и потребуется формула для расчетов.
Сколько краски нужно для металлопроката
Как рассчитать площадь покраски металла, если поверхность извилистая с многочисленными перепадами, углами и иными неровностями? Конструктивные элементы, выполненные из металлопроката, например, уголка, двутавра или швеллера, имеют различную конфигурацию. Формула проведения общего расчета позволяет вычислить с точностью количество квадратов обрабатываемого основания.
Рассчитать площадь проката можно, используя методику коэффициентов, которую найдете в интернет-ресурсах или в технической библиотеке. При расчете площадей можно пользоваться таблицами, в которых отражается зависимость веса от площади поверхности. К примеру, для одной тонны профиля № 5, площадь поверхности составляет 47,1 м2.
Таблицы площадей определены нормативными документами, а именно ГОСТами, в которых несложно найти поверхности 1 тонны изделия для соответствующего наименования профиля. Пример такой таблицы ниже.
Как рассчитать расход краски, зависимого от толщины слоя? Чтобы правильно выполнить расчет, следует придерживаться нормативов. Исходя из элементарных знаний алгебры школьного уровня, рекомендуется производить вычисления по данной формуле: А = (100 — ρ / Р — k1) — k2 — h. Эта формула получена после проведения исследований и позволяет высчитать площадь покраски металлических поверхностей с учетом их состояния и количества слоев).
Буквенные обозначения:
- А – норма расхода лакокрасочного материала для заданной площади, определяется 1 грамм на м2 окраски изделия;
- ρ – показатель плотности сухой пленки, количество граммов в см 3;
- Р – процентное содержание испаряющихся веществ при окраске изделия;
- k1– величина постоянная, равная 0,6 на основании действующих нормативов;
- k2 – используется в данной формуле на основании норм, его величина зависит от последовательности выполнения слоев окраски, или для 1 слоя – 1,15; для 2 – 1,05; для 3 – 1,0. Величины постоянные.
- h – толщина покрытия слоя окрашиваемой поверхности, измеряется в мкм.
Формула расхода, зависимая от толщины слоя краски, применяется не только на профессиональном уровне, ею может воспользоваться любой обыватель. Согласно произведенным расчетам, можно определить, какое количество краски следует приобрести, чтобы покрасить, к примеру, уголок.
О нормативах расхода ЛКМ
Чтобы правильно подсчитать количество квадратных метров окрашиваемых поверхностей, при расчете следует учитывать не только применение формулы, но и что литр ЛКМ уходит на покраску разного количества квадратов для различных оснований, например, расчетные данные следующие:
- 15 м2 – для металла;
- 16 м2 – для вновь оштукатуренной стены и отшлифованного дерева;
- 10 м2 – для обоев с рельефным узором;
- 8-10 м2 – для необработанного дерева;
- 15-17 м2 – для грунтованной поверхности штукатурки.
Важно учитывать, что при расходовании материала играет роль непосредственная зависимость от способа нанесения, к примеру, краскопультом или кистью. В последнем случае расход краски будет немного больше.
Программа для автоматического расчета площади (1 видео)
Что вам понадобится (16 фото)
Теория и материалы
Формулы и калькуляторы для расчета лакокрасочных покрытий
Формула 1. Определение толщины сухой пленки.
где,
ТСП – толщина сухой пленки, мкм;
ТМП – толщина мокрой пленки, мкм;
СО – сухой остаток по объему, %.
Пример. Необходимо определить толщину пленки после высыхания при нанесении лакокрасочного материала, имеющего объемный сухой остаток 70%, с толщиной мокрой пленки 200 мкм.
Используя формулу 1, получаем
200 * 70% = 140 мкм, т.е. толщина пленки после высыхания составит 140 мкм.
Калькулятор толщины сухой пленки:
Введите толщину мокрой пленки, мкм:
Введите объемный сухой остаток, %:
Толщина сухой пленки, мкм, равна:
Формула 2. Определение толщины мокрой пленки.
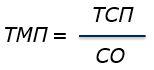
где,
ТСП – толщина сухой пленки, мкм;
ТМП – толщина мокрой пленки, мкм;
СО – объемный сухой остаток, %.
Пример. Определить толщину слоя, которую должен нанести маляр в процессе окраски. Объемный сухой остаток лакокрасочного материала составляет 60%, необходимая толщина сухой пленки 120 мкм.
Используя формулу 2, получаем
120/60% = 200 мкм, т.е. маляр должен наносить покрытие с толщиной 200 мкм, чтобы потом получить сухую пленку толщиной 120 мкм.
Калькулятор толщины мокрой пленки:
Введите толщину сухой пленки, мкм:
Введите объемный сухой остаток, %:
Толщина мокрой пленки, мкм, равна:
Формула 3. Определение толщины мокрой пленки при нанесении лакокрасочного материала с разбавлением.
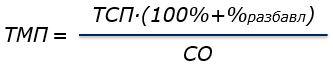
где,
ТСП – толщина сухой пленки, мкм;
ТМП – толщина мокрой пленки, мкм;
СО – сухой остаток, %;
%разбавл – степень разбавления материала, %.
Пример. Определить толщину слоя, которую должен нанести маляр в процессе окраски. Сухой остаток лакокрасочного материала составляет 60%, необходимая толщина сухой пленки 120 мкм. Материал разбавляется на 10%.
Используя формулу 3, получаем
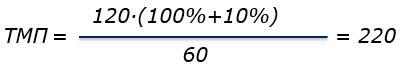
т.е. при разбавлении материала на 10% маляр должен наносить 220 мкм мокрой пленки, чтобы получить толщину сухого покрытия 120 мкм.
Калькулятор толщины мокрой пленки при разбавлении ЛКМ:
Введите толщину сухой пленки, мкм:
Введите объемный сухой остаток, %:
Укажите степень разбавления, %:
Толщина мокрой пленки, мкм, равна:
Формула 4. Расчет теоретического расхода.
О том, что такое теоретический расход, читайте по ссылке (Факт 1).
С помощью формулы можно определить теоретический расход для любой толщины сухой пленки.
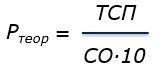
где,
Ртеор – теоретический расход, л/м2;
ТСП – толщина сухой пленки, мкм;
СО – сухой остаток по объему, %;
10 – безразмерный коэффициент, обеспечивающий переход от одних единиц измерения к другим (от мкм к л/м2).
Пример. Определить теоретический расход лакокрасочного материала с сухим остатком 60%, если необходимо получить покрытие с толщиной сухой пленки 150 мкм.
Используя формулу 4, получаем
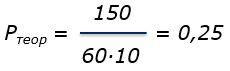
т.е. теоретический расход составит 0,25 л/м2 (или 250 мл/м2).
Калькулятор теоретического расхода:
Введите толщину сухой пленки, мкм:
Введите объемный сухой остаток, %:
Теоретический расход, лкв.м, равен:
Формула 5. Определение коэффициента потерь.

где,
Кпотерь – коэффициент потерь;
Потери(%) – совокупность всех потерь, возникающих при нанесении покрытия. Эту величину также называют фактор потерь.
О потерях, возникающих при нанесении покрытия, можно почитать здесь.
Пример. Потери при окраске составляют 40%. Чему равен коэффициент потерь?
Используя формулу 6, получаем

Калькулятор коэффициента потерь:
Введите сумму потерь при окраске, %:
Коэффициент потерь равен:
Формула 6. Определение практического расхода.
где,
Рпракт – практический расход, л/м2;
Ртеор – теоретический расход, л/м2;
Кпотерь – коэффициент потерь.
Практический и теоретический расходы могут также измеряться в литрах, если расчет был сделан для всей площади.
Пример. Вычислить практический расход, если теоретический расход равен 300 мл/м2, при коэффициенте потерь 1,43.
Используя формулу 5, получаем
300 * 1,43 = 429 (мл/м2)
С методикой расчета практического расхода по ВСН 447-84 можно ознакомиться по ссылке.
Калькулятор практического расхода:
Введите значение теоретического расхода, л/кв.м:
Введите сумму потерь при окраске, %:
(см. формула 5)
Введите коэффициент потерь:
Практический расход, л/кв.м, равен:
*Значение дробей вводятся с разделительным знаком “.”
Формула 7. Расчет потерь, связанных с шероховатостью поверхности.
Потери, связанные с шероховатостью поверхности, обусловлены необходимостью заполнения так называемого «мертвого объема». Информацию про «мертвый объем» см. по ссылке.
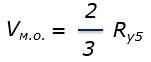
где
Vм.о. – величина «мертвого объема», мл/м2;
Ry5 – профиль (шероховатость) поверхности, мкм.
Пример. Определить дополнительное количество лакокрасочного материала, необходимое для компенсации шероховатости поверхности (заполнения «мертвого объема»). Профиль поверхности Ry5 (максимальное расстояние между пиками и впадинами шероховатости) составляет 75 мкм. Площадь окрашиваемой поверхности 500 м2.
Используя формулу 7, получаем
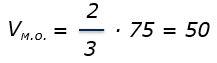
т.е. потери на шероховатость на 1 квадратном метре поверхности составят 50 мл/м2.
Для всей поверхности потери на шероховатость составят 50 мл/м2 * 500 м = 25000 мл (25 л) краски.
Формула 8. Расчет стоимости покрытия на 1 квадратный метр площади.
Для расчета стоимости покрытия на 1 квадратный метр площади поверхности необходимо умножить величину теоретического расхода на стоимость 1 литра лакокрасочного материала:
где,
R1 – стоимость покрытия на 1 квадратный метр площади поверхности (без учета потерь);
Ртеор – теоретический расход для заданной толщины сухой пленки, л/м2 (см. формулу 4 выше);
Rл – стоимость 1 л лакокрасочного материала.
Если вы хотите определить стоимость покрытия с учетом потерь, то формула будет иметь следующий вид:
где те же множители и
Кпотерь – коэффициент потерь (см. формула 5 выше).
Пример. Определить стоимость 1 квадратного метра площади для эпоксидной грунтовки, имеющей сухой остаток 60% и наносимой с заданной толщиной сухой пленки 80 мкм при величине потерь 30%. Стоимость грунтовки 700 руб/л.
Используя формулу 4, получаем
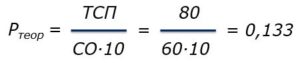
т.е. теоретический расход для данной грунтовки, нанесенной с толщиной 80 мкм, составляет 0,133 л/м2.
По формуле 5 определяем Кпотерь:
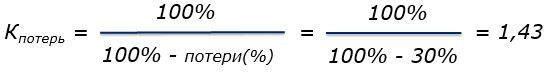
Стоимость 1 квадратного метра покрытия составит (с учетом потерь):
Калькулятор стоимости 1 квадратного метра покрытия:
Введите толщину сухой пленки, мкм:
Введите объемный сухой остаток, %:
Введите стоимость 1 литра ЛКМ, руб:
Введите сумму потерь, %:
Стоимость 1 квадратного метра покрытия с учетом потерь, руб, равна:
Во многих областях повседневной жизни геометрия помогает людям отвечать на важные вопросы и решать проблемы жизнедеятельности. По меньшей мере 4 тыс. лет назад эти знания уже использовались, например, в Древнем Египте для землеустройства. И сегодня многие профессии, от модельеров до архитекторов, нуждаются в базовых геометрических знаниях, чтобы знать, как рассчитать площадь.
Поверхность тела и ее площадь
Это мера того, сколько пространства находится внутри плоской формы. В общем случае площадь поверхности представляет собой сумму всех областей геометрических фигур, покрывающих поверхность объекта. Рассчитать площадь поверхности тела часто требуется в повседневной жизни, например, чтобы узнать сколько краски нужно купить, чтобы покрыть стену, или шифера для ремонта крыши дома.
Люди издавна научились определять площадь плоских геометрических фигур, используя метод сетки. Он заключается в том, что на измеряемую фигуру накладывают масштабированную сетку из простейших квадратов, например, 1х1 см. После чего можно легко рассчитать квадратную площадь, посчитав количество квадратов сетки внутри формы. В этом случае каждый квадрат сетки имеет ширину 1 см и высоту 1 см, и площадь этого квадрата сетки составляет один квадратный сантиметр.
Использование сетки для подсчета квадратов в форме — это очень простой способ определения площади, но он не может быть применен для определения площади сложных фигур. Площадь таких сложных объектов может быть рассчитана с использованием простых математических формул. Самые простые и наиболее часто используемые в жизни вычисления – это площади квадратов и прямоугольников, и надо знать, как рассчитать площадь в метрах.
Часто в реальности расчеты могут быть более сложными. Например, типичный план этажа комнаты может не состоять из простого прямоугольника или квадрата. В этом случае перед тем, как рассчитать общую площадь, нужно разделить измеряемую сложную поверхность на несколько простейших геометрических фигур.
Простой расчет прямоугольника
Если внимательно посмотреть вокруг, можно увидеть множество примеров прямоугольников. По определению, прямоугольник представляет собой четырехсторонний многоугольник, углы которой находятся под прямым углом, равным 90 градусам. Рассчитать площадь поверхности тела прямоугольника – простая математическая операция, которая наиболее часто применяется человеком в повседневной жизни. Почему важно знать формулу площади? Многие предметы и обстановка, окружающие человека, имеют прямоугольную форму: дом, стены, пол, крыша. И очень часто надо знать их площадь для строительства или ремонта.
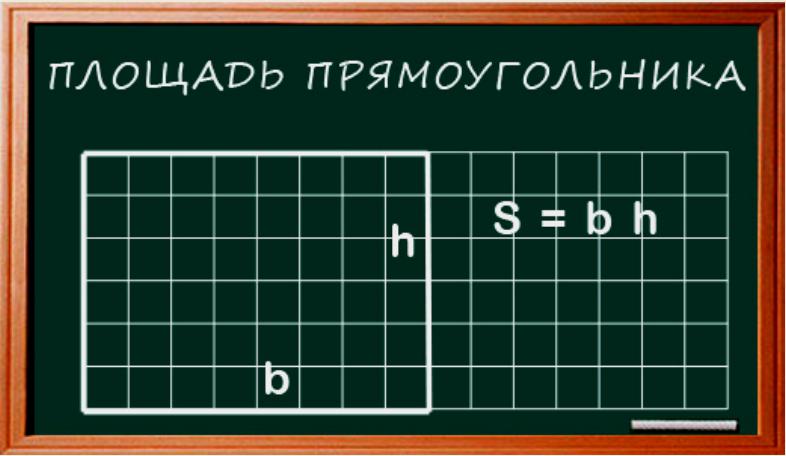
Если прямоугольник имеет длину b и ширину h, мы можем найти площадь S, умножив ширину на его длину. Следовательно: S=bxh.
Пример. Как рассчитать площадь прямоугольника, если известны сторона и ширина, например, длина 4 см и ширина 3 см, тогда: S=4х3=12.
Ответ: 12 см2.
Квадрат — разновидность прямоугольника с равными углами и сторонами.
S=bxb=b2.
Пример. Если квадрат имеет стороны 3 см, мы можем найти S, возведя в квадрат значение стороны. Следовательно, имеем: S=3х3=9.
Ответ: 9 см2.
Формулы параллелограмма
Параллелограмм является четырехсторонним многоугольником с двумя парами параллельных сторон одинаковой длины. По определению, прямоугольник также представляет собой тип параллелограмма, но с равными углами. Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных сторон, а расстояние между сторонами.
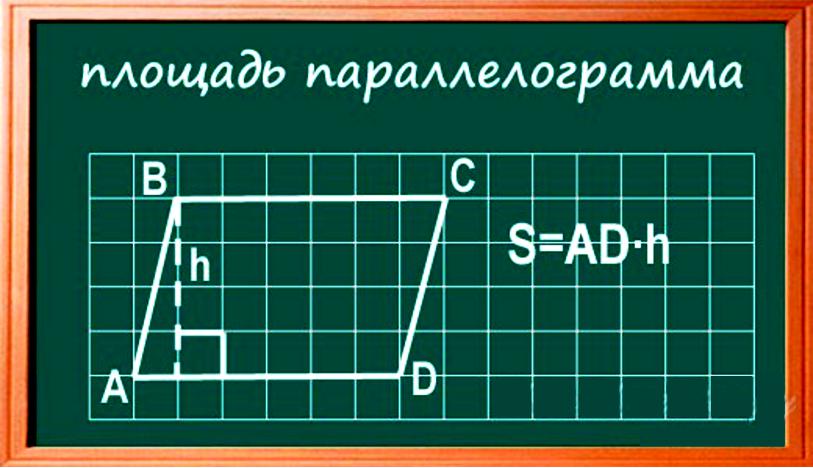
Из рисунка видно, что высота — это расстояние между двумя параллельными сторонами параллелограмма, расположенная под прямым углом между ними. S=ADxh. S=bxh, где AD=b – основание, h – высота.
Пример. Если параллелограмм имеет основание 3 см, а высоту 2 см, то площадь S равна произведению основания на высоту. Следовательно, имеем: S=3х2=6.
Ответ: 6 см2.
Основание трапеции
Рассмотрим, как правильно рассчитать площадь трапеции. Трапеция представляет собой четырехсторонний многоугольник с одной парой параллельных сторон. Если две непараллельные стороны имеют одинаковую длину, форма называется равнобедренной или обычной трапецией. Если непараллельные стороны имеют разную длину, она называется неравнобедренной. Однако, несмотря на эту дополнительную сложность в определении, площадь неправильной трапеции может быть рассчитана с помощью простой формулы.
Измерения для расчета площади трапеции:
- Выровнять прямой край транспортира вдоль более короткой из двух параллельных сторон.
- Использовать транспортир, чтобы провести линию перпендикулярно от основания трапеции вплоть до противоположной параллельной стороны.
- Измерить расстояние высоты с помощью линейки.
- Измерить длину более короткой параллельной стороны.
- Измерить длину более длинной параллельной стороны.
- Чтобы найти площадь трапеции, предварительно нужно вычислить среднюю величину двух ее параллельных сторон: (a+b)/2.
- Площадь равнобедренной (или любой) трапеции равна произведению средней длины основания и вершины на высоту.
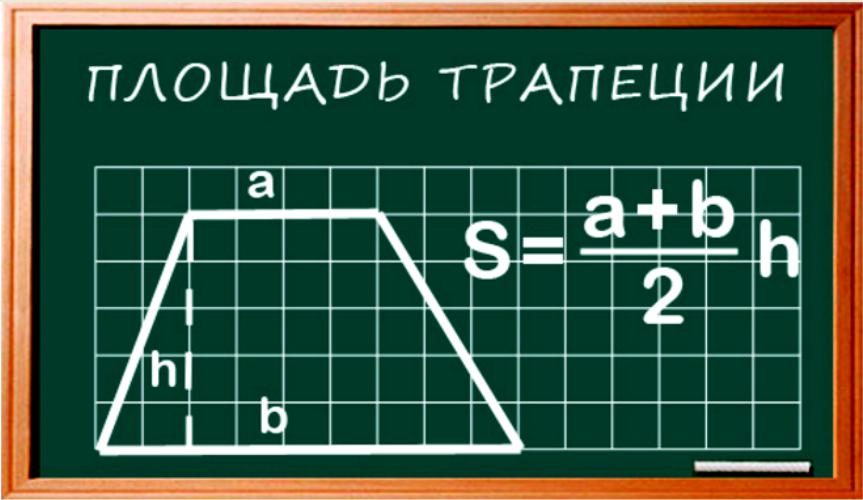
- Площадь трапеции: S=1/2×h×(a + b).
Нужно обратить внимание, что высота трапеции всегда перпендикулярна основанию, точно так же, как высота параллелограмма. Пример: a=3 см, b=5 см, h=4 см. S=4х(3+5)/2=16.
Ответ: 16 см2.
Виды треугольников
Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:
- Равносторонний треугольник имеет равные стороны и равные углы.
- Равнобедренный треугольник имеет две равные стороны и два равных угла.
- Разносторонний треугольник имеет три неравные стороны и три неравных угла.
- Прямоугольный треугольник имеет один прямой угол 90 градусов.
- Остроугольный треугольник имеет все углы меньше 90 градусов.
- Тупоугольный треугольник имеет один угол больше 90 градусов.
Площадь любого треугольника определяется по формулам.
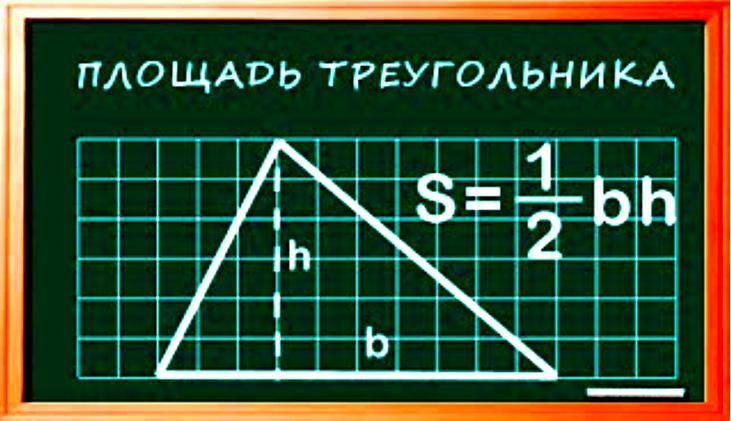
1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:
- S=1⁄2×a×h, где: h – высота, a – основание.
- S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α – угол между ними.
- S=p×r, где: p = (a+b+c) / 2 – полупериметр, a, b, c – три стороны, r – радиус круга.
Площадь равностороннего треугольника:
- S=a2х√3 ⁄4 , где a=b= c.
Площадь равнобедренного треугольника:
- S=1⁄4xbx√(4a2-b2).
2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:
- S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.
Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота – 10 см.
Решение: b=14 см, h=10 см, A=1⁄2х14х10=70
Ответ: 70 см2.
Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.
Решение: Площадь треугольника =1⁄2xaxbxsin 45.
Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)
Площадь =1⁄2×24,745=12,3725
Ответ: 12,3725 см2.
Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание – 12 м.
Решение: Площадь равнобедренного треугольника определяется:
A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48
Ответ: 48 м2.
Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).
Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.
Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50
Ответ: 35,50 м2.
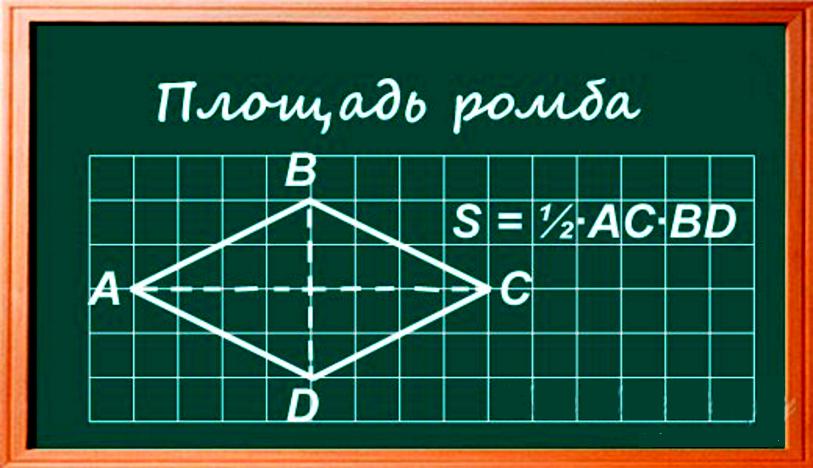
Измерение площади ромба
Ромб – особый вид параллелограмма, имеющий равные стороны и равные противоположные углы. Площадь ромба можно определить, используя три способа.
1. Метод высоты основания. Сначала выберите одну любую сторону в качестве базы, так как они имеют одинаковую длину. Затем определите высоту – перпендикулярное расстояние от выбранного основания до противоположной стороны.
- Площадь является произведением этих двух величин и определяется по формуле: S=a×h, где: S – площадь ромба, h – высота ромба, AB=BC=AD=DC=a – сторона ромба.
2. Метод диагоналей. Другая простая формула для площади ромба, когда известны длины диагоналей. Площадь составляет половину произведения диагоналей.
- В качестве формулы: S=1/2xACxBD, где: S – площадь ромба, AC– большая диагональ, BD – меньшая диагональ.
3. Использование тригонометрии. В тригонометрии, есть удобная формула, когда известны длина стороны и любой угол:
- S=a2×sin α, где: S – площадь ромба, B=BC=AD=DC= a – сторона ромба, α – острый угол, β – тупой угол.
Поверхность круга
Круг представляет собой форму, состоящую из замкнутой изогнутой линии. Каждая часть линии находится на одном и том же расстоянии от центра области, называемом радиусом. Еще с древних времен известно, как рассчитать площадь круга, если задан радиус. Площадь круга вычисляется по формуле S=πxr2, где: S – площадь круга,
π – число пи (3.1415), r – радиус круга.
Чтобы найти площадь круга, выполняем следующие действия. Запишите заданный радиус или диаметр величины как r или d соответственно. Как рассчитать площадь круга, если задан диаметр? Это совсем несложно, нужно вычислить радиус, разделив диаметр на 2, и перемножить данные с помощью калькулятора или вручную. Полученный ответ будет в квадратных единицах.
Задача: Найти площадь круга радиусом 10 см.
Решение: Мы имеем радиус окружности =10 см. Площадь круга =3,1416×10×10=314,16.
Ответ: 314,16 см2.
Найдите площадь круга диаметром 15 см.
Решение: У нас диаметр круга =15 см. Радиус =15/2=7,5 см. Площадь круга =3,14х7,5х7,5=176,625=176,63 (округлить до 2 знаков после запятой).
Ответ: 176,63 см2.
Простые геометрические фигуры крыш
Прежде чем выполнять кровельные работы, нужно знать, как рассчитать площадь крыши, чтобы определить, сколько материала потребуется. Его количество всегда нужно брать с запасом и добавлять не менее 10 процентов от общей площади кровли для учета отходов строительства.
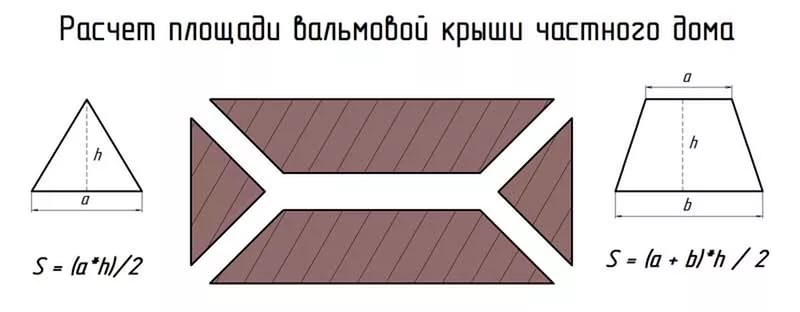
Предварительно перед расчетом схему кровли разбивают на простые геометрические фигуры, в нашем примере это две трапеции и два треугольника. Как рассчитать площадь крыши для трапециевидных элементов? Площадь вычисляется по следующей формуле: S=(a+b)xh/2, где: а – ширина нижнего свеса – 10 м, b – ширина по коньку – 7 м, h – высота – 5 м.
Для треугольных элементов применяется формула: S=axh/2, где: а – ширина ската по нижнему свесу – 7 м, h – высота ската – 3 м.
Порядок измерения:
- Измерить длину, ширину и высоту каждой геометрической фигуры крыши, включая ветровые окна. Эта информация может быть доступна в исходном плане здания дома или, если поверхность крыши относительно низкая и плоская, можно ее измерить самостоятельно. Если хозяин дома сам не может безопасно подняться на крышу, расчет можно выполнить по наружным замерам здания.
- Перемножить длину и ширину каждой треугольной или трапецеидальной плоскости в отдельности.
- Вычислить площадь для симметричных треугольных плоскостей, умножив длину основания треугольника (самую длинную сторону) на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
- Затем разделите итог на 2, чтобы получить результат в квадратных метрах. S=axh/2=7х3/2=10,5 м2.
- Вычислить площадь для трапеции, умножив ширину нижнего свеса плюс ширину по коньку на его высоту (расстояние от середины самой длинной стороны до противоположного угла).
- Затем разделить итог на 2, чтобы получить результат в квадратных метрах.
- Умножить площадь на 0,1, чтобы получить 10-процентную надбавку для запаса кровельного материала S=(a+b)xh/2=(10+7)*5/2= 42,5 м2.
- Сложить площади всех фигур вместе. S=10,5+10,5+42,5+42,5=106 м2.
- В результате получается общая площадь крыши 106 м2, с запасом – 116 м2.
Инструментальные обмеры дома
Для измерения площади дома потребуются инструменты, чтобы очень точно выполнить расчеты, которые могут стать основой для проведения ремонтных работ, купли-продажи или страхования дома. Перед тем как рассчитать площадь, нужно взять рулетку, карандаш и блокнот, на котором нарисовать простейшую схему плана дома. Ее можно взять из паспорта застройщика или других проектных документов. С последним источником нужно быть внимательным, указанные цифры могут быть не всегда точными, например, какие-то ремонтные работы могут быть в них не учтены. Поэтому правильнее будет выполнить измерение площади самостоятельно.
Как рассчитать площадь дома вручную? Если нужно измерять площадь пола вручную, лучше всего измерить внешние стены, не забывая различных строительных углублений, подсобных помещений, верхних этажей, отдельных зданий или гаражей. Когда сделаны простые основные измерения, площадь рассчитывается путем умножения длины дома на ширину.
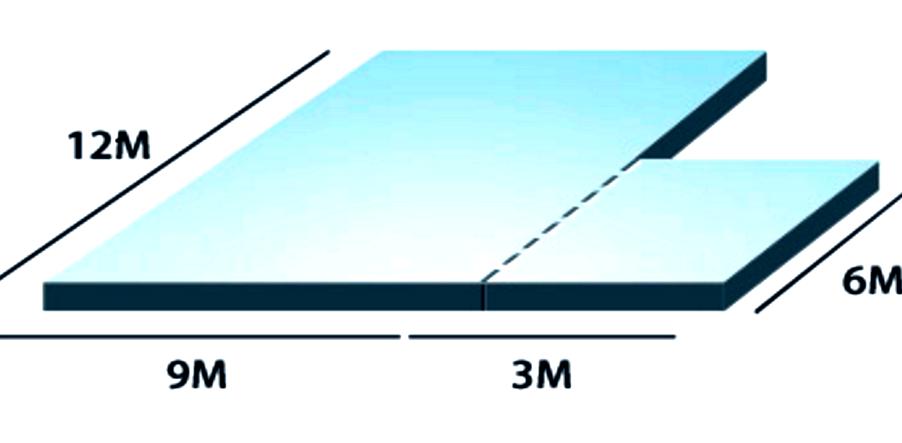
В зависимости от формы плана строительства может понадобится разбить его на простейшие геометрические фигуры. В этом примере дом имеет 9 метров на 12 метров, давая нам 108 квадратных метров. Гараж составляет 6 метров на 3 метра, что составляет 18 квадратных метров, общая площадь – 126 квадратных метров.
Предремонтные замеры пола
Как рассчитать площадь пола перед проведением ремонтных работ, например, замены линолеума или покраски? Для квадратного или прямоугольного помещения сначала нужно будет измерить длину и ширину комнаты. Затем умножить длину и ширину, получим длина x ширина = площадь. Таким образом, если комната имеет размеры 3 метра в ширину и 5 метров в длину, общая площадь составит 15 квадратных метров.
Это измерение можно использовать при расчете необходимого количества плиточного раствора, герметика, линолеума, которые владелец планирует использовать для своего проекта. Чтобы рассчитать площадь для подбора материалов, как правило, нужно добавить 10% коэффициент запаса: просто умножьте площадь на 1,1, а затем округлите до целого значения.
В примере, когда общая площадь составляет 15 м2, нужно будет заказать дополнительное количество плитки и раствора для 16,5 квадратных метра. Если комната не прямоугольная, нужно разделить ее на две или более элементарных геометрических фигур, чтобы рассчитать общую площадь.
Калькулятор для неправильной фигуры
Очень часто измеряемое пространство имеет очень сложную форму, которую не всегда удается разбить на простые элементы.
Чтобы просто определить такую площадь, стоит воспользоваться интернет-приложением SketchAndCalc. Он является калькулятором площади неправильных фигур для любой формы изображения. Это единственный калькулятор площади, способный вычислять по загруженным изображениям, он имеет уникальную функцию, которая позволяет пользователю установить масштаб чертежа любого изображения, прежде чем рисовать периметр. Таким образом, углы или кривые неправильной фигуры легко вычисляются.
Проще говоря, если есть изображение, которое можно загрузить, или адрес карты для поиска, можете рассчитать площадь неправильной фигуры независимо от того, насколько сложна она, просто рисуя периметр области. Калькулятор может даже суммировать вычисления нескольких площадей вместе путем рисования слоев. После вычисления первой области можно добавить новый слой чертежа, что позволяет выполнить неограниченное количество вычислений области.
Результаты калькулятора площади отображаются в дюймах и метрах, увеличивая его полезность и устраняя необходимость преобразования. Это наряду с точными инструментами рисования и увеличения гарантирует, что площади каждой неправильной фигуры рассчитываются точно. Он также может размещать правильные формы многоугольника с фиксированными углами и точными линиями.
Инструмент с ограниченным рисунком привязывается к общим углам, а линию длины можно редактировать вручную с помощью клавиатуры. Приложение полезно, если измеряемая область имеет прямую сторону или длину. Еще одной уникальной особенностью SketchAndCalc TM является то, что он имеет продвинутый инструмент рисования кривой для неправильных фигур. Некоторые приложения калькулятора области позволяют осуществлять поиск по карте.
SketchAndCalc делает это очень точно, используя поиск по долготе и широте. Независимо от того, находится ли замеряемая область на сельскохозяйственных землях или в море, пользователь будет тратить меньше времени на поиск и больше времени на расчет площади территории. Это универсальная утилита, применяемая во многих отраслях промышленности, в строительстве, садоводстве. Она используется и энтузиастами по благоустройству своего дома и придомовой территории. Калькулятор ландшафта или калькулятор земельной площади также нашел своих пользователей среди землеустроителей. Теперь они знают, как рассчитать площадь участка легко и быстро.
Однако, помимо этих общих применений, многие работающие в области образования, медицины, науки и исследований нуждаются в расчете площади неправильных форм, таких как клеточные мембраны или другие объекты, обнаруженные в биологии, и с удовольствием пользуются этим приложением.
Для применения математики в повседневной жизни недостаточно уметь считать один плюс один. Существенным аспектом окружающей среды являются геометрические структуры, то есть представление повседневных предметов в прямоугольной, квадратной, круглой или треугольной форме. И надо уметь рассчитать нужную площадь.
Кроме того, геометрические фигуры используются и при построении диаграмм, схем, презентаций. Вот почему так важно уметь делать различные расчеты, в том числе и вычисление площади.
Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-
1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-
3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-
4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-
3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-
4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-
5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-
6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-
3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-
4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-
5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-
6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-
3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-
4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-
5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-
3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-
4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-
5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-
3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-
4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-
5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-
3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-
4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-
5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-
6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 69 399 раз.
Была ли эта статья полезной?
Библиографическое описание:
Данилко, В. А. Расчет площади поверхности сложных деталей / В. А. Данилко. — Текст : непосредственный // Молодой ученый. — 2022. — № 16 (411). — С. 4-7. — URL: https://moluch.ru/archive/411/90473/ (дата обращения: 15.05.2023).
В работе осуществлен анализ способов измерения площади поверхности различных фигур. Представлен авторский метод расчета площади поверхности фигуры как площади поверхности вращения с предварительным аналитическим описанием контура фигуры.
Ключевые слова:площадь поверхности вращения, интегралы, тела сложной формы.
Для решения определённого рода задач гальваники и металлообработки требуется знать площадь поверхности тела, с которым придётся работать. Однако, не всегда получается быстро осуществить вычисления, ввиду того что некоторые детали имеют нетипичную, сложную форму. Поэтому возникает необходимость найти максимально простой, удобный и экономически выгодный способ для определения этой площади.
Существуют различные подходы к решению данной проблемы. Например, Яскеляин Б. В. и Череднеченко Т. Ф. предложили способ измерения площади поверхности тела, при котором на тело наносят плёнку из материала постоянной толщины, обладающего свойством гигроскопичности, предварительно покрывая поверхность смачивающим составом. Площадь поверхности при этом находят из её геометрической площади с учётом отношения приращения длины плёнки к геометрической длине поверхности [1].
Другой способ был предложен В. Г. Вохмяниным [2]. Он заключался в измерении веса двух тел, простого эталонного (образцового) и измеряемого (сложной формы). Сначала в обычных условиях измеряли вес тел, а затем их охлаждали до температуры конденсации воды и снова проводили взвешивание. Площадь вычисляли, находя частное от деления изменения веса измеряемого тела на изменение веса эталонного. При этом полученное число — это площадь поверхности, выраженная в единицах эталонного тела. Данный способ по сравнению с аналогичными отличается высокой производительностью, простотой, низкой стоимостью и высокой точностью.
Способ измерения площади поверхности, предложенный В. С. Аксельродом и Г. М. Рохлиной [3] позволяет измерить площадь плоской детали сложной формы и основывается на измерении емкости конденсатора. Площадь изделия равна произведению отношения емкости конденсаторов, одной из обкладок которых является измеряемое изделие или эталонное изделие.
Е. Д. Гражданников предложил способ определения величины поверхности твёрдых тел, основанный на измерении сокращения времён спин-решёточной и спин-спиновой магнитной релаксации ядер в слое жидкости, покрывающей поверхность твёрдой фазы [4]. Данный способ предназначен для определения поверхности широкого круга нанесённых веществ и носителей, причём измерения могут быть проведены непосредственно в процессе реакции. Для определения по этому способу площади поверхности нужен эталон изделия, площадь поверхности которого можно измерить другим способом.
Б. Д. Разуваева и К. С. Лыткин, исследуя методы определения площади поверхности сложных изделий, пришли к выводу о том, что метод растворения достаточно надёжен в измерении площади поверхности детали [5]. Он основан на том, что количество металла, растворяющегося в жидкости за единицу времени пропорционально величине поверхности металла. Для определения по этому способу площади поверхности требуется эталонное изделие с известной площадью поверхности.
Каждый из представленных способов предполагает осуществление определенных химические операции с изделием, а также зачастую наличие эталонного тела. В то же время, обратившись к математическому инструментарию, можно осуществить расчет площади поверхности тела аналитически с меньшими затратами.
Например, если изделие обладает центральной симметрией, то его можно рассматривать, как тело вращения. Тогда площадь его поверхности можно рассчитать, как площадь поверхности вращения по формуле:
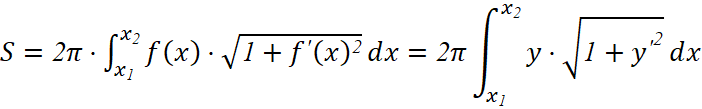
где — аналитическая функция, описывающая контур изделия,
x1 и x2 — границы, в которых задана функция.
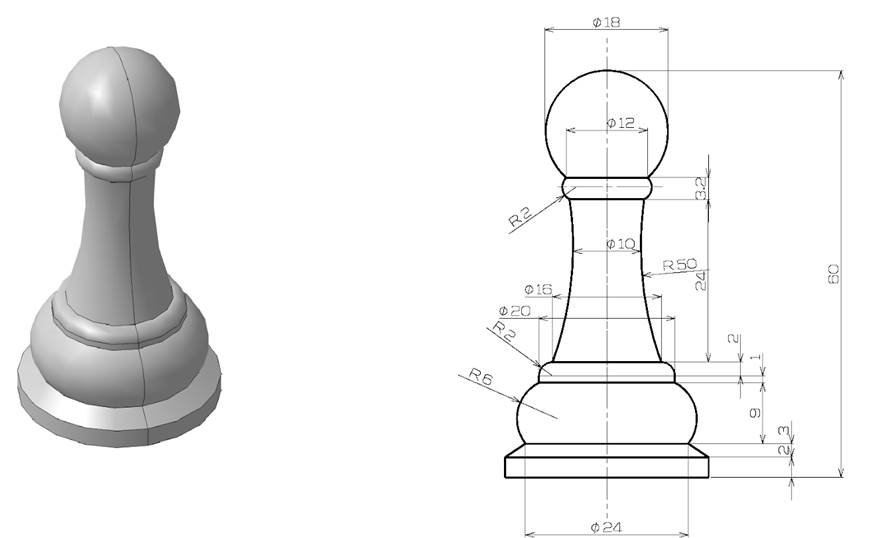
Рассмотрим более подробное применение данного способа на частном примере. Определим площадь поверхности шахматной пешки (рис.1.).
Рис. 1. Шахматная пешка
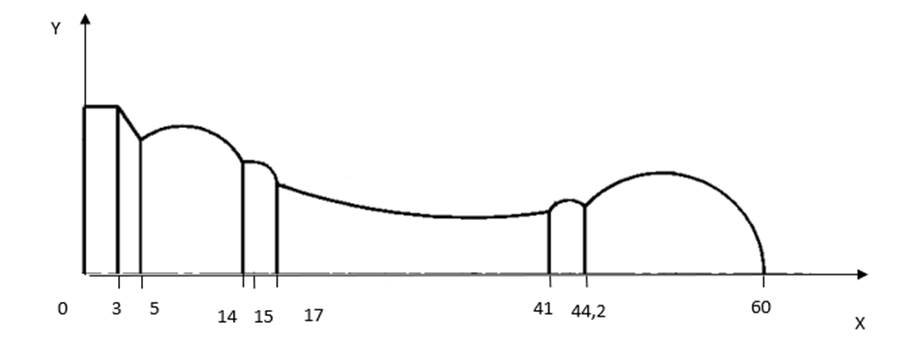
Поместим контур исследуемого тела в декартову систему координат XOY (рис.2.).
Разные участки контура можно задать различными функциями вида . Так можно выделить 8 таких функций, задающих контур боковой поверхности, для 8 участков. Так как ищем площадь боковой поверхности, то площадь основания фигуры не рассматриваем.
1) При — функция —
2) При — функция —
3) При — функция —
4) При — функция —
5) При — функция —
6) При — функция —
7) При — функция —
8) При — функция —
Рис. 2. Контур пешки в системе координат
Найдя данные функции, можно вычислить площадь поверхности этих участков. В ситуациях, когда функция имеет вид , площадь поверхности участка будет вычисляться также как площадь поверхности цилиндра, по формуле
, но в данном случае —
, а
, где
и
— координаты
начала и конца участка соответственно.
Так, для первого и четвёртого участков площадь поверхности равна соответственно: ,
.
Для других участков будет использоваться формула вычисления площади поверхности вращения вдоль оси OX.
Так вычисляем площадь поверхности второго участка:
Далее, аналогично, получаем значения площади поверхности остальных участков:
,
,
,
,
.
Конечную площадь поверхности находим как сумму площадей поверхностей участков:
.
Данный способ может быть использован для определения площади поверхности тел наряду с ранее упомянутыми. Он будет особенно удобен в случае, если изделие имеет центральную симметрию. Метод отличается точностью и экономической выгодой.
Литература:
1. Яскеляин Б. В., Чередненко Т. Ф. Способ измерения площади поверхности тела сложной формы [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://rusneb.ru/catalog/000224_000128_0093005691_19950720_A_RU/ (дата обращения 22.02.2022)
2. Вохмянин В. Г. Способ В. Г. Вохмянина измерения площади поверхности тела сложной формы [Электронный ресурс] // FREEPATENT: патентный поиск в РФ — URL: https://www.freepatent.ru/patents/2040776 (дата обращения 22.02.2022)
3. Аксельрод В. С., Рохлина Г. М. Способ определения площади поверхности электропроводящих изделий [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000273447_19700615_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
4. Гражданников Е. Д. Способ определения величины поверхности твёрдых тел [Электронный ресурс] // НЭБ: Национальная электронная библиотека — URL: https://viewer.rusneb.ru/ru/000224_000128_0000176457_19651102_A1_SU?page=1&rotate=0&theme=white (дата обращения 22.02.2022)
5. Разуваева Б. Д., Лыткин К. С. Экспресс-метод измерения криволинейных и фактурных поверхностей [Электронный ресурс] // Драгоценные материалы — URL: http://jewelpreciousmetal.ru/technology_other_surfacearea.php ((дата обращения 22.02.2022)
Основные термины (генерируются автоматически): площадь поверхности, сложная форма, функция, площадь поверхности вращения, XOY, боковая поверхность, центральная симметрия, шахматная пешка, эталонное изделие, эталонное тело.