как найти основание трапеции, зная площадь, другое основание и высоту??
Назипа Кумыкбаева
Знаток
(285),
на голосовании
10 лет назад
Голосование за лучший ответ
Олеся Сереброва
Просветленный
(26866)
10 лет назад
площадь=(большее основание+меньшее основание): 2*на высоту.
S=1/2(а+в) h
а=(2S / h ) – в
Похожие вопросы

{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
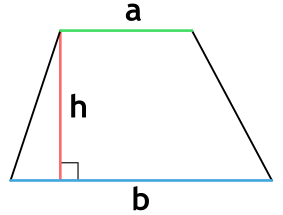
{S = dfrac{1}{2} (a + b) cdot h}
a и b – основания трапеции
h – высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
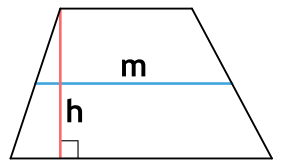
{S = m cdot h}
m – средняя линия трапеции
h – высота трапеции
Площадь трапеции через диагонали и среднюю линию
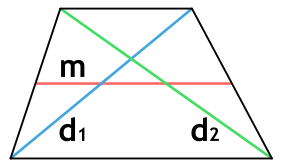
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 – диагонали трапеции
m – средняя линия трапеции
Площадь трапеции через 4 стороны
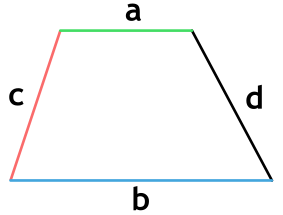
{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}
a, b, c и d – стороны трапеции
Площадь трапеции через диагонали и угол между ними
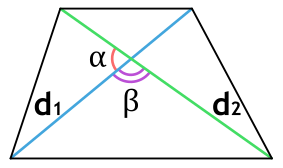
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 – диагонали трапеции
α или β – угол между диагоналями трапеции
Площадь трапеции через основания и углы при основании
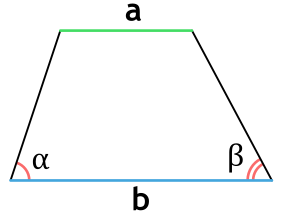
{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b – основания трапеции
α или β – прилежащие к основанию трапеции углы
Площадь трапеции через площади треугольников
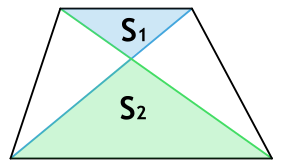
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 – площади образованных пересечением диагоналей трапеции треугольников
Площадь трапеции через диагонали и высоту
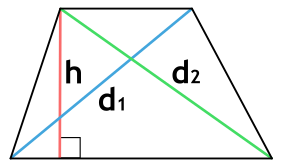
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 – диагонали трапеции
h – высота трапеции
Площадь трапеции через радиус вписанной окружности и основания

{S = (a+b)cdot r}
a и b – основания трапеции
r – радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 – перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
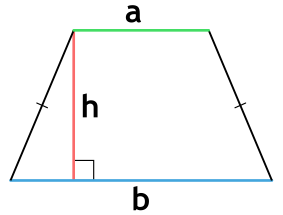
{S = dfrac{a+b}{2} cdot h}
a и b – основания равнобедренной трапеции
h – высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a – верхнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
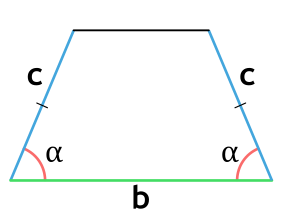
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b – нижнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащий к нижнему основанию трапеции угол
Площадь равнобедренной трапеции через основания и угол
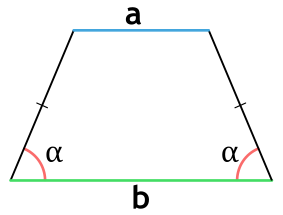
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b – основания равнобедренной трапеции
α – прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
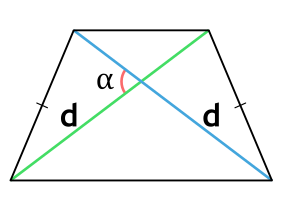
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a – диагональ равнобедренной трапеции
α – угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
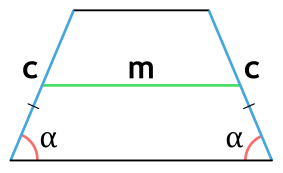
{S = m cdot c cdot sin(alpha)}
m – средняя линия равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}
r – радиус вписанной окружности
α – угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}
h – высота равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
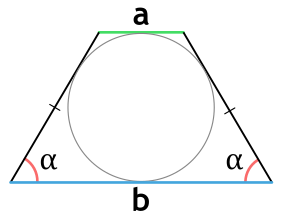
{S = dfrac{a cdot b}{sin(alpha)}}
a и b – основания равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
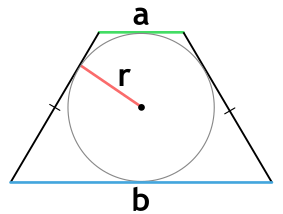
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b – основания равнобедренной трапеции
r – радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b – основания равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
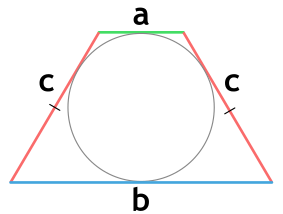
{S = c cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
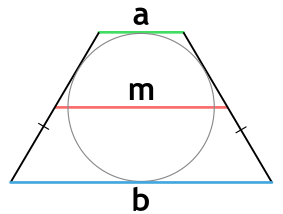
{S = m cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
m – средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Немного истории
Для начала вспомним, что такое трапеция.
Трапеция – это фигура, у которой две стороны параллельны, а две другие не параллельны.
Трапеция – одна из самых «загадочных» фигур школьной планиметрии. Она обладает некоторыми признаками параллелограмма, но сильно отличается от него разнообразием форм. Различают трапеции прямоугольные, равнобедренные, общего вида. Одно это разнообразие форм уже подозрительно.
На практике форма трапеции встречается более часто, чем прямоугольники, квадраты или параллелограммы. Поэтому нахождение площади для трапеции – более актуальная задача, чем для других фигур.
Покажем вам несколько формул, как найти площадь трапеции. Каждая формула площади трапеции подходит для решения соответствующего круга задач.
Основные формулы
- Площадь трапеции через её основания и высоту:
- Площадь трапеции через ее высоту и среднюю линию:
- Площадь трапеции через ее диагонали и угол между ними:
Давайте разберем задачу, иллюстрирующую применение одной из этих формул:
Задача
Основания трапеции общего вида равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Решение
Изобразим трапецию общего вида и введём обозначения, как показано на рисунке ниже.
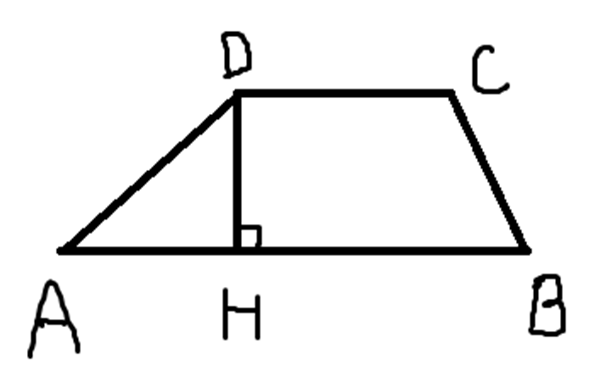
По условию задачи, один из углов трапеции равен 150°. Этим углом может быть угол ADC. По свойству трапеции, также как и параллелограмма, сумма углов, прилежащих к боковой стороне, равна 180°. Отсюда несложно вычислить, что второй угол, DAН, прилежащий к этой боковой стороне, будет равен 30°.
Отрезком DH на рисунке является высота трапеции. Найдем эту высоту из прямоугольного треугольника AHD, где DH является противолежащим катетом, AD является гипотенузой:
Воспользуемся формулой (1) площади трапеции через ее основания и высоту. По этой формуле площадь трапеции равна произведению полусуммы оснований на ее высоту:
Ответ: 42
Итак, зная длины двух оснований трапеции и ее высоту, вычислить ее площадь достаточно просто. Сложности могут быть, если нам не известны один из требуемых элементов, например, высота трапеции. Но здесь на помощь приходят знания свойств трапеций и соотношений в прямоугольном треугольнике.
Часто задаваемые вопросы
✅ Что такое трапеция?
↪ Трапеция – это четырехугольник, у которого две противоположные стороны параллельны, а две другие стороны непараллельны.
✅ Как найти площадь трапеции?
↪ Площадь трапеции можно найти по формуле: S = (a + b) * h / 2, где a и b – длины оснований трапеции, а h – высота трапеции, опущенная на основание.
✅ Что происходит с площадью трапеции, если увеличить одно из оснований?
↪ Если увеличить одно из оснований трапеции, то ее площадь увеличится, при этом высота трапеции останется неизменной. Если увеличить оба основания на одинаковую величину, то площадь трапеции увеличится в два раза.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Щебетун Виктор
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На данной странице вы можете ознакомиться со всеми формулами для нахождения площади трапеции, как обычной, так и равнобедренной или неправильной. Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.
Площадь трапеции по высоте и двум основаниям

Формула нахождения площади трапеции по высоте и двум основаниям:
$S = frac{a + b}{2} cdot h$,
$S$ – площадь трапеции, где
$a$ – малое основание трапеции,
$b$ – большее основание трапеции,
$h$ – высота трапеции.
Площадь трапеции по высоте и средней линии

Формула нахождения площади трапеции по высоте и средней линии:
$S = m cdot h$, где
$S$ – площадь трапеции,
$m$ – средняя линия,
$h$ – высота трапеции.
Ну а сейчас рассмотрим на примере, как найти площадь трапеции по высоте и средней линии. Быстро и без лишних действий самостоятельно найдем возможные ошибки в своем решении с помощью данного калькулятора и сверим с ним ответы.
Пример 1
Дано: высота $h = 7$ см, средняя линия $m = 8$ см.
Найти: площадь трапеции $S$.
Решение:
$S = 8 cdot 7 = 56$
Площадь трапеции по четырём сторонам

Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
$S = frac{a + b}{2} cdot sqrt{c^2 – (frac{(b – a)^2 + c^2 – d^2}{2 cdot (b – a)})^2}$, где
$S$ – площадь трапеции,
$a$ – малое основание,
$b$ – большее основание,
$c, d$ – боковые стороны.
Площадь трапеции по диагонали и углу между диагоналями

Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =frac12 cdot d1 cdot d2 cdot sin (α)$, где
$S$ – площадь трапеции,
$d1$ – первая диагональ,
$d2$ – вторая диагональ,
$α$ – угол между диагоналями.
Площадь трапеции через ее основание и углы

Формула нахождения площади трапеции через ее основание и углы при основании:
$S = frac12 cdot (b^2 – g^2) cdot frac{sin (α) cdot sin (γ)}{sin (α + γ)}$, где
$S$ – площадь трапеции,
$b$ – большее основание,
$g$ – малое основание,
$α$ – первый угол при основании,
$γ$ – второй угол при основании.
Площадь равнобедренной трапеции через стороны

Формула нахождения площади равнобедренной трапеции через ее стороны:
$S = frac{AB + CD}{2} cdot sqrt{AC^2 – frac{(CD – AB)^2}{4}}$, где
$S$ – площадь трапеции,
$AB$ – малое основание,
$CD$ – большее основание,
$AC = DB$ – боковая сторона.
Площадь равнобедренной трапеции через малое основание

Формула нахождения площади равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании
$S = c cdot sin (α) cdot (a + c cdot cos (α))$, где
$S$ – площадь трапеции,
$a$ – малое основание,
$c$ – боковая сторона
$α$ – угол.
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол

$S = c cdot sin (α) cdot (b – c cdot cos (α))$, где
$S$ – площадь трапеции,
$α$ – угол при большем основании,
$c$ – боковая сторона,
$b$ – большее основание.
Площадь равнобедренной трапеции через основания и угол при основании

Формула нахождения площади равнобедренной трапеции через основания и угол при основании:
$S = frac{(b^2 – a^2) cdot mathrm{tg}(α)}{4}$, где
$S$ – площадь трапеции,
$b$ – большее основание,
$a$ – малое основание,
$α$ – угол при основании.
Площадь равнобедренной трапеции через диагонали и угол между диагоналями

Формула нахождения площади равнобедренной трапеции через диагонали и угол между диагоналями:
$S = frac12 cdot D^2 cdot sin (α)$, где
$S$ – площадь трапеции,
$D$ – диагональ трапеции,
$α$ – угол между диагоналями.
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
$S = m cdot c cdot sin (α)$, где
$S$ – площадь трапеции,
$m$ – средняя линия трапеции,
$c$ – боковая сторона,
$α$ – угол при основании.
Чтобы проверить правильность своего решения и ответа или найти какие-либо ошибки в действиях необходимо решить пример данной задачи. Для наглядности выполним пример задачи на нахождение равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании.
Пример 2
Дано: средняя линия $m = 8$ см, боковая сторона $c = 10$ см, угол при основании $α = 30°$.
Найти: площадь трапеции $S$.
Решение:
$S = 8 cdot 10 cdot sin (30) = 80 cdot frac12 = 40$ см$^2$.
Ответ: $S = 40$ см$^2$
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами

Формула нахождения площади равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами:
$S = frac{4 cdot R^2}{sin (α)}$, где
$S$ – площадь трапеции,
$R$ – радиус вписанной окружности,
$α$ – угол между сторонами.
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности

Формула нахождения площади равнобедренной трапеции через два ее основания и радиус вписанной окружности:
$S = r cdot (a + b)$, где
$S$ – площадь трапеции,
$r$ – радиус вписанной окружности,
$a$ – малое основание,
$b$ – большее основание
Площадь равнобедренной трапеции через ее основания и угол при большем основании

Формула нахождения площади равнобедренной трапеции через ее основания и угол при большем основании:
$S = frac {d cdot b} {sin (α)}$, где
$S$ – площадь трапеции,
$d$ – малое основание,
$b$ – большее основание,
$α$ – угол при большем основании.
Площадь равнобедренной трапеции через основания и среднюю линию

Формула нахождения площади равнобедренной трапеции через основания и среднюю линию:
$S = m cdot sqrt {a cdot b}$, где
$S$ – площадь трапеции,
$m$ – средняя линия,
$a$ – малое основание,
$b$ – большее основание.
Для того, чтобы сверить свой ответ и решение с онлайн-калькулятором и найти какие-либо свои ошибки, будет полезно рассмотреть пример решения данной задачи на нахождение площади равнобедренной трапеции через заданные основания и среднюю линию.
Пример 3
Дано: малое основание $a = 5$ cм, большее основание $b = 8$ см, $m = 6$ см.
Найти: площадь трапеции $S$.
Решение:
$S = 6 cdot sqrt(5 cdot 8)=37,95$ см$^2$
Ответ:
$S = 37,95$ см$^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
