Загрузить PDF
Загрузить PDF
Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.
-
1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
-
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
-
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).[1]
- Площадь = сторона х сторона, или S = a2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a2 = 4 х 4 = 16 квадратных сантиметров.
-
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
-
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
-
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама
-
1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
-
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
-
3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
-
4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама
-
1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
-
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
-
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама
-
1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
-
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
-
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
-
Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
-
- = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
- = 84 × sin (80) + 22,5 × sin (110)
- = 84 × 0,984 + 22,5 × 0,939
- = 82,66 + 21,13 = 103,79 квадратных сантиметров.
-
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама
Советы
-
Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.[5]
- Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.
Реклама
Об этой статье
Эту страницу просматривали 439 694 раза.
Была ли эта статья полезной?
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
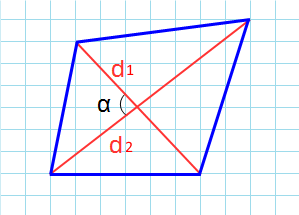
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 – диагонали; α – угол между диагоналями.
Через стороны и противолежащие углы
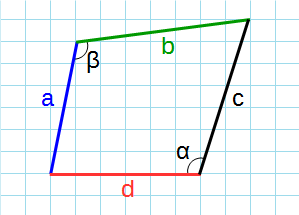
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Площадь вписанного четырехугольника в окружность
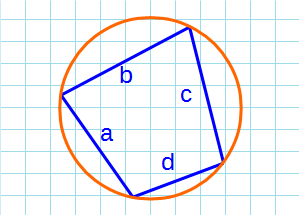
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
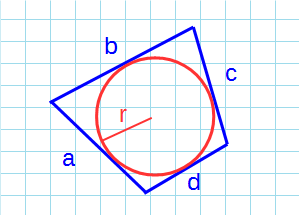
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
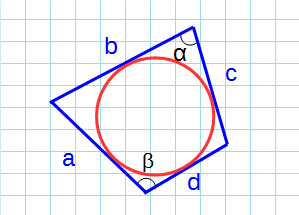
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Download Article
Quickly calculate the area of any 4-sided figure, including squares, rectangles, parallelograms, kites, and rhombuses
Download Article
- Area of Trapezoid and Kite Cheat Sheets
- Square
- Rectangle
- Parallelogram
- Trapezoid
- Rhombus
- Kite
- Any Quadrilateral Shape
- Q&A
- Tips
|
|
|
|
|
|
|
|
|
If you’re stuck on your geometry homework trying to figure out the area of a quadrilateral, you’ve come to the right place! Remember—the “area” of a shape is just how much 2-dimensional space it takes up. For some quadrilaterals, there’s a handy formula you can use to calculate the area. But what if all the sides are different? Just divide it into triangles! Read on to follow along with some examples and see how this works.
Things You Should Know
Area of Square, Rectangle, and Rhombus Cheat Sheets
Area of Trapezoid and Kite Cheat Sheets
-
Use
to find the area of a square. In the formula, “s” is the length of one side. Since all sides are equal, you only need the length of one of them to quickly find the area of any square. Then, express the area in units squared.
Advertisement
-
Use the formula
to find the area of a rectangle. Since a rectangle has sides of 2 different lengths, you multiply one value by the other to find out how much space the rectangle covers. Just get the length of one of the short sides and one of the long sides.
-
Find the area of a parallelogram with
. A parallelogram has 2 parallel sides—those are the bases (b). The height (h) is the distance from one base to the other. Multiply those 2 values together and you’ve got the area of a parallelogram.[1]
Advertisement
-
Use
to calculate a trapezoid’s area. Since the 2 bases (b) of a trapezoid aren’t the same length, the average is used for the area of this shape. Once you have the average length of the two bases, multiply that by the height (h)—the distance between the two bases—to easily find the area of a trapezoid.[2]
Advertisement
-
Find the area of a kite with
. A kite’s orientation can throw you off because your “diagonal” lines (d1 and d2) might not look diagonal at all—they might actually be vertical and horizontal. But as long as they’re connecting opposing corners, they’re still called diagonals. Multiply them together and then divide by
to get your area.
-
1
Divide the quadrilateral into 2 triangles. If you draw a diagonal line from one corner to the other, you create 2 triangles within the quadrilateral. The 2 triangles might not be the same size, but they share a common base—the diagonal that divides the quadrilateral.[4]
- If you’re working on a homework problem, the diagonal line might already be drawn for you. In fact, if you have a quadrilateral with a diagonal line, that’s a pretty big clue that you’ll use triangles to find the area.
-
2
Get the measurements for the base and heights of your triangles. To find the area of a triangle, you need to know the size of the base (b) and the height (h). Your diagonal line is serving as the base of your triangles, so they’ll both have the same measurement for the base. They might not be the same height, though, depending on the quadrilateral. The height isn’t the length of a side (unless you’re working with a right triangle). It’s the length from the base to the top point of the triangle.[5]
- If you’re working a problem for homework and you’re not given any way to measure these values, you can’t use triangles to find the area of that quadrilateral.
-
3
Find the area of each triangle. Recall that the formula for the area of a triangle is
. All you have to do is plug in the measurements you got for the base and the height, then simplify the equation to find the area of each triangle.[6]
-
4
Add the areas of the 2 triangles together to get the area of the quadrilateral. Since you originally divided your quadrilateral into 2 triangles, all you have to do is add those 2 areas together and you’ll have the total area of the quadrilateral. You could also think of the area of one of the triangles as being half the area of the quadrilateral.[7]
Advertisement
Add New Question
-
Question
Could I divide the quadrilateral into two triangles, find the area of each, and add them to find the area of the quadrilateral?
Yes. If you know the base and height of each triangle, you can just add the two areas together. It’s not always possible, however, to know the bases and heights.
-
Question
How do I calculate the area of a parallelogram?
Calculate as follows: Area = base multiplied by height.
-
Question
How would I know the angle for quadrilateral?
Assuming you’re not given the angle(s), you either have to use a protractor or analyze the quadrilateral and use trigonometry.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Since a square is also a rhombus, if you only know the measurement of a diagonal, you can also find the area of a square using the rhombus formula.
Advertisement
References
About This Article
Article SummaryX
Before you can find the area of a regular quadrilateral, start by identifying the type of quadrilateral in the problem, since different types of quadrilaterals require different equations. For rectangles or rhombuses, simply multiply the base by the height to find the area. For squares, multiply one side by itself to get the area. If you have a parallelogram, multiply the diagonals and divide by 2 to get the area. To find the area of a trapezoid, add the base and the height together, and divide that number by 2 times the height. If you want to find the area of an irregular quadrilateral, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,698,488 times.
Reader Success Stories
-
“Great, but I would be glad if you could find the angles for any quadrangular with given sides. But you put some…” more
Did this article help you?
Находить площадь фигуры можно не только по формулам, но чаще всего мы используем именно их. Первые формулы площади нам дают в 3 – 4 классах и это четырёхугольники – прямоугольник и квадрат. К сожалению, некоторые и эти формулы к экзамену не знают. Ну а мы рассмотрим задачу для решения которой будем использовать ещё более сложную формулу. Формулу площади произвольного (т.е. любого) четырёхугольника. Начнём?
Условие
Рассуждение
- В условии ни слова не сказано про диагонали;
- Точки M, F и K – середины сторон AB, AD и DC, а значит если их соединить, тополучатся отрезки соединяющие середины сторон (масло масляное);
- Отрезки FM и KF – известны, угол между ними ∠MFK – тоже, и это похоже на теорему косинусов, но MK – кажется бесполезным в решении отрезком.
Решение
Нарисуем произвольный четырёхугольник, то есть так, чтоб он не был похож ни на параллелограммы, ни на трапеции. И отметим середины сторон, известные отрезки и угол:
Отрезки MF и FK – соединяют середины сторон, что очень напоминает средние линии. Рассмотреть их помогут диагонали.
Теперь видно, что MF – средняя линия в ∆ABD, а FK – в ∆ACD.
Рассмотрим ∆ABD:
По свойству средне линии треугольника (равна половине параллельной ей стороны), можно найти диагональ BD, будет в 2 раза больше MF:
BD = 12√3 см.
Аналогично найдём диагональ AC через ∆ACD:
AC = 20 см.
Теперь нам известны обе диагонали найдём угол между ними. Для этого рассмотрим четырёхугольник NEHF:
Опять по свойству средней линий треугольника (только теперь параллельность стороне), определим тип четырёхугольника:
NEHF – параллелограмм ( противолежащие стороны параллельны).
Осталось найти площадь по формуле:
Подставим в формулу найденные диагонали и синус 120° (равен синусу 60°) и получим ответ.
Ответ: 180
Заключение
В этом решении мы применяли:
- Свойства средней линии треугольника.
- Формула площади произвольного четырёхугольника через диагонали и угол между ними.
Применение
Понять, что Вам нужна именно эта формула площади обычно проще, чем в рассмотренной задаче. Вам будут давать длины диагоналей или угол между ними, а найти нужно будет площадь. Могут наоборот дать площадь и попросить узнать диагональ или угол между ними. Формула встречается в первой части ОГЭ: ссылка на задания из открытого банка заданий ОГЭ.
Попробуйте решить и похожую на ту, что мы разобрали:
Пробуйте, решайте, изучайте, делитесь решениями в комментариях. Удачи!
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
-
Расчет площади
-
1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 3. Через полупериметр и радиус вписанной окружности
-
1. Через диагонали и угол между ними
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
3. Через полупериметр и радиус вписанной окружности
Формула расчета
S = p ⋅ r
































