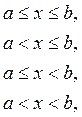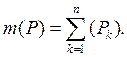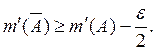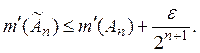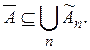Плоская мера множества как найти

Мера множества

Понятие меры множества является далеко идущим обобщением понятия длины отрезка. В простейшем случае (которым только мы и будем заниматься) задача состоит в том, чтобы дать определение длины не только для отрезков, но также и для более сложных точечных множеств, расположенных на прямой.

Примем за единицу измерения отрезок [0,1] . Тогда длина произвольного отрезка [a,b] , очевидно, равна b-a . Точно так же если имеется два непересекающихся отрезка [a_1,b_1] и [a_2,b_2] , то под длиной множества , состоящего из этих двух отрезков, естественно понимать число (b_1-a_1)+(b_2-a_2) . Однако далеко не так ясно, что следует понимать под длиной множества более сложной природы, расположенного на прямой; например, чему равна длина канторова множества. Отсюда вывод: понятие длины множества, расположенного на прямой, нуждается в строгом математическом определении.

Задача определения длины множеств, или, как говорят еще, задача измерения множеств, весьма важна, так как она имеет существенное значение для обобщения понятия интеграла. Понятие меры множества применяется и в других вопросах теории функций, а также в теории вероятностей, топологии, функциональном анализе и т.д.

Ниже излагается определение меры множеств, предложенное французским математиком А. Лебегом и лежащее в основе данного им определения интеграла.

Мера открытого и замкнутого множества

Начнем с определения меры произвольного открытого или замкнутого множества. Как уже отмечалось, всякое открытое множество на прямой является конечной или счетной суммой попарно не пересекающихся интервалов.

Мерой открытого множества называется сумма длин составляющих его интервалов.

Таким образом, если $textstyle{G=sum(a_i,b_i)}$ и интервалы попарно не пересекаются, то мера равна $textstyle{sum(b_i-a_i)}$ . Обозначая вообще меру множества через mu E , можем написать $textstyle{mu G=sum(b_i-a_i)}$ . В частности, мера одного интервала равна его длине mu(a,b)=b-a .

Всякое замкнутое множество , содержащееся в отрезке [a,b] и такое, что концы отрезка [a,b] принадлежат , получается из отрезка [a,b] путем удаления из него некоторого открытого множества . В соответствии с этим мерой замкнутого множества Fsubseteq[a,b] , где ain F,~bin F , называется разность между длиной отрезка [a,b] и мерой открытого множества , дополнительного к (относительно отрезка [a,b] ).

Итак,

mu F=(b-a)-mu G.~~~~~~~~~(2)

Нетрудно усмотреть, что, согласно этому определению, мера произвольного отрезка равна его длине mu[a,b]=b-a , а мера множества, состоящего из конечного числа точек, равна нулю.

Определение меры множества

Для того чтобы дать определение меры множеств более общей природы, чем открытые и замкнутые, нам понадобится одно вспомогательное понятие. Пусть — некоторое множество, лежащее на отрезке [a,b] . Рассмотрим всевозможные покрытия множества , т. е. всевозможные открытые множества V(E) , содержащие . Мера каждого из множеств V(E) уже определена. Совокупность мер всех множеств V(E) есть некоторое множество положительных чисел. Это множество чисел ограничено снизу (хотя бы числом 0) и потому имеет нижнюю грань, которую мы обозначим через mu_e E . Число mu_e E называется внешней мерой множества .

Пусть mu_e E — внешняя мера множества , а mu_e CE — внешняя мера его дополнения относительно отрезка [a,b] .

Если удовлетворяется соотношение

mu_eE+mu_eCE=b-a,~~~~~~~~~(3)

то множество называется измеримым, а число mu_eE — его мерой: mu E=mu_eE ; если соотношение (3) не удовлетворяется, то говорят, что множество неизмеримо; неизмеримое множество не имеет меры.

Отметим, что всегда

mu_eE+mu_eCEgeqslant b-a.~~~~~~~~(4)

Сделаем несколько пояснений. Длина простейших множеств (например, интервалов и отрезков) обладает рядом замечательных свойств. Укажем важнейшие из них.

1. Если множества E_1 и измеримы и E_1subseteq E , то mu E_1leqslant mu E , т.е. мера части множества не превосходит меры всего множества .

2. Если множества E_1 и E_2 измеримы, то множество E=E_1+E_2 измеримо и mu(E_1+E_2)leqslantmu E_1+mu E_2 , т.е. мера суммы не превосходит суммы мер слагаемых.

3. Если множества $E_i,~iinmathbb{N}$ измеримы и попарно не пересекаются, E_iE_j=varnothing~(ine j) , то их сумма $textstyle{E=sum E_i}$ измерима и $textstyle{mu!left(sum E_iright)=summu E_i}$ , т.е. мера конечной или счетной суммы попарно непересекающихся множеств равна сумме мер слагаемых. Это свойство меры называется ее полной аддитивностью.

4. Мера множества не меняется, если его сдвинуть как твердое тело.

Желательно, чтобы основные свойства длины сохранялись и для более общего понятия меры множеств. Но, как можно совершенно строго показать, это оказывается невозможным, если приписывать меру произвольному множеству точек на прямой. Поэтому-то в данном выше определении и появляются множества, имеющие меру или измеримые, и множества, не имеющие меры или неизмеримые. Впрочем, класс измеримых множеств настолько широк, что это обстоятельство не вносит каких-либо существенных неудобств. Даже построение примера неизмеримого множества представляет известные трудности.

Приведем несколько примеров измеримых множеств.

Мера канторова совершенного множества

При построении канторового множества из отрезка [0,1] выбрасывается сперва один смежный интервал длины 1/3 , затем два смежных интервала длины 1/9 , затем четыре смежных интервала длины 1/27 и т. д. Вообще, на -м. шаге выбрасывается $2^{n-1}$ смежных интервалов длины $3^{-n}$ . Таким образом, сумма длин всех выброшенных интервалов равна

$S=frac{1}{3}+frac{2}{9}+frac{4}{27}+cdots+frac{2^{n-1}}{3^n}+cdots=sum_{n=1}^{infty}frac{2^{n-1}}{3^n}.$

Члены этого ряда представляют собою геометрическую прогрессию с первым членом 1/3 и знаменателем 2/3 . Поэтому сумма ряда равна $frac{1/3}{1-2/3}=1$ .

Итак, сумма длин всех смежных к канторовому множеству интервалов равна 1. Иначе говоря, мера дополнительного к канторовому множеству открытого множества равна 1. Поэтому само множество имеет меру mu P=1-mu G=1-1=0 .

Как показывает этот пример, множество может иметь мощность континуума и тем не менее иметь меру, равную нулю.

Мера множества R всех рациональных точек отрезка [0, 1]

Покажем прежде всего, что mu_e R=0 . Как известно, множество счетно. Расположим точки множества в последовательность

r_1,r_2,ldots,r_n,ldots

Далее, зададим varepsilon>0 и окружим точку r_n интервалом delta_n длины $frac{varepsilon}{2^n}$ . Сумма $textstyle{delta= sumdelta_n}$ есть открытое множество, покрывающее . Интервалы delta_n могут пересекаться, поэтому

$mu(delta)=mu!left(sum_{n=1}^{infty}delta_nright)leqslantsum_{n=1}^{infty}mudelta_n=sum_{n=1}^{infty}frac{varepsilon}{2^n}=varepsilon.$

Так как varepsilon можно выбрать сколь угодно малым, то mu_eR=0 .

Далее, согласно (3) имеем mu_eR+mu_eCRgeqslant1 , т. е. . Так как содержится в отрезке [0,1] , то mu_eCRleqslant1 .

Итак, mu_eR+mu_eCR=1 , откуда

mu R=0,quadmu CR=1.~~~~~~~~~(5)

Этот пример показывает, что множество может быть всюду плотным на некотором отрезке и тем не менее иметь меру, равную нулю.

Множества меры нуль во многих вопросах теории функций не играют никакой роли, и ими следует пренебрегать. Например, функция f(x) интегрируема по Риману в том и только в том случае, если она ограничена и множество её точек разрыва имеет меру нуль. Можно было бы привести значительное число таких примеров.

Измеримые функции

Переходим к одному из наиболее блестящих приложений понятия меры множеств, а именно к описанию того класса функций, с которыми фактически оперирует математический анализ и теория функций. Точная постановка задачи такова. Если последовательность функций ${f_n(x)}$ , заданных на некотором множестве , сходится в каждой точке , кроме, быть может, точек множества mathbb{N} меры нуль, то будем говорить, что последовательность ${f_n(x)}$ сходится почти всюду.

Какие функции можно получить из непрерывных функций путем повторного применения операции построения предела почти всюду сходящейся последовательности функций и алгебраических операций?

Для ответа на этот вопрос нам потребуется несколько новых понятий.

Пусть функция f(x) определена на некотором множестве и alpha — произвольное действительное число. Обозначим через E[f(x)>alpha] множество тех точек , для которых . Например, если функция f(x) определена на отрезке [0,1] и на этом отрезке f(x)=x , то множества равны [0,1] для alpha<0 , равны (alpha,1] для 0leqslantalpha<1 и пусты для alpha>1 .

Функция f(x) , определенная на некотором множестве , называется измеримой, если само множество измеримо и для любого действительного числа alpha измеримо множество E[f(x)>alpha] .

Можно показать, что произвольная непрерывная функция, заданная на отрезке, измерима. Однако к числу измеримых функций принадлежат также и многие разрывные функции, например функция Дирихле, равная 1 для иррациональных точек отрезка [0,1] и равная 0 для остальных точек этого отрезка.

Отметим без доказательства, что измеримые функции обладают следующими свойствами.

1. Если f(x) и varphi(x) — измеримые функции, определенные на одном и том же множестве , то функции

f+varphi,quad f-varphi,quad fcdotvarphi и $frac{f}{varphi}$

также измеримы (последняя, если varphine0 ).

Это свойство показывает, что алгебраические операции над измеримыми функциями снова приводят к измеримым функциям.

2. Если последовательность измеримых функций ${f_n(x)}$ , определенных на множестве , сходится почти всюду к функции f(x) , то эта функция также измерима.

Таким образом, операция построения предела почти всюду сходящейся последовательности измеримых функций вновь приводит к измеримым функциям.

Эти свойства измеримых функций были установлены Лебегом. Глубокое исследование измеримых функций было произведено советскими математиками Д. Ф. Егоровым и Н. Н. Лузиным. В частности, Н. Н. Лузин показал, что всякую измеримую функцию, заданную на отрезке, можно превратить в непрерывную, изменив ее значения на некотором множестве сколь угодно малой меры.

Этот классический результат Н. Н. Лузина и перечисленные выше свойства измеримых функций позволяют показать, что измеримые функции и представляют собой тот класс функций, о котором шла речь в начале этого пункта. Измеримые функции имеют также большое значение для теории интегрирования, именно, понятие интеграла может быть обобщено таким образом, чтобы всякая ограниченная измеримая функция оказалась интегрируемой. Подробнее об этом рассказывается в разделе интеграл Лебега.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Дискретная математика

Множество
– совокупность предметов (объектов,
называемых элементами), объединенных
некоторым общим признаком (свойством).
Запись А = {х
/ х²
– 3 х
+ 2 = 0} означает, что множеству А принадлежат
все те элементы х,
которые являются корнями уравнения х²
– 3 х
+ 2 = 0, т. е. числа х
= 1 и х
= 2.

Бесконечное
множество, элементы которого возможно
занумеровать натуральными числами,
называется счётным.

Множество всех
рациональных чисел – счётное, а множество
всех действительных чисел – несчётное.

Если любой элемент
множества В принадлежит также множеству
А, то множество В называется подмножеством
множества А и записывают В
А
или А
В.
Например, всякое натуральное число
(множество N) принадлежит множеству
целых чисел (множество Z), т. е. N

Из определения
подмножества следует, что любое множество
является подмножеством самого себя, т.
е.справедливо утверждение А
А.

Множество,
состоящее из всех элементов, принадлежащих
и множеству А и множеству В, называется
пересечением
множеств А и В и обозначается А
В.

Множество,
состоящее из всех элементов, принадлежащих
или множеству А или множеству В,
называется объединением
множеств А и В и обозначается А
В.

Обозначим через
m (А) число элементов конечного множества
А, тогда для любых конечных множеств
А и В справедливо равенство

m (А
В)
= m (А) + m(В) – m(А
В),
если пересечение множеств А и В не
пусто. Когда множества А и В не пересекаются,
то m(А
В)
= 0 и

m (А
В)
= m (А) + m(В).

Разностью
множеств А
и В (дополнением множества В до множества
А) называется множество всех тех и только
тех элементов из множества А, которые
не содержатся в множестве В, обозначается
А В. Например, дополнением множества
целых чисел до множества всех рациональных
чисел является множество всех дробных
чисел.

Пример 1.
Даны множества А={- 3 < х ≤ 5}, В ={1 < х
< 5}. Найти количество целых х

.

Решение.
Объединением множеств А и В является
промежуток ( -3; 5], куда входит 8
целых чисел.

Пример 2.
А = {20,30,40,50}, В = {20, 25, 30, 35}, С = {30, 35, 40, 45}.
Найти число элементов множества Д = (
)
С .

Решение.
=
{20, 25, 30, 35, 40, 45, 50}. Множество Д = (
)
С содержит числа без чисел множества
С, т. е. Д = {20,
25, 50}.

Пример 3.
Даны множества А = {х : sin х
= 0}, В = {х : 0 < х < 10}. Сколько элементов
содержится в множестве А

В
?

Решение.
Множество А = {х : sin х
= 0} = {х : х = πk, k
Z}.

В
= {π; 2π; 3π}, следовательно, в нём 3
элемента.

Прямым или
декартовым
произведением множеств
А и В называется множество упорядоченных
пар (а,
b),
в котором а

А, b

В, т. е.

А × В = {(а,
b)
/ а

А и b

В}.

Плоскость в
выбранной прямоугольной системой
координат изображает произведение
множеств R×R (иногда пишут R²
).

Пример 4. Дано
множество А = {2, 3, 4, 5, 6, 7, 8, 9} и бинарное
отношение Р = {х,
у
/ х,
у

А, х
≤ 3 }, причём х делит у без остатка.
Найти количество элементов предиката
(неопределённое высказывание –
подмножество множества А)

Решение.
Так как множество А состоит из 8
элементов, то декартово произведение
А × А будет содержать n = 8 · 8 = 64 парных
элемента. Предикат Р является
подмножеством множества А × А . Нужно
из 64 парных элементов выбрать только
те, которые удовлетворяют условиям
нашего предиката, т. е. первый элемент
пары не должен быть больше 3, а второй
должен делиться на первый без остатка
. Тогда это предикат

Р = {(2; 2), (2; 4), (2;
6), (2; 8), (3; 3), (3; 6), (3; 9)}, который содержит
7 элементов.
( Ответ: 7
элементов.
)

Мера плоского
множества есть
площадь соответствующей фигуры

П
ример1.

S =
π r₂² – π r₁
²
= π (4²–
2²)
= 12π.

П
ример
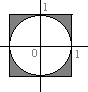
2. Найти меру
плоского множества А В, где

А
{ (х,
у)

R²:
mах (| х |, | у | <1} и

В{
(х,
у)

R²:
х ²
+ у ²<1}.

S = площадь квадрата
минус площадь круга = 4 – π.

(
ответ: 4 – π
)

Пример3.
Найти меру плоского множества { (х,
у)

R²:

<
у
< 2,5 – х}.
В начале находим точки пересечения
линий, решая совместно систему уравнений
у =

и у = 2,5 – х. Имеем

=
2,5 – х или 2х ²– 5х +2 = 0.

Отсюда
х₁=
2, х₂=
0,5.

S =

=

2,5 (2 – 0,5) – 0,5 (4 –
0,25) – ln 2 + ln 0,5 =

–
ln 4.

(ответ

–
ln 4 )

Пример 4.
Найти меру плоского множества { (х,
у)

R²:
х²+
у²
= 1}.

Так как множество
состоит только из точек кривой –
окружности, то мера данного плоского
множества равна нулю. (Ответ:
нуль )

Если по какому-то
правилу каждому элементу
х

А ставится в соответствие определенный
элемент у

В, то такое соответствие называется
отображением
множества А в множество В и пишут f
: А → В.

Символ f
обозначает правило заданного соответствия.
Это правило можно обозначать и другими
символами.

Отображение, в
котором различные элементы входного
множества А соединяются с различными
элементами выходного множества В и нет
неприсоединенных элементов, называется
биективным
или взаимно
однозначным соответствием.

Линейным
отображением
называется отображение φ, удовлетворяющее
условиям φ (х
+ у) = φ (х)
+ φ (у);
φ (λ х)
= λ φ (х).

Отображение f
: Х → У называется обратимым, если
существует

f
^-1
: У → Х такое, что f
○ f
^-1=
е _х,
f
^-1
○ f
= е _у,
где е _х,
е _у
– тождественные отображения на множества
Х и У соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Мера, интеграл Лебега, гильбертово пространство

Страницы работы

Содержание работы

Часть II

Мера, интеграл Лебега,

гильбертово пространство

Глава
V

Теория
меры

Понятие меры множества А является естественным
обобщением понятий:

1) длины отрезка

2) площади S(F) плоской фигуры F,

3) объема V(G) пространственной фигуры G,

4) приращения неубывающей функции на полуинтервале [а, b),

5) интеграла от
неотрицательной функции, взятого по некоторой линейной, плоской или
пространственной области, и т. п.

Понятие меры
множества, возникшее первоначально в теории функций действительного
переменного, нашло в дальнейшем многочисленные применения в теории вероятностей,
теории динамических систем, функциональном анализе и других областях математики.

В первом параграфе этой
главы мы изложим понятие меры для множеств на плоскости, отправляясь от понятия
площади прямоугольника. Общая теория меры будет изложена в § 35-39. Читатель
легко заметит, однако, что все рассуждения, проведенные в §33, имеют общий
характер и в абстрактной теории повторяются без существенных изменений.

§ 33. Мера плоских множеств

Рассмотрим систему множеств на плоскости (х,у), каждое
из которых определяется одним из неравенств вида

и одним из неравенств вида

где а, b, с, и d — произвольные
числа. Множества, принадлежащие этой системе, мы будем называть
«прямоугольниками». Замкнутый прямоугольник, определяемый неравенствами

представляет собой прямоугольник в обычном
смысле (вместе с границей), если и или отрезок (если и
или и ), или точку (при ),или, наконец, пустое множество (если а > b или с > d). Открытый «прямоугольник»

представляет собой, в зависимости от
соотношений между а, b, с и d, прямоугольник без границ
или пустое множество. Каждый из прямоугольников остальных типов (назовем их
полуоткрытыми) представляет собой либо настоящий прямоугольник без одной, двух
или трех сторон, либо интервал, либо полуинтервал, либо, наконец, пустое
множество.

Для каждого из
прямоугольников определим его меру, в соответствии с известным из элементарной
геометрии понятием площади, следующим образом:

а) мера пустого
множества равна нулю;

б) мера непустого
прямоугольника (замкнутого, открытого или полуоткрытого), определяемого числами
а, b, с и d, равна

Таким образом, каждому
прямоугольнику Р поставлено в соответствие число т(Р) —
мера этого прямоугольника; при этом выполнены, очевидно, следующие условия:

1) Мера т(Р)
принимает действительные неотрицательные значения;

2) Мера m(Р)
аддитивна, т. е. если и при то

Нашей задачей является
распространение, с сохранением свойств 1) и 2), меры т(Р), определенной
пока лишь для прямоугольников, на более широкий класс множеств.

Первый шаг в этом
направлении состоит в распространении понятия меры на так называемые
элементарные множества. Назовем плоское множество элементарным, если его
можно представить, хотя бы одним способом, как соединение конечного числа попарно
непересекающихся прямоугольников.

Для дальнейшего нам
понадобится следующая

Теорема 1. Соединение, пересечение, разность и симметрическая разность
двух элементарных множеств также являются элементарными множествами.

Доказательство. Ясно, что пересечение
двух прямоугольников есть снова прямоугольник. Поэтому, если

— два элементарных множества, то и

также является элементарным множеством.

Разность двух
прямоугольников есть, как легко проверить, элементарное множество.
Следовательно, вычитая из прямоугольника некоторое элементарное множество, мы
снова получим элементарное множество (как пересечение элементарных). Пусть
теперь A и В — два
элементарных множества. Найдется, очевидно, прямоугольник Р, содержащий
каждое из них. Тогда

есть элементарное множество, в силу сказанного
выше. Отсюда и из равенств

следует, что разность и симметрическая разность
элементарных множеств являются элементарными множествами. Теорема доказана.

Определим теперь меру для элементарных множеств следующим
образом: если

где — попарно не
пересекающиеся прямоугольники, то

Покажем, что не
зависит от способа представления множества А в виде суммы прямоугольников.
Пусть

где и —
прямоугольники, и при Так как
пересечение двух прямоугольников есть прямоугольник,
то, в силу аддитивности меры для прямоугольников,

Легко видеть, что мера элементарных множеств,
определенная таким образом, неотрицательна и аддитивна.

Установим следующее важное
для дальнейшего свойство меры элементарных множеств.

Теорема 2. Если А — элементарное
множество и — конечная или счетная система
элементарных множеств, такая, что

то

(1)

Доказательство. Для любого и данного А можно, очевидно, найти
такое замкнутое элементарное множество которое
содержится в А и удовлетворяет условию:

(Для этого достаточно каждый из k составляющих А прямоугольников заменить целиком лежащим в нем
замкнутым прямоугольником с площадью большей, чем )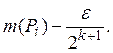

Далее, для каждого можно найти открытое элементарное
множество содержащее и
удовлетворяющее условию

Ясно, что

Информация о работе

Источник

Ме́ра мно́жества, понятие, обобщающее длину отрезка, площадь плоской фигуры и объём тела на множества более общей природы. Примером меры множества является мера Лебега (введённая А. Лебегом, 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m(Δ)m(Δ) любого квадрата ΔΔ полагают равной его площади в тех или иных единицах измерения. Затем заданное множество АА покрывают конечным или бесконечным набором квадратов Δ1,Δ2,…;Δ_1, Δ_2,…; нижнюю грань чисел ∑n=1∞m(Δn)sum_{n=1}^infty m(Δ_n), взятую по всевозможным покрытиям множества АА, называют верхней (внешней) мерой m∗(А)m^*(А) множества АА. Нижняя (внутренняя) мера m∗(А)m_*(А) множества АА определяется как разность m(Δ)−m∗(Aˉ)m(Δ)-m^*(Ā), где ΔΔ – какой-либо квадрат, содержащий множество АА, и AˉĀ – множество всех точек квадрата ΔΔ, не содержащихся в АА. Множества АА, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m(А)m(А) верхней и нижней мер – мерой Лебега множества АА. Геометрические фигуры, имеющие площадь в элементарном смысле, измеримы, и их мера Лебега совпадает с их площадью. Однако существуют неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.

Основные свойства меры Лебега состоят в том, что мера любого множества неотрицательна и мера объединения A=⋃n−1∞AnA=bigcup_{n-1}^infty A_n конечной или счётной системы попарно непересекающихся множеств A1,A2,…A_1, A_2, … равна сумме их мер, т. е. m(A)=∑n=1∞m(An)m(A)=sum_{n=1}^infty m(A_n).

Класс множеств, измеримых по Лебегу, достаточно широк; в частности, измеримыми по Лебегу являются множество АА рациональных точек интервала (0,1)(0, 1) и множество В иррациональных точек того же интервала. Эти множества сходны в том смысле, что каждое из них плотно на интервале (0,1)(0, 1), т. е. между любыми двумя точками указанного интервала найдутся как точки множества АА, так и точки множества ВВ; в то же время они резко различаются по мере, т. к. m(А)=0m(А)=0, а m(В)=1m(В)=1. Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (1898).

Развитие ряда разделов современной математики привело к дальнейшим обобщениям понятия меры множества – созданию т. н. абстрактной теории меры. При этом меру множества определяют аксиоматически. Пусть UU – произвольное множество и Mmathfrak {M} – некоторое семейство его подмножеств. Неотрицательную функцию μ(A)μ(A), определённую для всех АА, входящих в Mmathfrak {M}, называют мерой, если она вполне аддитивна, т. е. если для любой последовательности непересекающихся множеств A1,A2,…,A_1, A_2,…, входящих в Mmathfrak {M}, сумма АА которых также входит в Mmathfrak {M}, имеет место равенство μ(A)=∑n=1∞μ(An)μ(A)=sum_{n=1}^infty μ(A_n), и, кроме того, система Mmathfrak {M} удовлетворяет определённым дополнительным условиям. Множества, входящие в Mmathfrak {M}, называют измеримыми. После того как определена мера μμ, вводят понятие измеримых (по отношению к μμ) функций и операцию интегрирования.

Многие основные утверждения теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими изменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное А. Н. Колмогоровым (1933). Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества UU в себя.

Дата публикации: 25 января 2023 г. в 22:59 (GMT+3)

Источник

Мера множества, математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (D) любого квадрата D полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов D1, D2,…, Dn,…; нижнюю грань чисел

взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m*(А) множества А. Нижняя (внутренняя) мера m* (А) множества А определяется как разность

где D — какой-либо квадрат, содержащий множество А, и — множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер — мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.

Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)D ³ 0; 2) мера суммы

конечной или счётной системы попарно непересекающихся множеств A1, A2…, An… равна сумме их мер:

3) при перемещении множества как твёрдого тела его мера не меняется.

Своеобразие понятия «М. м.» можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А, так и точки множества В; в то же время они резко различаются по мере: m (А) = 0, а m (В) = 1.

Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.

Развитие ряда отделов современной математики привело к дальнейшим обобщениям — созданию т. н. абстрактной теории меры. При этом М. м. определяют аксиоматически. Пусть U — произвольное множество и — некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в

и если, кроме того, система удовлетворяет определённым дополнительным условиям. Множества, входящие в, называют измеримыми (по отношению к мере m). После того как определена мера m, вводят понятие измеримых (по отношению к m) функций и операцию интегрирования.

Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.

Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. — Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.

Ю. В. Прохоров.

Источник

Мера множества

Мера открытого и замкнутого множества

Определение меры множества

Мера канторова совершенного множества

Мера множества R всех рациональных точек отрезка [0, 1]

Измеримые функции

Дискретная математика