Рисунок 1: Точка O является внешним центром подобия для двух треугольников. Размер каждой фигуры пропорционален её расстоянию до центра подобия.
Центр подобия (или центр гомотетии) — это точка, из которой по меньшей мере две геометрически подобные фигуры можно видеть как масштабирование[en] (растяжение/сжатие) друг друга. Если центр внешний, две фигуры похожи друг на друга прямо — их углы одни и те же в смысле вращения. Если центр внутренний, две фигуры являются изменёнными в размерах отражениями друг друга — их углы противоположны.

Рисунок 2: Две геометрические фигуры относительно внешнего центра подобия S. Углы в соответствующих точках те же самые и имеют тот же смысл. Например, углы ABC и A’B’C’ оба равны по размерам и по направлению (по часовой стрелке/против часовой стрелки).
Многоугольники[править | править код]

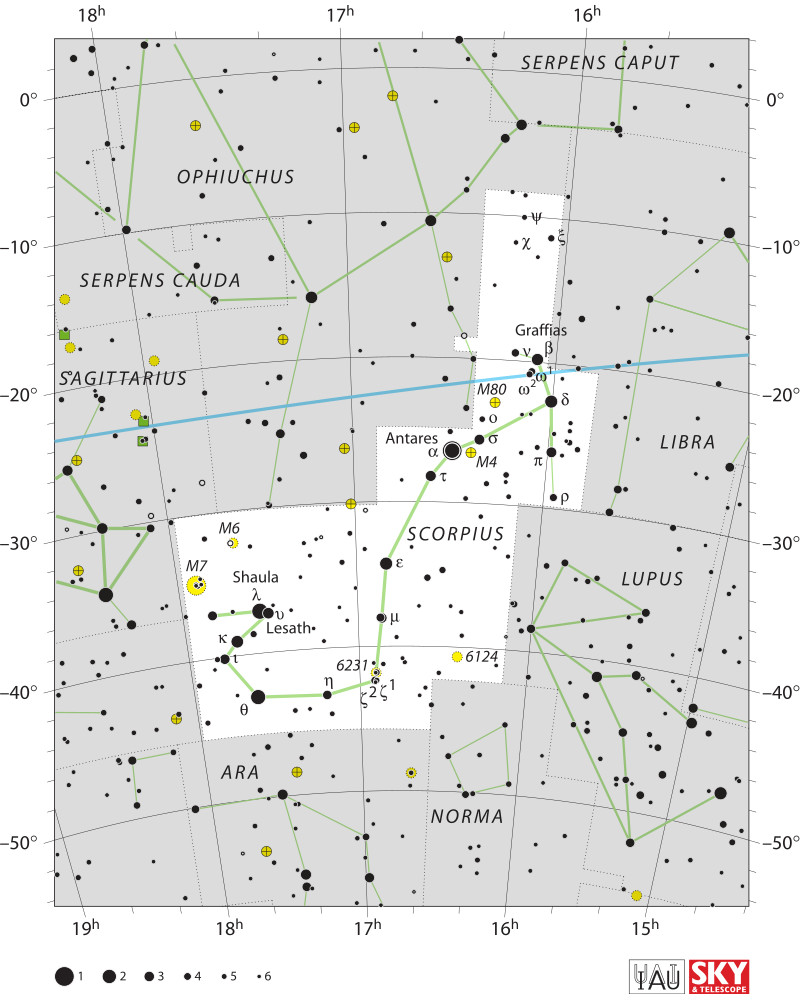
Внешний (сверху) и внутренний (внизу) центры подобия двух окружностей (выделены красным) показаны как зелёные точки.
Если две геометрические фигуры имеют центр подобия, они подобны друг другу. Другими словами, они должны иметь те же самые углы в соответствующих точках и отличаются только их относительными размерами. Центр подобия и две фигуры не обязательно должны принадлежать одной плоскости. Он может относиться к трёхмерной проекции[en] из центра подобия.
Центры подобия могут быть внешние или внутренние. Если центр внутренний, две геометрические фигуры являются изменёнными в размерах зеркальными отражениями друг друга. Говоря техническим языком, они имеют противоположную хиральность. Направленный по часовой стрелке угол одной фигуры будет соответствовать углу против часовой стрелки на другой. И наоборот, если центр подобия внешний, две фигуры прямо пропорциональны друг другу — их углы имеют тот же смысл.
Окружности[править | править код]
Окружности геометрически подобны друг другу и зеркально симметричны. Пара окружностей имеет оба типа центров подобия, внешний и внутренний, если только центры не совпадают или окружности имеют одинаковый радиус. Эти особые случаи трактуются как общие случаи. Эти два центра подобия лежат на прямой, проходящей через центры двух данных окружностей, которая называется линией центров (Рисунок 3). Окружности с нулевым радиусом можно тоже включать в рассмотрение (смотрите особые случаи), как и отрицательные радиусы, при этом происходит смена ролей внешних и внутренних центров подобий.
Вычисление центра подобия[править | править код]

Рисунок 3: Две окружности имеют оба вида центров подобия, внутренний (I) и внешний (E). Радиусы окружностей (r1 и r2) пропорциональны расстоянию (d) от каждого центра подобия. Точки A1 и A2 гомологичны, как точки B1 и B2.
Для данной пары окружности внутренний и внешний центры подобия можно найти различными путями. В аналитической геометрии внутренний центр подобия является средним взвешенным центров окружностей, где вес соответствует радиусу противоположной окружности – расстояние от центра окружности до внутренней точки подобия пропорциональны противоположным радиусам. Если обозначить центры окружностей 






Внешний центр можно получить из того же уравнения, если принять один из радиусов отрицательным. Какой бы радиус мы не приняли отрицательным, будем иметь то же самое уравнение:
Обобщая, если взять радиусы с одним и тем же знаком (оба положительны или оба отрицательных), получим внутренний центр, в то время как радиусы с разными знаками (один положительный, а другой отрицательный) дадут внешний центр подобия. Заметим, что уравнение для внутреннего центра остаётся верным для любых значений (если только оба радиуса не равны нулю или в сумме радиусы не дают нуль), но уравнение для внешних центров требует, чтобы радиусы были различны, иначе получим деление на ноль.
В элементарной геометрии, если нарисованы два параллельных диаметра, по одному в окружности, они будут составлять один и тот же угол α с линией центров. Прямые A1A2 и B1B2, проведённые через соответствующие конечные точки радиусов, являющиеся гомологичными токами, пересекают друг друга и линию центров во внешнем центре подобия. Прямые же A1B2 и B1A2, проведённые через одну конечную точку и противоположную конечную точку, пересекают друг друга и линию центров во внутреннем центре подобия.
Особые случаи[править | править код]
Если окружности имеют один и тот же радиус (но разные центры), не существует внешнего центра подобия в аффинной плоскости — в аналитической геометрии это приводит к делению на нуль, а в классической геометрии прямые 

Если окружности имеют один и тот же центр, но различные радиусы, внешний и внутренний центры подобия совпадают с общим центром окружностей. Это можно видеть из аналитической формулы, а также как предел двух центров подобия при движении центров друг к другу при сохранении радиусов, пока центры не совпадут.
Если один радиус равен нулю, а другой нулю не равен (точка и окружность), и внешний, и внутренний центры подобия совпадают с точкой (центром окружности нулевого радиуса).
Если две окружности идентичны (имеют один центр и одинаковые радиусы), внутренний центр подобия — это их общий центр, но нет хорошо определённого внешнего центра. В пределе, когда две окружности равного радиуса двигаются друг к другу до совпадения центров, внешний центр подобия находится на бесконечности и потому может быть где угодно, а потому никакого внешнего центра подобия для таких окружностей не существует.
Если оба радиуса равны нулю (две точки), но точки различны, внешний центр подобия можно определить как точку на бесконечности, соответствующую прямой, проходящей через линию центров, но в этом случае нет внутреннего центра.
Гомологичные и антигомологичные точки[править | править код]

Рисунок 4: Прямые через соответствующие антигомологичные точки пересекаются на радикальных осях двух заданных окружностей (зелёные и синие). Точки Q и P′ антигомологичны, как и S и R′. Эти четыре точки лежат на окружности, которая пересекает две данные окружности. Прямые через точки пересечения новой окружности с двумя заданными окружностями должны пересекаться в радикальном центре G трёх окружностей, который лежит на радикальных осях двух заданных окружностей.
В общем случае луч, исходящий из центра подобия, пересекает каждую окружность в двух местах. Из этих четырёх точек две гомологичны, если радиусы, проведённые из них, составляют один и тот же угол с линией центров, т.е. точки A1 и A2 на рисунке 3. Точки, которые лежат на одной прямой с центром подобия, но не гомологичные, называются антигомологичными,[1] как, например, точки Q и P′ на рисунке 4.
Пары антигомологичных точек, лежащих на окружности[править | править код]
Если два луча из одного центра подобия пересекают окружности, любой набор антигомологичных точек лежит на окружности.
Пусть даны треугольники EQS и EQ′S′ (рисунок 4).
Они подобны, поскольку имеют общий угол ∠QES=∠Q′ES′ и 
Из этого подобия следует, что ∠ESQ=∠ES′Q′=α.
Вследствие теоремы о вписанном угле ∠EP′R′=∠ES′Q′.
∠QSR′=180°-α, поскольку это дополнительный угол для ∠ESQ.
В четырёхугольнике QSR′P′ ∠QSR′+∠QP′R′=180°-α+α=180°, что означает, что четырёхугольник вписан.
Из теоремы о секущих следует, что EQ•EP′=ES•ER′.
Тем же способом можно показать, что PRS′Q′ может быть вписан в окружность и EP•EQ′=ER•ES′.
Доказательство аналогично доказательству для внутреннего центра подобия I.
PIR~P′IR′, следовательно, ∠RPI=∠IP′R′=α.
∠RS′Q′=∠PP′R′=α (теорема о вписанном угле).
Сегмент RQ′ виден под тем же углом из P и S′ что означает, что R, P, S′ и Q′ лежат на окружности.
Тогда из теоремы о пересекающихся хордах IP•IQ′=IR•IS′.
Похожим образом можно показать, что QSP′R′ может быть вписан в окружность и IQ•IP′=IS•IR′.
Связь с радикальными осями[править | править код]
Две окружности имеют радикальные оси, прямые, состоящие из точек, из которых отрезки от точки до точки касания обеих окружностей имеют одну длину. Обобщённо, любая точка на радикальной оси имеет свойство, что её степени относительно окружностей равны. Радикальная ось всегда перпендикулярна линии центров, и если две окружности пересекаются, их радикальная ось проходит через точки пересечения окружностей. Для трёх окружностей можно определить три радикальные оси, для каждой пары окружностей (C1/C2, C1/C3 и C2/C3). Замечателен факт, что эти три радикальные оси пересекаются в одной точке, радикальном центре. Касательные отрезки, проведённые из радикального центра до всех трёх окружностей, будут иметь одну и ту же длину.
Любые две пары антигомологичных точек могут быть использованы для нахождения точки на радикальной оси. Пусть два луча проведены из внешнего центра подобия E, как на рисунке 4. Эти лучи пересекают две заданные окружности (зелёная и синяя на рисунке 4) в двух парах антигомологичных точек, Q и P′ для первого луча, и S и R′ для второго луча. Эти четыре точки лежат на одной окружности, которая пересекает обе заданные окружности. По определению, прямая QS является радикальной осью для новой окружности и зелёной окружности, в то время как прямая P′R′ является радикальной осью для новой окружности и синей окружности. Эти две прямые пересекаются в точке G, которая является радикальным центром трёх окружностей — новой окружности и двух исходных. Таким образом, точка G также лежит на радикальной оси двух исходных окружностей.
Касательные окружности и антигомологичные точки[править | править код]
Для любой пары антигомологичных точек двух окружностей существует третья окружность, которая касается исходных окружностей в антигомологичных точках.
Обратное также верно — любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках.

Рисунок 5: Любая окружность, касающаяся двух других окружностей, касается их в антигомологичных точках
Пусть наши две окружности имеют центры O1 и O2 (Рисунок 5). Пусть E — их внешний центр подобия.
Строим произвольный луч из точки E, который пересекает две окружности в точках P, Q, P′ и Q′.
Продлим O1Q и O2P′ до пересечения (в точке
T1).
Легко показать, что треугольники O1PQ и O2P′Q′ подобны. Эти треугольники равнобедренны, поскольку O1P=O1Q (радиус), потому
∠O1PQ=∠O1QP=∠O2P′Q′=∠O2Q′P′=∠T1QP′=∠T1P′Q.
Но тогда T1P′Q также будет равнобедренным, и можно построить окружность с центром в T1 и радиусом T1P′=T1Q. Эта окружность касается двух исходных окружностей в точках Q и P′.
Аналогично доказывается утверждение для другой пары антигомологичных точек (P и Q′), а также для случая внутреннего центра подобия.

Рисунок 6: Семейство касательных окружностей для внешнего центра подобия

Рисунок 7: Семейство касательных окружностей для внутреннего центра подобия
Если мы построим касательные окружности для каждой возможной пары антигомологичных точек, мы получим два семейства окружностей — для каждого центра подобия. Семейство окружностей для внешнего центра подобия таково, что окружности этого семейства либо содержат обе исходные окружности внутри себя, либо ни одной (рисунок 6). С другой стороны, окружности из семейства для внутреннего центра содержат всегда одну из исходных окружностей (рисунок 7).

Рисунок 8: Радикальные оси касательных окружностей проходят через радикальный центр
Все окружности из семейства касательных окружностей имеют общий радикальный центр и он совпадает с центром подобия.
Для того, чтобы это показать, представим два луча из центра подобия, пересекающие заданные окружности (рисунок 8). Существуют две касательные окружности T1 и T2, которые касаются исходных окружностей в антигомологичных точках. Как мы уже показали, эти точки лежат на окружности C, а потому эти два луча являются радикальными осями для C/T1 и C/T2. Точка пересечения этих радикальных осей должна лежать также на радикальной оси T1/T2. Эта точка пересечения — центр подобия E.
Если две касательные окружности касаются в антигомологичных точках, лежащих на прямой через точку подобия, как на рисунке 5, то из-за подобия 
Центр подобия трёх окружностей[править | править код]
Любая пара окружностей имеет два центра подобия, поэтому три окружности будут иметь шесть центров подобия, по два на каждую пару (различных) окружностей. Интересно, что все эти шесть точек лежат на четырёх прямых, по три точки на каждой прямой. Вот один из способов показать это.

Рисунок 9: В случае трёх окружностей три центра подобия (для каждой пары окружностей) лежат на одной прямой
Представим на плоскости три окружности (рисунок 9). Добавим для каждого центра окружностей точку на перпендикуляре к плоскости, отстоящую от исходного центра на расстояние, равное соответствующему радиусу. Точки можно добавить с любой стороны плоскости. Три полученные точки определяют плоскость. В этой плоскости мы построим три прямых через каждую пару точек. Эти прямые пересекают плоскость окружностей в точках HAB, HBC и HAC. Поскольку геометрическим местом точек, которые принадлежат обеим непараллельным плоскостям, является прямая, эти три точки будут лежать на одной прямой. Из подобия треугольников HABAA′ и HABBB′ мы видим, что 
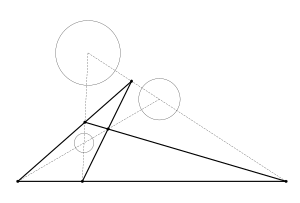
Рисунок 10: Все шесть центров подобия (точек) трёх окружностей лежат на четырёх прямых (жирные линии)
Повторяя процесс для различных комбинаций центров подобия (в нашем методе они определяются сторонами, с которых мы выбираем точки относительно плоскости), получим четыре прямых — по три центра подобия на каждой прямой (рисунок 10).
Существует и другой метод доказательства.

Рисунок 11: Синяя прямая является радикальной осью двух касающихся окружностей C1 и C2 (светло-красные). Каждая пара исходных окружностей имеет центр подобия, лежащий на радикальной оси двух касающихся окружностей. Поскольку радикальные оси — прямые, это означает, что три центра подобия лежит на одной прямой
Пусть C1 и C2 — пара сопряжённых окружностей ко всем трём исходным окружностям (рисунок 11). Под сопряжённостью здесь мы понимаем, что окружности принадлежат тому же самому семейству для одной из пары исходных окружностей. Как мы уже видели, радикальная ось любых двух касательных окружностей из одного класса проходит через центр подобия двух исходных окружностей. Поскольку касательные окружности являются общими для всех трёх пар исходных окружностей, их центры подобия лежат на радикальной оси C1 и C2, т.е. на одной прямой.
Это свойство используется в общем решении Жозефа Диаса Жергонна задачи Аполлония. Если даны три окружности, можно найти центры подобия, а затем радикальные оси пар искомых окружностей. Естественно, имеется бесконечно много окружностей с одними и теми же радикальными осями, так что нужна дополнительная работа, чтобы определить в точности, какая пара окружностей является решением.
См. также[править | править код]
- Подобие
- Гомотетия
- Радикальная ось двух окружностей, Радикальный центр
- Задача Аполлония
Примечания[править | править код]
- ↑ Weisstein.
Литература[править | править код]
- Johnson RA. Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle. — New York: Dover Publications, 1960.
- Paul Kunkel. The tangency problem of Apollonius: three looks. — 2007. — Т. 22, вып. 1. — С. 34–46. — doi:10.1080/17498430601148911.
- Eric W. Weisstein. Antihomologous Points. MathWorld–A Wolfram Web Resource.
Подобный центр
Cтраница 2
В пакет Fuzzy Logic Toolbox входит еще одна программа, позволяющая работу в режиме графического интерфейса, – программа Clustering ( Кластеризация) выявления центров кластеров, т.е. точек в многомерном пространстве данных, около которых группируются ( скапливаются) экспериментальные данные. Выявление подобных центров, надо сказать, является значимым этапом при предварительной обработке данных, поскольку позволяет сопоставить с этими центрами функции принадлежности переменных при последующем проектировании системы нечеткого вывода.
[17]
Стратегической линией развития системы услуг, рассчитанной на длительную перспективу, является создание современных центров обслуживания, ориентированных на высокомеханизированные и автоматизированные ресурсосберегающие технологические процессы. Заранее спланированное число подобных центров, интегрированных в единую сеть, должно поэтапно, с учетом особенностей размещения и динамики производительных сил каждого региона или республики, вводиться в действие в двенадцатой – тринадцатой пятилетках.
[18]
Наиболее распространенными типами их являются центры социального обслуживания населения различного ( регионального, муниципального и локального) уровня, а также центры социальной помощи семье и детям. Типология и названия подобных центров, набор их функций могут варьировать в зависимости от местных условий.
[19]
Носители тока как бы попадают в ловушку, выход из которой весьма затруднен. Оказывается также, что подобные центры захвата способствуют возникновению шумов в полупроводниковых усилителях.
[20]
ХШР-центров испускает попеременно то дырку, то электрон, которые удаляются из перехода под действием сильного электрического поля. Такая флуктуация в зарядовом состоянии подобного центра приводит к локальной модуляции ширины обедненного слоя и, следовательно, ширины канала, что в свою очередь приводит к флуктуациям тока, текущего во внешней цепи.
[22]
Образование КПЗ возможно и при неполном переносе заряда, хотя такие локальные центры, конечно, не будут давать сигнала ЭПР. Недавно Карпачевой удалось экспериментально подтвердить существование подобных центров. Изучая комплексы полишиффовых оснований с бромом, она обнаружила, что концентрации парамагнитных центров значительно ниже количества введенных молекул галогена.
[24]
Корреляция конфигурации может потребовать, чтобы в продукте образовался дополнительный центр асимметрии, и возникает вопрос о том, влияют ли первоначально имеющиеся асимметрические атомы на ход такой реакции. Это вещество не имеет асимметрического атома углерода, в то время как продукт его восстановления содержит подобный центр.
[25]
Модель центра и величина сверхтонкого взаимодействия указывают не только на существенно ковалентный характер связи в алюмосиликатах и изменение его в сторону увеличения ковалентности А1 – О-связи по сравнению с кварцем, но и на перекрывание орбит кислородных атомов, принадлежащих различным тетраэдрам. Было установлено также, что ни в одном из силикатов алюминия, ни при каком способе облучения подобные центры не образуются. Очевидно, наличие слабо связанных электронов и существенная ковалентность А1 – О-связи характерны для тетраэдрического алюминия.
[26]
Уже сегодня ряд областей знаний ( технические науки, геология, биология) обслуживаются информационными центрами, предоставляющими проверенные количественные или описательные данные в большинстве случаев в машиночитаемой форме. Интенсивно ведущиеся исследования, направленные на обеспечение доступа к этим центрам по каналам связи, реализует практическое включение подобных центров в сеть. Одной из организаций, работающих в этом направлении, является Новосибирский институт органической химии СО АН СССР, который создал Центр данных по масс-спектроскопии. Это дало возможность расширить коллекцию спектров, которая теперь непрерывно пополняется благодаря поступлениям от масс-спектроскопистов всего мира, а результаты, полученные в центре, распространять ка в нашей стране, так и в других странах. Хранение и поиск данных производится с помощью комплекса программ для ЭВМ.
[27]
Кроме того установлено, что отдельные пики термического высвечивания также обусловлены высвобождением электронов из центров окраски. Иными словами, упомянутыми исследованиями показано, что возбужденные электроны в процессе послесвечения и термического высвечивания высвобождаются из F -, М – и других подобных центров захвата, образованных тепловыми микродефектами, существующими в реальных кристаллах независимо от присутствия в них активирующей примеси.
[28]
Ноэто не всегда так для случая кремниевых диодов при комнатной температуре, отступление от характеристик идеального диода связано с наличием генерации и рекомбинации носителей в обедненном слое. Статистика генерационно-рекомбинационных процессов через центры с одиночным энергетическим уровнем в запрещенной энергетической зоне для полупроводниковых материалов была развита Холлом [8], Шокли и Ридом [21] и в настоящее время подобные центры общепринято называть как ХШР-центры. Этот статистический подход был использован Са-хом, Нойсом и Шокли [17] в качестве основы для получения отношения ток – напряжение для кремниевых р – / г-переходов. Эта теория показала, что в таких приборах в достаточно широком диапазоне напряжений смещения и температуры составляющая постоянного тока во внешней цепи, обусловленная актами рекомбинации и генерации носителей в обедненном слое, доминирует над диффузионной составляющей.
[29]
В начале января 1904 года в Женеве образовалась небольшая группа членов РСДРП, которая, отвечая давно уже назревшей потребности, положила начало устройству за границей центральной библиотеки и архива РСДРП, куда могли бы стекаться все произведения нелегальной печати как заграничной, так и российской, а также и все произведения печати легальной, необходимые для изучения общественной жизни в России. Группа эта, назвавшая себя группой инициаторов, приступила к своему делу с полной уверенностью, что найдет себе самую живую поддержку и сочувствие как среди товарищей, так и среди революционеров других фракций и людей общества, более или менее заинтересованных в создании подобного центра за границей. И действительно, несмотря на многие препятствия и осложнения, несмотря на постоянный недостаток в денежных средствах, прошло только пятнадцать месяцев, – и начинание небольшой группы товарищей превратилось в целое партийное книгохранилище с 4760 томами книг, со множеством русских и иностранных газет и журналов и с быстро увеличивающимся архивом партии.
[30]
Страницы:
1
2
3
4
Предложения со словосочетанием «подобные центры»

Одной из распространённых форм подобных центров являются инкубаторские центры, субсидируемые государством.
В чатике владельцев подобных центров по уходу за дошколятами мама кинула клич «Кто за?».
Многие исследователи приматов снова и снова убеждали меня, что то, что я наблюдаю, невозможно: ни одна обезьяна в неволе не захочет участвовать в эксперименте, даже таком безобидном, как этот, а руководитель подобного центра не будет настолько самоуверенным или глупым, чтобы попытаться это сделать.
Существовало несколько сильных политических центров, к которым тяготели все остальные области; каждый из подобных центров проводил вполне независимую внутреннюю политику и противостоял всем внешним врагам.
При этом торговля или оказание логистических услуг в подобных центрах если и осуществляется, то занимает в структуре товарооборота незначительную величину.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: сотик — это что-то нейтральное, положительное или отрицательное?
Владельцы подобных центров часто с удовольствием поддерживают такие мелкие розничные предприятия (иногда называемые точками розничной торговли или RMU), потому что они придают самобытность их комплексам, а иногда превращаются в постоянных арендаторов.
Моя тётя сотрудничала с подобными центрами.
Для экономики подобного центра не существует.
– Организация открыла множество подобных центров по всему миру.
Этот центр имел такой успех, что движение разрослось и возникло более 30 подобных центров, располагавшихся в основном в школах.
Он ведь и сам проводил много времени в подобном центре в детстве.
Военное ведомство должно создать и само финансировать подобные центры.
Сегодня я налажу связи с советом, и как только вернём нашу детвору, определим их в подобные центры.
Однако у подобных центров занятости населения существуют и некоторые минусы, с которыми мы считаем необходимым вас ознакомить.
Бывают и такие ситуации, когда подобные центры оказываются единственно правильным выбором для вашего больного родственника.
Жители подобных центров официально назывались «колонистами».
Подобный центр не требует больших инвестиций и сложной инфраструктуры из «стекла и бетона».
Для формирования подобного центра притяжения материальных стимулов, экономических методов мотивации недостаточно.
Подобные центры организуют сознательно.
Подобных центров имеется множество по всему земному шару.
Но, конечно, создание подобных центров – это не дело одного дня.
Им нужна постоянная практика общения не только со сверстниками, но и с людьми старшего возраста, а для этого должны быть созданы подобные центры.
Чаще всего подобные центры оказываются расположенными в «спальных» районах, либо за городом, фактически на пустыре, возле крупной магистрали.
Поэтому было решено создать здесь подобный центр, в котором были воспроизведены основные внутренние помещения знаменитого дома, где гости могли любоваться и неровным полом, и причудливыми линиями стен, и буйными красками, придающими дому сказочно-карнавальный вид.
На нём был монитор, что меня удивило, не думал, что подобный центр возможен в армии, куда я очевидно попал.
Главной целью подобных центров является повышение доступности первичного медицинского ухода, организация качественного лечения в удобное время, снижение нагрузки на дорогостоящие стационары.
Он даже не знал в деталях о существовании подобных центров.
Подобные центры должны быть в каждом крупном городе, в каждой европейской стране.
Ассоциации к слову «подобный»
Ассоциации к слову «центр»
Синонимы к словосочетанию «подобные центры»
Цитаты из русской классики со словосочетанием «подобные центры»
- В другом месте видел Райский такую же, сидящую у окна, пожилую женщину, весь век проведшую в своем переулке, без суматохи, без страстей и волнений, без ежедневных встреч с бесконечно разнообразной породой подобных себе, и не ведающую скуки, которую так глубоко и тяжко ведают в больших городах, в центре дел и развлечений.
- (все
цитаты из русской классики)
Сочетаемость слова «центр»
- торговый центр
музыкальный центр
учебный центр - в центре зала
в центре комнаты
в центре круга - в сторону центра
директор центра
здание центра - центр сообщил
центр работает
центр считает - находиться в центре
стоять в центре
оказаться в центре - (полная таблица сочетаемости)
Значение слова «подобный»
-
ПОДО́БНЫЙ, –ая, –ое; –бен, –бна, –бно. 1. кому-чему. Сходный с кем-, чем-л., похожий на кого-, что-л. (Малый академический словарь, МАС)
Все значения слова ПОДОБНЫЙ
Значение слова «центр»
-
ЦЕНТР, -а, м. 1. Мат., физ. Точка пересечения каких-л. осей, линий в фигуре, точка сосредоточения каких-л. отношений в теле. Центр давления. Центр линзы. Центр окружности. Центр подобия. Центр симметрии. Центр эллипса. (Малый академический словарь, МАС)
Все значения слова ЦЕНТР
Афоризмы русских писателей со словом «подобный»
- Тот счастлив, кто прошел среди мучений,
Среди тревог и страсти жизни шумной,
Подобно розе, что цветет бездумно,
И легче по водам бегущей тени. - О, Лермонтов презрением могучим
К бездушным людям, к мелким их страстям
Ты был подобен молниям и тучам,
Бегущим по нетронутым путям,
Где только гром гремит псалмом певучим. - Родина — это огромное, родное, дышащее существо, подобное человеку, но бесконечно более уютное, ласковое, беспомощное, чем отдельный человек.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
ПОДО́БНЫЙ, –ая, –ое; –бен, –бна, –бно. 1. кому-чему. Сходный с кем-, чем-л., похожий на кого-, что-л.
Все значения слова «подобный»
ЦЕНТР, -а, м. 1. Мат., физ. Точка пересечения каких-л. осей, линий в фигуре, точка сосредоточения каких-л. отношений в теле. Центр давления. Центр линзы. Центр окружности. Центр подобия. Центр симметрии. Центр эллипса.
Все значения слова «центр»
- региональный центр
- культурный центр
- крупные центры
- единый центр
- различные центры
- (ещё синонимы…)
- подобие
- аналогичный
- аналогия
- (ещё ассоциации…)
- город
- серёдка
- центробанк
- круг
- середина
- (ещё ассоциации…)
- подобный образ
- подобное развитие событий
- не ожидать подобного
- (полная таблица сочетаемости…)
- торговый центр
- в центре зала
- в сторону центра
- центр сообщил
- находиться в центре
- (полная таблица сочетаемости…)
- Разбор по составу слова «подобный»
- Разбор по составу слова «центр»
- Как правильно пишется слово «подобный»
- Как правильно пишется слово «центр»
Математика
260. Возьмем два круга O и O1 (чер. 254 и 255). Построим радиус OA и параллельный ему радиус другого круга O1A1, который имеет одинаковое направление с OA, или O1A11 тоже параллельный OA, но имеющий обратное с ним направление. Построим затем прямые AA1 и AA11, проходящие чрез концы этих радиусов. Тогда представляется следующая задача:
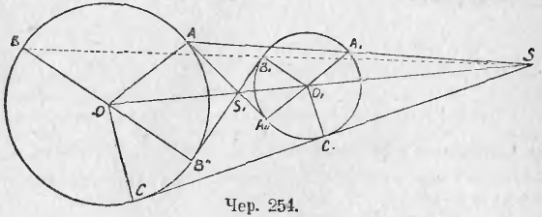
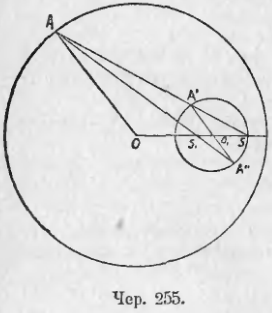
По данным радиусам R и r кругов и по расстоянию их центров OO1 = d найти расстояние от одного из центров (напр., от O) точек пересечения линий центров с прямою AA1 и с прямою AA11.
Назовем OS чрез x; тогда O1S = x – d. ∆OAS
∆O1A1S, следовательно, OS/O1S = OA/O1A1 или x/(x – d) = R/r, откуда rx = Rx – dR.
Определяя отсюда x, получим
Отсюда мы видим, что положение точки пересечения S прямых OO1 и AA1 не зависит от того, в каком направлении от центра мы построили параллельные радиусы OA и O1A1, так что прямая BB1, соединяющая концы другой пары параллельных радиусов OB и O1B1, должна пройти чрез точку S и, кроме того, имеем (∆O1SB1
∆OSB): SB1/SB = r/R. Таким образом точка S обладает всеми свойствами внешнего центра подобия двух подобно расположенных фигур.
Также, называя OS1 чрез y, получим S1O1 = d – y и из подобия ∆OAS1 и ∆O1A11S1: y(d – y) = R/r. Отсюда находим yr = dR – yR и
Отсюда видим, что положение точки S1 также не зависит от того, какую именно пару параллельных, но идущих в обратных направлениях, радиусов мы взяли. Чрез эти же точку S1 должна пройти прямая B1B11, соединяющая концы радиусов OB11 и O1B1 параллельных, но имеющих обратные направления. Кроме того, имеем (∆O1B1S1
Таким образом точка S1 обладает всеми свойствами внутреннего центра подобия двух кругов.
Если один круг лежит внутри другого (чер. 255), то оба центра подобия расположены внутри меньшего круга: внешний лежит вне отрезка OO1, а внутренний — внутри его.
Центры O и O1 также соответствуют друг другу, так как SO1/SO = r/R (из подобия ∆OAS и ∆O1A1S) и S1O1/S1O = r/R (из подобия ∆S1O1A11 и ∆S1OA).
Итак, всякие два круга подобно расположены и имеют два центра подобия — внутренний и внешний; центру одного круга соответствует центр другого и любой точке одного соответствует та точка другого, которая расположена на радиусе, параллельном радиусу первого круга, идущему чрез взятую точку, и имеющем то же или обратное направление. Обратно: если чрез S построить любую прямую A и соответствующие точки пересечения соединить с центрами, то полученные радиусы должны быть параллельны между собою.
261. Если окажется, что радиус, напр., O1C1 (чер. 254), перпендикулярен к прямой SC1, то и радиус OC, соединяющий центр O другого круга с его точкою C, соответствующей точке C1, должен быть также перпендикулярен к SC. Отсюда следует, что касательная из точки S к одному из наших кругов должна касаться и другого круга. Точно так же, если построим касательную к одному кругу чрез точку S1, то она должна касаться и другого круга.
Этим пользуются для решения задачи: построить общую касательную к двум данным кругам .
Надо найти сначала их центры подобия, для чего надо построить радиус OA и параллельный ему диаметр A1A11 второго круга (чер. 254). Соединив концы A и A1, найдем внешний центр подобия S и соединив A и A11, найдем внутренний центр подобия S1. Затем чрез найденные центры подобия S и S1 построим касательные к одному кругу — они и должны быть общими касательными. Всего общих касательных у двух кругов может быть 4. Если два круга имеют внешнее касание, то точка касания служит их внутренним центром подобия, и общих касательных тогда будем иметь 3; если два круга пересекаются, то внутренний ценр подобия лежит внутри обоих кругов, и из него нельзя построить касательных, – тогда получим только две общих касательных чрез внешний центр подобия; если 2 круга имеют равные радиусы, то внешний центр подобия удаляется в бесконечность и тогда две внешних касательных параллельны линии центров; если два круга имеют внутреннее касание, то точка касания служит их внешним центром подобия, – тогда возможна лишь одна общая касательная; если, наконец, один круг внутри другого, то оба центра подобия расположены внутри обоих кругов, и общих касательных вовсе не существует.
262. Можно применить понятие о центре подобия кругов к решению задачи, которую раньше мы решили другим способом (п. 227 зад. 3): построить круг, касающийся двух пересекающихся прямых и проходящий чрез данную точку .
Точка пересечения данных прямых является внешним центром подобия искомого круга и какого-либо еще касающегося данных прямых и расположенного внутри того же угла, где лежит данная точка, но не проходящего чрез эту точку. Последний круг легко построить. Затем найдем на нем точку, соответствующую данной, построим чрез найденную точку радиус построенного круга, а чрез данную точку построим прямую, параллельную этому радиусу, – точка пересечения ее с биссектором угла и должна быть центром искомого круга. Задача имеет 2 решения, так как у построенного сначала круга можно найти 2 точки, любую из которых можно принять за соответствующую данной.
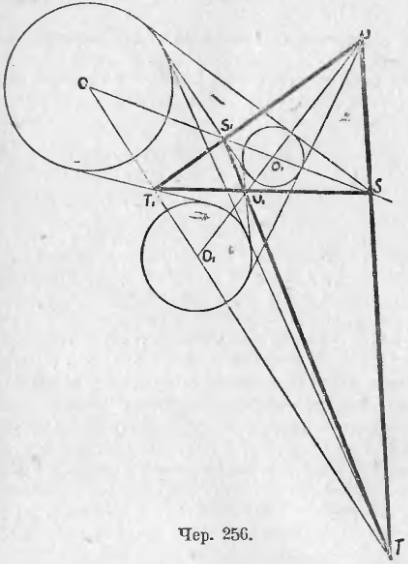
263. Если возьмем три каких-либо круга O, O1 и O2 (чер. 256), то они попарно подобно расположены и к ним применимо свойство п. 256. У этих трех кругов всего 6 центров подобия и они располагаются на четырех прямых: UST, US1T1, SU1T1 и TS1U1. Чрез каждый центр подобия проходят 2 из этих четырех прямых.
264. Степень точки относительно круга . В п. 222 мы познакомились с понятием о степени точки относительно круга. Этим именем называется, как мы знаем, произведение отрезков какой-либо прямой, проходящей чрез эту точку и пересекающей круг, от этой точки до точек пересечения прямой с кругом. Если точка вне круга, то это произведение равно квадрату касательной из нашей точки к ругу; если точка внутри круга, то это произведение равно квадрату половины хорды, делящейся в этой точке пополам. Чтобы отличить первый случай от второго, считают степень точки во втором случае отрицательною и перед указанным квадратом половины хорды ставят знак минус.
Пусть имеем круг O (чер. 257) и точку M вне его. Построив касательную MA и прямые MO и OA, найдем из прямоугольного треугольника AOM, что степень точки M = MA 2 = OM 2 – OA 2 = OM 2 – R 2 , где OA обозначаем чрез R.
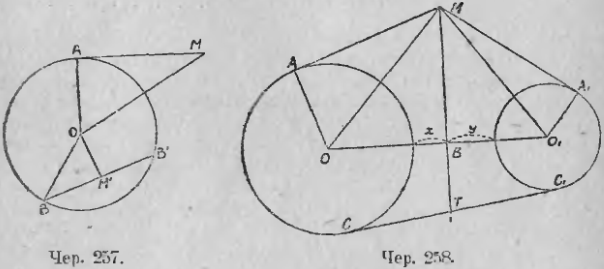
Возьмем теперь точку M1 внутри круга. Степень этой точки равна произведению отрезков хорды M1B и M1B’, взятому со знаком минус. Если эта хорда перпендикулярна к прямой OM1, соединяющей точку M1 с центром, то хорда делится в точке M1 пополам и M1B1 = M1B и, следовательно, степень точки M1 = –M1B 2 . Из прямоугольного треугольника OM1B найдем: M1B 2 = OB 2 – OM1 2 = R 2 – OM1 2 , а, следовательно, степень точки M1 = – M1B 2 = –(R 2 – OM1 2 ) = OM1 2 – R 2 .
В обоих случаях степень точки выражается одинаково: она равна квадрату расстояния точки от центра минус квадрат радиуса.
Если точка лежит на круге, то легко увидим, что ее степень равна нулю.
265. Пусть теперь имеем 2 круга O и O1 (чер. 258). Возникает вопрос, не существует ли таких точек, степени которых относительно обоих кругов равны между собой. Если такие точки существуют, то где они расположены? Допустим, что M такая точка. Называя радиус OA чрез R и радиус O1A1 чрез r, имеем для этой точки M

Из этого равенства и их равенства OB + O1B = d мы можем определить отрезки OB и O1B, – получим для каждого одно решение (уравнения первой степени), откуда заключаем, что точка B вполне определена. Отсюда выводим: если бы мы нашли другую точку M1, степени которой относительно наших кругов равны, и на нее опустим перпендикуляр на линию центров, то он должен пройти чрез ту же точку B и, следовательно, слиться с MB. Следовательно, все точки, степени которых относительно двух кругов равны, расположены на перпендикуляре к линии центров. Этот перпендикуляр носит название — радикальная ось двух кругов. Обратно, легко показать, что всякая точка перпендикуляра MB имеет равные степени относительно наших кругов.
Из равенства (2) видим: 1) если R = r, то OB – O1B = 0 и OB = O1B, т. е. радикальная ось двух равных кругов делит расстояние между их центрами пополам; 2) если R > r, то OB > O1B, т. е. радикальная ось расположена ближе к центру меньшего круга.
Но, если мы назовем чрез x и y расстояния точки B от круга O и от круга O1 (мы применяемся к случаю данному на чертеже: круги расположены один вне другого), то OB = R + x, O1B = r + y и, подставив в равенство (2), найдем:
f48
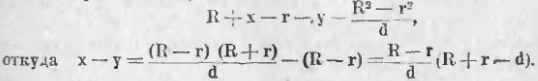
У нас R + r 0 (ибо считаем, что R > r). Тогда из последнего равенства вытекает x 2 = TC1 2 , или TC = TC1, т. е. общая касательная двух кругов делится радикальною осью пополам.
Если два круга пересекаются, то радикальная ось должна пройти чрез точки пересечения, так как степень каждой из этих точек одинакова относительно каждого круга (она равна нулю); для построения радикальной оси в этом случае следует лишь построить прямую, определяемую этими точками пересечения.
Если два круга касаются, то радикальная ось есть перпендикуляр к линии центров чрез точку касания.
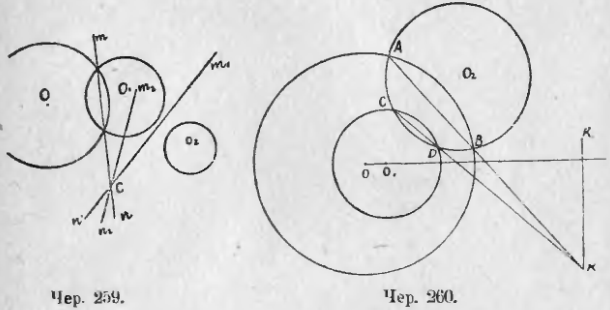
266. Пусть имеем 3 круга O, O1 и O2 (чер. 259). Построив радикальные ости mn и m1n1 двух пар кругов, мы найдем, что они пересекаются в какой-либо точке C, если только центры всех трех кругов не расположены на одной прямой. Так как точка C лежит на оси m1n1, то степени ее относительно кругов O1 и O2 одинаковы. Отсюда следует, что точка C имеет одинаковые степени и относительно кругов O и O2, т. е. она должна лежать на радикальной оси последней пары кругов. Итак,
Радикальные оси трех кругов, взятых попарно, пересекаются в одной точке, которая называется радикальным центром трех рассматриваемых кругов.
Если из радикального центра построить касательные ко всем трем кругам, то они равны между собою.
Если три круга попарно пересекаются, то их общие хорды проходят чрез одну точку (общая хорда двух пересекающихся кругов есть их радикальная ось).
267. Свойством предыдущего п. можно воспользоваться для построения радикальной оси для двух непересекающихся кругов . Пусть даны круги O и O1 (чер. 260). Построим третий круг O2 чтобы его центр не лежал на линии центров OO1 и чтобы он пересекался с каждым из данных кругов: с кругом O и точках A и B и с кругом O1 в точках C и D. Тогда AB есть радикальная ось кругов O и O2, CD — радикальная ось кругов O1 и O2, точка пересечения K прямых AB и CD есть радикальный центр наших трех кругов. Построив прямую KK1 ⊥ OO1, получим радикальную ось кругов O и O1.
268. Построить круг, касающийся данного круга и проходящий чрез две данных точки .
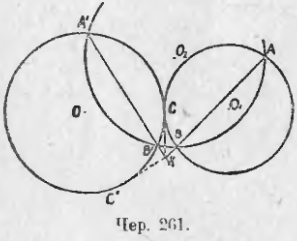
Пусть дан круг O и точки A и B (чер. 261). Воспользуемся предыдущею задачею. Искомый круг должен касаться данного; следовательно, радикальною осью этой пары кругов должна служить их общая касательная. Если бы ее удалось построить, то легко было бы построить и искомый круг. Для построения этой радикальной оси воспользуемся, как в предыдущем п., третьим кругом O2, пересекающим и данный и искомый круг. Но у искомого круга мы знаем пока только 2 точки A и B; следовательно, и этот третий круг O2 мы можем построить лишь так, чтобы он проходил чрез точки A и B. Итак, построим любой круг O2, проходящий чрез точки A и B и пересекающий круг O, напри., в точках A’ и B’. Тогда прямая AB есть радикальная ось искомого круга и круга O2, прямая A’B’ есть радикальная ось кругов O и O2, а точка их пересечения K есть радикальный центр всех трех кругов. Теперь нетрудно построить радикальную ось круга O и искомого, так как она должна касаться круга O: надо чрез точку K построить касательную к кругу O, а их можно построить две KC и KC’ (C и C’ точки касания). Тогда получим два решения: 1) искомый круг определяется точками A, B и C и 2) искомый круг определяется точками A, B и C’.
269. Мы имеем в виду решить еще две задачи на построение кругов: 1) построить круг, касающий двух данных кругов и проходящий чрез данную точку; и 2) построить круг, касающийся трех данных кругов (задача Аполлонин). Для этого надо познакомиться еще с некоторыми свойствами центра подобия и радикальной оси двух кругов.
Чрез центр подобия S кругов O и O1 (чер. 262) построена общая касательная SCC1 к этим кругам и секущая SB, соответственные точки которой суть A и A1, B и B1.

270. Пусть круг M касается кругов O и O1 (чер. 263), обоих внешним образом в точках A и B. Построим прямую AB и пусть эта прямая пересекает еще круг O в точке B1 и круг O1 в A1. Тогда OAM есть прямая, – следовательно, углы при основаниях в равнобедренных треугольниках OAB1 и MAB равны; также O1BM есть прямая и, следовательно, углы при основании в равнобедренном треугольнике O1A1B равны углам в ∆MAB (на чертеже равные углы отмечены). Отсюда заключаем, что O1A1 || OA и O1B || OB1, откуда следует, что прямая B1ABA1 проходит чрез внешний центр подобия кругов O и O1. Итак, если круг касается двух других, то точки касания расположены на прямой, проходящей чрез центр подобия, но не суть соответственные точки .
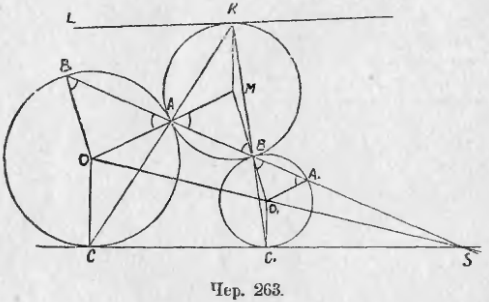
Мы разобрали случай, когда M с O и с O1 имеет внешнее касание; также будет и для случая, когда M с O и с O1 имеет внутреннее касание; но если M имеет с одним из кругов внешнее касание, а с другим внутреннее, то вместо внешнего центра подобия надо взять внутренний. Поэтому в предыдущем заключении мы и не указали, чрез какой именно центр подобия проходит прямая, соединяющая точки касания.
Если построить еще общую касательную SC1C, то прямые CA и C1B, как мы знаем, пересекаются в точке K, лежащей на радикальной оси кругов O и O1. Но можно выяснить еще, что точка K лежит на круге M.
Точка A есть внутренний центр подобия кругов O и M, причем точке O соответствует точка M, радиус OC (который ⊥ SC) соответствует некоторый радиус MX круга M, который параллелен OC, но имеет обратное с ним направление. Точка B есть внутренний центр подобия кругов O1 и M, причем точке O1 соответствует точка M и радиус O1C1 круга O1 соответствует некоторый радиус MY круга M, который параллелен радиусу O1C1, но имеет обратное с ним направление. Отсюда следует, что радиусы MX и MY параллельны друг другу (ибо O1C1 || OC) и одинаково направлены, но они имеют общую точку M, – следовательно, они совпадают. С другой стороны, точка X должна лежать на прямой CA и точка Y на прямой C1B. Поэтому совпадение радиусов MX и MY требует, чтобы точка X и точка Y совпали с точкою K, где пересекаются прямые CA и C1B. Следовательно, точка K есть конец радиуса MK круга, и M, и K лежит на круге M.
Далее прямой SC относительно центра подобия A должна соответствовать прямая KL, проходящая чрез K (ибо SC проходит чрез C) и параллельная SC. Кроме того, прямая KL ⊥ MK, ибо SC ⊥ OC (радиусы OC и MK соответствуют друг другу). Поэтому прямая KL касается круга M в точке K. К тому же результату придем, рассматривая соответствие относительно центра подобия B.
271. Теперь мы можем приступить к решению первой из намеченных задач: даны круги O и O1 и точка P (чер. 264). Требуется построить круг, касающийся кругов O и O1 и проходящий чрез P.
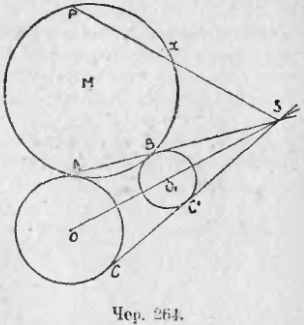
Пусть M искомый круг и точки A и B суть точки касания. Тогда легко найти точку X, где луч SP (S центр подобия кругов O и O1) пересекает круг M. Мы имеем:
SP · SX = SA · SB = SC · SC1 (п. 269)
Отсюда SX/SC = SC1/SP, т. е. отрезок SX есть четвертый пропорциональный к трем известным отрезкам SC, SC1 и SP, – построить его мы умеем. Тогда задача сведется к задаче п. 268.
272. Задача Апполония . Даны три круга O1, O2 и O3 (чер. 265). Построить круг, касающийся трех данных.
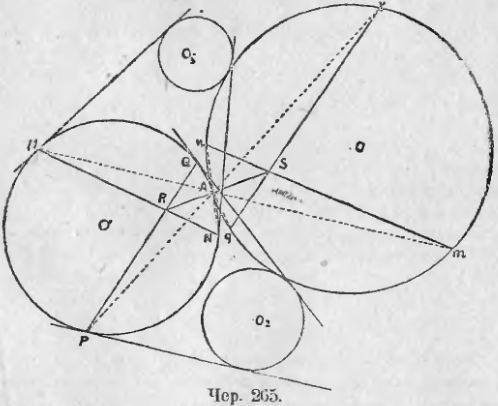
Мы будем рассуждать лишь в предположении, что мы ищем круг, касающийся каждого из данных внешним образом. Применить к другим случаям не представит затруднений (всего задача имеет 8 решений).
Пусть круг O есть искомый и A есть точка касания кругов O и O1; тогда прямой MN, соединяющей точки касания M и N общих касательных для кругов O1 и O3, соответствует относительно центра подобия A (точка A есть внутренний центр подобия кругов O1 и O) радикальная ось mn кругов O1 и O3: точке M соответствует точка m, лежащая на круге O и на радикальной оси кругов O1 и O3 (п. 270) и также точке N соответствует точка n, лежащая на радикальной оси кругов O1 и O. Точно так же прямой PQ, соединяющей точки касания круга O1 с общими касательными для кругов O1 и O2, соответствует радикальная ось pq кругов O1 и O2.
Точке R, где MN и PQ пересекаются, соответствует точка S, где mn и pq пересекаются, т. е. радикальный центр кругов O1, O2 и O3. Поэтому точки R и S лежат на одной прямой с A.
Точки R и S мы можем построить; соединив их, получим (между ними) точку касания искомого круга с кругом O1, после чего задача легко решается.
Подобие фигур
Подобие фигур — это две геометрические фигуры или два геометрических тела называются подобными, если одно представляет собой уменьшенную модель другого.
Содержание:
Понятие подобия фигур
В окружающем мире часто встречаются предметы, одинаковые по форме, но различные по размерам: мыльный пузырь и футбольный мяч, небольшая модель ледокола и сам корабль, карты, фотоснимки различных размеров одного и того же здания. В геометрии такие фигуры называют подобными.
Существуют фигуры, которые всегда подобны друг другу, например, круги, квадраты, кубы.
Для обозначения подобия фигур употребляется знак  . На рисунке 2.434 изображены подобные фигуры
. На рисунке 2.434 изображены подобные фигуры  . Запись
. Запись  читается: фигура
читается: фигура  подобна фигуре
подобна фигуре 
Для подобных фигур вводится понятие — коэффициент подобия, он обозначается k; k всегда больше нуля. Коэффициент подобия показывает, в каком отношении находятся соответствующие расстояния между точками фигур. На рисунке 2.434 коэффициент подобия можно определить, найдя отношения сторон квадратиков изображенной сетки.

Подобие фигур широко используется при разработке планов построек зданий или при изображении на картах городов или других участков земной поверхности. Всякий план или карта является подобным изображением реального объекта или участка земной поверхности, т. е. фигурой, подобной реальному объекту. При этом план или карта может изображать реальный объект в разном масштабе.
Определение. Масштаб — это коэффициент подобия соответствующих фигур.
Подобие треугольников
На рисунке 2.435 изображены два чертежных прямоугольных треугольника с острыми углами в 60° и 30°. Стороны второго треугольника по сравнению с первым уменьшены в два раза:  У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны:
У этих треугольников углы попарно равны. Стороны, лежащие против разных углов, пропорциональны:  Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.
Такие треугольники называют подобными. Стороны, лежащие против равных углов, называют сходственными.

Определение. Подобными называют треугольники, у которых углы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так:  Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия. В случае, изображенном на рисунке 2.435, коэффициентом подобия треугольников  будет число 2. Если же взять отношения
будет число 2. Если же взять отношения  , коэффициент подобия будет равен
, коэффициент подобия будет равен  .
.
Подобные треугольники могут быть произвольно расположены как на плоскости, так и в пространстве.
Если фигуры равны, то они подобны с коэффициентом подобия, равным 1. Если фигуры подобны, то они не обязательно равны.
Теорема 1. (Лемма о подобии треугольников). Прямая, пересекающая две стороны треугольника и проведенная параллельно третьей стороне, отсекает треугольник, подобный данному.
Для выявления подобия треугольников существуют признаки подобия треугольников.
Теорема 2. (Первый признак — по двум равным углам.) Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Следствия из этой теоремы.
1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Теорема 3. (Второй признак — по пропорциональности двух сторон и равенству углов между ними.) Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 4. (Третий признак — по пропорциональности трех сторон.) Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Подобие многоугольников
Определение. Если стороны одного многоугольника пропорциональны сторонам другого многоугольника и соответственные углы этих многоугольников равны, то такие многоугольники подобны.
На рисунке 2.436 изображены два подобных пятиугольника  , у них
, у них 
 а также
а также  k – коэффициент подобия.
k – коэффициент подобия.
Для многоугольников с числом сторон больше трех признак подобия, аналогичный третьему признаку подобия треугольников, будет неверен. Например, квадрат и ромб, отличный от квадрата, не будут подобны, хотя их стороны пропорциональны (рис. 2.437). Недостаточно для подобия двух прямоугольников и равенства их соответствующих углов. Например, квадрат не подобен четырехугольнику, не все стороны которого равны (рис. 2.438).


Теорема 6. Отношение периметров подобных многоугольников равно отношению их сходственных сторон (коэффициенту подобия).
Теорема 7. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
Смотрите также дополнительные лекции по предмету “Математика”:
Основные теоремы, связанные с окружностями
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Теорема 1.
1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
Доказательство:
1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) .
2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) .
Теорема 2.
Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large<angle K_1AK_2=90^circ>>]
Доказательство:
1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) .
2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) .
Теорема 3.
Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large<triangle AB_1C_1 sim triangle AB_2C_2>>] [(2) <large>]
Доказательство:
1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) .
2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) .
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]
Доказательство
Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) :
Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom <00000000000>(1)]
Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom <00000000000>(2)]
Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд.
Формула Эйлера:
Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>]
Доказательство:
а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) .
Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) .
Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)) .
С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y))
Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)) .
Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:
(dfrac=dfrac Rightarrow dfrac=dfrac <2R>Rightarrow BQcdot AB_1=2Rr) .
Подставим это в ((**)) и получим:
(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) .
б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).
Теорема о бабочке:
Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>]
Доказательство:
Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) .
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle PMO=angle NKO, angle MPO=angle KNO) .
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2, angle XOX_2=angle YOY_1) .
Следующие прямоугольные треугольники подобны:
1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac)
2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac)
3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac)
4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac)
Из 1) и 2) следует, что
Из 3) и 4) следует, что
Совместив последние два равенства, получим:
Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит:
Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)
[spoiler title=”источники:”]
http://natalibrilenova.ru/podobie-figur/
http://shkolkovo.net/theory/41
[/spoiler]
Антарес — сердце Скорпиона
Время на прочтение
4 мин
Количество просмотров 13K
У этой звезды есть двойник — на другой стороне неба
Видеоверсия статьи в конце

Короткими летними ночами над горизонтом северных широт крадучись поднимается одно из самых мистических (в нашем восприятии) зодиакальных созвездий — созвездие Скорпиона. Его возглавляет оранжевый Антарес — звезда со странным именем. В основе этого имени — название планеты, а если быть еще точнее — имя греческого бога войны — Ареса, который у греков всегда был связан с кроваво-красной планетой Марс. И только римляне потом навязали миру имя планеты — Марс — тоже по имени своего бога Войны.

В средних северных широтах Скорпион полностью не восходит. На широте Москвы (и большинства других российских городов) появляется только самая макушка — “Клешни Скорпиона”. А протяженный хвост с ядовитым жалом (в нем расположена пара звезд “Кошачьи глаза”) можно видеть только в субтропиках и южнее.

К счастью, Антарес находится недалеко от клешней. И хотя сейчас мы называем его именно — “Анти-Марс” — если переводить название буквально, поскольку название это возникло в результате хронической путаницы — звезду часто принимали за красную планету и наоборот, ведь каждые 2 года Марс заходит в созвездие Скорпиона — но в древности альфа Скорпиона имела сразу несколько названий, никак с планетами не связанных. Арабы, подарившие астрономии большую часть звездных имен, величали его Калб-аль-Акраб («Сердце Скорпиона»). У персов звезда называлась Сатевис. В Индии — Джьештха.
(Движение планеты Марс по созвездию Скорпиона в период с 20.02.2048 по 24.09.2048)
Забавно, что в средние века итальянцы назвали Антарес “Вечерней звездой” — Веспертелино, что вносило еще одну путаницу с планетой, но в данном случае уже — с Венерой.
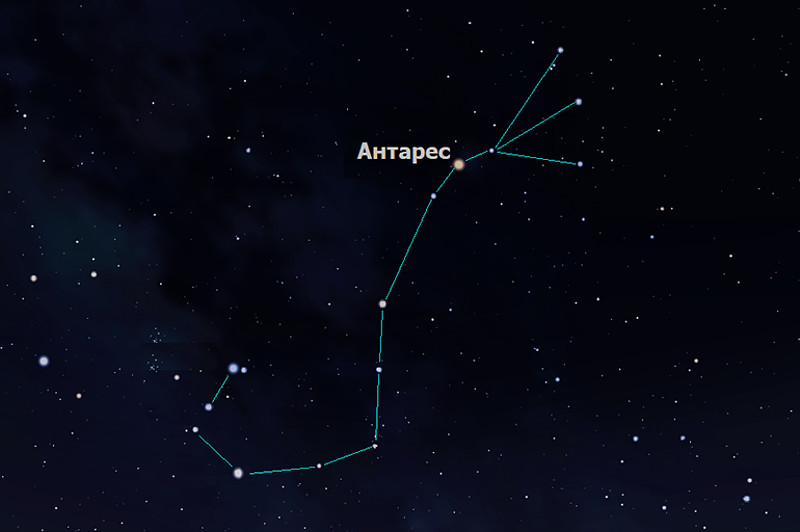
Лучшее время для наблюдения Антареса — вторая половина весны и все лето. Осенью Антарес теряется в вечерних сумерках и до середины весны вновь становится недоступным наблюдениям. У Антареса есть звезда-антипод — красно-оранжевая Бетельгейзе — альфа созвездия Ориона. Согласно греческой мифологии Орион был ужален Скорпионом и погиб от этого ядовитого укуса. Но Зевс спас душу величайшего из охотников, водворив её на небо в виде самого яркого созвездия. А чтобы Орион и Скорпион более не встречались, Скорпион оказался в противоположной части небесного глобуса, и как только восходит Орион, Скорпион тут же прячется за горизонт. Увидеть одновременно два этих созвездия в северных широтах нельзя. И главные звезды этих созвездий — Антарес и Бетельгейзе — никогда не сияют на небе одновременно.
Но эти звезды похожи.
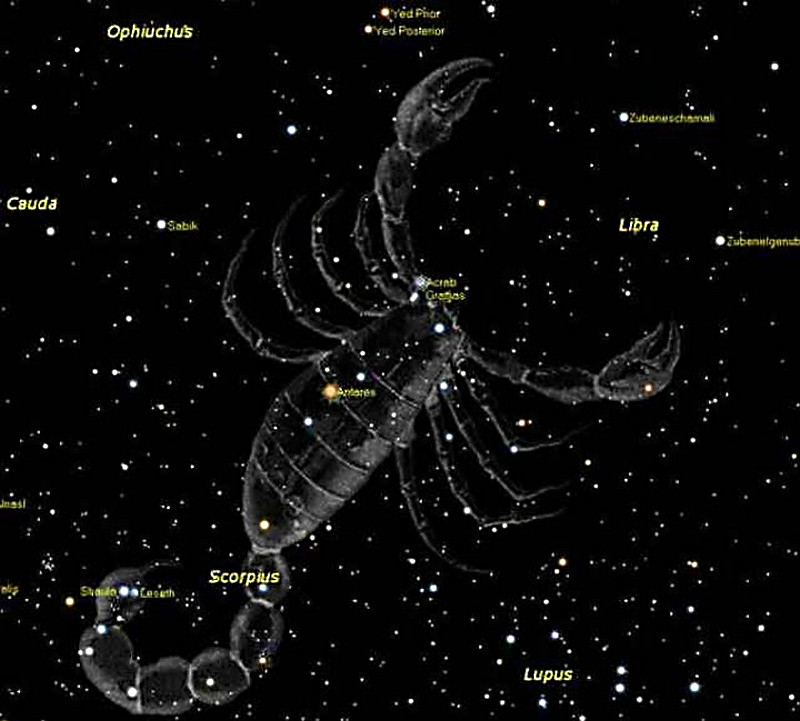
Красные сверхгиганты удаленные от Солнца на 600 световых лет, обладающие неправильной или полуправильной переменностью, находящиеся на финальной стадии эволюции, столь огромные в размерах, что любая из этих звезд (оказавшись на месте Солнца) поглотила бы своими раскаленными недрами все планеты, включая тот самый Марс (чтобы больше не путался под ногами). Используя VLT — “Очень Большой Телескоп” (расположенный в чилийской пустыне Атакама) — астрономы практически синхронно смогли построить первые карты поверхности и для Антареса, и для Бетельгейзе.

Пару последних лет вся мировая общественность астрономов-любителей ожидала взрыв Бетельгейзе. Этого пока не произошло. И теперь никто не знает, кто рванет раньше — Бетельгейзе или Антарес?
Однако, у Антареса есть спутник — это отличает его от Бетельгейзе. Хоть что-то нашлось, в противном случае эти звезды можно было бы считать звездами-близнецами.
Антарес B — имеет отчетливый зелено-голубой оттенок и является непростым объектом для наблюдений. Расстояние между звездами составляет чуть менее 3 секунд дуги, и яркий Антарес A чаще всего поглощает своим сиянием несколько более слабый Антарес B.
Блеск звезд составляет +1m и +5,5m.

Утверждается, что в любительский телескоп разделить Антарес на компоненты A и B можно только при покрытии звезды Луной — такое случается иногда. Луна поочередно закрывает один компонент, потом другой, а затем звезды так же поочередно появляются из-за лунного диска — с разницей в несколько секунд. Именно таким образом и был открыт Антарес B — в 1819 году. Но за 200 лет любительские телескопы успели заметно вырасти в размерах и качестве. И лично я хорошо помню, что видел Антарес B вне всяких покрытий в телескоп “Мицар” (диаметр зеркала 110 миллиметров) без особого труда.
Антарес B — только кажется слабым спутником оранжево-красного исполина. Сам по себе он тоже звезда-гигант — в 7 раз более массивный, чем Солнце, очень горячий (18 тысяч градусов — температура поверхности) и с общей светимостью превышающей солнечную почти в 3000 раз.
В спектре Антареса B обнаружено довольно много линий тяжелых химических элементов, очевидно захваченных от Антареса A, хотя звезды не столь близки в нашем понимании — их разделяет расстояние в 500 астрономических единиц или 80 млрд. километров — это можно сравнить с расстоянием между Солнцем и далекой холодной Седной — самой дальней из известных карликовых планет, подобных Плутону. Тем не менее звездный ветер Антареса A, постоянно “обдувает” Антарес B, обогащая его атмосферу теми химическими элементами, которые естественным путем там образоваться сами не могли.
Пара этих звезд совершает оборот вокруг общего центра масс более чем за тысячу лет. Для двойных звезд это очень небольшой период обращения.

На звездной карте Антарес расположен в крайне богатом интересными астрономическими объектами районе. Проходящий здесь Млечный путь наиболее широк и ярок — это не удивительно, ведь именно в этом направлении расположен центр нашей Галактики, скрытый темными пылевыми облаками и туманностями.
Антарес — являясь весьма ярким светилом (его светимость превосходит солнечную в 60 000 раз) подсвечивает обширную туманность, в которой идет активное звездообразование. Еще несколько туманностей — подсвеченных другими, более далекими, звездами — можно обнаружить в этой же области неба. Иногда кажется, что туманности практически сливаются друг с другом. Это иллюзия — все они находятся на очень разном расстоянии от нас, и только их проекции на небесную сферу накладываются друг на друга. Тем не менее эта совокупность туманностей называется комплексом туманностей Антареса, или даже — совсем просто — Туманность Антареса.
В завершении этого небольшого обзора оставляю Вам видеоролик, на котором Антарес и его небесное окружение видно во всей красе.
Звучит фрагмент моего музыкального альбома «Туманность Антареса». Полностью альбом можно послушать на специальной странице.
Видео-версия статьи