Показательный закон как найти плотность функции

Непрерывная случайная
величина
имеетпоказательный
(экспоненциальный)
закон распределения, если её плотность
вероятности задаётся равенствами:

(23)

гдепараметр
распределения.

График функции плотности
приведён
на рис. 32.

Рис. 32.

Теорема 9. 6. Для
показательного
закона непрерывной случайной величины

имеют
место формулы:

1.

2.
.

Доказательство.Вычислим функцию
распределения показательного закона.
По определению имеем

,

Найдём
числовые характеристики:

Согласно определению
математического ожидания н.с.в.(формула (7), пункта 1., Т. 8.), и с учётом
определения функции плотности имеем:

Вычисляя
интеграл по частям, получим

Вычислим
дисперсию на основе формулы (15) (п.2.,
Т.8.). С учётом равенства имеем

Дважды
применяя интегрирование по частям,
после несложных вычислений получим

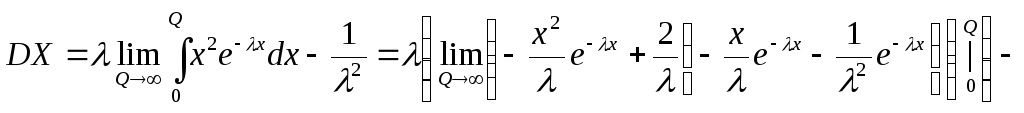
Извлекая,
квадратный корень из
получим,Теорема доказана.

Отметим,
также имеет место дифференциальный
закон
(проверьте!).

Характерное свойство
показательного распределения является
определением одним единственным
параметром
,
и все числовые характеристики также
определены тем же параметром. Обычно,
значения функциинаходят
по таблице.

Следствие. Вероятность
попадания с.в.
,
в интервале,
распределенной по показательному
закону, вычисляется по формуле

(24)

Доказательство прямо
выводится из формулы (13), п. 5., Т. 7., с
учётом равенства 1.
, теоремы 6. Действительно, имеем

Пример 8. Пусть
случайная величина
выражает
время работы некоторого элемента
микросхемы и имеет показательное
распределение. Найти вероятность того,
что элемент микросхемы проработает не
менее 800 часов, если среднее время работы
элемента равна 400 часов (т.е. м.о. равно
400).

Решение. Так
математическое ожидание равно 400, то
Следовательно, искомая вероятность

Пример 9.
Непрерывная случайная величина
распределена
по показательному закону с функцией
плотности

Найти
вероятность того, что в результате
испытания с.в.попадает
в интервал (0,3;1).

Решение.По условию задачиТогда по формуле (24) имеем

Задание.
Выписать явный вид функции распределения,
найти численные значения числовых
характеристик:

Замечаний:
1.
На практике часто встречаются показательно
распределённая случайная величина,
где параметр
неизвестен.
Если математическое ожидание также
неизвестно, то обычно находят его
приближенное значение, в качестве
которой принимают «выборочную среднюю».
Тогда приближенное значение параметранаходят с помощью равенства.

2.
Математическое ожидание и среднее
квадратическое отклонение показательного
закона равны между собой, поэтому в
приложениях их оценки должны различаться
незначительно. Если оценки окажутся
близкими одна к другой, то данные
наблюдений подтверждают гипотезу о
показательном распределении исследуемой
случайной величины; если же оценки
различаются существенно, то гипотезу
следует опровергнуть.

Показательное распределение широко
применяется в приложениях теории
вероятностей, особенно в теории массового
обслуживания, в физике, а также
используется для описания распределения
случайной величины вида: длительность
работы прибора до первого отказа,
длительность времени обслуживания в
системе массового обслуживания и т.д.
В частности в теории надёжности, где
одним из основных понятий является
функция надёжности.

Соседние файлы в папке Теория вероятностей от исмоилова

• #
• #
• #
• #
• #
• #
• #

  06.02.20162.36 Mб71~WRL0002.tmp

• #

  06.02.20161.87 Mб67~WRL0005.tmp

• #

  06.02.20161.01 Mб66~WRL0205.tmp

• #

  06.02.20162.41 Mб65~WRL0264.tmp

• #

  06.02.20162.17 Mб65~WRL0310.tmp

1 вопрос. Нормальное распределение.

2 вопрос. Нормальная кривая.

3 вопрос. Показательное распределение и его числовые характеристики.

1 вопрос. Нормальное распределение.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

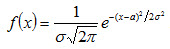. (4.14)

где а – математическое ожидание,

σ – среднее квадратическое отклонение Х.

Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и σ (σ >0).

Нормированным называют нормальное распределение с параметрами а=0 и σ =1.

Например, если Х – нормальная величина с параметрами а и σ, то U = (X – a) / σ – нормированная нормальная величина, причем M(U)=0, σ(U)=1.

Плотность нормированного распределения

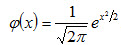. (4.15)

Эта функция табулирована (см. приложение 1).

Замечание 2. Функция F(x) общего нормального распределения

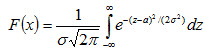, (4.16)

а функция нормированного распределения

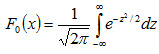. (4.17)

Функция F₀(x) табулирована. Легко проверить, что

.

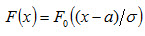Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал (0, x) можно найти, пользуясь функцией Лапласа 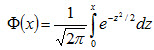. Действительно,

.

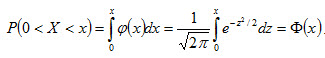Замечание 4. Учитывая, что 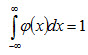(свойство 2), и, следовательно, в силу симметрии φ(x) относительно нуля

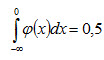, а значит, и  P (-∞ < X < 0) = 0,5,

легко получить, что

F₀(x) = 0,5 + Ф(x) .

Действительно,

F₀(x) = P(-∞ < X < x) = P(-∞ < X < 0) + P(0 < X < x) = 0,5 + Ф(x).

Вероятность того, что X примет значение, принадлежащее интервалу (α, β), равна

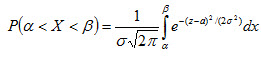. (4.18)

Преобразуя эту формулу, получим

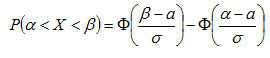, (4.19)

где 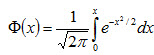– функция Лапласа.

Функцию Лапласа находим по таблице (см. приложение 2).

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероят­ность того, что X примет значение, принадлежащее интервалу (10, 50).

Решение.

Воспользуемся формулой (4.19). По условию, α=10, β=50, а=30, σ=10, следовательно,

.

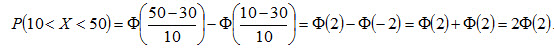По таблице приложения 2 находим  Ф(2) = 0,4772. Отсюда искомая вероятность

P(10 < X < 50) = 2 · 0,4772 = 0,9544.

2 вопрос. Нормальная кривая.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Исследуем функцию

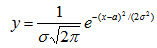
методами дифференциального исчисления.

Свойства нормальной кривой.

1. Очевидно, функция определена на всей оси х

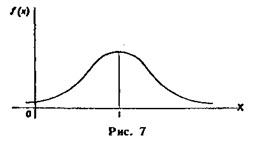
2. При всех значениях х функция принимает поло­жительные значения, т. е. нормальная кривая располо­жена над осью Ох.

3. Предел функции при неограниченном возрастании х по (абсолютной величине)

равен нулю: 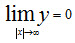, т.е. ось Ох служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум. Найдем первую производную:

.

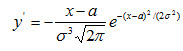Легко видеть, что у’=0 при х = а, у’>0 при х<а, у’ < 0 при х > а.

Следовательно, при х = а функция имеет максимум равный .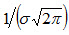

5. Разность х-а содержится в аналитическом выра­жении функции в квадрате, т. е. график функции симметричен относительно прямой х = а.

6. Исследуем функцию на точки перегиба. Найдем вторую производную:

.

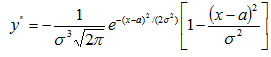Легко видеть, что при х=а+σ и х=а– σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 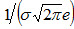). Таким образом, точки графика (а-σ, 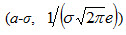) и (а+σ, 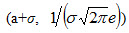) являются точками перегиба.

Как влияют на форму и расположение нормальной кривой значения параметров а и σ?

1. Изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает.
2. С возрастанием σ максимальная ордината нормальной кривой убывает, а сама кривая стано­вится более пологой, т. е. сжимается к оси Ох; при убывании σ нормальная кривая становится более «островершинной и растягивается в положительном направле­нии оси Оу.

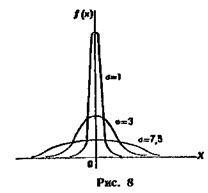
При а = 0 и σ = 1 нормальную кривую 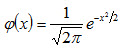называют нормированной.

3 вопрос. Показательное распределение и его числовые характеристики.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

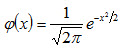(4.20)

где λ – постоянная положительная величина.

Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (показательный закон надежности).

Функция распределения показательного закона:

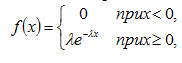(4.21)

Графики плотности и функции распределения показательного закона:

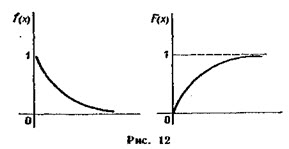
Пример 1. Написать плотность и функцию распределения показательного закона, если параметр λ = 8.

Решение.

Очевидно, искомая плотность распределения

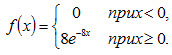
Искомая функция распределения

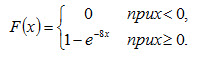
Вероятность попадания в интервал (а, b) непрерывной случайной величины X, распределенной по показательному закону,

P(a < X < b) = e-^λa – e^-λb. (4.22)

Значения функции е^-х находят по таблице.

Пример 2. Непрерывная случайная величина X распределена по показательному закону

f(x) = 2e^-2x при x ≥0; f(x) = 0 при x <0.

Найти вероятность того, что в результате испытания X попадает в интервал (0,3, 1).

Решение.

По условию, λ = 2. Воспользуемся формулой (4.22):

P(0,3 < X < 1) = e^-(2·0,3) – e^-(2·1) = e^-0,6 – e^-2 = 0,54881 – 0,13534 ≈ 0,41.

Числовые характеристики показательного распределения

Математическое ожидание показательного распределения равно обратной величине параметра λ:

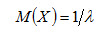. (4.23)

Дисперсия показательного распределения равна

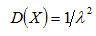. (4.24)

Среднее квадратическое отклонение показательного распределения равно

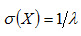. (4.25)

Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

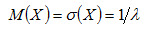
Пример 3. Непрерывная случайная величина X распределена по показательному закону

f(x) = 5e^-5x при x ≥0; f(x) = 0 при x <0.

Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Решение.

По условию, λ = 5. Следовательно,

.

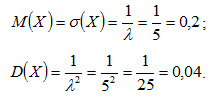Содержание:

1. Показательное распределение
2. Задача с решением

Во многих теоретических и практических вероятностных задачах, связанных, например, с анализом надежности технических систем, исследовании случайных промежутков времени между редкими событиями и др., используется показательный (экспоненциальный) закон распределения.

Показательный закон распределения непрерывной случайной величины описывается плотностью вида

Здесь — постоянный коэффициент, определяющий как начальное значение плотности вероятности так и темп изменения в зоне определения аргумента.

В соответствии с определением (4.6) найдем функцию распределения показательного закона:

Функция распределения (5.27) имеет характер восходящей экспоненты, которая стремится к 1 при и имеет нулевое начальное значение.

Вероятность попадания экспоненциально распределенной случайной величины заданный интервал на основании (4.11), (5.27) равна:

Определим теперь числовые характеристики показательного распределения.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

На основании (4.19) математическое ожидание непрерывной случайной величины с плотностью (5.26) равно:

Применяя к (5.29) интегрирование по частям при получим:

Для получения дисперсии воспользуемся выражением (4.29):

Интегрирование по частям позволяет преобразовать это выражение к виду:

Таким образом, математическое ожидание и дисперсия экспоненциально распределенной случайной величины определяются обратной величиной и квадратом обратной величины параметра При этом значения и средне-квадратического отклонения совпадают.

Легко убедиться в том, что и моменты высших порядков также являются функциями от Выполненные преобразования позволяют записать выражения для следующих интегралов:

которые могут быть использованы для нахождения значений первых четырех начальных моментов показательного распределения. Согласно (4.37) эти значения равны:

Из (5.32) следует, что начальный момент показательного распределения сеть отношение факториала степени

Центральные моменты показательного распределения могут быть получены с помощью выражений (4.41), связывающих центральные и начальные моменты. Применяя (5.32) к (4.41), получим

Значения центральных моментов (5.33) позволяют найти коэффициенты асимметрии (4.32) и эксцесса (4.33):

Возможно вам будут полезны данные страницы:

В среде Mathcad показательному закону распределения соответствуют встроенные функции, в названии имеющие корневое слово и начинающиеся с символов

— выводит значения плотности распределения

— выводит значения функции распределения

— выводит значение квантили порядка

— выводит массив (вектор-столбсц) из значений экспоненциально распределенных независимых случайных чисел с параметром На рис. 5.4 приведены плотности и функции показательного распределения для (плотность и функция распределения

Рис. 5.4. Вид плотностей и функции показательного распределения

Плотность (5.26) имеет характер ниспадающей кривой (экспоненты), асимптотически приближающейся к оси Начальное значение равно (см. рис. 5.4). В практических приложениях можно считать, что «достигает» установившегося значения (нуля) при

Функция показательного распределения практически достигает установившегося значения (единицы) также при

Показательное распределение

В этом подразделе будет рассмотрено показательное распределением времени , которое встречается, когда имеют дело с распределением времени совершенно случайных событий.

Задача с решением

Найти закон распределения времени перегорания лампочки, если вероятность ее перегорания не зависит от предыдущей работы лампочки, а зависит только от будущей работы.

Решение:

Введем обозначение событий:

— лампочка не перегорела до момента времени вероятность того, что лампочка не перегорела до момента времени

лампочка перегорит в следующие единиц времени;

лампочка перегорит в промежуток времени

Очевидно, что

Пусть время замены лампочки. Очевидно, что момент перегорания лампочки может быть абсолютно произвольным, начиная с некоторого момента начала отсчета времени: сделаем его равным нулю.

Таким образом, Тогда . Обозначим ее функцию распределения а плотность вероятности — С учетом возможности произвольного выбора начала отсчета Поэтому далее будем рассматривать плотность вероятности и функцию распределения только при

Тогда

При малых вероятность должна быть пропорциональна самому интервалу, т.е.

Разделим части уравнения на и вычислим предел при

Вспомнив, что получим дифференциальное уравнение с разделяющимися переменными

которое легко интегрируется: Постоянную интефирования найдем из условия Тогда и получим

Итак, показательным (экспоненциальным) называют распределение непрерывной случайной величины которое описывается функцией распределения: Тогда плотность вероятности показательного распределения равна

где — постоянная положительная величина.

Графики плотности вероятности (рис. 2.13, и функции распределения (рис. 2.13, б) приведены на рис. 2.13.

Показательное распределение, обозначаемое широко применяется в приложениях, в частности, в теории надежности,

одним из основных понятий которой является функция надежности.

Также закон показательного распределения используется в системах массового обслуживания.

В частности, по показательному закону изменяется промежуток времени между двумя последовательными событиями или соседними заявками для простейших потоков в теории массового обслуживания (см. подразд. 2.4).

Пусть непрерывная случайная величина распределена по показательному закону. Найдем ее математическое ожидание:

Таким образом, математическое ожидание показательного распределения равно величине, обратной параметру Поэтому, если переменная время некоего процесса, то имеет смысл времени релаксации этого процесса, когда плотность вероятности уменьшается в раз. Тогда вероятность, что событие произойдет (например, лампочка перегорит) за время равна

Найдем дисперсию:

откуда

Получили, что показательное распределение определяется всего одним параметром

Действительно, замеченная нами особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и в математической статистике приходится находить их оценки (приближенные значения). Очевидно, проще оценить один параметр, чем два, три и т.д.

Найдем вероятность попадания распределенной по показательному закону, на интервал Воспользуемся общей формулой вероятности попадания на заданный интервал:

Тогда имеем

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.