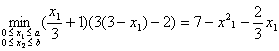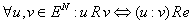Как
известно, на рынке потребитель сталкивается
с бесконечно большим количеством
товаров и услуг, однако для упрощения
нашего анализа мы предположим существование
всего двух товаров.
Пусть
потребитель выбирает первый товар в
количестве
q1,
а
второй – в количестве
q2.
Тогда
набор (q1,
q2)
определит
потребительский
набор
(потребительскую
корзину),
включающую то или иное количество
обоих товаров и обладающую для потребителя
некоторым качеством, которое можно
измерить.
Так,
если наборы пищевые, то таким качеством
будет калорийность данных благ, либо
содержание в них витамина С, либо
содержание сахара и т.д. Если рассматриваемые
товары — металлы, то таким качеством
будет прочность сплава, либо температура
его плавления, либо другая аналогичная
характеристика.
Естественно,
что не
всякое качество товара может быть
охарактеризовано числом.
Например, качество одежды оценивается
и продолжительностью носки (ее можно
охарактеризовать числом), и ее
соответствием современной моде или
красотой (а это числом охарактеризовать
невозможно). В дальнейшем будем
считать, что каждой потребительской
корзине
(q1,
q2)
соответствует
некоторое число
TU(total
utility),
называемое
совокупной полезностью.
Совокупная
полезность (TU)
есть
совокупное удовлетворение, получаемое
человеком в результате потребления
данного количества товаров или услуг
за данное время.
На
совокупную полезность блага влияют не
только его физические характеристики,
но и психология потребителя, его личный
опыт, социальная и культурная среда. И
хотя экономисты проявляют интерес
к этим факторам, однако на практике
обычно уделяют внимание только
количественным показателям (таким,
как объем продаж, количество единиц
товара, приобретенных покупателями, и
т.д.), предполагая постоянными все
прочие факторы, влияющие на поведение
человека. Допущение «при прочих равных
условиях» позволяет упростить анализ
условий максимизации полезности без
особого ущерба для модели.
Математически
это означает, что задается общая функция
полезности от потребления за определенный
период времени n-го
количества товаров:
TU=
U(q1,
q2,
…, qn).
где
q
–
количество товаров, включенных в
потребительский набор.
Функция
полезности
показывает количественную зависимость
между объемом потребления каждого из
n-благ
за данный промежуток времени и совокупной
полезностью блага, отражающей
индивидуальные предпочтения потребителя.
Как
и любая другая функция, функция полезности
может быть представлена в виде таблицы,
графика или уравнения.
Если
мы отвлечемся от отдельных случаев
функции полезности, то для большинства
товаров и услуг действует следующая
закономерность: чем
больше объем потребления, какого- либо
товара, тем больше значение совокупной
полезности, получаемой потребителем.
Изменение
(или приращение) совокупной полезности
отражается в показателе предельной
полезности.
Предельная
полезность
MU
(marginal
utility)
–
это дополнительная полезность,
получаемая человеком от потребления
одной дополнительной единицы данного
блага за единицу времени.
Математически
предельная полезность является первой
производной функции совокупной
полезности по количеству данного
блага и рассчитывается по формуле2:
MU
=
TU(q)
=
d(TU)/dq,
где
d(TU)
–
приращение совокупной полезности,
dq
–
приращение количества потребляемого
блага.
Существует
множество уравнений, которые могут
описывать функцию совокупной
полезности, однако наиболее простым
и наиболее часто применяемым является
общее уравнение
кубической функции:
TU
= а
+ bq
+
cq2–
dq3,
где
q
–
количество потребленного товара;
а,
d,
с, d
–
положительные константы.
Если
последовательное потребление какого-либо
блага постепенно приводит человека
к состоянию насыщенности, то дополнительная
полезность от использования одной
дополнительной единицы данного блага
начинает сокращаться. Эта закономерность
имеет универсальный характер и называется
законом
убывания предельной полезности или
первым законом Госсена.
Закон назван так в честь немецкого
экономиста Германа Госсена (1810-1858),
впервые сформулировавшего данный
принцип.
Начиная
с некоторого момента, дополнительная
полезность от потребления одного
дополнительного блага уменьшается по
мере того, как возрастает объем потребления
данного блага.
Математически
это означает, что вторая производная
общей полезности по количеству
данного блага является отрицательной
величиной.
Принцип
убывания предельной полезности был
использован английским экономистом
А. Маршаллом (1890) для объяснения
знаменитого
парадокса
воды и алмазов.
Суть
парадокса заключалась в том, что на
рынке алмазы ценятся неизмеримо
дороже, чем вода, и в то же время все
понимают, что если без алмазов человек
может обойтись, то без воды выжить
невозможно.
Объяснение
Маршалла состояло в следующем. Цена
товара определяется не его совокупной
полезностью для человека, а той предельной
полезностью, которую человек извлекает
из последнего глотка воды. Другими
словами, стоимость воды определяется
той суммой денег, которую индивидуум
захочет заплатить, чтобы получить
дополнительную меру воды. В силу того,
что предельная ценность убывает по мере
возрастания количества потребленной
воды, а запасов воды на земле существенно
больше, чем запасов алмазов, вода имеет
более низкую стоимость при обмене, чем
алмазы.
Рассмотрим
конкретные задачи 4.1 и 4.2.
Задача
4.1.
Определение точки насыщения
Пусть
дана функция полезности отдельного
потребителя:
TU
=
130q
–
2,5q2.
Определить
точку, при которой совокупная полезность
(TU)
является
максимальной и человек достигает
насыщения.
Решение:
Функция
совокупной полезности достигает своего
максимума при условии MU
=
0:
MU
=
dTU/dq
=
130 – 5q.
Приняв
функцию предельной полезности равной
нулю, получаем:
130 – 5q
= 0; q
= 26.
Это
и есть искомая точка насыщения.
Задача
4.2.
Закон убывания предельной полезности
Пусть
функция полезности задана уравнением:
TU=
18q
+7q2
– (l/3)
q3
Найти
объем потребления (q),
при
котором начинает действовать закон
убывания предельной полезности, т.е.
предельная полезность (MU)
начинает
уменьшаться.
Решение:
Очевидно,
что MU
начнет
уменьшаться в точке, в которой функция
предельной полезности имеет максимальное
значение:
MU
=
dTU/dq
=
18 + 14q
– q2.
Приравняв
dMU/dq
к
нулю и решая это уравнение относительно
q,
получим
q=7
это
степень потребления, при которой
начинается уменьшение MU.
Если
известны или могут быть оценены функции
потребительской полезности, то можно
судить о том, какие товары и услуги
потребители будут или не будут покупать
на рынке.
Для
дальнейшего анализа дополним наше
предположение о рациональности
потребителя допущениями о независимости
рассматриваемых нами функций полезности
(функция полезности одного товара
или услуги не зависит от степени
потребления других благ) и о полной
информированности потребителей.
Каждый потребитель обладает всей
необходимой для принятия решений
информацией, вполне определенными
вкусами и предпочтениями; знает,
какие товары и услуги доступны для
приобретения, качественные характеристики
этих товаров и их способность
удовлетворять его желания, цены, по
которым они продаются.
С
учетом представленных допущений
проанализируем поведение отдельного
потребителя, выбирающего комбинацию
из двух товаров
(q1,
q2)
и
располагающего доходом
(R),
равным
40 у.е. Эксперимент позволил выявить
следующие потребительские предпочтения
(табл. 4.1) для двух товаров (q1,
q2)
(в
баллах). Рыночные цены товаров
соответственно: p1
= 3 у.е., p2
=
5 у.е.
Таблица
4.1
Потребительские
предпочтения индивидуума
|
q1 |
TU1 |
MU1 |
MU1/P1 |
q2 |
TU2 |
MU2 |
MU2/P2 |
|
0 |
0 |
– |
– |
0 |
0 |
– |
– |
|
1 |
54 |
54 |
18 |
1 |
75 |
75 |
15 |
|
2 |
99 |
45 |
15 |
2 |
135 |
60 |
12 |
|
3 |
129 |
30 |
10 |
3 |
175 |
40 |
8 |
|
4 |
138 |
9 |
3 |
4 |
200 |
25 |
5 |
|
5 |
141 |
3 |
1 |
5 |
215 |
15 |
3 |
|
6 |
138 |
-3 |
-1 |
6 |
220 |
5 |
1 |
Как
видно из табл. 4.1, наибольшее удовольствие
потребителю принесло бы потребление
5 ед. товара
q1,
6 ед.
товара
q2.
Однако
на эти покупки пришлось бы потратить
45
у.е.
(5×3+5×6),
которых у человека нет.
Критерием
правильности
потребительского выбора является не
совокупная и даже не предельная
полезность, а предельная полезность на
1 у.е. затрат (MU/P).
Прибавочное
удовлетворение, получаемое на 1 у.е.
затрат, является наилучшим критерием,
поскольку объединяет и фактор
удовлетворения, и фактор затрат,
необходимые для обоснованного сравнения
товаров между собой.
В
нашем примере потребитель получит
наибольшее удовлетворение, распределяя
свой доход (40 у.е.) следующим образом:
4 ед. товара
q1
(4
х 3 у.е. = 12 у.е.), 5 ед. товара
q2
(5×6
у.е. = 30 у.е.).
3
у.е. (45 у.е. – (12 + 30 у.е.) = 3 у.е. останутся на
сбережениях.
С
учетом полученных результатов сформулируем
основное условие
потребительского оптимума, или второй
закон Госсена, для
двух и более товаров.
Для
максимизации полезности потребитель
должен таким образом распределить свой
ограниченный бюджет, чтобы предельные
полезности на один рубль, затраченный
на последнюю единицу каждого товара,
равнялись бы между собой
MU1/P1
=
MU2/P2
=
… = MUn
/Pn
а
сумма всех затрат потребителя на товары
и услуги плюс сбережения (S)
соответствовала
его денежному доходу (R),
т.е.
P1Q1
+P2
Q2 +…
+ PnQn
+S
= R
Если
эти предельные полезности не равны, то
совокупное удовлетворение может быть
увеличено путем уменьшения расходов
на товары с меньшей степенью полезности
и увеличения затрат на товары с большей
степенью полезности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
What Is Total Utility?
Total utility is the aggregate amount of satisfaction or fulfillment that a consumer receives through the consumption of a specific good or service. Total utility is often compared to marginal utility, which is the satisfaction a consumer receives from consuming one additional unit of a good or service. Total utility helps economists understand the demand for goods and services.
Key Takeaways
- Total utility is the aggregate summation of satisfaction or fulfillment that a consumer receives through the consumption of goods or services.
- Economists seek to quantify utility and total utility using utils.
- To best understand total utility, one should understand the Law of Diminishing Marginal Utility, which states that as more of a single good or service is consumed, the additional satisfaction, referred to as marginal utility, drops.
- Total utility is a core concept studied when seeking to analyze consumer behaviors.
- In general, economic theories believe that consumer actions are usually based on the goal of total utility maximization, which leads to purchasing units perceived to have the greatest utility satisfaction.
Understanding Total Utility
In economics, utility refers to the satisfaction gained from consuming a good or service. Total utility is usually defined as a quantifiable summation of satisfaction or happiness obtained from consuming multiple units of a particular good or service.
Utility and total utility are used in the economic analysis of consumer behaviors within a marketplace. Economists seek to quantify total utility using special calculations. Economists may also study several economic metrics in conjunction with total utility when seeking to understand how consumer behaviors align with supply and demand.
In economics, economists typically view changes in behavior and consumption by analyzing marginal increases and marginal decreases. Marginal changes will usually be either scaled increases or scaled decreases. In the case of total utility, marginal refers to the increasing or decreasing level of utility that is obtained with added consumptions.
Rational Choice Theory
Total utility is often studied alongside Rational Choice Theory and the Law of Diminishing Marginal Utility. Rational Choice Theory says that consumers seek to maximize their utility with each unit of consumption. Consumer theory and demand theory suggest that consumer actions are driven toward utility maximization by attempting to acquire the most satisfaction possible in the most affordable way. In general, classical economic theories show that most consumers want to get the highest possible level of utility per unit for the money they spend.
Total utility is usually measured in relative units called utils. When measuring total utility, analysis can span from one unit of consumption to multiple units. For example, a cookie provides a level of utility as determined by its singular consumption, while a bag of cookies may provide total utility over the course of time it takes to completely consume all the cookies in the bag.
The Law of Diminishing Marginal Utility
To better understand total utility, one must understand the Law of Diminishing Marginal Utility, which states that as more of a single good or service is consumed, the additional satisfaction, referred to as marginal utility, drops. The first good consumed provides the highest utility, the second good has a lower marginal utility, and so on. Therefore, total utility grows less rapidly with each additional unit consumed of the same good or service.
How to Calculate Total Utility
Each individual unit of a good or service has its own utility and each additional unit of consumption will have its own marginal utility. The total utility will be the aggregated sum of utility gained from all units being studied.
“Satisfaction” is a subjective measure and will vary from individual to individual, meaning that total utility acts more as a guide in understanding a consumer’s psychological decisions.
A total utility formula will include utils. Utils are typically relative and assigned a base value. Economists usually analyze utils across a spectrum to provide a comparative analysis of the amount of util or satisfaction gained from a unit of consumption. An assigned base value for utils is needed because theoretically there is no real value for utility satisfaction in general.
To find total utility economists use the following basic total utility formula:
TU = U1 + MU2 + MU3 …
TU = Total Utility
U = Utility
MU = Marginal Utility
The total utility is equal to the sum of utils gained from each unit of consumption. In the equation, each unit of consumption is expected to have slightly less utility as more units are consumed.
Total Utility Maximization
Economic theory regarding consumer activities suggests that the primary goal of the consumer is to achieve the largest amount of utility for the least amount of cost. This is partly due to the limited amount of funds a person may possess, as well as a desire to achieve as much satisfaction from the consumption of goods and services as possible.
For example, if a consumer is presented with two purchasing options with the same financial cost, and neither option is more necessary or functional than the other, the consumer will choose the good or service that provides the most utility for the money.
Example of Total Utility
John is hungry and decides to eat a chocolate bar. His total utility from eating one chocolate bar is 20 utils. He is still hungry so he eats another chocolate bar, where his total utility is 25 utils. John is still hungry and has two more chocolate bars. The third chocolate bar has a total utility of 27 utils, and the fourth has a total utility of 24 utils. This is best represented in the table below.
| Quantity Consumed | Total Utility |
| 0 Bars | – |
| 1 Bar | 20 utils |
| 2 Bars | 25 utils |
| 3 Bars | 27 utils |
| 4 Bars | 24 utils |
With each additional chocolate bar, John’s total utility increases, until it reaches its max at three chocolate bars. With the fourth chocolate bar, John’s total utility decreases. This can be understood with marginal utility; the utility that John derives from each additional chocolate bar.
| Quantity Consumed | Total Utility | Marginal Utility |
| 0 Bars | – | |
| 1 Bar | 20 utils | 20 utils |
| 2 Bars | 25 utils | 5 utils |
| 3 Bars | 27 utils | 2 utils |
| 4 Bars | 24 utils | – 3 utils |
With every additional chocolate bar after the first, John’s marginal utility is decreasing, meaning that he is deriving less satisfaction from another chocolate bar. This makes sense as he is getting more full with each bar. After the third bar, his marginal utility is negative, meaning he is deriving no satisfaction and in fact is made worse off; perhaps feeling sick after consuming so much chocolate and sugar.
Total Utility FAQs
What Is Total Utility?
Total utility is the aggregate satisfaction that an individual receives from consuming a specific quantity of a good or service.
What Is the Relationship Between Total Utility and Marginal Utility?
While total utility measures the aggregate satisfaction an individual receives from the consumption of a specific quantity of a good or service, marginal utility is the satisfaction an individual receives from consuming one additional unit of a good or service. If marginal utility is positive then total utility will increase. Once marginal utility is negative, then total utility will decrease.
How Do You Calculate Marginal Utility and Total Utility?
The basic formula to calculate total utility is as follows:
TU = U1 + MU2 + MU3 …
TU = Total Utility
U = Utility
MU = Marginal Utility
Marginal utility is calculated as follows:
MU = Change in Total Utility / Change in Units
Does Total Utility Always Increase?
Total utility does not always increase. When marginal utility is negative, then total utility will decrease. This means that an individual does not derive any satisfaction from the consumption of an additional unit of a good or service and is worse off by doing so.
The Bottom Line
Utility measures the satisfaction an individual receives from the consumption of a good or service. Total utility measures the total satisfaction from a specific quantity of goods or services. Total utility operates hand in hand with marginal utility, which measures the additional satisfaction received from the consumption of a good or service. As long as marginal utility is positive, total utility will increase. Once marginal utility is negative, then total utility will decrease.
Economists aim to study total utility and marginal utility to understand consumer behavior. Consumer behavior helps to predict the demand for goods and services, which impacts supply and their prices; all key metrics of analyzing an economy.
Предельная полезность товара
Полезность-это «ценность» или «удовлетворение», которое потребитель получает от потребления определенного количества товаров. Хороший способ понять полезность заключается в том, что это то, сколько денег потребитель гипотетически заплатит за удовлетворение, которое обеспечит товар.
Например, предположим, что вы голодны и покупаете рыбу, чтобы поесть на ужин. Допустим также, что одна рыба стоит 2000. Если вы так голодны, что заплатили бы 8000 за рыбу, говорят, что рыба обеспечивает полезность на 8000. Другими словами, вы готовы заплатить 8000, чтобы получить удовлетворение от рыбы, независимо от того, что она на самом деле стоит.
Предельная полезность измеряет увеличение удовлетворенности потребителей от потребления дополнительной единицы товара или услуги. Предельная полезность рассчитывается путем разницы в общей стоимости и деления на изменение потребляемого количества.
Предельная полезность = (TUf – TUi)/(Qf – Qi)
Где,
TUi — Общая полезность в единицах Q i
TUf — Общая полезность в единицах Q f
Qi — количество единиц потребления изначально
Qf — количество единиц потребления в конечном итоге
Полезность-это удовлетворение, которое человек получает от потребления товара или услуги. Общая полезность-это общее удовлетворение, полученное от потребления данного общего количества товара или услуги, в то время как предельная полезность-это удовлетворение, полученное от потребления дополнительного количества этого товара.
Пример: Таблица полезности
| Количество потребляемого | Общая полезность (сумма полезности от потребления) | Предельная полезность (изменение общей полезности, деленное на изменение потребленного количества) | Средняя полезность (общая полезность, деленная на общее количество потребленного) |
|---|---|---|---|
| 1 | 50 | 50 | = 50/1 = 50 |
| 2 | 90 | 40 | = 90/2 = 45 |
| 3 | 120 | 30 | = 120/3 = 40 |
Общая полезность
Общая полезность – удовлетворение, которое получают от потребления определенного набора товара или услуги.
Предельная полезность – это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.
Mu = (Tu1 – Tu0)/(Q1 – Q0)
Производная по количеству Q
Mu = dTu/dQ
Как найти производную.
Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2
Функция полезности – функция, показывающая убывание полезности блага с ростом его количества:
Tu = f(Qi)
Условия равновесия потребителя
Условия равновесия потребителя можно выразить формулой:Mux / Muy = Px / Pyгде Px и Py – цены на товары X и Y.
Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.
Пример задачи на нахождение оптимального набора покупок
Пример задачи на нахождение оптимального набора товаров при заданной функции полезности
Кривая безразличия
Кривая безразличия – это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.
Предельная норма замещения (marginal rate of substitution – MRS) – количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:
MRSxy = ΔY / ΔXΔY = Y1 – Y0ΔX = X1 – X0илиMRSxy = Mux / Muy
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Бюджетная линия
Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = PxX + PyYгде I – доход потребителя;
Px – цена блага Х;
Py – цена блага Y;
X,Y – составляют соответственно купленные количества благ.
Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.
Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x
Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x
Откуда: x = 20 ед., y = 1/2*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.
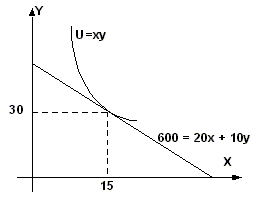
Пример решения определения оптимума потребителя
Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х – 20 рублей, а товара Y – 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = PxX + PyY 600 = 20X + 10Y
Предельная полезность товаров:
Mux = dU/dx = d(xy)/dx = yMuy = dU/dy = d(xy)/dy = x
Оптимум потребителя достигается при равенстве:
Mux / Muy = Px / PyMux / Muy = 20 / 10 = 2
Предельная норма замещения
MRSxy = Mux / Muy = 2
Выразим y через x.
Mux / Muy = y / x = 2y = 2x
Подставим в уравнение бюджетной линии:
600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.
При уменьшении цены товара X на 5 руб.
Px = 20 – 5 = 15
Найдем новый оптимум потребителя.
600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 – 15)
Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.
Пример нахождения цен товаров при оптимальном выборе покупателя
Утилитарное решение и решение, оптимальное по Нэшу
Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 – 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.
Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).
Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 – 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).
Независимость от масштаба
Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 – 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 – 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).
Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.
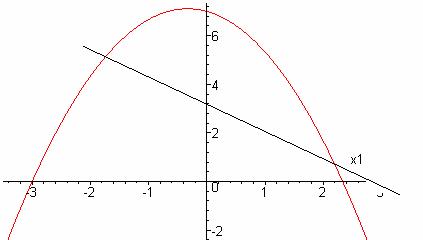
Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:
Минимум достигается x1 = 2,17; x2 = 0,83.
Видим, что соблюдается условия:
а) 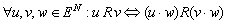
б)
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара – Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) – TU(1)=30 – 19 = 11
MU(3)= TU(3) – TU(2)=38 – 30 = 8
MU(4)= TU(4) – TU(3)=43 – 38=5
MU(5)= TU(5) – TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) – TU(2)=39 – 32=7
MU(4)= TU(4) – TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | 20 | 20 | 19 | 19 | 22 | 22 |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 |