Полезный сигнал как найти

1

Каждый электронщик должен знать основные параметры усилителя, так как усилитель в электронике используется абсолютно везде. В этой статье мы рассмотрим самые важные параметры усилителей.

Входное и выходное сопротивление

Кто в первый раз сталкивается с этими понятиями, читайте эту статью. Кому лень читать, вкратце объясню здесь из прошлой статьи. Каждый усилительный каскад имеем свое входное и выходное сопротивление. На схеме R_вх и R_вых

Входное сопротивление усилителя находится по формуле R_вх =U_вх / I_вх . Думаю, здесь вопросов возникать не должно. Эта формула справедлива как для постоянного тока, так и для переменного. В случае с постоянным током — это у нас будет усилитель постоянного тока (УПТ).

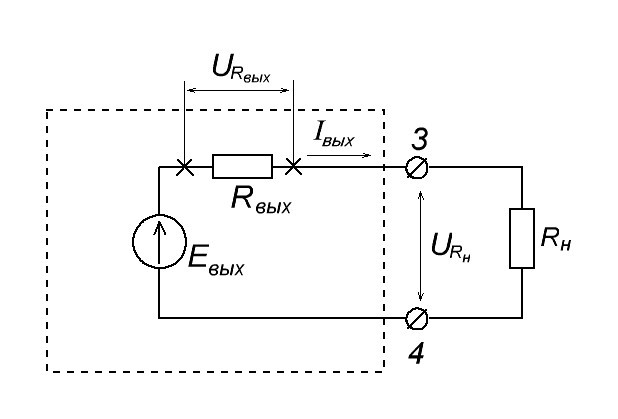
Немного иначе обстоят дела с выходным сопротивлением. В теории, можно замкнуть выходные клеммы 3 и 4 накоротко. В этом случае во выходной цепи усилителя у нас появится ток короткого замыкания I_кз

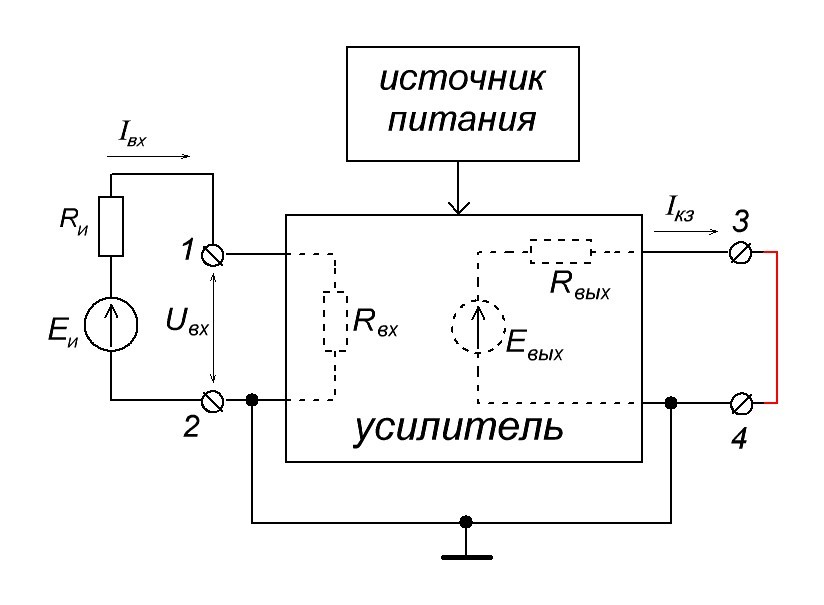
Более наглядно:

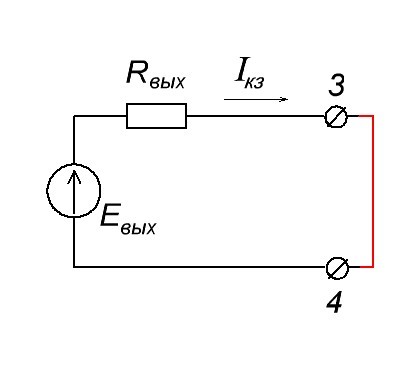
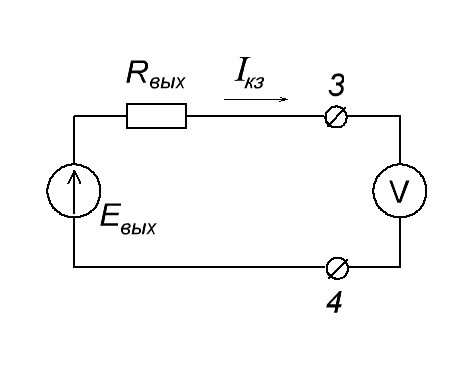
Ну и по закону Ома нетрудно догадаться, что R_вых = E_вых / I_{кз .} Но как же найти Е_вых ? Достаточно разомкнуть цепь и просто и замерить напряжение мультиметром. Это и будет E_вых. Физический смысл очень простой. Так как вольтметр обладает очень высоким входным сопротивлением, то в цепи у нас почти не будет течь ток, так как по закону Ома I=U/R. А если сопротивление нагрузки бесконечно большое, то, следовательно, I_кз будет бесконечно малое.

В этом случае этим бесконечно маленьким током можно пренебречь и считать, что в цепи нет никакой силы тока. А раз сила тока равна нулю, то  и падение напряжения на R_вых также будет равняться нулю или формулой: U_Rвых = IR_вых = 0 Вольт. Следовательно, на клеммах 3 и 4 мы будем замерять E_вых .

Выходное сопротивление усилителя можно найти двумя способами: теоретическим и практическим. Теоретический способ, часто сложен, поскольку неизвестны многие параметры «черного ящика», называемого усилителем. Проще определить выходное сопротивление практическим путем.

Как найти выходное сопротивление на практике

Что нужно для этого? Номинальная мощность усилителя и допустимое напряжение на выходе. Не важно — усилитель это постоянного или переменного тока (напряжения). Тестирование усилителя любого типа желательно выполнять на уровне 70% допустимой выходной мощности. Это общая практика.

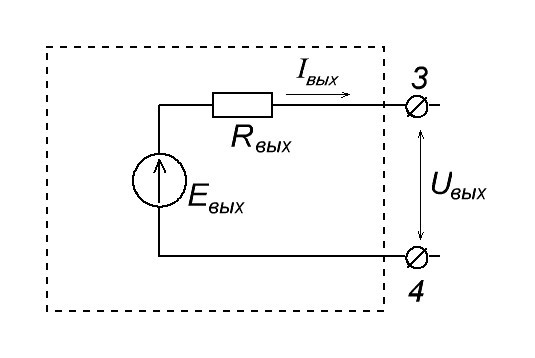
Если вы не забыли, мультиметр в этом случае нам покажет ЭДС  E_вых , т. е. в данном случае E_вых = U_вых . (Что такое ЭДС).

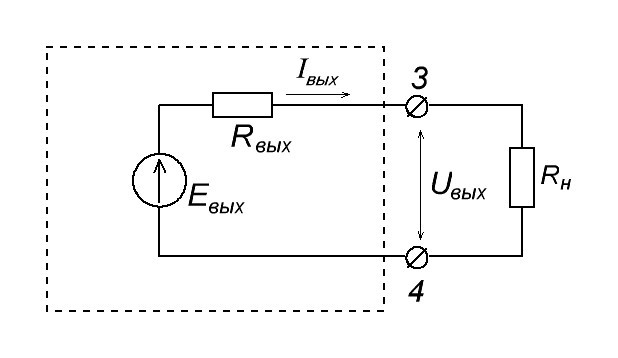
Номинал нагрузочного сопротивления должен выбираться исходя из допустимого тока и мощности усилителя.

Пример:

Выходная мощность усилителя 10 Вт, допустимое выходное напряжение (эффективное) 100 В. В этом случае, резистор нагрузки должен иметь сопротивление не менее R=U²/P = 10000/10 = 1 кОм. Мощность резистора: P_R = U²/R = 10000/1000 = 10 Вт

Какой же физический смысл этого опыта? В результате этих шагов,  у нас цепь станет замкнутой, а два сопротивления, R_вых и R_н , образуют делитель напряжения. Сюда же можно приписать закон Ома для полной цепи, который выражается формулой:

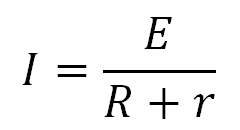
где

I — сила тока в цепи, А

E — ЭДС, В

R — сопротивление нагрузки, Ом

r — внутреннее сопротивление источника ЭДС, Ом

Применительно к нашей ситуации, формула будет иметь такой вид:

Отсюда получаем:

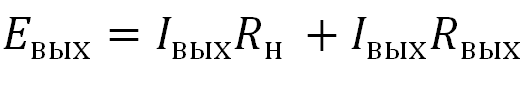
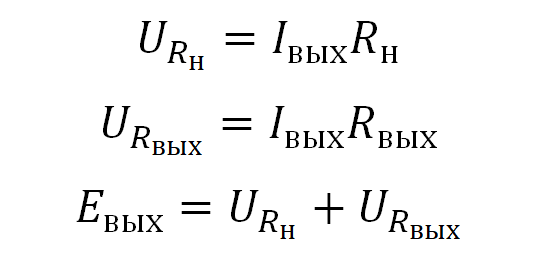
Или словами, ЭДС равняется сумме падений напряжения на каждом сопротивлении.

Как вы могли заметить, падение напряжения на сопротивлении R_вых зависит от силы тока в цепи. Чем больше сила тока в цепи, тем больше падение напряжения на выходном сопротивлении R_вых . Но от чего же зависит сила тока в цепи? От нагрузки R_н ! Чем она меньше, тем больше сила I_вых в цепи, тем больше будет падение напряжения на R_вых , а значит, падение напряжения на U_Rн будет меньше.

Теперь, зная этот принцип, можно косвенно вычислить выходное сопротивление R_вых .

Шаг номер 3: Замеряем напряжение на нагрузке U_Rн. Вспоминаем формулу выше:

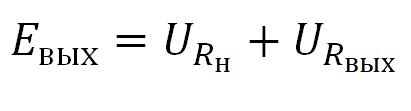
отсюда

из формулы

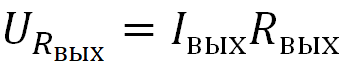
Получаем, что

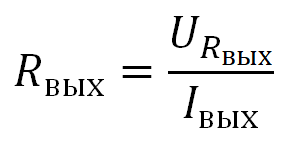
Далее что нам требуется — это увеличивать входное напряжение и снимать выходное напряжение — так мы увидим всю нелинейность выходной характеристики от тока и сможем замерить выходное сопротивление в диапазоне нагрузок, так как большинство усилителей мощности имеют нелинейность выходного сопротивления от допустимого тока нагрузки.

Коэффициент усиления

Про коэффициенты усиления мы писали еще в прошлой статье.

Рабочий диапазон частот

Рабочий диапазон — это диапазон частот, где коэффициент усиления изменяется в допустимых пределах, заданных в технических условиях на усилитель. Для этого надо построить АЧХ усилителя. Обычно этот предел устанавливается на уровне -3 децибел. Почему именно -3 дБ? В свое время так было удобнее учитывать передаваемую энергию. В полосе — 3 дБ передается 50% мощности сигнала.

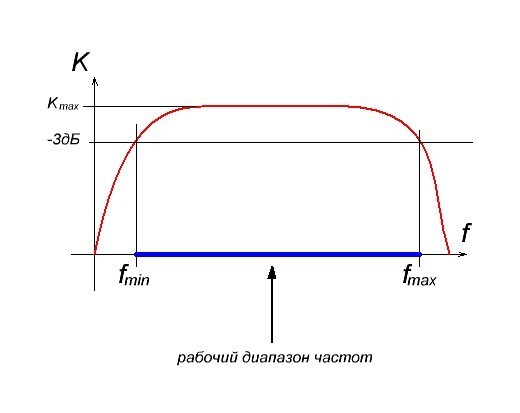
Но иногда требуется незначительное изменение коэффициента усиления. Например, в -1 дБ. В этом случае рабочий диапазон частот усилителя будет меньше:

Собственные шумы усилителя.

Что же такое шум?

В электронике шумом называют беспорядочные колебания амплитуды сигнала, которые глушат полезный сигнал. Сюда же относятся разного рода помехи. Собственные шумы усилителя — это шумы, которые зарождаются как внутри самого усилителя, так и могут быть вызваны внешним источником помех, либо некачественным питанием усилителя. Давайте рассмотрим основные виды шумов усилителя.

Фон

Этот шум вызван некачественным питанием усилителя. Если источник питания собран на сетевом трансформаторе, то шум  будет на частоте 100 Гц (2х50Гц, по схеме диодного моста). То есть на выходе такого усилителя мы услышим гудение, если подцепим к выходу динамик. Думаю, вы часто слышали такое выражение «что-то динамики фонят». Это все из этой серии.

Помехи и наводки

Это могут быть внешние источники, которые так или иначе действуют на усилитель. Это может быть наводка от сети 220 Вольт (очень часто ее можно увидеть, если просто прикоснуться к сигнальному щупу осциллографа), это также может быть какая-либо искра, которая образуется в свечах двигателей внутреннего сгорания.

Небольшое лирическое отступление. Помню, как смотрел диснеевские мультики по первому каналу, а через дорогу сосед пилил дрова с помощью бензопилы Дружба-2. Тогда на экране ТВ были такие помехи, что я  про себя тихо материл соседа.

Ну а как же без грозовых разрядов? Благодаря электромагнитному импульсу у нас появилось такое изобретение, как радио.

К источникам помех можно также отнести радио- и ТВ-станции, рядом лежащее и стоящее электрооборудование, типа мощных коммутационных механических ключей, разрядников и тд.

Ну и конечно, это шум самих радиоэлементов. Сюда относится тепловой шум (джонсоновский), дробовой шум, а также фликкер-шум.

Наиболее существенными являются шумы, которые возникают на входе усилителя в самом первом каскаде. Этот шум в дальнейшем усиливается также, как и входной полезный сигнал. В результате на выходе усилителя у нас будет усилен как полезный сигнал, так и шумовой. Поэтому, при проектировании качественных усилителей стараются как можно сильнее минимизировать шум на входе первого каскада усилителя.

Отношение сигнал/шум

Пусть у вас дома стоит телевизор, который ловит аналоговое вещание. На экране телевизора мы видим четкую картинку:

Но вдруг антенна на крыше вашего дома из-за сильного ветра чуток отклонилась в сторону и изображение ухудшилось

Потом антенна вообще упала с крыши, и на телевизоре мы видим теперь что-то типа этого

В каком случае отношение сигнал/шум будет больше, а в каком меньше? На первой картинке, где четкое изображение, отношение сигнала к шуму будет очень большое, так как не первой картинке мы простым взглядом не можем уловить каких-либо помех на изображении, хотя по идее они есть).

На второй картинке мы видим, что в изображении появились помехи, которые делают некомфортным просмотр картинки. Здесь отношение сигнала к шуму  уже будет намного меньше, чем на первой картинке.

Ну и на третьей картинке шумы почти полностью одолели изображение. В этом случае можно сказать , что отношение сигнала к шуму будет ну очень малым.

Отношение сигнал/шум является количественной безразмерной величиной.

В аналоговой электронике для нормальной работы усилителя полезный сигнал должен в несколько раз превышать шумы, иначе это сильно скажется на качестве усиления, так как полезный сигнал суммируется с шумовым.

Отношение сигнал/шум в англоязычной литературе обозначается как SNR или S/N.

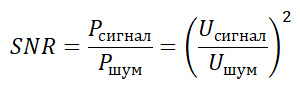
Так как порой это отношение достигает очень больших значений в цифрах, поэтому чаще всего его выражают в децибелах:

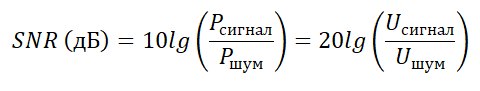
где

U_cигнал —  среднеквадратичное значение полезного сигнала, В

U_шум  — среднеквадратичное значение шумового сигнала, В

P_сигнал  — мощность сигнала

P_шум  — мощность шума

То есть в нашем случае с котиком на первой картинке амплитуда  полезного видеосигнала в разы превосходила амплитуду шума, поэтому первая картинка была четкой. На третьей картинке амплитуда полезного видеосигнала почти была равна амплитуде шума, поэтому картинка получилась очень зашумленной.

Еще один пример. Вот синусоидальный сигнал с SNR=10:

А вот тот же самый синус с SNR=3

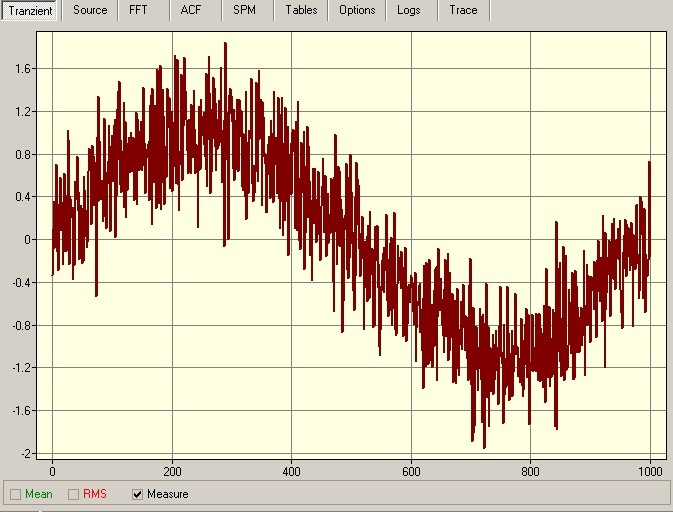
Как вы могли заметить, сигнал с SNR=10 намного «чище», чем с SNR=3.

SNR чаще всего можно увидеть при описании характеристик усилителя звука. Чем выше SNR, тем лучше по качеству звучания будет усилитель. Для HI-FI систем звучания этот показатель должен быть от 90 дБ и выше.  Для телефонных разговоров вполне достаточно и 30 дБ.

На практике SNR измеряется на выходе усилителя с помощью милливольтметра с trueRMS, либо с помощью анализатора спектра.

Амплитудная характеристика

Амплитудная характеристика усилителя — это зависимость амплитуды сигнала на выходе от входного сигнала при фиксированной частоте. Обычно она составляет 1 кГц.

Амплитудная характеристика идеального усилителя по идее должна выглядеть вот так:

Это луч, который начинается от нулевой точки отсчета координат и простирается в бесконечность.

Но на самом деле реальная амплитудная характеристика усилителя выглядит вот так:

Здесь мы видим, что если даже входное напряжение U_вх =0, то на выходе усилителя мы все равно получим какой-то уровень сигнала. Это будет напряжение шума U_ш .

Динамический диапазон усилителя

Динамический диапазон — это отношение максимально допустимого уровня выходного сигнала к его минимальному уровню, при котором  обеспечивается заданное отношение сигнал/шум:

Чтобы понять концовку определения «обеспечивается заданное отношение сигнал/шум» динамического диапазона, давайте рассмотрим наш рисунок:

Допустим, наш усилитель должен иметь SNR=90 дБ. Будет ли правильно, если мы возьмем U_{вых мин}  за  U_шум?

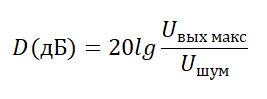
Конечно же нет!  В этом случае в этой точке на графике амплитуды сигнала и шума будут равны, а следовательно, по формуле

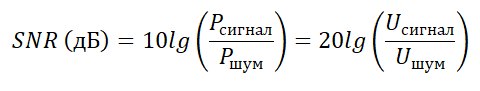
получим, что SNR=0 дБ.

Непорядок. Значит, надо взять такое значение U_вых , при котором бы соблюдалось равенство

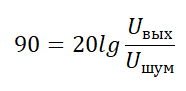
Допустим, что U_шум =1 мкВ, подставляем в формулу

Из этого уравнения находим U_вых . Это  будет как раз являться U_{вых. мин.} для формулы:

при SNR=90.  В нашем случае это будет точка А.

U_{вых макс} берем в точке B, так как в этом случае это максимальное значение, при котором у нас в усилителе не возникают нелинейные искажения (о них чуть ниже).

Рабочая область усилителя будет обеспечиваться на отрезке АВ. В этом случае у нас будут минимальные искажения в сигнале, так как эта область линейная. Отношение максимально допустимого выходного сигнала к уровню шума — это предельный уровень динамического диапазона для аналогового усилителя.

Для усилителей звука выход за пределы этой рабочей области в большую сторону будет чреват нелинейными искажениями, а в меньшую — полезный сигнал задавят помехи. Да вы и сами, наверное замечали, что выкрутив на полную катушку ручку громкости дешевой китайской магнитолы, у нас качество звучания оставляло желать лучшего, так как в дело «вклинивались» нелинейные искажения.

Коэффициент полезного действия (КПД)

КПД представляет из себя отношение мощности на нагрузке усилителя к мощности, которая потребляется усилителем от источника питания

где

P_вых  — это мощность на нагрузке, Вт

P_и.п.  — мощность, потребляемая источником питания, Вт

Искажения, вносимые усилителем

Искажения определяют сравнением формы сигнала на входе и на выходе. Идеальным является усилитель, который в точности повторяет форму сигнала, поданного на вход. Но так как наш мир не идеален, и радиоэлементы тоже не идеальны, то и на выходе у нас сигнал будет всегда немного искаженный. Главное, чтобы эти искажения не были столь критичны.

В основном искажения делятся на 4 группы:

• Частотные
• Фазовые
• Переходные
• Нелинейные

Частотные искажения

Частотные искажения возникают вследствие того, что коэффициент усиления во всем диапазоне частот не одинаковый. Или простыми словами, какие-то частоты усиливаются хорошо, а какие-то плохо). Чтобы в этом разобраться, достаточно посмотреть на АЧХ усилителя.

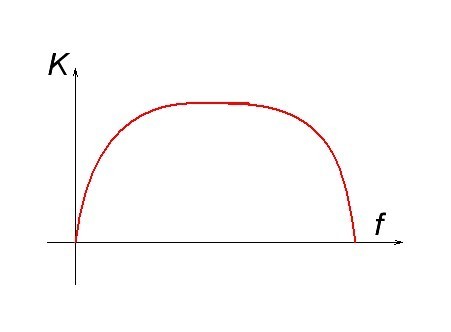
В данном случае мы можем увидеть, что низкие и высокие частоты будут усиливаться меньше, чем средние частоты. А так как сложный сигнал состоит из множества частотных составляющих, вследствие этого и возникнут частотные искажения.

Фазовые искажения

Фазовые искажения возникают из-за того, что разные частоты с разной задержкой по времени появляются на выходе усилителя. Какие-то частоты запаздывают больше, а какие-то меньше. Давайте все это рассмотрим на примере двух картинок.

Допустим, мы «загоняем» на вход синусоидальный сигнал с низкой частотой и на выходе получаем уже усиленный сигнал, но немного с небольшой задержкой.

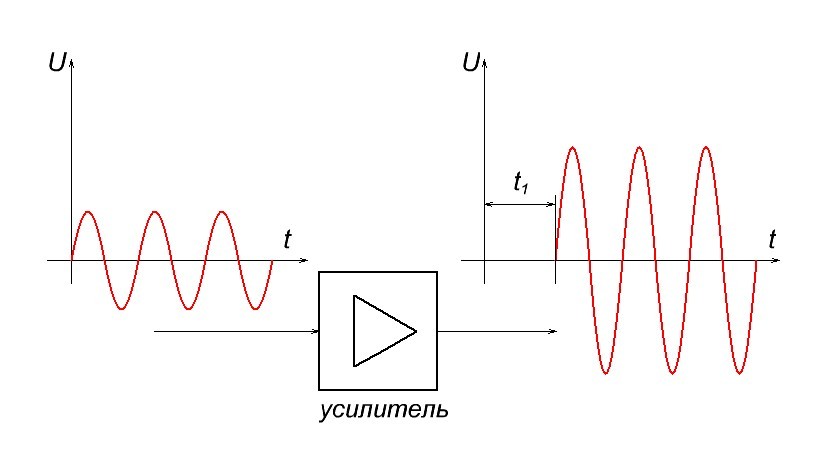
Но также не забывайте, что катушки и конденсаторы являются частото-зависимыми радиоэлементами. Их реактивное сопротивление зависит от частоты сигнала, поэтому, прогоняя через усилитель сигнал с другой частотой, мы получим уже совсем другую задержку сигнала

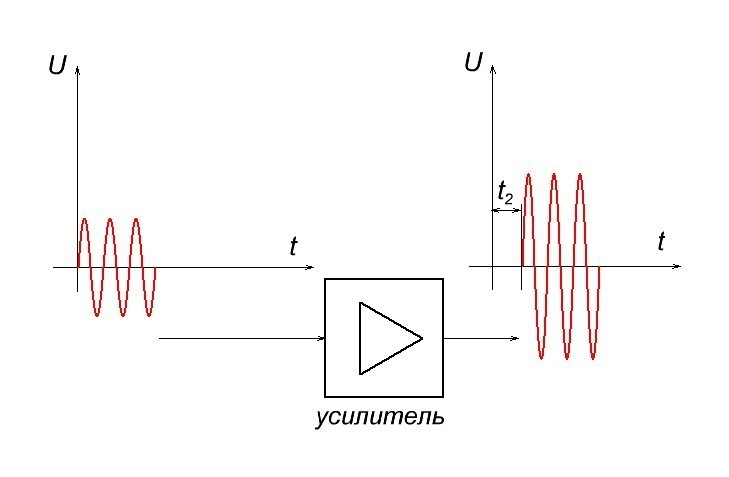
То есть в нашем случае t₁ ≠ t₂ . Хорошо это или плохо?  Если мы будем усиливать синусоиду, то в принципе нам по барабану. Какая разница раньше он появится на выходе или позже? Главное то, что сигнал будет усиленный.

Все бы ничего, но стоит помнить, что сложные сигналы состоят из суммы множества синусоид различных частот и амплитуд.

Чтобы понять, что такое сумма сигналов, достаточно рассмотреть вот такие примеры:

ну и еще один, мне не жалко)

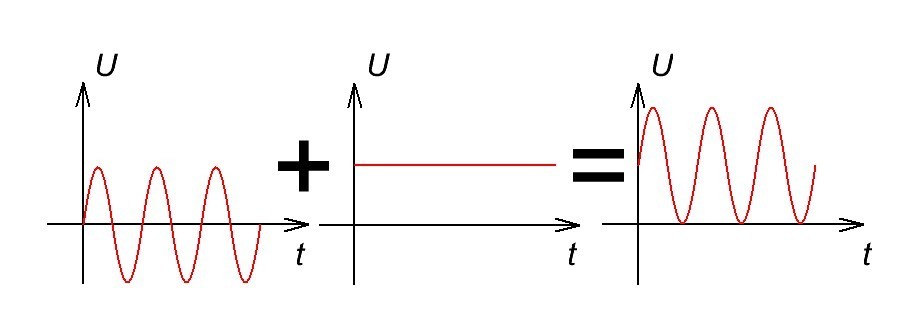
Складываем амплитуды в одинаковые моменты времени и получаем сумму этих двух сигналов.

А вот так из разных синусоид разных частот складывается прямоугольный сигнал:

В данном случае мы пытаемся «собрать» прямоугольный сигнал из суммы синусоид разных амплитуд и частот.

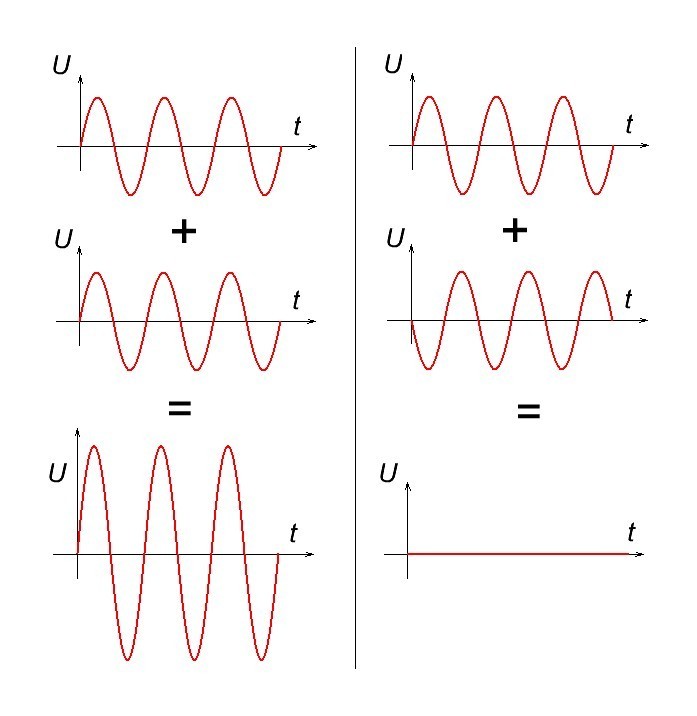
Но так как у нас усилитель задерживает разные сигналы по частоте по-разному, то у нас между сигналами происходит разнобой. Лучше всего это объяснит рисунок ниже. Имеем два синусоидальных сигнала с разной частотой и амплитудой:

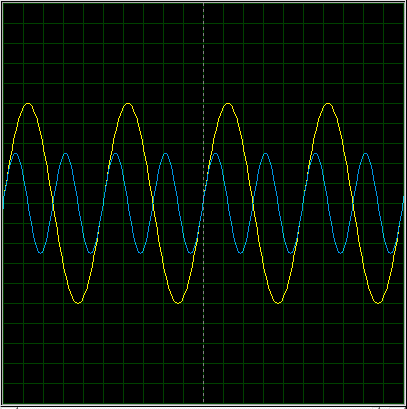
Если их сложить, получим сложный сигнал:

Но что будет, если второй сигнал сдвинется по фазе относительно первого?

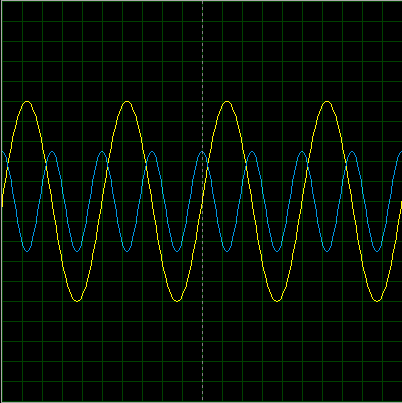
Смотрим теперь сумму этих сигналов:

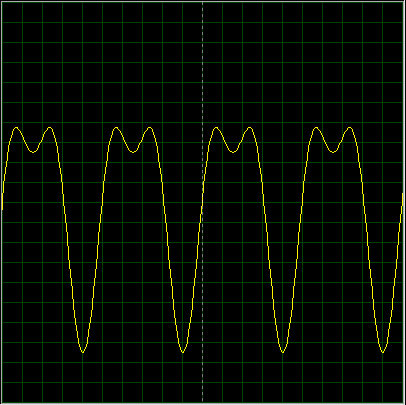
Абсолютно другой сигнал! Чувствуете разницу? Чуток сдвинули фазу, а форма сигнала уже поменялась.

То есть на выходе усилителя мы хотели получить вот такой усиленный сигнал:

а получили такой:

В результате фазовых искажений наш сложный сигнал, состоящий  из двух синусоид, поменял форму. На выходе усилителя мы получили совсем другой сигнал. А как вы помните, роль усилителя заключается в том, чтобы усиливать сигнал, сохраняя при этом его форму.

Фазо-частотная характеристика (ФЧХ) усилителя — это график зависимости угла сдвига фаз, вносимого усилителем, от частоты. Выглядеть она может примерно вот так:

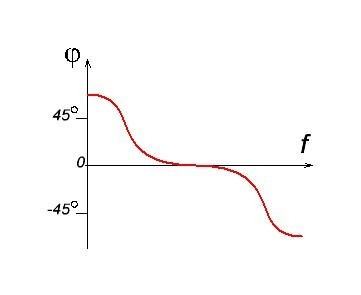
где

φ — это сдвиг фазы относительно входного и выходного сигнала

f — частота сигнала

Человеческое ухо не замечает фазовых искажений, несмотря на то, что даже изменяется форма сигнала. Поэтому при проектировании звуковых усилителей  фазовые искажения не принимают во внимание.

Частотные искажения и фазовые искажения относят к линейным искажениям, так как оба вида искажений  обусловлены линейными элементами схемы.  Если сказать по научному, у нас в спектре сигнала не появляется дополнительных гармоник.

Переходные искажения

Переходным искажением называют искажение прямоугольного импульса, которое подается на вход усилителя. На выходе такой импульс будет иметь уже другую форму, вызванную искажением сигнала внутри самого усилителя.

Для оценки переходных искажений используют переходную характеристику. Она представляет из себя зависимость напряжения или тока на выходе усилителя от времени от подачи на его вход прямоугольного импульса.

На рисунке ниже имеем прямоугольный сигнал, который подаем на вход усилителя, а на выходе усилителя уже будет искаженный усиленный сигнал. Это искажения вызваны, как обычно, с наличием в схеме усилителя реактивных радиоэлементов, то есть тех же самых катушек индуктивности и конденсаторов.

Для оценки переходных искажений используют такие параметры:

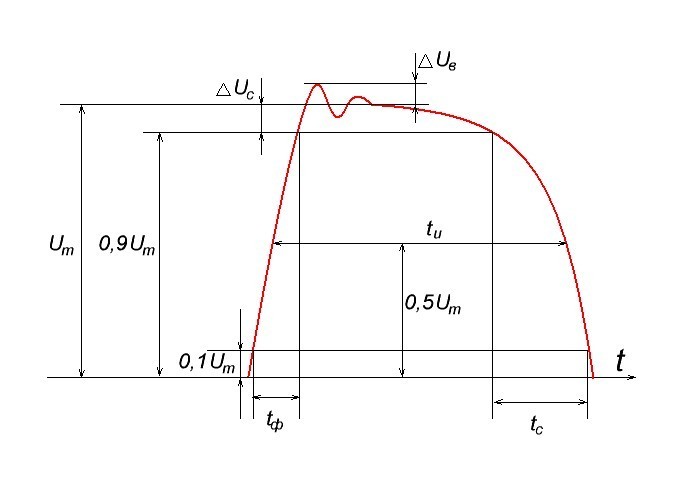
U_m — это амплитуда импульса, отсчитывается от плоской вершины импульса, В

ΔU_в — это выброс фронта импульса, В

ΔU_с — спад вершины импульса, В

Следующие два параметра измеряются в диапазоне от 0,1U_m  и до 0,9U_m :

t_ф  — длительность фронта импульса

t_c — длительность спада импульса

А длительность самого импульса t_и измеряется на уровне 0,5U_m .

Нелинейные искажения

Ну и напоследок мы с вами разберем нелинейные искажения. Нелинейными она называются из-за того, что такие искажения уже меняют форму сигнала, в отличие от линейных искажений. Все дело в том, что электронные лампы и полупроводники имеют нелинейную характеристику. Давайте рассмотрим все это дело более подробно.

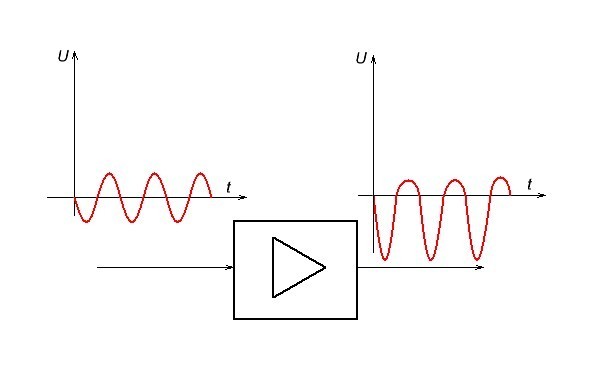
Как вы могли заметить, на выходе у нас форма сигнала изменилась. Нашу верхнюю часть синусоиды усиленного сигнала немного «придавило». То есть мы подавали сигнал одной формы, а вышел сигнал совсем другой формы. Это не есть хорошо и с этим надо бороться.

Если сказать более научным радиотехническим языком, в нашем сигнале появились дополнительные гармоники, которых не было в исходном сигнале. В данном случае мы на вход загоняли простой синусоидальный сигнал, состоящий из одной гармоники, а получили на выходе сложный сигнал, состоящий уже из нескольких гармоник.

Для количественной оценки нелинейных искажений используется коэффициент гармонических искажений (КГИ). Он выражается формулой:

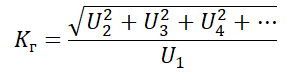
Эта величина находится как отношение среднеквадратичного напряжения суммы высших гармоник сигнала, кроме первой, к напряжению первой гармоники при воздействии на вход усилителя синусоидального сигнала.

или на английский манер

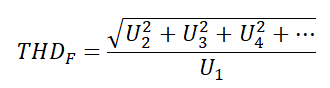
Также есть и подобный параметр коэффициент нелинейных искажений (КНИ). Он выражается формулой:

на английский манер

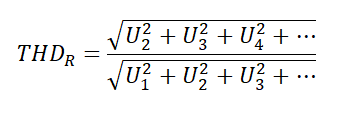
Эти два параметра выражаются в процентах. Для малых значений коэффициенты КГИ и КНИ почти совпадают. Так что коэффициент искажений можно считать как по первой, так и по второй формуле.

Консультант Jeer

Цель
работы:
Изучение структуры и характеристик
оптимального обнаружителя полезного
сигнала известной формы на фоне белого
гауссова шума.

1. Основные положения байесовой теории оптимального обнаружения

1.1
Постановка задачи, критерий обнаружения
и алгоритм обработки.
Сигнал на входе приемника – обнаружителя
на интервале
представим в виде

(1)

где
– случайная (постоянная на интервале
наблюдения) величина с двумя значениями
0 и 1;– полезный сигнал, форма которого в общем
случае полностью не известна «приемнику»;– случайная помеха (шум);– оператор, определяющий способ
взаимодействия полезного сигнала и
шума при образовании входного сигнала
приемника.

Проблема
обнаружения полезного сигнала состоит
в том, что приемник, получив
сигнал
,
должен принять решение о том, чему равна
величина.
Поскольку входной сигнал
содержит шум, то обнаружение полезного
сигнала, в особенности, если он по уровню
сравним с шумом, является не простой
задачей. Приемник, как впрочем, и человек,
в подобной ситуации может давать ошибки.
Интуитивно ясно, чтосамый
хороший (оптимальный) приемник должен
в среднем давать меньше ошибок.
В математическом плане необходимо найти
формулы (алгоритм), по которым оптимальный
приемник работает,
т.е. следует в явном виде записать
выражение для сигнала на выходе приемника.
В инженерном плане необходимо определить
структурную и далее функциональную
схему этого приемника,
чтобы его можно было выполнить и
использовать при решении задачи
обнаружения. Такой приемник необходим
в радиолокационных системах для
обнаружения объектов, в системах охранной
сигнализации и др. В системах цифровой
связи имеет место фактически та же самая
задача – задача различения двух ситуаций
(сигналов).

Метод
решения подобных задач дает статистическая
теория проверки гипотез. Выражение (1)
задает математическую (статистическую)
модель входного сигнала. Очевидно, можно
предполагать, что на входе
приемника
случайно могут сложиться две
взаимоисключающие ситуации (гипотезы):
нулевая гипотеза
– параметр
=0,
т.е. во входном сигнале нет полезного
сигнала
и противоположная (альтернативная)
гипотеза– параметр
=1,
когда входной сигнал содержит полезный
.
На выходе приемника – обнаружителя
(послевыполнения
действий
над входным
сигналом)
также возможны две ситуации (два решения):
нулевое решение
– приемник выдал результат об отсутствии
полезного сигналаво входном сигналеи альтернативное решение,
при котором формируется результат о
наличии сигналаво входном сигнале.

Конечно,
вероятностные свойства сигнала
длядолжны отличаться в зависимости от того
содержится или нет в нем полезный сигнал.
В противном случае задача обнаружения
теряет смысл. В байесовой теории
обнаружения статистические свойства
входного сигнала для двух гипотезидолжны
быть известны. При дискретном отборе
данных на интервалеэти свойства определены заданиемn
– мерных условных ПРВ:
.
Предполагается, что до получения сигналаприемнику известны вероятности появления
на входе каждой ситуации, т.е.– априорные вероятности гипотез.

Определение
оптимального алгоритма принятия решения,
т.е. правила обработки, связано с введением
количественного критерия оптимальности.
В байесовой теории критерий оптимальности
вводится следующим образом. Для каждой
ситуации, в которой случайно может
оказаться приемник – обнаружитель,
назначается число
– относительный штраф (плата за итог
работы). В итоге имеем четыре возможных
случайно возникающих в приемнике
ситуации со своей платой за «работу».
Перечислим их:

1. Правильное
   обнаружение
   – событие
   ;
   плата;
   вероятность штрафа –.

2. Пропуск
   сигнала –
   событие
   ;
   плата;
   вероятность штрафа –.

3. Правильное
   не обнаружение
   – событие
   ;
   плата;
   вероятность штрафа –.

4. Ложная
   тревога –
   событие
   ;
   плата;
   вероятность штрафа –.

Критерием
оптимальности является средний риск
(средний штраф)
– средний по ансамблю всех возможных
сигналов на входе приемника. Таким
образом, получаем

. (2)

Оптимальный
приемник работает так, что обеспечивает
наименьшую величину риска
.
В общем виде алгоритм работы оптимального
приемникапредусматривает вычисление отношения
правдоподобияи
принятие решения после сравнения
полученной величины отношения с пороговым
уровнем.
Аналитически оптимальный алгоритм
записывают в общем виде так: приемник
формирует решение

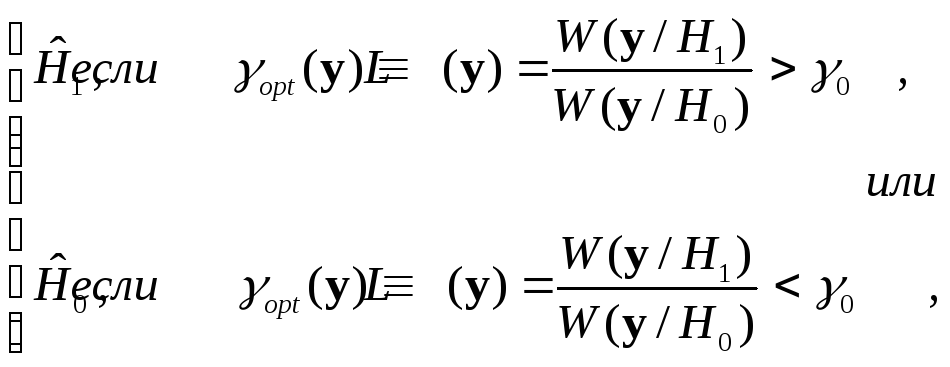(3)

где
оптимальный порог. Подробный вывод
этого результата приведен в [ 1, п.3.4 ].

1.2 Оптимальный
алгоритм обнаружения для случая
аддитивной смеси полностью известного
полезного сигнала с белым гауссовым
шумом. Для
данного конкретного случая выражение
(1) принимает вид

(4)

где

– аддитивный белый гауссов шум. Таким
образом, если,
то входной сигнал

,
(5)

в
противном случае
и тогда

.
(6)

Выражения
(5) и (6) утверждают, что присутствие во
входном сигнале
полностью известного полезного сигналаприводит лишь к изменению (в каждый
момент времени) среднего значения
входного сигнала. Таким образом,n
– мерные гауссовские условные ПРВ
,
соответствующие двум гипотезами, отличаются средними значениями. В
явном виде эти ПРВ приведены в [1, ф.
3.43]. После их подстановки в (3) и выполнения
простых алгебраических преобразований
получаем выражение для сигнала на выходе
оптимального приемника. В итоге алгоритм
принятия решения (алгоритм обнаружения)
принимает следующий вид [1, ф. 3.48, 3.49]

(7)

где
– модифицированный порог;– энергия сигнала;спектральная плотность средней мощности
шума.

Выражение
(7) содержит операцию интегрирования
произведения двух функций, которая
характерна для вычисления корреляционной
функции [1, ф. 1.11, 1.15а]. По этой причине
приемное устройство, реализующее
алгоритм обнаружения в виде (7) называют
приемником корреляционного типа.

Структурная
схема приемника – обнаружителя
корреляционного типа показана на рис.
1.

Устройство
синхронизации, показанное на схеме,
обеспечивает работу генератора опорного
сигнала на
том интервале времени, где ожидается
полезный сигнал.
Сравнение с порогом также происходит
в момент окончания сигнала. Здесь следует
помнить, что рассматривается задача
обнаружения полностью известного
сигнала, т. е. моменты времени начала и
окончания полезного сигнала известны.
Приемнику неизвестен лишь сам факт
наличия или отсутствия сигнала на
ожидаемом интервале времени.

Соседние файлы в папке Статистическая теория радиотехнических систем

• #
• #
• #
• #

  11.05.201530.98 Кб80Итог ЛАБ.1.mcd

• #

  11.05.201539.57 Кб89Итог ЛАБ.2.mcd

• #

  11.05.201541.99 Кб102Итог ЛАБ.3.mcd

• #

  11.05.201547.03 Кб78К. раб.№ 1.mcd

• #

  11.05.201550.54 Кб59К. раб.№ 2.mcd

Спасибо всем, кто откликнулся! В последние несколько недель был завален другими делами, поэтому не отвечал.

Условия поставлены очень неточно (к сожалению, на форуме это встречается постоянно). Приведите конкретные цифры, пожалуйста, а именно: частоту, диапазон ее изменения, модель шума, или хотя бы его спектральные хар-ки.

Далее, непонятно, что Вы подразумеваете под “амплитудой” шума?

Данная работа – мой дипломный проект. Моя задача – разработка общего алгоритма выделения полезного сигнала из шума и последующая его реализация в виде устройства. На данном этапе условия следующие: есть вихревой измеритель скорости, частота сигнала прямопропорциональна скорости потока. Пока “идеальные” условия – сигнал с датчика – синусоида. Частота меняется (скорость потока непостоянна). Шум более-менее постоянен (собственные шумы устройств и трубы) но может изменятся – помехи от других устройств, удары по трубе, “гул” в трубах, шум от насосов и т.д. Пока рассматриваю “идеальные” условия – белый шум, со временем не меняется.

Проблемма – амплитуда полезного сигнала уменшается с уменьшением скорости потока квадратично. Измерение на больших скоростях не представвляет сложности – соотношени сигнал/шум 10 к 1. Но при снижении частоты соотношение сигнал/шум составляет 1 к 1 (точка 200 – 300 Гц , в зависимости от датчика и среды, где проводятся измерения), при дальнейше сниженни частоты – 1 к 10. Из-за этого есть возможность измерять только большие скорости, на нижней же части диапазона измерений (0 – 5%) просто отключать измерения и не учитывать расход. Моя задача – отодвинуть нижнюю границу как можно ниже.

Первое, что приходит в голову – преобразование Фурье. При указанных Вами условиях “палка” от полезного сигнала будет выделяться на фоне “мусора” от шума так, что с шумом ее никогда не спутаешь. Точность оценки частоты – порядка Fд/N, где Fд – частота дискретизации, N – длина преобразования.

Если для заданной точности требуется нереальное N, но известно, что периодический сигнал только один, то можно попробовать адаптивный самонастраивающийся фильтр (как вариант – ФАПЧ типа аналоговой), после чего мерить частоту/период на его выходе.

Сам склоняюсь к работе со спектром. В ближайшие пару дней попытаюсь промоделировать.

попробуйте знаковый коррелятор

Слышал что неплох метод медианного центра

s_yakov и rar_а не могли бы Вы рассказать более подробно? Не совсем пойму о чем речь.

Можно попробовать БПФ.

Я обычно делаю БПФ а потом корреляторами уточняю до требуемого значения

Если рессурсы серьезно ограничены то можно попробовать достаточно инерционный ФАПЧ

А литература подойдет любая по системам автоматического регулирования

С точки зрения науки есть только один метод – узкополосная фильтрация, а как его реализовать – дело вкуса. В аналоговом виде проще фАПЧ, там, в зависимости от условий, можно реализовать фильтр до единиц гц шириной. В цифровом виде проще БПФ, Однако, у этого метода есть некоторые недостатки. АЧХ одного канала имеет вид sin(x)/x, да к тому же соседние каналы перекрываются. С первым недостатком борются применением оконных функций, а со вторым – дискриминаторной обработкой.

Была мысль использовать фазовую автоподстройку под частоту полезного синала, вот только есть сомнения, буду ли “успевать бегать” за изменением частоты, и не буду ли “застрявать” на точках, типа 50 Гц, где есть стабильные и сильные помехи…

БПФ – как это расшифровываеться?

Была еще мысль работать с амплитудами, т.к. амплитуда шума распределена по з-ну Гауса, а полезный сигнал будет периодически сдвигать распределение.

Вобщем впереди три свободных дня – буду моделировать.

Еще раз благодарю ВСЕХ, кто ответил и ответит!

Программирование микроконтроллеров, Разработка систем связи, Блог компании DIRECTUM

---

Рекомендация: подборка платных и бесплатных курсов дизайна интерьера – https://katalog-kursov.ru/

Часть 1 — Основы передачи данных по линиям электропередач

В первой части статьи мы кратко ознакомились с основными понятиями при передаче данных по линиям электропередач. Узнали, что такое “полезный сигнал”, как с его помощью можно кодировать передаваемую информацию. Но ни слова не было о том, как это устройство должно быть выполнено физически, как оно будет генерировать сигнал, и каким образом его вообще подключить к сети 220 В.

В этой и следующей частях статьи опишем, какие основные блоки должны быть в простейшем устройстве передачи данных по PLC. Постепенно, как конструктор, будем добавлять в общую картину блок за блоком и разберемся для чего нужен каждый блок и как он работает.

– Введение
– Мозги устройства — микроконтроллер
– Основные требования к микроконтроллеру
– Выбор подходящего микроконтроллера
– Особенности питания устройства

Дисклеймер: статья не является руководством по созданию устройства и не является справочником по электронным компонентам. Это просто результаты моих экспериментов и некоторый накопленный практикой опыт, который, надеюсь, будет полезен тем, кто интересуется темой. Если есть какие-то замечания, интересные ссылки и книги, обязательно оставляй это в комментах.

Введение

Для начала кратко вспомним из части 1, как происходит передача данных. На изображении одна из фаз ЛЭП. Красное устройство передает, синие слушают. Биты данных один за одним передаются в виде синусоидальных сигналов различной частоты (FSK модуляция).

В мозге устройства — микроконтроллере — зашит протокол, по которому передаются/принимаются данные. Также в прошивке микроконтроллера для каждого передаваемого символа (или бита) задана соответствующая частота сигнала.

Для примера: если передается символ “0”, то генерируется “полезный сигнал” в виде синусоиды 74 кГц. А если передается “1”, то генерируется синусоида с частотой, например, 80 кГц. Номиналы частот не особо важны, просто выбираются любые из разрешенных диапазонов. Главное, чтобы приемник смог их различить.

В первой части статьи упоминалось про третий символ “S”, который означал начало кадра. Он также кодировался своей определенной частотой. Когда устройство получало символ “S”, входной буфер очищался. Для простоты в этой статье будут упоминаться только “0” и “1”.

Передающие и принимающие устройства синхронизируются между собой с помощью отдельного блока устройства — “zero cross детектора”.

Представим передающее устройство, в котором есть подготовленный кадр данных — некий массив нулей и единиц, и этот кадр нужно передать по PLC каналу связи (ЛЭП). Передача/прием кадра происходит по одному биту за один синхросигнал из ZC детектора.

Физически это значит, что за один синхросигнал из ZC детектора генерируется один “полезный сигнал” определенной частоты. В нашем случае это синусоиды 74 кГц или 80 кГц.

Таким образом, бит за битом, передается кадр данных в PLC канал. Совместно с микроконтроллером генерацией сигналов будет заниматься отдельная часть схемы. Назовём её “Выходная цепь”.

Задача принимающих устройств — каждый раз, по сигналу ZC детектора, оцифровывать “полезный сигнал” из PLC канала и узнавать, какой символ там был закодирован.

Но сначала сырой сигнал нужно грубо очистить от шума, подогнать уровень “очищенного” сигнала под пригодный для оцифровки и уже затем передать на АЦП микроконтроллера для дальнейшего цифрового анализа. Этой подготовкой “полезного сигнала” для АЦП будет заниматься “Входная цепь”.

Чтобы не раздувать эту часть статьи, расскажу только про задачи, решаемые микроконтроллером и некоторые особенности питания устройства.

В следующей части рассмотрим как устройство можно согласовать с сетью 220 В, работу ZC детектора, а также про входную и выходную цепи.

Мозги устройства — микроконтроллер

Центральная часть устройства — микроконтроллер, который будет контролировать всю схему: обрабатывать входной сигнал, генерировать полезный сигнал, управлять усилителями, хранить данные и т.д.

Микроконтроллер — это такой мини-компьютер, который в одном корпусе содержит процессор (ЦПУ), память (ПЗУ и ОЗУ), ввод-вывод и периферийные устройства. По сути, внутри уже все есть для работы: подаем питание и поехали. Дальше все зависит уже от программы “прошивки”, которую мы в него записали.

Сейчас выпускают микроконтроллеры с большим количеством различной встроенной периферии. Это очень удобно, так как меньше необходимости во внешних компонентах, что экономит место на печатной плате (и, конечно же, ваши денежки). Внутри может иметь ЦАП и АЦП, часы с календарем. Даже встроенный USB уже не удивляет.

На рынке огромное разнообразие микроконтроллеров с разной вычислительной мощностью и периферией. Обычно они группируются в серии и подходят под разные классы задач. Например, чтобы помигать светодиодом в миниатюрном устройстве, нам не нужен мощный камень, на котором можно запустить Linux, подойдет “ATtiny”. Но для нашего устройства его уже не хватит, так как нужны ЦАП, АЦП и быстрые вычисления в реальном времени.

Поэтому к выбору камня нужно подойти немного поразмыслив. Подумаем, что же требуется от микроконтроллера в нашем случае.

Основные требования к микроконтроллеру

Производительность

Основной нагрузкой на ЦПУ будет обработка оцифрованного входного сигнала с помощью ДПФ для выяснения того, какой символ был закодирован в сигнале: “0” или “1”. Далее этот символ будет отправляться в протокол на уровень выше. Больше всего вычислений будет происходить именно при подсчете гармоник в ДПФ.

Циклично, с интервалом 10 миллисекунд, АЦП будет оцифровывать входящий сигнал и сохранять его в виде массива чисел. Затем этот массив несколько раз прогоняется через ДПФ для выяснения амплитуд гармоник каждой из интересующих нас частот в полезном сигнале.

Результат визуально можно представить в виде эквалайзера, на котором нарисованы полоски определенных частот разной высоты (амплитуды). Для подсчета высоты каждой отдельной полоски нужно сигнал прогонять через ДПФ.

После подсчета некоторого количества гармоник, делаются выводы о том, какой символ закодирован.

В самом простом случае можно просто сравнить амплитуды гармоник 74 и 80 кГц между собой. Если в сигнале преобладает гармоника с частотой 74 кГц, записываем в входной буфер бит “0”.

Если в сигнале преобладает гармоника с частотой 80 кГц, записываем в входной буфер “1”.

В таком случае, любой шум что-то означает: “0” либо “1”, даже если ничего не передавалось. Отделением зерен от плевел будет заниматься отдельная подпрограмма — уровнем выше — которая будет проверять целостность кадра и прочие прелести.

Задача же этого уровня — просто, как конвейер, подавать “0” и “1” наверх, а дальше из них будут складываться правильные целостные кадры данных. Или не будут.

Также можно заморочиться и дополнительно рассчитывать амплитуды смежных гармоник и узнавать уровень шума относительно полезного сигнала. Можно программно фильтровать сигнал и тд. Вариантов много.

Суть в том, что считать, возможно, придется много. Успевать считать нужно гарантированно, так как это реалтайм-конвейер.

Если разложить всю нагрузку на которую ЦПУ тратит время друг за другом, то получим примерно это:

• оцифровка сигнала

• подсчет амплитуд гармоник через ДПФ и анализ результата

• прочая нагрузка (обработка прерываний из интерфейсов USB или CAN, обработчики таймеров, моргания светодиодами, работа с памятью, какие-то вычисления по протоколу и т.д.)

Это должно циклично выполняться каждые 10 миллисекунд снова и снова. ЦПУ никогда не должен быть загружен на 100%, иначе есть риск не успеть посчитать что-то важное. Поэтому всегда нужно оставлять запас по производительности.

Энергоэффективность

Обратная сторона быстрых вычислений — большее потребление энергии. Чем быстрее контроллер считает, тем больше он потребляет энергии. Поэтому нам не нужен “слишком мощный” процессор.

Подобрать нужную производительность ЦПУ можно опытным путём: берём микроконтроллер с запасом вычислительной мощности и памяти, пишем код, запускаем и смотрим за какое время он справляется с конкретными задачами. Выбираем из линейки контроллеров подходящий, оставляя небольшой запас мощности и памяти (для возможных обновлений и улучшений).

Должен быть достаточно быстрый АЦП

Нам нужно оцифровывать входной аналоговый сигнал и желательно, чтобы был встроенный АЦП. Точность тут не так важна, как скорость. Так как измеряемый сигнал имеет частоту до сотни килогерц. Для корректных вычислений гармоник есть условие (из Теоремы Котельникова).

Частота дискретизации должна быть минимум в два раза больше частоты измеряемого сигнала.

Это значит, что для распознавания сигнала нужно сделать от двух точек измерения на период. А по-хорошему — 4-5. Посмотрим на примере.

Представим, что мы измеряем сигнал, в котором есть нужная нам гармоника частотой 80 кГц. У сигнала с частотой 80 кГц период микросекунд. Чтобы оцифровать 5 точек на период нужно успевать делать измерение раз в 2.5 микросекунды для адекватного распознавания сигнала.

С пятью точками измерений на период уже выглядит неплохо. ДПФ с этим отлично справится.

Но для чего брать с запасом? Что если измерять по минимуму, только две точки на период? Вот такой сигнал мы оцифруем при удачном попадании.

А так будет выглядеть оцифрованный сигнал, если попасть в момент, когда сигнал в нуле.

Не похоже на синусоиду.

Если интересно посмотреть, что будет, если проводить измерения частотой меньше двух точек за период, то поищите в гугле картинки “Эффект алиасинга”.

Должен быть достаточно быстрый ЦАП

Для полезного сигнала нужно сгенерировать синусоиду большой частоты. Чем больше точек на период синусоиды успеет генерировать ЦАП, тем плавнее будет сигнал на выходе (меньше лесенка, которую затем сгладит конденсатор).

Представим на примере синусоиды с частотой 80 кГц, период 12.5 микросекунд. Возьмем для начала 4 точки на период. Генерация каждые 3.125 микросекунды.

Такой сигнал сложновато будет сгладить конденсатором, чтобы сделать его похожим на синус.

Увеличим количество точек вдвое. Генерация каждые 1.56 микросекунды.

Нужна достаточная скорость ЦАП для того, чтобы сигнал был хотя бы похож на синус. В нашем случае, с сигналом частотой до 80 кГц, будет достаточно чтобы ЦАП успевал менять уровень сигнала раз в 1.5 микросекунды. Если успеет быстрее, то еще лучше.

С выхода ЦАП этот угловатый сигнал проходит через пассивный фильтр нижних частот и в сглаженном виде идет на усилитель “выходной цепи”.

Если нет АЦП

Помню, в самом начале я проводил эксперименты на 8-битных AVR от Atmel серии ATmega8, и у них в распоряжении не было АЦП. Но на них было очень удобно начинать знакомство с миром микроконтроллеров. Низкий порог вхождения и никаких танцев с бубнами при запуске.

Ну так вот, входной сигнал я решил “оцифровывать” простой ножкой в режиме входа. Если входное напряжение выше 2.5В, то у ножки было логическое состояние “1”, если ниже 2.5В, то “0”. В равные промежутки времени просто считывалось текущее состояние ножки и эти значения записывались в массив.

И этот “оцифрованный сигнал” прогонялся через ДПФ и вычислялось наличие нужных гармоник. Ни о какой точности или чувствительности речи и не шло, но это работало.

Если нет ЦАП

Аналогичная ситуация на ATmega8 была с ЦАП. Его там нет, и мне очень не хотелось заморачиваться с внешним ЦАП.

Оказалось, что можно пожертвовать логическими выходами микроконтроллера и подключить к ним резисторную матрицу R-2R. Таким образом из горстки резисторов собрать свой ЦАП с нужной разрядностью.

Подавая 0 и 1 на выходы микроконтроллера, можно получать нужный уровень напряжения на выходе “OUT”. Чем больше выходов будет использовано, тем выше разрядность ЦАП. По схеме R-2R оставил ссылку в конце.

Выбор подходящего микроконтроллера

После экспериментов на ATmega8 мне захотелось улучшить то, что есть. Выбирая из разных вариантов, я положил глаз на STM32. А конкретно — на STM32F103 — это 32-битные микроконтроллеры на ядре ARM Cortex-M3 (до 72 MHz).

Эксперименты проводил на отладочной плате, которая, наверное, есть в любом магазине электроники. На отладочной плате сразу располагался программатор, с помощью которого прошивается на МК.

Немного пострадав с его запуском, сразу же побежал проверять его по своему чек листу.

Производительность?

Схема тактирования позволяет работать ЦПУ на частоте 72 MHz, что после 8-битных на 20 MHz было с запасом. Хватало для более точных расчетов по алгоритму ДПФ.

Энергоэффективность?

При почти максимальной нагрузке потреблял около 40-50 мА. Дешевый стабилизатор напряжения в схеме питания на 100 мА с этим справлялся. Даже с учетом остальной маложрущей периферии этого было достаточно.

Достаточно быстрый АЦП?

Разобрался, как разогнать до максимальной скорости АЦП при частоте ЦПУ 72 MHz. Так как ранее было сказано, что полезный сигнал будет частотой в районе 80 кГц, то будем считать исходя из этого.

В доках для STM32 нашел, как вычислять минимальное время преобразования: нужно к настраиваемому времени семплирования (минимум 1.5 цикла) прибавить 12.5 машинных циклов. Получается 14 машинных циклов на одну точку измерения.

При определенной настройке схемы тактирования на модуль АЦП приходится 14 MHz. Если перевести в секунды, то 14 циклов при частоте тактирования 14 MHz — это одно измерение в 1 микросекунду.

Идеально! Даже если полезный сигнал будет частотой 100 кГц, я смогу измерить 10 точек за один период сигнала. С минимальной точностью, но быстро.

Примерно так будет выглядеть оцифровка синусоиды 80 кГц.

Достаточно быстрый ЦАП?

По той же логике нам нужно сгенерировать синусоиду частотой около 80 кГц. И если мы хотим, чтобы синусоида была похожа на синусоиду, а не на странную угловатую фигуру, нужно генерировать одну точку хотя бы раз в 1.5 микросекунды, как мы выяснили ранее.

Почитав документацию, я понял, что в ЦАП STM32F103 встроенный ОУ имеет ограничение в 1 MSPS. Получилось настроить генерацию каждой точки сигнала раз в 1 микросекунду.

Примерно так при этом будет выглядеть синусоида с частотой 80 кГц на выходе из ЦАП.

Периферия

Что еще мне понравилось в STM32F103 — это наличие встроенного USB. Там есть режим эмуляции COM порта. Мне показалось это очень удобным, особенно после внешних преобразователей USB-UART.

Можно подключать устройство к ПК обычным шнурком от телефона и через терминал посылать на устройство какие-нибудь отладочные команды.

Для экспериментов подключал два PLC устройства к двум компам, и они посылали друг другу ASCII символы, вводимые с клавиатуры. Получилось что-то вроде чата через розетку 220 В.

Особенности питания устройства

Сразу отмечу, что я не спец в проектировании блоков питания, для подробностей есть специализированная литература. Но считаю важным отметить некоторые моменты, которые влияют на стабильность системы, и с которыми у меня были проблемы.

Блок питания можно либо собирать самому, либо взять готовый модуль с нужными характеристиками, это неважно. В любом случае, нужно адекватно развести линии питания по печатной плате.

Схема питания устройства зависит от потребителей. В нашем случае основные “жрущие” потребители — это микроконтроллер и “выходная цепь”, так как в ней усилитель для отправки сигнала в ЛЭП.

Остальные потребители вроде усилителей входного сигнала во “входной цепи”, EEPROM памяти или какие-то UART конвертеры потребляют немного.

Стабильное питание микроконтроллера

Первое и самое важное на что нужно обратить внимание — это стабильность питания микроконтроллера. Он не любит скачки напряжения и может в самый неподходящий момент перезагружаться или просто начать себя странно вести (пропускать блоки кода).

И тут у нас проблемка: как назло, под боком у микроконтроллера находится “выходная цепь” с усилителем полезного сигнала. Этот блок устройства во время генерации сигнала импульсами потребляет мощность, что может прилично потрясти всю систему питания, обнулив при этом микроконтроллер.

При передаче кадра это происходит каждые 10 миллисекунд длиной в 1 миллисекунду.

С этим у меня возникли трудности. Иногда устройство работало нормально, но чаще — предсказуемо перезагружалось. Сначала пытался решить проблему блоком питания помощнее, но не помогало. В поисках решений много интересного узнал из форумов по робототехнике. Там похожие проблемы были в основном из-за сервоприводов, которые потребляют приличное количество энергии и, при неправильной разводке платы, могут внезапно перезагружать микроконтроллер.

Для тяжелых случаев есть пара советов, которые помогут уменьшить влияние скачков напряжения.

Совет 1 – Разделить землю на аналоговую и цифровую

Первый важный момент — это обеспечение минимального влияния аналоговой части схемы на цифровую.

Для этого нужно разделить дорожки “GND” в самом начале схемы питания — возле минуса блока питания. Ни в коем случае нельзя их пересекать или как-то замыкать в других частях схемы.

Для питания условно “цифровых” компонентов схемы (микроконтроллер, EEPROM память и т.д.) от самого блока питания должна идти отдельная линия, можно назвать её “DGND”.

Для питания аналоговой схемы генерации “полезного сигнала” от блока питания, соответственно, должна идти отдельная линия “AGND”. Подробнее можно почитать в статьях или литературе по заземлению.

Совет 2 – Не забыть про керамику

Конденсаторы нужно ставить перед каждой ножкой питания микроконтроллера и как можно ближе к ним. Обязательно выполнить минимум обвеса, который указан в Datasheet на микроконтроллер.

Также желательно добавить в цепи питания микроконтроллера дополнительную емкость, в виде электролитического или танталового конденсатора, чтобы он мог даже выдерживать кратковременное отключение питания.

С танталовыми осторожнее, они красиво взрываются :).

Еще надо не забыть “защитить” ножку “Reset” микроконтроллера, как указано в Datasheet. В противном случае микроконтроллер может внезапно перезагружаться. Если нет светодиодной индикации запуска программы микроконтроллера, то можно этого даже не заметить.

Совет 3 – Экранировать цифровые компоненты

Может получиться так, что недалеко от микроконтроллера расположен высокочастотный трансформатор, который во время передачи сигнала генерирует электромагнитные помехи.

Мне помогло расположение микроконтроллера на другой от ВЧ трансформатора стороне печатной платы и наличие земляного полигона под корпусом микроконтроллера.

Подробнее можно почитать в статье по ссылке в конце.

Заключение

В этой части мы в общих чертах разобрали чем занимается микроконтроллер. Узнали некоторые особенности питания устройства и возможные проблемы.

Статья вышла довольно объемной. Я постарался максимально коротко передать основные моменты. Может сложиться ощущение незаконченности и это нормально. Для углубленного изучения оставлю ссылки внизу.

В следующей части подробнее разберём оставшиеся блоки устройства: входная и выходная цепи, zc детектор и согласование устройства в сетью 220 В. После этого должна сложиться целостная картинка. В заключительной части пробежимся по программной части: обработке оцифрованного сигнала, генерация синуса и т.д.

У кого был/есть какой-либо опыт в PLC обязательно делитесь этим с остальными в комментариях 🙂

Полезные ссылки