Как находить нули функции 🚩 как найти нули функции примеры 🚩 Математика
11 марта 2011
Автор КакПросто!
Математическое понятие функции показывает наглядно то, как одна величина полностью определяет значение другой величины. Обычно рассматриваются числовые функции, которые ставят в соответствие одним числам другие. Нулем функции, обычно называют значение аргумента, при котором функция обращается в ноль.

Статьи по теме:
Инструкция
Для того, чтобы найти нули функции, необходимо приравнять ее правую часть к нулю и решить полученное уравнение. Предположим, вам дана функция f(x)=x-5.
Для нахождения нулей этой функции, возьмем и приравняем ее правую часть к нулю: x-5=0.
Решив это уравнение получим, что x=5 и это значение аргумента и будет нулем функции. То есть при значении аргумента 5, функция f(x) обращается в ноль.
Обратите внимание
При нахождение корней уравнения, могут появиться лишние корни. Проверить это легко: достаточно подставить полученное значение аргумента в функцию и убедиться обращается ли функция в ноль.
Полезный совет
Иногда функция не выражается в явном виде через свой аргумент, тогда просто необходимо знать, что представляет собой эта функция. Примером этому может служить уравнение окружности.
Источники:
- как найти ноль
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Нули функции | Алгебра
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
1) Найти нули линейной функции y=3x+15.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
3)Найти нули функции
Решение:
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)
x ∈ (-∞; -1)U(-1; 1)U(1;∞).
Решаем уравнение
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Ответ: x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
Например,
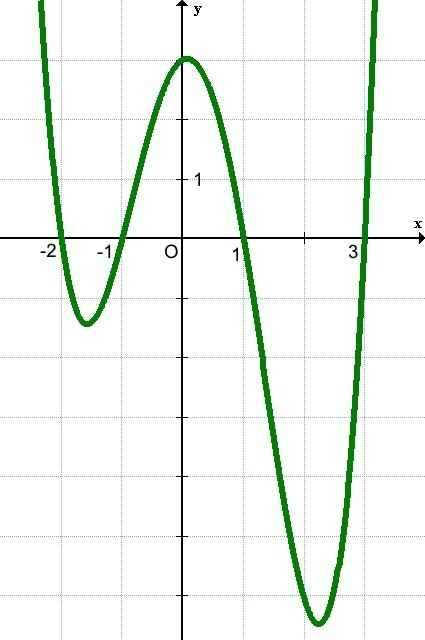
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
www.algebraclass.ru
Как находить нули функции | Сделай все сам
Математическое представление функции показывает наглядно то, как одна величина всецело определяет значение иной величины. Традиционно рассматриваются числовые функции, которые ставят в соответствие одним числам другие. Нулем функции, обыкновенно называют значение довода, при котором функция обращается в нуль.

Инструкция
1. Для того, дабы обнаружить нули функции, нужно приравнять ее правую часть к нулю и решить полученное уравнение. Представим, вам дана функция f(x)=x-5.
2. Для нахождения нулей этой функции, возьмем и приравняем ее правую часть к нулю: x-5=0.
3. Решив это уравнение получим, что x=5 и это значение довода и будет нулем функции. То есть при значении довода 5, функция f(x) обращается в нуль.
Под представлением функции в математике понимают связь между элементами множеств. Если говорить больше верно, это «закон», по которому всему элементу одного множества (называемому областью определения) ставится в соответствие определенный элемент иного множества (называемого областью значений).
Вам понадобится
- Знания в области алгебры и математического обзора.
Инструкция
1. Значения функции это некая область, значения из которой может принимать функция. Скажем область значения функции f(x)=|x| от 0 до бесконечности. Дабы обнаружить значение функции в определенной точке нужно подставить взамен довода функции его числовой эквивалент, полученное число и будет значение м функции . Пускай дана функция f(x)=|x| – 10 + 4x. Обнаружим значение функции в точке x=-2. Подставим взамен x число -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. То есть значение функции в точке -2 равно -16.
Обратите внимание!
Раньше чем искать значение функции в точке – удостоверитесь, что она входит в область определения функции.
Полезный совет
Аналогичным методом дозволено обнаружить значение функции нескольких доводов. Различие в том, что взамен одного числа нужно будет подставить несколько – по числу доводов функции.
Функция представляет собой установленную связанность переменной у от переменной x. Причем всем значению х, называемого доводом, соответствует исключительное значение у – функции. В графическом виде функция изображается на декартовой системе координат в виде графика. Точки пересечения графика с осью абсцисс, на которой откладываются доводы х, именуются нулями функции. Поиск допустимых нулей – одна из задач по изысканию заданной функции. При этом учитываются все допустимые значения самостоятельной переменной x, образующие область определения функции (ООФ).

Инструкция
1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк.
2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x).
3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений.
4. Рассматривая функцию с выражением под корнем четной степени, примите за область определения все доводы х, значения которых не обращают подкоренное выражение в негативное число (напротив функция не имеет смысла). Уточните, попадают ли обнаруженные нули функции в определенную область допустимых значений х.
5. Знаменатель дроби не может обращаться в нуль, следственно исключите те доводы х, которые приводят к такому итогу. Для логарифмических величин следует рассматривать лишь те значения довода, при которых само выражение огромнее нуля. Нули функции, обращающие подлогарифмическое выражение в нуль либо негативное число, обязаны быть отброшены из финального итога.
Обратите внимание!
При нахождение корней уравнения, могут возникнуть лишние корни. Проверить это легко: довольно подставить полученное значение довода в функцию и удостовериться обращается ли функция в нуль.
Полезный совет
Изредка функция не выражается в очевидном виде через свой довод, тогда легко нужно знать, что представляет собой эта функция. Примером этому может служить уравнение окружности.
jprosto.ru
Как определить нули функции 🚩 как найти ооф функции 🚩 Математика
27 декабря 2018
Автор КакПросто!
Функция представляет собой установленную зависимость переменной у от переменной x. Причем каждому значению х, называемого аргументом, соответствует единственное значение у — функции. В графическом виде функция изображается на декартовой системе координат в виде графика. Точки пересечения графика с осью абсцисс, на которой откладываются аргументы х, называются нулями функции. Поиск возможных нулей – одна из задач по исследованию заданной функции. При этом учитываются все возможные значения независимой переменной x, образующие область определения функции (ООФ).

Статьи по теме:
Инструкция
Нуль функции – это такое значение аргумента х, при котором значение функции равно нулю. Однако нулями могут быть лишь те аргументы, которые входят в область определения исследуемой функции. То есть в такое множество значений, для которых функция f(x) имеет смысл.
Запишите заданную функцию и приравняйте ее к нулю, например f(x) = 2х²+5х+2 = 0. Решите получившееся уравнение и найдите его действительные корни. Корни квадратного уравнения вычисляются с помощью нахождения дискриминанта.
2х²+5х+2 = 0;
D = b²-4ac = 5²-4*2*2 = 9;
х1 = (-b+√D)/2*а = (-5+3)/2*2 = -0,5;
х2 = (-b-√D)/2*а = (-5-3)/2*2 = -2.
Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих аргументам исходной функции f(x).
Все найденные значения х проверьте на принадлежность к области определения заданной функции. Найдите ООФ, для этого проверьте исходное выражение на присутствие корней четной степени вида √f (х), на наличие дробей в функции с аргументом в знаменателе, на присутствие логарифмических или тригонометрических выражений.
Рассматривая функцию с выражением под корнем четной степени, примите за область определения все аргументы х, значения которых не обращают подкоренное выражение в отрицательное число (иначе функция не имеет смысла). Уточните, попадают ли найденные нули функции в определенную область возможных значений х. Знаменатель дроби не может обращаться в ноль, поэтому исключите те аргументы х, которые приводят к такому результату. Для логарифмических величин следует учитывать лишь те значения аргумента, при которых само выражение больше нуля. Нули функции, обращающие подлогарифмическое выражение в ноль или отрицательное число, должны быть отброшены из конечного результата.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Ответы@Mail.Ru: Будьте добры объяснить как в алгебре (тема
D (f)-те значения, которые может принимать аргумент
E (f)-те значения, которые может принимать функция
R- искать не надо, это множество действительных чисел
Д (ф) значение функции по х (т. е. от чего до чего)
Е (ф) значения функции по у ( т. е. от чего до чего)
D(f) находят исходя из вида самой функции. Например многочлены имеют область определения R (множество всех действительных чисел).
Область определения функции — это множество всех тех значений аргумента (x), при которых функция определена ( или имеет смысл, или принимает действительные значения).
Например, для функции у = (7 — х) /(5 — х) область определения — все действительные числа, кроме х = 5. Потому что при х равном 5, знаменатель дроби равен нулю, а на ноль делить нельзя. Ещё говорят, что у этой функции в точке х = 5 разрыв.
E(f) — это множество всех значений, которые принимает функция при всех Х из области определения (т. е. при всех Х из D(f))
Найти область значений функции иногда сложнее, чем её D(f). В некоторых случаях она очевидна, как например у многочленов — R (все действительные числа). Или у обратной пропорциональности y=a/x, (где а-некоторое число), область значений — все действительные числа, кроме нуля. В большинстве же других случаев её приходится отыскивать разными аналитическими методами.
touch.otvet.mail.ru
Что такое нули функции и как их определить
Что такое нули функции? Ответит довольно прост — это математический термин, под которым подразумевают область определения заданной функции, на котором ее значение нулевое. Нули функции также называют корнями уравнения. Проще всего пояснить, что такое нули функции, на нескольких простых примерах.
Примеры
Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции — это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:
0=х+3;
х=-3.
В данном случае -3 и есть искомый нуль. Для данной функции существует только один корень уравнения, но так бывает далеко не всегда.
Рассмотрим другой пример:
у=х2-9.
Подставим 0 в левую часть уравнения, как и в предыдущем примере:
0=х2-9;
-9=х2 .
Очевидно, что в данном случае нулей функции будет два: х=3 и х=-3. Если бы в уравнении был аргумент третьей степени, нулей было бы три. Можно сделать простой вывод, что количество корней многочлена соответствует максимальной степени агрумента в уравнении. Однако многие функции, например у=х3 , на первый взгляд противоречат этому утверждению. Логика и здравый смысл подсказывают, что у этой функции только один нуль — в точке х=0. Но на самом деле корней три, просто все они совпадают. Если решать уравнение в комплексной форме, это становится очевидным. х=0 в данном случае, корень, кратность которого 3. В предыдущем примере нули не совпадали, потому имели кратность 1.
Алгоритм определения
Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:
- Записать функцию.
- Подставить у или f(x)=0.
- Решить получившееся уравнение.
Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.
Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.
Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.
Уравнение у=х2-16 имеет два корня, и оба лежат в комплексной плоскости: х1=4і, х2=-4і.
Типичные ошибки
Частая ошибка, которую допускают школьники, еще не разобравшиеся толком в том, что такое нули функции, — это замена на ноль аргумента (х), а не значения (у) функции. Они уверенно подставляют в уравнение х=0 и, исходя из этого, находят у. Но это неправильный подход.
Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти «потерянные» сомножители.
Графическое представление
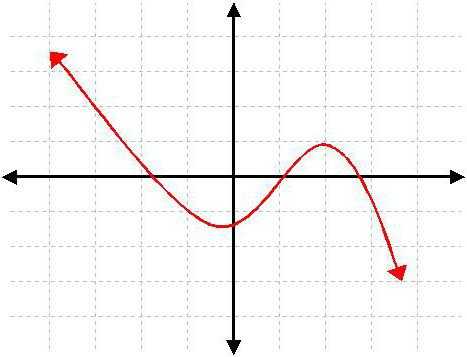
Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.
fb.ru

Как правильно: нУль или нОль????
Цифровой знак O обозначается словами «ноль» или «нуль», что одно и то же. Хотя нуль — старинное слово, ноль более современное.
Заглянем в Толковый словарь Ефремовой Т. Ф. и Ефремова, 2000 г.
Читаем:
Ноль и Нуль — слова мужского рода. Обозначают одно и то же, а именно:
1. Отсутствие величины.
2. Условленная величина, от которой начинается исчисление подобных ей величин (времени, температуры и т. п.).
3. Самый низкий балл оценки знаний и поведения в школе (в Российском государстве до 1917 г.).
4. Что-либо бесконечно малое, ничтожное.
5. Переносное значение: полное ничтожество, не имеющий никакого значения человек .
Значит, все равно, как вы будете говорить: ноль или нуль. А как вам больше нравится?!
Но все же разница в употреблении этих слов есть, хоть она и небольшая!
Есть случаи, когда следует употреблять только «нОль» и, наоборот, только «нУль» и никак иначе!
О человеке мы скажем: абсолютный нУль. Но в математике: абсолютный нОль!
Только ноль мы употребим в выражениях: «ноль-ноль», «ноль целых», «ноль часов», «ноль внимания», «ноль без палочки».
Только нуль в выражениях: «температура опустится ниже нуля», «стричься под нуль», «равно нулю», «на нуле кто-нибудь, что-нибудь», «с нуля начинать», «сводить к нулю» .
Одной из задач, возникающих при исследовании функции, является нахождение её нулей – т.е. точек пересения с осью абсцисс. Рассмотрим график некоторой функции
:
Нулями функции
являются точки
в которых, как было сказано выше, график функции пересекает ось абсцисс. Чтобы найти
нули функции
необходимо и достаточно
решить уравнение:
Нулями функции будут корни этого уравнения. Таким образом, нули функции находятся в точках
.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен найти нули практически любой, даже очень сложной функции.
Кто придумал ноль? Как он стал частью привычной нам математики? Да, тот самый ноль (или нуль – оба варианта правильны), который мы обозначаем знаком, похожим на букву «О», без него немыслима современная математика и десятичная система счёта. Нам, живущим в XXI веке, кажется, что ноль существует так же давно, как и само человечество. На самом деле ноль появился относительно недавно.
Непозиционные системы счёта
Развитие математики идёт нога в ногу с развитием человечества. Математика началась с самого простого, с того, что первобытному человеку понадобилось нечто, чем он мог бы обозначать количество предметов. Например, охотник, чтобы объяснить другому охотнику, что видел «трёх мамонтов в двух днях ходьбы, возле пяти скал» использовал жесты и пальцы рук. Но вскоре эти жесты получили конкретные письменные обозначения – так появились первые числа. Как вы сами догадываетесь первобытным людям незачем было использовать понятие ноль.
Ведь «ноль мамонта» или «ноль скал» в природе нет. То есть число ноль было невостребованным в древние времена.

Время шло, и человечеству понадобилось всё больше и больше чисел. Если раньше для обозначения стада из восьми коров, люди делали восемь чёрточек, то, когда их количество стало, например, сто, то для удобства счёта люди начали объединять объекты в группы по 3, 5, 7 и 10. Такая группировка упрощала счёт. Анатомия рук человека, а именно то, что мы имеем по пять пальцев, стала основой для популярности групп по 5 и 10. Далее люди начали группировать десятки по десяткам (так появились сотни), сотни по десяткам (так появились тысячи) и так далее. Для обозначения их тоже придумали специальные символы (числа). Например, в древнем Египте использовали следующие символы.

Любые другие числа записывались путём повторения этих цифр. Каждая цифра могла повторяться от 1 до 9 раз. Например, число 4622 обозначалось следующим образом:

Обратите внимание! Не важно, в какой последовательности расположены символы, в итоге у вас всегда получится ровно 4622. Подобные системы счёта называют непозиционными, так как расположение цифр (позиция в записи) не имеет значения. Первые системы счёта были непозиционными. Как видите, в этих системах, как правило, не требовалась цифра ноль.
Позиционные системы счёта
Недостатки непозиционных систем счёта – их громоздкость и непрактичность. Например, представим запись двух чисел 3000 и 2998. Эти числа отличаются только на две единицы и в привычной нам арабской записи эти числа займут одинаковое место в тетради, но давайте посмотрим, как они будут выглядеть в непозиционной древней египетской записи:

Как же люди решили эту проблему? Чтобы ответить на этот вопрос, перенесёмся в древний Вавилон. Тут произошло одно очень значимое для математики событие – была открыта позиционная система счёта. Вавилонские математики рассудили, что для обозначения всех чисел им достаточно будет только два символа: первый – стоячий клин для обозначения единиц, и второй – лежачий клин
для обозначения десятков (они использовали шестидесятеричную систему счисления, ниже мы объясним как это работает). Давайте разберёмся, как они пришли к этой простой идее. Для начала вспомним, что люди при счёте стремились группировать объекты: десятки десятков – это сотня, десятки сотен – это тысяча и так далее. Вавилонским математикам было удобно группировать по 12 объектов, но в 5 групп (помните про количество пальцев?), так появилась шестидесятеричная система счисления (12 х 5 = 60) Почему они выбрали за основу счёта 60, вместо, казалось бы, удобных нам 10? Кстати, мы тоже используем эту систему при измерении времени (60 минут – это 1 час и так далее). Из-за удобства, ведь 60 можно разложить на большее количество множителей ( 2*2*3*5 = 60), чем 10 ( 2*5 = 10).
Так как же выглядели вавилонские числа?

Как, например, вавилонцы записывали числа 62? Давайте попробуем разобраться. Число 62 имеет вид . Заглянем в таблицу, по ней видно, что эта запись имеет для нас такой смысл – «1 2». Как же так? Ведь мы имели ввиду число 62. Не торопитесь, всё верно, только нам следует обратить внимание на пробел между этими цифрами и вспомнить, что в зависимости от позиции цифры могут нести дополнительный смысл. Так вот, крайняя левая «единица» показывает число полных групп, в нашем случае это означает, что в числе есть 60 единиц, далее следует 2. В итоге
означает 1х 60 + 2 = 62. Всё просто. Но как случайно не спутать число
( число 2) с
(число 61)? Визуально они не сильно отличаются друг от друга (не каждый разглядит пробел). Сначала вавилонцы мирились с этой проблемой и должны были догадываться из контекста задачи, о каком числе идёт речь. Но в итоге нужно было заменить эту пустоту неким символом, так появился ноль.

Цифра ноль пришла к нам вместе с арабскими цифрами, которые в свою очередь попали к арабским математикам из Индии. Первое изображение ноля выглядело как кружок, чуть меньший по размеру, чем прочие цифры – его нашли в записи числа 270, которое было изображено в 876 году на стене индийского города Гвалиора.
Позже индийские математики Брахмагупта, Махавира и Бхаскара писали, что если из одного числа вычесть его же, то получится ноль. Это и есть знакомое нам определение числа ноль, то есть ноль – это не понятие отсутствия числа, а число, и он стал использоваться в расчётах. Теперь всего десятью цифрами можно было записать любое, даже самое большое число. Это была революция в математике.
Сперва цифру ноль называли индийским словом «сунья» («пустое»). Арабы перевели это как «сыфр», от которого и произошло слово «цифры».
Но даже узнав о «восточной диковинке» (ноле), европейские учёные долго не решались использовать её – ведь это число ничего не исчисляет!
Итальянский математик Леонардо Фибоначчи одним из первых заинтересовался индийской системой счёта, и это позволило ему сделать ряд важнейших открытий и закономерностей. Но его пропаганда столь удобного способа записи и счёта не возымела особого действия на средневековых учёных. И даже в XVI веке математики продолжали всячески избегать ноля, упорно придерживаясь античной системы счёта и полагаясь на счётные доски.
Однако, как показала практика, ноль был таким же решающим прогрессивным изобретением, как и колесо. Эту простую и удобную систему сразу же оценили банкиры и купцы, которые считали вполне реальные деньги, а не извлекали воображаемые корни из воображаемых чисел в пыльной библиотеке. Уже в XV веке простой, неучёный люд считал с помощью индийских цифр, опережая учёные умы на столетия. Окончательно же десять знаков, включая ноль, утвердились в европейской науке лишь к началу XVIII века.

Есть два способа использования ноля и оба – очень важные. Первый – ноль указывает пустой разряд в нашей десятичной позиционной системе счисления. Второй способ использования ноля – это число, которое мы обозначаем 0.
- Ноль (от лат.Nullus – никакой) – цифра и одновременно число.
- Ноль не имеет знака.
- Ноль – это число, отделяющее на числовой прямой положительные числа от отрицательных.
- Ноль – целое число.
- Ноль – чётное число, поскольку при делении ноля на 2 получается целое число ноль.
- Ноль – это нейтральный элемент для операции сложения. Любое число при сложении с ним не меняется:
- a + 0 = 0 + a = a
- При вычитании ноля из любого числа получается то же число:
- a – 0 = a
- Умножение любого числа на ноль даёт ноль:
- a 0 = 0 a = 0
- При делении ноля на любое ненулевое число получается ноль:
- 0 : a = 0, при этом а не равно нолю.
- На ноль делить нельзя!
- Выражение 0 : 0 не имеет смысла.
Последние два свойства ноля заслуживают особого внимания. Любой взрослый ещё со школы помнит, что на ноль делить нельзя. Почему нельзя – обычно никогда не объясняют. Просто нельзя и точка! Ну нельзя, значит, нельзя. Давайте сами разберёмся.
Предположим, что можно делить на ноль. Разделим любое число на ноль:
7 : 0 = х.
Следовательно,
0 х = 7.
То есть, надо найти такое число, которое при умножении на 0 даст 7. Но мы знаем, что при умножении на 0 всегда получается 0. Значит, такое число просто не существует. То есть, наша задача не имеет решения, а сама запись не имеет смысла. Поэтому бессмысленность этой записи кратко выражают фразой: «На ноль делить нельзя».
А можно ли ноль делить на ноль?
Опять предположим, что можно:
0 : 0 = х,
Следовательно,
0 x = 0, и это уравнение благополучно решается.
Например, можно взять x = 0, и тогда получаем 0 0 = 0. Но не будем спешить. Попробуем взять x = 1. Получим 0 1 = 0. Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 518 и т. д. Мы не можем остановить свой выбор на каком-то одном числе и сказать, что именно ему соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что ноль на ноль тоже делить нельзя.
«На ноль делить нельзя» – это правило и точка. А кто сказал, что нельзя? И почему нельзя? А что будет, если разделить? Давайте разбираться вместе.
У меня статьи вытекают одна из другой. Так получается само собой.
Когда я описывала статистику своих подписчиков, то в комментариях разразился спор, что не могут люди старшего возраста сидеть в интернете (хотя, это была статистика канала и я её никак подделать не могла). Дала развернутый ответ в статье о том, как 60-летние используют интернет.
Потихоньку в спорах дошло дело до обзора на “Торнадо-С” и Himars, тогда подписчики написали, что хорошо бы и про ракеты «Кинжал» написать. Написав про гиперзвуковые ракеты “Кинжал”, в комментариях-дискуссиях был поднят вопрос про скорость звука и число Маха.
Следующая статья, как Вы уже понимаете, была про скорость звука. А уже под этой статьей вышли на ещё одну тему, а почему на ноль делить нельзя? Вот, встречайте – подробное объяснение того, почему математика запрещает это делать.
Как будет правильно «нуль» или «ноль»
Отойдем немного от математики и выясним, как правильно писать: «ноль» или «нуль».
На самом деле «нуль» и «ноль» – это два разных понятия, хотя они оба произошли от одного и того же латинского слова «nullus» – «ничто».
Ноль – название цифрового знака 0, используется в математике.
Нуль – разговорная речь, используется в литературе. Например, чтобы показать никчемность человека – «он был нулем», события – «старания свелись к нулю», «настроение на нуле», но… «он был полный ноль».
Если речь идет о математических решениях, то правильнее писать: «делить на ноль» или «ноль в квадрате», но… «прибавить к нулю» или «стремится к нулю».
Вывод: даже в письменном виде ноль не имеет конкретного правила, и не понятно, как правильно писать «ноль» или «нуль» и как будет грамотно.
«На ноль делить нельзя» – почему?
Мы узнали это правило ещё в младших классах и, если спрашивали: «Почему?», то ответ получали: «Потому! Это правило такое». Ну нельзя, так нельзя.
Но многим не даёт покоя: «Так почему нельзя делить на ноль? А если разделить на него, то что получится?».
1. Деление на ноль обычных чисел в арифметике
Делить на ноль натуральные числа в «обычной математике» действительно нельзя. А знаете почему? Потому что в арифметике нет понятия «деление», а есть понятие «обратное действие умножению»!
Всем известно, что 100 : 25 = 4. Но…раз в математике деление работает как обратное действие умножению, тогда:
100 : 25 = Х это и есть
Х · 25= 100, Х = 4. Верно.
Значит:
100 : 0 = Х это и есть
Х · 0 = 100, Х =?. Неверно.
Это неверно, так как умножая число на 0, мы всегда получаем 0.
Таких чисел, которое при умножении на 0 дали бы нам 100 не существует.
Такая задача не имеет смысла.
Число, которое при умножении на 0 даст другое число, кроме 0 – не существует! Так как при обратном действии умножении, это не будет таким же числом.
2. Любое деление можно заменить вычитанием
Приведу простой, но довольно показательный пример:
100 : 25 = 4
Таким образом в 100 находится четыре 25 – это значит, что если из 100 вычесть 4 раза 25, то должен получиться ноль:
100 – 25 – 25 – 25 – 25 = 0. Верно.
А сколько нужно из 100 вычесть 0, чтобы остался 0:
100 : 0 = ?
Давайте попробуем решить:
100 – 0 – 0 – 0 – 0 – 0 – 0 …
Как видно, никогда мы не придем к тому, чтобы получился ноль.
Тут даже понятие «бесконечное количество» не правильное, так как бесконечно убирая нули мы всё равно не придем к тому, чтобы 100 стало нулем.
Именно поэтому на ноль делить нельзя! Это не запрет и не правило, это бессмысленное действие, без ответа.
3. Что будет если ноль разделить на ноль
Рассмотрим 0 : 0 = Х, значит Х · 0 = 0, значит Х = 0.
В данном раскладе вроде бы уравнение решено верно. Но…
В выражении Х · 0 = 0 вместо Х можно подставить абсолютно любое число. Ведь любое число, умноженное на ноль, даст нам ноль.
Значит если Х · 0 = 0, то Х может быть и 0, и 10, и 1000 и 1234567890.
Это противоречит первому условию, что мы делили 0 именно на 0.
Но так как при умножении, это может быть любое число, значит мы не можем уверенно ответить, что эта запись приводит к первоначальной записи 0 : 0.
Вывод: раз решение получается бессмысленным, значит и ноль на ноль делить нельзя!
Ноль в скоростях
Если нам нужно преодолеть 60 км со скоростью 0 км/час, то мы будем лететь/ехать/идти без движения, а точнее стоять/лежать/сидеть на месте бесконечное количество времени!
Другими словами, со скоростью 0 км/час мы 60 км преодолеем за бесконечное количество времени. Ну или пока не умрём. С точки зрения математики – время равно бесконечности.
Курьезный пример с нулями
Покажу вам пример, который ставит в тупик уже давно не только простых обывателей.
Мы с 4 класса знаем, если с обоих сторон уравнения стоят одинаковые числа, то их можно сократить:
3 · 5 = 3 · 5
Сократив 3 получаем: 5 = 5. Верно.
Сократив 5 получаем 3 = 3. Верно.
Но, мы также знаем, что при умножении на 0 любое число будет равно 0:
0 · 8 = 0
0 · 77 = 0
Также есть правило, что если правые стороны одинаковые, значит и левые тоже одинаковые, получаем:
0 · 8 = 0 · 77.
Сокращаем 0 и получаем: 8 = 77. Неверно.
Курьёз, абсурд. Поэтому с нулём шутки плохи.
А если делить на число приближенное к нулю
Например, если знаменатель 0,000000000000000000001 и он бесконечно стремится к нулю, но его так и не достигает. Формально он уже ноль, но на самом деле нет.
Так вот если взять калькулятор и разделить на этот псевдоноль любое натуральное число, то получится огромное число. И чем больше мы будем уменьшать делитель, приближая его к нулю, тем больше мы будем приближать частное к бесконечности.
А если всё-таки разделить на ноль, что будет?
Итак, мы выяснили, что с математической точки зрения делить на ноль нельзя.
Но такого понятия в математике как «нельзя» – не существует. Тогда делить на ноль всё-таки можно?
Например, ноль на ноль делить можно при вычислении пределов функций. Если окунуться в мир математического анализа, то правило Лопиталя, на основании метода Бернулли, раскрывает решение вот таких вот неопределенностей как 0 : 0 или 0/0.
По теореме Лопиталя, которая была опубликована в 1696 году (это не опечатка, это XVII век) получается, что два ноля делённых на ноль равно два.
Однако, в теореме рассматриваются примеры, когда в числителе и знаменателе выражения стремятся к нулю. Не конкретно нули, а число предельно близкое к нулю. Фи… опять не чистый ноль.
А это и есть – неопределенность, чего математика не приемлет! Математика – наука точная!
Вместо заключения
В школьной математике действительно на ноль делить нельзя. Так как дети маленькие и в их головы невозможно вместить понятия о лимитах, множествах, термины из математического анализа и высшей математики.
Таким образом, запрет на деление на ноль введен как раз из-за неопределенности ответа! Из-за того, что его невозможно объяснить простыми словами.
Главный вывод из всего вышесказанного: А если не в школьной математике, то на ноль делить можно? Можно, но не на ноль, а на очень сильно приближенное к нулю значение. Потому что (фанфары и злобный смех за кадром) на ноль делить нельзя…
Так что думайте сами, решайте сами – делить или не делить.
Понравилась статья? Если «да», то ставьте лайк. Лайк – лучшее спасибо! Пишите комментарии – это возможность поспорить и найти истину. Подписывайтесь, будет интересно!
