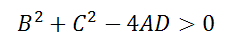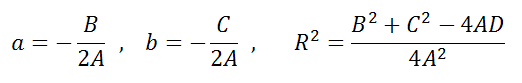Полуокружность как найти точку

Прежде чем
приступить к изучению нового материала, давайте вспомним, что

Для любого угла  синусом
угла  называется
ордината  точки
М,

а косинусом угла
 –
абсцисса  точки
М.

Тангенсом угла  называется
.

Котангенсом угла
 называется
.

 основное
тригонометрическое тождество

Если ,
то:

Если ,
то:

Еще сегодня нам
надо вспомнить о том, что координаты векторы равны разности соответствующих
координат его конца и начала.

Координаты вектора  равны
разности соответствующих координат его конца и
начала :
.

Еще вспомним лемму
о коллинеарных векторах.

Лемма. Если
векторы  и
 коллинеарны
и ,
то существует такое число ,
что .
 

Рассмотрим задачу.
Определить координаты точки А, которая расположена в верхней координатной
полуплоскости.

Построим в этой полуплоскости
единичную полуокружность. Соединим точку А с центром полуокружности и обозначим
за М точку пересечения отрезка ОА с полуокружности. Координаты точки М (.

Определим
координаты вектора ,
поскольку координаты точки О (0;0).

,
 

С другой стороны,

Теперь давайте
проанализируем знаки координат точки А.

Координаты точки зависят от
величины отрезка ОА, (а это всегда положительное число), и от знака синуса и
косинуса угла α. Синус произвольного угла из промежутка от 0 до 180
градусов находится в промежутке от 0 до 1, то есть принимает не отрицательные
значения. Косинус угла может принимать значения от -1 до 1, то есть быть как
положительным, так и отрицательным. Значит, можно записать, что ;
;
.

Решим несколько
задач.

Задача. Угол
между лучом ,
пересекающим единичную полуокружность, и положительной полуосью равен
.
Найдите координаты точки ,
если:

а) , 
; 
б) , 
; 
в) , 
.

Решение.

 

 

а)  

  

      

б)   

 

 

в)  

 

 

Задача. Найти
угол между лучом  и
положительной полуосью ,
если:

а) ; 
б) ; 
в) ;
г) .

Решение.

 

 

 

 

Запишем формулы для
определения координат точки А.

а)

 

 

 

б)

 

 

 

в)

 

 

 

г)  

 

 

 

Подведем итоги
урока. Сегодня на уроке мы вывели формулы для вычисления координат точки и
рассмотрели, как они используются при решении задач.

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Формулы для вычисления координат точки

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы выведем формулы для определения координат точки с помощью понятий синуса и косинуса.
Вначале решим типовую задачу на данную тему и на ее примере рассмотрим, как выражаются координаты точки через длину отрезка и угол. Далее выразим координаты вектора и точки через произведение тригонометрических функций и длины отрезка и проанализируем знаки полученных координат.
На примере типовой задачи решим несколько конкретных задач на нахождение координат точки через синус и косинус угла.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

[spoiler title=”источники:”]

http://interneturok.ru/lesson/geometry/9-klass/sinus-kosinus-i-tangens-ugla/formuly-dlya-vychisleniya-koordinat-tochki

[/spoiler]

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

«Базовые элементы» для решения задач с параметрами

В задачах с параметрами Профильного ЕГЭ по математике вам встретятся не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.

Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова. Чтобы лучше почувствовать эту разницу, повторите тему «Что такое функция».

Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать 5 типов элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:

1. Уравнение задает окружность с центром в начале координат и радиусом

2. Уравнение задает окружность с центром в точке (a;b) и радиусом

3. Неравенство задает круг вместе с границей.

4. Уравнение задает верхнюю полуокружность с центром в начале координат и радиусом

5. Уравнение задает нижнюю полуокружность с центром в начале координат и радиусом

6. Уравнение задает верхнюю полуокружность центром в точке и радиусом

7. Уравнение при положительных и задает ромбик, симметричный относительно начала координат.

8. Уравнение (сумма модулей) задает график следующего вида:

9. Расстояние между точками и находится по формуле:

Координаты середины М отрезка АВ находятся по формуле:

Уравнение отрезка концы отрезка и

В левой части уравнения сумма расстояний от точки P с координатами до точек и В правой расстояние между точками и

Пара чисел соответствует координатам любой точки этого отрезка.

Кратко это можно записать так: Это значит, что точка P лежит на отрезке

Окружность на координатной плоскости

Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

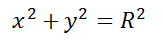
Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

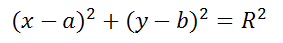
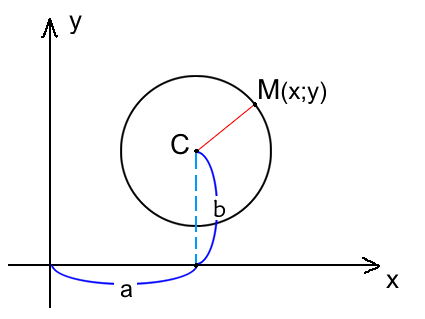
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде: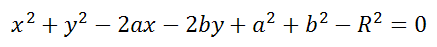

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида: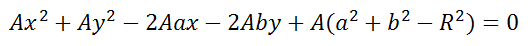

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

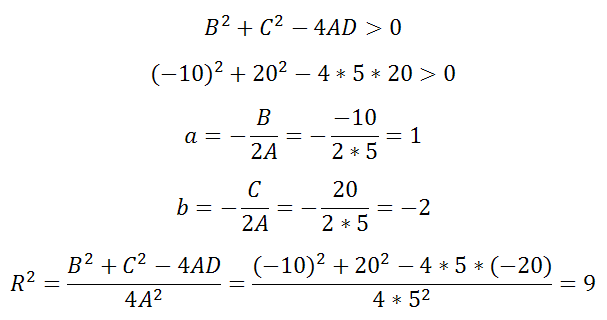
Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Конспект
На координатной плоскости изобразим окружность с центром в начале координат и радиусом, равным единице.

Эта окружность задаётся следующим уравнением: x² + y² = 1
Рассмотрим часть этой окружности – полуокружность, расположенную в первой и второй четвертях. Координаты любой точки этой полуокружности должны удовлетворять уравнению данной окружности.

Координаты точки М – это значения косинуса и синуса угла α, который соответствует этой точке.

x = cos⁡α, y = sin⁡α
Подставив в формулу окружности выражения для x и y получим следующее равенство: cos² α + sin² α = 1 (0° ≤ α ≤ 180°).
Это равенство называется основным тригонометрическим тождеством и выполняется для любого угла от нуля градусов до ста восьмидесяти градусов.
В математике существуют формулы, которые позволяют упростить вычисления синусов и косинусов углов. Эти формулы называются формулами приведения:
Если 0° ≤ α ≤ 90°, то
sin⁡(90° – α) = cos⁡α,
cos(90° – α) = sin⁡α.
Если 0° ≤ α ≤ 180°, то
sin⁡(180° – α) = sin⁡α.
cos(180° – α) = –cos⁡α
Вычислим с помощью формул приведения значения синуса угла, равного 150°. Представим угол, равный 150° в виде разности 180° и 30°, воспользуемся соответствующей формулой приведения: sin⁡150° = sin⁡(180° – 30°) = sin⁡30° = 0,5

В верхней полуплоскости прямоугольной системы координат Оху отметим точку А и выразим координаты этой точки через длину отрезка ОА и угол α между лучом ОА с положительной полуосью Ох. Построим в верхней полуплоскости единичную полуокружность. Проведём отрезок ОА и обозначим точку пересечения построенного отрезка с полуокружностью точкой М. Абсцисса точки М равна косинусу соответствующего угла α, а ордината точки М – синусу угла α. Определим координаты вектора ОА. Каждая координата вектора равна разности соответствующих координат его начала и конца.
Найдём координаты вектора ОМ:
(ОМ) ⃗(cos α – 0; sin α – 0),
(ОM) ⃗(cos α; sin α).
(ОА) ⃗↑↑(ОМ) ⃗, тогда (ОА) ⃗= ОА ∙ (ОМ) ⃗
Запишем равенство векторов в координатах. ((х;у)) ⃗= ((ОА ∙ cos⁡α; ОА ∙ sin⁡α)) ⃗
Так как векторы равны, то равны их соответствующие координаты.
x = ОА ∙ cos α
у = ОА ∙ sin α
Мы выразили координаты точки А через длину отрезка АО и угол α между лучом ОА с положительной полуосью Ох: А (ОА ∙ cos α; ОА ∙ sin α)

Wiki-учебник

Поиск по сайту

Реклама от партнёров: