Полюса как найти уравнение – Сайт, где вы сможете решить свои вопросы

Изолированные особые точки функций и полюсы

Классификация особых точек

Важное место в изучении и применении теории функций комплексного переменного занимает исследование их поведения в особых точках, где нарушается аналитичность функции. В частности, это точки, где функция не определена.

Исследование функции в особой точке z_0 определяется поведением ее в окрестности этой точки, т.е. исследованием $limlimits_{zto z_0}f(z)$ . Очевидно, имеют место три возможности:

а) $limlimits_{zto z_0}f(z)$ не существует;
б) $limlimits_{zto z_0}f(z)$ существует и равен конечному числу;
в) $limlimits_{zto z_0}f(z)$ равен бесконечности.

Исследование пределов функции в комплексной области — задача более сложная, чем в действительной области, так как, согласно определению, переменная стремится к z_0~(zto z_0) по любому направлению. Вычисление пределов в точках аналитичности не представляет интереса, так как в этих случаях $limlimits_{zto z_0}f(z)=f(z_0)$ .

Будем рассматривать $limlimits_{zto z_0}f(z)$ , где z_0 — особая точка.

Пример 4.1. Исследовать существование $limlimits_{zto0}exp frac{1}{z},~ limlimits_{zto0} exp frac{1}{z^2}$ в случаях a) z=xinmathbb{R} ; б) zinmathbb{C} .

Решение

a) В действительной области $limlimits_{zto0}exp frac{1}{z}$ не существует, так как не равны односторонние пределы $limlimits_{xto0+0}exp frac{1}{x}=infty,~ limlimits_{xto0-0}exp frac{1}{x}=0$ , но существует предел второй функции: $limlimits_{xto0}exp frac{1}{x^2}=infty$ .

б) В комплексной области, очевидно, $limlimits_{zto0}exp frac{1}{z}$ не существует, так как он не существует в частном случае z=x .

Но для второй функции полученного выше результата $limlimits_{xto0}exp frac{1}{x^2}=infty$ не достаточно, так как рассмотрены только два направления на плоскости — по действительной положительной и действительной отрицательной полуосям.

Рассмотрим еще какое-нибудь направление, например по мнимой оси, т.е. z=iy,~ yto0colon

$limlimits_{zto0}exp frac{1}{z^2}= limlimits_{zto0}exp frac{1}{(iy)^2}= limlimits_{zto0}exp frac{-1}{y^2}=0.$

Сравнивая этот результат с полученным выше $limlimits_{xto0}exp frac{1}{x^2}=infty$ , заключаем, что в комплексной области $limlimits_{zto0}exp frac{1}{z^2}$ не существует.

Аналогично можно показать, что не существует $limlimits_{zto0}exp frac{1}{z^4}$ , хотя $limlimits_{zto0}exp frac{1}{z^4}=infty$ для случаев z=x и z=iy (по действительной и мнимой осям).

Эти простые примеры показывают, что исследование функции в особой точке с помощью $limlimits_{zto z_0}f(z)$ может представлять большие сложности. Но, с другой стороны, в примере 3.36 при вычислении пределов функции в особых точках было использовано разложение функции в ряд.

Представление функции в виде ряда как один из способов ее аналитического задания, может быть использовано для исследования функции, в частности, в особых точках.

Будем рассматривать изолированные особые точки функций, т.е. особые точки, для каждой из которых существует такая ее окрестность, в которой нет других особых точек функции.

В частности, конечная особая точка $z_0inmathbb{C}$ является изолированной особой точкой функции f(z) , если существует число r>0 , такое, что в круге |z-z_0|<r эта точка- единственная особая точка f(z) , а в проколотой окрестности, т.е. в 0<|z-z_0|<r функция f(z) аналитическая.

Бесконечно удаленная особая точка z_0=infty является изолированной особой точкой функции f(z) , если существует число R>0 , такое, что в области |z|>R эта точка — единственная особая точка f(z) , а в кольце R<|z|<infty функция f(z) — аналитическая.

Согласно теореме Лорана, функция, аналитическая в кольце, в частности, в проколотой окрестности особой точки, может быть представлена рядом Лорана. Это позволяет свести исследование функции в изолированной особой точке к исследованию соответствующего ряда. Особенности рядов как представления аналитических функций можно заметить, проанализировав некоторые примеры предыдущих лекций.

Пример 4.2. Исследовать поведение и вид ряда Лорана в окрестности особой точки z=0 функций:

а) $frac{sin z}{z}$ ; б) $frac{sin z}{z^n},~n>1$ ; в) $exp frac{1}{z}$ .

Решение

Эти простые примеры показывают, что поведение функции в особой точке связано с видом главной части ряда Лорана: трем отмеченным выше случаям нахождения предела функции в точке z_0 соответствуют три различных случая вида главной части ряда Лорана в окрестности точки. В примере 4.2 исследовалась конечная особая точка. Такой же результат можно получить, рассматривая точку z=infty , например, для функций $exp frac{1}{z},~ z^2+frac{1}{z}$ и e^z .

Типы особых точек функции

В зависимости от трех случаев поведения функции в особой точке (исследования $limlimits_{zto z_0}f(z)$ ) особые точки функций делят на три типа — производится классификация особых точек. В качестве определения типа особых точек можно выбрать либо поведение функции в особой точке, либо вид ряда Лорана. Выберем первый подход.

Изолированная особая точка $z_0in overline{C}$ функции f(z) называется:

– устранимой особой точкой, если $limlimits_{zto z_0}f(z)$ существует и конечен (4.1);
– полюсом, если $limlimits_{zto z_0}f(z)=infty$ (4.2);
– существенно особой точкой, если $limlimits_{zto z_0}f(z)$ не существует (4.3).

Замечание 4.1. Если в случае устранимой особой точки z_0 положить $f(z_0)= limlimits_{zto z_0}f(z)$ , то f(z) будет аналитической в $O_{delta}(z_0)$ и точку z_0 можно считать правильной, т.е. не особой. В этом случае говорят, что в точке z_0 устранена особенность.

Пример 4.3. Определить тип особой точки z=0 для функций $frac{sin z}{z};~~frac{sin z}{z^n},~n>1;~~exp frac{1}{z},~~ exp frac{1}{z^2}$ .

Решение

На основании результатов решения примеров 4.1, 4.2 заключаем, что z=0 является устранимой особой точкой функции $frac{sin z}{z}$ ; полюсом для $frac{sin z}{z^n}$ при любом n>1 ; существенно особой точкой для функций $exp frac{1}{z}$ и $exp frac{1}{z^2}$ .

Пример 4.4. Определить тип особой точки z=infty для функций $f_1(z)=z^nsin frac{1}{z}$ и f_2(z)=e^z .

Решение

Рассмотрим $limlimits_{ztoinfty}f(z)$ . Для удобства введем обозначение $frac{1}{z}=xi$ . Для функции f_1(z) получим $limlimits_{ztoinfty}f_1(z)= limlimits_{xito0} frac{sinxi}{xi^n}=infty~(n>1)$ (см. пример 4.2), поэтому z=infty является полюсом функции $f_1(z)=z^nsin frac{1}{z}$ . Для функции f_2(z)=e^z точка z=infty является существенно особой, так как $limlimits_{ztoinfty}e^z= limlimits_{xito0}exp frac{1}{xi}$ не существует (см. пример 4.1).

Пример 4.5. Найти все конечные особые точки функций: а) $f_1=frac{sin z}{z^4+1}$ б) $f_2(z)= frac{sin z}{sin z^{-1}}$ и определить их тип.

Решение

Особыми точками дробей являются особые точки числителя, особые точки знаменателя и нули знаменателя.

а) Так как числитель и знаменатель функции f_1(z) — функции аналитические, то ее особыми точками являются только нули знаменателя, т.е. корни уравнения z^4+1=0 . Это четыре точки $z_k=exp frac{(pi+2kpi)i}{4},~k=0,1,2,3$ , или в алгебраической форме: $z_{1,2}= frac{pm1+i}{sqrt{2}},~ z_{3,4}= frac{pm1-i}{sqrt{2}}$ . Заметим, что точки расположены в вершинах квадрата, вписанного в окружность радиуса R=1 с центром в начале координат, и справедливы равенства $z_2=iz,~ z_3=-z_1,~ z_4= overline{z}_1$ .

Очевидно, все точки изолированные и являются полюсами, так как $limlimits_{zto z_k}f_1(z)=infty$ для любой точки z_k,~k=1,2,3,4 .

б) Особыми точками функции f_2(z) являются нули знаменателя, т.е. точки, для которых $frac{1}{z_k}=kpi$ или $z_k=frac{1}{kpi},~ k=pm1,pm2,ldots$ , а также z=0 — особая точка знаменателя. Точки z_k являются полюсами, так как $limlimits_{zto z_k}f_2(z)=infty$ . Точка z=0 — неизолированная особая точка функции, так как в любой ее окрестности |z|<r ( — любое число, r>0 ), кроме этой точки, расположено бесконечное множество особых точек вида $z_k=frac{1}{kpi},~ k=pm1,pm2,ldots$ . Точку z=0 в таком случае называют предельной точкой полюсов $z_k=frac{1}{kpi}$ , так как $limlimits_{ktoinfty}z_k=0$ .

Теоремы Сохоцкого и Пикара

Для исследования поведения функции в существенно особой точке имеют место следующие две теоремы.

Теорема 4.1 (Сохоцкого). Если r_0 — существенно особая точка функции f(z) , то для любого Ain overline{mathbb{C}} существует последовательность ${z_n}$ , сходящаяся к точке z_0 , такая, что $limlimits_{ntoinfty}f(z_n)=A$ .

Теорема 4.2 (Пикара). В любой окрестности существенно особой точки функция f(z) принимает любое значение (причем бесконечное число раз) кроме, быть может, одного.

Пример 4.6. Исследовать поведение следующих функций в существенно особых точках, проиллюстрировать теоремы Сохоцкого и Пикара:

a) $f_1(z)=exp frac{1}{z},~ f_2(z)= exp frac{1}{z^2},~ z_0=0$ ; б) f_3(z)=e^z,~ z_0=infty .

Решение

В примерах 4.3 и 4.4 показано, что точки z_0=0 и z_0=infty являются существенно особыми точками соответствующих функций. Исследуем пределы функций.

а) Для иллюстрации теоремы Сохоцкого выбираем A=0 и A=infty . Используя результат примера 4.1, имеем $limlimits_{zto0}exp frac{1}{z}=0$ , если z=x<0 , и $limlimits_{zto0}exp frac{1}{z}=infty$ , если z=x>0 , то есть $limlimits_{ntoinfty}f_1(z_n)=0$ для последовательности z_n=x_n , такой, что $limlimits_{ntoinfty}x_n=0$ и x_n<0 , и $limlimits_{ntoinfty}f_1(z_n)=0$ для последовательности z_n=x_n , такой, что $limlimits_{ntoinfty}x_n=0$ и x_n>0 .

Аналогично исследуем функцию f_2(z) . Для числа A=0 выбираем z_n=iy_n , где $limlimits_{ntoinfty}y_n=0$ и тогда $limlimits_{ntoinfty}f_2(z_n)=0$ , а для A=infty выбираем z_n= x_n , где $limlimits_{ntoinfty}x_n=0$ и тогда $limlimits_{ntoinfty} f_2(z_n)=infty$ .

Справедливость теоремы Пикара для этих функций следует из рассмотрения уравнений $exp frac{1}{z}=A,~ exp frac{1}{z^2}=A$ , которые, как известно, имеют бесконечное множество решений для любого Ain mathbb{C},~ Ane0 .

Например, для функции $f_1(z)= expfrac{1}{z}$ имеем $expfrac{1}{z}=A$ . Отсюда получаем

$frac{1}{z}= operatorname{Ln}A,quad frac{1}{z}= ln|A|+i(arg A+2kpi),quad k=0,pm1,pm2,ldots$ или $z_k=frac{1}{ln|A|+i(arg A+2kpi)}$ .

В частности, функция $exp frac{1}{z}$ в любой окрестности точки z_0=0 принимает значение A=1 бесконечное множество раз: в точках $z_k=frac{-i}{2kpi},~ k=pm1,pm2,ldots$ (рис. 4.1).

Рис. 4.1.

б) Точка z=infty является существенно особой точкой функции e^z (пример 4.4). Обозначив $z=frac{1}{xi}$ , можно повторить рассуждения предыдущего пункта для функции $expfrac{1}{xi}$ и точки xi=0 .

Ряд Лорана в окрестности особой точки

В предыдущем разделе на примере простых функций (см. пример 4.2) было высказано предположение, что вид ряда Лорана в окрестности особой точки зависит от типа особой точки и потому задача исследования функции в особой точке может быть сведена к исследованию соответствующего ряда Лорана . Подтверждением этого предположения в общем случае является доказательство соответствующих утверждений.

Утверждение 4.1

1. Для того чтобы особая точка функции была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z_0 — устранимая особая точка, то ряд Лорана функции f(z) имеет вид

$f(z)= sum_{n=0}^{infty} c_n(z-z_0)^n,quad 0<|z-z_0|<r$

(4.4)

для z_0 — конечной точки $z_0inmathbb{C}$ , и (для z_0=infty )

$f(z)= c_0+sum_{n=1}^{infty} frac{c_{-n}}{z^n},quad R<|z|<infty.$

(4.5)

2. Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов. Ряд Лорана функции f(z) в случае z_0 полюса имеет вид

$f(z)=sum_{k=-n}^{infty} c_k(z-z_0)^k,quad 0<|z-z_0|<r,$

(4.6)

если $z_0inmathbb{C}$ , и (если z_0=infty )

$f(z)=sum_{k=-infty}^{n}c_kz^k,quad R<|z|<infty,$

(4.7)

3. Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции f(z) в случае z_0 — существенно особой точки имеет вид

$f(z)= sum_{n=-infty}^{infty} c_n(z-z_0)^n,quad 0<|z-z_0|<r,$

(4.8)

если $z_0inmathbb{C}$ , и (если z_0=infty )

$f(z)= sum_{n=-infty}^{infty}c_nz^n,quad R<|z|<infty.$

(4.9)

Замечания 4.2

1. Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.

Так, точка $z_0inmathbb{C}$ является полюсом порядка (Pi(n)) функции f(z) , если в разложении (4.6) $c_{-n}ne0,~ c_k=0$ при k<-n . Точка z_0=infty является полюсом порядка (Pi(n)) функции f(z) , если в разложении (4.7) c_nne0,~ c_k=0 при k>n .

2. Главная часть ряда Лорана в случае полюса порядка и записывается следующим образом:

а) в случае $z_0inmathbb{C}$ в виде $sum_{k=-n}^{-1} c_k(z-z_0)^n$ , или $sum_{k=1}^{n} frac{c_{-k}}{(z-z_0)^k}$ , или, подробнее:

$frac{c_{-n}}{(z-z_0)^n}+frac{c_{-n+1}}{(z-z_0)^{n-1}}+ ldots+ frac{c_{-1}}{z-z_0},quad c_{-n}ne0,;$

(4.10)

б) в случае z_0=infty в виде $sum_{k=1}^{n}c_nz^k$ , или $sum_{k=-n}^{-1} frac{c_{-k}}{z^k}$ (см. (4.7)), или, подробнее:

$c_ncdot z^n+ c_{n-1}cdot z^{n-1}+ldots+c_1cdot z,quad c_nne0.$

(4.11)

3. Главная часть ряда Лорана в случае существенно особой точки записывается так:

а) в случае $z_0inmathbb{C}$ в виде $sum_{n=-infty}^{-1} c_n(z-z_0)^n$ , или $sum_{n=1}^{infty} frac{c_{-n}}{(z-z_0)^n}$ (см.(4.8)), или, подробнее:

$frac{c_{-1}}{z-z_0}+ frac{c_{-2}}{(z-z_0)^2}+ ldots+ frac{c_{-n}}{(z-z_0)^n}+ldots;$

(4.12)

б) в случае z_0=infty в виде $sum_{n=-infty}^{-1} frac{c_{-n}}{z^n}$ или $sum_{n=1}^{infty}c_nz^n$ (см.(4.9)), или, подробнее:

c_1cdot z+c_2cdot z^2+ldots+c_ncdot z^n+ldots

(4.13)

Пример 4.7. Определить тип особых точек функций: а) $f_1(z)=frac{z+2}{z^2-2z-3}$ ; б) $f_2(z)=frac{z+2}{(z+1)^2(z-3)}$ .

Решение

Особыми точками функций являются z_1=-1,~z_2=3,~z_3=infty . Чтобы определить тип особой точки, используем разложения функций в окрестности каждой точки, полученные в примерах 3.31 , 3.33 , 3.34.

a) $f_1(z)= frac{-1}{4}cdot frac{1}{z+1}-sum_{n=0}^{infty} frac{5(z+1)^n}{4^{n+2}},~ 0<|z+1|<4$ . В главной части разложения — один член ряда: $frac{-1}{4}cdot frac{1}{z+1}$ , здесь $c_{-1}=frac{-1}{4}ne0$ , все c_n=0 для n<-1 . Следовательно, в точке z=-1 — полюс первого порядка, т.е. простой полюс функции f_1(z) .

Аналогично из разложения $f_1(z)= frac{5}{4}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}}{4^{n+2}}(z-3)^n,~ 0<|z-3|<4$ получим такой же результат: точка z=3 — простой полюс функции f_1(z) .

Разложение $f_1(z)= sum_{n=1}^{infty} frac{(-1)^n+5cdot3^{n-1}}{4}cdot frac{1}{z^n},~ |z|>3$ . Функции в окрестности z=infty не содержит главной части — разложение имеет вид (4.5). Следовательно, точка z=infty — устранимая особая точка функции f_1(z) .

б) Из разложения $f_2(z)= frac{5}{16}cdot frac{1}{z-3}+ sum_{n=0}^{infty} frac{(-1)^{n+1}(n+6)}{4^{n+3}}(z-3)^n,~ 0<|z-3|<4$ следует, что z=3 — простой полюс функции f_2(z) .

Из разложения $f_2(z)= frac{-5}{16}cdot frac{1}{z+1}+ frac{-1}{4}cdot frac{1}{(z+1)^2}+ sum_{n=0}^{infty} frac{-5(z+1)^n}{4^{n+3}},~ 0<|z+1|<4$ , где $c_{-2}=frac{-1}{4}ne0$ и все c_n=0 для n<-2 , получаем, что z=-1 — полюс второго порядка функции f_2(z) .

Разложение f_2(z) в окрестности z=infty и не содержит положительных степеней, в чем можно убедиться, проанализировав разложения элементарных дробей (см. пример 3.34). Поэтому z=infty — устранимая особая точка функции f_2(z) .

Пример 4.8. Определить тип конечных особых точек для функций:

а) $exp frac{1}{z-a},~ sin frac{1}{z-a},~ cos frac{1}{z-a}$ ; б) $frac{sin z}{z^n},~ frac{1-cos z}{z^3}$ .

Решение

а) Используем разложения функций по степеням (z-a)colon

$begin{gathered}exp frac{1}{z-a}= 1+frac{1}{z-a}+ frac{1}{2!(z-a)^2}+ldots;qquad sinfrac{1}{z-a}= frac{1}{z-a}- frac{1}{3!(z-a)^3}+ldots;\ cosfrac{1}{z-a}= 1-frac{1}{2!(z-a)^2}+ldots end{gathered}$

Убеждаемся, что для всех указанных функций точка z=a является существенно особой точкой, так как в разложениях главная часть содержит бесконечное число членов, т.е. имеется бесконечное число членов с отрицательными степенями (см. п.1 утверждения 4.1).

б) Запишем разложения функций по степеням zcolon

$begin{aligned}frac{sin z}{z^n}&= frac{1}{z^n}! left(z-frac{z^3}{3!}+ldotsright)= frac{1}{z^{n-1}}-frac{1}{z^{n-3}cdot3!}+ldots;\ frac{1-cos z}{z^3}&= frac{1}{z^3}! left(1-left(1-frac{z^2}{2!}+frac{z^4}{4!}+ldotsright)right)= frac{1}{2!z}-frac{z}{4!}+ldots end{aligned}$

Для первой функции при n=1 в разложении отсутствует главная часть — совокупность членов с отрицательными степенями. Следовательно, согласно п.1 утверждения 4.1, точка z=0 для $frac{sin z}{z}$ является устранимой особой точкой.

При n>1 главная часть разложения содержит конечное число членов, поэтому точка z=0 для $frac{sin z}{z^n}$ является полюсом (см. п.2 утверждения 4.1). Кроме того, так как при n>1 в разложении старшая отрицательная степень равна (n-1) , то, согласно п. 1 замечаний 4.2, заключаем, что z=0 для $frac{sin z}{z^n}$ при n>1 является полюсом порядка (n-1) . Рассуждая аналогично, получаем, что z=0 является полюсом первого порядка — простым полюсом для функции $frac{1-cos z}{z^3}$ .

Сравнивая разложения функций по степеням в окрестности z_0=0 (формулы (4.4),(4.6),(4.8) при z_0=0 ) и z=infty (формулы (4.5), (4.7), (4.9)), можно сделать следующее заключение.

Утверждение 4.2

1. Чтобы z=infty была устранимой особой точкой функции f(z) , необходимо и достаточно, чтобы точка xi=0 была устранимой (или не особой) для $varphi(xi)= f!left(frac{1}{xi}right)$ .

2. Чтобы z=infty была полюсом порядка функции f(z) , необходимо и достаточно, чтобы точка xi=0 была полюсом порядка функции $varphi(xi)= f!left(frac{1}{xi}right)$ .

3. Чтобы z=infty была существенно особой точкой функции f(z) , необходимо и достаточно, чтобы точка xi=0 была существенно особой точкой функции $varphi(xi)= f!left(frac{1}{xi}right)$ .

Замечание 4.3. Как и в случае конечной особой точки z_0 , в которой функция не определена, но $limlimits_{zto z_0}f(z)=0$ (см. утверждение 3.5) , так и для z=0 в случае $limlimits_{ztoinfty}f(z)=0$ , устранимую особую точку z=infty можно считать нулем функции f(z) . Порядок нуля можно определить как порядок нуля функции varphi(xi) в точке xi=0 .

Пример 4.9. Исследовать точку z=infty для функций: a) $f(z)=frac{1}{z^2(z-2)}$ ; б) $f(z)=frac{z^2+1}{3z^2-2}$ ; в) $f(z)= zsinfrac{1}{z}$ .

Решение

Правила определения порядка полюса

Используя формулу (4.6) разложения функции в ряд в окрестности полюса, можно получить практически удобные правила определения порядка полюса, не требующие записи разложений в ряд в каждом конкретном случае.

Пусть $z_0~(z_0in mathbb{C})$ — полюс порядка n~(Pi(n)) функции f(z) . Разложение (4.6), где главная часть имеет вид (4.10) , преобразуем следующим образом:

$f(z)=frac{1}{(z-z_0)^n}bigl[c_{-n}+c_{-n+1}cdot (z-z_0)+ ldots+c_0(z-z_0)+ ldotsbigr]$ или $f(z)=frac{varphi(z)}{(z-z_0)^n}$ ,

где varphi(z) — функция, аналитическая в точке z_0 , как сумма степенного ряда, записанного в скобках, и $varphi(z_0)=c_{-n}ne0$ .

Далее рассмотрим функцию $F(z)=frac{1}{f(z)}$ , то есть $F(z)=frac{(z-z_0)^n}{varphi(z)}$ или F(z)=(z-z_0)^n varphi_1(z) , где — аналитическая в точке z_0 и varphi_1(z_0)ne0 . Из этого, согласно утверждению 3.5, следует, что z_0 является нулем порядка функции F(z) . Можно доказать и обратное утверждение.

А именно, если функция представлена в виде $f(z)=frac{varphi(z)}{(z-z_0)^n}$ , где — функция, аналитическая в точке z_0 , и varphi(z_0)ne0 , то z_0 — полюс порядка функции f(z) , а также, если z_0 — нуль порядка функции F(z) , то для функции $f(z)=frac{1}{F(z)}$ эта точка является полюсом порядка .

Кроме того, рассмотрим частное $f(z)=frac{f_1(z)}{f_2(z)}$ , где точка z_0 является нулем порядка для функции f_1(z) и нулем порядка для функции f_2(z) , то есть $f(z)= frac{(z-z_0)^k varphi_1(z)}{(z-z_0)^m varphi_2(z)}$ . При m>k получаем $f(z)= frac{varphi(z)}{(z-z_0)^{m-k}}$ , из чего, с учетом приведенных выше рассуждений, находим, что z_0 — полюс порядка (m-k) . Заметим, что при m=k точка z_0 — устранимая особая точка; случай m<k рассмотрен ранее. Результаты приведенных рассуждений запишем в виде утверждения.

Утверждение 4.3

1. Для того чтобы точка z_0 была полюсом порядка функции f(z) , необходимо и достаточно, чтобы ее можно было записать в виде

$f(z)= frac{varphi(z)}{(z-z_0)^n},quad varphi(z_0)ne0.$

(4.14)

2. Для того чтобы точка z_0 была полюсом порядка функции f(z) , необходимо и достаточно, чтобы она была нулем порядка функции $frac{1}{f(z)}$ (связь нулей с полюсами).

3. Если точка z_0 является нулем порядка функции f_1(z) и нулем порядка функции f_2(z)~(m>k) , то она — полюс порядка (m-k) для $frac{f_1(z)}{f_2(z)}$ .

Пример 4.10. Определить порядок полюсов функций из примеров: а) 4.7 ; б) 4.8.

Решение

Замечания 4.4

1. Так как конечными особыми точками рациональной дроби $frac{P_n(z)}{Q_m(z)}$ являются только нули знаменателя, то это либо полюсы, либо устранимые особые точки функции.

2. Такое же заключение можно сделать и для функции вида $f(z)= frac{varphi(z)}{Q_m(z)}$ , где — аналитическая функция. При этом, используя определение устранимой особой точки (4.1) и правила определения порядка нуля и полюса (утверждения 3.5 и 4.3), можно сделать следующие выводы относительно особой точки z_0 — нуля порядка k~[0(k)] знаменателя:

а) z_0 — полюс порядка функции f(z) , если varphi(z_0)ne0 ;
б) z_0 — полюс порядка (k-n) , если z_0 — нуль порядка функции varphi(z) и k>n ;
в) z_0 — устранимая особая точка функции f(z) , если z_0 — нуль порядка функции ;

г) z_0 — нуль порядка (n-k) функции f(z) , если z_0 — нуль порядка функции varphi(z) и n>k ; при этом полагаем $f(z_0)= limlimits_{zto z_0}f(z)=0$ .

▼ Примеры нахождения особых точек и определения их типа

Пример 4.11. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{z^2-4z+3}{(z-1)^3(z+2)^2}$ ; б) $f(z)= frac{z+2i}{z^3+8i}$ .

Решение

Конечными особыми точками этих рациональных дробей являются нули знаменателя. Чтобы для каждой их этих точек определить, является ли она полюсом или устранимой особой точкой, нужно, согласно определению, найти предел функции в этой точке. В случае полюса, т.е. когда $limlimits_{zto z_0}f(z)=infty$ , далее следует определить его порядок. Для этого используется утверждение 4.3.

Можно поступить иначе — согласно замечанию 4.4. Для этого нужно найти и нули числителя.

а) Особые точки функции z_1=1,~ z_2=-2 . Для точки z_2=-2 можно применить формулу (4.14) и из $f(z)= frac{varphi(z)}{(z+2)^2}$ , где $varphi(z)= frac{z^2-4z+3}{(z-1)^3}$ и varphi(-2)ne0 , получить, что эта точка — полюс второго порядка. Для точки z_1=1 формула (4.14) не применима, так как из $varphi(z)= frac{z^2-4z+3}{(z+2)^2}$ имеем varphi(1)=0 . Поступаем далее согласно замечанию 4.4. Раскладываем на множители числитель и записываем функцию

$f(z)= frac{(z-1)(z-3)}{(z-1)^3(z+2)^2}= frac{z-3}{(z-1)^2(z+2)^2}= frac{varphi(z)}{(z-1)^2},quad varphi(1)ne0.$

Получаем, что z=1 — полюс второго порядка для f(z) .

б) Особые точки функции — корни уравнения z^3+8i=0 , то есть z=sqrt[LARGE{3}]{-8i} или $z_k= exp left[left(-frac{pi}{6}+ frac{2kpi}{3}right)!iright],~ k=0,1,2$ . Все эти точки: $z_{1,3}=2! left(pmfrac{sqrt{3}}{2}-i frac{1}{2}right)!,~ z_2=2i$ — простые нули знаменателя, и так как числитель в этих точках не обращается в нуль, то они — простые полюсы функции f(z) .

Пример 4.12. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{z^6+z^4-z^2-1}{(z^2-4z+3)^2}$ ; б) $f(z)= frac{z-2i}{z^3+8i}$ .

Решение

Пример 4.13. Найти конечные особые точки функций и определить их тип:

а) $f(z)=frac{cospi z}{(4z^2-1)(z^2+3)}$ ; б) $f(z)=frac{sinpi z}{z^4-1}$ .

Решение

Конечными особыми точками этих функций вида $f(z)= frac{varphi(z)}{Q_4(z)}$ , где — аналитическая функция, являются только нули знаменателя.

а) Особые точки функции: $z_1=frac{2}{2},~ z_2=-frac{1}{2},~ z_3=isqrt{3},~-i sqrt{3}$ . Точки z_3 и z_4 — простые полюсы, так как числитель в этих точках не обращается в нуль и функцию можно представить в виде $f(z)= frac{varphi(z)}{z-z_0},~ varphi(z_0)ne0,~ z_0$ — точка z_3 или z_4 . В точках $z=pmfrac{1}{2}$ числитель обращается в нуль. Очевидно, это простые нули числителя, и поэтому его можно записать в виде cospi z= (z-z_0)cdot varphi(z),~ varphi(z_0)ne0,~ z_0 — точка z_1 или z_2 . Тогда для функции f(z) получаем

$f(z)= frac{(z-z_0)cdot varphi(z)}{4 left(z-dfrac{1}{2}right)!! left(z+ dfrac{1}{2}right)! (z^2+3)},.$

Так как $limlimits_{zto z_k} f(z)neinfty$ для $z_0=z_1=frac{1}{2}$ или $z_0=z_2=-frac{1}{2}$ , то эти точки — устранимые особые точки функции f(z) .

б) Особые точки функции: $z_{1,2}=pm1,~ z_{3,4}=pm i$ . Точки z_3=i и z_4=-i — простые полюсы.

Для точек z_1=1 и z_2=-1 проводим рассуждения, как в предыдущем пункте, и находим, что они — устранимые особые точки f(z) .

Пример 4.14. Определить тип особой точки z=0 для следующих функций: а) $f(z)= frac{e^z-1-z}{e^{z^5}-1}$ ; б) $f(x)= frac{cos z^2-1}{z^3sin^2z^2}$ .

Решение. В точке z=0 и числитель, и знаменатель каждой из функций обращается в нуль. Определим порядок нуля в каждом случае и используем п.3 утверждения 4.4.

а) Из разложений по степеням функций

$begin{gathered} e^z-1-z&= left(1+z+frac{z^2}{2!}+ldotsright)-1-z= frac{z^2}{2!}+frac{z^3}{3!}+ldots\ e^{z^5}-1&= left(1+z^5+frac{z^{10}}{2!}+ldotsright)-1= z^5+frac{z^{10}}{2!}+ldots end{gathered}$

находим, что z=0 — нуль второго порядка для числителя (0(2)) и нуль пятого порядка для знаменателя (0(5)) . Следовательно, z=0 — полюс третьего порядка для функции f(z) .

б) Используя правила определения порядка нуля, в частности, как и в предыдущем пункте, раскладывая функции в ряды по степеням , находим, что z=0 является 0(2) для числителя и 0(7) для знаменателя. Следовательно, z=0 -полюс пятого порядка для f(z) .

Пример 4.15. Найти конечные особые точки следующих функций и определить их тип:

а) $f(z)= frac{e^{2+2i}}{z^4-16}$ ; б) $f(z)= frac{(z+pi) sin frac{pi z}{2}}{zsin^2z}$ .

Решение

Пример 4.16. Определить тип особой точки z=0 для следующих функций:

а) $f(z)= frac{sin z-z}{cos z-1-dfrac{z^2}{2}}$ ; б) $f(z)= frac{sin z+z}{operatorname{ch}z-1-dfrac{z^2}{2}}$ ; в) $f(z)= frac{sin z-z}{cos z-1+dfrac{z^2}{2}}$ ; г) $f(z)= frac{sin z+z}{operatorname{ch}z-1+dfrac{z^2}{2}}$ .

Решение

Точка z=0 является нулем и знаменателя, и числителя для каждой из функций. Определим порядок нуля в каждом случае, используя правило определения порядка нуля (утверждение 3.5), в частности, раскладывая соответствующую функцию по степеням .

а) Из разложений

$begin{aligned}sin z-z&= left(z-frac{z^3}{3!}+ldotsright)-z=-frac{z^3}{3!}+ frac{z^5}{5!}+ldots\ cos z-1-frac{z^2}{2}= left(1-frac{z^2}{2!}+ frac{z^4}{4!}-ldotsright)-1-frac{z^2}{2}=-z^2+frac{z^4}{4!}-ldots end{aligned}$

находим, что z=0 является 0(3) для числителя и 0(2) — для знаменателя, поэтому она — устранимая особая точка. Так как

$limlimits_{zto0}f(z)= limlimits_{zto0} frac{z^3! left(-frac{1}{3}+ frac{z^2}{5!}+ ldotsright)}{z^2! left(-1+frac{z^2}{4!}-ldotsright)}=0,$

то, полагая f(0)=0 , можно считать, что z=0 — нуль для f(z) , причем 0(1) (см. замечания 4.4).

б) Из разложений

$sin z+z=2z-frac{z^3}{3!}+ldots$ и $operatorname{ch}z-1-frac{z^2}{2}= left(1+frac{z^2}{2!}+ frac{z^4}{4!}+ldotsright)-1-frac{z^2}{2}= frac{z^4}{4!}+ frac{z^6}{6!}+ldots$

находим, что z=0 является 0(1) для числителя и 0(4) — для знаменателя. Поэтому z=0 — полюс третьего порядка для f(z) .

в) Как и в предыдущих пунктах, находим, что z=0 является 0(3) для числителя и 0(4) — для знаменателя. Поэтому z=0 — простой полюс для f(z) .

г) Точка z=0 является простым нулем числителя, нулем второго порядка для знаменателя. Следовательно, это простой полюс для f(z) .

Определение порядка полюса в бесконечно удаленной точке

Рассмотрим бесконечно удаленную точку. Тип особой точки можно определить, вычисляя $limlimits_{ztoinfty}f(z)$ или раскладывая функцию в ряд Лорана (см. примеры 4.4, 4.7). Можно свести задачу к исследованию конечной точки $xi=0,left(frac{1}{z}= xiright)$ (см. утверждение 4.2 и пример 4.9). В двух последних случаях определяется и порядок полюса.

Практически удобное правило определения порядка полюса z=infty можно получить, используя п. 2 утверждения 4.2 и правила определения порядка полюса в конечной точке (утверждение 4.3). Действительно, пусть z=infty-Pi(n) для функции f(z) , тогда xi=0-Pi(n) для $f! left(frac{1}{xi}right)$ и можно записать $f! left(frac{1}{xi}right)= frac{F(xi)}{xi^n},~ F(xi)ne0$ (см. (4.14)). Поэтому, обозначив $f! left(frac{1}{z}right)= varphi(z)$ , для f(z) получим

$f(z)=z^ncdot varphi(z),qquad limlimits_{ztoinfty} varphi(z)ne0,qquad limlimits_{ztoinfty} varphi(z)neinfty.$

(4.15)

Представление функции в виде (4.15) является необходимым и достаточным условием полюса порядка функции f(z) в точке z=infty .

Замечание 4.5. Используя формулу (4.15), нетрудно убедиться, что если z=infty-Pi(m) для f_1(z) и Pi(k) для f_2(z) , то z=infty — полюс порядка (m-k) для функции $f(z)= frac{f_1(z)}{f_2(z)}$ .

Пример 4.17. Определить тип особой точки z=infty для функций: а) f(z)= z^2(z-2) ; б) $f(z)=frac{z^5+z^2+1}{z^3-2z}$ .

Решение

Так как $limlimits_{ztoinfty}f(z)=infty$ в обоих случаях, то z=infty для данных функций — полюс. Определим порядок полюса.

а) Точка z=infty является полюсом третьего порядка, в чем можно убедиться любым из следующих способов.

Первый способ. Разложение функции по степеням имеет вид f(z)=z^3-2z,~c_3ne0 , все c_n=0,~n>3 , и по определению (см. формулы (4.7), (4.11)) заключаем, что z=infty-Pi(3) .

Второй способ. Обозначим $z=frac{1}{xi}$ , получим функцию $f! left(frac{1}{xi}right)= frac{1-2xi}{xi^3}$ , для которой xi=0-Pi(3) . Поэтому, согласно п. 2 утверждения 4.2, точка z=infty-Pi(3) для f(z) .

Третий способ. Запишем функцию в виде $f(z)=z^3! left(1-frac{2}{z}right)$ и, так как функция $varphi(z)=left(1-frac{2}{z}right)$ — удовлетворяет условиям формулы (4.15), получим, что z=infty-Pi(3) для f(z) .

б) Разложение функции в ряд по степеням представляет некоторые трудности. Используем другие способы.

Первый способ. Обозначим $z=frac{1}{xi}$ , получим $f! left(frac{1}{xi}right)= frac{(xi^5+xi^3+1)cdotxi^3}{xi^5cdot(1-2xi^2)}$ , или $f! left(frac{1}{xi}right)= frac{xi^5+xi^3+1}{xi^2cdot(1-2xi^2)}$ .

Поэтому xi=0 является Pi(2) для $f!left(frac{1}{xi}right)$ и, следовательно, z=infty-Pi(2) для f(z) .

Второй способ. Представим функцию в виде $f(z)= frac{z^5cdot left(1+ dfrac{1}{z^3}+dfrac{1}{z^2}right)}{z^3cdot left(1-dfrac{2}{z^2}right)}$ или f(z)= z^2cdot varphi(z) , где $limlimits_{ztoinfty} varphi(z)=1$ , и, согласно формуле (4.15), z=infty-Pi(2) для f(z) .

Третий способ. Используем замечание 4.5. Можно определить порядок полюса z=infty для дроби $frac{f_1(z)}{f_2(z)}$ , зная соответствующие порядки полюсов числителя и знаменателя. Здесь, очевидно, z=infty-Pi(5) для числителя и Pi(3) — для знаменателя (см. формулы (4.7), (4.11)). Поэтому z=infty-Pi(2) для f(z) .

Пример 4.18. Определить порядок полюса в точке z=infty для следующих функций: а) $f(z)= frac{z^3}{z-1}$ ; б) $f(z)=z^2+1+frac{1}{z^2-1}$ .

Решение

Определение типа особых точек для суммы, разности, произведения и частного функций

Пусть z_0 — особая точка функций f_1(z) и f_2(z) и тип особой точки для каждой из функций известен. Требуется определить тип особой точки для функций $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ . Рассмотрим следующие случаи.

Первый случай. Пусть точка го является полюсом порядка m~(Pi(m)) для функции f_1(z) и полюсом порядка k~(Pi(k)) для функции f_2(z) .

а) При исследовании суммы f(z)= f_1(z)+ f_2(z) воспользуемся формулой (4.14) (п.1 утверждения 4.3) и запишем слагаемые в виде

$f_1(z)=frac{varphi_1(z)}{(z-z_0)^m},~~ f_2(z)=frac{varphi_2(z)}{(z-z_0)^k}$ , где varphi_1(z_0)ne0,~varphi_2(z_0)ne0 .

При k=m для суммы f(z)= f_1(z)+ f_2(z) получаем $f(z)= frac{varphi_1(z)+varphi_2(z)}{(z-z_0)^m}$ или $f(z)=frac{varphi(z)}{(z-z_0)^m}$ , где varphi(z)= varphi_1(z)+ varphi_2(z) . Если varphi(z_0)ne0 , то z_0-Pi(m) для функции f(z) . Однако для функций f_1(z),, f_2(z) может выполняться условие varphi_1(z_0)+ varphi_2(z_0)=0 и’ следовательно, varphi(z_0)=0 . В этом случае формула (4.14) не применима и точка z_0 не будет полюсом порядка для f(z) . В соответствии с п.3 утверждения 4.3 порядок полюса будет меньше, чем , и равен (m-p) в случае m>p , где — порядок нуля функции varphi(z) . Если p=m , то z_0 — устранимая особая точка для f(z) .

Таким образом, при сложении функций порядок полюса в точке может оказаться равным или меньше, чем наибольший из порядков слагаемых.

б) Для исследования произведения f_1(z)cdot f_2(z) воспользуемся формулой связи нулей с полюсами (п.2 утверждения 4.3) и рассмотрим вспомогательные функции $F_1(z)= frac{1}{f_1(z)},~ F_2(z)= frac{1}{f_2(z)}$ . Для первой из этих функций z_0-0(m) , для второй соответственно z_0-0(k) . а поэтому для F(z)= F_1(z)cdot F_2(z) она будет 0(m+k) . Согласно п.2 утверждения 4.3, z_0 является Pi(m+k) для .

в) Аналогичные рассуждения для частного $frac{f_1(z)}{f_2(z)}$ приводят к результату: при m>k точка z_0 является Pi(m-k) для $frac{f_1(z)}{f_2(z)}$ .

Второй случай. Пусть точка z_0 является полюсом, устранимой особой точкой или не особой для f_1(z) и существенно особой для f_2(z) . Так как $limlimits_{zto z_0}f_2(z)$ не существует, то по свойству пределов он не существует для каждой из рассматриваемых комбинаций $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ . Следовательно, для каждой из них z_0 — существенно особая точка. Заметим, что для функции $frac{1}{f_2(z)}$ эта точка является либо существенно особой точкой, либо не является изолированной особой точкой. Последнее проиллюстрировано в примере 4.5 для функции $frac{1}{sin z^{-1}}$ .

Третий случай. Пусть z_0 — полюс порядка для f_1(z) и устранимая особая точка для f_2(z) . Разложения этих функций в ряд в окрестности z_0 имеют вид (4.6) и (4.4) соответственно.

а) При сложении рядов в общей области сходимости получится ряд, главную часть которого будет составлять главная часть ряда функции f_1(z) . Следовательно, для f(z)= f_1(z)pm f_2(z) точка z_0 — полюс порядка .

б) Аналогичные рассуждения приводят к заключению, что такой же результат получится и для f(z)= f_1(z)cdot f_2(z) , если $limlimits_{zto z_0}f_2(z)ne0$ .

Если $limlimits_{zto z_0}f_2(z)=0$ и z_0-0(p),~ p<n для функции f_2(z) , то из равенства

$f_1(z)cdot f_2(z)= frac{varphi_1(z)}{(z-z_0)^n}cdot varphi_2(z)cdot (z-z_0)^p= frac{varphi(z)}{(z-z_0)^{n-p}}$ заключаем, что z_0-Pi(n-p) .

в) Для частного $frac{f_1(z)}{f_2(z)}$ при условии $limlimits_{zto z_0} f_2(z)ne0$ из равенства $f(z)= frac{f_1(z)}{f_2(z)}= frac{varphi_1(z)}{(z-z_0)^n f_2(z)}= frac{varphi(z)}{(z-z_0)^n}$ заключаем, что z_0-Pi(n) для f(z) .

Если $limlimits_{zto z_0}f_2(z)=0$ и z_0-0(p) для f_2(z) , то, используя условие кратного нуля, из равенства

$f(z)= frac{f_1(z)}{f_2(z)}= frac{varphi_1(z)}{(z-z_0)^n varphi_2(z) (z-z_0)^p}= frac{varphi(z)}{(z-z_0)^{n+p}}$

заключаем, что z_0 является Pi(n+p) для $frac{f_1(z)}{f_2(z)}$ , где — порядок полюса функции f_1(z),~p — порядок нуля функции f_2(z) в точке z_0 .

Подводя итог, запишем следующее утверждение.
Утверждение 4.4

1. Пусть точка z_0 является Pi(m) для функции f_1(z) и Pi(k) для функции f_2(z) . Тогда:

а) для f_1(z)pm f_2(z) она будет Pi(n),~ n leqslant max(m,k) , а при n=0 — устранимой особой точкой;

б) для f_1(z)cdot f_2(z) она является Pi(n),~ n=m+k ;

в) для $frac{f_1(z)}{f_2(z)}$ она будет Pi(n),~ n=m-k .

2. Пусть z_0 — существенно особая точка для функции f_2(z) и устранимая особая точка или полюс для функции f_1(z) . Тогда z_0 — существенно особая точка для $f_1(z)pm f_2(z);~ f_1(z)cdot f_2(z);~ frac{f_1(z)}{f_2(z)}$ .

3. Пусть точка z_0 является Pi(n) для функции f_1(z) и устранимой особой точкой для функции f_2(z) . Тогда:

а) для f_1(z)pm f_2(z) она будет Pi(n) ;

б) для f_1(z)cdot f_2(z) она является Pi(n) , если $limlimits_{zto z_0}f_2(z)ne0$ , и Pi(n-p) , если $limlimits_{zto z_0}f_2(z)=0$ и — порядок нуля f_2(z) в точке z_0 ;

в) для $frac{f_1(z)}{f_2(z)}$ она будет Pi(n) , если $limlimits_{zto z_0}f_2(z)ne0$ , и Pi(n+p) , если $limlimits_{zto z_0}f_2(z)=0$ и — порядок нуля f_2(z) в точке z_0 ;

4. Если точка z_0-Pi(n) для varphi(z) , то она существенно особая точка для сложной функции f(varphi(z)) . В этом можно убедиться, рассматривая ряды для и в окрестности z_0 .

Пример 4.19. Определить тип особой точки z=0 для функции f(z) , если f(z)= f_1(z)+ f_2(z) , где $f_1(z)= frac{1}{z^2}$ , а функция f_2(z) определяется следующим образом:

а) $f_2(z)= frac{1}{z}-frac{2}{z^2}$ ; б) $f_2(z)= frac{1}{z}-frac{1}{z^2}$ ; в) $f_2(z)=1-frac{1}{z}$ .

Решение

Пример 4.20. Найти особые точки функции $f(z)= frac{1}{e^z-1}-frac{1}{z}$ . Определить их тип.

Решение

Особыми точками функции являются особые точки первого слагаемого z=2kpi i,~ kinmathbb{Z} , особая точка второго слагаемого z=0 входит в это множество. Точки z_k=2kpi i,~kne0 являются простыми нулями знаменателя и поэтому простыми полюсами первой функции; для второго слагаемого эти точки не являются особыми. Поэтому точки -простые полюсы f(z) (см. п. 3 “а” утверждения 4.4).

Точка z=0 — простой полюс и для первого, и для второго слагаемого. Для f(z) — это или простой полюс, или устранимая особая точка (см. п.1 “а” утверждения 4.4). Преобразуем разность в дробь: $f(z)= frac{z-e^z+1}{(e^z-1)z}$ . Точка z=0 является нулем второго порядка и для числителя, и для знаменателя. Следовательно, это — устранимая особая точка, в чем можно убедиться, используя определение, т.е. находя $limlimits_{zto0}f(z)$ . Действительно,

$limlimits_{zto0}f(z)= limlimits_{zto0} frac{-1-z-dfrac{z^2}{2!}+ldots+z+ 1}{left(-1-z-dfrac{z^2}{2!}+ldots-1 right)!z}= limlimits_{zto0} frac{-dfrac{z^2}{2!}-dfrac{z^3}{3!}-ldots}{z^2! left(1+dfrac{z}{2!}+ldotsright)}= limlimits_{zto0} frac{-z^2! left(dfrac{1}{2!}+ dfrac{z}{3!}+ldotsright)}{ z^2!left(1+dfrac{z}{2!}+ldotsright)}=-frac{1}{2},.$

Точка z=infty для данной функции является неизолированной особой точкой, так как в любой ее окрестности |z|>R содержится бесконечное множество особых точек вида z_k=2kpi i . Эта точка- предельная точка полюсов. Заметим, что для знаменателя первого слагаемого функции она — существенно особая точка.

Пример 4.21. Найти особые точки следующих функций, определить их тип:

а) $f(z)= frac{z-pi}{sin^2z}cos frac{1}{z-2i}+ frac{1}{z^6+1}$ ; б) $f(z)= frac{1}{z^2-1} sin frac{pi z}{2z+1}+ frac{1}{e^z+i}$ .

Решение

Обозначим f_1(z) — первое слагаемое, f_2(z) — второе слагаемое функции f(z) , т.е. имеем f(z)=f_1(z)+f_2(z) .

а) Для f_1(z) точка z=2i является существенно особой точкой, так как это существенно особая точка для $cos frac{1}{z-2i}$ множителя этой функции. Поэтому она — существенно особая точка для f(z) (п. 2 утверждения 4.4).

Точки z_k=kpi,~kne1 — полюсы второго порядка функции f_1(z) , так как ее можно записать в виде $f_1(z)=frac{varphi(z)}{sin^2z}$ , где varphi(z_k)ne0 , а для знаменателя эти точки — нули второго порядка . Так как для f_2(z) эти точки не особые, то z_k=kpi,~znepi — полюсы второго порядка для f(z) (п. 3 утверждения 4.4).

С помощью аналогичных рассуждений получаем, что z=pi — простой полюс для f(z) .

Особыми точками f_2(z) являются корни уравнения z^6+1=0 , то есть $z_k=exp frac{(-pi+2kpi)i}{6},~ k=0,1,ldots,5$ . Все они — простые нули знаменателя- функции F(z) , а потому — простые полюсы для $f_2(z)= frac{1}{F(z)}$ . Так как эти точки не являются особыми для f_1(z) , то для f(z) — это простые полюсы.

Точка z=infty — неизолированная особая точка f(z) .

б) Точка $z=frac{-1}{2}$ — полюс дроби $frac{pi z}{2z+1}$ является существенно особой точкой для $sinfrac{pi z}{2z+1}$ (п.4 утверждения 4.4), поэтому она — существенно особая точка для f_1(z) и, следовательно, для f(z) .

Точка z=1 — простой полюс для f_1(z) , так как можно записать $f_2(z)= frac{varphi(z)}{z-1},~ varphi(z)ne0$ . Поскольку z=1 не является особой точкой для f_2(z) , то она — простой полюс для f(z) .

Точка z=-1 — устранимая особая точка для f_1(z) , так как она — простой нуль и для числителя, и для знаменателя дроби $frac{sindfrac{pi z}{2z+1}}{z^2-1}$ . Так как z=-1 не является особой точкой для f_2(z) , то она — устранимая особая точка для f(z) .

Особыми точками f_2(z) являются простые нули знаменателя — корни уравнения e^z+i=0 , или e^z=-i , то есть z=operatorname{Ln}(-i) . Все точки

z_k=ln|-i|+ibigl(arg(-i)+2kpibigr) , или $z_k=i! left(2kpi-frac{pi}{2}right)!,~ kin mathbb{Z}$

являются простыми полюсами для f_2(z) и, следовательно, простыми полюсами для f(z) .

Точка z=infty — неизолированная особая точка f(z) .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Полюс и поляра

Рассмотрим овальную
квадрику Х^Т∙Q∙Х
= 0 и точки А
и В
не принадлежащие квадрике.

Пусть
M
и L
точки пересечения квадрики и прямой
(АВ).

Определение:
Если (AB,ML)=-1,
то говорят что овальная квадрика
гармонически разделяет пару АВ,
или точки А
и В
гармонически
сопряжены
относительно овальной квадрики.

На прямой (АВ)
рассмотрим репер R(A,B,M),
тогда в этом репере и точки А,
В
,
М

и пусть
точка L
.

Если (AB,ML)=
-1, тогда =
-1 α
= 1 и β
= -1 , т.е. L
.

Таким образом,
М = А+В
и L = А –
В.

Значит, для точек
пересечения прямой (АВ)
с квадрикой
.

Но

являются корнями уравнения λ²∙а
+ 2∙λ∙μ∙с
+ μ²∙b=0,

где а
= А^Т∙Q∙А,
b = В^Т∙Q∙В,
с = А ^Т∙Q∙В
= В^Т∙Q∙А.

По теореме Виета
сумма корней равна среднему коэффициенту,
взятому с противоположным знаком:
+=
– с

с = 0

А^Т∙Q∙В
= В^Т∙Q∙А
= 0 – условие
гармонической сопряженности точек А
и В
относительно квадрики.

Фиксируем точку
А

КВП. Рассмотрим все прямые проходящие
через эту точку в каждом случае будет
своя точка В
гармонически сопряженная с А
относительно овальной квадрики. Сделаем
точку В
переменной, по условию гармонической
сопряженности точек относительно
овальной квадрики получим: А^Т∙Q∙Х
= 0
– это уравнение I степени, то есть прямая,
причем это прямая единственна. Эту
прямую будем называть полярой точки
А.
Если точка А

КВП, то уравнение А^Т∙Q∙Х
= 0
определяет касательную к квадрике в
точке А.

Определение:
Полярой
точки А
называется прямая, состоящая из точек
гармонически сопряженных с данной
точкой относительно овальной квадрики.

Вывод:
Полярой
точки А
является прямая, которая имеет
уравнение: А^Т∙Q∙Х
= 0
и

в случае А

КВП является касательной к овальной
квадрике,

в случае А

КВП состоит из точек гармонически
сопряженных с точкой А
относительно овальной квадрики.

Определение:
Уравнение
А^Т∙Q∙Х
= 0
называется уравнением
поляры
точки А
относительно овальной квадрики.

Если уравнение
прямой а∙Х=0,
тогда λ∙а
=
А^Т∙Q
(с точностью до пропорциональности).

λ∙а
= А^Т∙Q

λ∙а∙Q^-1
= А^Т∙Q∙Q^-1

μ∙А^Т=
а∙Q^-1
или μ∙А=
Q^-1∙а^Т

(Почему существует
Q^-1
и почему (Q^-1)^Т=
Q^-1 ? )

Вывод:
Для любой прямой существует точка, для
которой эта прямая является полярой
относительно квадрики.

Определение:
Точка, для которой данная прямая
относительно овальной квадрики является
полярой, называется полюсом
прямой.

Свойства:

1. Если точка А
внешняя по отношению к овальной квадрике,
то ее поляра проходит через точки касания
касательных проведенных из точка А
к КВП.

Доказательство.
Координаты точек касания Х₁
и Х₂
находятся из системы
,
первое уравнение это уравнение квадрики,
второе уравнение это уравнение поляры,
а значит это точки пересечения поляры
и квадрики. □

2. Если точка и
прямая инцидентны, то их поляра и полюс
тоже инцидентны.

Доказательство.
Пусть а –
поляра точки
А
и В –
полюс прямой b,

значит λ∙а
= А^Т∙Q
и μ∙В=
Q^-1∙b^Т. Докажем,
что А

b

B

a.

Уравнение прямой
b∙Х
= 0, тогда А

b

b∙А
=0.

Найдем
а∙В=(А^Т∙Q)∙(Q^-1∙b)=А^Т∙(Q∙Q^-1)∙b^Т=А^Т∙Е∙b^Т=А^Т∙b^Т=(А∙b)^Т=0
– это означает, что точка В
лежит на
прямой а. □

Замечание:
Свойство 2 позволяет находить полюс
прямой. Выбрав на данной прямой две
любые точки и построив их поляры, точка
их пересечения будет полюсом данной
прямой.

Задача.
Дана квадрика х₁²
– 2∙х₂²+
4∙х₂∙х₃
=0 . Найти уравнение поляры для А
и координаты полюса прямой b:
х₁+х₂–2∙х₃=0.

Решение. Q=

Q^-1=

λ∙а=А^Т∙Q=(
1: 3 :-1) ∙=(1
:-8: 6)

х₁
–8∙х₂+6∙х₃=0.

μ∙В=Q^-1∙b^Т=∙=
В=.

Задача.
Дана квадрика 2∙х₁²
+ х₃²
– 2∙х₁∙х₂
-2∙х₁∙х₃
=0 . Найти уравнения касательных к квадрике
из точки А.

Решение.
Воспользуемся свойством (1). Q=. Найдем
уравнение поляры.

λ∙а
= А^Т∙Q=(
1: 8 : 5 )∙=(
-11 : -1 : 4 )

11∙х₁
+ х₂
– 4∙х₃
=0.

Найдем точки
пересечения квадрики поляры.

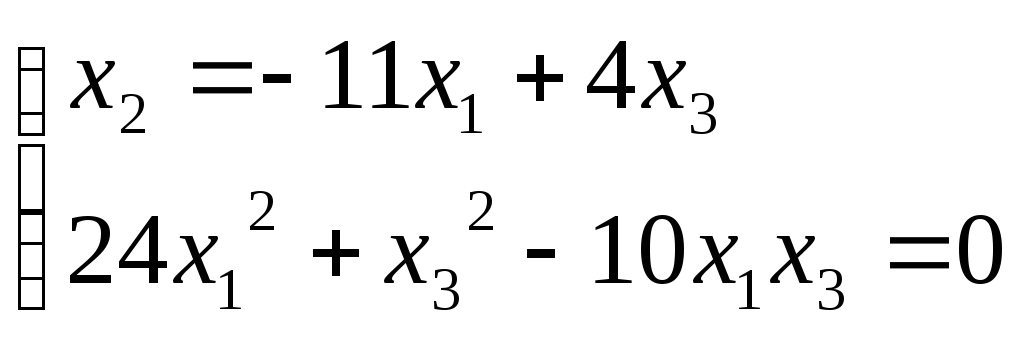
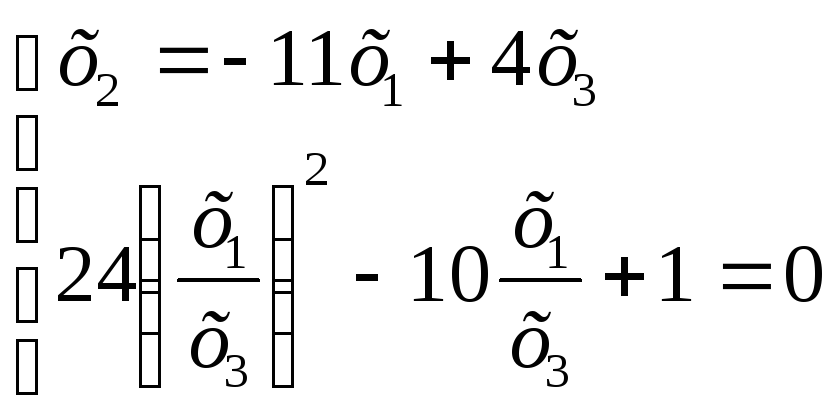
D=100–96
= 4
и
.
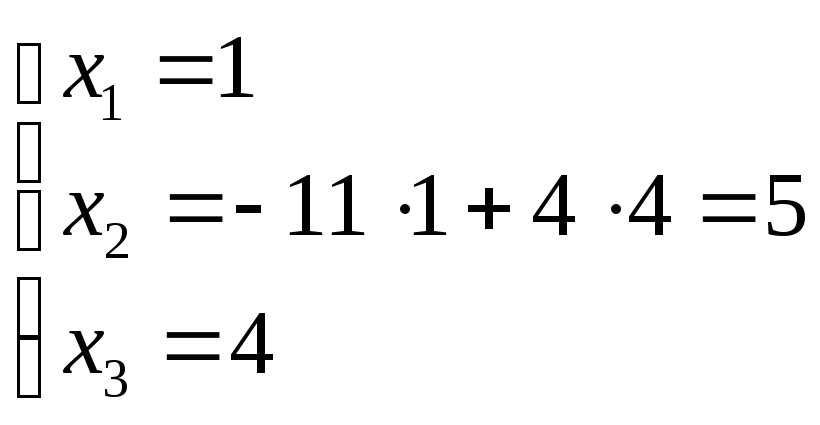
и

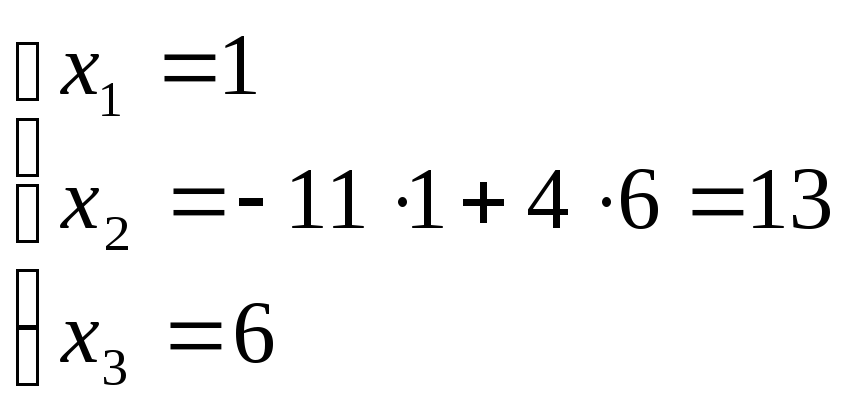
В
и С
– точки пересечения поляры и квадрики,
тогда прямые (АВ)
и (АС)
будут касательными.

(АВ)
:
=0 –
7∙х₁
– х₂
+ 3∙х₃
=0.

(АС)
:
=0 17∙х₁
+ х₂
–
5∙х₃
=0.

Определение:
Трехвершинник называется автополярным
относительно овальной квадрики, если
каждая его вершина является полюсом
противоположной стороны.

Замечание:
Автополярных трехвершинников может
быть много.

Теорема.
Для того чтобы уравнение овальной
квадрики было каноническим необходимо
и достаточно, чтобы ΔЕ₁Е₂Е₃
был автополярным относительно данной
квадрики.

Доказательство.
Необходимость:

Дано q₁₁∙х₁²
+
q₂₂∙х₂²
+ q₃₃∙х₃²
=0
.

Доказать что
ΔЕ₁Е₂Е₃
автополярный трёхвершинник.

Достаточность: Найти
матрицу Q
, используя то, что точка Е₁

является полюсом
прямой (Е₂Е₃
) и т.д. (самостоятельно).

Определение:
Четырехвершинник называется вписанным
в овальную квадрику, если его вершины
инцидентны квадрике.

Теорема.
Если четырехвершинник вписан в овальную
квадрику, тогда диагональный трехвершинник
является автополярным относительно
квадрики.

Доказательство.
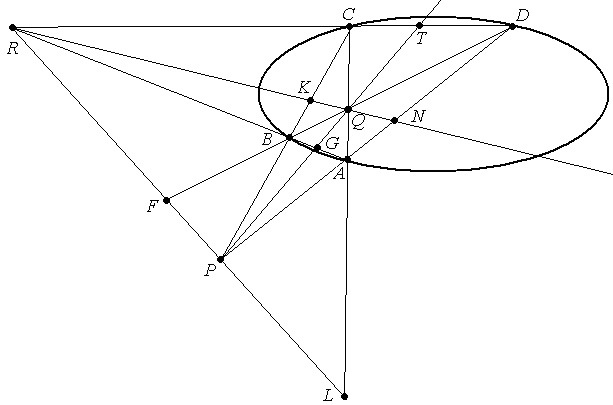
Пусть АВСD –
четырёхвершинник
вписанный в овальную квадрику и ΔPQR
– диагональный
трёхвершинник.

Докажем, что Р
– полюс
прямой (QR).

По гармоническим
свойствам полного четырехвершинника
гармоническими будут: (CB,PK)=(AD,PN)=
-1, т.е. точки K
и N
гармонически
сопряжены с точкой Р
относительно овальной квадрики, а значит
они принадлежат поляре точки Р.
В тоже время точки K
и N
лежат на
прямой (QR)

(QR)
– поляра точки Р.
Для точек Q
и R
доказательство аналогично. □

Замечание:
Эта теорема позволяет строить поляру
точки если она не инцидентна овальной
квадрике.

Задачи на
построение

Задача 1.
Дана овальная
квадрика и точка Р
ей не
инцидентная.
Построить поляру точки Р.

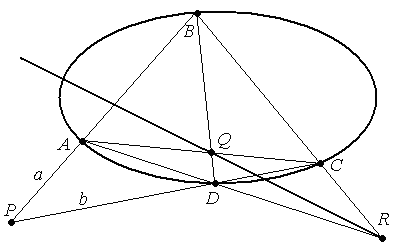
Решение.
Пусть для определенности Р
– внешняя точка. Необходимо восстановить
какой-либо четырёхвершинник инцидентный
овальной квадрике, так чтобы точка Р
была одной
из диагональных точек. Через точку P
проводим две произвольные прямые а
и b
так чтобы они пересекали квадрику: а
∩ КВП =А,
В, b
∩ КВП = С,
D.

АВСD
– является вписанным четырехвершинником
и точка P
является диагональной точкой. Строим
две другие диагональные точки:
(АС)∩(ВD)=Q,
и
(АD)∩(ВС)=R.

Прямая (RQ)
является полярой.

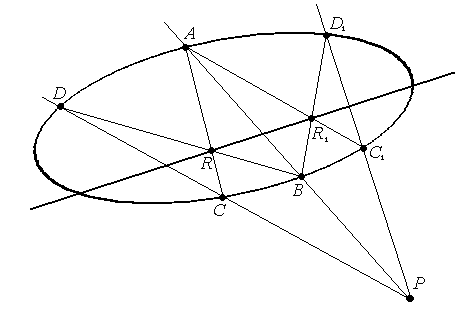
Замечание:
В некоторых случаях одну из диагональных
точек построить сложно, она может выйти
за пределы чертежа. В этом случае можно
построить ещё один какой-либо
четырехвершинник вписанный в овальную
квадрику.

Замечание:
Если P
– внутренняя точка построение аналогичное.

Задача 2.
Дана овальная квадрика и прямая а.
Построить полюс прямой.

Решение.
Воспользуемся свойством (2).

На прямой а
возьмем две различные точки В
и С, построим
их поляры – b
и с (см.
пред. задачу).

b ∩ с = А –
полюс прямой а
.

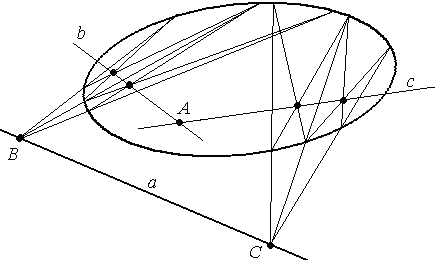
Задача
3.
Дана овальная квадрика и точка А
ей инцидентная, построить поляру точки.

Решение.
Поляра точки в этом случае будет
касательной.

Воспользуемся
свойством (2): если через точку А
провести какую-либо прямую b,
то её полюс – В
пройдет через поляру точки А.

Построение полюса
прямой – задача 2.

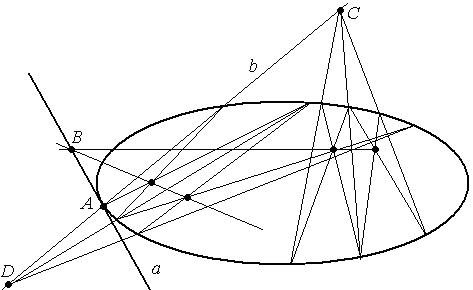
Задача
4.
Дана овальная квадрика и точка А.
Через точку А
провести касательную к квадрике.

Решение.

1. А
– внутренняя
точка – касательных нет.

2 А

КВП – касательная является полярой
(см. задачу 3).

3. А
– внешняя
точка – касательные две. По свойству
(1), если а
поляра точки А,
тогда а ∩
КВП = В
и С –
эти точки являются точками касания.
Т.е. (АВ)
и (АС)
– касательные.

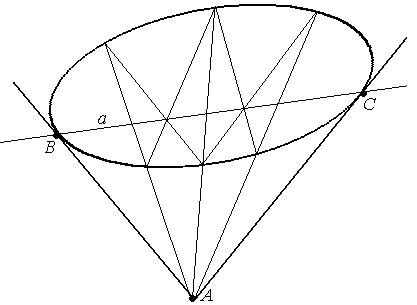
Задача 5.
Дана овальная квадрика и прямая
а , касающаяся
квадрики, построить полюс прямой.

Р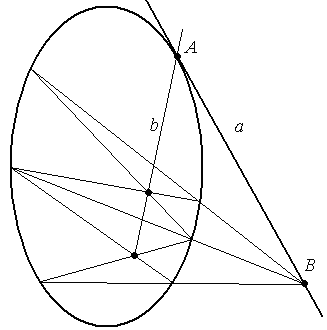ешение.
Полюс прямой в этом случае будет точкой
касания.

Воспользуемся
свойством (2). Если на данной прямой а
взять какую-либо точку В,
то её поляра – b
пройдет через полюс прямой а.

Построение поляры
точки – задача 1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

У этого термина существуют и другие значения, см. Полюс.

Модуль Гамма-функции $Gamma(z)$ . Слева (Re z<0) у функции есть полюса, в них она стремится к бесконечности. Справа (Re z>0) полюсов нет, функция всюду конечна.

Изолированная особая точка $z_{0}$ называется полюсом функции $f(z)$ ,
голоморфной в некоторой проколотой окрестности этой точки,
если существует предел

$lim _{{zto {z_{0}}}}f(z)=infty$ .

Критерии полюса[править | править код]

$f(z)=sum _{{k=-infty }}^{{infty }}{f_{k}}(z-z_{0})^{k}=P(z)+f_{{-n}}(z-z_{0})^{{-n}}+ldots +f_{{-1}}(z-z_{0})^{{-1}}$ ,

где $P(z)$ — правильная часть ряда Лорана.
Если $f_{{-n}}neq 0$ , то $z_{0}$ называется полюсом порядка $n$ .
Если $n=1$ , то полюс называется простым.

См. также[править | править код]

Нуль (комплексный анализ)
Мероморфная функция
Вычет
Интегральная формула Коши

Другие типы изолированных особых точек:
- Устранимая особая точка
- Существенно особая точка

Литература[править | править код]

Бицадзе А.В. Основы теории аналитических функций комплексного переменного — М., Наука, 1969.
Шабат Б. В., Введение в комплексный анализ — М., Наука, 1969.

Источник

Макеты страниц

Мы доказали в § 2, что если точка есть точка (нераспадающейся) кривой , определенной уравнением

то прямая

т. е. прямая с координатами

есть касательная к кривой (1) в ее точке Но прямую с координатами (2) можио рассматривать для любой точки независимо от того, лежит ли точка P на кривой (1) или нет. Эта прямая (2) называется полярой точки относительно кривой (1). Поляра точки P, лежащей на касательная к кривой в точке P.

Замечание 1. Это определение поляры годится как для нераспадающейся кривой второго порядка, так и для распадающейся на пару пересекающихся прямых.

Одиако во втором случае не будет определена поляра точки координаты которой удовлетворяют системе уравнений

Единственной такой точкой P является точка пересечения обеих прямых, на которые распалась данная кривая. В этом и двух следующих параграфах мы не будем рассматривать кривые, распадающиеся на пару слившихся прямых.

Будем теперь предполагать (если не оговорено противное), что кривая у нераспадающаяся. Тогда

и уравнения (2) однозначно разрешаются относительно

Другими словами, если дана произвольная прямая, координаты которой обозначим через , то существует единственная точка имеющая прямую своей полярой. Эта точка называется полюсом прямой

Пусть какая-нибудь точка плоскости. Тогда уравнение (2), которое можно записать в виде

представляет собою условие для того, чтобы точка лежала на поляре точки P. Но выражение симметрично относительно троек чисел поэтому равенство (3) выражает также условие того, что точка лежит на поляре точки X. Итак, имеем следующий основной результат.

Теорема 8 (теорема взаимности). Если точка X лежит на поляре точки P, то и точка P лежит на поляре точки X.

Пусть прямая q с координатами есть поляра точки Р. Обозначим через точки пересечения прямой q с кривой (1) (эти точки могут быть различными или совпадающими, действительными или мнимыми) (рис. 248).

Точка лежит на поляре точки P; значит, по теореме взаимности точка P лежнт на поляре точки т. е. на касательной К кривой (1) в точке

Другими словами, точка есть точка прикосновения касательной, проведенной из точки P.

Рис. 248.

Итак, всякая точка пересечения поляры точки P с кривой (1) есть точка прикосновения касательной, проведенной из точки P. Так как имеется две точки пересечении поляры точки P с кривой (1), то из точки P можно провести к кривой (1) две касательные — одна будет касаться нашей кривой в точке другая — в . Доказана

Теорема 9. Из каждой точки P плоскости можно провести к кривой (1) две касательные, совпадающие между собою, если точка P лежит на кривой, и только в этом случае. Поляра точки P есть прямая, соединяющая точки прикосновения обеих касательных, проведенных к кривой (1) из точки P.

Тот же факт можно высказать и так:

Полюс прямой q есть точка пересечения двух касательных, проведенных к кривой (1) в точках пересечения прямой q с кривой (1).

Это определение гголяры и полюса не зависит от того, каким именно уравнением и в какой системе координат мы определим данную кривую второго порядка.

Приведенное определение годится независимо от того, будут ли касательные, проведенные из точки P, действительными или мнимыми. Однако рисунок осуществим, конечно, лишь если касательные из точки P действительные. В этом случае говорим, что точка P лежит вне кривой (1).

Если же касательные к кривой (1), проведенные из точки P, мнимые, то мы говорим, что точка P лежит внутри кривой (1); в этом случае рисунок уже не имеет реального смысла. Спрашивается: как в этом случае свести построение поляры точки P к построению касательных?

Для этого проведем через точку две какие-нибудь прямые АВ и АВ (рис. 249), точки пересечения этих прямых с кривой (1) обозначим через А, В, соответственно А, В. Касательные в точках А, В, А, В к нашей кривой обозначим соответственно через . Точку пересечения прямых а и b обозначим через С, точку пересечения прямых а и обозначим через С. Прямая и есть поляра точки P.

В самом деле, прямая АВ есть поляра точки С, и P лежит на этой поляре; так как P лежит на поляре точки С, то точка С лежит на поляре точки P; точно так же точка P лежит на поляре точки С, значит, точка С лежит на поляре точки P. Поляра точки P, таким образом, проходит через обе точки С и С, а значит, эта поляра есть прямая .

Это построение применимо не только к случаю, когда P — внутренняя точка кривой (1) (см. рис. 249), а к любому случаю. На рис. 250 наше построение сделано для точки P, внешней к кривой (1).

Рис. 249.

Определение поляры точки и полюса прямой относительно данной нераспадающейся кривой второго порядка (1) устанавливает взаимно однозначное соответствие между всеми точками и всеми прямыми проективной плоскости: каждой точке X плоскости соответствует вполне определенная прямая этой плоскости, а именно поляра точки X; каждая прямая является полярой лишь одной точки (своего полюса). Если точка X дана своими однородными координатами

то координаты ее поляры находятся по формулам:

Обратно, если дана прямая своими координатами то координаты ее полюса находятся по формулам:

где коэффициенты получаются, если решить уравнения (4) относительно (что возможно, так как матрица есть матрица, обратная к матрице

Рис. 250.

Только что описанное соответствие между точками и прямыми плоскости называется полярным соответствием, порожденным данной нераспадающейся кривой второго порядка (1). При полярном соответствии сохраняется отношение инцидентности между точками и прямыми, именно в этом заключается содержание теоремы 8. Эта теорема может быть сформулирована и так:

Теорема 8. Если данная точка X пробегает некоторую прямую d, то ее поляра пробегает весь пучок прямых с центром в полюсе D прямой

Обратно, если прямая пробегает весь пучок прямых с центром в данной точке D, то ее полюс X пробегает прямую d, а именно поляру точки

В самом деле, если точка X пробегает поляру d точки D, то точка D лежит на поляре каждой из точек X, т. е. поляры всех точек X пробегают весь пучок прямых с центром

Другое определение поляры. Пусть снова

есть уравнение кривой второго порядка.

Назовем две точки сопряженными относительно кривой , если точки М и образуют пару точек, гармонически сопряженную к паре точек пересечения прямой MN с кривой , т. е. если

Параметрическое уравнение прямой MN может быть записано в виде

а координаты точек пересечения P и Q определяются подстановкой в эти уравнения значений отношение которых определяется из квадратного уравнения

где

Корни уравнения (7) обозначаем через и так что теперь

Из формулы (10) § 8 главы XXI нам известно, что четверка точек М, N, P, Q тогда и только тогда будет гармонической, когда

т. е. если в квадратном уравнении (7) коэффициент . А это значит, что

Если теперь точка дана, а точка определена требованием быть гармонически сопряженной точке М относительно кривой , то координаты точки N, которые мы теперь будем обозначать через должны удовлетворять уравнению

Но это уравнение есть не что иное, как уравнение поляры точки М относительно кривой

Итак:

Теорема 10. Поляра точки М относительно данной кривой второго порядка есть геометрическое место точек, гармонически сопряженных с точкой М относительно этой кривой .

Теорема 10 может рассматриваться как новое определение поляры. Это определение может быть перенесено и на случай распадающейся кривой второго порядка. Существенно при этом, что уравнение поляры точки есть

что тоже может быть принято за определение поляры. Однако при обращении в нуль дискриминанта А формы соответствие между полярой и полюсом перестает быть однозначным.

Замечание 2. Если кривая распалась на пару различных прямых , пересекающихся в некоторой точке О, то, как мы знаем, определенное этой кривой полярное соответствие между точками и прямыми плоскости перестает быть взаимно однозначным. Тем не менее для каждой точки М, отличной от точки О, имеется единственная поляра, и эта поляра проходит через точку О. Для самой точки О поляра перестает быть определенной (если угодно, можно считать любую прямую, проходящую через точку О, касательной, а следовательно, и полярой этой точки).

Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
§ 1. Отношение отрезков
§ 2. Направленные отрезки (векторы); их отношение
§ 3. Ось. Алгебраическое значение (координата) вектора на оси
§ 4. Сложение векторов на прямой
§ 5. Система координат на прямой
§ 6. Деление отрезка в данном отношении
§ 7. Пропорциональность пар чисел
§ 8. Бесконечно удаленная точка прямой
§ 9. Пропорциональность двух последовательностей, состоящих из и чисел
ГЛАВА II. ВЕКТОРЫ
§ 1. Равенство векторов. Свободный вектор
§ 2. Линейные операции над векторами (сложение и умножение на число)
§ 3. Проекции
§ 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
§ 5. Линейная зависимость и независимость векторов
§ 6. Геометрический смысл линейной зависимости векторов
§ 7. Векторные многообразия
ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 1. Определение аффинной системы координат
§ 2. Перенос начала координат
§ 3. Деление отрезка в данном отношении
ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
§ 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
§ 2. Скалярное произведение векторов; угол между двумя векторами
§ 3. Угол от одного вектора до другого на плоскости
§ 4. Полярная система координат на плоскости
§ 5. Полярная система координат в пространстве
ГЛАВА V. ПРЯМАЯ ЛИНИЯ
§ 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
§ 2. Расположение двух прямых на плоскости
§ 3. Частные случаи общего уравнения прямой
§ 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
§ 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
§ 6. Две полуплоскости, определяемые данной прямой на плоскости
§ 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
§ 8. Расстояние от точки до прямой (на плоскости)
§ 9. Углы, образуемые двумя прямыми на плоскости
§ 10. Прямая в пространстве, снабженном прямоугольной системой координат
ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
§ 1. Парабола
§ 2. Определение и каноническое уравнение эллипса
§ 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
§ 4. Эллипс как проекция окружности и как сечение круглого цилиндра
§ 5. Определение гиперболы. Каноническое уравнение гиперболы
§ 6. Основной прямоугольник и асимптоты гиперболы
§ 7. Директрисы эллипса и гиперболы
§ 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
§ 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
ГЛАВА VII. ДЕТЕРМИНАНТЫ
§ 1. Плошадь ориентированного параллелограмма и треугольника
§ 2. Детерминант второго порядка. Матрицы
§ 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
§ 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
§ 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
§ 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
§ 8. Правило Крамера для решений систем и уравнений с n неизвестными
§ 9. Общее определение миноров матрицы. Теорема Лапласа
§ 10. Умножение детерминантов
§ 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
§ 1. Переход от одной аффинной системы координат к другой
§ 2. Перемножение матриц. Новое определение обратной матрицы
§ 3. Переход от одной прямоугольной системы координат к другой
§ 4. Действия над матрицами в общем случае
ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
§ 1. Ориентация пространства (плоскости)
§ 2. Углы Эйлера
§ 3. Объем ориентированного параллелепипеда
§ 4. Векторное произведение двух векторов
ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 1. Уравнения плоскости
§ 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
§ 3. Взаимное расположение двух плоскостей
§ 4. Прямая как пересечение двух плоскостей
§ 5. Пучок плоскостей
§ 6. Взаимное расположение двух прямых в пространстве
§ 7. О двух полупространствах, определяемых данной плоскостью
§ 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
§ 9. Угол между прямой и плоскостью; угол между двумя плоскостями
§ 10. Две задачи
ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§ 1. Определение движений и аффинных преобразований
§ 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
§ 3. Аналитическое выражение аффинных преобразований
§ 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
§ 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
§ 6. Движения как изометрические преобразования
§ 7. Преобразования подобия
§ 8. Классификация движений прямой и плоскости
ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
§ 1. Определение векторного пространства
§ 2. Размерность. Базис. Координаты
§ 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
§ 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
§ 5. Алгебраическая (в частности, прямая) сумма подпространств
§ 6. Линейные отображения векторных пространств
§ 7. Теорема о ранге матрицы
§ 8. Системы линейных однородных уравнения
ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
§ 1. Линейные функции
§ 2. Билинейные функции и билинейные формы
§ 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
§ 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
§ 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
§ 1. Определение n-мерного аффинного пространства
§ 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
§ 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
§ 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
§ 5. Системы линейных уравнений
§ 6. Аффинные преобразования n-мерного аффинного пространства
ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
§ 1. Определение алгебраических линий и поверхностей
§ 2. Преобразование многочлена второй степени при преобразовании координат
§ 3. Аффинная эквивалентность линий и поверхностей
§ 4. Комплексная плоскость
§ 5. Прямая линия на комплексной плоскости
§ 6. Замечание о действительных и мнимых линиях
§ 7. Комплексное пространство
§ 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
§ 9. Несколько заключительных замечаний о линиях и поверхностях
ГЛАВА XVI. Различные виды кривых второго порядка
§ 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
§ 2. Инварианты многочлена второй степени
§ 3. Центральный случай
§ 4. Параболический случай
§ 5. Аффинная классификация кривых второго порядка
§ 6. Несколько заключительных замечаний
ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
§ 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
§ 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
§ 3. Асимптотические направления кривых второго порядка
§ 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
§ 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
§ 6. Центр кривой второго порядка
§ 7. Диаметры кривой второго порядка
§ 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
§ 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
§ 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
§ 11. Оси симметрии и главные направления кривой второго порядка
§ 12. Основная теорема об аффинных преобразованиях
ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
§ 1. Распадающиеся поверхности
§ 2. Цилиндрические поверхности
§ 3. Конусы второго порядка
§ 4. Эллипсоиды и гиперболоиды
§ 5. Параболоиды
§ 6. Прямолинейные образующие
ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
§ 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
§ 2. Пересечение поверхности второго порядка с плоскостью
§ 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
§ 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
§ 5. Центр поверхности второго порядка
ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
§ 1. Диаметральные плоскости. Особые направления
§ 2. Диаметральные плоскости поверхностей различных видов
§ 3. Сопряженные направления
§ 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
§ 5. Теорема единственности
§ 6. Главные направления
§ 7. Приведение к каноническому виду уравнения поверхности второго порядка
§ 8. Аффинная классификация поверхностей второго порядка
ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
§ 1. Перспективное соответствие между плоскостью и связкой
§ 2. Однородные координаты точек на плоскости и лучел в связке
§ 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
§ 4. Принцип двойственности для проективной плоскости
§ 5. Проективная система координат в связке и на проективной плоскости
§ 6. Проективные преобразования и отображения проективной плоскости
§ 7. Проективные координаты на прямой. Проективные отображения прямой
§ 8. Двойное отношение
ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
§ 1. Определение. Теорема единственности
§ 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
§ 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
§ 4. Поляры и полюсы
§ 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
§ 6. Диаметры как поляры несобственных точек
§ 7. Автополярный треугольник
§ 8. Проективная классификация кривых второго порядка
ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
§ 1. Проективное пространство; его плоскости и прямые
§ 2. Проективные координаты. Проективные преобразования.
§ 3. Понятие об n-мерном проективном пространстве
§ 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
§ 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
§ 6. Полюсы и полярные плоскости
§ 7. Проективная классификация поверхностей второго порядка
§ 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
§ 1. Введение. Ортогональные матрицы
§ 2. Положительно определенные симметричные билинейные функции в векторном пространстве
§ 3. Определение евклидовых пространств и простейших относящихся к ним понятий
§ 4. Неравенство Коши—Буняковского и его следствия. Углы
§ 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
§ 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
§ 2. Ортогональные преобразования n-мерного евклидова пространства
§ 3. Движения трехмерного евклидова пространства
§ 4. Преобразования подобия. Дальнейшие проблемы
§ 5. Самосопряженные операторы
§ 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
§ 7. Билинейные и квадратичные формы в евклидовых пространствах
§ 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
§ 1. Перестановки
§ 2. Множества
§ 3. Отображения или функции
§ 4. Разбиение множества на подмножества. Отношение эквивалентности
§ 5. Определение группы
§ 6. Простейшие теоремы о группах
§ 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
ЗАДАЧИ
Задачи к главе IV
Задачи к главе V
Задачи к главе VI
Задачи к главе VIII
Задачи к главе IX
Задачи к главе X
Задачи к главе XI
Задачи к главе XII
Задачи к главе XIII
Задачи к главе XIV
Задачи к главе XV
Задачи к главам XVI и XVII
Задачи к главе XVIII
Задачи к главам XIX и XX
Задачи к главе XXI
Задачи к главе XXII

Источник

Нули функции. Рассмотрим функциюАналитическую в точкеТочка называется нулем функцииПорядка (или кратности)Когда выполняются условия:

(37.47)

ЕслиТо точкаНазывается простым нулем.

ЗначениеТогда и только тогда является нулем и-го порядка функции f(z), аналитической в точкеКогда в некоторой ее окрестности верно равенство

(37.48)

Где– функция, аналитическая в точкеИ

Особые точки. Особой точкой функцииНазывается точкаВ которой эта функция не является аналитической. ТочкаНазывается изолированной особой точкой функции, когда существует окрестность этой точки, в которой Аналитическая всюду, кроме. Особая точкаФункцииНазывается устранимой, когда существует конечный предел этой функции в данной точке: ТочкаНазывается полюсом функцииКогда

Для того, чтобы точкаБыла полюсом функцииНеобходимо и достаточно, чтобы эта точка была нулем. функции

(37.49)

ТочкуНазывают полюсом порядкаФункции, когда эта

Точка является нулем порядкаДля функцииВ случае

Полюс называют простым.

Для того, чтобы точкаЯвлялась полюсом порядкаФункции, необходимо и достаточно, чтобы функциюМожно было привести к виду

(37.50)

Где– функция, аналитическая в точкеИ

ТочкаНазывается существенно особой точкой функцииКогда в ней

ФункцияНе имеет ни конечного ни бесконечного предела.

Справедливы следующие утверждения.

1. ТочкаЯвляется устранимой особой точкой функцииТогда и только тогда, когда ее лорановское разложение в окрестности точкиНе содержит главной части.

2. ТочкаЯвляется полюсом функцииТогда и только тогда, когда главная часть ее лорановского разложения в окрестности точкиСодержит только конечное число членов:

(37.51)

Наибольший из показателей степени разностиВ знаменателях

Совпадает с порядком полюса.

3. ТочкаЯвляется существенно особой точкой функцииТогда и только тогда, когда главная часть ее лорановского разложения в окрестности точкиСодержит бесконечное множество членов.

Пример 37.31. Доказать, что точкаЯвляется нулем второго по

Рядка для функции

Разложим в ряды данную функцию и ее первую и вторую производные:

ПосколькуТ. е. выполняются условия (37.47)

При, то— нуль второго порядка для функции

Пример 37.32. Найти порядок нуляДля функции

Использовав разложение функцииВ ряд Тейлора, получим

Таким образом, функция _. j записана в виде (37.48), где– функция, аналитическая в точкеПричемЗначит, точка– нуль

Четвертого порядка для данной функции.

Пример 37.33. Найти нули функцииИ определить их порядки.

КогдаИлиТоЛибоИз первого

Равенства следует, чтоА со второго, что

ПустьТогда функциюМожно представить в виде (37.48):

Где функцияЯвляется аналитической в

ТочкеПричемЗначит, точкаЕсть нуль

Третьего порядка. Аналогично доказывается, что—нуль третьего порядка. ФункцияИмеет нулиДействительно,

Это нули первого порядка для функцииНо

Ибо

Пример 37.34. Доказать, что точкаДля функции

Является устранимой особой точкой.

Действительно, поскольку

То— устранимая особая точка.

Пример 37.35. Найти полюсы функции

Так как для функцииТочки–

Нули первого порядка,—нули второго порядка, то для функции

Точки— полюсы первого порядка, точки– полюсы второго порядка.

Замечание. Если, гдеИ– многочлены,

Не имеющие общих корней, то корни многочлена(и только они) являются полюсами функцииПорядок полюсовСовпадает с кратностью соот

Ветствующих корней многочленаНапример, когда

То– простой полюс,— полюс второго порядка,– полюс третьего порядка Пример 37.36. Исследовать особые точки функции

Поскольку

То функция имеет особые точкиИсследуем точкуФункцию

Приведем к виду (37.50):

Где– функция, аналитическая в окрестности точкиПричем

Следовательно, точкаЯвляется полюсом второго порядка. Аналогично, записав функциюВ виде

Заключаем, что– простой полюс данной функции.

Пример 37.37. Найти особые точки функцииИ опреде

Лить их типы.

Принимая во внимание, что (см. (37.3))

ПриПолучим

Этот ряд сходится всюду, кроме точкиЕго можно рассматривать как

Разложение функцииВ ряд Лорана в окрестности точкиПоскольку

Главная часть ряда имеет бесконечное множество членов, то точка является существенно особой точкой для функции

< Предыдущая		Следующая >

Источник

Изолированные особые точки функций и полюсы

Классификация особых точек

Типы особых точек функции

Теоремы Сохоцкого и Пикара

Ряд Лорана в окрестности особой точки

Правила определения порядка полюса

Определение порядка полюса в бесконечно удаленной точке

Определение типа особых точек для суммы, разности, произведения и частного функций

Полюс и поляра

Критерии полюса[править | править код]

См. также[править | править код]

Литература[править | править код]

Вам также может понравиться

Сервисы гугл плей не поддерживаются как исправить

Как найти номер лицевого счета по газу

Как найти радио на колонке блютуз

Добавить комментарий Отменить ответ