Алгебраический порядок точности численного метода (порядок точности численного метода, степень точности численного метода, порядок точности, степень точности) — наибольшая степень полинома, для которой численный метод даёт точное решение задачи.
Другое определение: говорят, что численный метод имеет порядок точности 



Очевидно, что метод левых (или правых) прямоугольников имеет порядок точности 0, метод Рунге — Кутты (решения дифференциальных уравнений) четвёртого порядка — 4. Широко известный метод Гаусса по пяти точкам имеет порядок точности 9. Менее очевидно, но легко показывается, что порядок точности метода трапеций — 1, а метода Симпсона — 3.
Наивысшая возможная алгебраическая степень точности для методов численного интегрирования достигается для метода Гаусса.
Для метода Рунге — Кутты решения ОДУ порядок точности имеет другое значение — максимальное число первых членов ряда Тейлора полученного решения, совпадающих с действительным решением ОДУ
Другие определения[править | править код]
Зачастую порядком точности называют порядок зависимости точности от величины шага и обозначают как 


Примечания[править | править код]
- ↑ Лекция 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера. Дата обращения: 31 мая 2020. Архивировано 10 мая 2020 года.
Алгебраический порядок точности численного метода (порядок точности численного метода, степень точности численного метода, порядок точности, степень точности) — наибольшая степень полинома, для которой численный метод даёт точное решение задачи.
Другое определение: говорят, что численный метод имеет порядок точности d, если его остаток Rn равен нулю для любого полинома степени d, но не равен нулю для полинома степени d+1
Очевидно, что метод левых (или правых) прямоугольников (ССЫЛКА ТУТ) имеет порядок точности 0, метод трапеций — 1 (ССЫЛКА ТУТ) , метод Рунге — Кутты (ССЫЛКА ТУТ) (решения дифференциалных уравнений) четвёртого порядка — 4. Широко известный метод Гаусса (ССЫЛКА ТУТ) по пяти точкам имеет порядок точности 9. Менее очевидно, но легко показывается, что порядок точности метода трапеций — 2, а метода Симпсона — 4 (ССЫЛКА ТУТ).
ЛЕКЦИЯ
4.
Решение
нелинейных уравнений
ЛИТЕРАТУРА.
Учебник [1] §4.4.
§4.7, §4.2.
§4.1.
Метод простой итерации с параметром
Дано
нелинейное уравнение:

(4.1)
Уравнение
(4.1) преобразуется к виду

,
который называется видом,
удобным для итераций,
а функция

— итерационной
функцией.
Далее задается начальное приближение

и строится последовательность приближений
к корню по формуле

(4.2)
На
прошлой лекции была доказана теорема.
Теорема
3.2.
Если в окрестности корня функция
непрерывно дифференцируема и удовлетворяет
условию

,
(3.10)
то
метод простой итерации сходится и
справедливы априорная оценка погрешности

(3.11)
означающая,
что метод сходится со скоростью
геометрической прогрессии со знаменателем

,
и апостериорная оценка погрешности

(3.12)
из
которой для заданной точности

следует критерий окончания итераций

(3.13)
В
этом случае

является искомым приближением с точностью
.
Не
всегда возможно простым преобразованием
уравнения найти итерационную функцию,
удовлетворяющую
условию (3.10). Однако есть способ, при
котором гарантированно выполнено это
условие.
Метод
простой итерации с параметром.
В
этом способе приведения к виду, удобному
для итераций, итерационная функция
имеет вид

(4.3)
где

— параметр, выбираемый таким образом,
чтобы величина

была минимальной. Тогда метод (4.3) будет
сходиться максимально быстро, т.е. для
достижения заданной точности требуется
минимальное количество итераций.
Если
в окрестности корня функция
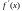
строго знакопостоянна, например,
выполняется
условие
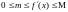
,
то оптимальное значение параметра
находится по формуле
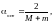
(4.4)
при
этом метод сходится со скоростью
геометрической прогрессии со знаменателем

Поскольку
для нахождения каждого корня необходимо
вычислить лишь величины
и

,
преобразование (4.3) называют универсальным.
ПРИМЕР
4.1.
Найти корень уравнения

на отрезке

методом простой итерации с точностью
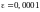
.
Решение.
Воспользуемся параметрической формой
метода простой итерации. В данной задаче
можно воспользоваться этим методом,
так как производная функции

строго
положительна и на заданном отрезке
монотонно возрастает. Следовательно,

По
формуле (2.6) получаем значение оптимального
параметра

и
тогда

.
Также находим знаменатель сходимости
метода
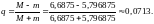
Возьмем
в качестве начального приближения
середину отрезка локализации:

.
Вычисляем

и
проверяем критерий окончания итераций

В
нашем случае имеем

Выполняем
следующую итерацию

и
проверяем критерий окончания итераций:

.
На этот раз неравенство верное, а значит
итерации можно прекратить. В соответствии
с погрешностью ответ записываем с
четырьмя знаками после запятой.
Ответ.
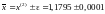
.
Пояснение
выбора параметра.
Рассмотрим
итерационную функцию
и
попробуем выбрать параметр, исходя из
достаточного условия сходимости (3.10).
Найдем
производную: 
и решим неравенство:

.
Тогда:

или

Это
означает, что знак параметра должен
совпадать со знаком производной. Мы
предположили, что производная
знакопостоянна и выполнено неравенство:
Тогда
параметр можно выбирать из интервала:
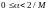
.
В
случае, когда производная отрицательна,
можно умножить исходное уравнение на
-1 и функция из убывающей превратится
в возрастающую, то есть знак производной
будет положительным.
Порядок
(скорость) сходимости.
Пусть в некоторой окрестности (вообще
говоря, малой) корня

уравнения (2.1) итерационная последовательность
удовлетворяет неравенству

где

— постоянная и

.
Тогда

называется порядком
сходимости
метода.
Метод
простой итерации с параметром является
линейно сходящимся методом, то есть p=1
§4.2.
Модификации метода Ньютона.
Упрощенный
метод Ньютона.
В этой модификации метода Ньютона
производная функции

вычисляется только один раз — в начальном
приближении
.
Расчетная формула имеет вид
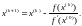
(4.5)
Упрощённый
метод Ньютона представляет собой метод
простой итерации с итерационной функцией
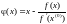
и
обладает линейной сходимостью. Для
достижения заданной точности требуется
тем меньше итераций, чем ближе к корню
лежит точка
.
Метод
ложного положения.
Метод основан на следующей аппроксимации
производной

(4.6)
где

— некоторая точка из окрестности корня.
Расчетная формула:

Метод
ложного положения представляет собой
метод простой итерации с итерационной
функцией

(4.7)
и
обладает линейной сходимостью. Для
достижения заданной точности требуется
тем меньше итераций, чем ближе к корню
лежит точка
.
Метод
секущих. Метод
основан на следующей аппроксимации
производной

(4.8)
Расчетная
формула метода

Метод
имеет порядок сходимости

,
т.е. обладает сверхлинейной сходимостью.
Метод
Стеффенсена.
Идея аппроксимации производной основана
на малости значения

в малой окрестности корня. Поэтому
берется в качестве приращения аргумента:

(4.9)
Расчетная
формула метода

Метод
имеет второй порядок сходимости, т.е.
обладает квадратичной сходимостью.
Модификация
метода Ньютона для кратных корней. Если
искомый корень имеет кратность

,
то классический метод Ньютона из п.8
сходится к нему лишь линейно (со скоростью
геометрической прогрессии со знаменателем

).
Однако метод

(4.10)
обладает
квадратичной сходимостью в окрестности
такого корня.
§4.3.
Интервал неопределенности корня.
Пусть
между абсолютными погрешностями входных
данных x
и решения y
установлено
неравенство:

.Тогда
величина

–
называется
абсолютным
числом обусловленности. Если выполнено
неравенство для относительных
погрешностей:

То
число

называется относительным числом
обусловленности.
Если
число
достаточно велико, то задача называется
плохо обусловленной.
При
вычислениях на компьютере значения
функции
вычисляются с погрешностью:

,
причём предположим, что в окрестности
корня

.
Это приводит к тому, что существует
такая окрестность корня
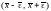
,
что при попадании в нее итерационной
последовательности невозможно определить,
какая точка представляет собой корень
уравнения (2.1). Эта окрестность называется
интервалом
неопределенности.
Внутри этого интервала любую точку
можно принять за роиближение к корню.
Найдем оценку радиуса интервала
неопределенности корня.

Отсюда
можно написать приближенное равенство:

Взяв
модуль и, используя понятии абсолютной
погрешности, имеем:

Если
корень

простой, то радиус интервала неопределенности
оценивается по формуле
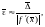
(4.11)
а
если
имеет кратность
,
то по формуле

Поскольку
значение корня
на практике неизвестно, то вместо него
можно взять любую достаточно близкую
к нему точку.
Также
величина

заведомо не превышает величины, примерно
равной

,
так как внутри такой окрестности может
не оказаться чисел, представимых на
компьютере, кроме одного (близкого или
равного
).
Соседние файлы в папке Все за 2й курс
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.
В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.
Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.
Нам нужно найти такое значение при котором такие называются корнями функции
Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.
Метод деления пополам
Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .
Поделим отрезок пополам и введем среднюю точку .
Тогда либо , либо .
Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .
Уравнение касательной к функции в точке имеет вид:
В уравнении касательной положим и .
Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.
Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).
Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:
1) функция y= f(x) определена и непрерывна при ;
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f ”(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
Рисунок 2. Результат первой итерации
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = .
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = ()
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:
= 1.5.
Второе приближение корня определяется по формуле:
=
Третье приближение корня определяется по формуле:
Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e – до выполнения неравенства |xi–xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:
/
Итерационный процесс имеет вид:
где .
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что .
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .
После подстановки имеем: и
Для сходимости необходимо, чтобы было положительным, поэтому .
Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.
Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Метод парабол
Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .
Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .
В форме Ньютона она имеет вид:
Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .
Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.
Этот метод очень удобен для поиска корней многочленов высокой степени.
Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.
Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).
По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение — произвольная точка промежутка .
Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа
Таким образом, если производная меньше единицы, то является сжатием.
Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.
Рассмотрим уравнение: .
Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .
Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .
Эти итерации сходятся к неподвижной точке для любого начального приближения :
Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.
Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь нетрудно убедиться, что при существует окрестность корня, в которой .
то если корень кратности , то в его окрестности и, следовательно,.
Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).
Поскольку , то
Таким образом, сходимость метода Ньютона очень быстрая.
Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.
Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.
Повторяя указанную процедуру, можно найти все корни с учетом кратности.
Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.
Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
Численные методы решения нелинейных уравнений
Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение:
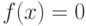 |
( 4.1) |
Необходимо решить это уравнение, т. е. найти его корень  .
.

Если функция имеет вид многочлена степени m,
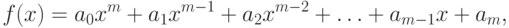
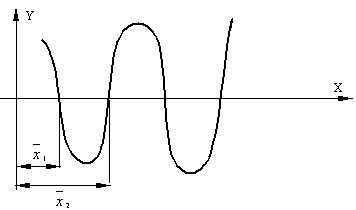
где ai – коэффициенты многочлена,  , то уравнение f(x)=0 имеет m корней (рис. 4.2).
, то уравнение f(x)=0 имеет m корней (рис. 4.2).
Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .


Такие уравнения обычно имеют бесконечное множество решений.
Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .
Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).
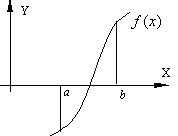
Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
- отделение корней, – т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
- уточнение корней, – т.е. сужение интервала [a,b] до величины равной заданной степени точности
 .
.
Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
Метод итераций
Правила ввода функции
- Примеры
 ≡ x^2/(1+x)
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)


На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A – номер итерации, столбец B – корень уравнения X , столбец C – значение функции F(X) , столбец D – точность eps .
[spoiler title=”источники:”]
http://intuit.ru/studies/courses/2260/156/lecture/27239
http://math.semestr.ru/optim/iteration_method.php
[/spoiler]
