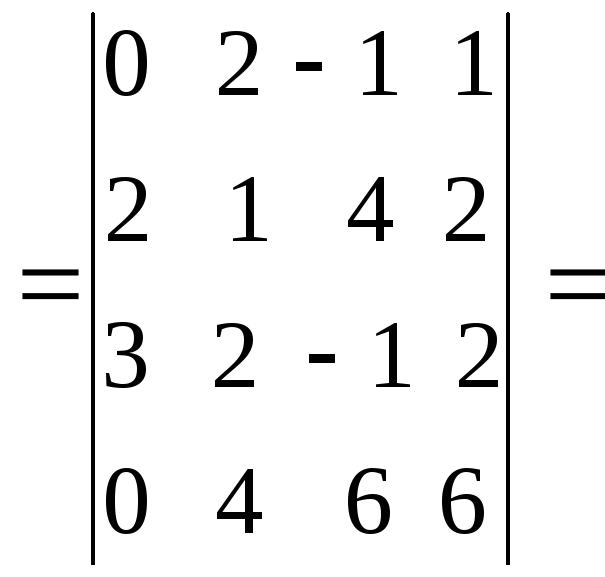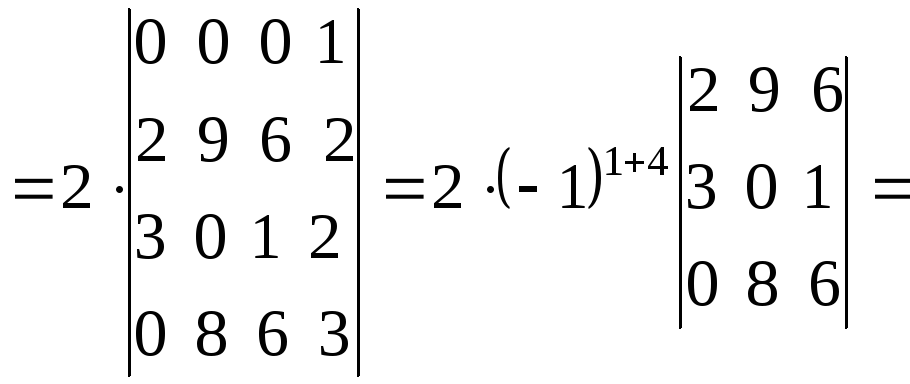Порядок системы уравнений как найти

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4  (*)

(*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+          =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

	x + 5y = 7 | ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+          =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 |:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+          =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8         | :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

---

Ваши комментарии

Оставить комментарий:

---

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = – 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 – t при – ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 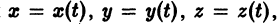выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

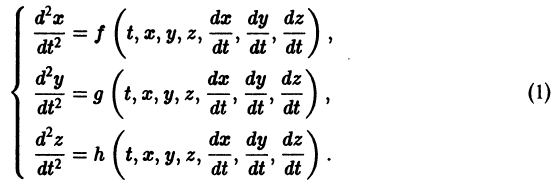
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 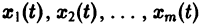аргумента t, назовем канонической систему вида

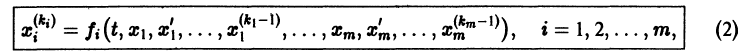
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

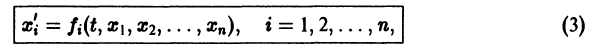
Если 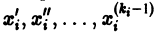в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из 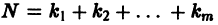уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

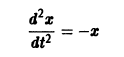
является мастным случаем канонической системы. Положив 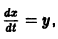в силу исходного уравнения будем иметь

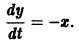
В результате получаем нормальную систему уравнений

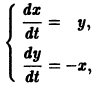
эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

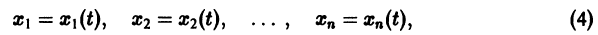
дифференцируемых на интервале а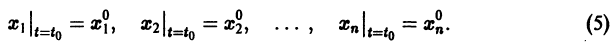

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

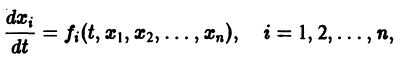
и пусть функции 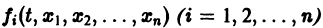определены в некоторой (n + 1) — мерной области D изменения переменных 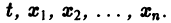Если существует окрестность точки 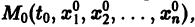в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал 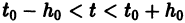изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

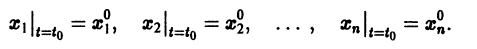
Определение:

Система n функций

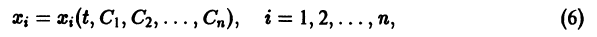
зависящих от t и n произвольных постоянных 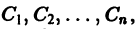называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях 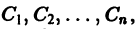система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных 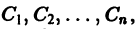называются частными решениями.

Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 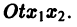Решение

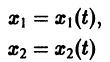
системы (7), принимающее при 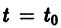значения 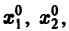определяет в пространстве некоторую линию, проходящую через точку 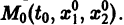Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку 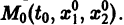(рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

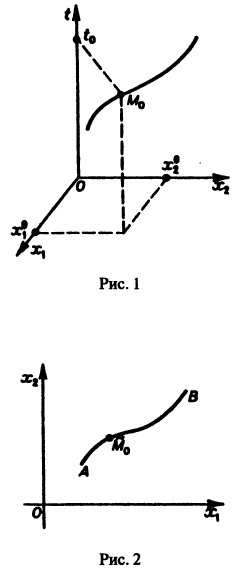
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

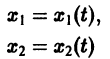
системы — как параметрические уравнения кривой на плоскости 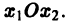Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение 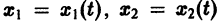системы (7), принимающее при t = to начальные значения 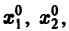изображается кривой АВ, проходящей через точку 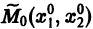(рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

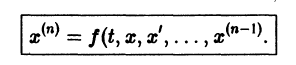
Введя новые функции 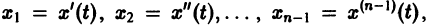заменим это уравнение следующей нормальной системой n уравнений:

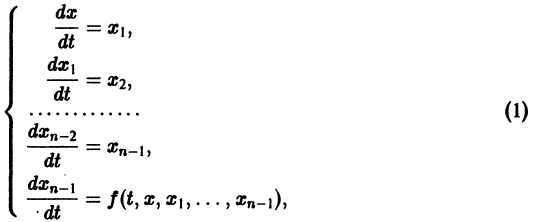
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

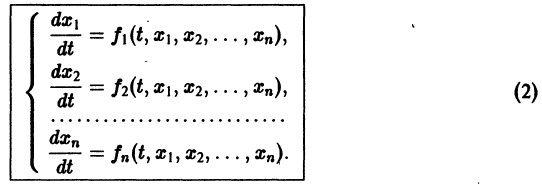
Продифференцируем первое из уравнений (2) по t. Имеем

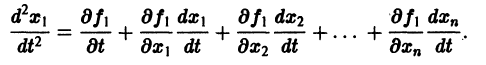
Заменяя в правой части производные 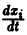их выражениями 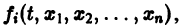получим

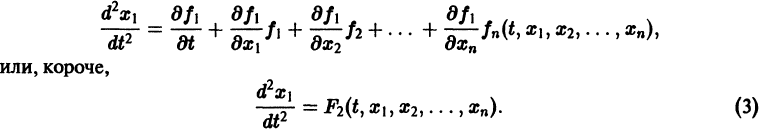
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

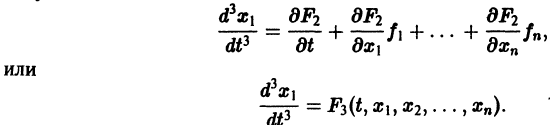
Продолжая этот процесс, найдем

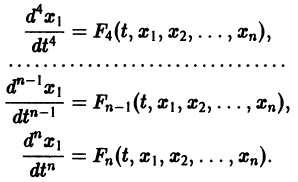
Предположим, что определитель

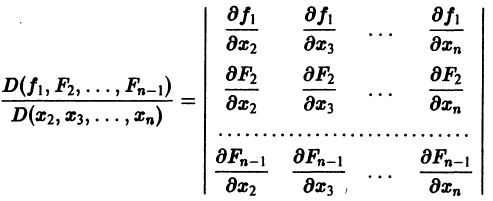
(якобиан системы функций отличен от нуля при рассматриваемых значениях

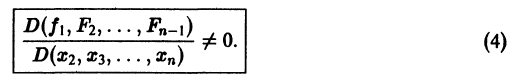
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

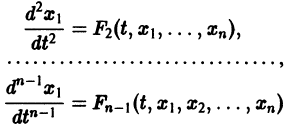
будет разрешима относительно неизвестных 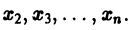При этом 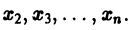выразятся через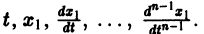

Внося найденные выражения в уравнение

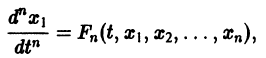
получим одно уравнение n-го порядка

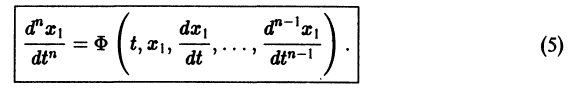
Из самого способа его построения следует, что если 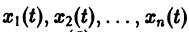есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 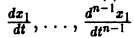и подставим найденные значения как известные функции

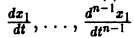
от t в систему уравнений

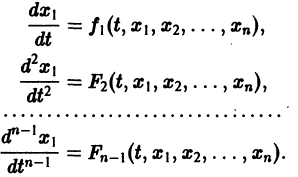
По предположению эту систему можно разрешить относительно 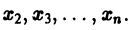т. е найти как функции от t.

Можно показать, что так построенная система функций

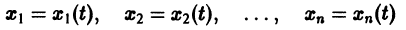
составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

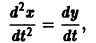
откуда, используя второе уравнение, получаем

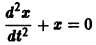
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

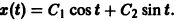
В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

Функции x(t), y(t) можно представить в виде

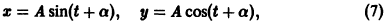
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 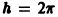и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

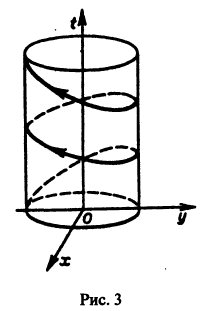
Исключая в формулах (7) параметр t, получаем уравнение

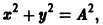
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

Может оказаться, что функции 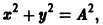нельзя выразить через 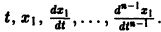Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

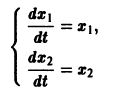
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

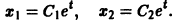
Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

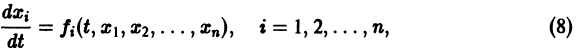
иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

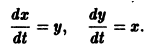
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

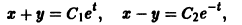
из которых легко определяется общее решение системы:

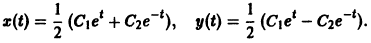
Одна интегрируемая комбинация дает возможность получить одно уравнение

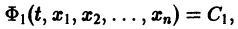
связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция 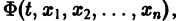не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

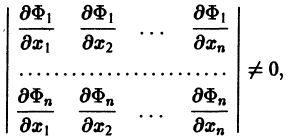
то задача интефирования системы (8) решена (так как из системы

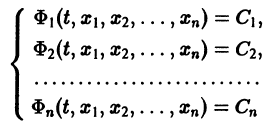
определяются все неизвестные функции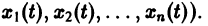

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

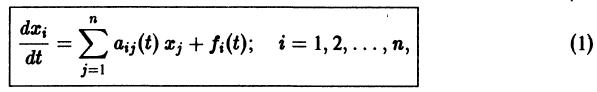
или, в матричной форме,

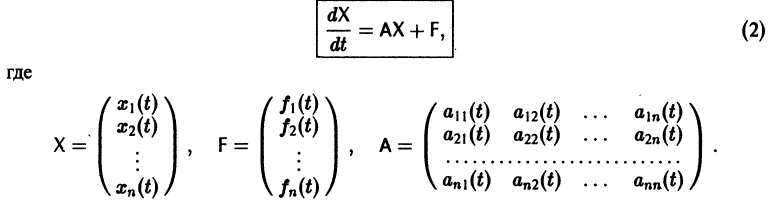
Теорема:

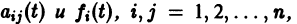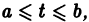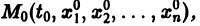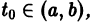Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по 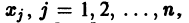ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам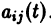

Введем линейный оператор

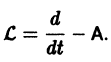
Тогда система (2) запишется в виде

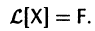
Если матрица F — нулевая, т. е. 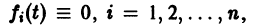на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

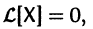
то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

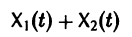
двух решений 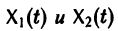однородной линейной системы уравнений является решением той же системы.

Следствие:

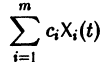
с произвольными постоянными коэффициентами сi решений 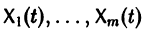линейной однородной системы дифференциальных уравнений

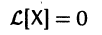
является решением той же системы.

Теорема:

Если 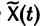есть решение линейной неоднородной системы

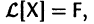
a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы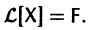

Действительно, по условию,

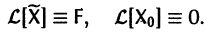
Пользуясь свойством аддитивности оператора 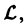получаем

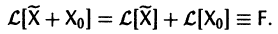
Это означает, что сумма 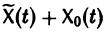есть решение неоднородной системы уравнений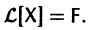

Определение:

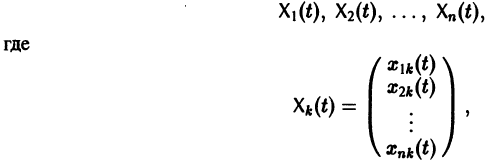
называются линейно зависимыми на интервале a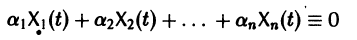

при 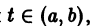причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы 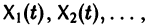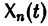называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

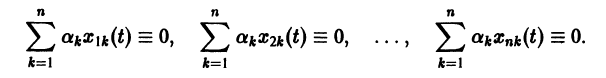
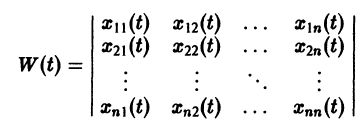
называется определителем Вронского системы векторов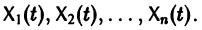

Определение:

Пусть имеем линейную однородную систему

где 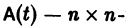матрица с элементами 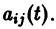Система n решений

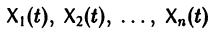
линейной однородной системы (6), линейно независимых на интервале а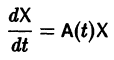

с непрерывными на отрезке 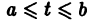коэффициентами 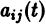является линейная комбинация п линейно независимых на интервале а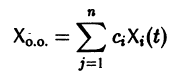

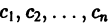() — произвольные постоянные числа).

Пример:

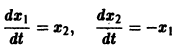
имеет, как нетрудно проверить, решения

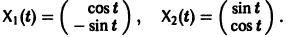
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

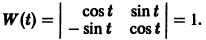
Общее решение системы имеет вид

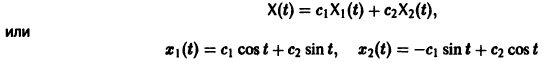
(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

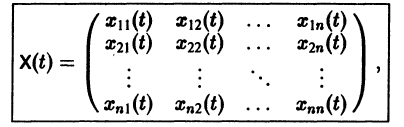
столбцами которой являются линейно независимые решения системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

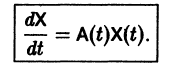
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

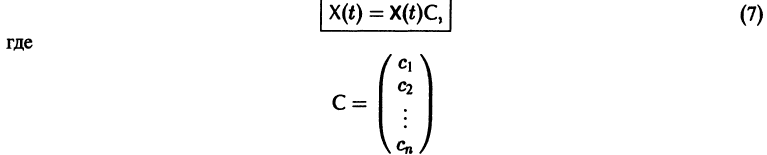
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

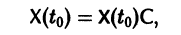
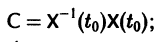
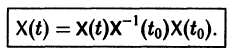
Матрица 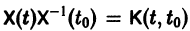называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

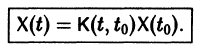
Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 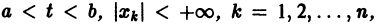линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке 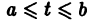коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

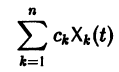
соответствующей однородной системы и какого-нибудь частного решения 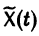неоднородной системы (2):

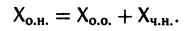
Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

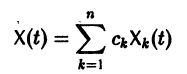
есть общее решение однородной системы (6), тогда

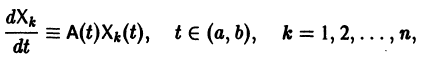
причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

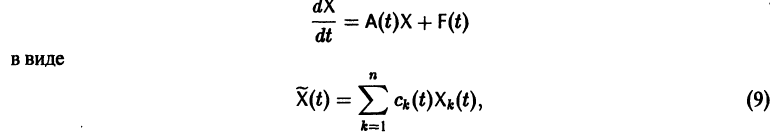
где 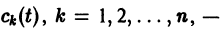неизвестные функции от t. Дифференцируя 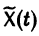по t, имеем

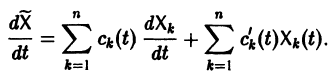
Подставляя 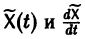в (2), получаем

то для определения получаем систему

или, в развернутом виде,

Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где — известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения в (9), находим частное решение системы (2)

(здесь под символом понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты — постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) получаем

откуда а21 = а11. Следовательно,

Полагая в находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

Напомним некоторые понятия из линейной алгебры. Вектор называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как есть нуль-матрица.

Теорема:

Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь — произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

где с1, с2 — произвольные действительные числа.

Понятие о системах дифференциальных уравнений

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/issledovanie-slau/slau/

http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/

[/spoiler]

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0: 

1. Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

2. Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

3. Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

4. Провести прямую через эти две точки и вуаля — график готов. 

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

1. Выразить одну переменную через другую из более простого уравнения системы.

2. Подставить то, что получилось на место этой переменной в другое уравнение системы.

3. Решить полученное уравнение, найти одну из переменных.

4. Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

5. Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Решим систему уравнений методом подстановки

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

1. Решите систему уравнений:

   x − y = 4
   x + 2y = 10

2. Выразим x из первого уравнения:

   x − y = 4
   x = 4 + y

3. Подставим получившееся выражение во второе уравнение вместо x:

   x + 2y = 10
   4 + y + 2y = 10

4. Решим второе уравнение относительно переменной y:

   4 + y + 2y = 10
   4 + 3y = 10
   3y = 10 − 4
   3y = 6
   y = 6 : 3
   y = 2

5. Полученное значение подставим в первое уравнение вместо y и решим уравнение:

   x − y = 4
   x − 2 = 4
   x = 4 + 2
   x = 6

Ответ: (6; 2).

Пример 2

1. Решите систему линейных уравнений:

   x + 5y = 7
   3x = 4 + 2y

2. Сначала выразим переменную x из первого уравнения:

   x + 5y = 7
   x = 7 − 5y

3. Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

   3x = 4 + 2y
   3 (7 − 5y) = 4 + 2y

4. Решим второе линейное уравнение в системе:

   3 (7 − 5y) = 4 + 2y
   21 − 15y = 4 + 2y
   21 − 15y − 2y = 4
   21 − 17y = 4
   17y = 21 − 4
   17y = 17
   y = 17 : 17
   y = 1

5. Подставим значение y в первое уравнение и найдем значение x:

   x + 5y = 7
   x + 5 = 7
   x = 7 − 5
   x = 2

Ответ: (2; 1).

Пример 3

1. Решите систему линейных уравнений:

   x − 2y = 3
   5x + y = 4

2. Из первого уравнения выразим x:

   x − 2y = 3
   x = 3 + 2y

3. Подставим 3 + 2y во второе уравнение системы и решим его:

   5x + y = 4
   5 (3 + 2y) + y = 4
   15 + 10y + y = 4
   15 + 11y = 4
   11y = 4 − 15
   11y = −11
   y = −11 : 11
   y = −1

4. Подставим получившееся значение в первое уравнение и решим его:

   x − 2y = 3
   x − 2 (−1) = 3
   x + 2 = 3
   x = 3 − 2
   x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

1. При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

2. Складываем почленно левые и правые части уравнений системы.

3. Решаем получившееся уравнение с одной переменной.

4. Находим соответствующие значения второй переменной.

5. Запишем ответ в в виде пар значений (x; y).

Пример.

Домножим первое уравнение системы на -2, второе оставим без изменений. Система примет вид:

Сложим уравнения, получим

Отсюда y = -3, а, значит, x = 2

Ответ: (2; -3).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

• ax + by + cz = d

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

Как решаем:

1. 5x − 8y = 4x − 9y + 3

2. 5x − 8y − 4x + 9y = 3

3. x + y = 3

Задание 2. Как решать систему уравнений способом подстановки

Как решаем:

1. Выразить у из первого уравнения:
   

2. Подставить полученное выражение во второе уравнение:
   

3. Найти соответствующие значения у:
   

Ответ: (2; −1), (−1; 2).

Задание 3. Как решать систему уравнений методом сложения

Как решаем:

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
   

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:
   

1. Найти у, подставив найденное значение в любое уравнение:
   

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Как решаем:

Решим второе уравнение и найдем х = 2, х = 5.
Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Ответ: (2; 4); (5; 13).

Задание 5. Как решить систему уравнений с двумя неизвестными

Как решаем:

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Ответ: (-4; 2); (4; 2).

---

---

1. Определители и системы линейных уравнений

1.1.
Системы двух линейных уравнений и
определители второго порядка

Рассмотрим
систему двух линейных уравнений с двумя
неизвестными:

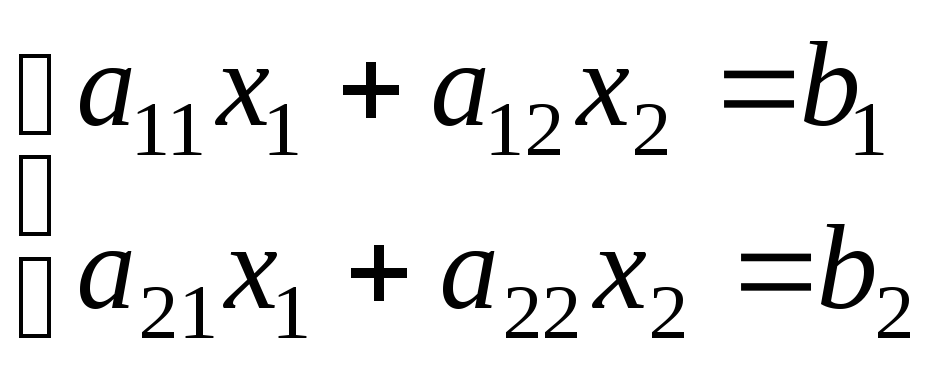
Коэффициенты

при неизвестных
и
имеют два индекса: первый указывает
номер уравнения, второй – номер
переменной.

Главным определителем системы называется таблица, составленная из коэффициентов при неизвестных и заключенная в прямые скобки:

Вспомогательным определителем называют определитель, полученный из главного определителя заменой одного из столбцов на столбец свободных членов:

Главнаядиагональ определителя – это диагональ, направленная из левого верхнего угла в правый нижний угол. Вторая диагональ называетсяпобочной.

Определитель второго порядка равен разности между произведением элементов главной диагонали и произведением элементов побочной диагонали:

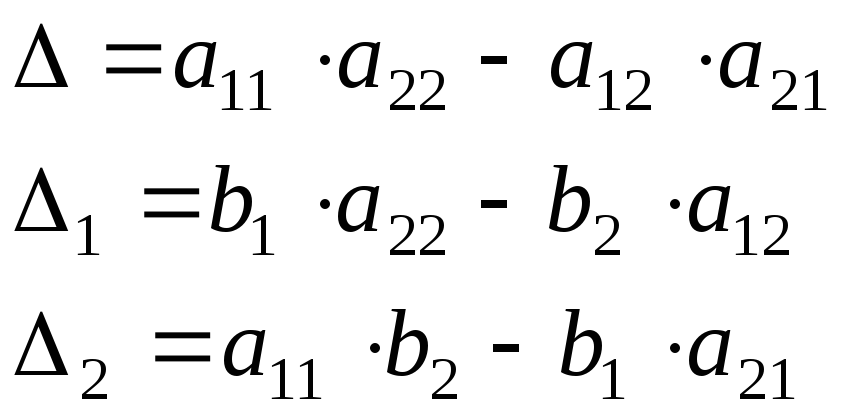
Правило
Крамера: Решение системы находят
путем деления вспомогательных
определителей на главный определитель
системы

,

Замечание
1.Использование правила Крамера
возможно, если определитель системы
не равен нулю.

Замечание
2.Формулы Крамера обобщаются и на
системы большего порядка.

Пример
1. Решить систему:
.

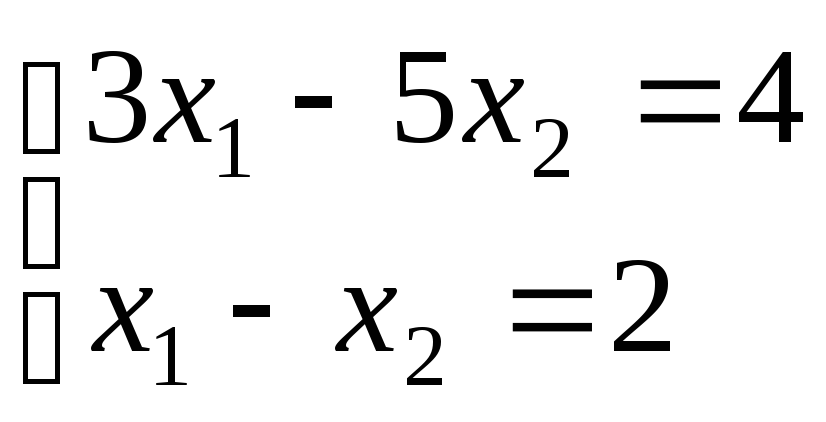Решение.

;

;

;

Проверка:

Вывод:
Система решена верно:
.

1.2. Системы трех линейных уравнений и определители третьего порядка

Рассмотрим
систему трех линейных уравнений с тремя
неизвестными:

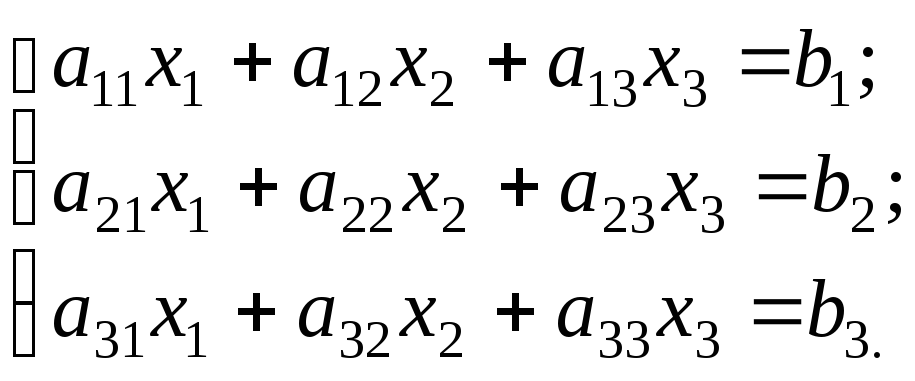
Определитель,
составленный из коэффициентов при
неизвестных, называется определителем
системы или главным определителем:

.

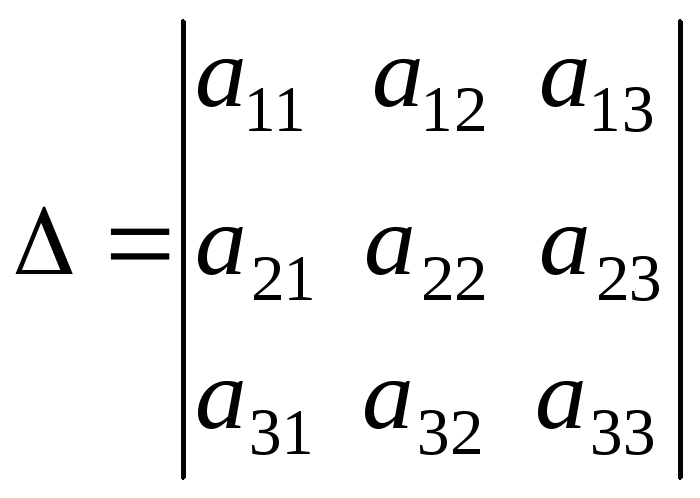Если

то система имеет единственное решение,
которое определяется по формулам
Крамера:

где

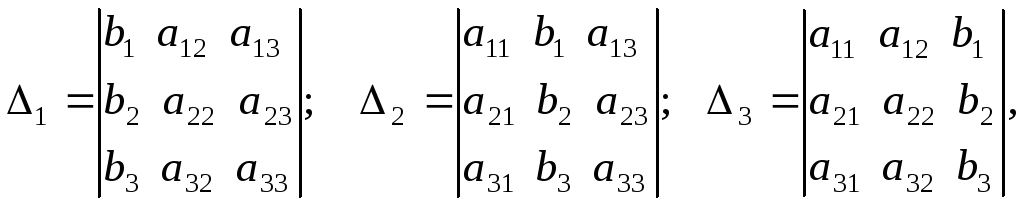
где
определители
– называются вспомогательными и
получаются из определителя
путем замены его первого, второго или
третьего столбца столбцом свободных
членов системы.

Пример
2.Решить систему
.

Сформируем
главный и вспомогательные определители:

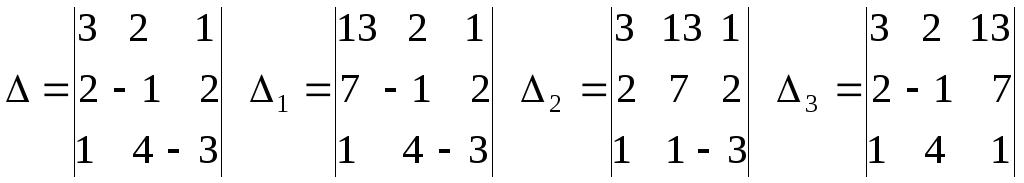
Осталось
рассмотреть правила вычисления
определителей третьего порядка. Их три:
правило дописывания столбцов, правило
Саррюса, правило разложения.

а)
Правило дописывания первых двух столбцов
к основному определителю:

.

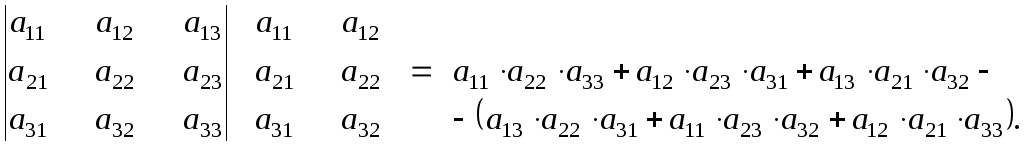
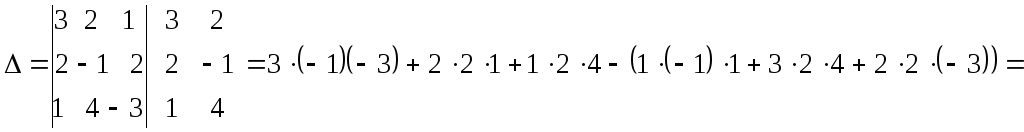
Вычисление
проводятся следующим образом: со своим
знаком идут произведения элементов
главной диагонали и по параллелям к
ней, с обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней.

б)
Правило Саррюса:

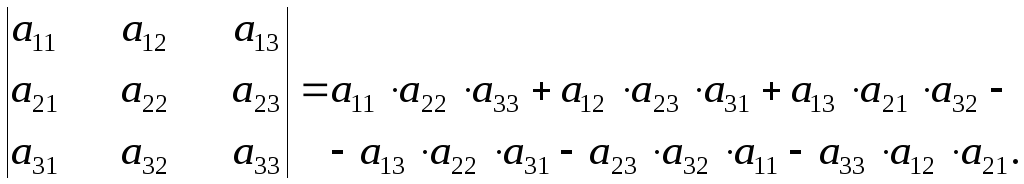
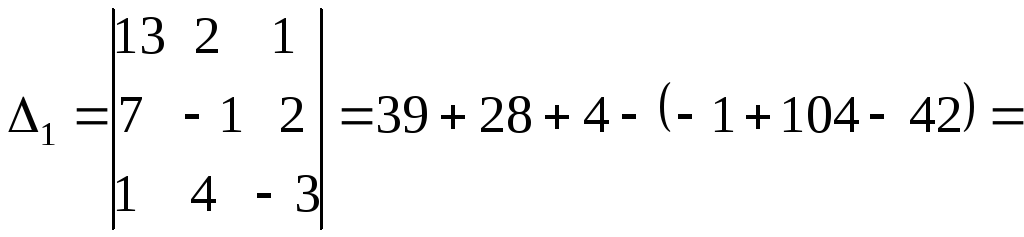
Со
своим знаком берут произведения элементов
главной диагонали и по параллелям к
ней, причем недостающий третий элемент
берут из противоположного угла. С
обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней, третий элемент берут
из противоположного угла.

в)
Правило разложения по элементам строки
или столбца:

Определитель равен сумме произведений элементов какой-нибудь строки (столбца) на их соответствующие алгебраические дополнения.

Если

,
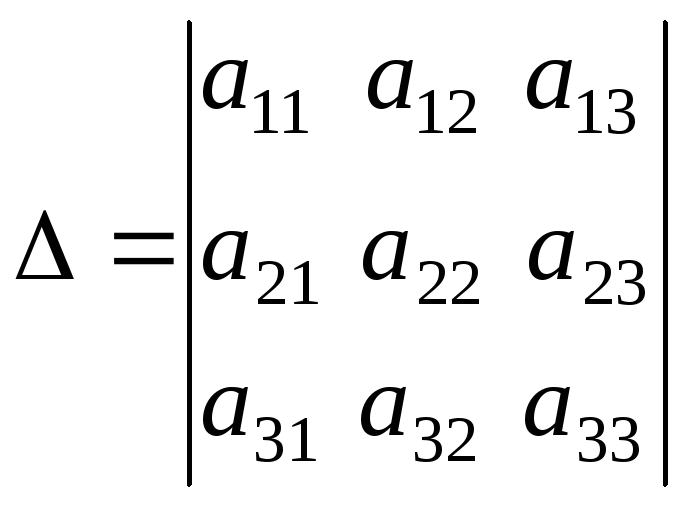тогда
.

Алгебраическое
дополнение– это определитель более
низкого порядка, получаемый путем
вычеркивания соответствующей строки
и столбца и учитывающий знак
,
где– номер строки,– номер столбца.

Например,

,

,
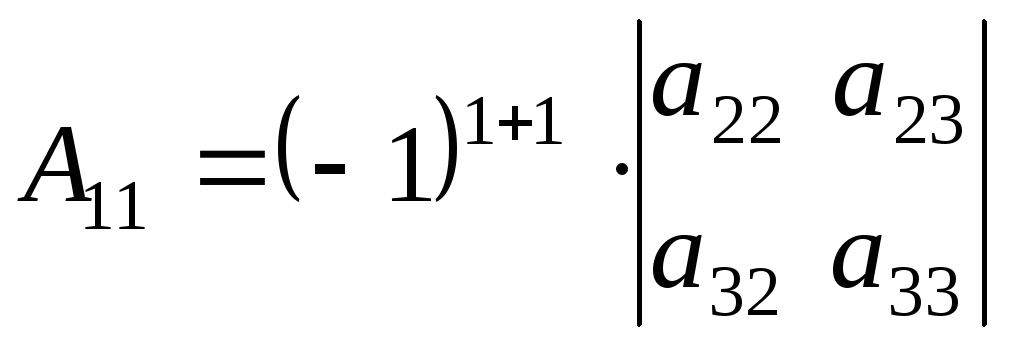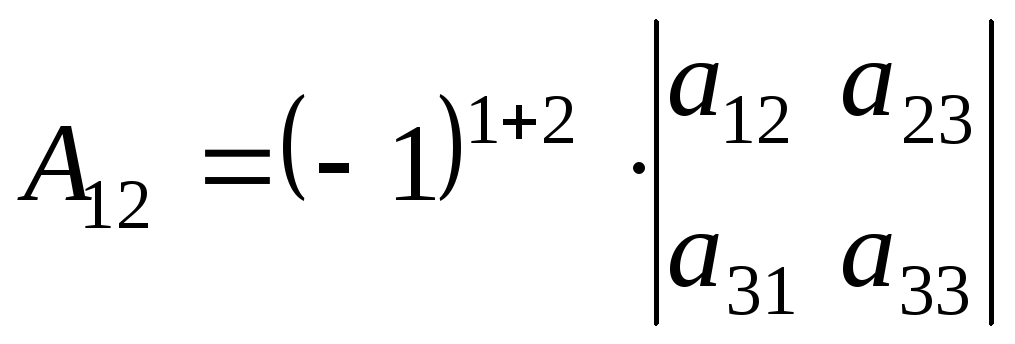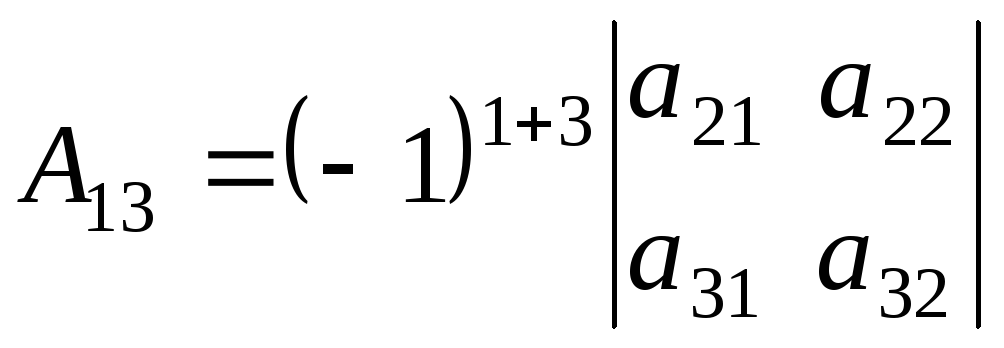и т.д.

Вычислим
по этому правилу вспомогательные
определители
и
,
раскрывая их по элементам первой строки.

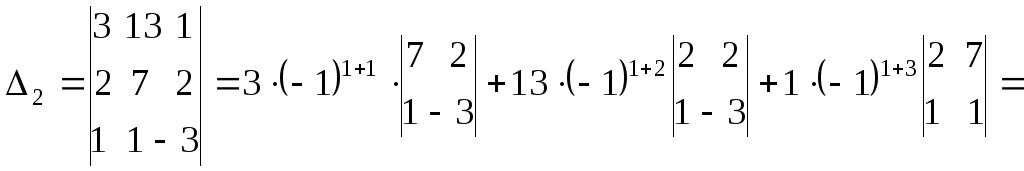
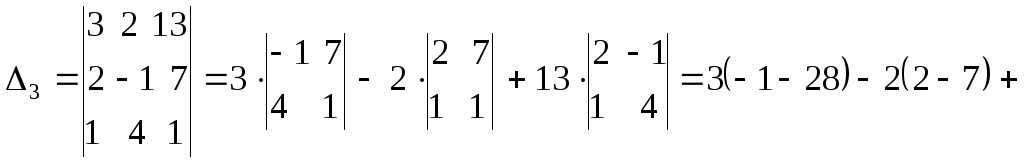
Вычислив
все определители, по правилу Крамера
найдем переменные:

Проверка:

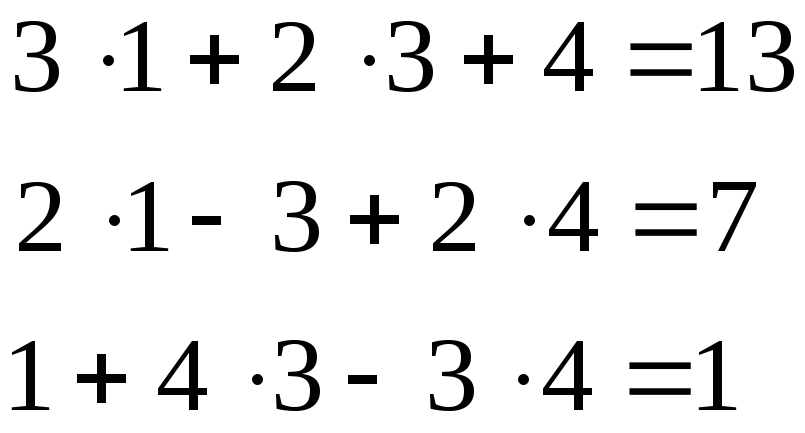
Вывод:
система решена верно:
.

1. Основные
   свойства определителей

Необходимо
помнить, что определитель – это число,
найденное по некоторым правилам. Его
вычисление может быть упрощено, если
пользоваться основными свойствами,
справедливыми для определителей любого
порядка.

Свойство
1.Значение определителя не изменится
от замены всех его строк соответствующими
по номеру столбцами и наоборот.

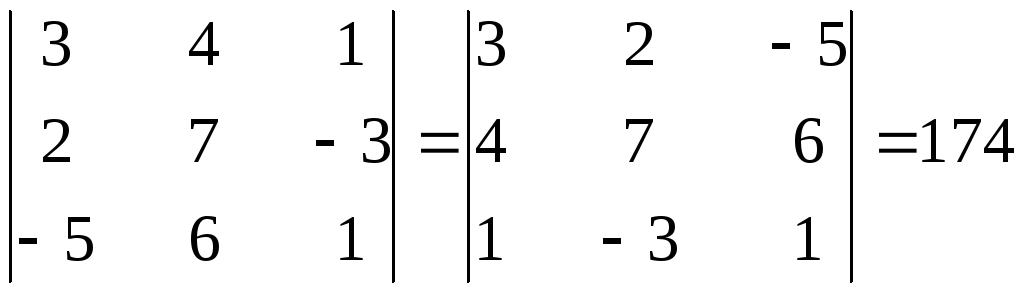
Операция
замены строк столбцами называется
транспонированием. Из этого свойства
вытекает, что всякое утверждение,
справедливое для строк определителя,
будет справедливым и для его столбцов.

Свойство
2.Если в определителе поменять
местами две строки (столбца), то знак
определителя поменяется на противоположный.

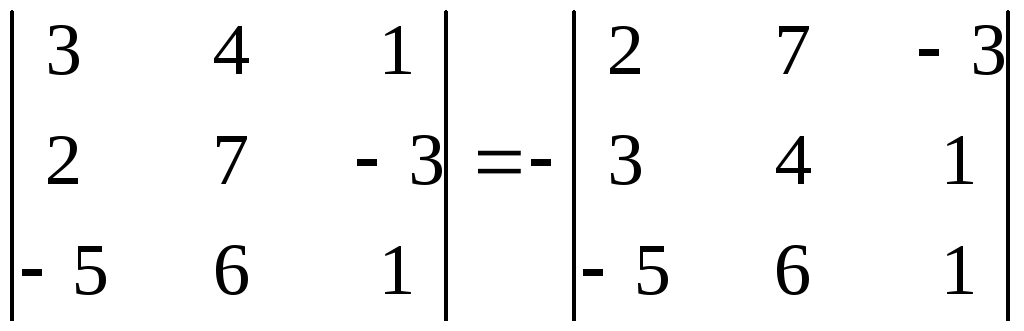
Свойство
3.Если все элементы какой-нибудь
строки определителя равны 0, то определитель
равен 0.

Свойство
4.Если элементы строки определителя
умножить (разделить) на какое-нибудь
число
,
то и значение определителя увеличится
(уменьшится) в
раз.

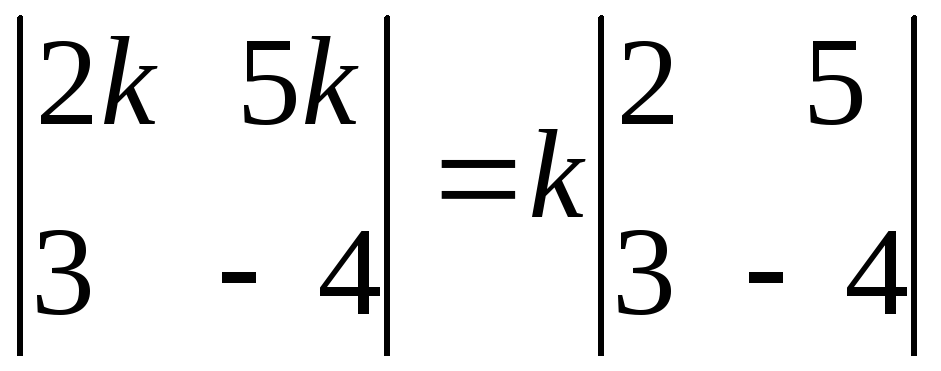
Если
элементы какой-нибудь строки, имеют
общий множитель, то его можно вынести
за знак определителя.

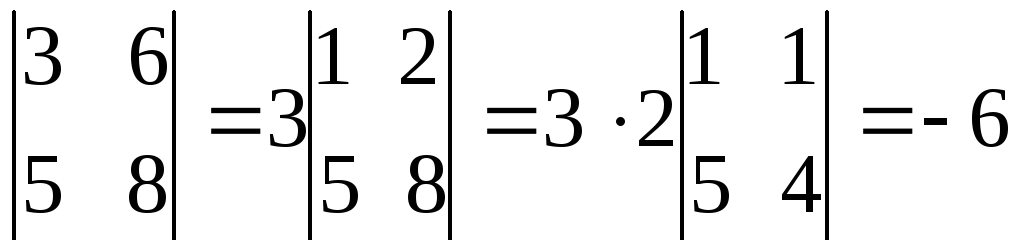
Свойство
5. Если определитель имеет две
одинаковые или пропорциональные строки,
то такой определитель равен 0.

Свойство
6. Если элементы какой-нибудь строки
определителя представляют собой сумму
двух слагаемых, то определитель равен
сумме двух определителей.

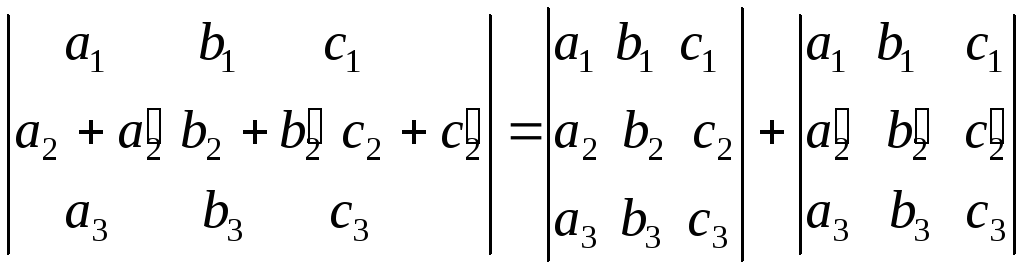
Свойство
7. Значение определителя не изменится,
если к элементам какой-нибудь строки
добавить элементы другой строки,
умноженной на одно и то же число.

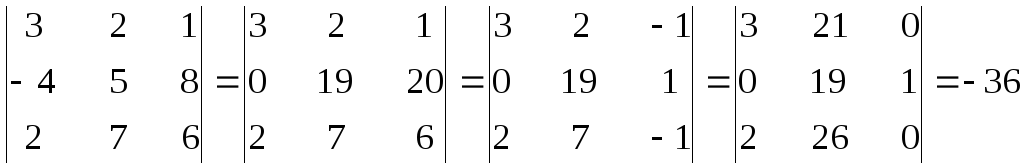
В
этом определителе вначале ко второй
строке прибавили третью, умноженную на
2, затем из третьего столбца вычли второй,
после чего вторую строку прибавили к
первой и третьей, в результате получили
много нулей и упростили подсчет.

Элементарными
преобразованиями определителя
называются упрощения его благодаря
использованию указанных свойств.

Пример
1.Вычислить определитель

Непосредственный
подсчет по одному из рассмотренных выше
правил приводит к громоздким вычислениям.
Поэтому целесообразно воспользоваться
свойствами:

а)
из І строки вычтем вторую, умноженную
на 2;

б)
из ІІ строки вычтем третью, умноженную
на 3.

В
результате получаем:

Разложим
этот определитель по элементам первого
столбца, содержащего лишь один ненулевой
элемент.

.

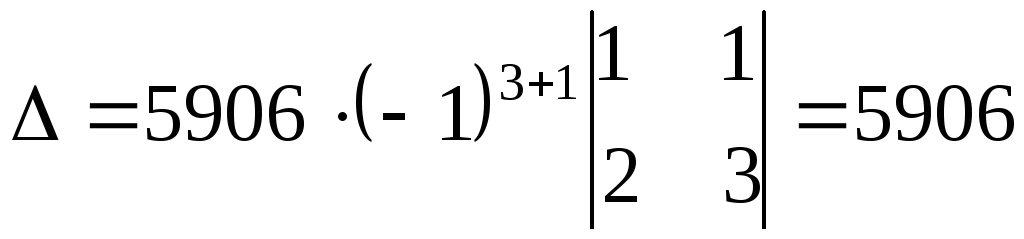1. Системы
   и определители высших порядков

Систему

линейных уравнений с
неизвестными можно записать в таком
виде:

Для
этого случая также можно составить
главный и вспомогательные определители,
а неизвестные определять по правилу
Крамера. Проблема состоит в том, что
определители более высокого порядка
могут быть вычислены только путем
понижения порядка и сведения их к
определителям третьего порядка. Это
может быть осуществлено способом прямого
разложения по элементам строк или
столбцов, а также с помощью предварительных
элементарных преобразований и дальнейшего
разложения.

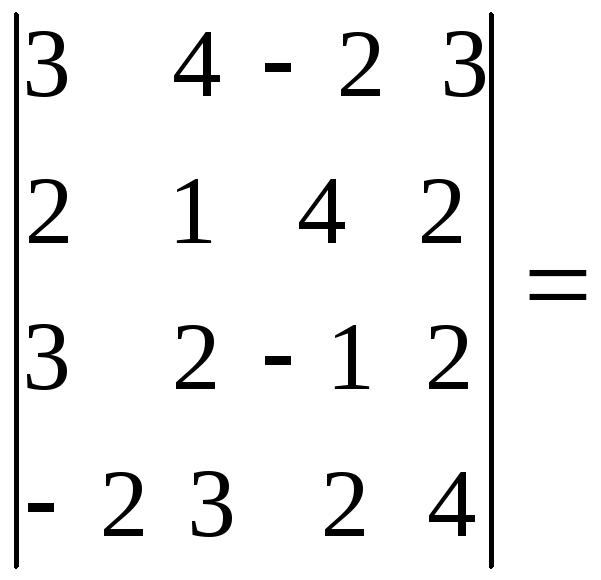
Пример
4. Вычислить определитель четвертого
порядка

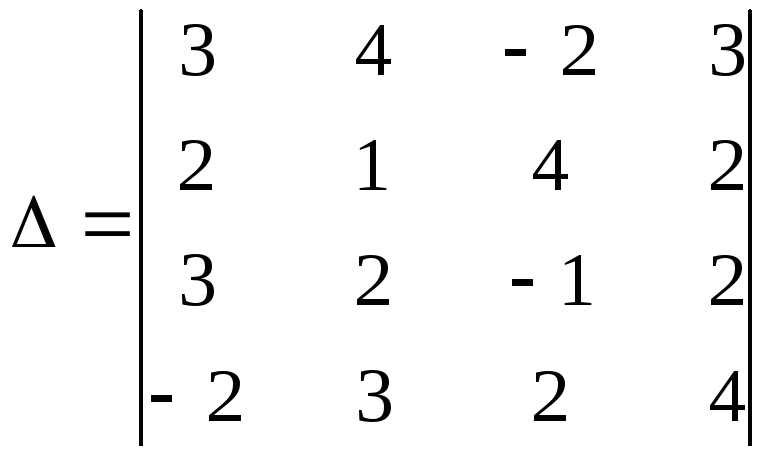
Решение
найдем двумя способами:

а)
путем прямого разложения по элементам
первой строки:

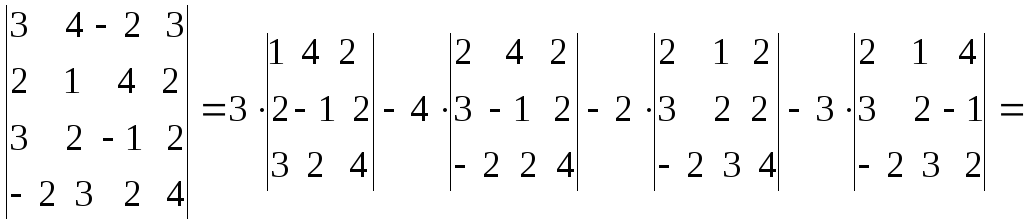
б)
путем предварительных преобразований
и дальнейшего разложения

	а) из І строки вычтем ІІІ
б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

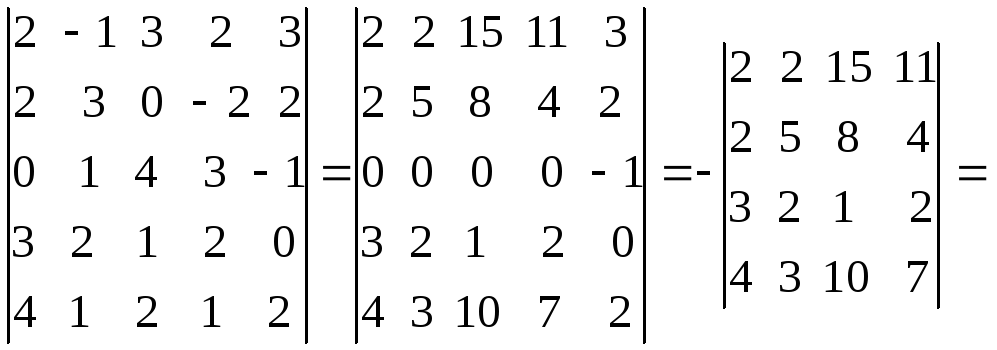
Пример
5.Вычислить определитель пятого
порядка, получая нули в третьей строке
с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

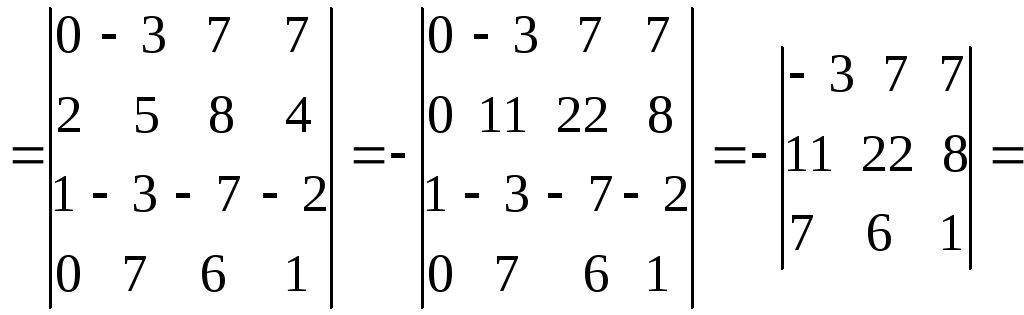
из
второго столбца вычтем третий:

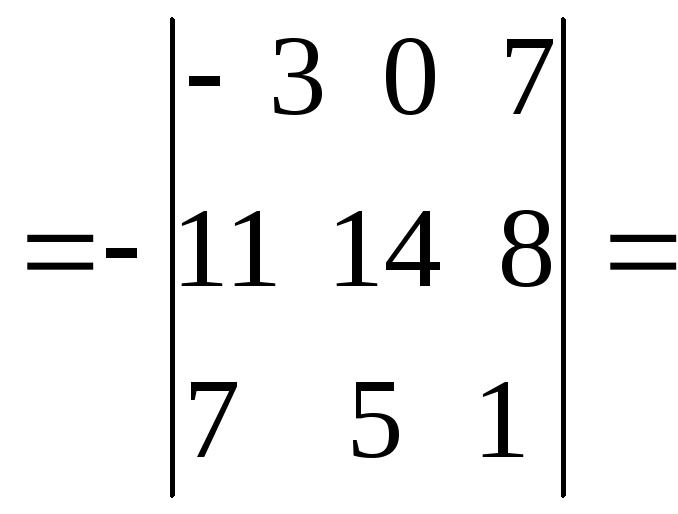
из
второй строки вычтем третью:

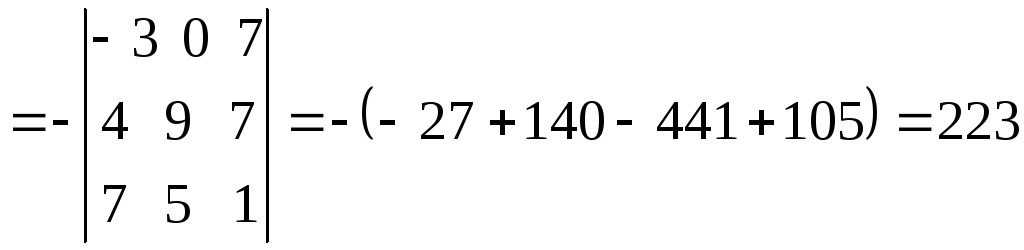
Пример
6.Решить систему:

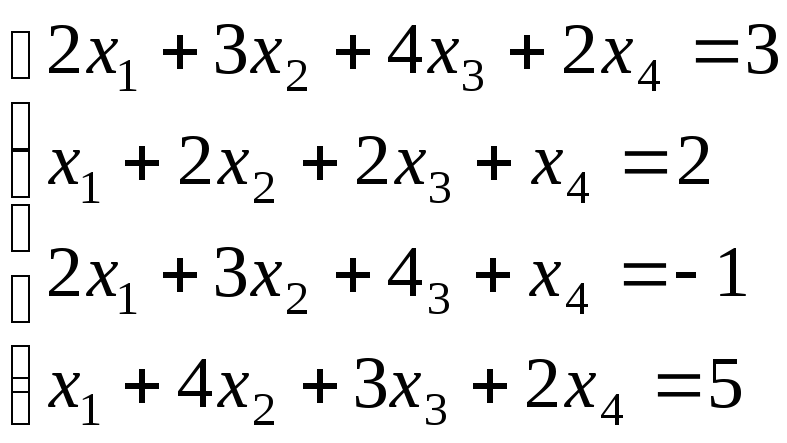
Решение.Составим определитель системы и, применив
свойства определителей, вычислим его:

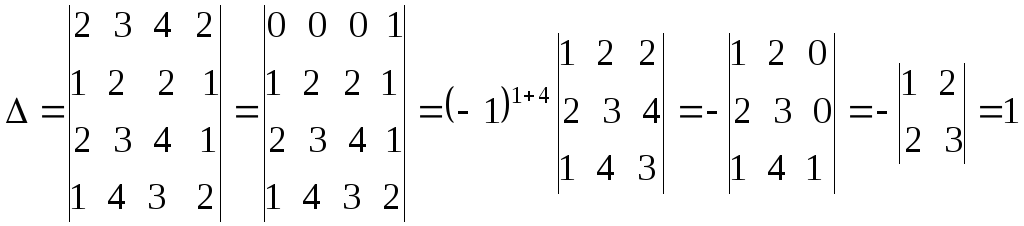
(из
первой строки вычтем третью, а затем в
полученном определителе третьего
порядка из третьего столбца вычитаем
первый, умноженный на 2). Определитель

,
следовательно, формулы Крамера применимы.

Вычислим
остальные определители:

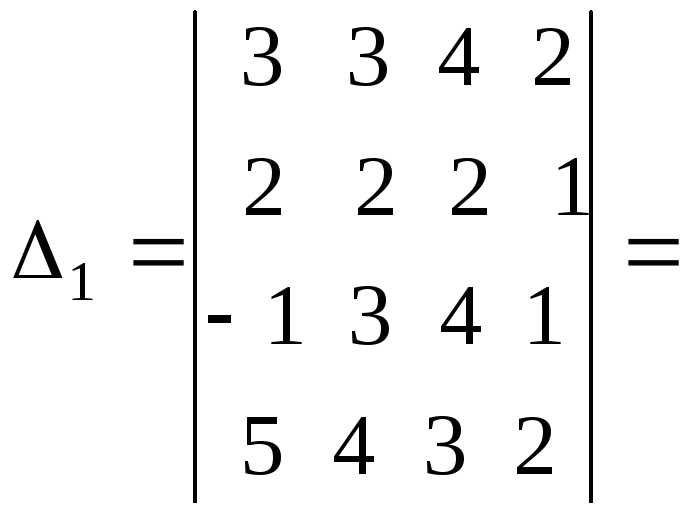
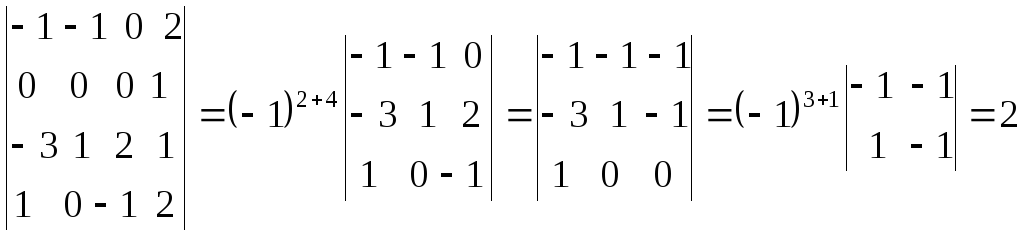
Четвертый
столбец умножили на 2 и вычли из остальных

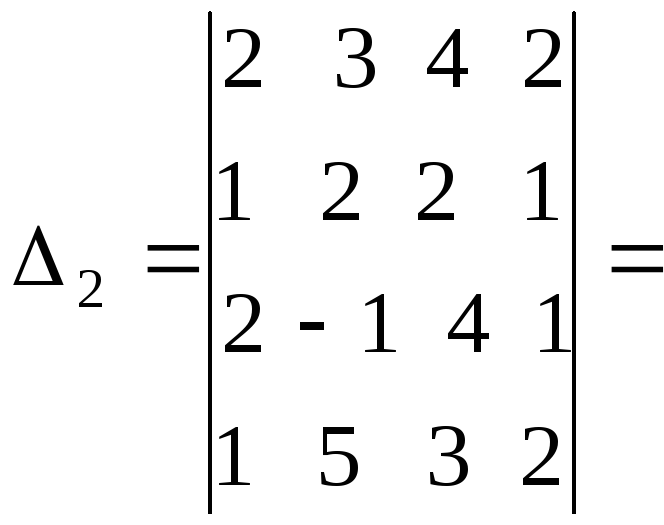
Четвертый
столбец вычли из первого, а затем, умножив
на 2, вычли из второго и третьего столбцов.

.

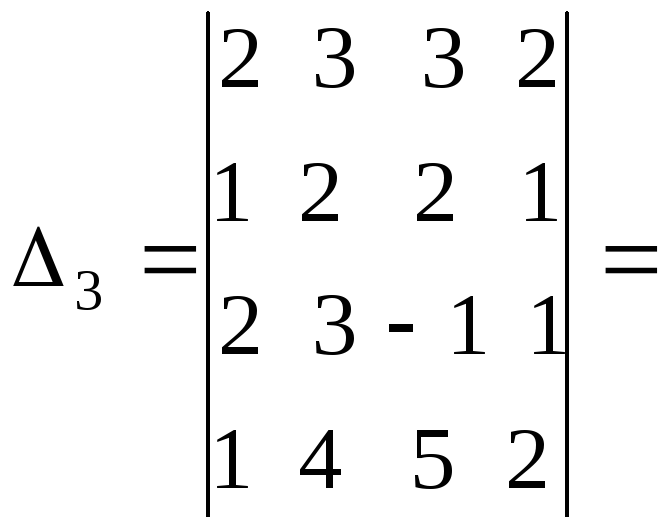
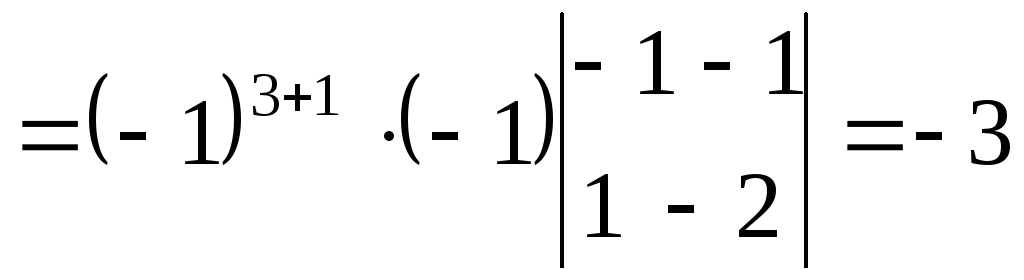Здесь
выполнили те же преобразования, что и
для
.

.

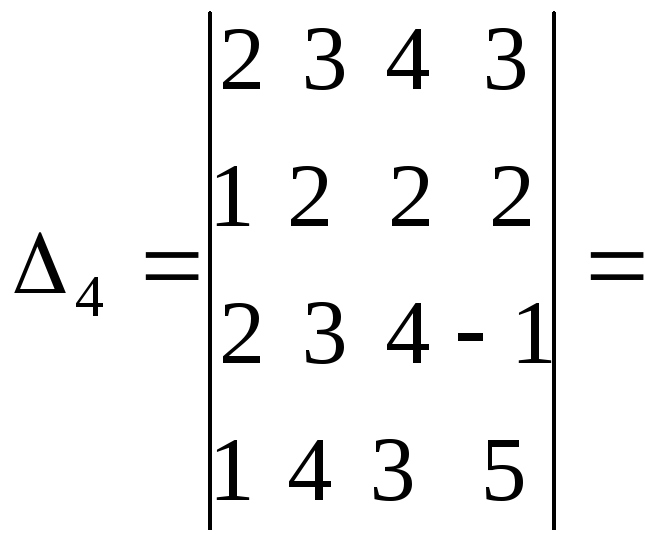
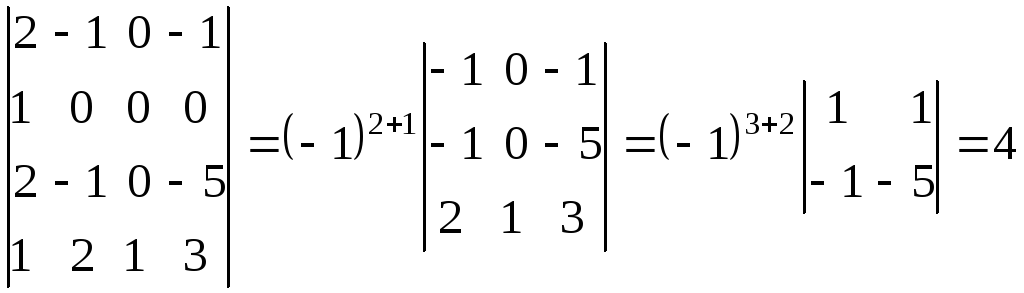При
нахождении
первый столбец умножили на 2 и вычли из
остальных.

По
правилу Крамера имеем:

.

После
подстановки в уравнения найденных
значений убеждаемся в правильности
решения системы.

2.
МАТРИЦЫ и
ИХ
ИСПОЛЬЗОВАНИЕ

В
РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Системы дифференциальных уравнений: понятия и определения

Система обыкновенных дифференциальных уравнений

разрешенная относительно старших производных , называется канонической системой. Она имеет вид

Порядком системы (1) называется число , равное .

---

Пример 1. Привести к каноническому виду систему дифференциальных уравнений

Решение. Данная система имеет третий порядок, так как и, значит, . Разрешая первое уравнение относительно , а второе относительно , получим каноническую систему

Система обыкновенных дифференциальных уравнений первого порядка вида

где — независимая переменная; — неизвестные функции от , называется нормальной системой.

Число называется порядком нормальной системы (3). Две системы дифференциальных уравнений называются эквивалентными, если они обладают одними и теми же решениями.

Любую каноническую систему (2) можно привести к эквивалентной ей нормальной системе (3), причем порядок этих систем будет одним и тем же.

---

Пример 2. Привести к нормальной системе следующую систему дифференциальных уравнений:

Решение. Положим . Тогда будем иметь , и данная система приведется к следующей нормальной системе третьего порядка:

---

Пример 3. Привести дифференциальное уравнение к нормальной системе.

Решение. Положим , тогда Подставляя эти выражения в данное уравнение, получим

Нормальная система будет иметь вид

Решением системы (3) в интервале называется совокупность любых функций

определенных и непрерывно дифференцируемых в интервале , если они обращают уравнения системы (3) в тождества, справедливые для всех значений .

---

Пример 4. Показать, что система функций , определенных в интервале , является решением системы дифференциальных уравнений

Решение. Имеем . Подставляя в уравнение данной системы вместо и их выражения через , получим тождества

---

Задачей Коши для системы (3) называется задача нахождения решения

этой системы, удовлетворяющего начальным условиям

где — заданные числа.

Теорема существования и единственности решения задачи Коши.

Пусть имеем нормальную систему дифференциальных уравнений (3) и пусть функции , определены в некоторой n+1-мерной области изменения переменных . Если существует окрестность точки , в которой функции а) непрерывны, 6) имеют ограниченные частные производные по переменным , то найдется интервал изменения , в котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям (4).

Система дифференцируемых функций

независимой переменной и произвольных постоянных называется общим решением нормальной системы (3), если: 1) при любых допустимых значениях система функций (5) обращает уравнения (3) в тождества, 2) в области, где выполняются условия теоремы Коши, функции (5) решают любую задачу Коши.

---

Пример 5. Показать, что система функций

является общим решением системы уравнений

Решение. В данном примере область есть

Подставляя функции и из (6) в систему уравнений (7), получаем тождества по , справедливые при любых значениях постоянных . Таким образом, условие 1), определяющее общее решение, выполнено.

Проверим выполнение условия 2). Заметим, что для системы уравнений (7) условия теоремы существования и единственности решения задачи Коши выполняются во всей области , определяемой соотношениями (8). Поэтому в качестве начальных условий можно взять любую тройку чисел . Тогда соотношения (6) дадут для определения систему

Определитель этой системы ; следовательно, она однозначно разрешима относительно при любых и . Это равносильно тому, что разрешима любая задача Коши. Итак, система функций (6) является общим решением системы уравнений (7).

---

Решения, получающиеся из общего при конкретных значениях постоянных , называются частными решениями.

Пример 6. Имея общее решение (6) системы (7), найти частное решение этой системы, удовлетворяющее начальным условиям .

Решение. Задача сводится к нахождению таких значений постоянных и , чтобы выполнялись соотношения

Решая эту систему, находим . Искомое частное решение

---

Замечание 1. Не всякую систему дифференциальных уравнений можно свести к одному уравнению. Например, система

распадается на два независимых уравнения. Общее решение в этом случае получается интегрированием каждого уравнения в отдельности:

Замечание 2. Если число уравнений в системе равно , а число искомых функций , причем , то такая система является неопределенной. В этом случае можно выбирать произвольно искомых функций (лишь бы они были нужное число раз дифференцируемыми) и в зависимости от них находить остальные функций.

Замечание 3. Если система состоит из уравнений, а число искомых функций , причем , то эта система может оказаться несовместной, т.е. не имеющий ни одного решения.

---

Пусть дана (для простоты) нормальная система двух дифференциальных уравнений

Будем рассматривать систему значений как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат . Решение принимающее при значение , изображает в этом пространстве некоторую линию, проходящую через точку . Эта линия называется интегральной кривой (линией) нормальной системы (9).

Задача Коши для системы (9) получает следующую геометрическую формулировку: в пространстве переменных найти интегральную кривую, проходящую через данную точку . Теорема Коши устанавливает существование и единственность такой линии.

Нормальной системе (9) и ее решению можно дать еще такое истолкование. Будем независимую переменную рассматривать как время, а систему значений функций как прямоугольные декартовы координаты точки плоскости . Эту плоскость переменных называют фазовой плоскостью. В фазовой плоскости решение системы (9), принимающее при начальные значения , изображается линией (рис.28), проходящей через точку . Эту линию называют траекторией системы (фазовой траекторией). Очевидно, что траектория системы (9) есть проекция интегральной кривой на фазовую плоскость.

Система (9) определяет в каждый момент времени в данной точке фазовой плоскости координаты скорости движущейся точки.

---

Пример 7. Решить систему уравнений

при начальных условиях

Решение. Дифференцируя один раз по первое уравнение системы (10) и подставляя в полученное уравнение , сведем систему (10) к одному уравнению второго порядка , образующее решение которого

Так как , то ; итак, общее решение системы (10):

Частным решением системы (10), удовлетворяющим начальным условиям (11), будет

Исключая из уравнений (13) (путем возведения в квадрат и почленного сложения), получаем фазовую траекторию

где . Это окружность, проходящая через точку . Представив уравнения (13) в виде

где , замечаем, что уравнения (15) выражают зависимость от времени текущих координат точки , или коротко , которая начинает свое движение при от точки и движется по окружности (14) (рис.29,а).

Направление движения точки определим с помощью заданной системы (10). При , согласно уравнению , величина убывает (как, например, в точке ), а при величина возрастает (как, например, в точке ). Таким образом, точка движется по кривой (14) по ходу часовой стрелки. Изменяя произвольно начальные условия (11) (оставаясь, однако, в физически допустимых пределах), т. е. изменяя как угодно положение начальной точки , получаем всевозможные фазовые траектории (14).

Дадим теперь другое истолкование уравнений (15) (или, что то же, уравнений (13)). В трехмерном пространстве возьмем правую декартову систему координат . Легко убедиться, что точка (или коротко ) с координатами (рис. 29,б)

начинает свое движение при от начальной точки и с возрастанием поднимается по винтовой линии (16), расположенной на цилиндре с окружностью (14) в основании и образующими, параллельными оси .

Очевидно, что точка совпадает с точкой и что при любом точка проектируется в точку на фазовой траектории. Так как точка движется по ходу часовой стрелки, то интегральная кривая, описываемая точкой , есть левая винтовая линия на цилиндре с окружностью (14) в основании и образующими, параллельными оси . При различных положениях точки интегральные кривые системы (10), соответствующие различным значением , проектируются на плоскость в раз личные кривые (14), а интегральные кривые, соответствующие одному и тому же значению , проектируются в одну и ту же кривую (14).

---

Интегралом нормальной системы (3) называется функция , определенная и непрерывная вместе со своими частными производными первого порядка , в области , если при подстановке в нее произвольного решения системы (3) она принимает постоянное значение, т.е. функция зависит только от выбора решения , но не от переменной .

Первым интегралом нормальной системы (3) называется равенство

где — интеграл системы (3), а — произвольная постоянная. Иногда первым интегралом системы (3) называют интеграл этой системы.

---

Пример 8. Показать, что функция

определенная в области , является интегралом системы уравнений

если общее решение этой системы есть

Решение. Подставляя (19) в (17), получаем

в области . Следовательно, функция (17) является в области интегралом системы уравнений (18), а значит первый интеграл этой системы будет , где — произвольная постоянная.

---

Теорема. Для того чтобы функция была интегралом системы (3), необходимо и достаточно выполнения условия

в области .

---

Пример 9. Показать, что функция

является интегралом системы уравнений

Решение. В данном случае

Находим частные производные данной функции . Имеем

Подставляя (23) и (24) в левую часть (20), получаем

в области .

Итак, функция (21) есть интеграл системы уравнений (22) и, следовательно, первый интеграл системы (22) будет

где — произвольная постоянная.

---

Нормальная система (3) имеет бесконечное множество систем первых интегралов.

Интегралы системы (3) называются независимыми относительно искомых функций , если между функциями не существует соотношения вида ни при каком выборе функции , не зависящей явно от .

Теорема. Для того чтобы функции , имеющие частные производные , были независимыми относительно в некоторой области , необходимо и достаточно, чтобы якобиан этих функций был отличен от нуля в области ,

Общим интегралом нормальной системы (3) называется совокупность независимых первых интегралов этой системы.

Если известны , где , независимых первых интегралов системы (3), то ее порядок можно понизить на единиц.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.