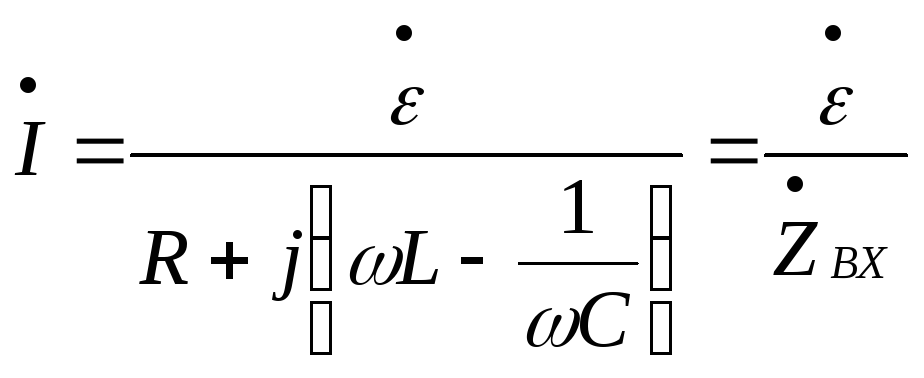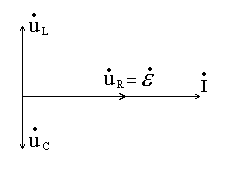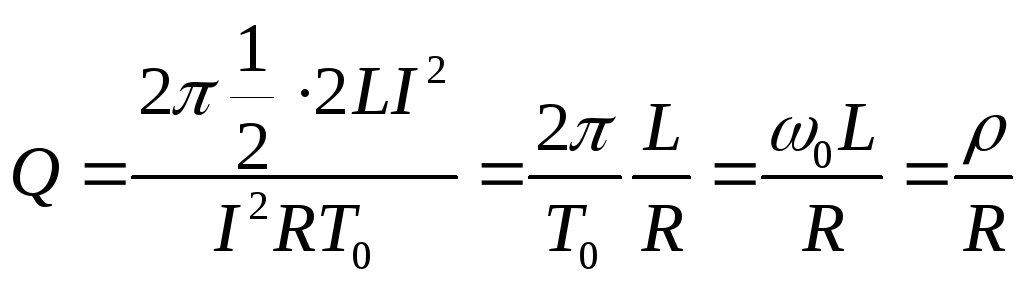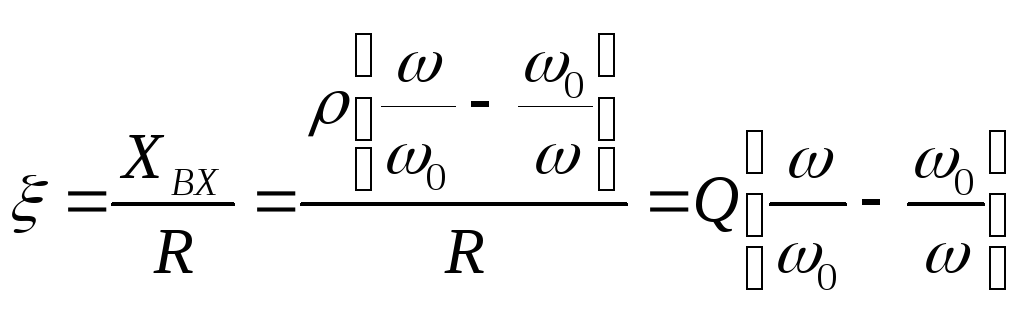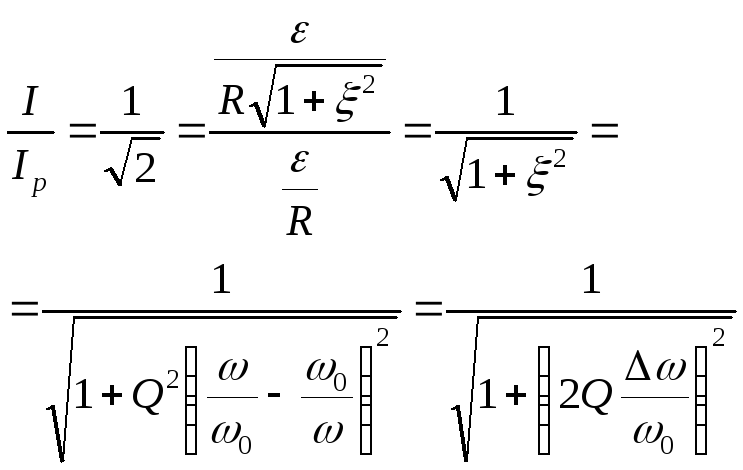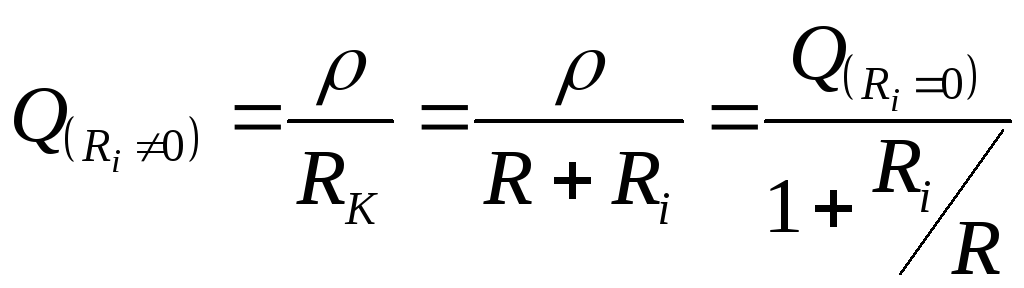Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L — индуктивность, Гн
С — емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН .
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
Последовательный
колебательный контур – это цепь,
состоящая из катушки индуктивности
(L), конденсатора (С) и активного
сопротивления (R), соединенных
последовательно относительно входных
зажимов, к которым можно подключать
генератор (рис. 1).
Рис.
1. Последовательный колебательный
контур.
Для нахождения тока
в цепи составляем уравнение второго
закона Кирхгофа для комплексных амплитуд:
где
– мнимая единица,
– входное комплексное сопротивление
контура;– активная составляющая входного
сопротивления;– реактивная составляющая входного
сопротивления.
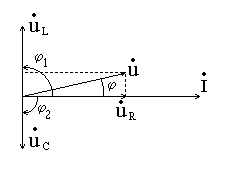
Векторная
диаграмма токов и напряжений в
последовательном контуре (рис. 2) построена
с учетом того, что напряжение на
индуктивности опережает ток по фазе на
,
а напряжение на емкости отстает от тока
на.
Рис.
2. Векторная диаграмма тока и напряжений
в последовательном колебательном
контуре.
Возможны три случая:
1),
2),
3)
,
На
рис. 2 представлена векторная диаграмма
для первого случая. Здесь
– сдвиг фаз между током в контуре и
напряжением на нем:
Особый
интерес представляет случай, когда
,
при этом.
Режим цепи, при котором,
несмотря на наличие реактивных элементов,
называется резонансом.Для
последовательного контура говорят о
резонансе напряжений, так как
.
Векторная диаграмма резонанса представлена
на рис. 3.
В
контуре с заданными
и
резонанс наступает при определенной
частоте:
;
.
В
настроенном в резонанс контуре
,
,
где
– характеристическое сопротивление
контура.
Рис.
3. Векторная диаграмма тока и напряжений
в последовательном контуре при резонансе.
Энергетические
соотношения в контуре характеризуются
величиной его добротности
,
которая равна отношению энергии,
запасенной в реактивном элементе
контура, к энергии, расходуемой за период
при резонансе, умноженному на:
Так
как
,
,
где– амплитуда тока,
– среднеквадратическое (действующее)
значение тока, а для синусоидального
тока, то
Обратная
величина добротности называется
декрементом затухания
.
Рассмотрим входное
сопротивление ненагруженного
последовательного контура:
где
– обобщенная растройка контура.
Так
как
,
,
то
Обычно
исследуют контура вблизи резонансной
частоты
,
то есть при малых расстройках частоты
(при малом уходе от резонансной частоты)
.
Тогда
.
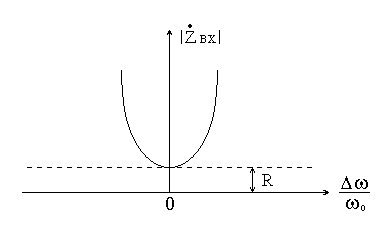
Зависимость
модуля
от расстройки представленна на рис. 4.
Рис. 4.
Ток в контуре
определяется выражением
При
резонансе ток достигает максимального
значения
.
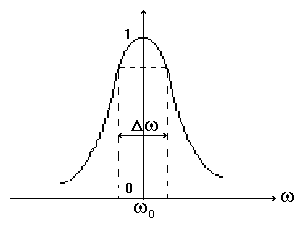
Кривая, показывающая отношение,
называется резонансной кривой контура
(рис. 5).
Рис. 5.
Для сравнения работы
последовательных контуров вводится
понятие полосы пропускания по уровню
0.7, как интервала частот
,
для которых отношение.
Считается, что эти сигналы не подавляются
контуром. Рассмотрим, как связаны
добротность контура и полоса пропускания:
или
,
отсюда,
где– полоса пропускания по уровню 0,707.
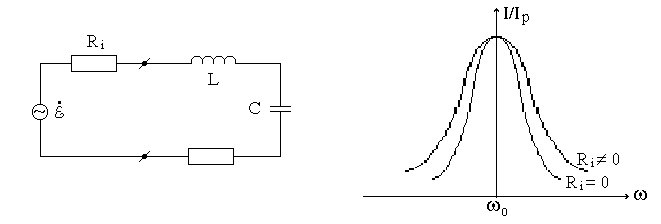
Вынужденные
колебания в контуре создаются генератором
с определенным внутренним сопротивлением
(рис. 6). Внутреннее сопротивление
генератора ухудшает избирательные
свойства контура, т.е. делает резонансную
кривую более пологой (рис. 7), т.е. уменьшает
добротность контура, т.к..
|
Рис. 6. |
Рис. 7. |
Откуда
Кривые зависимостей
напряжений на индуктивности и емкости
от частоты выглядят аналогично, по ним
так же можно определить добротность
контура.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных
параметров. Онлайн калькулятор резонансной
частоты колебательного контура,
добротности и коэффициента затухания в зависимости от величин индуктивности,
ёмкости и сопротивления потерь
Колебательный контур – это пассивная электрическая цепь, состоящая из конденсатора и катушки индуктивности, в которой
возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный
контур называется последовательным.
Для начала рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного
чаще последовательного.
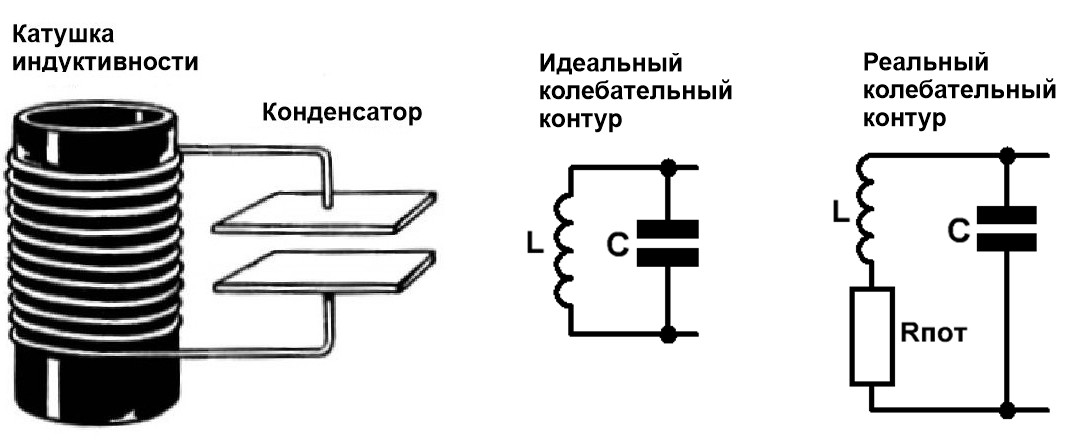
Рис.1 Параллельный колебательный контур, его изображение на схеме (идеальный
колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного
сопротивления потерь катушки – Rпот.
Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
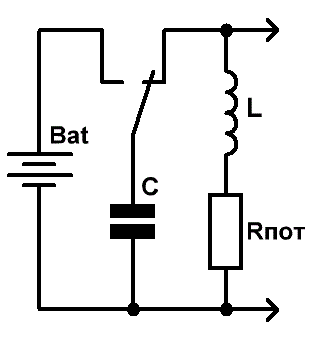
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд
qmax от внешнего источника Bat напряжением
Umax.
После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие
электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь,
суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу
колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в
еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её
измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
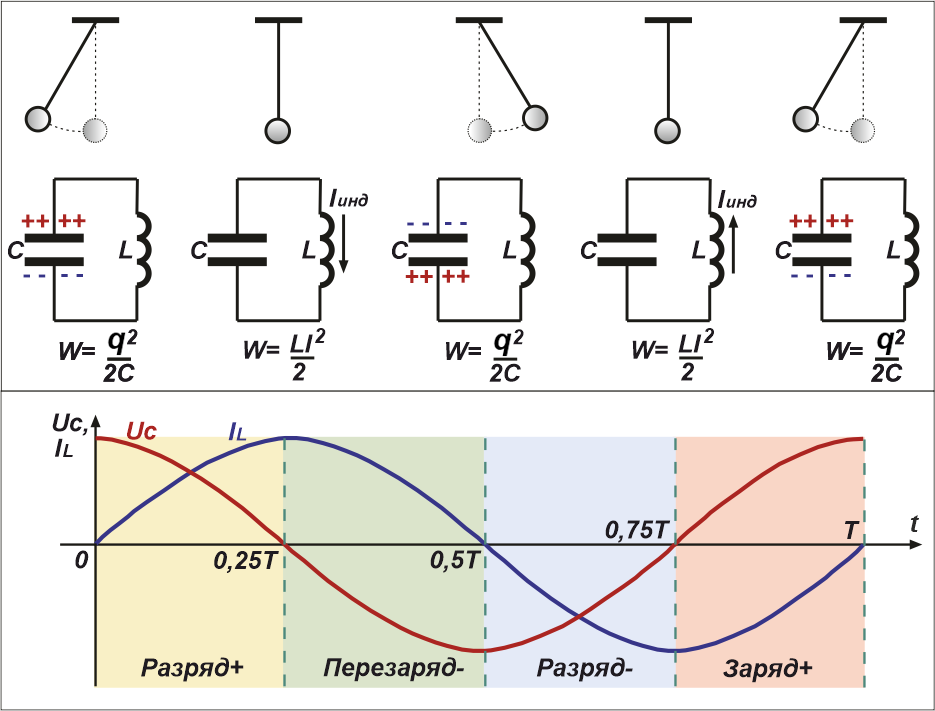
Рис.3 Фазы колебаний, происходящих в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна
W = q2/2C ).
Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС
самоиндукции, препятствующая этому росту.
2. t = 0,25Т – конденсатор полностью разряжен.
Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки
W = L*I2/2.
Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0,5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через
катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0,75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен
в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь – формулы, которые могут понадобиться при расчёте колебательного LC контура:
Период колебаний: T0 = 2π√LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 =
2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура:
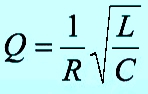
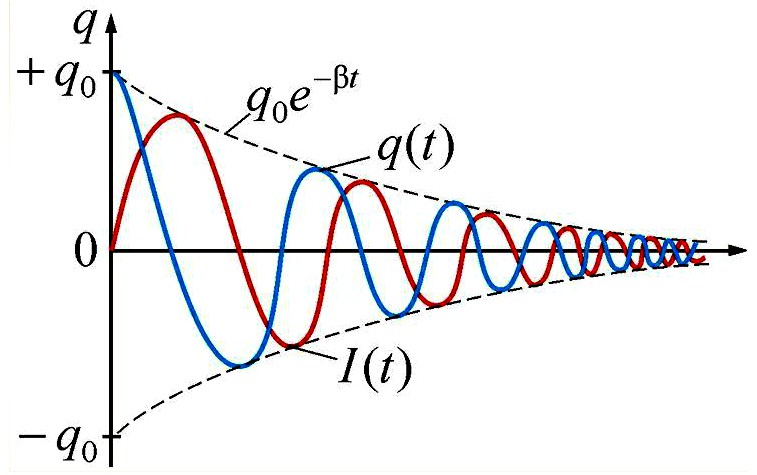
Мгновенные значения напряжения, силы тока и энергии можно рассчитать по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров
(с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания
β и логарифмический декремент колебаний λ.
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно
пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в
е раз.
Для колебательного контура данная величина вычисляется по формуле:
β = Rпотерь /(2L).
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения
двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент колебаний равен коэффициенту затухания,
умноженному на период колебаний:
λ = βT.
С учётом коэффициента затухания наши формулы приобретают следующий вид:
Заряд: q(t) = qmax cos(ωt) e(-βt) ;
Напряжение: U(t) = Umax cos(ωt) e(-βt) ;
Сила тока: I(t) = Imax sin(ωt) e(-βt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) ;
Период:
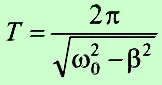
Круговая (циклическая) частота:
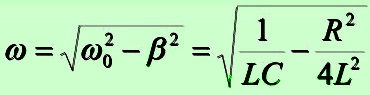
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие
β2 << ω02, круговая частота контура равна
ω ≈ ω0 ,
а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
РАСЧЁТ РЕЗОНАНСНОЙ ЧАСТОТЫ, ДОБРОТНОСТИ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОНТУРА
Ёмкость конденсатора контура |
||
Индуктивность катушки контура L |
||
Сопротивление потерь Rпот |
||
Резонансная частота |
||
Добротность = кол-во колебаний |
||
Коэффициент затухания β (сек-1) |
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые
выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и
имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.
4. Последовательный колебательный контур
4.1. Схема последовательного колебательного контура

ное напряжение сни- Рис. 4.1
мается с конденсатора
или с катушки индуктивности).
Конденсатор и катушка индуктивности имеют внутренние потери энергии, которые учитываются последовательно соединенными с ними эквивалентными сопротивлениями потерь 


Рис. 4.2
Рекомендуемые материалы
В дальнейшем будем рассматривать схему на рис. 4.2а, в которой выходное напряжение снимается с емкости, а схему
71
на рис. 4.2б аналогично рассмотрите самостоятельно.
4.2. Входное сопротивление последовательного
колебательного контура
Определим входное сопротивление последовательного колебательного контура показанного на рис. 4.3. Полное комплексное сопротивление 

Рис. 4.3 Его модуль 



Зависимости этих функций от частоты сигнала при 



реактивное сопротивление 

72
ное значение, равное 

Рис. 4.4
При отклонении частоты от 




4.3. Ток и напряжения в контуре, резонансные явления
Подключим к контуру рис. 4.2а идеальный источник гармонического напряжения, получим схему на рис. 4.5.
73


Рис. 4.5 
а для его амплитуды 



Зависимости амплитуды и начальной фазы тока от частоты при 




Рис. 4.6
74
Ток в контуре резко нарастает при приближении частоты источника к частоте 

Однако резонанс тока в последовательном колебательном контуре отсутствует, так как ток в контуре равен току источника, а не возрастает по сравнению с ним.
Так как изменения тока происходят в малой окрестности около частоты 

то есть производится смещение начала координат в точку 
Те же графики, что и на рис. 4.6, но в координатах 
Рис.4.7
Как видно, координаты абсолютной расстройки удобны для построения графиков частотных характеристик колебательного контура.
75
Определим комплексные амплитуды напряжений на элементах контура:



Тогда для амплитуд этих напряжений получим:



76
а их начальные фазы равны



На рис. 4.8 показаны зависимости амплитуд напряжений на элементах контура при 




Рис. 4.8
77
На рис. 4.8а кривые представлены в широком диапазоне частот, а на рис. 4.8б – в координатах абсолютной расстройки и узком частотном интервале в окрестности 
Как видно на частоте 


Частоты, на которых напряжения 


называют резонансной.
Точные значения резонансных частот нетрудно найти, определив производные 






Принимая резонансную частоту равной 


78

Подстановкой 

тогда резонансные напряжения на реактивных элементах одинаковы и равны

Величину

называют добротностью колебательного контура. Согласно (4.22) добротность является важнейшей характеристикой резонансных явлений.
На рис. 4.9 приведены зависимости от частоты сдвигов фаз напряжений на элементах контура относительно фазы ЭДС источника,



начальные фазы напряжений определяются из (4.15)-(4.17). Как видно, напряжение на индуктивности опережает по фазе
79
напряжение на сопротивлении на 




Рис. 4.9
4.4. Вторичные параметры колебательного контура
Последовательный колебательный контур полностью описывается своими первичными параметрами 


Резонансная частота контура

измеряется в радианах делить на секунду, или

80
которая измеряется в герцах. Ее значение сразу определяет частоту настройки колебательного контура.
Характеристическое сопротивление контура

измеряется в Омах и численно равно модулю реактивного сопротивления индуктивности или емкости (отдельно) на резонансной частоте 
Добротность контура

– величина безразмерная, характеризует резонансные свойства колебательного контура. Физический смысл добротности – это отношение максимальной энергии, накапливаемой в реактивных элементах, к энергии потерь в контуре за период колебаний на резонансной частоте.
Как видно из (2.28), добротность возрастает с уменьшением сопротивления потерь контура, которое практически полностью определяется потерями мощности сигнала в катушке индуктивности. На практике добротность 
Явление резонанса и понятие добротности используются и в механических колебательных системах. Например,
81
в кристаллах кварца (горного хрусталя) очень малы потери энергии механических колебаний, то есть они имеют высокую добротность. Поэтому изготовленные из него бокалы при слабом ударе издают продолжительный звон. В железе, алюминии или пластмассе эти потери велики, поэтому сделанные их них бокалы не обладают соответствующим звучанием.
Помимо малых потерь энергии механических колебаний монокристаллы кварца характеризуются явлением пьезоэффекта (повторите материал по физике): при возникновении в кварцевой пластине механических колебаний на ее гранях возникает переменное напряжение и наоборот, приложенное к кристаллу переменное напряжение вызывает механические колебания кристалла. Из кварцевых пластин изготавливают электронные устройства – кварцевые резонаторы. С электрической точки зрения они эквивалентны последовательному колебательному контуру с очень высокой добротностью 
4.5. Частотные характеристики контура
Под частотными характеристиками последовательного колебательного контура (рис. 4.2) понимают зависимость от частоты характеристик комплексного коэффициента передачи по напряжению вида

или

где 

82
единении индуктивности 

Рассмотрим комплексный коэффициент передачи напряжения емкости 


Из (4.31) АЧХ 



Частотные характеристики последовательного колебательного контура при 





83
на частоте 

Рис. 4.10
На рис. 4.10а приведены АЧХ в абсолютном, а на рис. 4.10б в относительном масштабах по оси ординат. На рис. 4.11 показаны ФЧХ этих контуров.

Как видно, с ростом сопротивления потерь 
84
тельном контуре максимум АЧХ падает (так как уменьшается добротность) и кривая АЧХ становится «шире», а ФЧХ – более пологой.
По форме АЧХ видно, что последовательный колебательный контур является узкополосным частотным фильтром.
4.6. Обобщенная расстройка
Исследование частотных характеристик колебательного контура удобнее всего проводить в координатах обобщенной расстройки 

Как видно, она зависит от частоты сигнала и параметров контура. Проведем преобразования

Обозначая абсолютную расстройку

85
и приближенно полагая в первой дроби 

Из (4.38) видно, что обобщенная расстройка прямо пропорциональна абсолютной расстройке, то есть частоте сигнала (начало координат смещено в точку 
4.7. Частотные характеристики в координатах обобщенной
расстройки
Комплексное входное сопротивление контура (4.1) в координатах 

а его модуль, аргумент, активную и реактивную составляющие соответственно

Эти характеристики как функции обобщенной расстройки показаны на рис. 4.12. Сплошной линией показаны точные, а пунктирной – приближенные значения, полученные из (4.40).
86
Рис. 4.12
Проведем расчет комплексного коэффициента передачи, приближенно заменив в числителе (4.31) 


Частотные характеристики последовательного колебательного контура в координатах обобщенной расстройки имеют вид


Зависимости АЧХ 

Как видно, расчеты частотных характеристик в координатах обобщенной расстройки имеют вполне удовлетворитель-
87
ную точность в достаточно широкой окрестности резонансной частоты, то есть там, где они и представляют практический интерес.
Рис. 4.13
С помощью обобщенной расстройки можно проводить расчеты токов и напряжений в контуре:




Выражения и вычисления существенно упрощаются.
Запишите самостоятельно выражения для амплитуд и начальных фаз тока и напряжений на элементах контура. Постройте их зависимости от частоты и обобщенной расстройки, оцените погрешность вычислений в координатах 
88
4.8. Полоса пропускания и коэффициент
прямоугольности
Определим полосу пропускания контура, расчет проведем в координатах обобщенной расстройки (рис. 4.14).



С учетом (4.42) урав-
нение имеет
вид Рис. 4.14

и его решения равны
Интервал обобщенной расстройки в полосе пропускания

с другой стороны из (4.38)

89
тогда получим уравнение

а полоса пропускания будет равна

Как видно, полоса пропускания контура с заданной частотой настройки 

Для определения коэффициента прямоугольности 



решения которого равны
90
Интервал величин обобщенной расстройки в полосе пропускания на уровне 1/10 от максимума равен

тогда получим уравнение

а полоса пропускания 

В результате коэффициент прямоугольности колебательного контура оказывается равным

Как видно, последовательный колебательный контур является полосовым частотным фильтром с низкой избирательностью.
4.9. Влияние внутреннего сопротивления источника
сигнала и нагрузки на резонансные свойства контура
Рассмотрим контур с подключенным реальным источником напряжения 


91
ее к уже рассмотренной цепи вида рис. 4.5 (с идеальным источником напряжения и без нагрузки) и воспользоваться уже полученными результатами анализа.
Рис. 4.15





Рис. 4.16 казано на рис. 4.16). Эти
цепи эквивалентны, если равны их полные комплексные сопротивления, тогда получим

Преобразуя дроби и приводя обе части равенства к алгебраической форме записи комплексных чисел, можно записать

92
Комплексные числа равны тогда и только тогда, когда равны отдельно их действительные и мнимые части, поэтому после алгебраических преобразований получим два уравнения для неизвестных 


Проделайте необходимые преобразования самостоятельно.
Как видно, эквивалентные параметры последовательной цепи зависят от частоты и, строго говоря, такое преобразование возможно только на фиксированной частоте. При анализе колебательного контура интерес представляет окрестность его резонансной частоты 


получим


Эти равенства является точными на частоте 


93
расстройки при 





Рис. 4.17


Рис. 4.18 ное

Контур рис. 4.18 уже изучен, его резонансные свойства определяются эквивалентной добротностью 
94

Как видно, внутреннее сопротивление источника сигнала 


Собственное сопротивление потерь 
Нагрузка контура также снижает его добротность, чем больше 



На практике величина характеристического сопротивления 

Для ослабления влияния нагрузки на добротность контура используют ее неполное включение, один из вариантов схемы показан на рис. 4.19.
95
Рис. 4.19
Проведите самостоятельно анализ этой цепи аналогично предыдущей, преобразовав параллельное соединение 

где 

Требования к сопротивлению нагрузки определяются неравенством

что значительно слабее (4.59). Например, при 


96
4.10. Расчеты цепей с последовательными
колебательными контурами
Расчет гармонических токов и напряжений в электрических цепях с колебательными контурами проводится методом комплексных амплитуд чаще всего в координатах обобщенной расстройки.









Резонансная частота
контура равна

а добротность соответственно

В координатах обобщенной расстройки 

97
сопротивление 


Сопротивление 

Вычислим общее сопротивление цепи,

в результате получим

Комплексная амплитуда тока в цепи равна
а напряжения на нагрузке соответственно

Переход к координатам обобщенной расстройки существенно упрощает расчеты цепей с колебательными контурами. При расчетах широко используют известные выражения для коэффициента передачи и других характеристик контура.
98







Резонансная частота 



тогда для обобщенной расстройки получим

Комплексный коэффициент передачи 

тогда комплексная амплитуда напряжения на емкости равна

а для его мгновенных значений получим

99
4.11. Моделирование последовательного колебательного
контура
На рис. 4.22 показана модель последовательного колебательного контура 




кривые) с шагом 50 Ом.
Рис.4.22 На рис. 4.24 пока-
заны аналогичные зависимости при 


Как видно по результатам моделирования, максимум АЧХ снижается с ростом сопротивления потерь и уменьшением сопротивления нагрузки, причем даже при большом 
На рис. 4.25 представлены результаты моделирования контура при изменении его емкости от 100пФ (правая кривая) до 200пФ (левая кривая) с шагом 50 пФ для 
Проведите расчеты, подтверждающие результаты моделирования, например, вычислите максимальные значения АЧХ при соответствующих параметрах цепи.
100
101
102
103
4.12. Применение последовательного колебательного
контура
Последовательный колебательный контур широко используется как узкополосный частотный фильтр. Таким фильтром является преселектор (предварительный селектор), который присутствует в любом супергетеродинном радиоприемнике (факультативно поинтересуйтесь у преподавателя, как работает супергетеродинный радиоприемник), его условная схема показана на рис. 4.26. Антенна приемника включена в контур как источник сигнала, а напряжение с емкости 
Рис. 4.26 кое входное сопротивление,
то используется неполное включение нагрузки. Задача преселектора – фильтрация «зеркального канала» приема в супергетеродинном приемнике.




лении потерь катушки ин-
дуктивности 
Рис. 4.27 
АЧХ и ФЧХ.
104
Рис. 4.28
Рис. 4.29
Как видно, фильтр подавляет сигнал в окрестности частоты 160 кГц. Нетрудно спроектировать такой фильтр на частоту 50 или 100 Гц, что часто необходимо в биомедицинской аппаратуре, питающейся от силовой сети переменного тока 220В с частотой 50 Гц (проведите необходимые расчеты и схемотехническое моделирование).
105
4.13. Задания для самостоятельного решения
Задание 4.1. Определите сопротивление потерь колебательного контура при 


Задание 4.2. Определите сопротивление потерь колебательного контура при полосе пропускания 

Задание 4.4. Определите полосу пропускания колебательного контура при 


Задание 4.4. Определите добротность 


Задание 4.5. Определите напряжение на катушке индуктивности контура рис. 4.30 при 





Рис. 4.30
Задание 4.6. Определите напряжение на емкости контура рис. 4.31 при 





106

сравните результаты. Рис. 4.31
Рекомендуем посмотреть лекцию “9. Районирование в экономической и социальной географии”.
Задание 4.7. Вычислите резонансные значения тока и напряжение на емкости контура при 
















Рис. 4.33
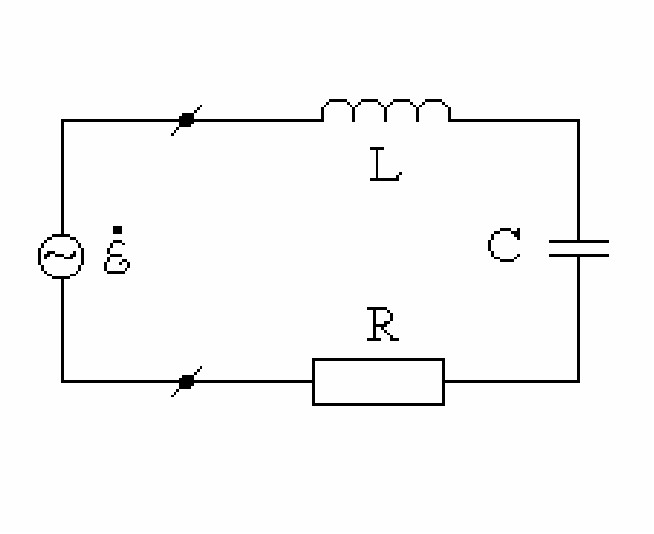
В теории цепей различают два случая резонансного контура: последовательный и параллельный. Они отличаются способом подключения внешней вынуждающей силы. В случае последовательного резонанса — это генератор напряжения, включенный последовательно в колебательный контур, а в случае параллельного тока — генератор тока подключенный параллельно.
Схема последовательного колебательного контура приведена на рисунке 1, 
[U_{R} =Icdot R, U_{L} =Lcdot frac{dI}{dt} , U_{C} =frac{Q}{C} =frac{1}{C} int I(t)dt . ]
Если задать переменное напряжение источника в виде гармонической функции с частотой $omega =2cdot pi cdot f$:
[U_{G} (t)=U_{0} cdot sin (omega cdot t), ]
то установившийся ток в цепи с линейными элементами будет также гармонической функцией с той же частотой, но, в общем случае, с другой начальной фазой $varphi $:
[I(t)=I_{0} cdot sin (omega cdot t)]
begin{equation}
U_{R} =I_{0} cdot Rcdot sin (omega cdot t)=U_{R} cdot sin (omega cdot t) (1)
end{equation}
begin{equation}
U_{L} =I_{0} cdot Lcdot omega cdot sin (omega cdot t+pi /2)=U_{L, } cdot sin (omega cdot t+pi /2)
(2)
end{equation}
begin{equation}
U_{C} =I_{0} cdot frac{1}{omega cdot C} cdot sin (omega cdot t-pi /2)=V_{C} cdot sin (omega cdot t-pi /2) (3)
end{equation}
Из полученных выражений видно, что падение напряжения на ёмкости запаздывает на четверть периода ($varphi =-90^{circ }$) относительно тока, а напряжение на индуктивности опережает ток на ту же величину ($varphi = 90^{circ }$). Кроме того, видно, что ток и напряжение на конденсаторе и индуктивности, которые называются реактивными элементами цепи, не совпадают по фазе, что отличает их от активного элемента – сопротивления, где фазы тока и напряжения совпадают. При этом напряжение на конденсаторе и индуктивности меняются в противофазе.
Второй закон Кирхгофа для рассматриваемой цепи выглядит следующим образом
begin{equation}
U_{G} =U_{R} +U_{L} +U_{C} (4)
end{equation}
Векторная диаграмма, соответствующая уравнению (4) приведена на рисунке 1. Каждый вектор представляет собой комплексное число характеризующееся амплитудой и фазой. Отметим, что вся диаграмма, как целое вращается с частотой гармонического сигнала $omega $. Наблюдаемое физическое значение напряжения или тока есть проекция соответствующего вектора на ось $Re$.
Из рассмотрения диаграммы следует соотношение для модулей векторов
[U_{0} =sqrt{U_{R} {}^{2} +(U_{L} -U_{C} )^{2} } =I_{0} cdot Z, ]
где выражение для полного сопротивления цепи $Z$
[Z=sqrt{R^{2} +left(omega cdot L-frac{1}{omega cdot C} right)^{2} } ]
получается подстановкой уравнений (1-3) в (4), а фаза $varphi $ равна
begin{equation}
varphi (omega )=arctgleft(frac{omega cdot L-frac{1}{omega cdot C} }{R} right). (5)
end{equation}
Исходя из выражений для полного сопротивления последовательного колебательного контура и используя формулы (1-3), можно определить полный ток $I_0 =frac{U_0}Z$ и амплитуды падения напряжения на элементах контура: сопротивлении, индуктивности и конденсаторе
begin{equation}
U_{{}_{R} } =frac{U_{0} cdot R}{sqrt{R^{2} +left(omega cdot L-frac{1}{omega cdot C} right)^{2} } } ,
(6)
end{equation}
begin{equation}
U_{L} =frac{U_{0} cdot Lcdot omega }{sqrt{R^{2} +left(omega cdot L-frac{1}{omega cdot C} right)^{2} } } , (7)
end{equation}
begin{equation}
U_{C} =frac{U_{0} }{Ccdot omega cdot sqrt{R^{2} +left(omega cdot L-frac{1}{omega cdot C} right)^{2} } } . (8)
end{equation}
Выражения (6-8) позволяют построить частотные зависимости напряжений на всех элементах последовательного колебательного контура, пример таких зависимостей приведён на рисунке 2.
Рис. 2. Зависимость напряжения (в вольтах) на элементах последовательного колебательного контура $R$, $L$ и $C$ от частоты для разных интервалов перестройки частоты внешнего сигнала (а, слева) $0.1cdot omega _{0} <omega <10cdot omega _{0} $, (б, в центре)- $0.5cdot omega _{0} <omega <1.5cdot omega _{0} $ (в, справа) $0.05cdot omega _{0} <omega <1.05cdot omega _{0} $. Величины напряжений $U_{L} $ и $U_{C} $ уменьшены в $Q$ раз, где добротность $Q$ определяется формулой (10). Напряжение на генераторе 1 вольт, $Q=5$.
Из рис. 2 (а) видно, что на малых частотах всё напряжение генератора падает на конденсаторе, который согласно формуле 2 (ч. I, раздел 1.2) имеет очень большое реактивное сопротивление. На больших частотах падение напряжение определяется индуктивностью (ч. I, раздел 1.3). Все резонансные кривые имеют максимум вблизи резонансной частоты, значение которой
begin{equation}
omega _{0} =frac{1}{sqrt{Lcdot C} } (9)
end{equation}
При этом оказывается, что резонанс напряжения на сопротивлении точно соответствует частоте (9), а резонансные частоты для $U_{C} $ и $U_{L} $ немного отличаются от $omega _{0} $ (см. ч. I, раздел 3.6), что заметно при точном измерении частоты при малых значения параметра $Q$ (см. рис. 2, в). Из рис. 2 (в) видно также, что максимум напряжения на сопротивлении равен напряжению источника переменного напряжения ($U_{R}^{res} =U_{G} $), а максимумы на реактивных элементах контура $C$ и $L$ превышают $U_{G} $ приблизительно на фактор добротности $Q$
begin{equation}
Q=frac{omega _{0} cdot L}{R} =frac{1}{omega _{0} cdot Rcdot C} =frac{1}{R} cdot sqrt{frac{L}{C} } =frac{rho }{R} , (10)
end{equation}
Где $rho sqrt{frac{L}{C} } $ характеристическое или волновое сопротивление контура. Собственные колебания возникают в контуре только при $Q <1.$
Оценим величину энергии, запасённой в реактивных элементах контура, используя формулы (1–3).
$$
W=frac{Lcdot I^{2} }{2} +frac{Ccdot U_{C}^{2} }{2} = (11)
$$
$$
=frac{L}{2} cdot I_{0}^{2} cdot sin (omega cdot t+varphi )^{2} +I_{0}^{2} cdot frac{1}{2cdot omega ^{2} cdot C} cdot cos (omega cdot t+varphi )^{2} $$
При резонансе ($omega =omega _{0} $) выражение (11) принимает вид
[W_{Res} =frac{L}{2} cdot I_{0}^{2} cdot left(sin (omega cdot t+varphi )^{2} +cos (omega cdot t+varphi )^{2} right)=frac{L}{2} cdot I_{0}^{2} ]
Из которого видно, что запасённая энергия попеременно сосредотачивается в конденсаторе и в индуктивности, сохраняясь постоянной при постоянной подпитке от источника напряжения. Поглощение энергии происходит в активном элементе цепи – сопротивлении. Средняя за период диссипация энергии в сопротивлении
[Delta W=leftlangle Icdot V_{R} rightrangle cdot frac{2cdot pi }{omega _{0} } =leftlangle I_{max }^{2} cdot Rcdot sin ^{2} (omega cdot t+varphi )rightrangle cdot frac{2cdot pi }{omega _{0} } =frac{I_{max }^{2} cdot R}{2} cdot frac{2cdot pi }{omega _{0} } ]
Отношение запасённой в резонансной системе энергии к потерям за период оказывается равным добротности с множителем $2cdot pi $.
Любая резонансная система характеризуется двумя экспериментально наблюдаемыми зависимостями — амплитудно-частотной (АЧХ) $I=Ileft(fright)$ и фазо–частотной (ФЧХ) $varphi =varphi left(fright)$. Для того, чтобы получить обобщенные характеристики контуров, эти характеристику строят в относительных величинах $Aleft(fright)=frac{Ileft(fright)}{I_0} $, где $I_0$ — максимальное значение тока в контуре при резонансной частоте.
Свойства амплитудно–частотной характеристики описываются выражениями 6–8 и показаны на рис. 2. Ширина резонансной кривой определяется добротностью колебательной системы. Чем выше добротность колебательной системы, тем уже резонансный пик, тем меньше относительные потери в системе. Напряжение на реактивных компонентах контура на фактор добротности $Q$ превышает напряжение на задающем источнике, что иногда приводит к разрушительным последствиям. Так при $Q=100$, напряжение на реактивных элементах $C$ и $L$ будет на два порядка больше напряжения источника, что может вызвать пробой изоляции в элементах цепи. Заметим, что при столь сильном возрастании напряжения на реактивных элементах в резонансе, эти напряжения остаются в противофазе друг с другом, поэтому суммарное падение напряжения на реактивных элементах $C$ и $L$ уменьшается при резонансе до нуля, а сопротивление всей цепи последовательного колебательного контура становится чисто резистивным и определяется только величиной $R$.
Частотная зависимость фазы тока в цепи (и напряжения $U_{R} $), определяемая формулой (5) показана на рисунке 3.
Рис. 3. Частотная зависимость разности фаз напряжения источника и тока в цепи для последовательного колебательного контура. Штриховые линии соответствуют значениям фазы $pm frac 12 pi $ Диапазон изменения частоты $0.5cdot omega _{0} <omega <1.5cdot omega _{0} $.
В низкочастотной части амплитуда тока определяется емкостью, и фаза тока опережает напряжение на четверть периода. В точке резонанса емкостные и индуктивные вклады в импеданс сравниваются и взаимно вычитаются, при этом разность фаз между током и напряжением источника равна нулю. После прохождения точки резонанса в высокочастотной части зависимости постепенно нарастает индуктивный вклад, и фаза тока стремится к чисто индуктивному запаздыванию относительно напряжения на четверть периода колебаний. При этом диапазон частот, на котором происходит перестройка от ёмкостного к индуктивному типу поведения фазы, соответствует ширине резонансной кривой на рис. 2 (б).
Изложенная выше теория колебательного контура имеет дело с идеализированными моделями физических процессов. При применении теории к эксперименту ограничения реальной аппаратуры часто требуют внесения дополнительных корректив в описание процессов. Практическая схема последовательного колебательного контура, используемого в настоящей работе, приведена на рисунке 4. Сопротивления R1 и R2 на этой схеме дополняют стандартный генератор, делая его более похожим на идеальный источник напряжения. Генераторы переменного тока, используемые в работе, не являются идеальными источниками тока или напряжения из-за того, что обладают конечным собственным внутренним сопротивлением. Внутреннее сопротивление идеального источника напряжения равно нулю, а у идеального источника тока оно равно бесконечности.
Рис. 4. Практическая схема последовательного колебательного контура.
Внутреннее сопротивление используемого в работе генератора составляет 50 Ом и является сравнимым или даже большим по отношению к характерным активным и реактивными сопротивлениям. Выход модифицированного генератора с сопротивления R2 позволяет уменьшить эквивалентное внутреннее спротивление до 2.5 ома ценой значительного уменьшения подаваемого на контур переменного напряжения. Тем не менее, при минимальном сопротивлении нагрузки, возможном в схеме и равном $R=R_{L}=4.4$ Oма, условие большой малости выходного сопротивления генератора напряжения $R2 ll R$ выполняется не достаточно хорошо и должно быть учтено при анализе результатов. Схема даёт возможность измерения напряжения непосредственно с сопротивления $R2.$ Появление сопротвления $R_L$ связано с тем, что реактивные элементы, и особенно индуктивность, не являются идеальными и обладают активными потерями. Для катушки индуктивности потери связаны с активным сопротивлнием ($R_L$) провода, которым намотана катушка. В данной схеме $R$ представляет собой минимальную величину активной нагрузки $R,$ используемой в теоретических формулах 1–11 выше, $R=(R_L+R3+R4).$ Сопротивление $R3$ переменное и служит для изменения уровня активных потерь в контуре, а $R4$ используется для измерения тока в цепи контура. Падение напряжения на активных элементах контура измерить непосредственно без изменения схемы невозможно. Это связано с тем, что внешний контакт коаксиальных разъёмов, на генераторе и осциллографе заземлён. Поэтому напряжение в точке 2 на схеме измеряется относительно земли и состоит из падения напряжения на конденсаторе $С$ и на сопротивлении $R4.$ Поскольку вкладом последнего можно пренебречь из за его относительной малости, то напряжение в точке 2 соответсвует падению напряжения на конденсаторе С. Напряжение между точками 1 и 2 может быть определено с помощью вычитания сигналов с соответствующих каналов непосредственно на осциллографе. Такая операция может быть выбрана из меню, включаемого кнопкой «math menu» на осциллографе. Сигналы, подаваемые на осциллограф с контура, особенно с сопротивления $R4,$ имеют малую величину и могут искажаться высокочастотными хаотическими шумами осциллографа, которые уширяют линии осциллограмм. Для уменьшения этого эффекта следует использовать усреднение осциллограмм, которое можно выбрать из меню, включаемого кнопкой «acquire», расположенной в верхнем ряду кнопок панели управления осциллографа. В меню вместо «sample» нужно выбрать «aver 16», принимая во внимание при этом, что реакция осциллограмы, на изменение условий в контуре, например, частоты генератора, будет в режиме усреднения осциллограмм немного замедленной.
Схема параллельного колебательного контура приведена на рис. 5. В данном случае вынужденные колебания в контуре создаются за счет источника тока подключенного параллельно колебательному контуру. Особенностью идеального источника тока является то, что он питает цепь током фиксированной амплитуды независимо от величины нагрузки, т.е. импеданса или сопротивления подсоединённой к нему цепи. При параллельном соединении элементов цепи складываются токи в разветвляющихся участках цепи, а не падения напряжения, как в случае последовательного соединения. Падение напряжение одинаково на всех элементах, соединённых параллельно, аналогично тому, как это было с током, одинаковым во всей последовательной цепи
[I_{R} =frac{U}{R} =Ucdot g, I_{C} =Ccdot frac{dU}{dt} , I_{L} =frac{1}{L} int U(t)dt . ]
Нетрудно видеть, что уравнения эти точно повторяют уравнения для последовательного резонанса, если в последних заменить ток на напряжение, сопротивление $R$ на проводимость $g=frac 1R, $ а емкость на индуктивность. Первый закон Кирхгофа для токов в параллельном контуре имеет вид:
[I_{g} =I_{R} +I_{L} +I_{C} , ]
а векторная диаграмма токов изображена на рис. 4. Ток на конденсаторе опережает ток источника на $frac 12pi$, а ток на индуктивности на столько же запаздывает относительно тока источника.
Рис. 5. Параллельный колебательный контур и векторная диаграмма токов в нем
Характерные функции для токов в параллельном контуре могут быть получены аналогично таким функциям для последовательного контура. Комплексная проводимость параллельного контура получается аналогично комплексному сопротивлению последовательного колебательного контура (см. уравнение (19) в разделе 4 настоящего сборника:
begin{equation}
Y=g-ileft(frac{1}{omega L} -omega Cright)=g-iomega Cleft(frac{omega _{0} }{omega } -frac{omega }{omega _{0} } right), (12)
end{equation}
где $omega _{0} =frac{1}{sqrt{Lcdot C} } $ частота резонанса в параллельном контуре.
Полная проводимость контура
$$
left|Yright|=sqrt{left(g^{2} +left(frac{1}{omega L} -omega Cright)^{2} right)} =sqrt{left(g^{2} +left(frac{omega _{0} }{omega } -frac{omega }{omega _{0} } right)^{2} right)} , (13)
$$
а фаза
begin{equation}
varphi (omega )=arctgfrac{omega _{0} C}{g} left(frac{omega _{0} }{omega } -frac{omega }{omega _{0} } right) . (14)
end{equation}
Частотная зависимость разности фаз приведена на рисунке 6.
Рис.6 Частотная зависимость тока источника и напряжения на параллельном контуре от частоты.
Здесь зависимость разности фаз напряжения на контуре и тока источника для низких частот носит индуктивный характер и емкостной характер на частотах, значительно превышающих резонансную частоту. Для идеального источника тока, у которого величина тока I остаётся постоянной, напряжение U($omega$) на контуре
begin{equation}
U(omega )=frac{I}{sqrt{left(g^{2} +left(frac{1}{omega L} -omega Cright)^{2} right)} } , (15)
end{equation}
а токи в ветвях контура пропорциональны их проводимостям.
begin{equation}
I_{L} (omega )=frac{I}{omega Lsqrt{left(g^{2} +left(frac{1}{omega L} -omega Cright)^{2} right)} } , (16)
end{equation}
begin{equation}
I_{R} (omega )=frac{Ig}{sqrt{left(g^{2} +left(frac{1}{omega L} -omega Cright)^{2} right)} } , (17)
end{equation}
begin{equation}
I_{C} (omega )=frac{Iomega C}{sqrt{left(g^{2} +left(frac{1}{omega L} -omega Cright)^{2} right)} } , (18)
end{equation}
Как и в случае последовательного контура, АЧХ образует острый пик на резонансной частоте, но, если в последовательном контуре наблюдается резонанс напряжений, то в параллельном контуре возникает резонанс токов. При этом добротность и острота резонансного пика в первом случае увеличиваются с уменьшением сопротивления, а во втором случае это происходит при увеличении сопротивления. Физически это понятно, поскольку сопротивление $R$, моделирует в последовательном контуре потери на элементах самого контура, и полное отсутствие потерь соответствует $R=0$. Обозначенное той же буквой сопротивление в параллельном контуре моделирует потери, вызванные внешней по отношению контура цепью, и в этом случае при отсутствии потерь $Rto infty $.
Практическая схема параллельного колебательного контура приведена на рисунке 7. 
Сигналы, подаваемые на осциллограф с этих сопротивлений, имеют малую величину и могут искажаться высокочастотными хаотическими шумами осциллографа, которые уширяют линии осциллограмм. Для уменьшения этого эффекта, как и в случае с последовательным контуром, рекомендуется использовать усреднениее осциллограмм, которое можно выбрать из меню, включаемого кнопкой «acquire», расположенной в верхнем ряду кнопок панели управления осциллографа. В меню вместо «sample» нужно выбрать «aver 16», принимая во внимание при этом, что реакция осциллограмы, на изменение условий в контуре, например, частоты генератора, будет в режиме усреднения осциллограмм немного замедленной.
-
Часть I, разделы 1.1-1.5, 2.1-2.4, 3.4$-$3.7 настоящего сборника.
-
Физическая энциклопедия, Ред. А.М. Прохоров, М., Советская энциклопедия, 1988–1998.
Назад к описаниям лабораторных работ «Электрические цепи» или далее к описанию эксперимента