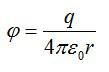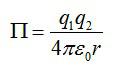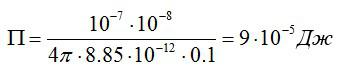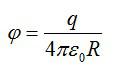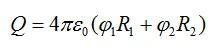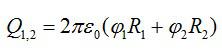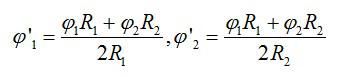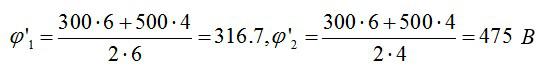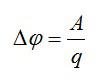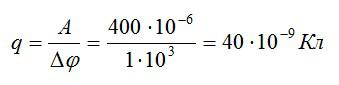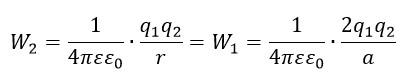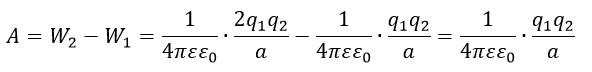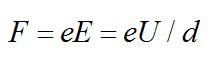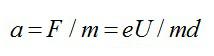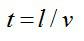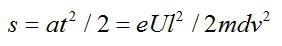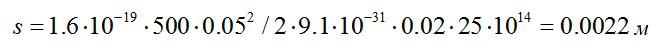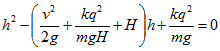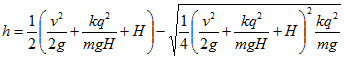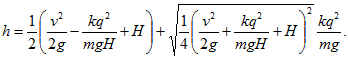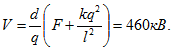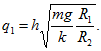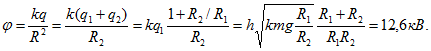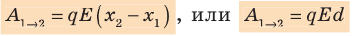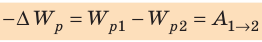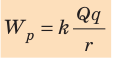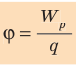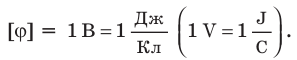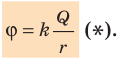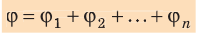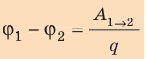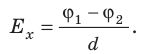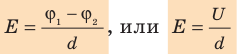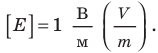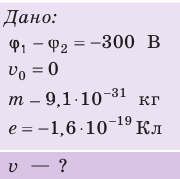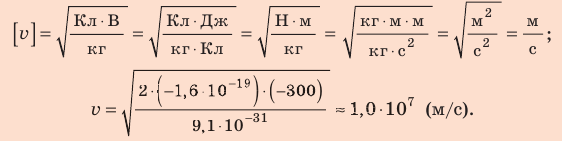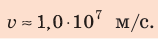Потенциал электрического поля как найти работу

Работа сил электростатического поля. Понятие потенциала

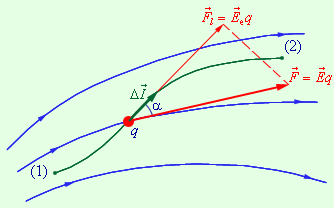
Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.

Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.

Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.

При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.

У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.

Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:

Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.

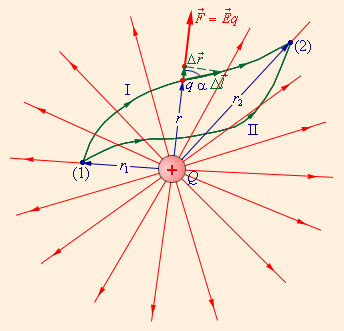
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→  на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:

∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.

Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:

A=∫r1r2E·q·dr=Qq4πε01r1-1r2.

Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.

Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.

Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.

Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.

Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.

Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:

Wp1=A10.

Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.

Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.

Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.

A12=A10+ A02= A10 – A20 =Wp1 – Wp2.

Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.

Понятие потенциала электрического поля

Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.

φ=Wpq.

Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.

A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).

Потенциал электрического поля измеряется в вольтах (В).

1 В=1 Дж1 Кл.

Разность потенциалов в формулах обычно обозначается Δφ.

Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:

Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.

φ∞=A∞q.

Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:

φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr

С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.

Изображение электрических полей с помощью эквипотенциальных поверхностей

Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.

Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.

Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.

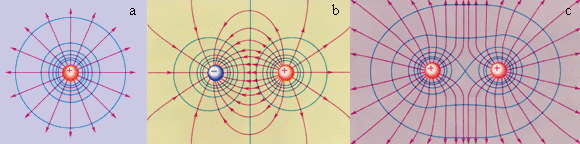
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.

Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.

Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.

В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:

ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,

где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что: 

E=-∆φ∆l, (∆l→0) или E=-dφdl.

Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.

Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:

φ=φ1+φ2+φ3+…

Физические задачи по электростатике мало кто любит. Но что поделать, решать их надо. Разберемся, как это делать по-быстрому и с использованием подробных примеров решений задач на разность потенциалов, задач на работу электрического поля и напряженность.

Наш телеграм – полезная информация для абитуриентов и студентов всех специальностей, присоединяйтесь!

Решение задач на разность потенциалов и работу поля: примеры

Задача №1 на потенциальную энергию системы зарядов

Условие

Два точечных заряда величиной 100 нКл и 10 нКл находятся на расстоянии r=10 см друг от друга. Вычислить потенциальную энергию системы этих зарядов.

Решение

Потенциал поля точечного заряда равен:

Так что, потенциальная энергия зарядов будет равна:

Подставим значения из условия и найдем:

Ответ: П=9*10^-5 Дж.

Задача №2 на определение потенциала заряженных шаров

Условие

Шар радиусом R1=6 см заряжен до потенциала 300 В , а шар радиусом R2=4 см – до потенциала 500 В. Найдите потенциал шаров после того, как их соединили металлическим проводом, емкостью которого можно пренебречь.

Решение

Потенциал шара равен:

Суммарный заряд двух шаров будет равен:

После соединения шаров заряд каждого будет равен:

Тогда суммарный потенциал шаров вычислится по формуле:

Подставим значения и найдем:  

Ответ: 317 В; 475 В.

Задача №3 на разность потенциалов и работу по перемещению заряда

Условие

Заряд переместился между двумя точками с разностью потенциалов 1 кВ, при этом поле совершило работу, равную 40 мкДж. Найдите величину заряда.

Решение

По определению, разность потенциалов равна работе по перемещению заряда, деленной на величину этого заряда:

Отсюда можно выразить заряд и вычислить ответ:

Ответ: 40 нКл.

Задача №4 на работу электрического поля по перемещению заряда

Условие

Два точечных заряда q1=6 мкКл  и  q2=2 мкКл, находятся на расстоянии а=60 см друг от друга. Какую работу необходимо свершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

Решение

Находясь на расстоянии a, точечные заряды обладали потенциальной энергией:

На вдвое меньшем расстоянии энергия зарядов равна:

Работа, затраченная на сближение зарядов:

Подставляем числовые данные и вычисляем:

Ответ: A=0,18 Дж.

Задача №5 на движение заряженной частицы в поле

Условие

Электрон влетает в плоский воздушный конденсатор параллельно его пластинам со скоростью V=5·107 м/с. Расстояние между пластинами d=2 см, разность потенциалов U=500 В. Найти отклонение электрона, вызванное полем конденсатора, если длина его пластины l=5 см.

Решение

При движении в электрическом поле конденсатора на электрон действует сила:

Ускорение электрона, по 2 закону Ньютона, определяется формулой:

Время движения электрона в конденсаторе вычислим, зная длину пластины и скорость частицы:

Отклонение электрона будет равно:

Найдем:

Ответ: 2.2 мм

Вопросы на тему «Работа электрического поля и разность потенциалов»

Вопрос 1. Что такое потенциал электрического поля?

Ответ. Потенциал – скалярная физическая величина, являющаяся энергетической характеристикой электростатического поля.

Потенциал поля равен отношению потенциальной энергии поля (или работы по перемещению заряда из данной точки на нулевой уровень потенциальной энергии) к величине заряда.

Для потенциала применим принцип суперпозиции.

Вопрос 2. Что такое разность потенциалов?

Ответ. Разность потенциалов – это работа по перемещению заряда из одной точки в другую. Разность потенциалов еще называют напряжением, обозначая его как разность потенциалов в начальной и конечной точках траектории заряда.

Вопрос 3. Что происходит с зарядом, когда он попадает в электрическое поле?

Ответ. На заряд со стороны поля действует сила, способная перемещать заряд в поле и совершать работу.

Вопрос 4. Какую природу имеет сила, действующая на заряд? Зависит ли величина работы от траектории заряда в поле?

Ответ. Сила, действующая со стороны поля на заряд, является проявлением электромагнитного взаимодействия. Величина работы поля не зависит от траектории заряда, так как это работа потенциальных (консервативных) сил.

Для наилучшего понимания сути задач на потенциал и работу поля, можно провести параллель между работой по перемещению заряда, потенциальной энергией в механике и работой силы тяжести.

Вопрос 5. Что такое эквипотенциальная поверхность?

Ответ. Это поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значения.

Какие бы задачи вы не решали и где ни учились, профессиональный образовательный сервис для студентов готов оказать помощь с проблемами по учебе любой сложности.

Работа электростатического поля

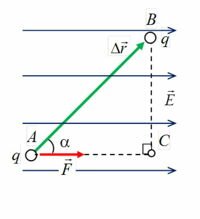
На электрические заряды в электростатическом поле действуют силы. Поэтому, если заряды перемещаются, то эти силы совершают работу. Рассчитаем работу сил однородного электростатического поля при перемещении положительного заряда q из точки A в точку B (рис. 1).

На заряд q, помещенный в однородное электрическое поле с напряженностью E, действует сила (~vec F = q cdot vec E ). Работу поля можно рассчитать по формуле

(~A_{AB} = F cdot Delta r cdot cos alpha,)

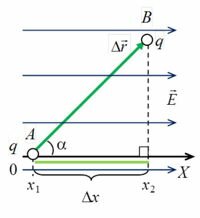
где Δr⋅cos α = AC = x₂ – x₁ = Δx — проекция перемещения на силовую линию (рис. 2).

Тогда

(~A_{AB} = q cdot E cdot Delta x. (1))

Рассмотрим теперь перемещение заряда по траектории ACB (см. рис. 1). В этом случае работа однородного поля может быть представлена как сумма работ на участках AC и CB:

(~A_{ACB} = A_{AC} + A_{CB} = q cdot E cdot Delta x + 0 = q cdot E cdot Delta x)

(на участке CB работа равна нулю, т.к. перемещение перпендикулярна силе (~vec F )). Как видно, работа поля такая же, как и при перемещении заряда по отрезку AB.

Не сложно доказать, что работа поля при перемещении заряда между точками AB по любой траектории будет находиться все по той же формуле 1.

Таким образом,

• работа по перемещению заряда в электростатическом поле не зависит от формы траектории, по которой двигался заряд q, а зависит только от начального и конечного положений заряда.
• Это утверждение справедливо и для неоднородного электростатического поля.

Найдем работу на замкнутой траектории ABCA:

(~A_{ABCA} = A_{AB} + A_{BC} + A_{CA} = q cdot E cdot Delta x + 0 – q cdot E cdot Delta x = 0.)

Поле, работа сил которого не зависит от формы траектории и на замкнутой траектории равна нулю, называется потенциальным или консервативным.

Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система “заряд — электростатическое поле” обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

(~A_{12} = -(W_{2} – W_{1}) = W_{1} – W_{2} . )

Сравнивая полученное выражение с уравнением 1, можно сделать вывод, что

(~W = -q cdot E cdot x, )

где x — координата заряда на ось 0Х, направленную вдоль силовой линии (см. рис. 1). Так как координата заряда зависит от выбора системы отсчета, то и потенциальная энергия заряда так же зависит от выбора системы отсчета.

Если W₂ = 0, то в каждой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q. Будем помещать в некоторую точку этого поля различные пробные заряды q₀. Потенциальная энергия их различна, но отношение (~dfrac{W}{q_0} = operatorname{const}) для данной точки поля и служит характеристикой поля, называемой потенциалом поля φ в данной точке.

• Потенциал электростатического поля φ в данной точке пространства — скалярная физическая величина, равная отношению потенциальной энергии W, которой обладает точечный заряд q в данной точке пространства, к величине этого заряда:

(~varphi = dfrac{W}{q} .)

Единицей потенциала в СИ является вольт (В): 1 В = 1 Дж/Кл.

• Потенциал — это энергетическая характеристика поля.

Свойства потенциала.

• Потенциал, как и потенциальная энергия заряда, зависит от выбора системы отсчета (нулевого уровня).

  В технике за нулевой потенциал выбирают потенциал поверхности Земли или проводника, соединенного с землей. Такой проводник называют заземленным.

  В физике за начало отсчета (нулевой уровень) потенциала (и потенциальной энергии) принимается любая точка, бесконечно удаленная от зарядов, создающих поле.

• На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой

(~varphi = k cdot dfrac{q}{r}.)

• Потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:

  если q > 0, то φ > 0; если q < 0, то φ < 0.

• Потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R, в точке, находящейся на расстоянии r от центра сферы

  (~varphi = k cdot dfrac{q}{R}) при r ≤ R и (~varphi = k cdot dfrac{q}{r}) при r > R .

• Принцип суперпозиции: потенциал φ поля, созданного системой зарядов, в некоторой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

(~varphi = varphi_1 + varphi_2 + varphi_3 + … = sum_{i=1}^n varphi_i .)

Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q₀ помещенного в эту точку: W₁ = q₀⋅φ. Если положить, что вторая точка находится в бесконечности, т.е. W₂ = 0, то

(~A_{1infty} = W_{1} = q_0 cdot varphi_1 .)

Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q₀ из данной точки в бесконечность. Из последней формулы имеем

(~varphi_1 = dfrac{A_{1infty}}{q_0}.)

• Физический смысл потенциала:

  потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в бесконечность.

Потенциальная энергия заряда q₀ помещенного в электростатическое поле точечного заряда q на расстоянии r от него,

(~W = k cdot dfrac{q cdot q_0}{r}.)

• Если q и q₀ — одноименные заряды, то W > 0, если q и q₀ — разные по знаку заряды, то W < 0.

• Отметим, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение W выбрано ее значение при r = ∞.

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q₀ из точки 1 в точку 2 поля

(~A_{12} = W_{1} – W_{2} .)

Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

(~W_{1} = q_0 cdot varphi_1 , W_{2} = q_0 cdot varphi_2 .)

Тогда

(~A_{12} = q_0 cdot (varphi_1 – varphi_2) .)

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

(~varphi_1 – varphi_2 = dfrac{A_{12}}{q_0} .)

• Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

• 1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ – φ₂ часто называют электрическим напряжением между данными точками поля и обозначают U:

(~U = varphi_1 – varphi_2 .)

• Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах.

• 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10^-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10^-19 Кл·1 В = 1,6·10^-19 Дж.

1 МэВ = 10⁶ эВ = 1,6·10^-13 Дж.

Разность потенциалов и напряженность

Рассчитаем работу, совершаемую силами электростатического поля при перемещении электрического заряда q₀ из точки с потенциалом φ₁ в точку с потенциалом φ₂ однородного электрического поля.

С одной стороны работа сил поля (~A = q_0 cdot (varphi_1 – varphi_2)).

С другой стороны работа по перемещению заряда q₀ в однородном электростатическом поле (~A = q_0 cdot E cdot Delta x).

Приравнивая два выражения для работы, получим:

(~q_0 cdot (varphi_1 – varphi_2) = q_0 cdot E cdot Delta x, ;; E = dfrac{varphi_1 – varphi_2}{Delta x},)

где Δx — проекция перемещения на силовую линию.

Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м).

Литература

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 228-233.
2. Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 86-95.

Решение:


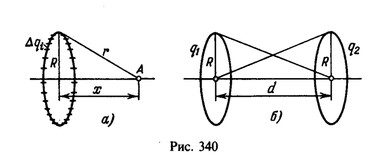
15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение:

Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:


18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:

Решая его, найдем

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение:


21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

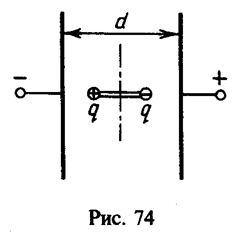
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:


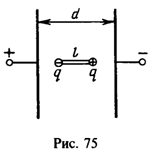
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.

Решение:


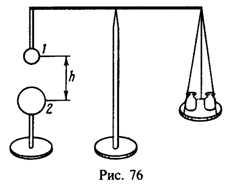
29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью

Вычислим работу А, которую совершает сила 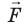, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

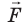
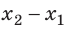
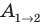
Поле однородное, поэтому сила постоянна, ее модуль равен: F=qE, а scosα=d=является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( ) равна:

Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 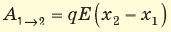будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 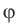электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

Единица потенциала в Си — вольт:

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 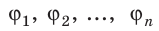полей, созданных каждым зарядом:

Как определяют разность потенциалов

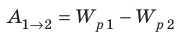
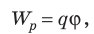
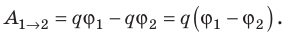
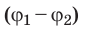
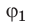
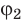
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: . Поскольку то Выражение называют разностью потенциалов, где — значение потенциала в начальной точке траектории движения заряда, — значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

Единица разности потенциалов в Си — вольт: 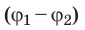= 1 В (V).

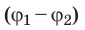
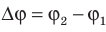
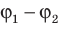
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов − также называют напряжением (U). Важно не путать изменение потенциала и разность потенциалов (напряжение) .

Как связаны напряженность однородного электростатического поля и разность потенциалов

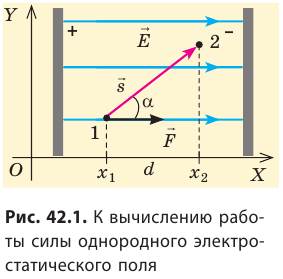
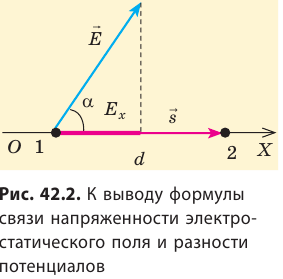
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

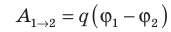
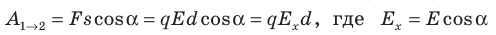
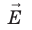
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2:; 2) через напряженность поля: — проекция вектора на ось Ох, проведенную через точки 1 и 2.

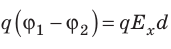
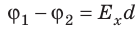
Приравняв оба выражения для работы, получим: , откуда: , или

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

Из последней формулы следует единица напряженности в Си — вольт на метр:

Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

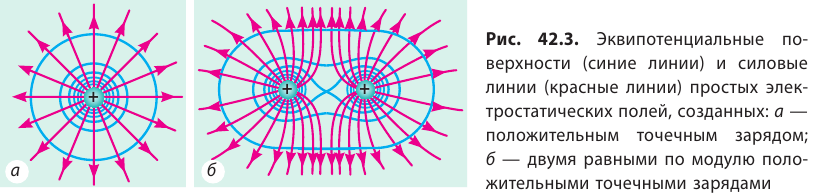
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

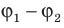
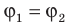
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( ), а на эквипотенциальной поверхности .

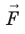
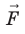
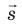
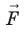
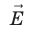
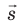
Работу электростатического поля также можно представить через силу , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами и . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы , а следовательно, и вектор напряженности поля в любой точке перпендикулярны вектору перемещения .

Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

• Заказать решение задач по физике

Пример решения задачи

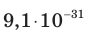
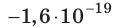
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона кг, заряд Кл.

Заряд электрона — отрицательный, его начальная скорость 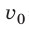= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

— работа сил поля.

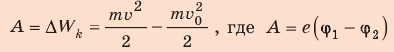
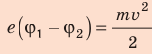
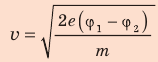
Таким образом, , отсюда .

Проверим единицу, найдем значение искомой величины:

Ответ:

Выводы: