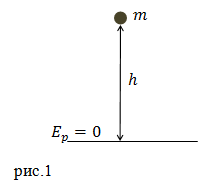Энергия является важнейшим понятием в механике. Данный термин определяет способность тела совершать работу. Универсальная количественная мера в физике характеризует движение и взаимодействие объектов. Она может быть двух типов: потенциальной и кинетической.
Потенциальная и кинетическая энергия
Потенциальной энергией называют энергию взаимодействия тел.
Определить потенциальную энергию тела можно, зная его массу, ускорение свободного падения и положение относительно земли. Формула для расчета имеет следующий вид:
E = m * g * h
В международной системе СИ потенциальная энергия обозначается буквой Е и измеряется в Дж (Джоуль).
В вышеуказанной формуле m является массой тела, h представляет собой высоту, а g – ускорением свободного падения, которое приблизительно равно 9,8 м/с2.
Величина потенциальной энергии определяется выбранной системой отсчета. Это связано с тем, что отсчет высоты можно выполнять не только относительно земной поверхности, но и от какой-то точки или определенного уровня.
Кинетической энергией называют энергию, которой обладает тело во время движения.
Кинетическая энергия служит для определения запаса энергии тела, обладающего определенной скоростью. Определить кинетическую энергию можно с помощью формулы:
(E=frac{mv^{2}}{2})
В международной системе СИ кинетическая энергия обозначается буквой Е и измеряется в Дж (Джоуль).
В уравнении m является массой тела, а v представляет собой его скорость.
Скорость тела определяется выбранной системой отсчета. Поэтому кинетическая энергия также зависит от того, каким образом рассчитывают характеристики системы, в которой движется тело.
Представленное уравнение для расчета кинетической энергии справедливо в том случае, когда рассматривают скорости, намного меньшие, чем скорость света в вакуумной среде в 300 тысяч километров в секунду. Если скорость близка к световой, то расчеты необходимо производить с учетом теории относительности, созданной Эйнштейном.
Каким законам подчиняется, формулы
Потенциальная энергия характерна не только для тела, находящегося на определенной высоте. Несколько иначе выполняют расчет потенциальной энергии упруго деформированного тела. При деформации изменяется его форма и объем, при этом объекту передается определенный запас энергии. К примеру, если растянуть пружину или, напротив, сжать ее, то такие действия меняют расстояние, на которое удалены атомы и молекулы друг от друга. Таким образом, создается потенциальная энергия.
Расчет потенциальной энергии деформированного объекта выполняют с помощью уравнения:
(E=frac{k(Delta x)^{2}}{2})
k является жесткостью пружины, (Delta x) — это изменение длины пружины.
Следует отметить, что значение потенциальной энергии пружины будет всегда положительным, так как формула содержит ее изменение в квадрате. Даже в случае, когда изменение будет иметь знак «-», потенциальная энергия в любом случае останется положительной.
Говоря об энергии, следует учитывать, что объект обладает несколькими типами энергии одновременно. К примеру, летящий на большой высоте самолет имеет запас потенциальной энергии, так как удален от поверхности земли, и кинетической энергии из-за своей скорости движения.
Ели принять земную поверхность за уровень нулевой энергии, то данное утверждение будет справедливо. В случае, когда рассматривают объект в других системах отсчета, его энергия будет отличаться.
Рассматривая качели, можно сказать, что они обладают запасом и кинетической, и потенциальной энергии. Когда конструкция максимально отклоняется от равновесного положения, энергия будет рассчитываться таким образом:
Еп = макс
Ек = 0, так как скорость имеет нулевое значение.
В момент, когда качели пересекают точку равновесного положения, энергия будет распределена следующим образом:
Ек = макс
скорость качелей в этой точке будет максимальна;
Еп = мин
высота, на которой тело находится над землей, будет минимальной.
При сложении двух видов энергии получают полную механическую энергию тела. Она включает потенциальную и кинетическую энергии.
Задачи по теме с подробными решениями
Задача 1
Самолет, масса которого составляет 50 тонн, пролетает на высоте 10 километров. Скорость транспортного средства равна 900 км/ч. Требуется рассчитать, какова полная механическая энергия самолета.
Решение
Первым шагом является перевод искомых данных, согласно системе СИ. В таком случае масса самолета составит 50 000 кг, скорость – 250 м/с, а высота – 10 000 м.
Самолет обладает запасом полной энергии, которая включает и потенциальную, и кинетическую.
E = Eп + Ек
Eп = m * g * h
Ек = m * v2 / 2
Таким образом, полная энергия составит:
(E=mtimes gtimes htimes frac{mv^{2}}{2})
Если подставить в полученную формулу числовые значения величин из условия задачи, то получим полную энергию:
(E=6.5625times 10^{9}) Дж
Если записать ответ сокращенно, то он примет такой вид:
(Е = 6,5625) Гдж.
Ответ: в рассмотренной системе отсчета значение полной механической энергии самолета составит 6.5625 Гдж.
Однако, данную задачу можно решить, принимая за нулевой уровень отметку в 10 километров. Тогда транспортное средство будет характеризоваться лишь запасом кинетической энергии, а значение потенциальной энергии будет равно нулю.
Задача 2
Пружину закрепили к стене и поместили на гладкую поверхность. На конце пружины зафиксировали тело. Растяжение пружины, которая обладает жесткостью в 400 Н/м, происходит при воздействии силы в 80 Н. Требуется рассчитать запас энергии в пружине.
Решение
Согласно условию задачи, поверхность обладает гладкостью, что позволяет сделать вывод о нулевом значении силы трения. Таким образом, потери энергии исключены. Воздействуя на пружину, можно наблюдать ее деформацию. Весь запас энергии будет сосредоточен в ней. Найти данную величину можно по формуле:
(E=frac{k(Delta x)^{2}}{2})
Сила упругости равна произведению жесткости на изменение длины пружины:
(ktimes Delta x=F)
Деформацию пружины можно рассчитать таким образом:
(Delta x=frac{F}{k})
Используя последнее равенство, можно преобразовать формулу для расчета энергии:
(E=frac{k(frac{F}{k})^{2}}{2}=frac{kF^{2}}{2k^{2}}=frac{F^{2}}{2k})
Далее следует подставить числовые значения в полученное выражение:
(E=frac{80^{2}}{2times 400}=8) Дж
Ответ: запас энергии в пружине составляет 8 Дж.
Задача 3
Масса пули составляет 9 грамм. Ее выпустили из оружия вертикально в верхнем направлении. Скорость пули при этом составила 700 м/с. Требуется рассчитать ее кинетическую энергию.
Решение
Условия задачи удобно представить в виде рисунка.
Расчет нужно выполнить по формуле:
(E=frac{mv^{2}}{2})
Перед тем, как подставить в уравнение числовые значения, требуется перевести их в систему СИ. Тогда масса пули составит 0,009 кг. Выражение будет записано следующим образом:
(E=frac{0.009times 49times 10^{4}}{2}=2200) Дж
Ответ: запас кинетической энергии пули равен 2200 Дж.
Задача 4
Масса ракеты составляет 0,2 кг. Ее выпустили из орудия вертикально вверх. После этого ракета достигла высоты в 60 метров. Требуется рассчитать значение потенциальной энергии ракеты, характерной для этой отметки.
Решение
Условие задачи можно представить с помощью рисунка.
Для того чтобы рассчитать потенциальную энергию, требуется воспользоваться формулой:
E = m * g * h
Далее необходимо подставить в выражение числовые значения:
Е = 0,2 * 9,8 * 60 = 118 Дж
Ответ: потенциальная энергия ракеты на заданной высоте составит 118 Дж.
Задача 5
Пружину растянули на 5 мм. Коэффициент ее жесткости составляет 10000 Н/м. Требуется вычислить, какова энергия пружины.
Решение
Следует представить условия задачи на рисунке.
Уравнение, с помощью которого можно рассчитать энергию пружины, имеет такой вид:
(E=frac{k(Delta x)^{2}}{2})
Далее необходимо привести к системе СИ расстояние, на которое растянули пружину. Оно составит 0,005 м.
После преобразований можно подставить числовые значения в искомую формулу:
(E=frac{10^{4}times 25times 10^{-6}}{2}=0.125) Дж
Ответ: энергия пружины составляет 0,125 Дж.
Знание основных формул для расчета кинетической, потенциальной и полной энергии тела позволит решить задачи любой сложности. Наиболее простым способом является выполнение последовательных действий, включая запись условий задачи, графическое изображение системы, представление формул для вычисления энергии, решение уравнения с помощью подстановки числовых значений. Важно отметить, что механическая энергия представляет собой сумму потенциальной и кинетической энергии.
Если в процессе поиска решений уравнений возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Потенциальная энергия, теория и онлайн калькуляторы
Потенциальная энергия
Определение
Определение
Потенциальной энергией ($E_p$) взаимодействующих тел называют энергию, которая зависит от взаимного расположения рассматриваемых тел. Работа ($A$) консервативных сил равна изменению потенциальной энергии системы тел находящихся во взаимодействии:
[A=E_{p1}-E_{p2}left(1right).]
Потенциальную энергию можно вычислить с точностью до произвольной постоянной величины. Добавляя ко всем значениям потенциальной энергии постоянную величину, получают новое значение потенциальной энергии. При таком изменении потенциальной энергии работа (1) не изменяется. Это результат можно сформулировать так: Ноль потенциальной энергии можно выбрать произвольно. При переходе к другому нулевому уровню потенциальной энергии величина потенциальной энергии изменится во всех точках на одну и ту же величину.
Когда говорят о потенциальной энергии тела, всегда следует указывать, в каком поле находится это тело (с каким телом взаимодействует).
Потенциальная энергия разных видов потенциальных сил
Потенциальная энергия упругих сил равна:
[E_{p_u}=frac{k{Delta x}^2}{2}left(2right),]
где $k$ – коэффициент упругости пружины; $Delta x$ – величина удлинения пружины. Потенциальная энергия упругих сил равна нулю,
когда пружина не деформирована $(Delta x=0).$
Потенциальная энергия сил Кулона в системе СИ равна:
[E_{p_k}=frac{q_1q_2}{4pi {varepsilon }_0r}left(3right),]
где $q_1{,q}_2$ – точечные электрические заряды; ${varepsilon }_0$ – электрическая постоянная; $r$ – расстояние между зарядами. Потенциальная энергия приближается к нулю, если расстояние между зарядами увеличивается до бесконечности. Если оба взаимодействующих заряда обладают одинаковыми знаками, то они отталкиваются, при этом потенциальная энергия больше нуля. Если заряды имеют противоположные знаки, то они притягиваются, а потенциальная энергия их взаимодействия отрицательна.
Потенциальную энергию сил гравитации находят как:
[E_{p_G}=-gamma frac{m_1m_2}{r}left(4right),]
где $gamma $ – гравитационная постоянная; $m_1;;m_2$ – массы материальных точек; $r$ – расстояние между точками. В данном случае потенциальная энергия является отрицательной величиной, так как сила гравитации – это сила притяжения. Потенциальная энергия стремится к нулю, если расстояние между массами бесконечно велико.
Потенциальная энергия тела поднятого над поверхностью Земли равна:
[E_{p_G}=гfrac{mMh}{R_Zleft(R_Z+hright)}left(5right),]
где $M$ – масса Земли; $R_Z$ – радиус Земли; $h$ – высота над поверхностью Земли, на которое поднято тело; $m$ – масса тела. Если расстояние от поверхности Земли до рассматриваемого тела невелико ($hll R_Z$), то можно использовать приближенную формулу расчета потенциальной энергии для этого тела в поле Земли:
[E_p=mgh left(6right).]
Единицей измерения потенциальной энергии в Международной системе единиц служит джоуль (Дж):
[left[E_pright]=Дж=Нcdot м=frac{кгcdot м^2}{с^2}.]
Потенциальная энергия и потенциальная сила
В общем случае потенциальная сила, которая действует на тело в некоторой точке потенциального поля и потенциальная энергия тела связывает соотношение:
[overline{F}=-gradE_p=-left(frac{partial E_p}{partial x}overline{i}+frac{partial E_p}{partial y}overline{j}+frac{partial E_p}{partial z}overline{k}right)left(7right),]
где $overline{i}, overline{j},overline{k}$ – единичные векторы (орты). Если поле сил имеет сферическую симметрию, то выражение (7) можно преобразовать к виду:
[F=-frac{dE_p}{dr}left(8right).]
Примеры задач с решением
Пример 1
Задание. При действии некоторой силы $F$ был поднят груз массой $m=10$кг на высоту $h=10$ м. Какой потенциальной силой обладает груз?
Решение. Сделаем рисунок.
Тело поднято над землей на высоту много меньшую, чем радиус Земли, значит для вычисления потенциальной энергии тела поднятого над Землей воспользуемся формулой:
[E_p=mgh left(1.1right).]
Поверхность Земли примем за ноль потенциальной энергии. Проведем вычисления потенциальной энергии нашего тела, принимая во внимание, что ускорение свободного падения равно $g=9,8 frac{м}{с^2}$:
[E_p=10cdot 9,8cdot 10=980 left(Джright).]
Ответ. $E_p=980$Дж
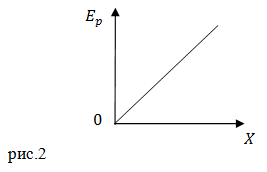
Пример 2
Задание. Материальная точка движется по оси OX в положительном направлении оси в силовом поле, потенциальная энергия которого задана графиком (рис.2). Как изменяется модуль ускорения этой материальной точки?
Решение. Потенциальная энергия задана прямой (рис.2), уравнение которой запишем как:
[E_p=alpha x left(2.1right),]
где $alpha =const$. Материальная точка движется под воздействием потенциальной силы, которая с потенциальной энергией связана выражением:
[overline{F}=-gradE_p=-left(frac{partial E_p}{partial x}overline{i}+frac{partial E_p}{partial y}overline{j}+frac{partial E_p}{partial z}overline{k}right)left(2.2right).]
Так как потенциальная энергия зависит только от координаты x, то формула (2.2) предстанет в виде:
[overline{F}=-frac{dE_p}{dx}overline{i} left(2.3right).]
Из уравнений (2.1) и (2.2), получим:
[overline{F}=-frac{d(alpha x)}{dx}overline{i}=-alpha overline{i} left(2.4right).]
Сила равна:
[overline{F}=moverline{a }left(2.5right),]
где $m$ – масса нашей материальной точки; $overline{a }$ – ее ускорение, тогда:
[moverline{a }=-alpha overline{i}to mleft|aright|=alpha to left|aright|=frac{alpha }{m}.]
Ответ. Модуль ускорения не изменяется.
Читать дальше: сила трения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Потенциальная энергия
Потенциальная энергия положения
Чтобы увеличить расстояние тела от центра Земли (поднять тело), над ним следует совершить работу. Эта работа против силы тяжести запасается в виде потенциальной энергии тела.
Если:
Wп — Потенциальная энергия тела, энергия положения (Джоуль),
G — гравитационная сила (Ньютон),
m — масса тела (кг),
h — высота на которую поднято тело (метр)
g — ускорение свободного падения 9.81 (м/c2)
то, поскольку, работа, затраченная на подъем тела Wп = Gh = mgh, потенциальная энергия тела равна:
[
W_{п} = Gh = mgh
]
Потенциальная энергия, определяемая по формуле (1), не является полной потенциальной энергией тела, а представляет собой только приращение потенциальной энергии при подъеме тела на высоту h, поскольку начало отсчета выбирается произвольно.
Вычислить, найти потенциальную энергию положения по формуле (1)
Потенциальная энергия положения на большой высоте
Формула (1) верна при условии, что ускорение свободного падения g постоянно по всей высоте подъема, т.е. в случае подъема на относительно небольшую высоту. В гравитационном поле любого небесного тела сила тяжести и соответственно ускорение свободного падения тела убывают пропорционально квадрату расстояния от центра этого тела. Поэтому при подъеме на большую высоту следует учитывать, что g = g(h) и, следовательно G = G(h):
[
W = int_{r_1}^{r_2} F dr
= int_{r_1}^{r_2} γ frac{m_a m_b}{r^2} dr
]
[
W = γ m_a m_b int_{r_1}^{r_2} frac{1}{r^2} dr
]
[
W = γ m_a m_b bigg(frac{1}{r_1} – frac{1}{r_2}bigg)
]
Здесь:
W — работа против гравитационной силы (Джоуль),
G — гравитационная сила, с которой два тела притягиваются друг к другу (Ньютон),
ma — масса первого тела (кг),
mb — масса второго тела (кг),
r — расстояние между центрами масс тел (метр),
r1 — начальное расстояние между центрами масс тел (метр),
r2 — конечное расстояние между центрами масс тел (метр),
γ — гравитационная постоянная 6.67 · 10-11
(м3/(кг · сек2)),
Вычислить, найти потенциальную энергию положения на большой высоте
Потенциальная энергия (примечания)
— Если тело опускается с высоты h, то выделяется определяемая формулами (1) и (4) энергия Wп, зависящая от расстояния, на которое опустилось тело.
— Если тело падает с высоты h, то его потенциальная энергия Wп целиком превращается в кинетическую энергию Wк (энергию движения).
Потенциальная энергия |
стр. 468 |
|---|
| Земля | 9,81 м/с² | 1,00 g | Солнце | 273,1 м/с² | 27,85 g |
| Луна | 1,62 м/с² | 0,165 g | Меркурий | 3,70 м/с² | 0,378 g |
| Венера | 8,88 м/с² | 0,906 g | Марс | 3,86 м/с² | 0,394 g |
| Юпитер | 24,79 м/с² | 2,528 g | Сатурн | 10,44 м/с² | 1,065 g |
| Уран | 8,86 м/с² | 0,903 g | Нептун | 11,09 м/с² | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с² | 0,084 ± 0,002 g | Плутон | 0,617 м/с² | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести (или, иными словами, ускорение тела при свободном падении), при исключении из рассмотрения других сил.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно округляют до 9,81, 9,8 или даже до 10 м/с².
Физическая сущность[править | править код]
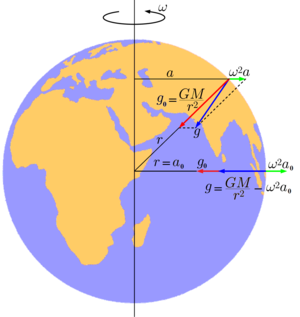
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центробежное ускорение[править | править код]
Центробежное ускорение является следствием вращения Земли вокруг своей оси. Именно центробежное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центробежное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с², причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с² | h, км | g, м/с² |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с² |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.