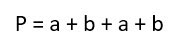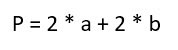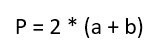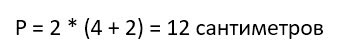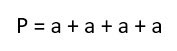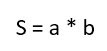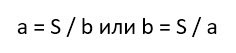Пример:
измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.
Найдём сумму длин всех сторон этого прямоугольника.
Для этого сложим все эти длины.
Получим:
(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.
Периметр — это сумма длин всех сторон фигуры.
Значит,
складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.
Периметр обозначается заглавной латинской буквой (Р).
Итак,
периметр прямоугольника (Р = 12) см.
Найдём периметр треугольника.
Сначала измерим стороны треугольника.
Длины сторон треугольника равны (4) см, (3) см, (6) см.
Значит,
сумма длин всех сторон треугольника, т. е. периметр треугольника
равен:
(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.
Дан квадрат, длина стороны которого равна (4) см.
У квадрата все стороны равны.
Периметр квадрата равен сумме длин всех сторон квадрата.
Получим:
(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.
Если у треугольника все стороны равны, такой треугольник называется равносторонний.
Для определения периметра данного треугольника найдём сумму длин всех его сторон.
Получим:
(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.
Источники:
Рис. 1. Прямоугольник. © ЯКласс
Рис. 2. Треугольник. © ЯКласс
Рис. 3. Квадрат. © ЯКласс
Рис. 4. Равносторонний треугольник. © ЯКласс
Математика, 2 класс. Урок № 49
Периметр прямоугольника
Перечень вопросов, рассматриваемых в теме:
Изучение правила вычисления периметра прямоугольника.
Глоссарий по теме:
Прямоугольник – четырёхугольник, у которого все углы прямые.
Периметр – сумма длины всех сторон плоской фигуры.
Основная и дополнительная литература по теме урока:
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –
8-е изд. – М.: Просвещение, 2017. – с.16.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова –
7-е изд., дораб. – М.: Просвещение, 2016. – с.22.
Открытые электронные ресурсы по теме урока:
Интересные факты о математике. Познай мир. URL:
https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/ (дата обращения: 18.08.2018)
Теоретический материал для самостоятельного изучения
Прямоугольные предметы окружают нас повсюду.
Рамки, телефоны, тетради и многое другое.
Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны.
Рассмотрим следующую задачу: «Вокруг дачного участка необходимо поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится?»
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.
длина

длина
У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров.
Составим выражение для подсчета длины забора. Это первый способ вычислений: 5 + 10 + 5 + 10
Воспользуемся переместительным законом сложения:
5 + 10 + 5 + 10 = 5 + 5 + 10 + 10
В данном выражении есть суммы одинаковых слагаемых
5 + 5 и 10 + 10
В этой записи рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно заменить умножением. Это второй способ вычислений:
5 + 5 + 10 + 10 = 5 · 2 + 10 · 2
Теперь воспользуемся распределительным законом умножения относительно сложения. Это третий способ вычислений: 5 · 2 + 10 · 2 = (5 + 10) · 2
Этот способ можно назвать рациональным, то есть, наиболее удобным и коротким, потому что в нём меньше действий, чем в предыдущих способах.
Найдём значение выражения (5 + 10) · 2
Сначала выполняем действие в скобках: 5 + 10 = 15
А затем повторяем число 15 два раза: 15 · 2 = 30.
Ответ: 30 метров забор вокруг участка.
Забор вокруг участка – это периметр этого участка. Периметр прямоугольника – сумма длин всех его сторон.
Делаем вывод: периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.
Тренировочные задания.
1. Решите задачу: Длина листа картона 4 см. Ширина 3 см. Вычислите периметр данного листа. Запишите решение тремя способами.
Правильный ответ:
1 способ. 4+3+4+3=14 (см)
2 способ. 4 · 2+ 3·2=14 (см)
3 способ. (4+3) ·2=14 (см)
Ответ: 14 сантиметров периметр листа картона.
2. Выберите верное решение:
Длина прямоугольника 5 см, ширина 3 см. Чему равен периметр прямоугольника?
А) 8 см Б) 13 см В) 16 см
Правильный ответ В) 16 см
По какой формуле высчитывают периметр прямоугольника?
Анонимный вопрос
2 ноября 2018 · 156,0 K
Мне интересны множество тем: от психологии до космоса…) · 2 нояб 2018
Периметр фигуры – это сумма длин ее сторон. Для простотого прямоугольника подойдет формула:
P=2*(a+b), a и b -длины прилегающих сторон прямоугольника.
Для правильного прямоугольника (квадрат), у которого все стороны равны, формулу можно упростить до:
P=4*a, где a – длина стороны квадрата.
90,0 K
Спасибо, Выручили! А то формулу подзабыла.
Комментировать ответ…Комментировать…
Не перестаю узнавать новое. Люблю путешествия и все с этим связанное. Много лет работаю в… · 2 нояб 2018
Периметр прямоугольника равен сумме длин его сторон. А так как у прямоугольника противоположные стороны равны, то периметр можно найти по формуле:
P=2(a+b), где a и b – стороны прямоугольника.
17,5 K
Комментировать ответ…Комментировать…
Начнем с того, что периметр прямоугольника можно посчитать по разным формулам.
Самая известная формула периметра прямоугольника: P = a * b, где P – периметр, a и b – длины двух смежных сторон прямоугольника.
Смотри на картинку ниже.
Кроме того, зная площадь прямоугольника и длину одной из сторон прямоугольника, можно также найти периметр. Это менее известная формула… Читать далее
1,4 K
Комментировать ответ…Комментировать…
Периметр высчитывают сложением(как нас раньше учили),а площадь умножением; Р=а+а+а+а: а площадь S=4*а. Вот и все вроде бы как это и есть правильная формула
11,3 K
А как найти формулу периметра прямоугольного параллелепипеда???
Комментировать ответ…Комментировать…
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Периметр многоугольника
Любой многоугольник – это замкнутая ломаная линия.
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
Значит, периметр многоугольника – это сумма длин всех его сторон.
В математике периметр обозначают буквой P (пэ).
Периметр прямоугольника
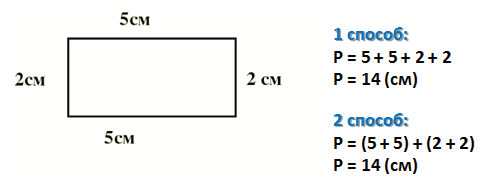
Например, найдём периметр данного прямоугольника.
1 способ:
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
2 способ:
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
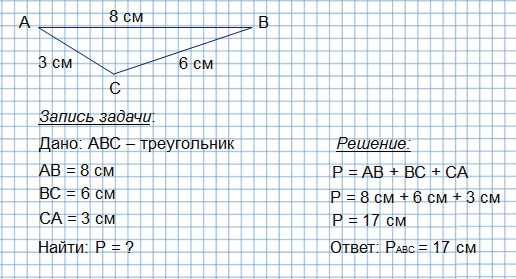
Периметр треугольника
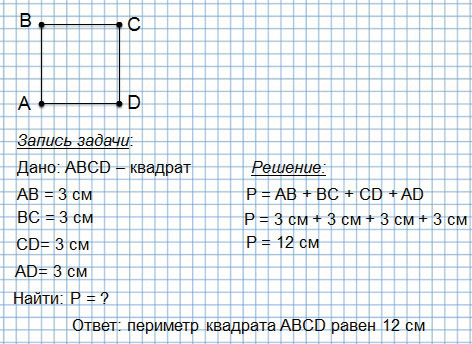
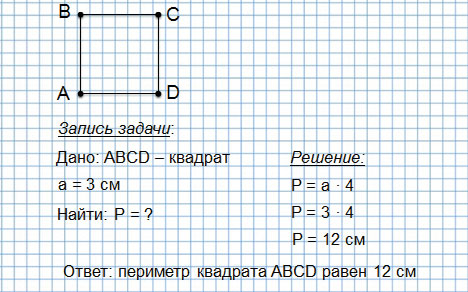
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
1 класс
Страница 4. Урок 3,
Петерсон, Учебник, часть 3
Страница 5. Урок 3,
Петерсон, Учебник, часть 3
Страница 87. Урок 44,
Петерсон, Учебник, часть 3
2 класс
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 65,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63. Урок 25,
Петерсон, Учебник, часть 2
Страница 85. Урок 35,
Петерсон, Учебник, часть 2
3 класс
Страница 16,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 43. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70. Урок 24,
Петерсон, Учебник, часть 1
Страница 88. Урок 38,
Петерсон, Учебник, часть 2
Страница 91. Урок 40,
Петерсон, Учебник, часть 2
Страница 20. Урок 9,
Петерсон, Учебник, часть 3
4 класс
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 43,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 56,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 80. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 207,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 208,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 210,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Задание 389,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
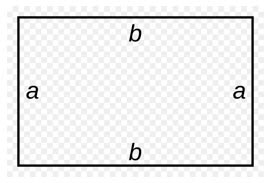
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
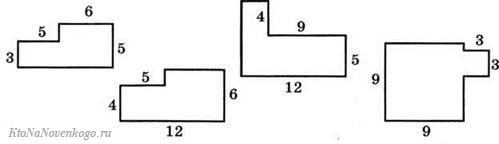
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.