Задача
В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.
Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2
Треугольник OKN — прямоугольный, OK — высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как α .
tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°
Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.
Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как β ) равен
tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°
Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°
Двугранные углы пирамиды и методика их расчета
Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.
Пространственная фигура пирамида
Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.
 Вам будет интересно: Популяция людей: определение, виды, свойства и примеры
Вам будет интересно: Популяция людей: определение, виды, свойства и примеры
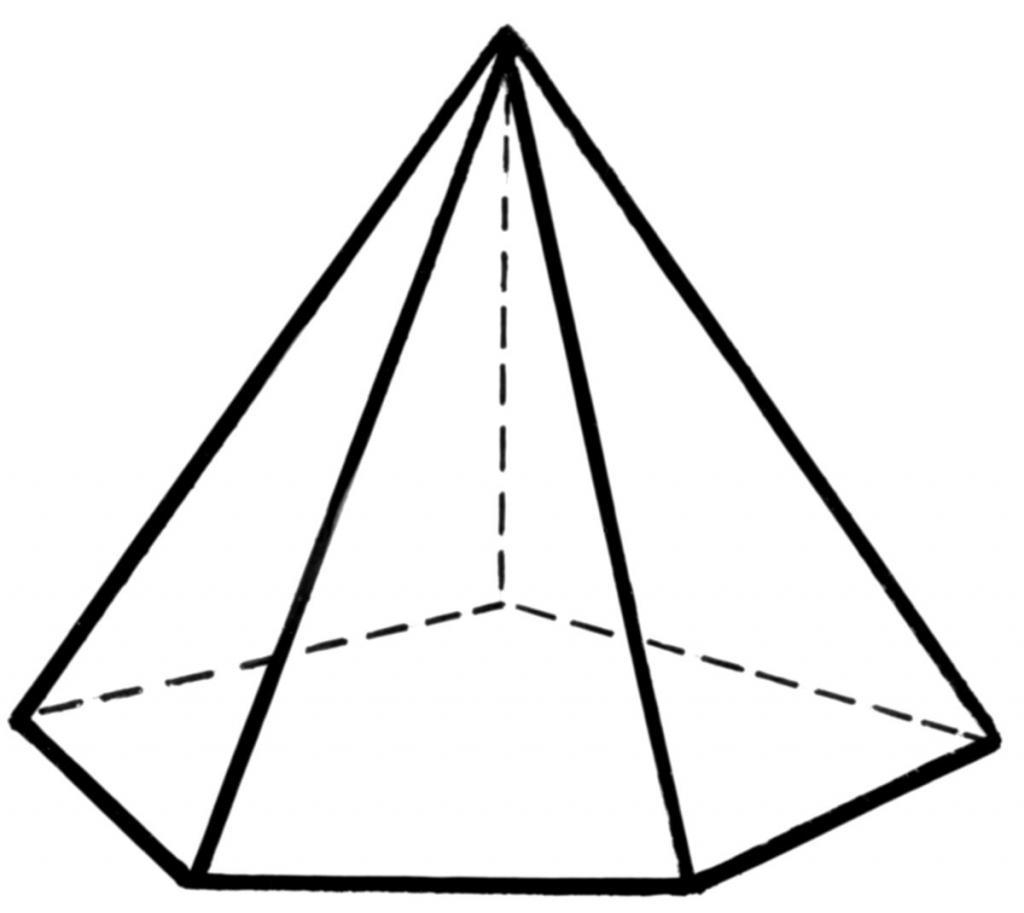
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.
Двугранные углы фигуры
 Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?
Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?
Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.
Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:
- При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
- Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.
Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.
Как рассчитать углы пирамиды?
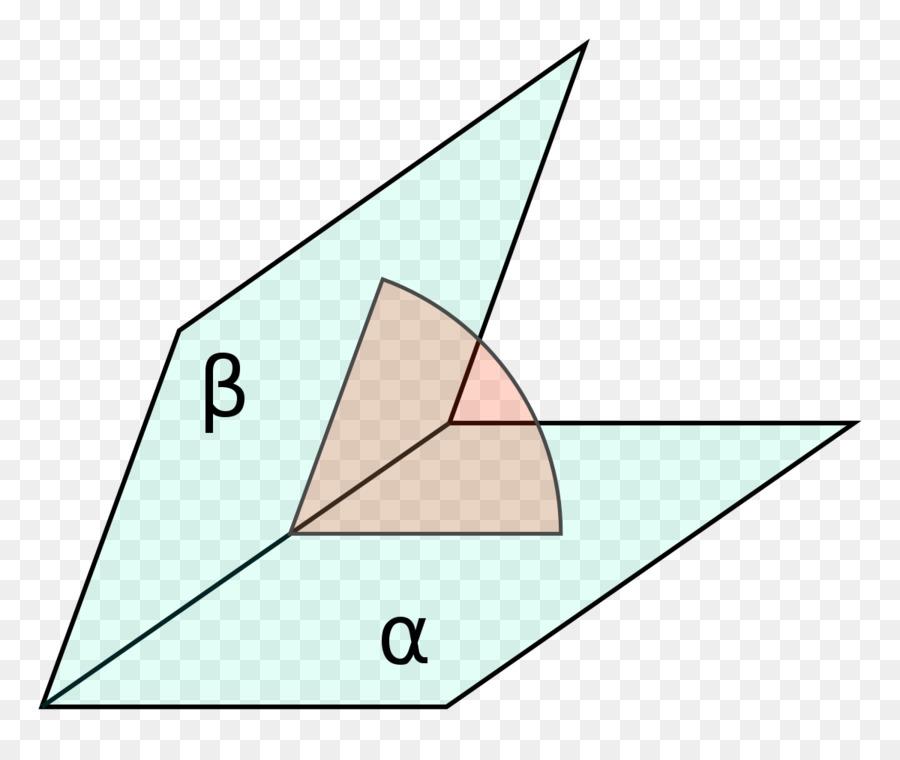
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.
В трехмерном пространстве плоскость задается следующим выражением:
A*x + B*y + C*z + D = 0
Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:
Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.
Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:
Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:
Или в координатной форме:
φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))
Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.
Углы правильной пирамиды четырехугольной
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.
Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.
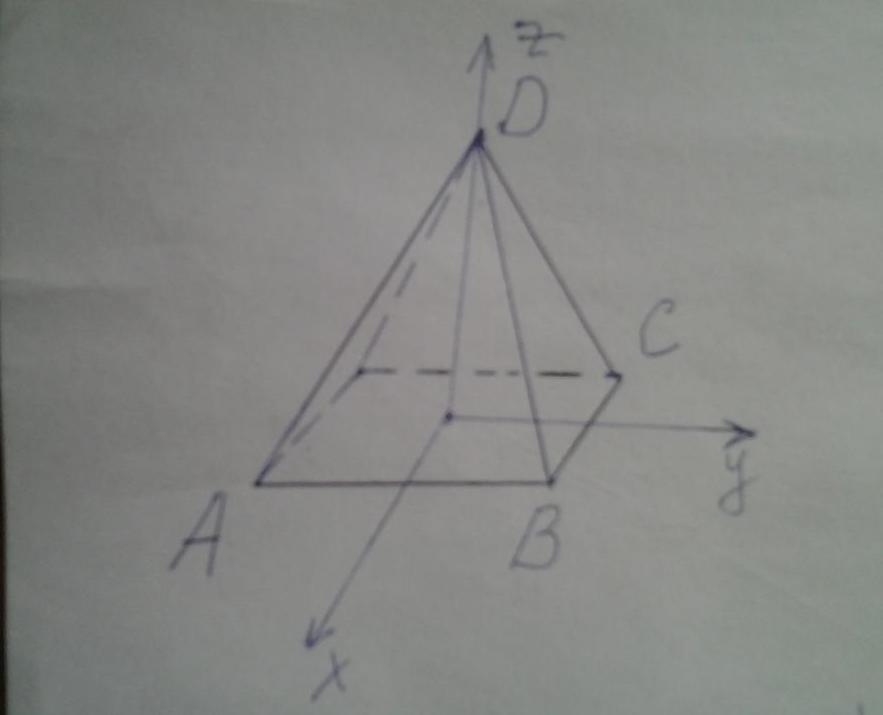
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:
Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:
Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:
Угол между ABC и ABD:
Угол между ABD и BDC:
φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o
Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.
Углы треугольной правильной пирамиды
На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.
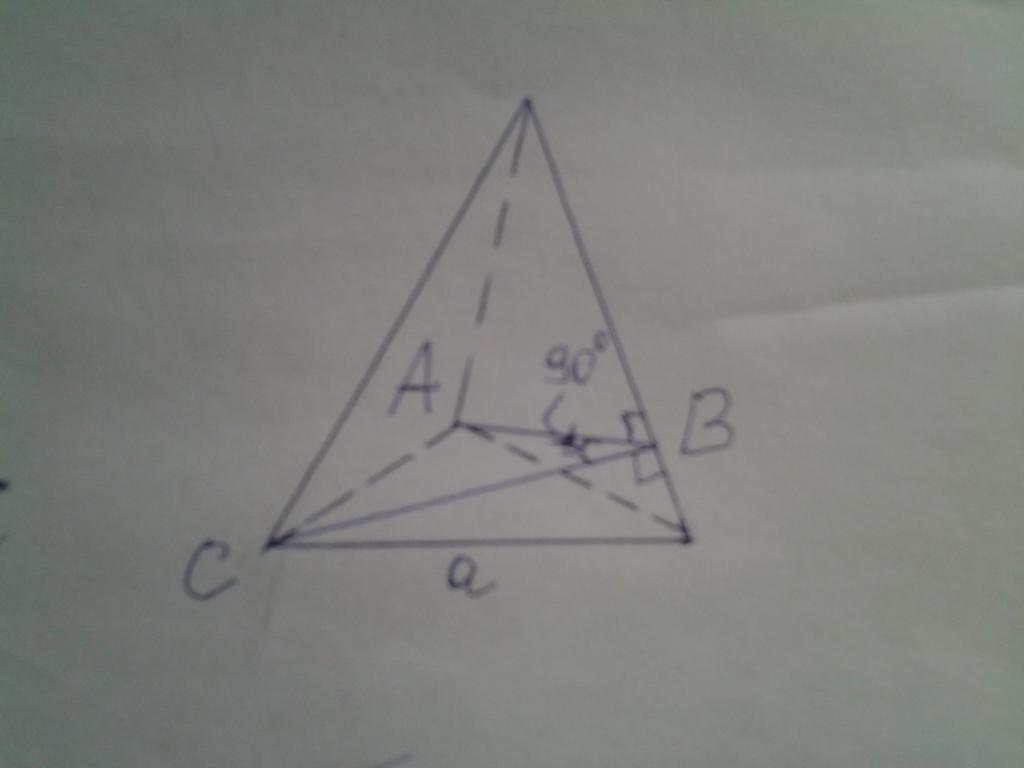
Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — hb и боковое ребро — b. Теперь можно записать следующие формулы:
Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:
Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:
Площадь равностороннего треугольника рассчитывается так:
Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.
Пирамида и ее элементы
Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.
Рассмотрим плоскость  , многоугольник
, многоугольник  , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки
, лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки  называются боковыми ребрами.
называются боковыми ребрами.  Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.
Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания. 
Пирамида называется правильной, если  правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.
правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.
Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства  следует совпадение центра P многоугольника
следует совпадение центра P многоугольника  с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.
с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.
Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно. 
Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA 
Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.
Формула объема пирамиды:
1)  -высота пирамиды
-высота пирамиды
2)  – радиус вписанного шара, а
– радиус вписанного шара, а  – площадь полной поверхности пирамиды.
– площадь полной поверхности пирамиды.
3)  – площадь параллелограмма, образованного серединами четырех оставшихся ребер.
– площадь параллелограмма, образованного серединами четырех оставшихся ребер.
Свойство основания высоты пирамиды:
 Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням
Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.
 Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте
Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны  все проекции боковых ребер будет равны
все проекции боковых ребер будет равны  P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.
P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.
Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней  .
.
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле  , где p — полупериметр основания, а SK-апофема.
, где p — полупериметр основания, а SK-апофема.
Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.
Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.
Колпаков Александр,
репетитор по математике в Москве. Строгино
Примечание. Это урок с решениями задачам по геометрии (раздел стереометрия, пирамида с четырехугольником в основании). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача
В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.
Решение.
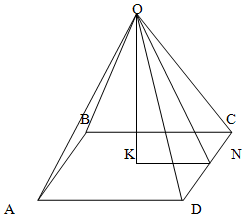
Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это – квадрат. Поскольку высота пирамиды проецируется в центр основания, то это – точка пересечения диагоналей. Откуда KN = а/2
Треугольник OKN – прямоугольный, OK – высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как
α.
tg
α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°
Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.
Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как
β ) равен
tg
β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°
Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°
0
Правильная пирамида с четырехугольником в основании (часть 3) |
Описание курса
| Нахождение величины наклона боковых граней правильной прамиды
.
Пирамида. Правильная пирамида.
Определение.
Пирамидой
называется многогранник, одна грань
которого – произвольный многоугольник
(основание), а все остальные грани
(боковые) – треугольники, имеющие общую
вершину (вершина пирамиды).
|
Определение. M MO MOABC MO∩ |
M
A B O D C четырехугольная |
Определение.
Пирамида называется правильной,
если её основание – правильный
многоугольник и высота пирамиды проходит
через центр этого многоугольника.
Определение.
Высота боковой грани правильной пирамиды,
проведённая из её вершины, называется
апофемой.
|
Правильная МО МК МКО МАО DMC |
A B D C K M
О |
|
Правильная АВС Если |
M
B
A1 C1
A C B1 О |
Для
решения задач полезно знать.
Для
правильной пирамиды справедливы
следующие утверждения:
– боковые
рёбра равны между собой;
– боковые
рёбра одинаково наклонены к плоскости
основания;
– боковые
грани – равные друг другу равнобедренные
треугольники;
– боковые
грани одинаково наклонены к плоскости
основания (т.е. все двугранные углы при
рёбрах основания равны);
– апофемы
равны;
– плоские
углы при вершине равны.
Для
пирамиды, все боковые рёбра которой
равны между собой, справедливы следующие
утверждения:
– все
боковые рёбра одинаково наклонены к
плоскости основания;
– около
основания можно описать окружность,
вершина пирамиды проецируется в центр
этой окружности;
– около
такой пирамиды можно описать шар, центр
которого лежит на прямой, содержащей
высоту пирамиды.
Для
пирамиды, все двугранные углы при рёбрах
основания которой равны между собой,
справедливы следующие утверждения:
– в
основание можно вписать окружность,
вершина пирамиды проецируется в центр
этой окружности;
– в
такую пирамиду можно вписать шар, центр
которого лежит на высоте пирамиды.
.
Усечённая пирамида.
|
Определение. |
B1
A1 C1
B
A C усеченная |
Определение.
Усечённая пирамида называется правильной,
если она получена сечением правильной
пирамиды плоскостью, параллельной
основанию. Боковые грани правильной
усечённой пирамиды – равнобедренные
трапеции, а её основания – правильные,
подобные друг другу многоугольники.
.
Объём и площадь поверхности пирамиды.
|
Пирамида |
|
|
полная |
усечённая |
|
V
Для
|
V
Для
|
Здесь
S1
и
S2
– площади нижнего и верхнего оснований,
P
– периметр основания, P1
и P2
– периметры нижнего и верхнего оснований,
h
– апофема.
|
Вопросы |
-
Найдите
объём пирамиды с высотой H,
если:
а)
H
= 2 м, а основанием служит квадрат со
стороной 3 м;
б)
H=
2,2 м, а основанием служит треугольник
АВС, в котором АВ = 20 см, ВС = 13,5 см, угол
АВС равен 30°.
-
Найдите
объём правильной треугольной пирамиды,
высота которой равна 12 см, а сторона
основания равна 13 см. -
Для
молока из картона склеен пакет, имеющий
форму правильного тетраэдра с ребром
10 см. Найдите площадь потраченного
картона. -
Молоко
планируют разливать в пакеты, имеющие
форму прямоугольного параллелепипеда
с высотой 20 см и квадратным основанием,
сторона которого 7 см, и в пакеты, имеющие
форму правильного тетраэдра с ребром
15 см. Укажите, в какие пакеты входит
больше молока. -
Найдите
объём правильной четырёхугольной
пирамиды, все рёбра которой 2. -
Рассматривается
четырёхугольная пирамида MABCD
такая, что в основании её лежит квадрат
со стороной 2, а её высота MA
равна 3. Найдите площадь поверхности
этой пирамиды. -
Вычислите
площадь боковой поверхности правильной
треугольной пирамиды, если её высота
равна 9, апофема – 18. -
В
правильной шестиугольной пирамиде
апофема равна 15, высота – 12. Найдите
площадь полной поверхности пирамиды. -
Пусть
KMNLP
и
ABCDA1B1C1D1
соответственно
правильная четырёхугольная пирамида
и правильная призма, имеющие равные
высоты длины 1 и равные стороны оснований
длины 2. Сравните их объёмы и площади
полных поверхностей. -
Пирамида
равновелика кубу с ребром 1 и основанием
её является грань куба. Найдите её
высоту. -
Рассматривается
куб ABCDA1B1C1D1
с ребром 1. Назовите какую-либо пирамиду
с вершинами в вершинах куба, такую, что
её объём равен: а)
 ;
;
б)
 .
. -
Площадь
основания пирамиды SABC
равна 4 см², а высота – 2 см. Через середину
высоты проведено сечение MNK,
параллельное основанию. Найдите:
а)
объём пирамиды SABC;
б)
объём пирамиды SMNK;
в)
объём тела ABCMNK,
ограниченного основанием пирамиды и
плоскостью MNK
(усечённой пирамиды).
-
Рассматривается
правильная треугольная пирамида MABC,
сторона основания которой равна 4, а
угол наклона плоскости боковой грани
MAB
к плоскости основания равен 60°. Пусть
MO
– высота пирамиды, точка K
– середина ребра AB.
Найдите:
а)
длину отрезка OK;
б)
длину высоты MO;
в)
площадь основания ABC;
г)
объём пирамиды MABC.
-
Найдите
объём треугольной пирамиды MABC,
если:
а)
все плоские углы с вершиной А прямые и
AM
= AB
= AC
= 1 см;
б)
АВС – правильный треугольник со стороной
2 см, а ребро МА равно 3 см и наклонено к
плоскости основания под углом 30°;
в)
АВС – равнобедренный треугольник со
сторонами АВ = ВС = 2 см и углом АВС = 120°,
грань МАВ имеет площадь, равную 4 см², и
перпендикулярна основанию АВС;
г)
АВС – прямоугольный треугольник,
гипотенуза АВ которого равна 13 см, а
катет АС = 12 см, вершина М проектируется
в середину гипотенузы АВ, грань МАС
образует с основанием угол 45°;
д)
она является правильной пирамидой,
ребро основания которой равно 2 см, а
боковое ребро наклонено к плоскости
основания под углом 45°;
е)
она является правильным тетраэдром,
все рёбра которого равны 1.
-
Все
рёбра правильной четырёхугольной
пирамиды SABCD
равны а.
Найдите:
а)
плоский угол при вершине S;
600
б)
угол ACS;
в)
высоту пирамиды;
г)
угол наклона бокового ребра к основанию;
д)
угол наклона боковых граней к основанию.
-
Высота
правильной треугольной пирамиды SABC
равна 3 а
а
высота её основания равна 9. Найдите:
а)
боковое
ребро;
б)
апофему;
в)
сторону
основания;
г)
плоский
угол при вершине S;
д)
угол
наклона боковой грани к основанию.
-
Высота
правильной четырехугольной пирамиды
SABCD
равна h,
а сторона основания равна а.
Найдите:
а)
диагональ
основания;
б)
боковое
ребро;
в)
апофему;
г)
расстояние
от точки пересечения диагоналей основания
O
до плоскости боковой грани;
д)
расстояние
от вершины A
до плоскости SCD.
-
Сторона
основания правильной шестиугольной
пирамиды равна 2 ,
,
высота пирамиды равна 4. Найдите:
а)
боковое
ребро;
б)
высоту
основания пирамиды;
в)
апофему;
г)
расстояние
от центра основания O
до плоскости боковой грани;
д)
расстояние
от вершины A
до плоскости BSC.
-
Все
боковые рёбра пирамиды равны 10, а радиус
окружности, описанной около её основания,
равен 8. Найдите высоту пирамиды.
-
Найдите
объём четырёхугольной пирамиды MABCD,
если ABCD
– квадрат со стороной 4 и вершина М
проецируется:
а)
в точку А,
а МВ
= 5;
б)
в точку В
и ребро МА
наклонено к плоскости основания под
углом 45°;
в)
в точку С
и грань MAB
наклонена к плоскости основания под
углом 30°.
-
Найдите
площадь боковой поверхности правильной
треугольной пирамиды MABC,
если:
а)
MA
= 5, AB
= 6;
б)
AB
= 2, а высота пирамиды MO
=
1;
в)
AB
= 2 и медиана боковой грани (апофемы) MK
наклонена
к плоскости основания под углом 300;
г)
высота MO
равна
3, а плоскость боковой грани MAB
наклонена
к плоскости основания ABC
под углом 450.
-
Основанием
пирамиды является параллелограмм,
стороны которого равны 20 см и 36 см, а
площадь равна 360 см². Высота пирамиды
проходит через точку пересечения
диагоналей основания и равна 12 см.
Найдите площадь боковой поверхности
пирамиды. -
Основанием
пирамиды является параллелограмм со
сторонами 5 м и 4 м и меньшей диагональю
3 м. Высота пирамиды проходит через
точку пересечения диагоналей основания
и равна 2 м. Найдите площадь полной
поверхности пирамиды. -
Основанием
пирамиды является квадрат, одно из
боковых рёбер перпендикулярно к
плоскости основания. Плоскость боковой
грани, не проходящей через высоту
пирамиды, наклонена к плоскости основания
под углом 45°. Наибольшее боковое ребро
равно 12 см. Найдите: а) высоту пирамиды;
б) площадь боковой поверхности пирамиды. -
Основанием
пирамиды DABC
является треугольник АВС, у которого
АВ = АС = 13 см, ВС = 10 см; ребро AD
перпендикулярно к плоскости основания
и равно 9 см. Найдите площадь боковой
поверхности пирамиды. -
Основанием
пирамиды DABC
является прямоугольный треугольник
АВС, у которого гипотенуза АВ равна 29
см, катет АС равен 21 см. Ребро DA
перпендикулярно к плоскости основания
и равно 20 см. Найдите площадь боковой
поверхности пирамиды. -
Основанием
пирамиды является прямоугольник,
диагональ которого равна 8 см. Плоскости
двух боковых граней перпендикулярны
к плоскости основания, а две другие
боковые грани образуют с основанием
углы 30° и 45°. Найдите площадь поверхности
пирамиды. -
Основание
пирамиды – квадрат со стороной 16 см,
две боковые грани перпендикулярны
плоскости основания. Вычислите площадь
полной поверхности пирамиды, если её
высота равна 12 см. -
Основанием
пирамиды является треугольник со
сторонами 12 см, 10 см и 10 см. Каждая боковая
грань наклонена к основанию под углом
45°. Найдите площадь боковой поверхности
пирамиды. -
Основание
пирамиды – прямоугольный треугольник,
катеты которого равны 3 и 4. Каждая
боковая грань наклонена к плоскости
основания под углом 60°. Найдите площадь
полной поверхности пирамиды. -
Основание
пирамиды – ромб с диагоналями, равными
6 м и 8 м. Высота равна 1 м. Вычислите
площадь полной поверхности пирамиды,
если все двугранные углы при основании
равны. -
Основанием
пирамиды является ромб со стороной 6
см. Каждый из двугранных углов при
основании равен 45°. Найдите объём
пирамиды, если её высота равна 1,5 см. -
Основание
пирамиды – ромб со стороной 15 см, каждая
грань пирамиды наклонена к основанию
под углом 45°. Найдите объём пирамиды,
если площадь её боковой поверхности
равна 300 см². -
Основание
пирамиды – равнобедренная трапеция,
у которой параллельные стороны составляют
3 см и 5 см, а боковая сторона – 7 см.
Высота пирамиды проходит через точку
пересечения диагоналей основания, а
большее боковое ребро равно 10 см. Найдите
объём пирамиды. -
Основание
пирамиды – прямоугольник, площадь
которого равна 1 м². Две боковые грани
перпендикулярны основанию, а две другие
наклонены к нему под углами 30° и 60°.
Найдите объём пирамиды. -
Основание
пирамиды – прямоугольный треугольник
с катетом a
и прилежащим к нему углом 30°. Боковые
рёбра наклонены к плоскости основания
под углом 60°. Найдите объём пирамиды. -
Основание
четырёхугольной пирамиды – прямоугольник
с диагональю b
и углом α между диагоналями. Боковые
рёбра наклонены к плоскости основания
под одним и тем же углом. Найдите этот
угол, если объём пирамиды равен V. -
Найдите
объём треугольной пирамиды SABC,
если:
а)
угол САВ
равен 90°, ВС
= c,
угол АВС
равен φ и каждое боковое ребро составляет
с плоскостью основания угол θ;
б)
АВ
=
12 см, ВС
= СА
= 10 см и двугранные углы при основании
равны 45°;
в)
боковые рёбра попарно перпендикулярны
и имеют длины а,
b
и с.
-
Основанием
пирамиды является прямоугольный
треугольник с катетами a
и b.
Каждое её боковое ребро наклонено к
плоскости основания под углом φ. Найдите
объём пирамиды. -
Объём
правильной пирамиды MABC
равен 2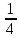
см³. Основание АВС пирамиды – правильный
треугольник со стороной 3 см. Найдите
угол наклона к основанию бокового ребра
МА. -
Объясните,
какой должна быть длина ребра правильного
тетраэдра, чтобы его площадь полной
поверхности была равна 4 см2. -
Основаниями
усечённой пирамиды являются правильные
треугольники со сторонами 5 см и 3 см.
Одно из боковых рёбер перпендикулярно
к плоскости основания и равно 1 см.
Найдите площадь боковой поверхности
усечённой пирамиды. -
В
правильной четырёхугольной усечённой
пирамиде стороны оснований равны 24 см
и 8 см, высота – 15 см. Вычислите площадь
полной поверхности пирамиды. -
В
правильной четырёхугольной усечённой
пирамиде площади оснований равны 25 см²
и 9 см², боковое ребро образует с
плоскостью нижнего основания угол 45°.
Вычислите площадь боковой поверхности
пирамиды. -
Найдите
объём правильной треугольной пирамиды
с боковым ребром l,
если:
а)
боковое ребро составляет с плоскостью
основания угол φ;
б)
боковое ребро составляет с прилежащей
стороной основания угол α;
в)
плоский угол при вершине равен β.
-
В
правильной треугольной пирамиде плоский
угол при вершине равен φ, а сторона
основания равна а. Найдите объём
пирамиды. -
Найдите
объём правильной четырёхугольной
пирамиды, если:
а)
её высота равна H,
а двугранный угол при основании равен
β;
б)
сторона основания равна m,
а плоский угол при вершине равен α.
-
Боковое
ребро правильной четырёхугольной
пирамиды равно m
и составляет с плоскостью основания
угол φ. Найдите объём пирамиды. -
Найдите
объём пирамиды и площадь боковой
поверхности правильной шестиугольной
пирамиды, если её боковое ребро равно
13 см, а диаметр круга, вписанного в
основание, равен 6 см.
Соседние файлы в папке 23-11-2015_20-04-52
- #
- #
Геометрические фигуры. Правильная пирамида.
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.

Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:

Боковое ребро правильной пирамиды находят по формуле:

где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Правильная треугольная пирамида.

Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:

Еще одним частным случаем правильно пирамиды является тетраэдр.
Источник
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
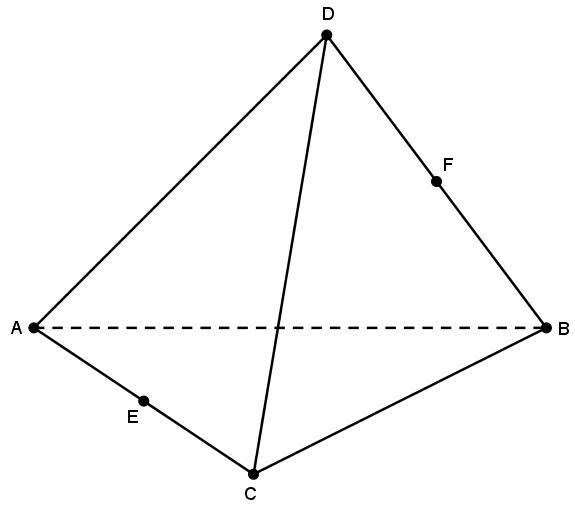
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
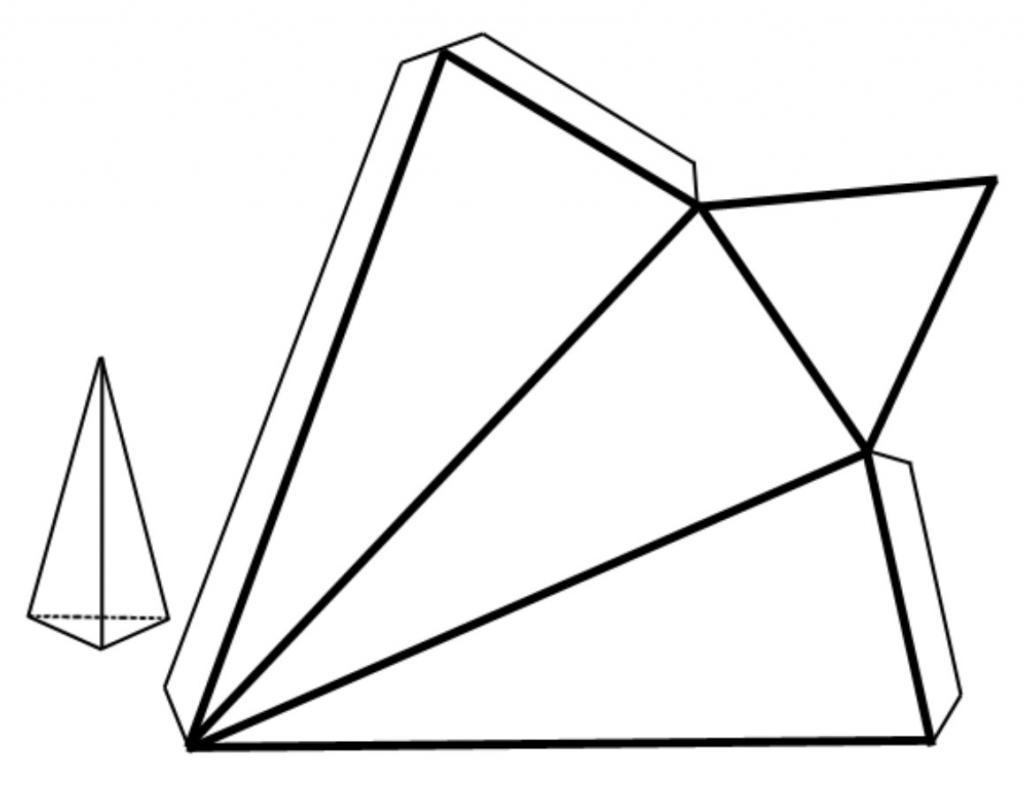
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
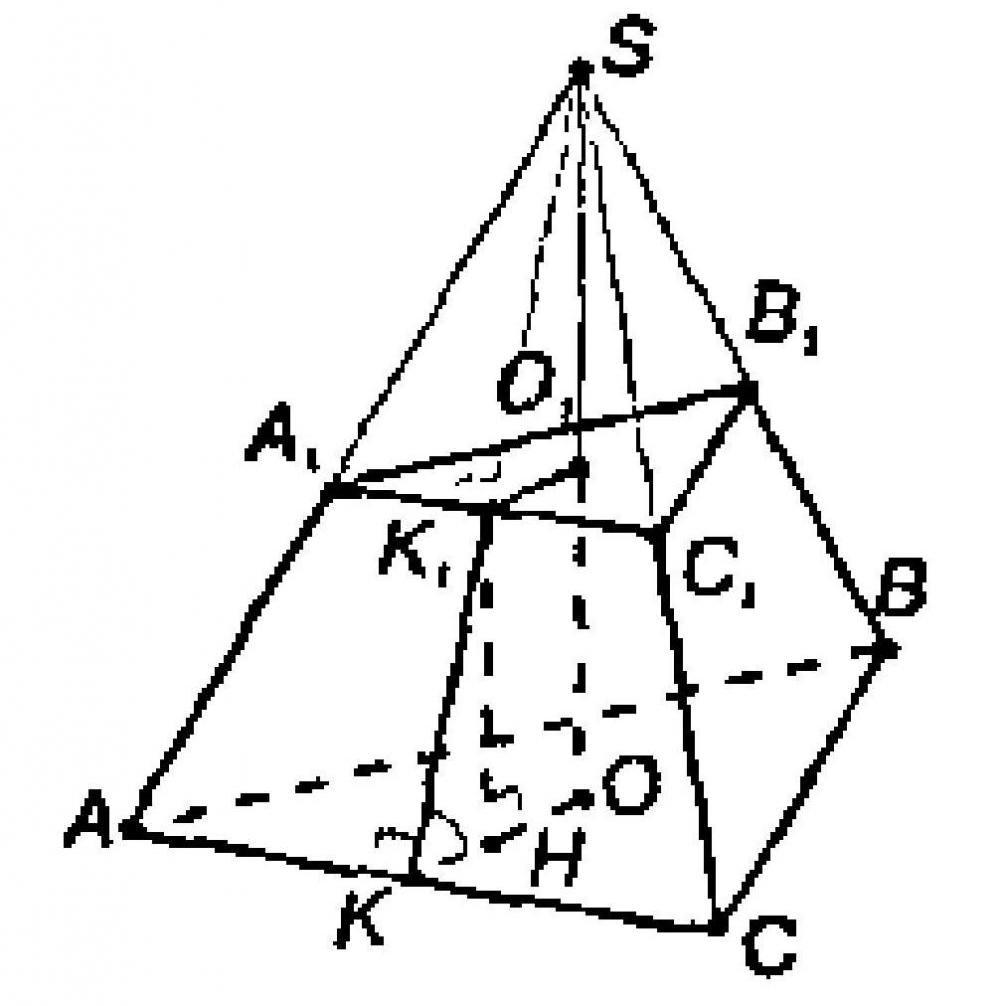
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Источник
Чему равны углы в правильной треугольной пирамиде

|
|||
|

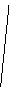






































 h
h















 — двугранный угол при основании пирамиды.
— двугранный угол при основании пирамиды.


