В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
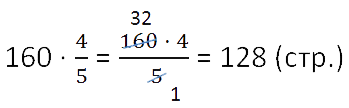
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
Начнем с довольно простой, но в то же время интересной темы, в которой школьники зачастую делают ошибки – нахождение дроби от числа.
Что такое часть от целого? Если у нас есть некоторое значение и нам необходимо вычислить некоторую долю или дробь от этого значения. Например, зная вес пиццы, найти вес нескольких ее кусочков.
При этом нужная доля может быть выражена как в виде обыкновенной дроби, так и в виде десятичной дроби или процентов. Для нахождения процента от числа стоит предварительно перевести проценты в десятичную дробь, просто разделив на 100. Например, 28 % = 0,28.
Для того, чтобы найти, сколько весят x кусочков пиццы, порезанной на равные y кусков, нужно общий вес пиццы разделить на y и умножить на x. Допустим, пицца весит Q грамм. То есть нам необходимо найти вес x/y части пиццы.
Немного парадоксальная ситуация: нужно найти часть, а мы умножаем, а не делим. Но на самом деле никакого парадокса в этом нет, если вспомнить, что дробь, вернее, горизонтальная черта дроби – это деление.
Да и при умножении на десятичную дробь меньше 1 мы тоже получим значение меньшее, чем исходное.
Немного запутать может ситуация, когда целая часть выражена в виде обыкновенной или десятичной дроби. Не стоит обращать на это внимание. Алгоритм действий точно такой же.
Рассмотрим еще несколько примеров.
Для закрепления материала предлагаем несколько примеров для самостоятельного решения. Ответы размещайте в комментариях.
Надеемся, эта тема была вам интересна. Если что-то осталось непонятным, задавайте вопросы в комментариях.
Завтра разберемся, как найти число, если нам известна только его часть.
Ставим лайки, подписываемся, в комментариях пишем темы, которые вам хотелось бы разобрать, задаем вопросы.
До скорой встречи!
Содержание материала
- Правильная и неправильная дробь
- Видео
- Дроби
- Нахождение части от целого (дроби от числа)
- Вычитание дробей
- Нахождение целого числа по дроби
- Как перевести десятичную дробь в обыкновенную или смешанную
- Применение нахождения дроби от числа для решения задач
- Нахождение числа по значению дроби
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Дроби
Дроби вида $frac{n}{m}$ называют «обыкновенные дроби». В дроби $frac{n}{m}$ число над чертой называют числителем дроби, а число под чертой – знаменателем дроби.
Знаменатель показывает, на сколько долей делят, а числитель — сколько таких долей взято.
Таким образом, если нам нужно обозначить не один «кусочек» числа, а больше, мы просто пишем в верхней части дроби не единицу, а другое число, например, так:
Дроби нужно уметь читать правильно: числитель читается как количественное числительное женского рода (одна, две и т.д.), а знаменатель как порядковое числительное (вторая, пятая) и согласуется с первым числительным.Например: $frac{1}{2}$ — одна вторая, $frac{2}{5}$ — две пятых, $frac{6}{11}$ — шесть одиннадцатых.
На рисунке 6 изображён отрезок АВ, его длина 10 см, то есть 1 дм. Длина отрезка АС будет 1 см.
А какую долю составит сантиметр от метра?
Показать ответ
Скрыть
$frac{1}{100}$
А грамм от килограмма?
Показать ответ
Скрыть
$frac{1}{1000}$
Видео
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 
длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби 
. Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби 
. Известно, что 
длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 
это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби 
это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
от всего числа. Найдите это число.
Знаменатель дроби 
показывает, что число, которое мы должны найти, разделено на пять частей. Если 
этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти 
(одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби 
20 : 4 = 5
Мы нашли 
от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби 
5 × 5 = 25
Мы нашли 
от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби 
показывает, что общее время приготовления каши разделено на три части. Если 
времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
времени приготовления. Для этого 10 нужно разделить на числитель дроби 
10 мин : 2 = 5 мин
Мы нашли 
времени приготовления каши. 
времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби 
показывает, что общая масса мешка разделена на четыре части. Если 
массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби 
.
30кг : 2 = 15кг
Мы нашли 
массы мешка. 
массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби 
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Применение нахождения дроби от числа для решения задач
В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.
Задача 1
Остап зарабатывает 40 000 рублей в месяц.
Из них (mathbf{frac{1}{4}}) это подработка.
Сколько рублей Остапу приносит подработка?
Решение:
В данной случае числом будет являться сумма заработка за месяц — 40 000
Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).
Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.
(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})
Ответ: 10 000 рублей.
Теперь рассмотрим что-нибудь посложнее.
Задача 2
Порфирий живет в комнате площадью 18 квадратных метров.
3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.
Какую площадь занимает одна кровать?
Решение:
Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.
1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати
2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать
Ответ: 2 квадратных метра.
Теперь посмотрим, как в задачах применяются проценты.
Задача 3
Пересвет работает на заводе и производит 100 деталей в день.
Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.
Сколько деталей в день должен делать Пересвет, чтобы получить премию?
Решение:
Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.
Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% — это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.
1) (mathbf{20%=20div100=0.2})
2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить
Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.
3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии
Ответ: 120 деталей.
В некоторых задачах нужно несколько раз применять нахождение процентов от числа.
Задача 4
Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.
Решение:
Исходное число- 10 метров, дробь задана в виде процентов.
Первым действием нужно будет найти глубину реки в начале июня.
Здесь можно пойти двумя разными путями:
I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.
0) (mathbf{10%=10div100=0.1})
1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня
II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.
Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.
0) (mathbf{100-10=90}) (процентов) останется
1) (mathbf{90%=90div100=0.9})
2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня
Как мы видим, эти два подхода дают одинаковый результат.
Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.
Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.
Используем в этом случае второй способ.
3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня
4) (mathbf{85%=85div100=0.85})
5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля
Ответ: 7.65 метра.
Пройти тест Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации Вход Регистрация
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
m = m : a / b
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет2 / 5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :2 / 5
= 20 ⋅5 / 2
=20 ⋅ 5 / 2
= 50
Теги
Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, 
от пиццы это половина пиццы:
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:
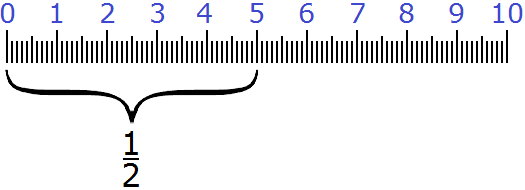
Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.
Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.
Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.
Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12.
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:
Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби
Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2
10 см : 2 = 5 см
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:
5 см × 1 = 5 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:
Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.
Пример 2. Найти 
от 10 см.
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Сначала делим 10 сантиметров на знаменатель дроби
10 см : 5 = 2 см
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
2 см × 2 = 4 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют четыре сантиметра.
Весь процесс решения можно увидеть на следующем рисунке:
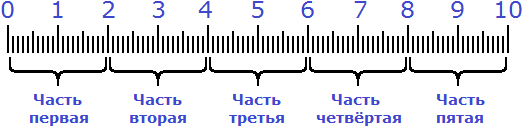
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
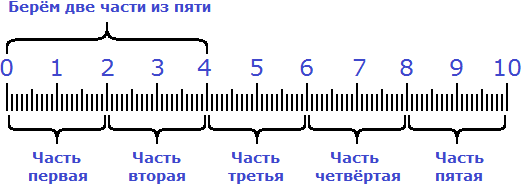
Пример 3. Найти 
от числа 56.
Чтобы найти от числа 56, нужно это число разделить на знаменатель дроби 
, и полученный результат умножить на числитель дроби .
Итак, сначала делим число 56 на знаменатель дроби
56 : 8 = 7
Теперь умножаем полученное результат на числитель дроби
7 × 3 = 21
Получили ответ 21. Значит от числа 56 составляет 21.
Пример 4. Найти 
Один час это 60 минут. Задание можно понимать, как нахождение
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит
Пример 5. Найти 
от одного метра.
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит от одного метра составляют 80 см.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
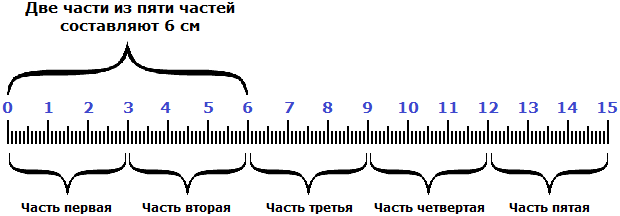
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
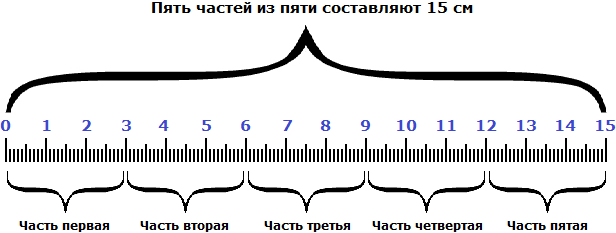
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
Знаменатель дроби 
времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:
И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:
А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:
Забавно, но дробь 
это ответ к нашей задаче. Каждому другу достанется яблока. Почему так произошло?
Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:
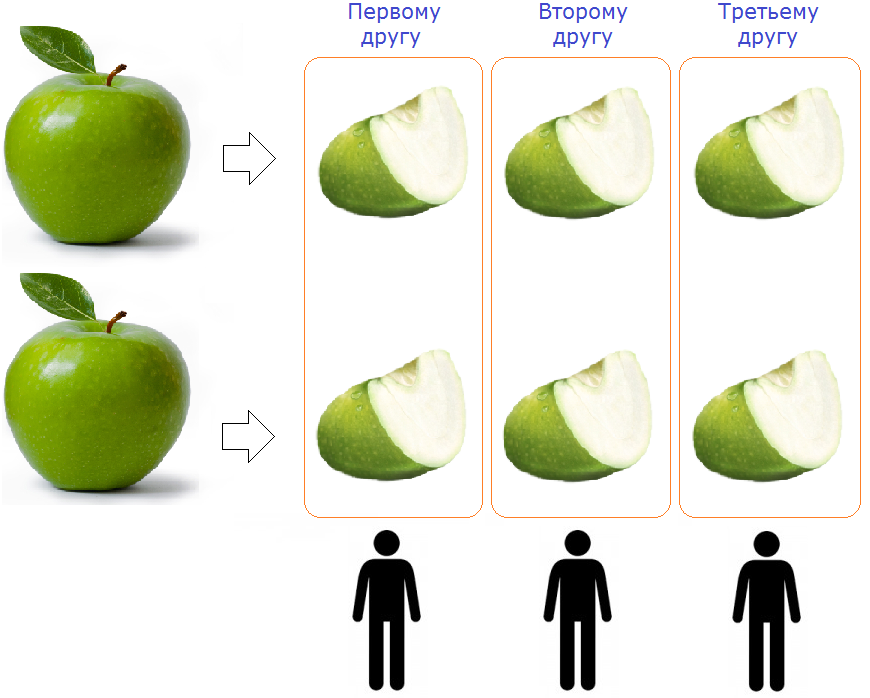
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось яблока (два кусочка из трёх).
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь 
.
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
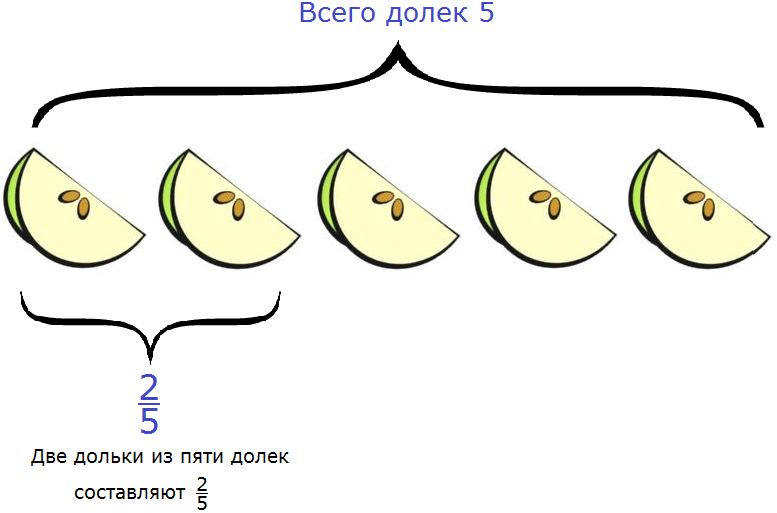
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь 
. Значит число 2 от числа 10 составляет (две десятых).
Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.
Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь 
.
Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.
Таким образом, число 2 составляет (одну пятую) от числа 10.
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь 
. Эту дробь можно сократить на 5
Получили аккуратную дробь 
. Значит ответ будет выглядеть следующим образом:
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.
Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем
15 : 3 = 5
5 × 1 = 5
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь 
. Эту дробь можно сократить на 3
Получили ответ 
. Значит 3 см составляют (одну четвёртую) от 12 см.
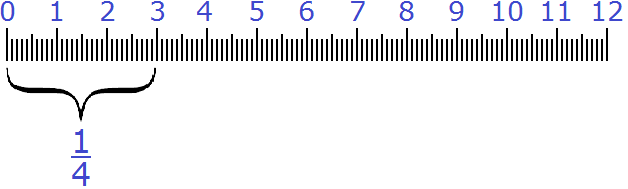
Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.
Делим 12 на знаменатель дроби
12 см : 4 = 3 см
Умножаем полученные 3 см на числитель дроби
3 см × 1 = 3 см
Получили ответ 3 см. Значит задача была решена правильно.
Задания для самостоятельного решения
Задание 1. Найдите от числа 30.
Задание 2. Найдите
Задание 3. Найдите от числа 30.
Задание 4. Найдите 
от числа 48.
Задание 5. Найдите 
от числа 48.
Задание 6. Найдите
120 см : 3 = 40 см
40 см × 2 = 80 см
Задание 7. Найдите
150 см : 3 = 50 см
50 см × 2 = 100 см
Задание 8. Найдите целое число по дроби, если известно, что
Задание 9. Найдите целое число по дроби, если известно, что этого числа составляет число 32.
Задание 10. Найдите целое число по дроби, если известно, что этого числа составляет число 150.
150 : 5 = 30
30 × 8 = 240
Задание 11. Найдите длину пути от дома до школы, если известно, что
4 км : 2 = 2 км
2 км × 3 = 6 км
Задание 12. Найдите длину рулетки, если известно, что этой рулетки составляют 100 см.
100 см : 5 = 20 см
20 см × 8 = 160 см
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
