Когда вы пользуетесь навигатором, вы указываете точку А и точку Б, и дальше навигатор как-то сам строит маршрут. Сегодня посмотрим, что лежит в основе алгоритма, который это делает. Просто ради интереса.
Графы и «задача коммивояжёра»
Ещё до появления навигаторов у людей была такая же проблема: как найти кратчайший путь из одного места в другое, если есть ограниченное количество промежуточных точек? Или как объехать ограниченное количество точек, затратив минимальные усилия. В общем виде это называется «задачей коммивояжёра», и мы уже рассказывали, в чём там идея:
- есть несколько городов, и мы знаем расстояния между двумя любыми городами;
- в классической задаче нельзя дважды заезжать в один и тот же город, но в жизни — можно;
- если городов мало, то компьютер справится с задачей простым перебором, а если их больше 66 — то уже нет;
- кроме расстояния, иногда важно учесть время, комфорт и общую длительность поездки;
- есть много приблизительных алгоритмов, которые дают более-менее точный результат.
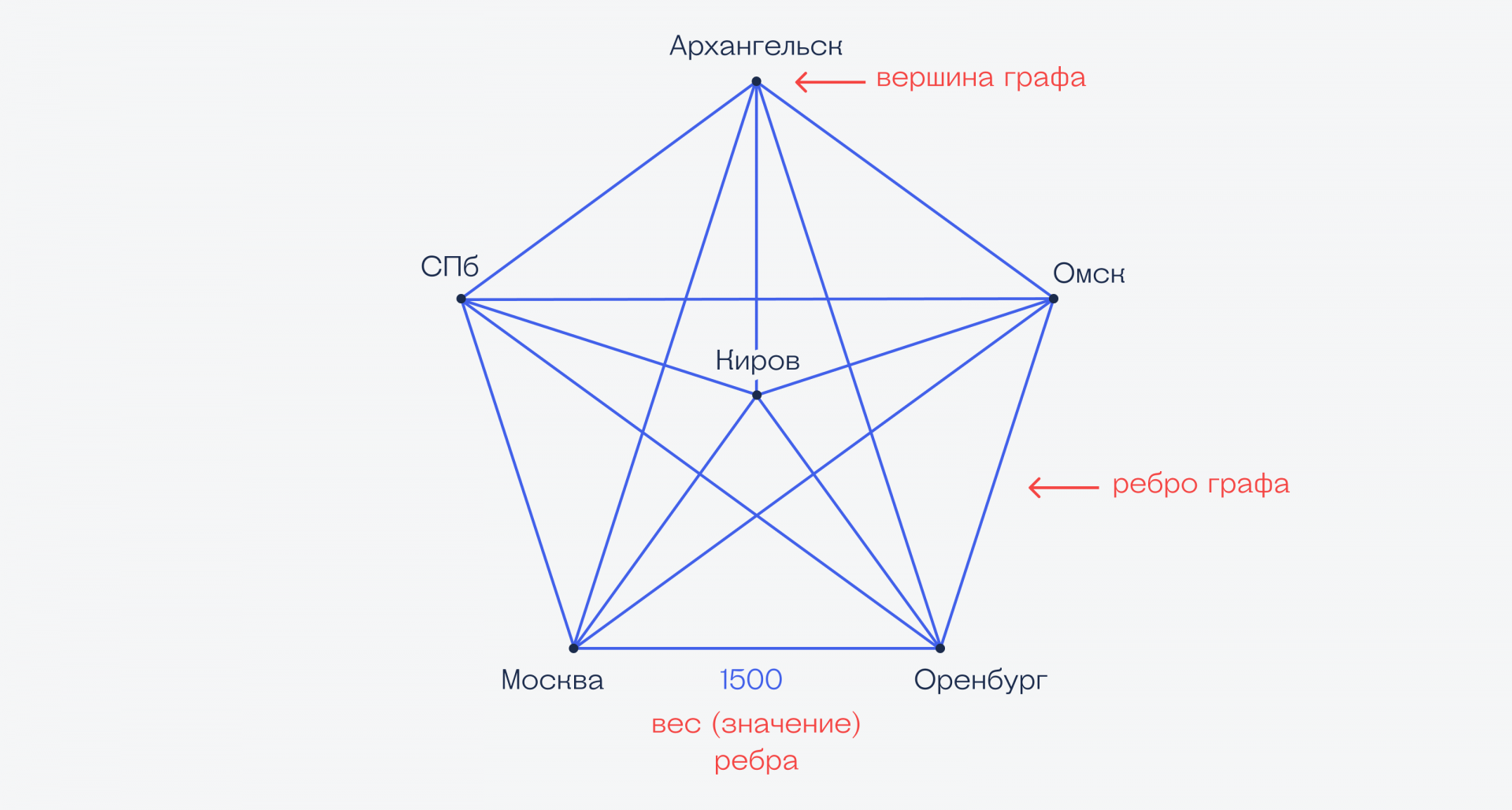
Если взять просто города и расстояния между ними, то с точки зрения математики это называется графом: города будут вершинами графа, а дороги между ними — рёбрами графа. Если мы знаем длину каждой дороги, то это будет значением (весом) рёбер графа. Этой теории нам уже хватит, чтобы понять, как работает навигатор в машине.
Алгоритм Дейкстры — ищем самый быстрый путь
Как только появилось решение полным перебором, математики стали искать другой подход, который работал бы гораздо быстрее и не требовал бы вычисления такого огромного объёма данных. В 1959 году Эдсгер Дейкстра придумал свой алгоритм, которым пользуются до сих пор. Идея его в том, чтобы не перебирать все варианты, а находить самый короткий путь только между соседними графами — и так, шаг за шагом, продвигаться к конечной точке.
Допустим, у нас есть улицы, перекрёстки и мы знаем время пути между ними. Нарисуем это в виде графа, а чтобы было проще ориентироваться — сделаем визуально всё одинаковой длины:
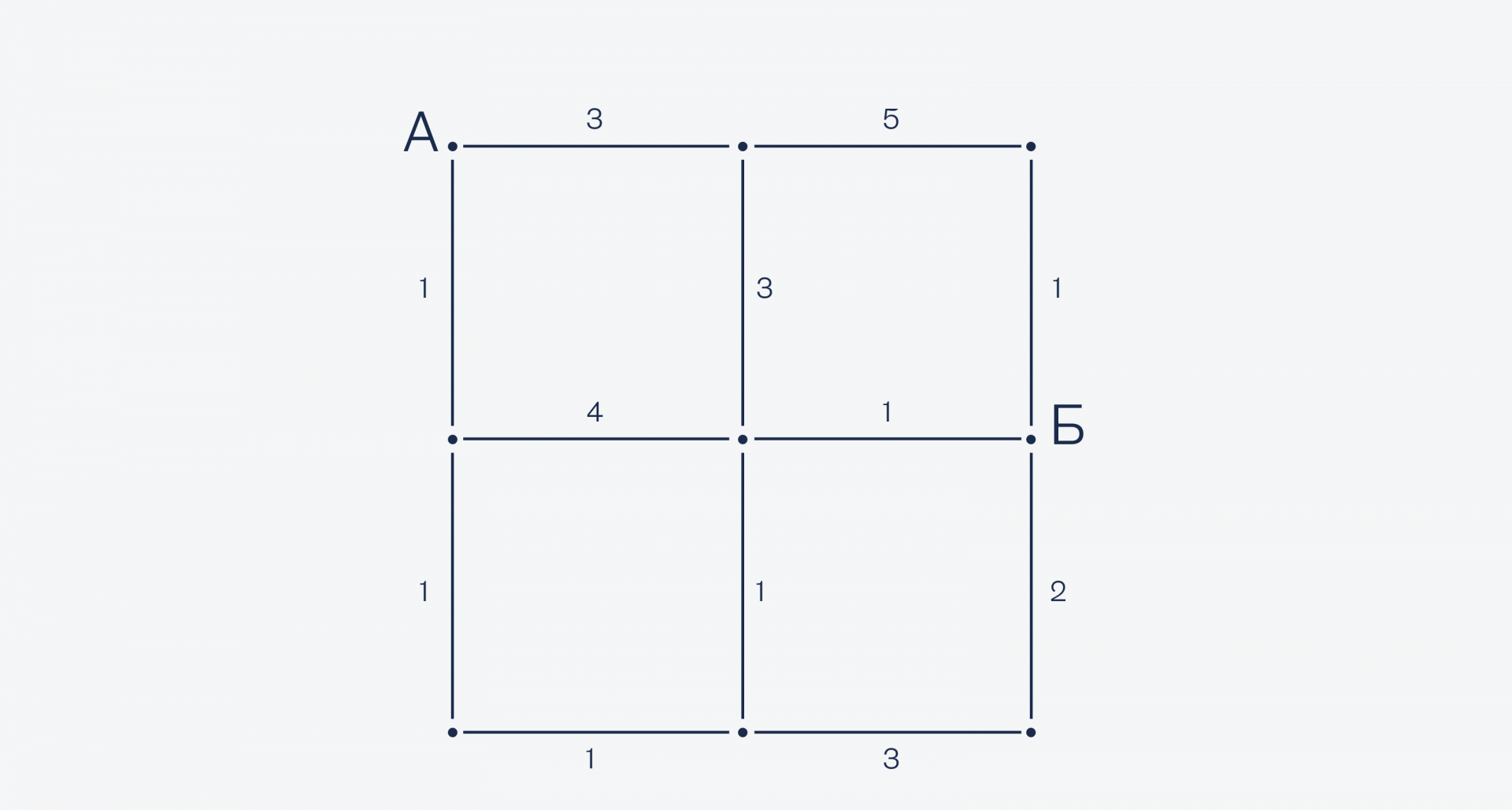
Чтобы найти самый быстрый путь из А в Б, мы смотрим сначала, какие пути у нас выходят из точки А. Видно, что поехать вниз будет быстрее, чем поехать направо:
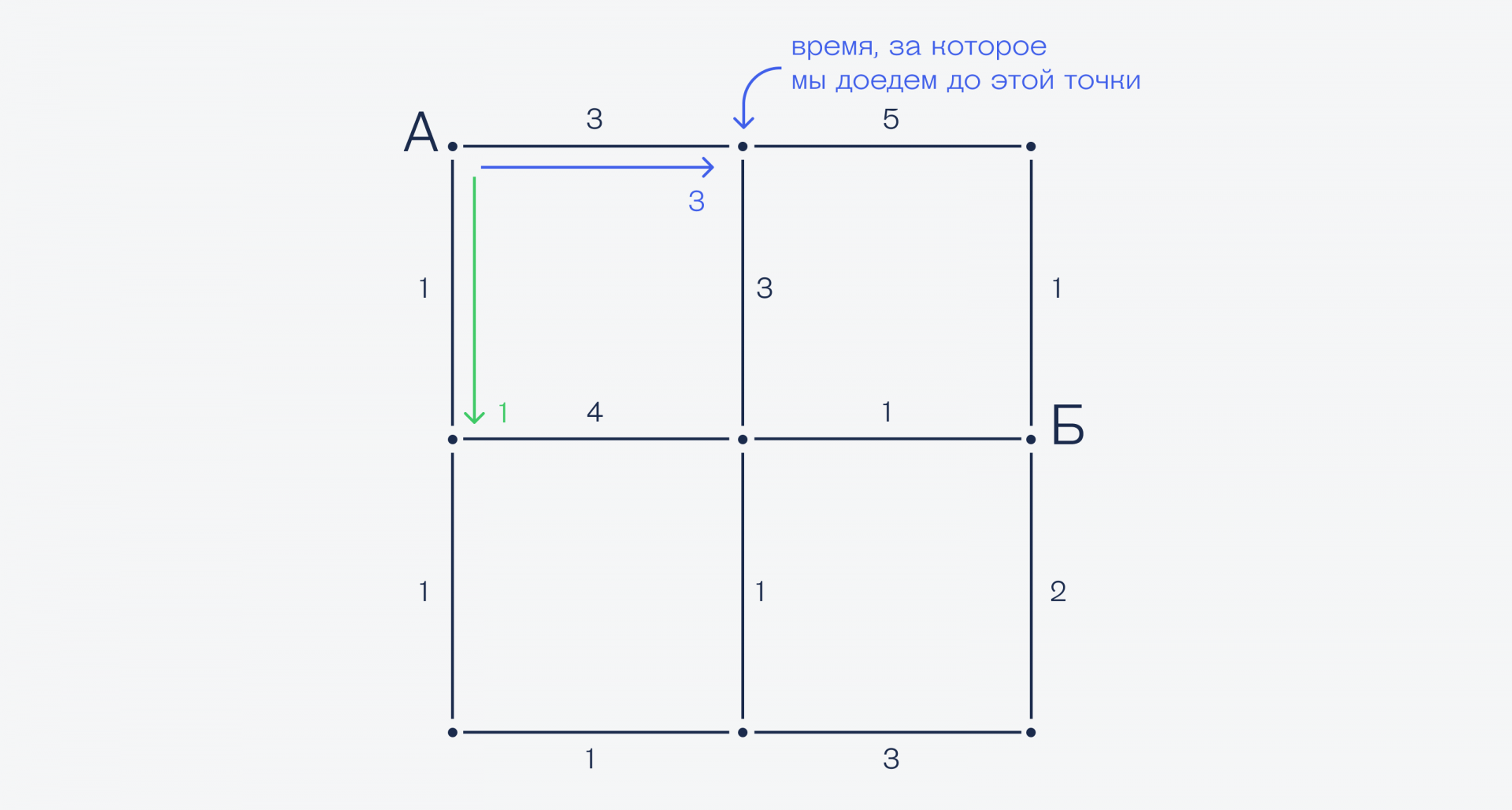
Значит, выбираем путь вниз. Теперь делаем то же самое для этой точки — смотрим, где быстрее: справа или внизу. Вниз быстрее (1 меньше, чем 4), поэтому едем по ней:
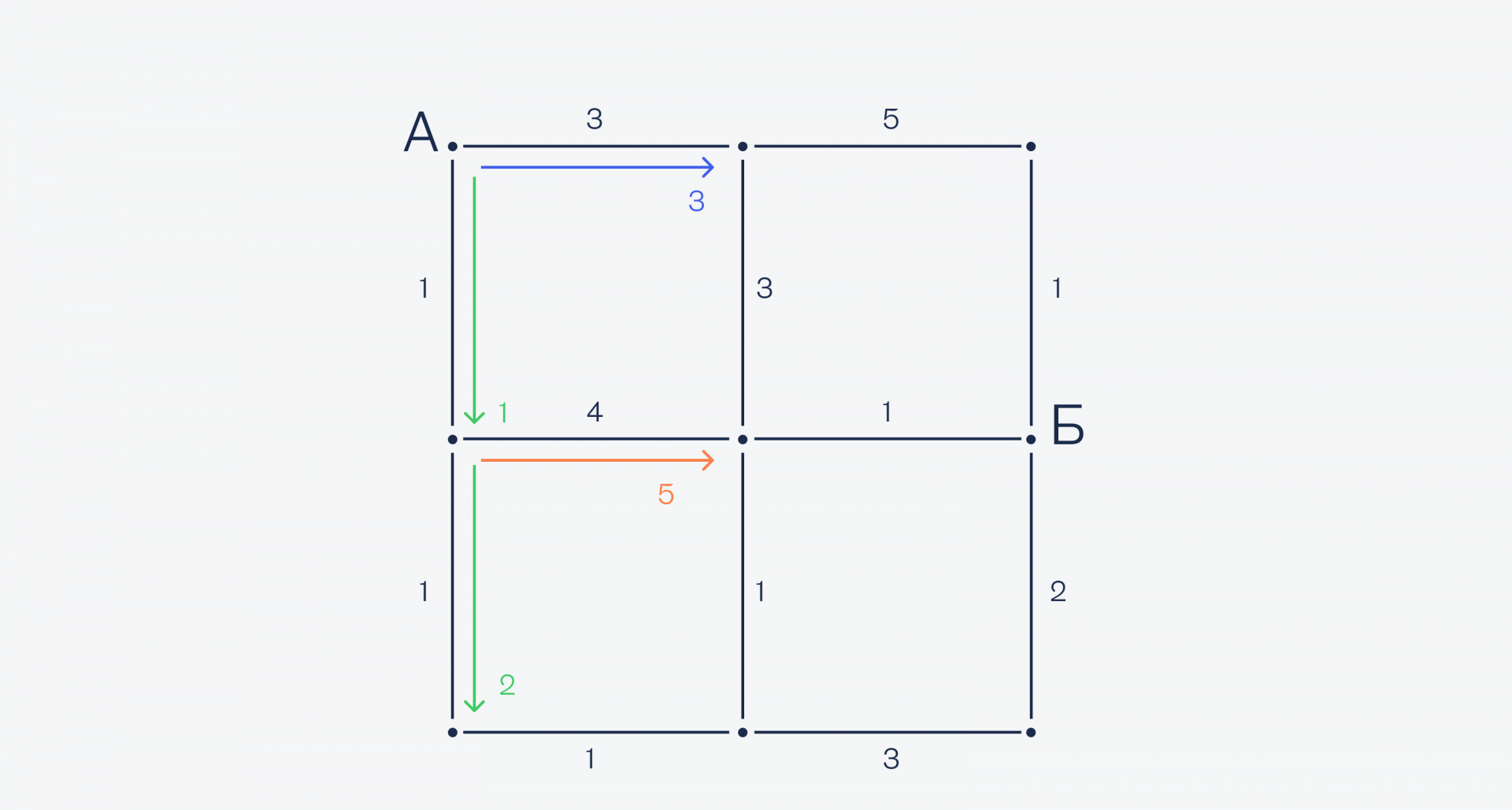
При этом мы не отбрасываем уже сделанные вычисления (всё равно уже посчитали), а запоминаем их на всякий случай. Из нижней точки есть только одна дорога — направо, поэтому едем по ней:
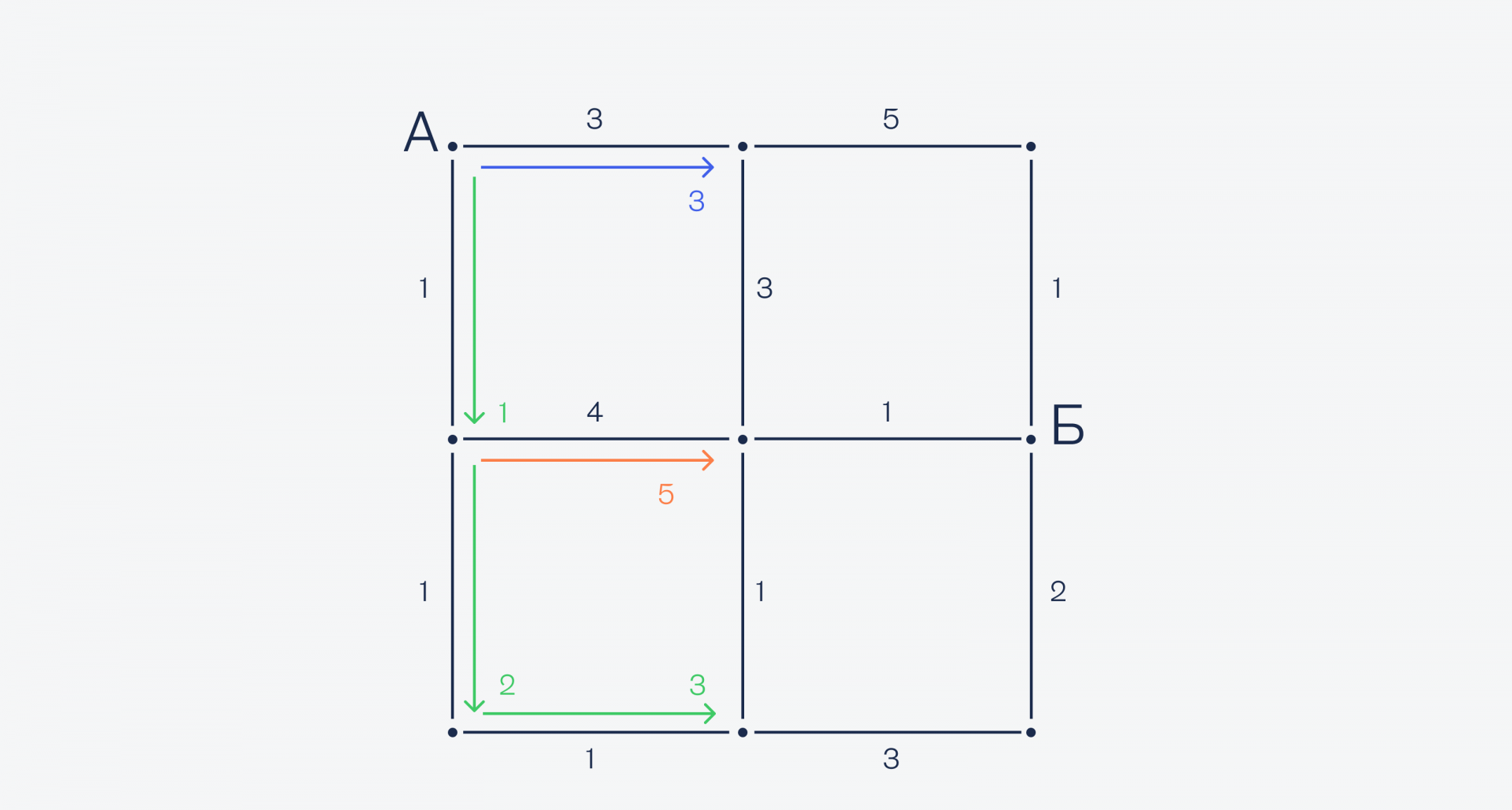
А теперь у нас получилась интересная ситуация: в центральную точку мы можем попасть как сверху, так и снизу, при этом и там, и там у нас одинаковое время — 3 минуты. Значит, посчитаем оба варианта — вдруг сверху будет быстрее и нам нужно будет перестроить маршрут заново:
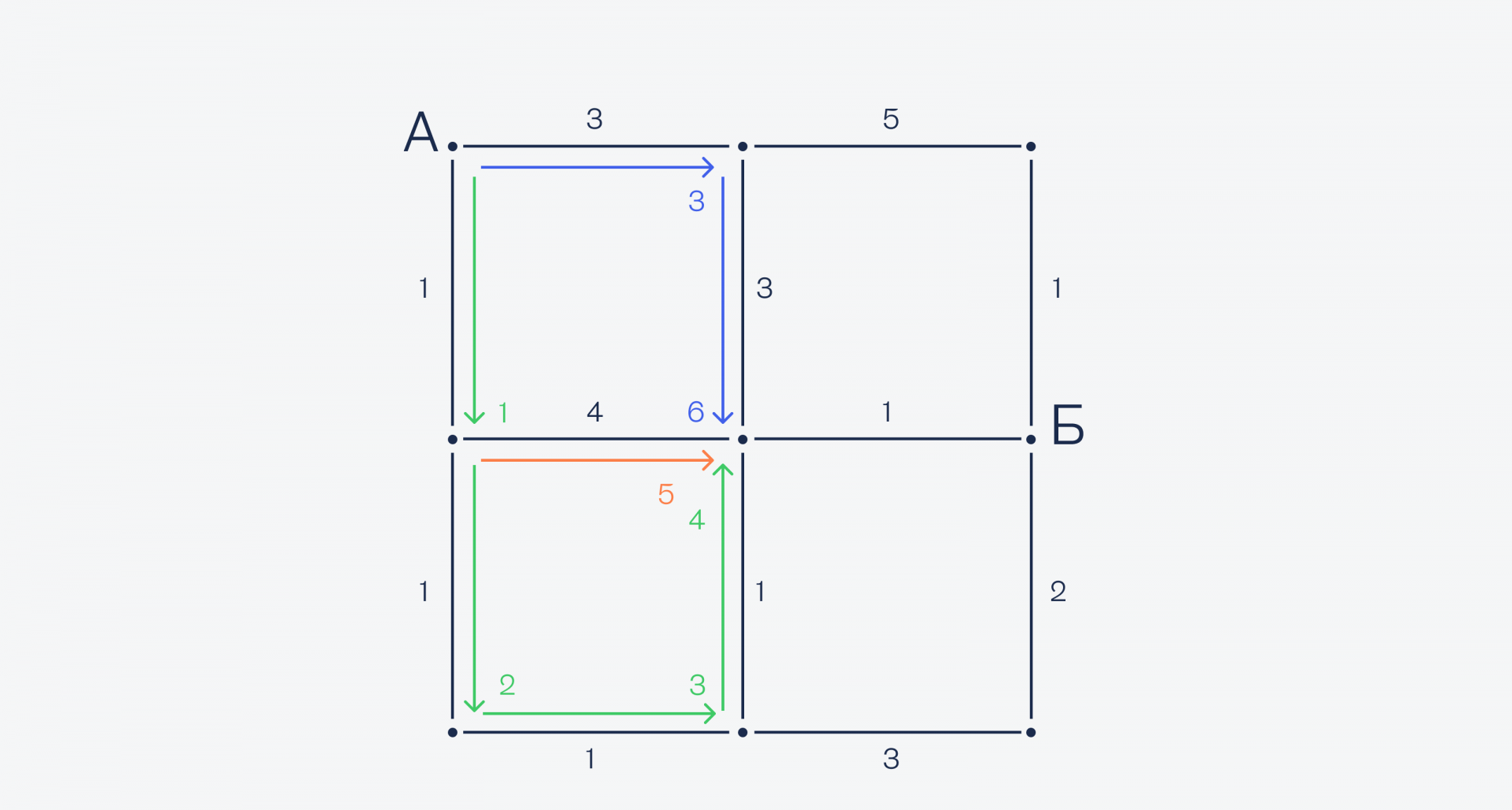
Оказывается, снизу ехать до центра быстрее, чем сверху — 4 минуты вместо 6, поэтому оставляем нижний маршрут. Наконец, из центральной точки до точки Б всего один путь — направо, поэтому выбираем его:
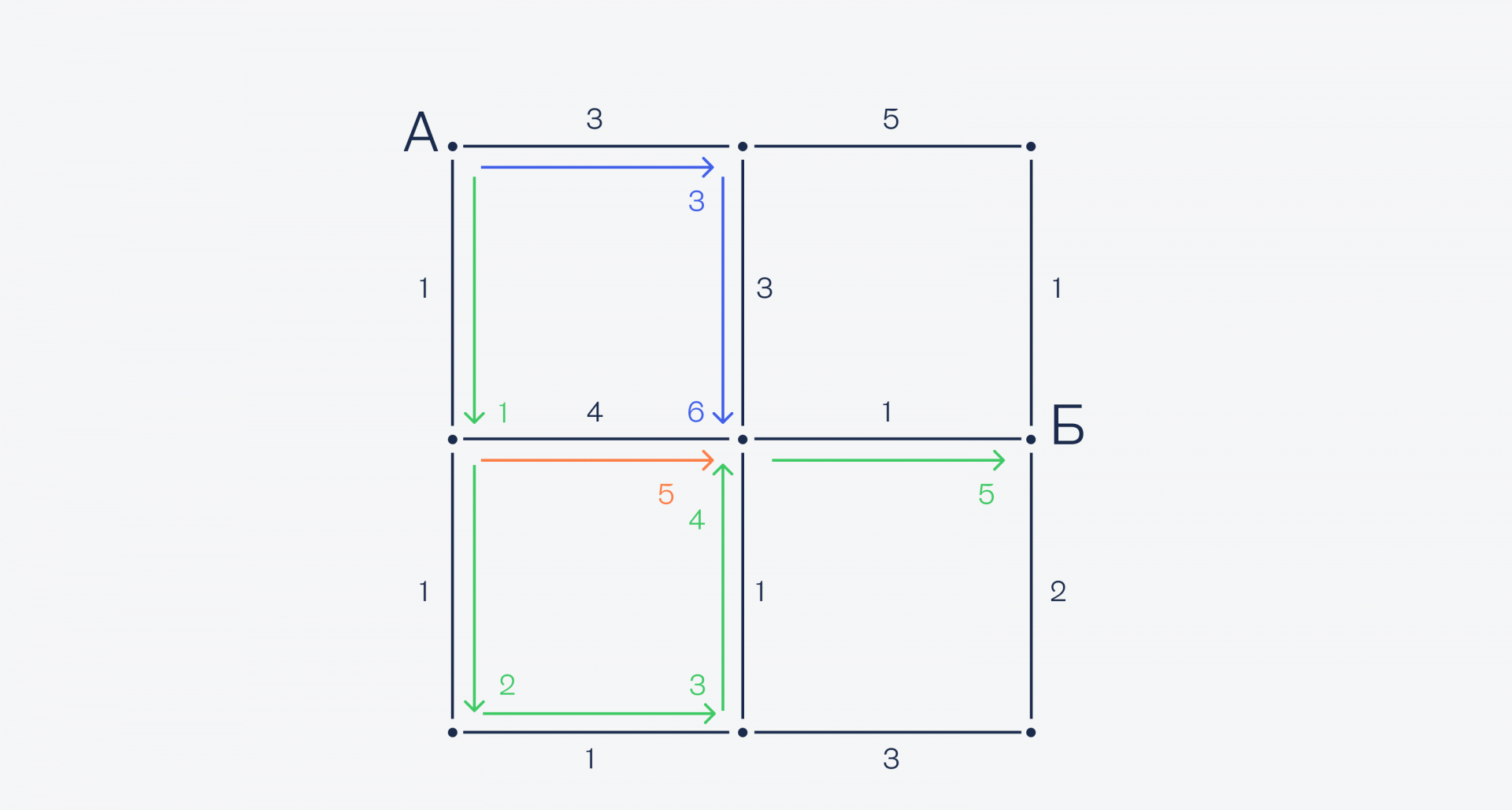
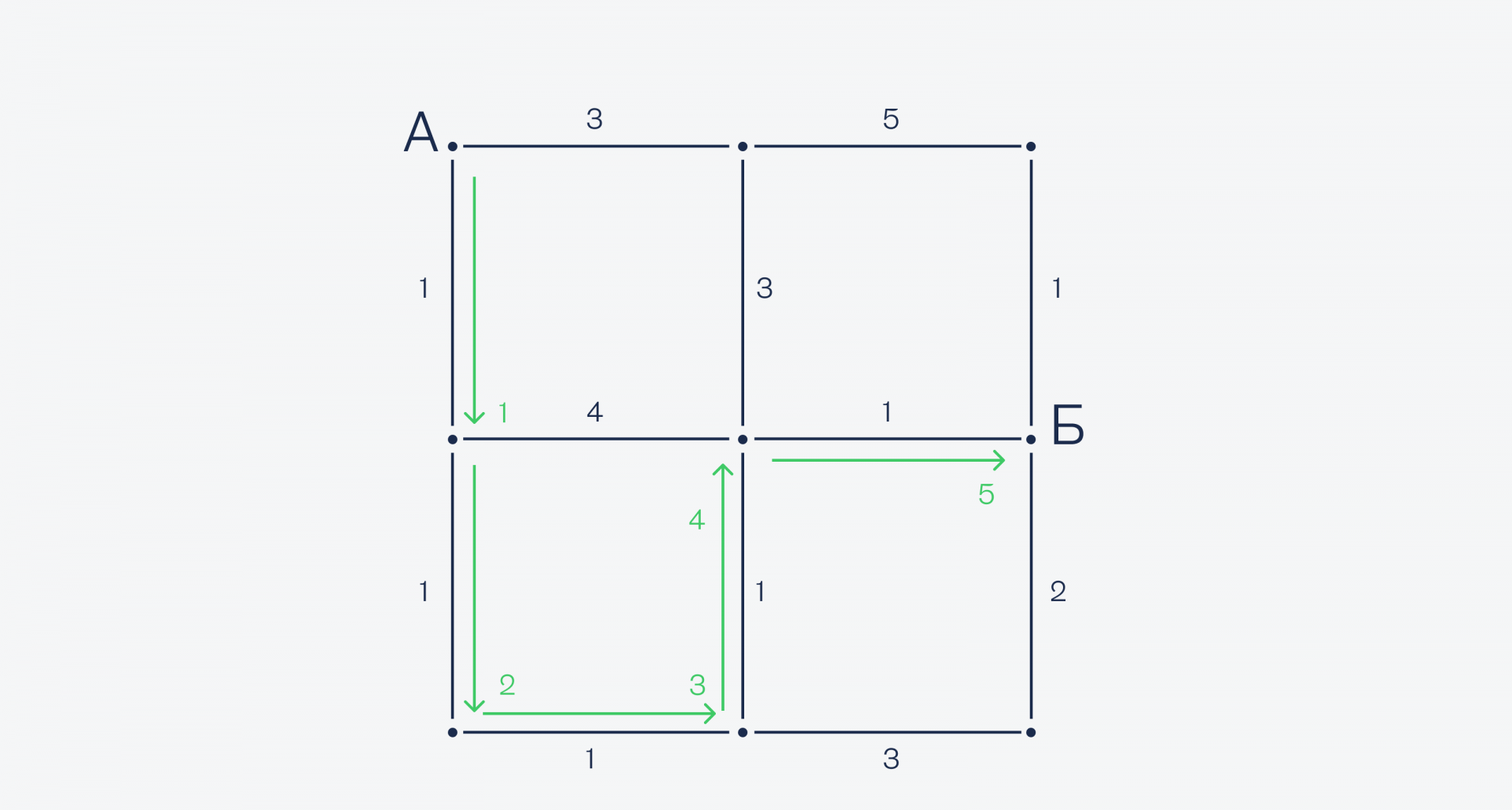
Как видите, нам не пришлось считать все варианты со всеми точками, а до некоторых мы просто не добрались. Это сильно сэкономило время и потребовало меньше ресурсов для вычисления.Такой алгоритм и лежит в основе автомобильных навигаторов — с вычислениями справится даже бюджетный смартфон.
Что ещё учитывает навигатор
Чтобы алгоритм оставался простым и работал только со временем, все остальные параметры дорог тоже привязывают ко времени. Покажем, как это работает, на паре примеров.
Комфорт. Если нам нужно построить не самый быстрый, а самый комфортный маршрут, то мы можем отдать предпочтение автомагистралям и дорогам с несколькими полосами — на них обычно и асфальт получше, и резких поворотов поменьше. Чтобы навигатор выбирал именно такие дороги, им можно присвоить коэффициент 0,8 — это виртуально сократит время на дорогу по ним на 20%, а навигатор всегда выберет то, что быстрее.
С просёлочными и грунтовыми дорогами ситуация обратная. Они редко бывают комфортными, а значит, им можно дать коэффициент 1,3, чтобы они казались алгоритму более долгими и он старался их избегать. А лесным дорогам можно поставить коэффициент 5 — навигатор их выберет, только если это единственная дорога то точки назначения.
Сложность маршрута и реальное время. Маршрут из А в Б почти никогда не бывает прямым — на нём всегда есть повороты, развороты и съезды, которые отнимают время. Чтобы навигатор это учитывал, в графы добавляют время прохождения поворота — либо коэффициентом, либо отдельным параметром. Из-за этого алгоритм будет искать действительно быстрый маршрут с учётом геометрии дорог.
Пробки. Если есть интернет, то всё просто: навигатор получает данные о состоянии дорог и добавляет разные коэффициенты в зависимости от загруженности. Иногда навигатор ведёт дворами, когда трасса свободна — это не ошибка навигатора, а его прогноз на время поездки: если через 10 минут в этом месте обычно собираются пробки, то там лучше не ехать, а заранее поехать в объезд.
Если интернета нет, то алгоритм просто использует усреднённую модель пробок на этом участке. Эта модель скачивается заранее и постоянно обновляется в фоновом режиме.
Как построить маршрут по всей России
Если нам нужно построить маршрут из Брянска в Тулу, то с точки зрения компьютера это безумно сложная задача: ему нужно перебрать десятки тысяч улиц и миллионы перекрёстков, чтобы понять, какой путь выбрать. С этим плохо справляется даже обычный компьютер, не говоря уже о телефоне.
Если мы в Яндекс Картах построим такой маршрут, то навигатор нам предложит сразу 4 варианта:
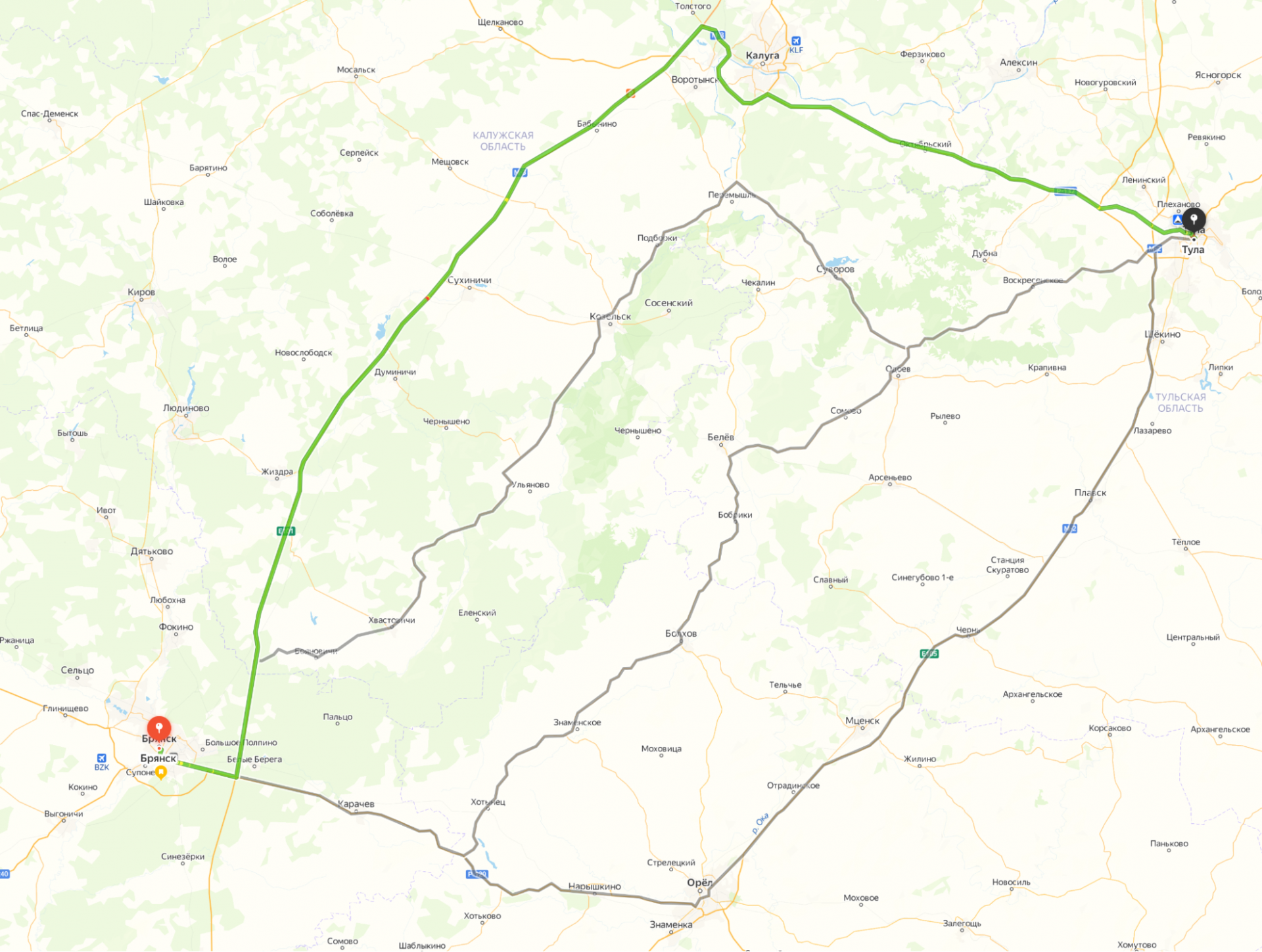
Но мы не ждали полчаса, пока сервер на той стороне посчитает все перекрёстки, а получили результат через пару секунд. Хитрость в том, что алгоритм использует уже заранее просчитанные варианты маршрутов и подставляет их для ускорения.
Например, если мы поедем в Тулу не из Брянска, а из Синезёрок, то поменяется только начальный маршрут по трассе М3, а всё остальное останется прежним:
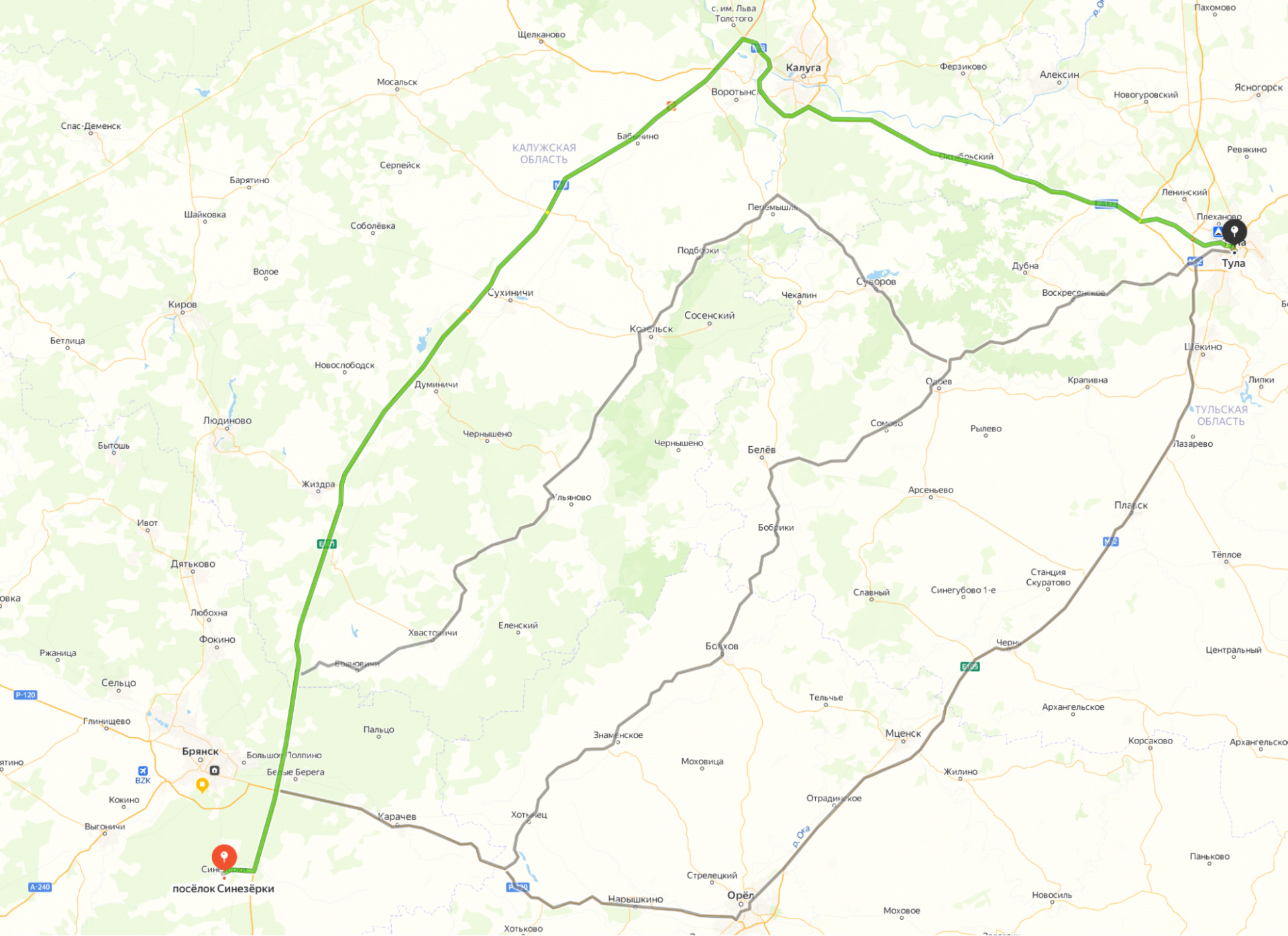
Получается, что навигатору не нужно всё пересчитывать — он находит только ключевые точки пути, а маршрут между ними уже просчитан до этого. Этот приём работает и при перестроении маршрута во время движения: навигатор смотрит, как нужно поменять путь, чтобы вернуть вас на уже известную дорогу.
Что дальше
Следующий этап — напишем алгоритм Дейкстры сами и посмотрим, как он работает по шагам.
Вёрстка:
Кирилл Климентьев
Составление маршрута – одна из наиболее сложных задач, стоящих перед руководителем любого похода. Хороший маршрут можно пройти, а можно и не пройти. Но пройти плохо задуманный или плохо проработанный маршрут не удается почти никогда, никакими усилиями. Чрезвычайно важно избежать даже элементарных ошибок при его составлении, потому что каждая может привести к неприятным последствиям, вплоть до аварийного выхода с маршрута.
Пешие маршруты можно условно классифицировать следующим образом:
1. Однодневные
2. Многодневные и степенные
3. Походы 1-2 (низких) категорий сложности
4. Походы 3-6 (высоких) категорий сложности.
Для каждого из этих видов при разработке маршрута применяются свои правила и маленькие хитрости, упрощающие жизнь туриста в походе.
Прежде чем составлять маршрут любой сложности и продолжительности, необходимо четко определиться с его целями и задачами. Если не договориться о них “на берегу”, то в походе неизбежны столкновения, вызванные разными мнениями участников. Как правило, реализуется одна из двух стратегий:
1. Руководитель лично определяет цели и задачи похода, затем набирает участников, согласных с ним.
2. Руководитель комплектует группу, затем путем обсуждения все вместе определяют цели и задачи похода.
Первый вариант более приемлем:
– для небольших походов, где существенные вариации целей и задач просто невозможны;
– в условиях большого турклуба, где всегда есть возможность выбрать участников;
– в неопытных, новичковых группах под началом руководителя со стажем.
На маршруте такой руководитель обычно является монопольным командиром, единолично принимающим решения по всем вопросам.
Второй вариант, как правило, применяется для категорийных походов в условиях ограниченного выбора участников. Начиная обсуждение целей и задач с участниками – по одному или со всеми вместе – руководитель ставит себя в положение не командира, но старшего товарища. На маршруте ему не стоит применять авторитарные методы управления, участникам будут ближе демократичность и стремление обсуждать решения.
Определение целей и задач, мотивов участников
В зависимости от возраста и склонностей, физической и технической подготовки, у участников могут возникнуть разные желания в отношении предстоящего похода. В рамках спортивного пешего похода наряду с выполнением обязательных требований (свыше 130 км и 6 дней) это могут быть более спортивные либо более развлекательно-познавательные цели. К спортивным относятся, например:
– сделать очередной разряд или пройти поход следующей категории сложности;
– получить хорошую физическую нагрузку;
– покорить вершину (порог, пещеру).
К развлекательно-познавательным:
– стремление отдохнуть на природе;
– пообщаться с друзьями или любимой девушкой;
– сходить в какой-нибудь (любой) поход из интереса;
– половить рыбку в отдаленном озере.
Выяснение мотивов – дело непростое, требующее хорошего знания людей, с которыми собираешься идти. Усложняет ситуацию то, что человек редко сообщает (а иногда и не может сформулировать) такую информацию о себе. Сделать вывод о действительных побудительных мотивах можно, собрав косвенную информацию по направлениям:
– уровень здоровья, наличие хронических заболеваний
– общая физическая подготовка
– специальная подготовка (туристская, альпинистская, медицинская, картографическая, музыкальная, ремонтная и т.д.)
– психологические особенности (склонность к лидерству, конфликтность, инициативность, исполнительность, лень, ответственность и многое другое)
– предыдущий опыт
– установившиеся личные симпатии и антипатии
Подбор в группу участников с сильно отличающимися мотивами приводит к двум наиболее распространенным последствиям:
1. Невозможно составить маршрут, удовлетворяющий всех участников
2. Если маршрут и составлен, при прохождении возникнут множественные конфликты между очень разными участниками. Например, половина группы хочет пройти заявленный маршрут, а другой уже ничего не надо, кроме возвращения домой (рыбалки, выпивки …).
В принципе, обе проблемы разрешимы, если руководитель осуществляет очень жесткое командование и способен подчинить участников своим интересам. Но такой подход требует специфического подбора участников, иначе весьма сомнительно, что они получат удовольствие от похода. Поэтому надо стремиться либо создать группу из людей со сходной мотивацией, либо задолго до похода внушить им нужные побуждения. Первое – проще: практика показывает, что хорошо подобранный состав группы – необходимое (но не достаточное) условие успеха любого похода. Во втором случае руководитель полностью принимает на себя командование группой, но вместе с ним и полную ответственность за принятые решения. Такое возможно, только если руководитель на голову выше участников в любом отношении.
Когда мотивы группы (или большей ее части) ясны, можно определяться с целями похода. Кроме прохождения маршрута, который должен соответствовать нормативам, это может быть:
– просто побыть, отдохнуть на природе (ну и что, что под рюкзаком);
– добиться высокого спортивного результата (достижение, исследование или покорение чего-то);
– краеведческий результат (что-то посмотреть, с кем-то пообщаться, ознакомиться с новым районом);
– поохотиться за дарами природы (золотым корнем, провиантом, драгоценностями).
Цели похода, по мере возможности, должны быть согласованы со всеми участниками. Даже если руководитель собирается быть в группе абсолютно непререкаемым, есть смысл хотя бы информировать коллег, чего, собственно, предполагается достичь по результатам похода. Такой стиль зачастую позволяет добиться более высоких результатов, чем демократичный, но кто категорически не согласен, пусть лучше останется дома.
Еще раз хочу подчеркнуть, что вопросы “зачем” и “для чего” при продумывании предстоящего похода являются значительно более важными, чем все прочие – “как”, “на чем”, “с кем” и т.п. Их проработка и понимание – безусловно, залог успеха любого похода, а пренебрежение ими ведет к конфликтам, срыву планов, возникновению опасных ситуаций и прочим неприятностям.
Подготовка маршрута
Обычно проводится параллельно с подготовкой группы, но после определения целей и задач похода. Как правило, подготовкой маршрута единолично занимается руководитель.
Подготовка маршрута включает:
1. выбор района путешествия
2. выбор категории (степени) сложности похода
3. собственно, разработка маршрута
4. разработка запасных вариантов и аварийных выходов.
5. подготовка заброски и выброски из района.
6. составление сметы на поход.
Подготовка однодневного маршрута
Однодневные и многодневные с базовым лагерем походы, как правило, проводятся для ознакомления с каким-либо одним объектом, например, скальным массивом, несложной пещерой (без организации подземного базового лагеря), водопадом и т.п. Поэтому нитка маршрута, от остановки общественного или заказного транспорта до объекта и обратно, обычно вполне очевидна. Могут возникнуть только транспортные варианты, например, заехать по одной дороге, а выехать по другой, чтобы не скучно было.
Подготовка сводится к распределению сил на переходе, планированию времени и набора мероприятий, которые предполагается провести (осмотр, восхождение, скальные тренировки и т.п.). В многодневном походе с базовым лагерем важным становится выбор места бивака, на котором предстоит стоять несколько дней.
Подготовка многодневных и категорийных маршрутов
Для многодневных (категорийных и степенных) походов необходимо составить маршрут, охватывающий, как правило, несколько интересных объектов, с логичными переходами между ними и правильно выбранными местами ночлегов.
Сложность составления маршрута, на мой взгляд, неоднозначно зависит от степени или категории сложности похода. Нельзя сказать, что, чем сложнее поход, тем труднее его придумать. Это связано с тем, что в степенных походах редко ставится цель прохождения какого-либо трудного участка, отнимающего много времени и сил. Как правило, многодневные степенные походы служат для обучения бивачным работам, самообеспечению на природе, в лучшем случае – это многодневный подход к какой-то одной Цели и отход от нее. Перед разработчиком пешего маршрута 1-2 категории сложности стоит задача, во-первых, более амбициозная, а во-вторых, отягощенная более суровыми требованиями. Пройти в день 21 км, что соответствует нормативам для похода 1 к.с., можно только по дороге или хорошей тропе, без больших перепадов высот. Впрочем, в зачет локальных препятствий в походе 1 к.с. идут всего 2 балла. То есть достаточно пройти перевал н/к или, максимум, вершину н/к, а остальное идти именно по тропам и дорогам. Но это довольно скучно, поэтому в любом среднегорном районе можно найти примеры более интересных “единичек”.
Если на маршруте есть лес, бурелом, осыпи, любой перевал и другие препятствия, максимально возможный дневной переход существенно уменьшается. При движении по глухой местности вряд ли возможно за день пройти больше 13-15 километров. К тому же, участниками похода 1 к.с. являются обычно как раз те, кто привык к небольшим нагрузкам и особенностям степенных походов. Выходя в “копейку”, они плохо представляют, что их ждет, и немало сюрпризов встретится им по пути. Причем сюрпризов неприятных, которые ведут к вопросам: “А как же теперь быть?”, “А почему никто не предупредил?”, “Почему все не так?” и т.п.
У начинающего руководителя на маршруте тоже всплывет немало сюрпризов. Начнем с того, что впервые разрабатывая маршрут, нормально составить его очень трудно, почти невозможно. В нем будет много ошибок, элементарно ясных для более продвинутых руководителей. Поэтому более правильным для “руководителя впервые” будет подыскать подходящий маршрут (или несколько), возможно, несколько модифицировать его (или скомбинировать из нескольких) и смело идти, опираясь на чужой опыт.
Разработка маршрута 3-5 к.с., как мне кажется, уже проще. Здесь закладываются меньшие дневные переходы, а дней планируется больше, поэтому возможны различные запасные варианты и т.п. Малейшее отставание от графика в походе 1 к.с. может очень плохо сказаться на результате похода, потому что нагонять упущенное некогда: нет ни запасных дней, ни резервов в течение каждого дня – переходы и так приходится планировать большие. А аварийный выход, который, разумеется, всегда есть, приводит к тому, что поход не удается защитить.
В походах более высоких категорий сложности потерять день, например, на непогоде – обычное дело. Это никого не нервирует и не создает угрозы непрохождения маршрута.
Выбор района путешествия
Это вопрос, требующий особого рассмотрения. Очень трудно дать не то, что исчерпывающие, а вообще какие-либо осмысленные рекомендации по выбору района, особенно для большого похода. На практике выбор района для походов различной продолжительности и сложности происходит примерно так.
Однодневный или многодневный с базовым лагерем
Здесь выбирать нечего. Цель такого похода однозначно определяет и его район. Как правило, этот район находится неподалеку от места проживания и связан с ним удобным транспортом. Исключения составляют многодневные “походы”, например, в высокогорные районы для покорения сложной вершины, то есть организация базового лагеря с последующими восхождениями из него, но и в них с выбором района проблемы не возникает.
Многодневный степенной поход или поход 1-2 к.с.
Такие походы, как правило, малобюджетные. Нет смысла ехать через всю страну, пусть даже в очень интересный район, чтобы несколько дней там побродить. Поэтому, как правило, это район, близкий к месту проживания, связанный с ним доступным и недорогим транспортом. Проблем не возникает, даже если местом проживания является какой-либо “неудачный” с точки зрения интересных природных объектов регион центра России, так как требования к походу 1 к.с. позволяют провести его практически где угодно. Другое дело, что при выходе в следующий раз в район среднегорья (или из среднегорья – в высокогорный район) группа оказывается не подготовлена к усложнившимся условиям, но это решается проведением несложного акклиматизационно-исследовательского похода в новом районе.
Редкое исключение составляют случаи, когда поход небольшой категории сложности совершается в отдаленном районе в составе, например, семинара. Тогда организуется совместная заброска нескольких групп (скажем, 5, 3 и 1-2 к.с.), что удешевляет транспорт. Это позволяет организовать интересные варианты взаимодействия групп на маршруте, разнообразные заброски, в лыжных походах – взаимную тропежку и т.п. Например, в 2003 году несколько групп уфимских туристов в походах 3…6 к.с. за один семинар исследовали и качественно описали огромную часть Северного Забайкалья, существенно обогатив общедоступную информацию о районе. Но и в этом случае район путешествия определяет руководитель семинара, а руководителю похода остается только составить маршрут, наилучшим образом вписывающийся в семинар.
Поход высокой категории сложности
Группа выросла, успешно прошла несколько категорийных походов, хочется большего. При выборе района сложного похода, как правило, проводимого для каждого участника один раз в год, в отпуск, исходят из двух вариантов.
Как правило, спортивным туризмом занимаются не самые богатые люди. Всегда есть желание придумать как можно более дешевый поход. Чем ближе к месту проживания, тем транспорт получается дешевле. Поэтому возможности своего района, обычно, реализуются до предела, а когда предел достигнут, хитрый и небогатый руководитель пытается найти способ за него запрыгнуть. Так, для Северного Урала определена максимальная третья категория пеших походов, но были прецеденты успешной защиты походов 4 к.с. (например, охватывающих Денежкин камень, Главный Уральский хребет и Кваркуш). Обычно, в любом районе среднегорья можно найти основания для защиты походов 3-4 к.с.
Есть еще одна причина ходить раз за разом в один и тот же район – привычка. Каждый район содержит столько интересных мест, что, если поставить задачу изучить его досконально, в него можно ходить десятки раз. Многие находят в этом удовольствие.
Более сложные походы требуют выезда в более сложный район. Походы 5-6 к.с. в России возможны на Полярном и Приполярном Урале, Кавказе, Алтае, в Саянах и более экзотических районах за Байкалом. Как правило, и здесь одним из определяющих выбор района факторов является расстояние от места жительства, а следовательно, стоимость железнодорожного (авиа-) и автомобильного транспорта на заброску. Сначала выбирается самый дешевый район, затем, когда он поднадоел, планируются более длительные заезды и отъезды.
Условно можно все районы классифицировать по бюджетному признаку:
1. Дешевые – в пределах своей и соседней области, куда можно доехать на местном авто, железнодорожном или недорогом (“знакомом”) заказном транспорте.
2. Бюджетные – куда можно доехать пусть не очень коротким, но регулярным железнодорожным транспортом. Для жителей центральной России это Алтай, Саяны, Урал и другие подобные районы. Удельная стоимость заказного транспорта еще не слишком большая, билеты все можно брать заранее.
3. Отдаленные – Кодар, Тува, Тянь-Шань и т.п., где либо очень дорогой и проблемный железнодорожный подъезд, либо требуется дорогая заказная заброска автотранспортом.
4. Дорогие – Камчатка, Якутия, крайний Север, где требуется авиазаброска.
Согласно существовавшей когда-то классификации (Ганопольский В.И. Туризм и спортивное ориентирование.- М.:ФиС, 1987.- С.30-41.), в основных районах РФ и стран СНГ возможны пешие походы следующих категорий сложности:
| Туристский район | Максимальная к.с. |
| Северо-Запад РФ (Кольский п-ов, Карелия) | 3 |
| Архангельская область и Республика Коми (кроме горной части) | 4 |
| Вологодская область | 3 |
| Восточно-Европейская равнина | 2 |
| Крым | 2 |
| Карпаты | 2 |
| Кавказ (Западный и Восточный) | 4 |
| Закавказье (Азербайджан, Армения, Грузия) | 3 |
| Полярный Урал | 5 |
| Приполярный Урал | 5 |
| Северный Урал | 3 |
| Средний Урал | 2 |
| Южный Урал | 3 |
| Север Западной Сибири | 3 |
| Средняя и южная часть Западной Сибири | 2 |
| Казахский мелкосопочник и Тургайское плато | 3 |
| Пустынные и полупустынные районы Средней Азии | 3 |
| Копетдаг и Западный Таджикистан | 3 |
| Западный Тянь-Шань | 4 |
| Алтай | 6 |
| Кузнецкий Алатау | 4 |
| Восточный и Западный Саян | 5 |
| Тува | 6 |
| Прибайкалье, Забайкалье, Кодар, Удокан, Становой хребет | 6 |
| Средняя Сибирь (Горы Бырранга, Таймыр, плато Путорана, Среднесибирское плоскогорье, Центрально-Якутский район) | 6 |
| Северо-Восточная Сибирь (Верхоянский, Момско-Черский, Колымский районы, Приполярье) | 6 |
| Север Дальнего Востока (Чукотский, Анадырский, Корякский, Охотский районы, Камчатка) | 6 |
| Курильские острова | 4 |
| Юг Дальнего Востока (Приамурье, Приморье, Сихотэ-Алинь, Нижний Амур) | 5 |
| Сахалин | 4 |
В современной методике расчета сложности формально нет ограничений на максимальную категорию сложности походов в районе, но регионы СНГ оцениваются как:
| Туристский район | Показатель, баллы |
| Средняя равнинная часть европейской территории | 0-2 |
| Карпаты, Крым | 3 |
| Карелия, Вологодская обл., Кавказ, Армения | 4 |
| Средний и Южный Урал, Тянь-Шань | 6 |
| Алтай, Кузнецкий Алатау | 7 |
| Западно-Сибирская низменность | 07.окт |
| Архангельская обл., Респ. Коми, Памиро-Алай, Зап. И Вост. Саян | 8 |
| Северный Урал, Приморье | 9 |
| Кольский полуостров, Памир | 10 |
| Хабаровский край | 11 |
| Полярный Урал, Прибайкалье, Забайкалье, Кодар, Удокан, Сахалинская обл. | 12 |
| Пустынные и полупустынные районы Средней Азии | 13 |
| Становый хребет и Алданское нагорье | 14 |
| Камчатка и Курильские острова | 15 |
| Плато Путорана | 16 |
| Магаданская обл., Чукотка | 18 |
| Верхоянский хребет, хр. Черского и Сунтар-Хаянта, Корякское нагорье | 19 |
| Таймыр (г. Бырранга), о. Врангеля | 24 |
| Северная Земля и Земля Франца-Иосифа | 30 |
Чем больше баллов указано для района, тем выше, при прочих равных условиях, будет оценен по методике маршрут.
Используя приведенную информацию, можно выбрать район похода либо исходя из финансовых соображений, либо из требуемой сложности. Составленный маршрут должен, кроме соответствия района, иметь продолжительность и протяженность не меньше установленной:
| Вид туризма | Категория сложности похода | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Продолжительность, дней | 6 | 8 | 10 | 13 | 16 | 20 |
| Протяженность, км | ||||||
| пеший | 130 | 160 | 190 | 220 | 250 | 300 |
| … |
Разработка маршрута, планирование запасных и аварийных выходов
После выбора района, категории сложности и определения целей похода надо приступать к составлению нитки. Так как, на мой взгляд, сложнее всего придумать красивую нитку похода 1-2 к.с., рассмотрим логику действия руководителя при составлении пеших маршрутов начальных категорий сложности.
1. Необходимо убедиться, что в выбранном районе возможно проведение маршрута заданной сложности.
2. Собрать материалы о выбранном районе. Изучить карты, ознакомиться с особенностями климатических условий, особенностями совершения путешествия в данном районе, оценить наличие и взаимное расположение перевалов и вершин требуемой категории сложности и возможность найти их описания, оценить сложность подходов и отходов, аварийных выходов. Много информативного материала можно найти в сети Internet. Правда, доверять им можно не всегда – на практике, практически в каждом отчете встречаются “приписки”, повышающие сложность препятствий. Лучший метод – списаться с автором отчета и попросить у него консультацию.
3. Определить оптимальные сроки путешествия.
4. Разработать маршрут (см. ниже)
5. Разработать краткие и предельно простые запасные и аварийные выходы из любой точки маршрута.
Пеший маршрут 1 к.с. должен быть протяженностью не менее 130 км и продолжительностью не менее 6 ходовых дней. Надо иметь в виду, что 160 км и 8 ходовых дней – это уже маршрут 2 к.с., то есть не надо делать слишком длинную или долгую “единичку”. Протяженность может быть уменьшена по согласованию с МКК (маршрутно-квалификацонной комисией) не более чем на 25% от норматива, если на маршруте много сложных препятствий.
Протяженность маршрута определяется умножением расстояния, измеренного по карте 1:2 км, на поправочный коэффициент 1,2.
После выбора района путешествия надо определиться с точками входа и выхода на маршрут, и какой он будет:
– линейный (идем из А в Б);
– кольцевой (откуда выходим, туда и возвращаемся, причем путь “туда” и “обратно” не совпадает);
– комбинированный (содержит и кольцевую, и линейную часть).
По существующим правилам, не менее 75% протяженности маршрута должна составлять линейная часть или одно кольцо. Остальную часть могут составлять небольшие кольца (с возвратом через несколько дней к оставленной продуктовой заброске), линейные и кольцевые радиальные выходы (без рюкзаков) на перевалы и вершины. Выбор линейной или кольцевой нитки в первую очередь определяется возможностью организации заброски и выброски с маршрута. Если такая точка существует только одна, маршрут может получиться только кольцевой.
Затем для маршрутов разных типов надо сделать примерно следующее.
Линейный маршрут
1. Прикинуть, сколько километров между А и Б по кратчайшему и самому легкому для прохождения пути. Отсюда становится ясно, можно ли отклоняться от этого пути и насколько, чтобы набрать нужные 130 км.
2. Посмотреть, что есть интересного около кратчайшего пути: куда можно залезть, что можно посмотреть, в какой населенный пункт можно зайти для пополнения продуктов. Надо помнить, что сложность перевалов и вершин в пеших “единичках”, как правило, не должна превышать 1А. Но если перевальный опыт участников это позволяет, нет никаких противопоказаний для включения в маршрут более сложного и интересного объекта.
3. Решить, куда заходить с рюкзаками, а какие объекты посетить в радиальном выходе. Радиальные выходы также могут быть линейными (тогда учитывается только путь в одну сторону) или кольцевыми.
4. Проложить нитку маршрута через найденные интересные объекты, посчитать протяженность. Если она вышла за 150 км, надо исключить какие-то отклонения и снова пересчитать длину.
Кольцевой маршрут
1. Прикинуть, что интересного попадает в радиусе 40-60 км от пункта входа-выхода. Наметить интересные для посещения объекты, провести через них пробную нитку.
2. В зависимости от получившейся длины, либо уменьшать ее исключением объектов (по хорде), либо добавлять отклонения от “кольца”, пока не наберется нужная длина.
Очевидной представляется необходимость соединять точки, связанные с выполнением задач похода, по кратчайшему времени (или наилегчайшему способу) передвижения, избегать ненужных трудностей и перенапряжения, согласовать (или хотя бы обсудить) маршрут с группой.
Во всех случаях, планируя пробную нитку, надо обратить внимание на наличие дорог, троп, поселков и изб; постараться избежать сложных переправ через реки, обширных болот (или обходить их по краю), траверсов хребтов, сложных перевалов. Выбирать характер движения надо примерно в следующем порядке:
1. Дороги.
2. Тропы.
3. Просеки, если известно, что они действительно прорублены; легко проходимый (“парковый”) лес по азимуту.
4. Плоские, протяженные хребтовые плато.
5. Участки леса рядом с высотной границей, где он начинает переходить в хребтовые курумники.
6. Моховые болота, если известно, что они проходимы.
7. Траверсы склонов хребтов.
8. Буреломный лес по азимуту.
После составления нитки необходимо получить как можно более полную информацию о препятствиях: перевалах, вершинах, бродах и переправах, растительном покрове, болотах, в межсезонье или при прохождении снежных перевалов – о лавинной опасности. Руководитель должен четко представлять свои действия и действия участников при преодолении этих препятствий, какое специальное снаряжение и как планируется использовать, какие могут быть аварийные пути отхода или обхода препятствия, например, при внезапном ухудшении погоды или травмировании участника. Очень желательно иметь не только точные карты, но и фотографии вершин и перевалов, чтобы легче и увереннее потом ориентироваться на местности. Если в ходе уточнения характера препятствий выявились непреодолимые для группы (в смысле сложности или продолжительности преодоления) препятствия, нитку придется менять.
На основании нитки составляется календарный план похода – разбивка нитки по дням с учетом дневок и запасных дней. Определяются места удобных стоянок (биваков и дневок), протяженность и содержание дневных переходов. Практика показывает, что если не рваться, то за день по пересеченной местности можно пройти, в среднем за поход, не более 13…17 км, учитывая дневки и отсидки. Планировать более длительные дневные переходы (до 20…25 км) можно в отдельных случаях, если есть надежная информация о наличии дорог, хороших троп, ровных плато,
Дальнейшие действия для любого типа маршрута примерно одинаковые.
1. Наметить (по карте или по чужим описаниям) все удобные места для ночлегов. Около них должны быть дрова и (летом) вода, и характер местности должен позволять поставить палатку. То есть это должны быть не крутые склоны, не курумники, не очевидные болота и т.п. Лучше избегать и обширных открытых мест из-за возможного там сильного ветра, и глухого бурелома. Важен также красивый вид вокруг. Если все эти места не подойдут сейчас, их можно будет использовать при (почти неизбежных) отклонениях от заявленного маршрута. По карте, даже масштаба 1:100 000…1:50 000, найти хорошую стоянку невозможно, приходится пользоваться чужим опытом, здравым смыслом и собственным опытом. Ночевки в безлесной зоне весьма нежелательны, если нет примусного хозяйства.
2. Разбить маршрут по дням, чтобы каждый день начинался и заканчивался в подходящем для ночлега месте. Протяженность дневного перехода зависит от характера местности: по лесу, по наклонному курумнику (перевал, траверс) летом реально можно проходить 12-14 км, по тропам и просекам до 16, по дороге порядка 20. К концу похода, когда рюкзаки становятся легче, несмотря на накопленную усталость, дневной переход по слабо пересеченной местности можно сделать на 10-25% больше.
3. Наметить аварийные и запасные варианты.
Запасной вариант используется, когда обнаруживается, что какое-то препятствие труднее пройти, чем предполагалось, или произошло отклонение от маршрута, или плохая погода вынудила отсиживать либо не проходить перевал. Запасной вариант выбирается так, чтобы в целом сложность маршрута не менялась. Обычно это обход препятствия по более легкому пути, “срез” угла на участке маршрута и т.п. Наличие запасного варианта прохождения, как правило, обязательно для каждого определяющего препятствия маршрута. Оно обычно составляется к составлению набора правил типа: “если перевал не удается пройти (из-за плохой погоды, сложной лавинной обстановки, болезни участника, поломки или утери снаряжения и т.п.), то…”.
Аварийный выход необходим в экстренных ситуациях, чтобы как можно быстрее выйти к людям. Он производится по самой легкой местности и по кратчайшему пути. Варианты аварийных выходов с маршрута прорабатываются до каждого населенного пункта, находящегося вблизи пути группы. Они должны пролегать по максимально легкой для преодоления местности, где к тому же просто ориентироваться. При планировании выхода по дорогам (особенно лесовозным) необходимо запастись свежим описанием (а не картой) местности, потому что такие дороги имеют обыкновение очень быстро изменяться, изобилуют не обозначенными на карте развилками, движение транспорта по ним меняется от времени года и т.п. Аварийные варианты предназначены для экстренного прекращения похода и обычно при их использовании заявленная категория сложности не сохраняется.
4. Наметить дневки. На маршруте 1 к.с. обычно предусматривается не более 1 дневки на 3-4 день, или они вообще не делаются (для сильной группы). На месте для дневки должно быть много дров, желательно, хороший вид, оно должно быть удобно во всех отношениях. Количество дневок планируют, исходя из одного из правил:
– какая категория маршрута, столько и надо планировать дневок плюс отсидок;
– количество дневок должно составлять примерно 1/5 от общего количества дней.
Реально даже за большой поход редко удается сделать более 1 дневки, остальное уходит на отсидки и компенсацию отставания.
5. Запланировать как минимум один запасной день (по другой методике – один на 10 полных и неполных дней похода) и рассчитать время на заброс и выброс с маршрута и возможные отсидки. Отсидка – вынужденный отказ от движения, как правило, из-за сложных метеорологических условий (пурга, туман, плохая видимость при прохождении перевала, проливной дождь) или болезни участников. Опыт показывает, что в сложных климатических условиях почти все запланированные дневки, на самом деле, используются для отсидки или чтобы нагнать незапланированное отставание от графика. Но излишнее количество плановых дневок, во-первых, рассматривается как снижение спортивности маршрута, а во-вторых, ведет к увеличению веса рюкзаков за счет продуктов и, следовательно, к снижению скорости.
6. Планирование водной части пеше-водного маршрута обычно сводится к разбивке участка реки, предназначенного для сплава, сразу в календарный график движения, поскольку нитка маршрута определяется рекой, и известны все препятствия на маршруте. Единственным запасным вариантом прохождения здесь, как правило, является обнос препятствия. При разработке маршрута желательно получить информацию об удобных точках начала и окончания обноса, о том, по какому берегу удобнее обноситься, чтобы не тратить время на разведку. Аварийные выходы просчитываются аналогично пешему маршруту до населенных пунктов, как правило, от места пересечения реки и какой-либо дороги, торной тропы, прорубленной просеки.
Планируемая продолжительность сна для дежурных, если они вообще назначаются, 8 часов, для остальных не менее 9 (к концу похода, 20 дней и более – 10) часов. Все равно среднестатистические дежурные быстрее, чем за час, не управятся. Общий подъем разумно объявлять в момент закипания воды. Планируемая продолжительность перекуса 0,5 часа, горячего обеда 1,5…2 часа, утренних сборов 1…2 часа, вечерних бивачных работ до 2,5 часов, но не менее 1 часа. Отсюда планируемая продолжительность рабочего времени (от начала первого перехода до конца последнего) порядка 24 – 9…10 – 0,5…2 – 1…2 – 1…2,5 = 7…12 часов.
Режим движения, в зависимости от нагрузки, обычно меняется от 40/20 (40 минут хода, 20 минут отдыха) до 50/10, то есть используется от 67% до 83% рабочего времени. То есть чистого ходового времени можно планировать от 4 до 10 часов. Опыт показывает, что возможно идти и 12 часов, но, по моим наблюдениям, более 6 часов чистого ходового времени, если такое случается регулярно, очень утомляют группу. Реальное чистое время движения – от 3 часов в походе 1…2 к.с. до 5…6 в походе 4…5 к.с. Обычно до перекуса проходится 4…5 переходов, реже 3 (первый можно сделать укороченным, даже 30/10), после перекуса 3…4.
Отсюда можно планировать дневные переходы, как чистое ходовое время, умноженное на характерную скорость движения:
| Характер местности | Скорость, км/час | Протяженность в день, не более, км |
| Бурелом, топкое болото | 1…1,5 | 10 |
| Перевал 1А – 1Б | 1,5…2 | 5 |
| Осыпь крупная | 1 … 2 | 5 |
| Глухой лес | 2 | 10 |
| Снег с фирном | 2…3 | 5 |
| Осыпь мелкая | 1…2 | 5 |
| Болото моховое | 3…4 | 10 |
| Осыпь средняя | 1,5…2,5 | 15 |
| Перевал н/к (плотная каменистая тропа) | 2…3 | 10 |
| Водораздел травянистый | 3…4 | 10 |
| Плато, пустошь | 4 | 15 |
| Тропа плохая | 3…4 | 15 |
| Тропа хорошая | 4 … 5 | 20 |
| Тропа магистральная | 5 … 5,5 | 20 |
| Дорога грунтовая | 5 | 20 |
| Дорога с покрытием | 5 … 5,5 | 20 |
Максимальная скорость сильно зависит от опыта участников. Для новичковой группы скорость 5 км/ч достижима с трудом, а бывалые люди на перехват вездехода по тундре с рюкзаками бегают.
В продолжительных походах (более 10 дней) непременно накапливаются общая усталость, голод, переохлаждение, плохое настроение и множество прочих неприятностей. Работоспособность группы к этому моменту может существенно упасть, что надо учитывать при составлении маршрута. Случалось, что из-за усталости девальвировались или утрачивались цели похода, нагнеталось раздражение, возникали конфликты, в результате чего прохождение маршрута срывалось. Уставший и злой человек всегда идет неохотно и неустойчиво, что увеличивает риск получения травм даже на простых участках. Поэтому не рекомендуется планировать прохождение сложных препятствий в конце маршрута.
Также не следует планировать большие дневные переходы и сложные препятствия на первые 1…3 дня, пока не прошла акклиматизация к условиям похода. Прохождение технически сложных препятствий рекомендуется в первой половине дня. Перед прохождением особо сложных препятствий рекомендуется сделать облегченный день или даже дневку. Распределение сложности в целом по маршруту рекомендуется следующее:
– начальная часть (1…3 дня). Идет акклиматизация, группа движется с максимальной загрузкой, поэтому рекомендуется уменьшать как дневные переходы (до 10…12 км), так и время хода (делать переходы не по 50…60, а по 30…40 минут). Надо избегать преодоления как локальных, так и серьезных протяженных препятствий, особенно сложных в техническом плане или опасных. Предпочтительны тропы, плато, пустоши, парковые леса.
– основная часть (50…75% похода). Проходятся определяющие препятствия, наибольшие дневные переходы, радиальные выходы. Группа уже немного разгрузилась за счет съеденных продуктов (а здесь чувствуется каждый килограмм на плечах), прошла адаптация к условиям похода, “вспомнились” технические приемы передвижения, поэтому можно увеличить как дневные переходы, так и продолжительность хода до 50…60 минут. Главное, чтобы вместе с продолжительностью перехода не росла и продолжительность “перекура”, иначе ускорение получается сомнительное.
Хорошо бы и здесь постепенно наращивать сложность, например, сначала пройти простой перевал, а уже потом более сложный. Положительный эффект иногда дают полудневки, то есть неполные дневные переходы, к которым можно отнести и восхождения на несложные вершины без груза. Режим движения 8…17 км/день, 20 в исключительных случаях.
– заключительная часть (20…30% похода). Выход “в цивилизацию”, продукты почти все съедены, рюкзаки легкие, поэтому допустимы большие переходы, но без прохождения сложных препятствий, так как накопленная усталость снижает технические возможности участников. Режим движения 13…18 км/день, допустимо и 23…25, но не больше 2…3 дней подряд.
Правильность составленной нитки маршрута можно проверить следующим образом. Нитка может быть (но не всегда является!) правильной, если обладает следующими свойствами:
– приводит к выполнению всех поставленных задач похода;
– не противоречит целям похода;
– начинается и заканчивается в разумных точках входа-выхода;
– верно распределены трудности маршрута;
– технически и физически выполнима;
– имеет заранее продуманные запасные и аварийные выходы.
Особенности разработки маршрутов высоких категорий сложности
Разработать хороший маршрут 3…5 категорий сложности в каком-то смысле даже проще, чем 1…2. Большее значение приобретают красота и логичность маршрута. Составить красивый маршрут становится проще, чем для начальных категорий, так как нитка длиннее, легче можно придумывать варианты прохождения разных участков, запасные выходы. Маршрут уже не так стиснут во времени, появляется возможность существенного перераспределения нагрузки по дням, выделения бОльшего времени для прохождения сложных препятствий и т.п. Так, в походе 1 к.с. практически невозможно выделить запасной день (дневку) под красивой вершиной на случай выжидания погоды: слишком мало всего дней в маршруте. А в походах высоких категорий сложности, например, подождать погоду под Манарагой – обычное дело.
Кажущаяся простота разработки продолжительных маршрутов связана еще и с тем, что составляют их, как правило, бывалые руководители, а не новички. Человек, отводивший несколько походов, может навскидку прикинуть разумный вариант маршрута между заданными точками, видит его потенциальные сложности и опасности, по карте может предложить варианты мест ночлега, интересные объекты и т.п. Эти навыки, к сожалению, приходят со временем и говорить о целенаправленном обучении им достаточно сложно. Но проблемы начинающего руководителя перестают возникать именно тогда, когда руководитель перестает быть начинающим. У него появляется аксиоматическая ясность того, что, например, нет смысла подходить под сложный перевал во второй половине дня, нельзя планировать переправу широкой неизвестной реки далеко от верховий, включать в маршрут без запасного варианта перевал определяющей сложности, на который нет описаний, и так далее. Он начинает видеть красоту и логичность маршрута. Это, в первую очередь, надо именно уметь увидеть, чтобы потом суметь доказать, но не наоборот. Понятие красоты вообще трудно формализуемое. Экспертной оценке, скорее, поддается уродство, то есть, в данном случае, признаки некрасивого, нелогичного маршрута. Ими, например, могут быть:
– затянутые, слишком продолжительные подходы или отходы от интересных участков;
– неравномерная загрузка, неправильное распределение сил на маршруте, дневных переходов, избыток или недостаток дневок;
– нелогичные пути следования между определяющими препятствиями (Целями) маршрута – без посещения расположенных неподалеку интересных объектов, через сложные или утомительные протяженные препятствия и т.п.
– отсутствие разумных запасных вариантов на каждое определяющее препятствие маршрута.
К вопросу о красоте длительного маршрута можно также отнести меры по облегчению физической трудности не в ущерб сложности. Я считаю достоинством для руководителя умение организовать заброску продуктов, или договориться со сплавной группой о переправе через реку, чтобы не делать неразумный крюк в верховья, или предусмотреть логичную закладку продуктов на кольцевом участке маршрута, или предпринять другие меры по уменьшению тонно-километров. Транспортировка груза никогда не является Целью похода! Примерами таких мер могут быть.
– Организация кольцевого однодневного радиального выхода. По существующим правилам, его протяженность (в отличие от линейного радиального выхода) полностью учитывается, а разницы между препятствиями, проходимыми налегке и с грузом, не делается. Разве что на чемпионатах, но на оценку категорию сложности они не влияют.
– Односторонние восхождения на перевалы по определяющей стороне. Как правило, они (и линейно-радиальные, и кольцевые по схеме перевал – вершина – перевал) учитываются МКК наряду с перевалами, пройденными насквозь.
– Организация заказных транспортных забросок и выбросок к интересным районам. Внутримаршрутный транспорт, как известно, строго запрещен.
– Использование сплавного выхода из района для уменьшения стоимости. Это особенно разумно, если планируется кольцевой пеший маршрут: суда забрасываются транспортом и лежат, пока группа не пройдет пешую часть. Как вариант, можно планировать маршрут-восьмерку с судами на берегу реки, которую нельзя перейти вброд. Это позволяет сделать два кольца по обоим берегам.
– Включение в начало маршрута акклиматизационного участка (обычно, кольцевого и с пониженной нагрузкой). Это особенно важно при походах в высокогорных районах.
– Правильная комплектация маршрута участками, учитываемыми при расчете сложности.
Последний пункт требует некоторых пояснений. Существующая методика расчета сложности пешего маршрута довольно трудоемка, вызывает множество вопросов, споров и непонимания, но она есть, и ею необходимо уметь пользоваться. Если изложить методику простыми словами, то прикинуть минимальный набор препятствий для выбранной категории сложности будет очень просто (см. таблицу).
| Категория сложности | Категория сложности препятствия | ||
| Минимальная | Нормальная | Максимальная | |
| 6 | 2А | 2Б | 3А в зачет за 2Б |
| 5 | 1Б | 2А | 2Б |
| 4 | 1А | 1Б | 2А |
| 3 | н/к | 1А | 1Б |
Для того, чтобы сумма баллов за локальные препятствия оказалась достаточной для выбранной категории сложности, достаточно выполнения одного из трех условий:
1. Пройдены локальные препятствия 4 видов от н/к до минимальной сложности. Например, для похода 5 к.с. это могут быть перевалы, вершины, траверсы и переправы н/к, 1А и 1Б – как минимум, один на каждую полукатегорию сложности. Переправы дают 0,5+1+3=4,5 балла, вершины 4+5+7=16, траверсы 4+5+7=16, перевалы 2+4+6=12, итого 4,5+16+16+12=48,5 баллов из 55 максимальных для похода 5 к.с. Добавляем 80 за протяженные, Г*А*К 10…15, и в сумме имеем свыше 138,5 баллов при минимуме 135 для походов 5 к.с.
2. Пройдены локальные препятствия 2 видов от н/к до минимальной сложности и 1 препятствия от н/к до нормальной сложности. Например, для похода 4 к.с. это могут быть траверсы и перевалы н/к и 1А, а вершины н/к, 1А и 1Б. Траверсы дают 4+5=9 баллов, перевалы 2+4=6, вершины 4+5+7=16, итого 9+6+16=31 балл. Плюс 60 за протяженные, Г*А*К 8…10, итого в сумме свыше 99 баллов при минимуме 95 для походов 4 к.с.
3. Пройден хотя бы один вид локальных препятствий от н/к до максимальной включительно. Например, для похода 5 к.с. это могут быть вершины от н/к до 2Б, которые сразу дают 4+5+7+9+9=34 балла (9 баллов дает вершина 2А и 9 – вершина 2Б в зачет за 2А). Поскольку по одним вершинам ходить невозможно, все равно придется и переправы бродить, и перевалы проходить, оставшиеся 11 легко набираются даже перевалами н/к и 1А (2+4=6), переправами н/к и 1А (4*0,5+3*1=7) или траверсами н/к и 1А (4+5=9).
Сумму баллов за протяженные препятствия набрать можно практически всегда, только надо на маршруте озаботиться фотографиями, подтверждающими болото по колено, бурелом, снег и т.п. А без осыпей и не обойдется, причем если внимательно читать правила, то при прохождении перевала или вершины почти всегда встречается осыпь, соответствующая по описанию сложности на полкатегории выше, например, на перевале 1Б сплошь и рядом встречаются “Камни “живые” размером до 1 м, крутизна склона 30-35 , индивидуальная страховка”, то есть осыпь 2А.
Следует отметить, что каждое локальное препятствие, кроме переправ и каньонов, учитывается только один раз. Исключение составляют походы 6 к.с., в которых препятствия нормальной сложности учитываются дважды. То есть повторное прохождение, например, перевала 2А либо вообще не добавляет баллов, либо идет в зачет за более простое препятствие, а сил и времени требует именно на 2А. Поэтому возможна “оптимизация” маршрута под правила – каждое препятствие каждой полукатегории сложности включать в маршрут не более одного раза.
Для повышения количества баллов за протяженные препятствия в маршрут может быть включен водный участок. Но, как правило, разумнее включать участок протяженностью, достаточной для категорийного водного похода соответствующей категории сложности. Тогда поход из пешего станет комбинированными (пеше-водными). По сложившейся практике, категория сложности комбинированного похода определяется на 1 меньше суммы категорий составляющих. Например, маршрут, составленный из 3 пешей + 2 водной в сумме дает 4 пеше-водную. Отсюда следует, что включение водного участка первой категории сложности вообще не повышает суммарную категорию, но может быть учтено, например, в походах 2 и 3 к.с. для увеличения количества баллов.
Организация заброски и выброски
Очень важно до похода надежно проработать варианты подъезда к району путешествия и заброски на заказном транспорте. Лишние задержки в пути, кроме собственно увеличения количества дней, приводят к удорожанию похода и нервируют группу. Сейчас при проведении похода почти в каждом районе можно заранее приобрести билеты, созвониться или списаться с владельцами транспорта и обеспечить надежный проезд группы к началу маршрута.
– Заброска должна состояться! Поэтому надо договориться либо с абсолютно надежным человеком (это должно быть подтверждено не единичным личным или почерпнутым из отчетов опытом), либо с несколькими. Не слишком красиво, конечно, отказываться от запасного перевозчика, но интересы группы для руководителя должны быть важнее. Помните, что перевозчик все-таки находится в своем городе, а вы находитесь в чужом, где проблематично пожить несколько дней, подыскивая заброску взамен несостоявшейся. Правда, отказать надо тактично, чтобы вследствие отказа не возникли проблемы с дружественным перевозчику местным населением…
– Если Вы уверены в своих дипломатических качествах и финансовой обеспеченности, договаривайтесь с одним, оптимальным по каким-либо параметрам, перевозчиком, но найдите в свежих отчетах контактные телефоны или адреса альтернативных. До похода желательно позвонить им и просто поинтересоваться – а что, Вы правда туристов возите? А почем? Заодно и оптимальный вариант подыщете.
– Выброска, заказанная на конкретный день, опасна – при отставании от графика Вы теряете, как правило, сделанную заранее предоплату. Поэтому либо планируйте ее на день после запасного и сидите лишний день в лесу, либо… не опаздывайте.
– Для удешевления заброски и выброски можно либо самому организовать несколько групп в машину на один день, либо присоединиться к компании. Компанию можно найти в специализированных форумах в Internet, а бывает, и перевозчик порекомендует дату, на которую заявлена загруженная наполовину машина.
Также будьте готовы к тому, что по прибытии на место можете обнаружить несоответствие договорной цены с фактической, как правило, в сторону увеличения…
Составление сметы и определение стоимости похода
Затраты на поход складываются из следующих категорий:
1. Затраты на подъезд (отъезд) регулярным транспортом.
2. Затраты на заброску (выброску) заказным транспортом.
3. Затраты на питание в пути.
4. Затраты на питание на маршруте.
5. Затраты на расходные материалы (фотопленка, печать фотографий, бумага и картриджи для печати отчета и т.п.).
6. Затраты на покупаемое многократно используемое снаряжение (кошки, скальное снаряжение, веревки, бивачное оборудование и т.п.).
7. Затраты на покупаемое оборудование, используемое только в этом походе (локальные петли, шлямбуры и т.п. – вплоть до бросаемых на переправах катамаранов).
8. Организационные затраты (оплата посещения особо охраняемых природных территорий, оплата участия в чемпионатах и конкурсах отчетов, организация и проведение до- и послепоходных мероприятий и т.п.)
9. Внеплановые затраты (дополнительное питание и напитки в пути, взятки, внезапное увеличение стоимости транспорта и т.п.).
Каждая группа определяет для себя, какие из этих затрат являются общими, а какие участники оплачивают независимо друг от друга. Обычно пп. 1, 2, 4, 7, 9, частично 3, 5, 6 являются общественными, а п. 7, как правило, относят к индивидуальным затратам. Но возможны, конечно, и другие варианты. В смету похода, естественно, входят только общие затраты. Деньги на них собираются заранее руководителем или казначеем, он отчитывается о расходе средств по окончании похода перед группой.
Оценка стоимости похода, то есть суммы общих затрат, начинается с определения допоходных затрат, к которым относятся пп. 1, 4, 6, 7, частично пп. 2, 3, 5, 8. Основную долю сметы составляют п. 1(2) и п. 3(4).
Транспортные затраты определяются стоимостью билетов и договоренностями о заказном транспорте. Стоимость железнодорожных, авиа и автобусных билетов можно выяснить точно и заранее по телефону или через Internet. В некоторых случаях надо не забыть заложить в смету стоимость провоза багажа. Стоимость заказного транспорта, как правило, не ниже тройной стоимости горючего, то есть от 10 руб/км за “Газель” по асфальту до 150 руб/км за вездеход “ГАЗ-71” по тундре (при оплате расстояния в одну сторону).
Стоимость питания в пути, как правило, не ниже 70…100 рублей в день, особенно если прибегать к услугам общепита. Стоимость питания на маршруте при разумном подборе продуктов порядка 50…70 рублей в день. При использовании дорогих или сублимированных продуктов она возрастает до 200…250 рублей в день.
В целом, опыт показывает, что любой (однодневный, многодневный, категорийный) поход обходится не дешевле 100…120 рублей в день. Это минимальная сумма, на которую можно ориентироваться. Она увеличивается при длинных подъездах к району путешествия.
Часть затрат (пп. 5, 8) приходится на послепоходный период. Вероятно, имеет смысл оценить сумму этих затрат до похода, собрать заранее с участников и иметь с собой на случаи, предусмотренные в п.9 и, частично, в пп. 2, 4, 5.
По окончании похода смета уточняется по фактическим затратам и включается в отчет о походе.
Резюме
Определение целей и задач похода, подбор участников и составление маршрута в соответствии с ними – важнейшая стадия подготовки похода. По окончании разработки маршрута у руководителя в голове (или на бумаге) должен сложиться цельный образ предстоящего путешествия, где учтены все материальные и моральные моменты, непредвиденные ситуации. Только таким образом руководитель может увериться в своей способности успешно провести группу по маршруту, несмотря ни на какие трудности. А без этого и билеты на поезд брать не стоит…
На статью получены рецензии К.В. Бекетова, В.В. Геллера и В.И. Самборского. Часть замечаний рецензентов учтена, в статью внесены дополнения и изменения.
Часть 1. Общий алгоритм поиска
Введение
Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.
Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.
Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.
В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.
Простая схема
Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.
Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».
Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.
Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.
Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.
Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.
Пример
Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.
Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.
Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?
Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.
Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».
Общий алгоритм
Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.
К тому же этот раздел невероятно прост.
Давайте попробуем формализовать наш пример, превратив его в псевдокод.
Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:
reachable = [start_node]
Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:
explored = []Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.
Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.
Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).
while reachable is not empty:Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:
node = choose_node(reachable)
Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:
if node == goal_node:
path = []
while node != None:
path.add(node)
node = node.previous
return pathНет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:
reachable.remove(node)
explored.add(node)Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:
new_reachable = get_adjacent_nodes(node) - exploredМы берём каждый из них:
for adjacent in new_reachable:
Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:
return NoneИ… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
if adjacent not in reachable
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
# If we get here, no path was found :(
return None
Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return pathВот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.
Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:
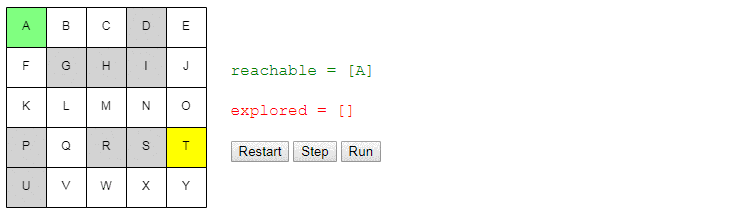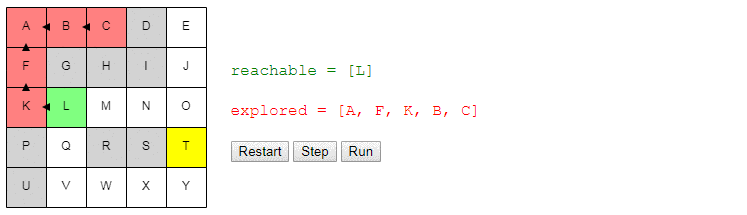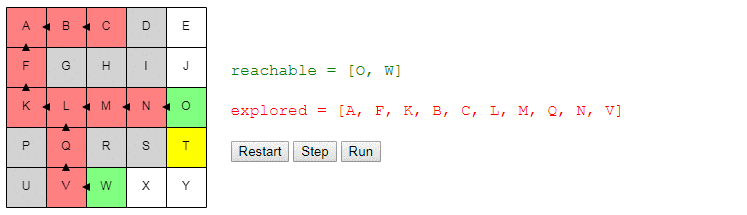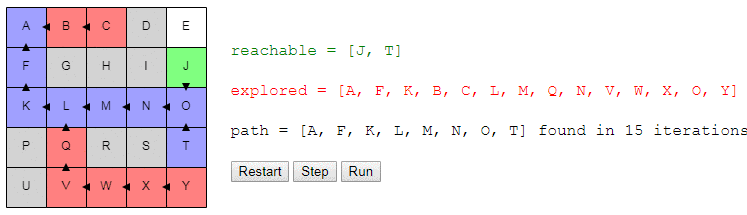
Интерактивное демо
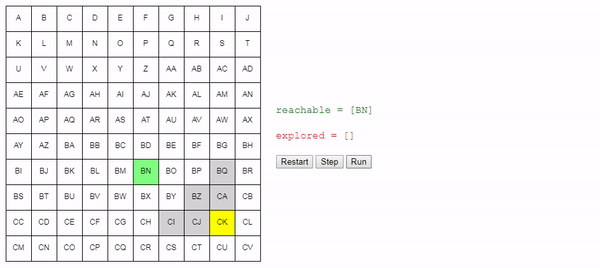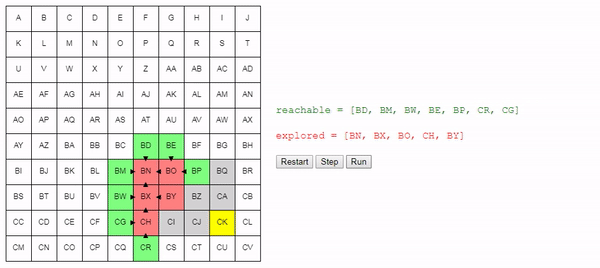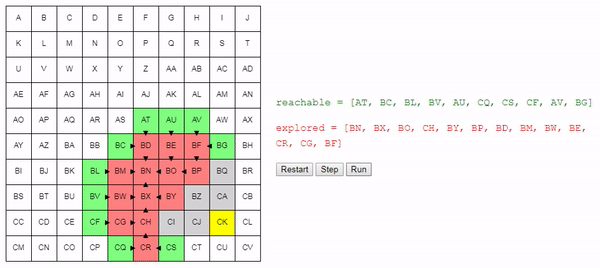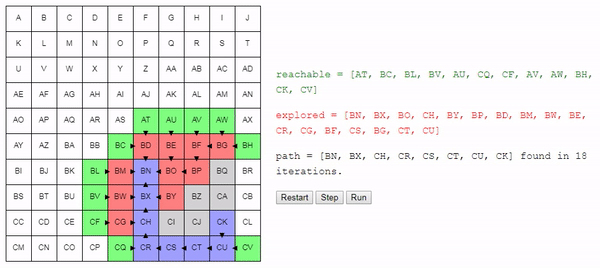
Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.
Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.
Заключение
Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.
Но что же отличает каждый алгоритм от другого, почему A* — это A*?
Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?
Часть 2. Стратегии поиска
Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.
Секретный ингредиент
В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?
Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:
node = choose_node(reachable)
Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.
Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.
Длина имеет значение
Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.
Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.
Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.
Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.
Тогда вот как будет выглядеть код:
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1Одинаковая стоимость поиска
Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.
Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.
Вот возможный пример функции choose_node:
function choose_node (reachable):
best_node = None
for node in reachable:
if best_node == None or best_node.cost > node.cost:
best_node = node
return best_nodeИнтуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:
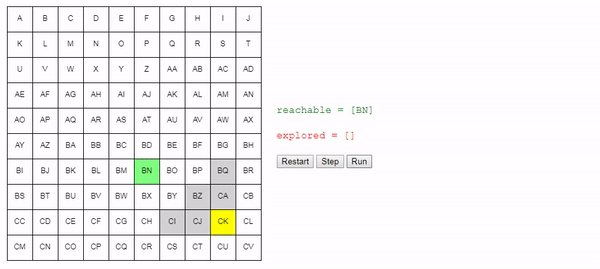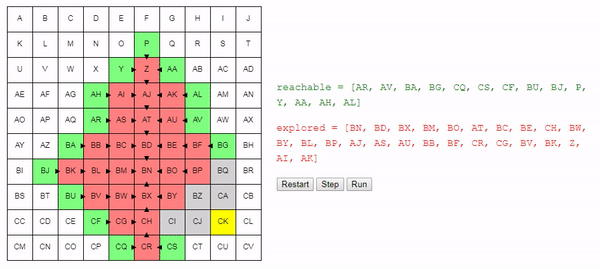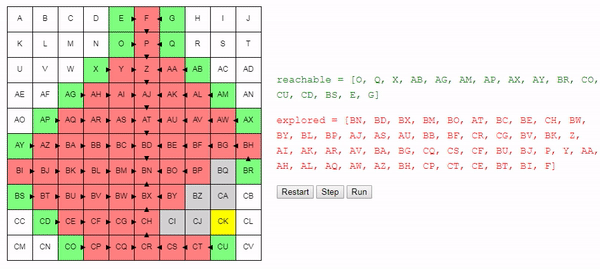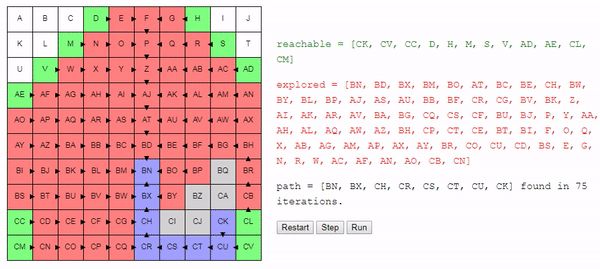
Заключение
Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.
Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?
Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?
Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.
Часть 3. Снимаем завесу тайны с A*
Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?
Волшебный алгоритм
Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:
function choose_node (reachable):
return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = magic(node, "кратчайший путь к цели")
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeЭто отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.
Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.
Не магический, но довольно потрясающий A*
К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:
# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:
cost_node_to_goal = distance(node, goal_node)Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.
Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.
Итак, вот немагическая версия choose_node:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeФункция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.
Интерактивное демо
Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение
Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.
Вот вам для справки полный псевдокод основного метода:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here that we haven't explored before?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
# First time we see this node?
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1
# If we get here, no path was found :(
return None
Метод build_path:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return path
А вот метод choose_node, который превращает его в A*:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_nodeВот и всё.
А зачем же нужна часть 4?
Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.
Часть 4. A* на практике
Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.
Например, что будет, если наш мир не является сеткой?
Что если персонаж не может мгновенно поворачиваться на 90 градусов?
Как построить граф, если мир бесконечен?
Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?
Как найти кратчайший путь к любому из двух конечных узлов?
Функция стоимости
В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?
Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.
В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.
Функция критерия
Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.
Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.
Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.
В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».
Полная определённость не обязательна
Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.
Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.
Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!
Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.
Так почему бы нам просто не строить граф в процессе исследования?
Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.
За пределами трёх измерений
Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?
Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.
Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].
Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].
Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.
Заключение
Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.
Дальнейшее чтение
У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).
Вы хотите добраться на автомобиле из точки А в точку Б по оптимальному маршруту? По маршруту с нужными вам промежуточными пунктами? Поможем вам инструкцией к одному из самых популярных у автомобилистов приложений «Яндекс.Карты».
Для корректной работы приложения не забудьте включить спутниковую навигацию на своём смартфоне.
📍Поездка между двумя точками или стандартный маршрут
Откройте главную страницу приложения и выберите раздел «Маршруты» в нижнем меню.
Если вам нужно выехать из той точки, где вы находитесь, строчку «Откуда» не трогайте. В ней будет отмечено ваше местоположение. Выберите пункт «Куда». Приложение предложит отметить точку прибытия. Это можно сделать тремя способами:
- вбить руками адрес или, скажем, название населённого пункта в поисковую строку;
- то же самое сделать с помощью голосового ввода;
- указать точку с помощью карты.
Далее мы использовали карту.
Рекомендация лучшего маршрута от «Яндекс.Карт» — не истина в последней инстанции. С опытом, в знакомой местности вы время от времени станете выбирать альтернативный путь и добираться при этом быстрее.
📍 Не из точки нахождения, а от точки до точки
Если вы хотите увидеть в качестве начала маршрута какую-то произвольную точку, а не то место, где вы сейчас, то на экране построения маршрута нажмите на пункт «Откуда». Точно так же с помощью карты или поиска задайте пункт старта.
📍Поездка по маршруту через несколько точек
Очень часто по пути к конечной точке нам нужно заехать в пару мест — скажем, по дороге на дачу заскочить на строительный рынок и в магазин за продуктами или развезти приятелей после вечеринки. Все промежуточные пункты можно учесть при планировании поездки.
Откройте страницу построения маршрута. Как мы уже разобрали в предыдущем разделе, если вы стартуете из той точки, где находитесь сейчас, отметьте только точку прибытия. Если вас интересует старт из произвольного места на карте, то укажите и точку старта.
Далее для внесения в маршрут промежуточных точек на том же экране нажмите пункт «Добавить точку». С помощью карты или голосового ввода найдите и отметьте места, где хотите остановиться по пути.
Последовательность точек на маршруте можно менять — не всегда ближайшее место требуется посетить первым. Для изменения порядка зажмите кнопку в виде двух полосок напротив точки маршрута и перетащите его на нужную позицию. В примере ниже мы последний пункт сделали первой промежуточной остановкой.
Кроме маршрута, ещё важно, на чём ехать. На своей? Взять у каршеринга? Кстати, с МТС Premium каршеринг у BelcaCar будет на 10% дешевле.
Узнать больше
Подписывайтесь на наш канал. Рассказываем о гаджетах и технологиях.
✔ ПОДПИСАТЬСЯ НА МТС/МЕДИА
Ещё интересные статьи:
🔴 Как сэкономить на заправке авто? Простой способ для заправок «ЛУКОЙЛ»
🔴 Регистрация авто в 2022 году: документы, сроки и способы
🔴 Регистрация авто в 2022 году: документы, сроки и способы
Маршрутизация работает на сетевом уровне модель взаимодействия открытых систем OSI. Маршрутизация — это поиск маршрута доставки пакета в крупной составной сети через транзитные узлы, которые называются маршрутизаторы.

Маршрутизация состоит из двух этапов:
- На первом этапе происходит изучение сети, какие подсети есть в этой составной сети, какие маршрутизаторы и как эти маршрутизаторы объединены между собой.
- Второй этап маршрутизации выполняется когда сеть уже изучена и на маршрутизатор поступил пакет, для этого пакета нужно определить куда именно его отправить. Иногда для второго этапа маршрутизации используется отдельный термин “продвижение” по-английски forwarding.

Варианты действий маршрутизатора
В качестве примера, рассмотрим схему составной сети, здесь показаны отдельные подсети, для каждой подсети есть ее адрес и маска, а также маршрутизаторы, которые объединяют эти сети.
Рассмотрим маршрутизатор D, на него пришел пакет, и маршрутизатор должен решить, что ему делать с этим пакетом. Начнем с того, какие вообще возможны варианты действий у маршрутизатора. Первый вариант, сеть которой предназначен пакет подключена непосредственно к маршрутизатору. У маршрутизатора D таких сетей 3, в этом случае маршрутизатор передает пакет непосредственно в эту сеть.

Второй вариант, нужная сеть подключена к другому маршрутизатору (А), и известно, какой маршрутизатор нужен. В этом случае, маршрутизатор D передает пакет на следующий маршрутизатор, который может передать пакет в нужную сеть, такой маршрутизатор называется шлюзом.

Третий вариант, пришел пакет для сети, маршрут которой не известен, в этом случае маршрутизатор отбрасывает пакет. В этом отличие работы маршрутизатора от коммутатора, коммутатор отправляет кадр который он не знает куда доставить на все порты, маршрутизатор так не делает. В противном случае составная сеть очень быстро может переполнится мусорными пакетами для которых не известен маршрут доставки.
Что нужно знать маршрутизатору для того чтобы решить куда отправить пакет?
- Во-первых у маршрутизатора есть несколько интерфейсов, к которым подключены сети. Нужно определить в какой из этих интерфейсов отправлять пакет.
- Затем нужно определить, что именно делать с этим пакетом. Есть 2 варианта, можно передать пакет в сеть (192.168.1.0/24), либо можно передать его на один из маршрутизаторов подключенные к этой сети. Если передавать пакет на маршрутизатор, то нужно знать, какой именно из маршрутизаторов подключенных к этой сети, выбрать для передачи пакета.

Таблица маршрутизации
Эту информацию маршрутизатор хранит в таблице маршрутизации. На картинке ниже показан ее упрощенный вид, в которой некоторые служебные столбцы удалены для простоты понимания.

Первые два столбца это адрес и маска подсети, вместе они задают адрес подсети. Затем столбцы шлюз, интерфейс и метрика. Столбец интерфейс говорит о том, через какой интерфейс маршрутизатора нам нужно отправить пакет.
Таблица маршрутизации Windows
Продолжим рассматривать маршрутизатор D, у него есть три интерфейса. Ниже на картинке представлен вид таблицы маршрутизации для windows, которые в качестве идентификатора интерфейса используют ip-адрес, который назначен этому интерфейсу. Таким образом в столбце интерфейс есть 3 ip-адреса, которые соответствуют трем интерфейсам маршрутизатора.

Столбец шлюз, говорит что делать с пакетом, который вышел через заданный интерфейс. Для сетей, которые подключены напрямую к маршрутизатору D, в столбце шлюз, указывается «подсоединен», которое говорит о том, что сеть подключена непосредственно к маршрутизатору и передавать пакет нужно напрямую в эту сеть.

Если же нам нужно передать пакет на следующий маршрутизатор то в поле шлюз указывается ip-адрес этого маршрутизатора.

Таблица маршрутизации Linux
В операционной системе linux таблица маршрутизации выглядит немного по-другому, основное отличие это идентификатор интерфейсов. В linux вместо ip-адресов используется название интерфейсов. Например, wlan название для беспроводного сетевого интерфейса, а eth0 название для проводного интерфейса по сети ethernet.

Также здесь некоторые столбцы удалены для сокращения (Flags, Ref и Use). В других операционных системах и в сетевом оборудовании вид таблицы маршрутизации может быть несколько другой, но всегда будут обязательны столбцы ip-адрес, маска подсети, шлюз, интерфейс и метрика.
Только следующий шаг!
Часто возникает вопрос, что делать, если сеть для который пришел пакет находится не за одним маршрутизатором? Чтобы в неё попасть, нужно пройти не через один, а через несколько маршрутизаторов, что в этом случае нужно вносить в таблицу маршрутизации.

В таблицу маршрутизации записываем только первый шаг, адрес следующего маршрутизатора, все что находится дальше нас не интересует.
Считаем, что следующий маршрутизатор должен знать правильный маршрут до нужной нам сети, он знает лучше следующий маршрутизатор, тот знает следующий шаг и так далее, пока не доберемся до нужные нам сети.

Метрика
Можно заметить, что в нашей схеме в одну и ту же сеть, например вот в эту (10.2.0.0/16) можно попасть двумя путями, первый путь проходят через один маршрутизатор F, а второй путь через два маршрутизатора B и E.

В этом отличие сетевого уровня от канального. На канальном уровне у нас всегда должно быть только одно соединение, а на сетевом уровне допускаются и даже поощряются для обеспечения надежности несколько путей к одной и той же сети.
Какой путь выбрать? Для этого используются поле метрика таблицы маршрутизации.

Метрика это некоторое число, которые характеризует расстояние от одной сети до другой. Если есть несколько маршрутов до одной и той же сети, то выбирается маршрут с меньшей метрикой.

Раньше, метрика измерялось в количестве маршрутизаторов, таким образом расстояние через маршрутизатор F было бы один, а через маршрутизаторы B и E два.

Однако сейчас метрика учитывает не только количество промежуточных маршрутизаторов, но и скорость каналов между сетями, потому что иногда бывает выгоднее пройти через два маршрутизатора, но по более скоростным каналам. Также может учитываться загрузка каналов, поэтому сейчас метрика — это число, которое учитывает все эти характеристики. Мы выбираем маршрут с минимальной метрикой в данном примере выше, будет выбран первый маршрут через маршрутизатор F.
Записи в таблице маршрутизации
Откуда появляются записей в таблице маршрутизации? Есть два варианта статическая маршрутизация и динамическая маршрутизация.
При статической маршрутизации, записи в таблице маршрутизации настраиваются вручную, это удобно делать если у вас сеть небольшая и изменяется редко, но если сеть крупная, то выгоднее использовать динамическую маршрутизацию, в которой маршруты настраиваются автоматически. В этом случае маршрутизаторы сами изучают сеть с помощью протоколов маршрутизации RIP, OSPF, BGP и других.
Преимущество динамической маршрутизации в том, что изменение в сети могут автоматически отмечаться в таблице маршрутизации. Например, если вышел из строя один из маршрутизаторов, то маршрутизаторы по протоколам маршрутизации об этом узнают, и уберут маршрут, который проходит через этот маршрутизатор. С другой стороны, если появился новый маршрутизатор, то это также отразится в таблице маршрутизации автоматически.
Маршрут по умолчанию
Если маршрутизатор не знает куда отправить пакет, то такой пакет отбрасывается. Таким образом получается, что маршрутизатор должен знать маршруты ко всем подсетям в составной сети. На практике для крупных сетей, например для интернета это невозможно, поэтому используются следующие решения.
В таблице маршрутизации назначается специальный маршрутизатор по умолчанию, на которой отправляются все пакеты для неизвестных сетей, как правило это маршрутизатор, который подключен к интернет.
Предполагается что этот маршрутизатор лучше знает структуру сети, и способен найти маршрут в составной сети. Для обозначения маршрута по умолчанию, в таблице маршрутизации используются четыре нуля в адресе подсети и четыре нуля в маске (0.0.0.0, маска 0.0.0.0), а иногда также пишут default.
Ниже пример маршрута по умолчанию в таблице маршрутизации в операционной системе linux.

Ip-адрес и маска равны нулю, в адрес и шлюз указываются ip-адрес маршрутизатора по умолчанию.
Длина маски подсети
Рассмотрим пример. Маршрутизатор принял пакет на ip-адрес (192.168.100.23), в таблице маршрутизации есть 2 записи (192.168.100.0/24 и 192.168.0.0/16) под который подходит этот ip-адрес, но у них разная длина маски. Какую из этих записей выбрать? Выбирается та запись, где маска длиннее, предполагается, что запись с более длинной маской содержит лучший маршрут интересующей нас сети.
Чтобы понять почему так происходит, давайте рассмотрим составную сеть гипотетического университета. Университет получил блок ip-адресов, разделил этот блок ip-адресов на две части, и каждую часть выделил отдельному кампусу.

На кампусе находятся свои маршрутизаторы, на которых сеть была дальше разделена на части предназначенные для отдельных факультетов. Разделение сетей производится с помощью увеличения длины маски, весь блок адресов имеет маску / 16, блоки кампусов имеют маску / 17, а блоки факультетов / 18.
Ниже показан фрагмент таблицы маршрутизации на маршрутизаторе первого кампуса. Он содержит путь до сети первого факультета, 2 факультета, до обще университетской сети, который проходит через университетский маршрутизатор, а также маршрут по умолчанию в интернет, который тоже проходит через обще университетский маршрутизатор.

Предположим, что у на этот маршрутизатор пришел пакет предназначенный для второго факультета, что может сделать маршрутизатор? Он может выбрать запись, которая соответствует второму факультету и отправить непосредственно в сеть этого факультета, либо может выбрать запись, которая соответствует всей университетской сети, тогда отправит на университетский маршрутизатор, что будет явно неправильным.
И так получается, что выбирается всегда маршрут с маской максимальной длины. Общие правила выбора маршрутов следующие.
- Самая длинная маска 32 — это маршрут конкретному хосту, если в таблице маршрутизации есть такой маршрут, то выбирается он.
- Затем выполняется поиск маршрута подсети с маской максимальной длины.
- И только после этого используется маршрут по умолчанию, где маска / 0 под которую подходят все ip-адреса.
Следует отметить, что таблица маршрутизации есть не только у сетевых устройств маршрутизаторов, но и у обычных компьютеров в сети. Хотя у них таблица маршрутизации гораздо меньше.
- Как правило такая таблица содержит описание присоединенной сети, который подключен данный компьютер.
- Адрес маршрутизатора по умолчанию (шлюз или gateway) через который, выполняется подключение к интернет, или к корпоративной сети предприятия.
- А также могут быть дополнительные маршруты к некоторым знакомым сетям, но это необязательно.
Для того чтобы просмотреть таблицу маршрутизации, можно использовать команды route или ip route (route print (Windows); route и ip route (Linux)).
Маршрутизация — поиск маршрута доставки пакета между сетями через транзитные узлы — маршрутизаторы.
