Правило как найти площадь квадрата прямоугольника

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

Была ли эта статья полезной?

Площадь прямоугольника и квадрата

Площадь прямоугольника или квадрата – это часть плоскости, занимаемая данной фигурой.

Рассмотрим два прямоугольника  ABCD  и  A₁B₁C₁D₁:

Чтобы узнать сколько места они занимают, надо вычислить их площадь. Так как размеры прямоугольников даны в сантиметрах, то и за единицу измерения площади можно взять квадратный сантиметр.

Прямоугольник  ABCD  состоит из  4  строк, в каждой из которых по  6  квадратных сантиметров, значит всего в нём  6 · 4,  или  24 см².  A₁B₁C₁D₁  состоит из  3  строк, по  8  квадратных сантиметров, значит в нём  8 · 3,  или  24 см².  Оказалось, что несмотря на то, что прямоугольники имеют разные размеры, они занимают одинаковую площадь.

Из данного примера можно сделать вывод, что площадь прямоугольника равна произведению длин его смежных сторон. Общая формула:

S = a · b,

где  S  — площадь прямоугольника, а  a  и  b  — его смежные стороны.

Рассмотрим квадрат  ABCD:

так как квадрат — прямоугольник, у которого все стороны равны, то в любом квадрате количество строк будет совпадать с количеством квадратных сантиметров, содержащихся в каждой строке. Квадрат  ABCD  состоит из  4  строк, по  4  квадратных сантиметра в каждой, значит в нём  4 · 4,  или  16 см².

Из примера можно сделать вывод, что площадь квадрата равна длине любой его стороны во второй степени. Общая формула:

S = a²,

где  S  — площадь квадрата, а  a  — его сторона.

Чтобы узнать площадь прямоугольника, надо взять его длину и ширину (в одинаковых единицах измерения) и найти их произведение (площадь должна быть выражена в соответствующих единицах измерения).

Формулы площади геометрических фигур

Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

2. Формула площади треугольника по трем сторонам

   Формула Герона

   S = √p(p – a)(p – b)(p – c)

3. Формула площади треугольника по двум сторонам и углу между ними
   
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   где S – площадь треугольника,
   a, b, c – длины сторон треугольника,
   h – высота треугольника,
   γ – угол между сторонами a и b,
   r – радиус вписанной окружности,
   R – радиус описанной окружности,

   p =	a + b + c	– полупериметр треугольника.
   2

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.

   S = a²

2. Формула площади квадрата по длине диагонали
   Площадь квадрата равна половине квадрата длины его диагонали.

   где S – площадь квадрата,
   a – длина стороны квадрата,
   d – длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

   S = a · b · sin α

3. Формула площади параллелограмма по двум диагоналям и углу между ними
   Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

   где S – Площадь параллелограмма,
   a, b – длины сторон параллелограмма,
   h – длина высоты параллелограмма,
   d₁, d₂ – длины диагоналей параллелограмма,
   α – угол между сторонами параллелограмма,
   γ – угол между диагоналями параллелограмма.

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади ромба по длине стороны и углу
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

   S = a² · sin α

3. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.

   где S – Площадь ромба,
   a – длина стороны ромба,
   h – длина высоты ромба,
   α – угол между сторонами ромба,
   d₁, d₂ – длины диагоналей.

Формулы площади трапеции

1. Формула Герона для трапеции

   S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
   |a – b|

2. Формула площади трапеции по длине основ и высоте
   
   Площадь трапеции равна произведению полусуммы ее оснований на высоту

   где S – площадь трапеции,
   a, b – длины основ трапеции,
   c, d – длины боковых сторон трапеции,

   p =	a + b + c + d	– полупериметр трапеции.
   2

Формулы площади выпуклого четырехугольника

1. Формула площади четырехугольника по длине диагоналей и углу между ними

   Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

   где S – площадь четырехугольника,
   d₁, d₂ – длины диагоналей четырехугольника,
   α – угол между диагоналями четырехугольника.

2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

   S = p · r

3. 

   Формула площади четырехугольника по длине сторон и значению противоположных углов

   S = √(p – a)(p – b)(p – c)(p – d) – abcd cos²θ

   где S – площадь четырехугольника,

   a, b, c, d – длины сторон четырехугольника,

   p = a + b + c + d2 – полупериметр четырехугольника,

   θ = α + β2 – полусумма двух противоположных углов четырехугольника.

4. Формула площади четырехугольника, вокруг которого можно описать окружность

   S = √(p – a)(p – b)(p – c)(p – d)

Формулы площади круга

1. Формула площади круга через радиус
   Площадь круга равна произведению квадрата радиуса на число пи.

   S = π r²

2. Формула площади круга через диаметр
   Площадь круга равна четверти произведения квадрата диаметра на число пи.

   где S – Площадь круга,
   r – длина радиуса круга,
   d – длина диаметра круга.

Формулы площади эллипса

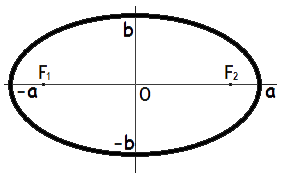
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S – Площадь эллипса,

a – длина большей полуоси эллипса,

b – длина меньшей полуоси эллипса.

План урока:

Площадь прямоугольного треугольника

Площадь произвольного треугольника

Площадь параллелограмма

Площадь ромба

Площадь трапеции

Площадь прямоугольного треугольника

Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?

Прямоугольный треугольник можно достроить до прямоугольника:

Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что

Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.

Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:

Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.

Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:

Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:

x = 10

Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.

Ответ: 10; 20.

Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:

Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:

Подсчитаем площадь каждой из трех фигур по отдельности:

Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:

Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):

Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:

Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S₁, S₂ и S₃:

Площадь произвольного треугольника

Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:

В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:

Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:

В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:

Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):

На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:

Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:

Итак, можно сформулировать следующее правило:

Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.

Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.

Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:

Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.

Решение.

Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что

Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:

Получили одно и то же значение, то есть площади треуг-ков равны.

В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.

Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:

Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:

Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:

Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:

Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:

Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.

Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.

Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.

Решение.

Зная ТН и РЕ, мы сможем найти площадь треуг-ка:

Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ

Величину S_РЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:

Площадь параллелограмма

Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:

На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.

Опустим в параллелограмме АВСD высоты ВН и СК:

В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).

Раз они равны, то одинаковы и их площади:

Но величину S₃ можно заменить на S₂. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:

Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:

Задание. Найдите площадь параллелограмма, изображенного на рисунке:

Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:

Далее надо просто перемножить эти длины:

Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:

Дальше можно просто посчитать по отдельности S₁, S₂и S₃, после чего сложить их. Попробуйте сделать это самостоятельно.

Задание. Площадь параллелограмма равна 162 см², а одна из его высот вдвое короче основания, к которому она проведена. Найдите эту высоту и основание.

Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:

Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.

Ответ: 9 и 18.

Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.

Решение. Опустим на сторону длиной 14 см высоту:

Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:

Площадь ромба

Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.

Построим ромб и проведем в нем диагонали:

Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:

Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, S_AOB:

В результате мы доказали следующее утверждение:

Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.

Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:

Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.

Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:

Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30

Ответ: 10 и 30 см.

Площадь трапеции

Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.

В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:

Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:

Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:

В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:

Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.

Решение. Это простая задача на использование формулы площади трапеции:

Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):

Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:

Считаем площадь:

Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?

Решение. Выполним построение:

Найдем острый угол трапеции. Так как CD||АВ, то

Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:

ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:

Из равенства треуг-ков следует, что

Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.