Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Сложение дробей
Поддержать сайт
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
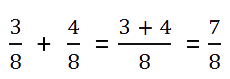
C помощью букв это правило сложения можно записать так:
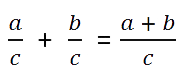
Запомните!
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
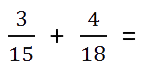
Как найти общий знаменатель
Находим НОК (15, 18).
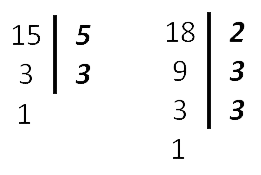
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
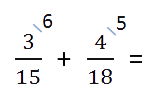
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
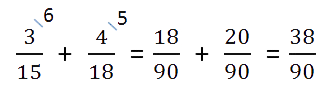
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
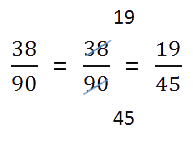
- Eсли в результате получилась
- Ещё раз весь пример целиком.
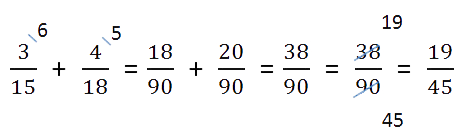
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
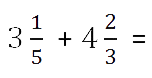
Складываем целые части.
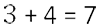
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем.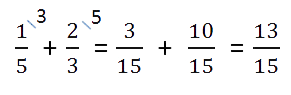
- Сложить полученные результаты из пунктов 1 и 2.
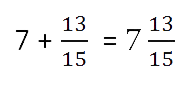
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
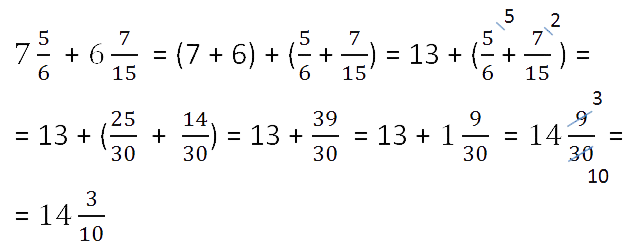
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( – ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + + 
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
Чтобы сложить смешанные числа, надо записать их в виде неправильных дробей, а затем сложить как обыкновенные дроби.
Часто удобней вначале сложить целые части, а затем дробные части, избегаю преобразования в неправильную дробь.
Пример Сложить смешанные числа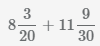
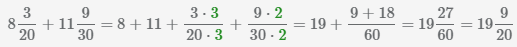
Сократим дробь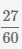 
с помощью нахождения наибольшего общего делителя числителя и знаменателя
и деления полученного числа на числитель и знаменатель, НОД(27,60)=3,
получим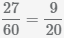 
.
Пример Найти сумму смешанных чисел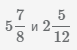
.
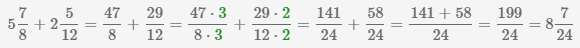В результате сложения также получим смешанное число.
Сложение нескольких дробей
Пример Сложить 3 дроби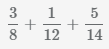
.
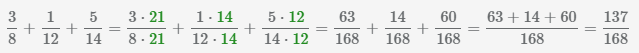Сложение обыкновенных и десятичных дробей
Пример Найти сумму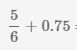
Для сложения десятичных и обыкновенных дробей нужно преобразовать их к одному формату. В данном примере преобразуем десятичную дробь
0.75 в обыкновенную дробь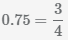 
.
.
Сложение и вычитание дробей
30 июля 2011
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
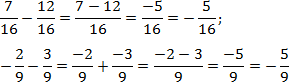
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
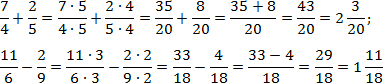
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
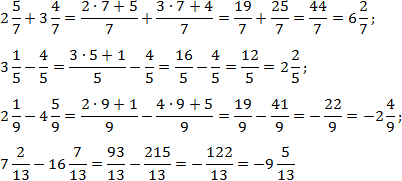
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Смотрите также:
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Приведение дробей к общему знаменателю
- Тест к уроку «Десятичные дроби» (1 вариант)
- Метод узлов в задаче B5
- Задача B5: площадь кольца
- Сфера, вписанная в куб
Содержание:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Сложение смешанных дробей
Сложение дробей с одинаковыми знаменателями
Определение
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме
числителей исходных дробей, а знаменатель – знаменателю дробей, то есть
$frac{a}{b}+frac{c}{b}=frac{a+c}{b}$
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить
их числители и результат записать в числитель, а
знаменатель оставить без изменения.
Пример
Задание. Найти сумму дробей
$frac{3}{11}$ и
$frac{7}{11}$
Решение. $frac{3}{11}+frac{7}{11}=frac{3+7}{11}=frac{10}{11}$
Ответ. $frac{3}{11}+frac{7}{11}=frac{10}{11}$
Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить,
то для конечного результата выполняем и сокращение дроби.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму дробей
$frac{3}{14}$ и
$frac{11}{14}$
Решение. Складываются дроби с одинаковым знаменателем,
поэтому просто складываем числитель, а знаменатель оставляем исходный:
$frac{3}{14}+frac{11}{14}=frac{14}{14}$
Полученная дробь $frac{14}{14}$ является
неправильной, у которой числитель равен знаменателю, и такая дробь равна единице, то есть
$frac{3}{14}+frac{11}{14}=frac{14}{14}=1$
Ответ. $frac{3}{14}+frac{11}{14}=1$
Сложение дробей с разными знаменателями
Определение
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а
далее складывать как дроби с общим знаменателем.
Пример
Задание. Сложить дроби
$frac{2}{3}$ и
$frac{1}{8}$
Решение. Так как дроби с разными знаменателями, то вначале приведем их к
наименьшему общему знаменателю. Для этого найдем НОК чисел 3 и 8:
НОК (3, 8) = 24
Дополнительные множители к каждой из дробей соответственно:
$24 : 3=8,24 : 8=3$
то есть
$frac{2}{3}+frac{1}{8}=frac{2^{8}}{3}+frac{1^{3}}{8}=frac{2 cdot 8+1 cdot 3}{24}=frac{16+3}{24}=frac{19}{24}$
Ответ. $frac{2}{3}+frac{1}{8}=frac{19}{24}$
Замечание. После первого знака равенства справа вверху у каждой дроби указан дополнительный множитель к ней.
Сложение смешанных дробей
Определение
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример
Задание. Вычислить сумму дробей
3$frac{2}{5}$ и
4$frac{7}{10}$
Решение. В данном случае складываем отдельно целые и дробные части:
$3 frac{2}{5}+4 frac{7}{10}=(3+4)+left(frac{2}{5}+frac{7}{10}right)$
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 10, так как НОК
знаменателей 5 и 10. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 2 и 1:
$3 frac{2}{5}+4 frac{7}{10}=7+frac{2^{2}}{5}+frac{7^{1}}{10}=7+frac{2 cdot 2+7 cdot 1}{10}=7+frac{11}{10}=7 frac{11}{10}$
Так как дробная часть представляет собой
неправильную дробь, то выделяем целую часть:
$3 frac{2}{5}+4 frac{7}{10}=7 frac{11}{10}=7left(1+frac{1}{10}right)=8 frac{1}{10}$
Ответ. $3 frac{2}{5}+4 frac{7}{10}=8 frac{1}{10}$
Читать следующую тему: вычитание дробей.
Математика
6 класс
Урок № 38
Сложение дробей
Перечень рассматриваемых вопросов:
- правила сложения рациональных чисел с одинаковыми знаками, разными знаками;
- свойства сложения рациональных чисел, свойство нуля при сложении.
Тезаурус
Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и суммой их числителей.
Чтобы сложить две дроби с разными знаменателями, необходимо сначала привести их к общему положительному знаменателю, а потом сложить числители получившихся дробей.
Сумма противоположных дробей равна нулю.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Продолжаем изучать тему «Рациональные числа». Сегодня узнаем правила, с помощью которых мы будем складывать дроби любого знака.
Определение
Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и суммой их числителей.
Правила сложения рациональных чисел, записанных в виде дробей.
- Если у дробей общий знаменатель, записываем его в знаменатель результата.
- Числители складываем по правилам сложения целых чисел и записываем в числитель результата.
Если требуется, результат сокращаем и преобразовываем в смешанную дробь.
Выполните сложение рациональных чисел, записанных в виде дробей с одинаковыми знаменателями.
Решение
Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых чисел с разными знаками. Результат сокращаем на два.
Выполните сложение рациональных чисел, записанных в виде дробей с одинаковыми знаменателями.
Решение
Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых отрицательных чисел.
Сложение рациональных чисел, записанных в виде дробей с разными знаменателями.
Чтобы сложить две дроби с разными знаменателями необходимо сначала привести их к общему положительному знаменателю, а потом сложить их числители.
Алгоритм действия при сложении рациональных чисел, записанных в виде дробей с разными знаменателями:
найти общий положительный знаменатель;
найти сумму дробей по правилам сложения рациональных чисел, записанных в виде дробей с одинаковыми знаменателями.
Допустим, у нас есть две дроби с разными знаменателями. Необходимо, чтобы знаменатели стали одинаковыми. Используем основное свойство дроби.
Дробь не изменится, если её числитель и знаменатель умножить на одно и то же число.
Значит, если правильно подобрать множители, то знаменатели уравняются. Этот процесс называется приведением к общему знаменателю. А числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Рассмотрим способы нахождения чисел, при умножении на которые знаменатели дробей станут равными.
Умножение «крест-накрест»
Самый простой способ: умножаем первую дробь на знаменатель второй дроби, вторую — на знаменатель первой дроби. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей.
Сложим дроби
При этом способе нахождения общего знаменателя могут получиться большие числа.
Этот способ используется в случае, если знаменатели дробей – взаимно простые числа.
Метод общих делителей
Этот приём помогает сократить вычисления.
Метод заключается в следующем:
если больший знаменатель делится на меньший, то число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем; дробь с большим знаменателем остаётся прежней.
Вычислим сумму
Метод наименьшего общего кратного
Определение
Наименьший общий положительный знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Алгоритм приведения дробей к наименьшему общему положительному знаменателю:
- разложить на простые множители знаменатели дробей;
- найти наименьшее общее кратное (НОК) для знаменателей данных дробей;
- Привести дроби к общему положительному знаменателю, умножив числитель и знаменатель каждой дроби на соответствующие дробям дополнительные множители.
Найдём сумму дробей
Решение
Найдём НОК.
16 = 2 ∙ 8
24 = 3 ∙ 8
НОК:
2 ∙ 8 ∙ 3 = 48
Дополнительные множители:
к первой дроби
48 : 16 =3
ко второй дроби
48 : 24 =2
Сложение противоположных рациональных чисел
Правило сложения противоположных рациональных чисел:
результатом сложения противоположных рациональных чисел будет ноль.
Выполним сложение дробей.
Свойство нуля
Дополнительный материал
Решим задачу.
Решение
Найдём, сколько Кощей израсходовал сам за второй век. 
Дроби с разными знаменателями. Общий знаменатель 10, тогда дополнительный множитель к первой дроби 2. Перемножим и получим:
Перемножим и получим:
Общий знаменатель 8. Дополнительный множитель к первой дроби 4.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
Варианты ответов:
сложение дробей с нулём
сложение дробей с разными знаменателями
сложение дробей с одинаковыми знаменателями
Для выполнения задания обратимся к теоретическому материалу урока.
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Сумма … дробей равна нулю.
Варианты слов для вставки:
противоположных
положительных
отрицательных
положительных и отрицательных
Для выполнения задания обратимся к теоретическому материалу урока.
Правильный ответ
Сумма противоположных дробей равна нулю.
