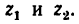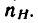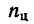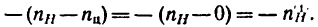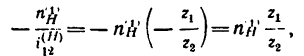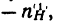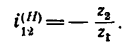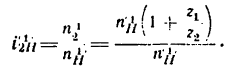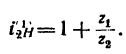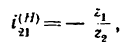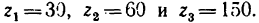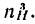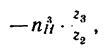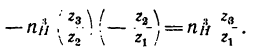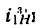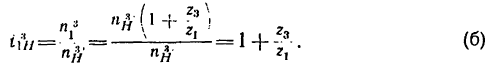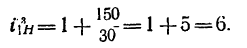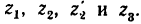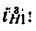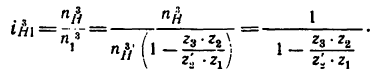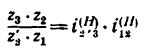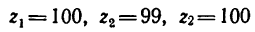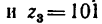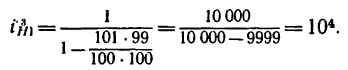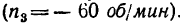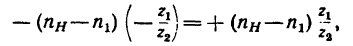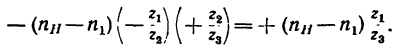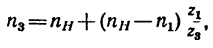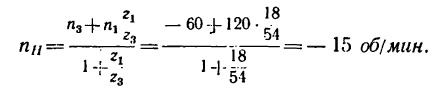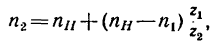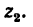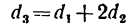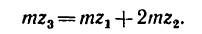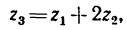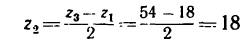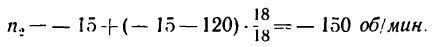Загрузить PDF
Загрузить PDF
В машиностроении передаточное отношение является показателем отношения частоты вращения двух или более сцепленных шестерен. Как правило, когда мы имеем дело с двумя шестернями, и ведущая шестерня (получающая поворачивающую силу непосредственно от двигателя) больше ведомой шестерни, то последняя вращается быстрее (и наоборот). Формула для вычисления: передаточное отношение = T2/ T1, где T1 — количество зубьев первой шестерни, Т2 — количество зубьев второй шестерни.[1]
Две шестерни
-
1
Для того чтобы определить передаточное отношение, у вас должно быть по крайней мере две шестерни, сцепленных друг с другом; такое сцепление называется зубчатой передачей. Как правило, первая шестерня является ведущей шестерней (крепится к валу двигателя), а вторая — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть сколь угодно много шестерен. Они называются промежуточными.
- Сейчас рассмотрим зубчатую передачу с двумя шестернями. Для определения передаточного отношения эти шестерни должны быть сцеплены друг с другом (то есть их зубья сцеплены и одна шестерня поворачивает другую). Например, дана небольшая ведущая шестерня (шестерня 1) и большая ведомая шестерня (шестерня 2).
-
2
Посчитайте количество зубьев на ведущей шестерне. Простейший способ найти передаточное отношение между двумя шестернями — сравнить количество зубьев на каждой из них. Начните с определения количества зубьев на ведущей шестерне. Вы можете сделать это вручную или посмотреть на маркировку шестерни.
- В нашем примере допустим, что меньшая (ведущая) шестерня имеет 20 зубьев.
-
3
Посчитайте количество зубьев на ведомой шестерне.
- В нашем примере допустим, что большая (ведомая) шестерня имеет 30 зубьев.
-
4
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В зависимости от условий задачи вы можете записать ответ в виде десятичной дроби, обыкновенной дроби или в виде отношения (х:у).
- В нашем примере: 30/20 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
- Такое передаточное отношение означает, что меньшая ведущая шестерня должна совершить полтора оборота, чтобы большая ведомая шестерня совершила один оборот. Это имеет смысл, так как ведомая шестерня больше, а значит вращается медленнее.[2]
Реклама
Более двух шестерен
-
1
Зубчатая передача может включать сколь угодно большое количество шестерен. В этом случае первая шестерня является ведущей шестерней (крепится к валу двигателя), а последняя — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть несколько промежуточных шестерен; они используются для изменения направления вращения или для сцепления двух шестерен (когда сцепление напрямую невозможно).[3]
- Рассмотрим пример, приведенный выше, но теперь ведущей шестерней станет шестерня с 7 зубьями, а шестерня с 20 зубьями превратится в промежуточную шестерню (ведомая шестерня с 30 зубьями остается той же).
-
2
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни. Помните, что при определении передаточного отношения зубчатой передачи с несколькими шестернями важно знать только количество зубьев ведомой шестерни и количество зубьев ведущей шестерни, то есть промежуточные шестерни на значение передаточного отношения не влияют.
- В нашем примере: 30/7 = 4,3. Это означает, что ведущая шестерня должна совершить 4,3 оборота, чтобы ведомая (большая) шестерня совершила один оборот.
-
3
Если необходимо, найдите передаточные отношения для промежуточных шестерен. Для этого начните с ведущей шестерни и двигайтесь в направлении ведомой шестерни. При каждом новом вычислении передаточного отношения для промежуточных шестерен рассматривайте предыдущую шестерню в качестве ведущей (и делите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни).
- В нашем примере передаточные отношения для промежуточной шестерни: 20/7 = 2,9 и 30/20 = 1,5. Заметьте, что передаточные отношения для промежуточной шестерни отличаются от передаточного отношения всей зубчатой передачи (4,3).
- Также заметьте, что (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Реклама
-
1
Определите частоту вращения ведущей шестерни. Используя передаточное отношение и частоту вращения ведущей шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (rpm).
- Рассмотрим пример зубчатой передачи, описанной выше (с тремя шестернями). Здесь частота вращения ведущей шестерни равна 130 оборотам в минуту. Вычислим частоту вращения ведомой шестерни.
-
2
Подставьте соответствующие значения в формулу: S1 × T1 = S2 × T2, где S1, Т1 — частота вращения и количество зубьев ведущей шестерни; S2, Т2 — частота вращения и количество зубьев ведомой шестерни.
- В нашем примере нужно найти S2, но по этой формуле вы можете найти любую переменную.
- 130 rpm × 7 = S2 × 30
-
3
Теперь просто обособьте неизвестную переменную на одной стороне уравнения, чтобы получить ответ. Не забудьте приписать к нему соответствующую единицу измерения.
- В нашем примере:
- 130 rpm × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30,33 rpm = S2
- Другими словами, если ведущая шестерня вращается со скоростью 130 оборотов в минуту, ведомая шестерня будет вращаться со скоростью 30,33 оборотов в минуту. Это имеет смысл, так как ведомая шестерня значительно больше, а значит вращается намного медленнее.
Реклама
Советы
- Для того, чтобы понять принцип передаточного отношения в действии, покатайтесь на велосипеде! Обратите внимание, что проще всего ехать в гору, когда у вас небольшая шестерня спереди, а большая сзади. Хотя педалями легче крутить меньшую шестерню, понадобится множество вращений, чтобы заставить заднее колесо вращаться, то есть скорость велосипеда будет ниже.
- Мощность, необходимая для движения нагрузки, может увеличиваться или уменьшаться (относительно мощности двигателя) посредством зубчатой передачи. При проектировании двигателя необходимо учитывать передаточное отношение, чтобы мощность двигателя соответствовала характеру будущей нагрузки. Повышающая система (в которой обороты вала нагрузки выше, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при меньших скоростях вращения ведущего вала.
- С другой стороны, понижающая система (в которой обороты вала нагрузки ниже, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при больших скоростях вращения ведущего вала.
Реклама
Об этой статье
Эту страницу просматривали 256 555 раз.
Была ли эта статья полезной?
Пример 1
Определить
передаточное отношение зубчатой передачи
(рис. 19), число оборотов ведомого вала и
общий коэффициент полезного действия
(кпд), если количества зубьев колес
равны: z1=30,
z2=20,
z3=45,
z4=30,
z5=20,
z6=120,
z7=25,
z8=15;
число оборотов ведущего вала n1=1600
об/мин.
Рис.
19
Решение
Механизм состоит
из четырех ступеней: двух цилиндрических
z1–z2,
z3–z4
с внешним зацеплением, цилиндрической
z5–z6
с внутренним зацеплением и конической
z7–z8.
Общее передаточное
отношение многоступенчатой передачи
равно произведению передаточных
отношений каждой ступени, образующих
этот зубчатый механизм. Для данного
случая
.
Знак (–) показывает,
что направление вращения колес в этих
парах противоположное. Направление
вращения колес в данном случае так же
можно определить путем простановки
стрелок на схеме (рис. 19).
Число оборотов
ведомого вала определяем через
передаточное отношение
об/мин.
Общий кпд зубчатого
механизма равен
,
где числовые
значения приняты согласно условию
задачи Т1.
Пример 2
|
Рис. 20 |
Для редуктора Решение
Рассматриваемый |
Здесь
,
,
– передаточные отношения преобразованного
механизма (водилоН
остановлено, а вращается неподвижное
колесо z3).
Полученное передаточное отношение со
знаком «+» свидетельствует о совпадении
направлений вращения ведущего и ведомого
валов.
Пример 3
|
Рис. 21 |
Для редуктора |
Решение
Как и в примере 2
этот механизм относится к одноступенчатой
планетарной передаче и передаточное
отношение от водила Н
к колесу z1
определяется отношением

Пример 4
|
Рис. 22 |
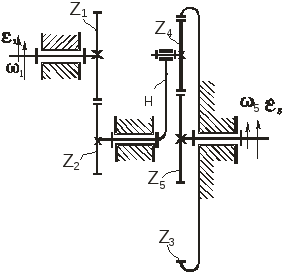
Для зубчатой
z1=20,
|
Решение
Сложная зубчатая
передача состоит из двух ступеней:
первая ступень – простая цилиндрическая
пара с внешним зацеплением z1-z2,
вторая ступень – планетарный механизм
Н-z5,
передающий вращательное движение от
водила Н
к колесу z5
через сателлит z4.
Направление вращения выходного вала
определяется алгебраическим знаком.
1. Для двухступенчатой
передачи общее передаточное отношение
находим через передаточные отношения
каждой ступени, т.е.
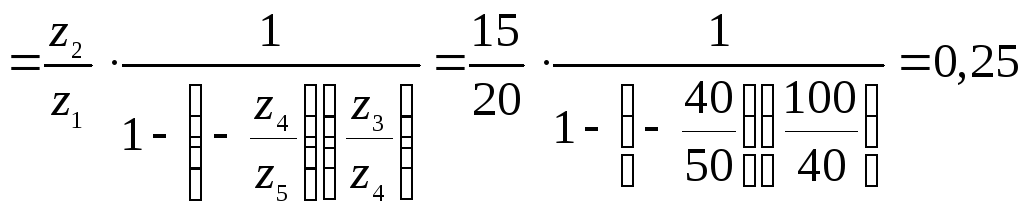
Полученное
передаточное отношение
,
что свидетельствует о повышении частоты
вращения выходного вала, а знак «+»
показывает, что направления вращения
валов совпадают.
2. Определяем
угловую скорость выходного звена
и его угловое ускорение
рад/с,
рад/с2.
3. Поскольку вращение
колес ускоренное (принимаем равноускоренное),
то время, в течение которого угловые
скорости увеличатся в два раза, определим
из зависимости
,
где
и
– угловые скорости соответственно в
начале и в конце рассматриваемого
периода времени.
Отсюда
с.
4. Определяем общий
коэффициент полезного действия передачи
.
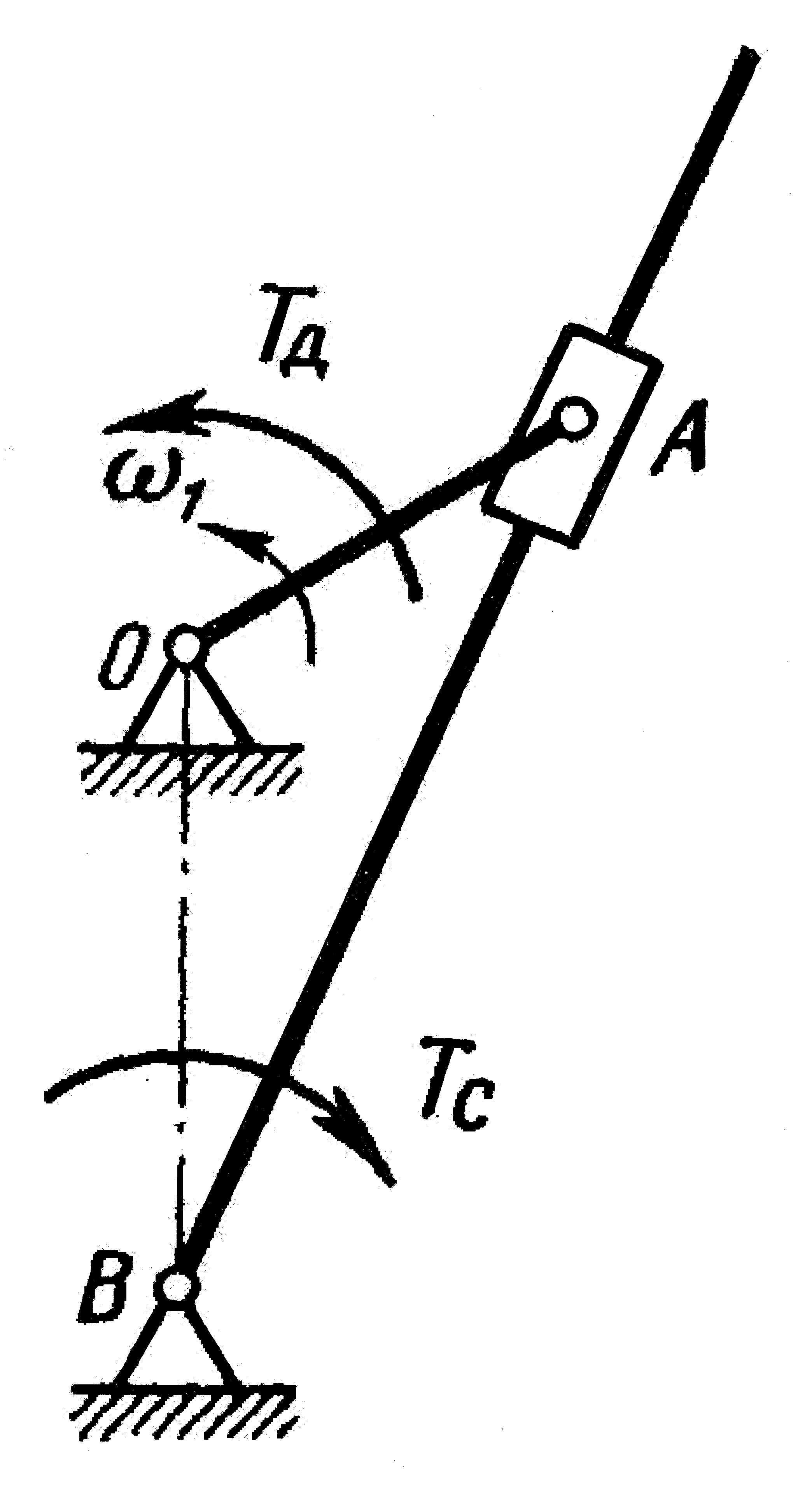
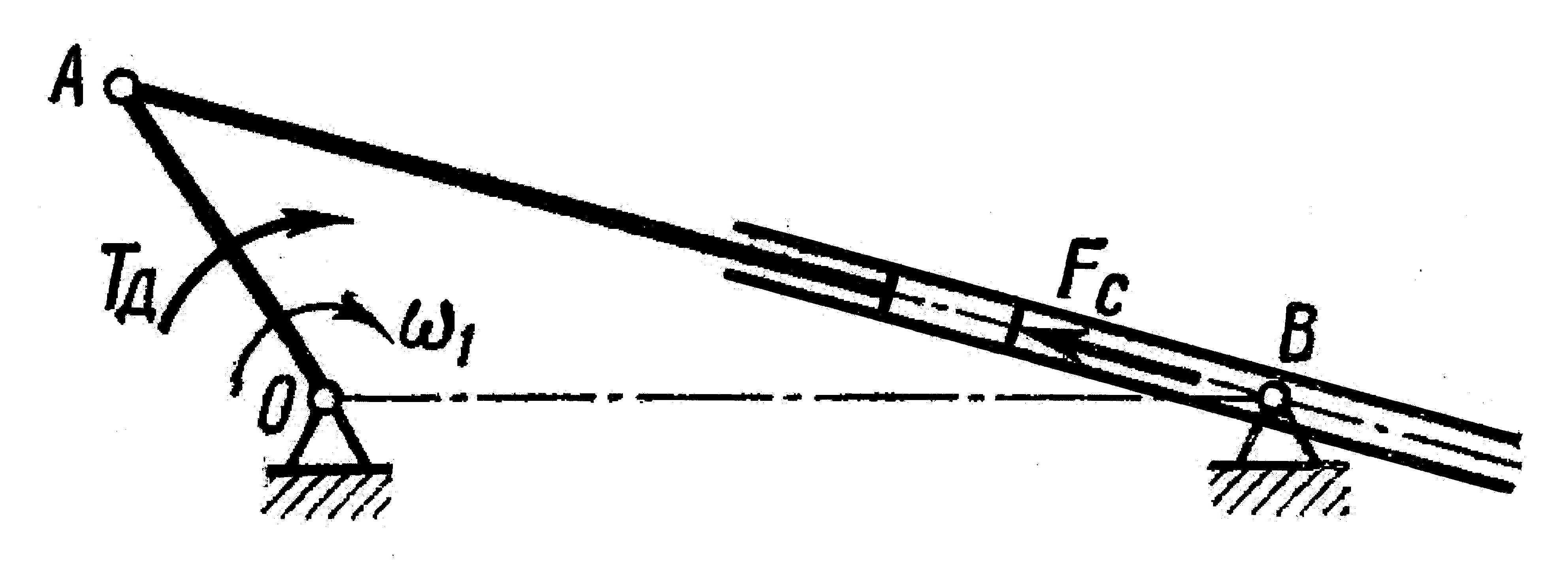
Задача Т2
Выходное
звено механизма, показанного на схемах
(рис. 23–32), совершает возвратно-поступательное
(или возвратно-вращательное) движение
и нагружено на рабочем ходу постоянной
силой Fc
(или
моментом Тс)
полезного сопротивления. На холостом
ходу, при обратном направлении движения
выходного звена, полезное сопротивление
отсутствует, но продолжают действовать
вредные. Учитывая действие трения в
кинематических парах, по коэффициенту
полезного действия
механизма необходимо определить:
1)
движущий момент Тд,
постоянный по величине, который нужно
приложить к входному звену при
установившемся движении с циклом,
состоящим из рабочего и холостого ходов;
2) работы сил трения
на рабочем и холостом ходах, считая, что
вредное сопротивление постоянно на
каждом из ходов, но на рабочем ходу оно
в три раза больше, чем на холостом;
3)
изменение кинетической энергии механизма
за время рабочего хода и за время
холостого хода;
4)
мощность, требуемую от привода при
вращении входного звена со
средней скоростью
и средние (за целый оборот) мощности
полезного сопротивления и сил трения.
Решение
этой задачи основано на уравнении
движения механизма, устанавливающем
связь между изменением кинетической
энергии и работами сил (законе кинетической
энергии). Работа сил и моментов
определяется соответственно по линейным
или угловым перемещениям звеньев,
на которые они действуют. В связи с этим
требуется определить положения механизма
при крайних положениях выходного звена.
Перемещения звеньев, линейные и угловые,
можно определить по чертежу,
выполненному в масштабе, или рассчитать
аналитически. Размеры звеньев,
согласно их обозначениям на схеме
механизма, и другие необходимые величины
приведены в таблицах числовых данных,
где
– коэффициент полезного действия, а в
варианте 9m
– модуль реечного зацепления, z
–
число зубьев колеса.
|
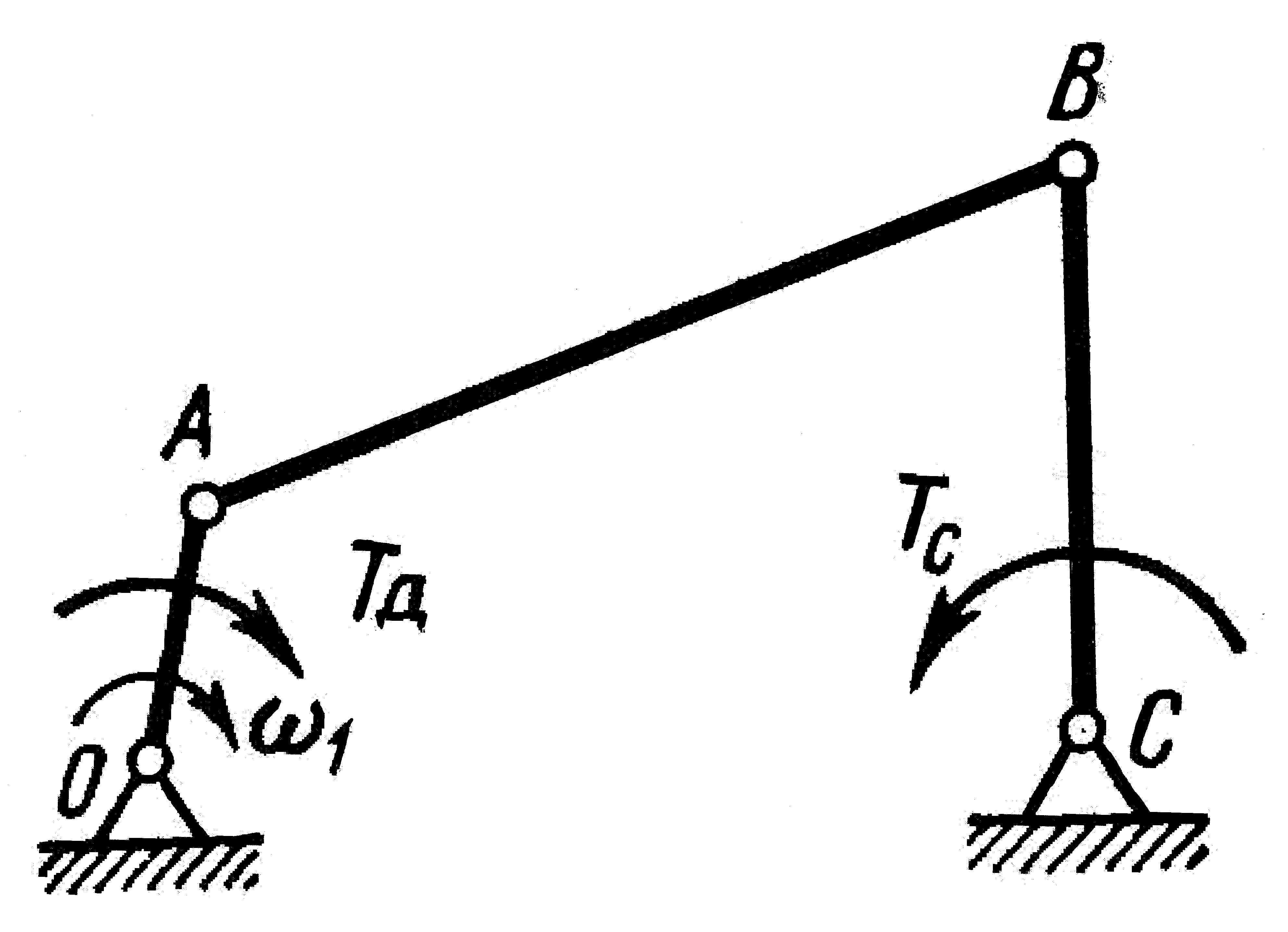
Вариант 1. Шарнирный (рис. 23, табл. 17) Рис. |
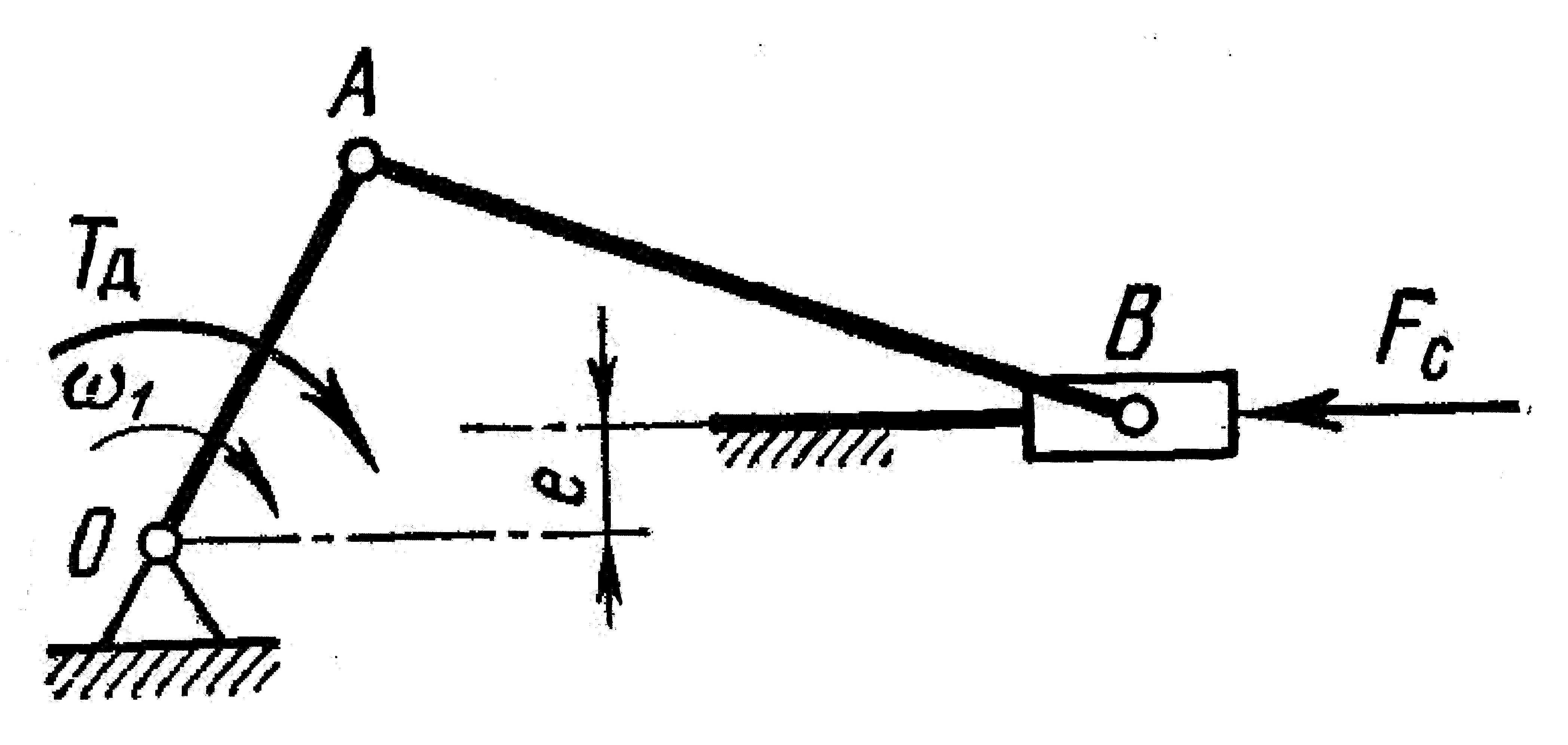
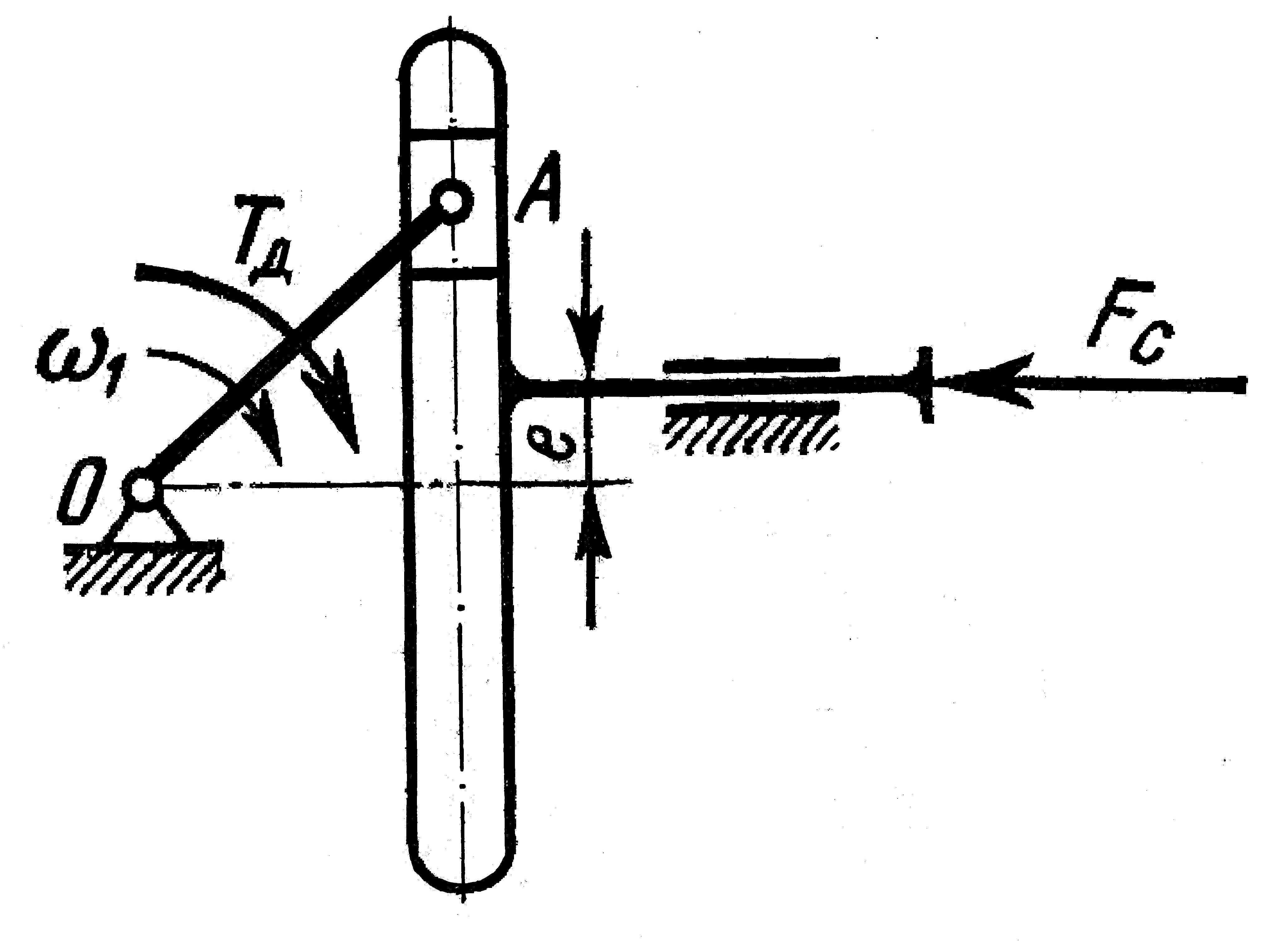
Вариант 2. Рис. |
Таблица
17
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
70 |
100 |
60 |
120 |
50 |
100 |
40 |
80 |
30 |
60 |
|
ОС, |
160 |
250 |
120 |
240 |
120 |
200 |
100 |
160 |
70 |
120 |
|
ВС, |
150 |
250 |
160 |
200 |
100 |
250 |
250 |
200 |
80 |
150 |
|
АВ, |
130 |
250 |
180 |
300 |
150 |
250 |
250 |
200 |
80 |
150 |
|
Т |
240 |
600 |
250 |
300 |
200 |
120 |
20 |
150 |
25 |
90 |
|
|
0,90 |
0,92 |
0,93 |
0,89 |
0,94 |
0,91 |
0,92 |
0,9 |
0,93 |
0,84 |
|
|
120 |
10 |
60 |
80 |
250 |
80 |
150 |
50 |
160 |
100 |
Таблица
18
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
120 |
120 |
25 |
100 |
100 |
80 |
20 |
50 |
40 |
50 |
|
е, |
60 |
50 |
10 |
4 |
30 |
20 |
10 |
25 |
8 |
10 |
|
АВ, |
400 |
300 |
100 |
30 |
300 |
300 |
90 |
200 |
100 |
100 |
|
Fc, |
8000 |
9000 |
1000 |
90 |
7000 |
8000 |
1000 |
2000 |
800 |
500 |
|
|
0,76 |
0,7 |
0,8 |
0,9 |
0,86 |
0,9 |
0,75 |
0,7 |
0,8 |
0,85 |
|
|
60 |
100 |
240 |
400 |
30 |
150 |
300 |
250 |
200 |
100 |
|
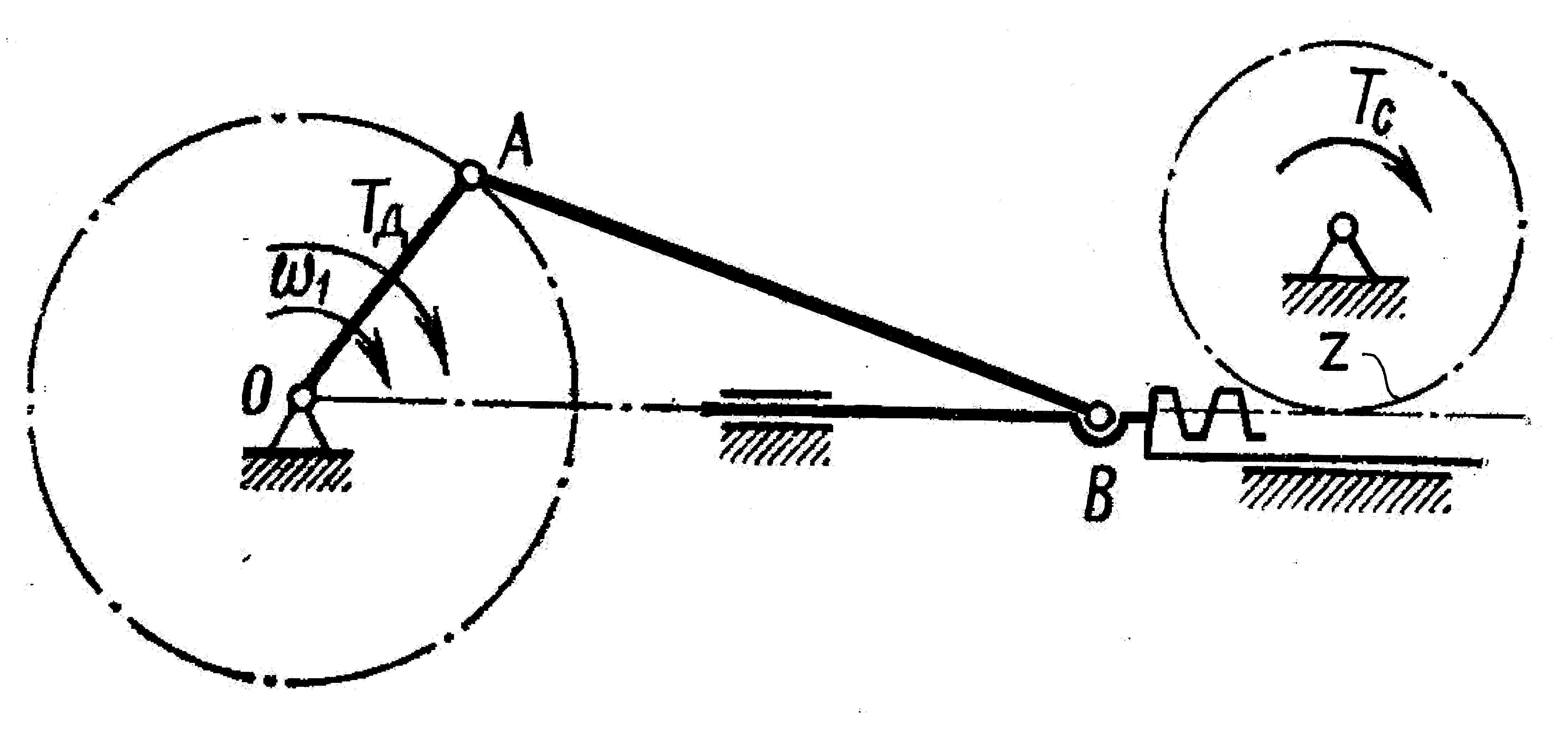
Вариант 3. Кулисный
Рис. |
Вариант 4. Механизм Рис. |
Таблица
19
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
60 |
30 |
60 |
180 |
120 |
25 |
200 |
150 |
100 |
50 |
|
ОВ, |
120 |
80 |
150 |
700 |
500 |
100 |
500 |
400 |
200 |
100 |
|
Тс, |
150 |
1 |
700 |
900 |
300 |
4 |
800 |
450 |
500 |
50 |
|
|
0,72 |
0,69 |
0,74 |
0,73 |
0,75 |
0,71 |
0,68 |
0,7 |
0,7 |
0,75 |
|
|
60 |
160 |
40 |
12 |
25 |
12 |
10 |
15 |
8 |
10 |
Таблица
20
|
Величина |
Предпоследняя |
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
ОА, |
50 |
100 |
160 |
200 |
25 |
120 |
150 |
60 |
30 |
50 |
|
|
ОВ, |
120 |
250 |
400 |
500 |
100 |
500 |
450 |
180 |
100 |
100 |
|
|
ВС=ВD, |
150 |
400 |
600 |
900 |
180 |
650 |
600 |
300 |
150 |
180 |
|
|
Fc, |
600 |
3000 |
5000 |
8000 |
250 |
2000 |
9000 |
500 |
100 |
150 |
|
|
|
0,6 |
0,62 |
0,64 |
0,65 |
0,6 |
0,61 |
0,63 |
0,64 |
0,6 |
0,65 |
|
|
|
40 |
30 |
20 |
10 |
40 |
25 |
15 |
30 |
80 |
ЕО |
|
|
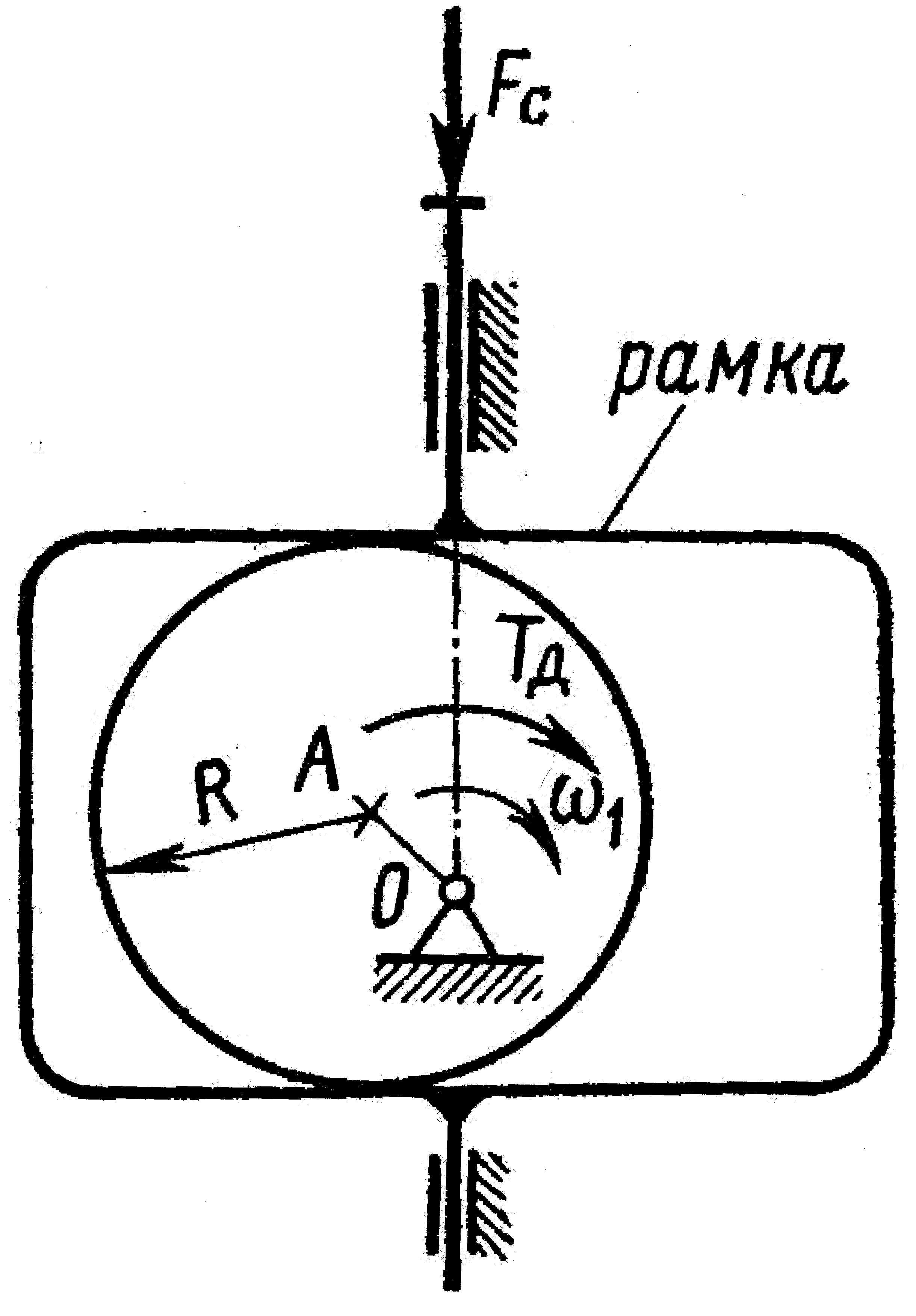
Вариант 5. Механизм (рис. 27, табл. 21) Рис. |
Вариант 6. Кулисный (рис. 28, табл. 22)
Рис. |
Таблица
21
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
R, |
40 |
15 |
20 |
30 |
25 |
45 |
50 |
20 |
60 |
40 |
|
ОА, |
25 |
10 |
12 |
15 |
15 |
20 |
20 |
10 |
25 |
15 |
|
Fc, |
65 |
30 |
45 |
65 |
60 |
90 |
120 |
50 |
100 |
40 |
|
|
0,72 |
0,7 |
0,71 |
0,69 |
0,7 |
0,72 |
0,68 |
0,71 |
0,72 |
0,7 |
|
|
75 |
150 |
120 |
100 |
90 |
90 |
70 |
100 |
60 |
80 |
Таблица
22
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
30 |
30 |
65 |
180 |
120 |
25 |
200 |
160 |
100 |
50 |
|
ОВ, |
100 |
80 |
200 |
650 |
480 |
100 |
620 |
400 |
220 |
90 |
|
BD, |
250 |
150 |
300 |
900 |
650 |
200 |
900 |
650 |
360 |
150 |
|
Fc, |
100 |
50 |
500 |
9000 |
2000 |
20 |
800 |
500 |
3000 |
600 |
|
|
0,64 |
0,62 |
0,65 |
0,63 |
0,61 |
0,6 |
0,65 |
0,64 |
0,62 |
0,6 |
|
|
50 |
150 |
30 |
12 |
25 |
40 |
10 |
16 |
10 |
20 |
|
Вариант 7. Синусный Рис. 29 |
Вариант 8. Механизм Рис. |
Таблица
23
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
60 |
25 |
100 |
10 |
40 |
20 |
80 |
60 |
50 |
30 |
|
е, |
30 |
15 |
40 |
5 |
0 |
10 |
30 |
30 |
10 |
12 |
|
Fc, |
400 |
120 |
200 |
10 |
400 |
50 |
2000 |
800 |
200 |
100 |
|
|
0,65 |
0,80 |
0,68 |
0,75 |
0,72 |
0,75 |
0,71 |
0,65 |
0,80 |
0,7 |
|
|
100 |
150 |
60 |
180 |
80 |
150 |
80 |
140 |
120 |
100 |
Таблица
24
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
R, |
40 |
60 |
25 |
50 |
42 |
25 |
30 |
20 |
15 |
35 |
|
ОА, |
15 |
20 |
10 |
20 |
15 |
10 |
18 |
14 |
7 |
22 |
|
r, |
10 |
15 |
6 |
12 |
10 |
7 |
8 |
4 |
5 |
8 |
|
|
0,81 |
0,8 |
0,82 |
0,84 |
0,8 |
0,85 |
0,83 |
0,8 |
0,81 |
0,8 |
|
Fc, |
55 |
120 |
50 |
100 |
90 |
60 |
65 |
45 |
30 |
70 |
|
|
80 |
60 |
100 |
80 |
90 |
110 |
180 |
120 |
140 |
70 |
|
Вариант 9. Синусный
Рис. 31 |
Вариант 10. Механизм
Рис. |
Таблица
25
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
38 |
150 |
35 |
22 |
15 |
40 |
25 |
30 |
20 |
10 |
|
АВ, |
100 |
450 |
80 |
55 |
40 |
100 |
75 |
80 |
50 |
30 |
|
m, |
3 |
5 |
1,5 |
2 |
1,5 |
3 |
2,5 |
2 |
2 |
1,5 |
|
z |
25 |
20 |
30 |
35 |
40 |
30 |
20 |
50 |
30 |
40 |
|
|
0,72 |
0,7 |
0,69 |
0,76 |
0,73 |
0,76 |
0,74 |
0,71 |
0,72 |
0,7 |
|
Тс, |
200 |
2500 |
15 |
400 |
20 |
120 |
45 |
60 |
30 |
20 |
|
|
50 |
75 |
50 |
60 |
85 |
70 |
120 |
90 |
80 |
100 |
Таблица
26
|
Величина |
Предпоследняя |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
ОА, |
150 |
130 |
25 |
10 |
150 |
20 |
100 |
80 |
40 |
50 |
|
ОВ, |
280 |
300 |
70 |
30 |
350 |
80 |
350 |
300 |
100 |
150 |
|
Fc, |
4000 |
9000 |
1500 |
1000 |
5000 |
1800 |
8000 |
4000 |
1500 |
1200 |
|
|
0,75 |
0,77 |
0,79 |
о.а |
0,74 |
0,8 |
0,75 |
о,7а |
0,76 |
0,75 |
|
|
25 |
50 |
120 |
100 |
20 |
90 |
30 |
40 |
80 |
60 |
Последовательность
выполнения задания. Во-первых необходимо
построить механизм в крайних положениях,
и по заданным направлениям угловой
скорости входного звена
и постоянной силыFс
(или
момента Тс)
полезного сопротивления установить
рабочие и холостые ходы.
При
графическом определении линейных и
угловых перемещений звеньев необходимо
снять с чертежа:
1) для
входного звена его углы поворота на
рабочем ходу
и на холостом
х;
2) для
выходного звена при его возвратно-поступательном
движении линейное перемещение, т.е.
ход s,
или при его возвратно-вращательном
движении угол размаха
.
Для
того чтобы определить зоны рабочего и
холостого ходов для входного звена,
нужно учитывать связь движения с
показанным направлением действия
полезного сопротивления, которое на
рабочем ходу должно препятствовать
движению выходного звена.
В
вариантах 5 и 8 применено геометрическое
замыкание звеньев в высшей паре,
предупреждающее отход звеньев друг от
друга: в варианте 8 ролик радиуса r
перекатывается
в круговом пазу входного звена, охваченный
наружным и внутренним профилями паза,
в варианте 5 круглый эксцентрик охвачен
рамкой выходного звена.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
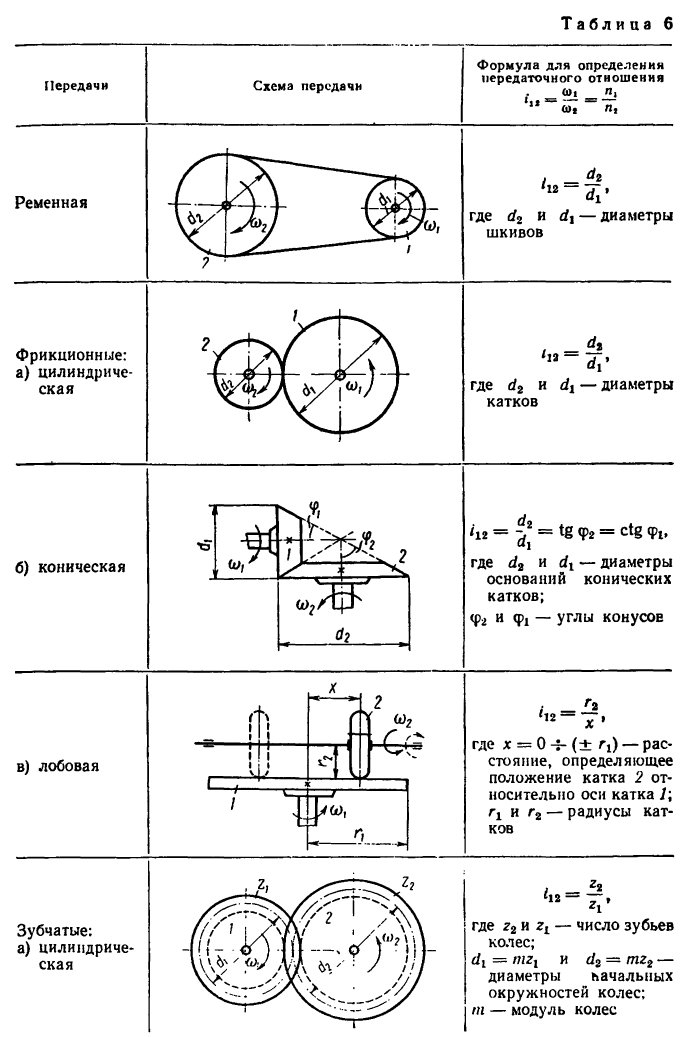
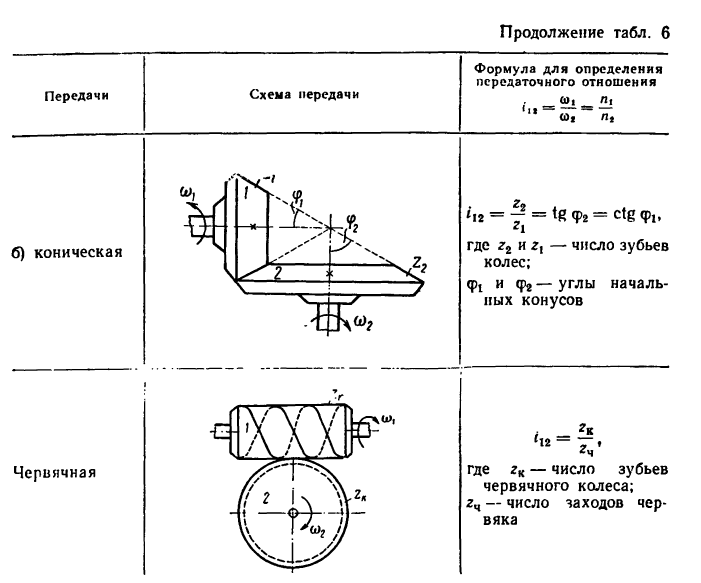
Определение передаточных отношений различных передач:
Передаточное отношение — основная кинематическая характеристика любой передачи.
Передаточные отношения определяются при помощи тех или иных геометрических элементов звеньев передачи. Найденное его значение выражает отношение угловых скоростей
Даны формулы, при помощи которых определяются передаточные отношения различных простейших передач, составленных из пары звеньев.
Передаточное отношение сложной передачи — передачи, составленной из нескольких простейших передач, равно произведению передаточных отношений простейших передач:
Передаточное отношение между двумя элементами передачи считается положительным, если оба элемента вращаются в одну сторону, например пара зубчатых колес с внутренним зацеплением.
Передаточное отношение между двумя элементами считается отрицательным, если оба элемента вращаются в противоположные стороны, например пара зубчатых цилиндрических колес с внешним зацеплением.
Задача №1
На каком расстоянии х необходимо установить каток 2 лобовой фрикционной передачи (см. эскиз к лобовой передаче в табл. 6), чтобы при угловой скорости 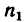
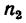
Определить также, какие наименьшую и наибольшую угловые скорости может получить вал катка 2 при различных положениях последнего.
Решение.
1. Необходимое значение х (расстояние от катка 2 до оси катка I) найдем непосредственно из формулы передаточного отношения любой передачи:
2. Если начать передвигать каток 2 ближе к краю катка 1 (увеличить х), то точки на ободе катка 2 будут вступать в контакт с точками на торцовом поверхности катка 1, имеющими возрастающую скорость (по зависимости
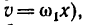
Если в выражение
вместо х подставить наибольшее, теоретически возможное значение х — 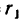
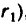
3. Если каток 2 установить у противоположного края катка 1, то угловая скорость у катка 2 также получится 10000 об/мин, но он будет вращаться в обратную сторону.
Таким образом, при
Благодаря способности изменять направление вращения вала, на котором укреплен каток 2, лобовую фрикционную передачу называют фрикционным вариатором (передача, способная варьировать направлением вращения).
4. При х = 0 (положение катка 2 совпадает с осью катка 1)
Точки на ободе катка 2 касаются практически неподвижных точек на торце катка 1 и поэтому не двигаются.
Иначе говоря, если в выражении 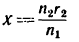
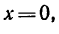
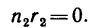
Задача №2
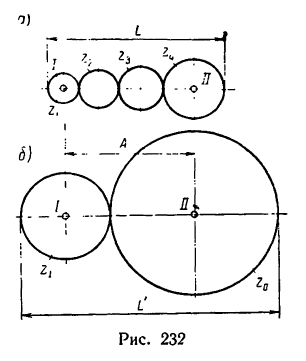
Передача вращательного движения между валами I и II осуществляется при помощи четырех зубчатых колес, два из которых помещены на промежуточных валах (рис. 232, а). Числа зубьев колес:
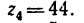
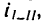
Решение.
1. Передаточное отношение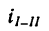
Как видно, зубчатые колеса, находящиеся на промежуточных осях, не влияют на величину передаточного отношения; поэтому их иногда называют «паразитными».
2. Находим межосевое расстояние А (см. рис. 232, а):
где 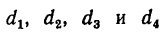
Подставляем вместо значений диаметров их выражения через модуль m и соответствующие числа зубьев:
Откуда
3. Находим габариты передачи L (см. рис. 232, а):
4. Если осуществить передачу при помощи двух колес с числами зубьев 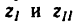
Здесь имеются два неизвестных 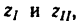
Из уравнения (2)
(как уже известно,
Подставим найденное значение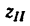
откуда
Теперь, зная число зубьев, легко определить габариты двухколесного варианта передачи:
Как видно, габариты увеличиваются на 300 мм, т. е почти в 1,5 раза (на 47,5%).
Отсюда следует сделать вывод, что при значительных межосевых расстояниях, которые по конструктивным причинам нельзя уменьшить, целесообразнее (для уменьшения габаритов) применять рядовое соединение нескольких зубчатых колес.
Задача №3
Какую угловую скорость л, нужно сообщить валу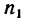
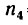
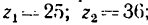
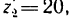
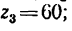
Решение.
1. Передаточное отношение от вала I к валу IV равно в данном случае произведению трех передаточных отношений:
где 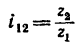
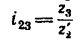
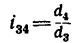
2. Таким образом,
После подстановки в эту формулу числовых значений получаем, что угловая скорость первого вала
Задача №4
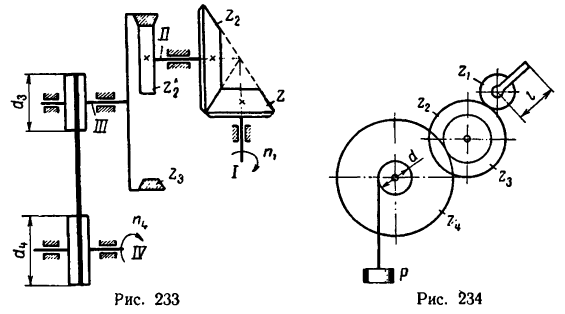
Изображенный на рис. 234 механизм лебедки при вращении рукоятки, имеющей длину I, в вертикальном на-
правлении перемещает груз Р. Диаметр барабана d = 200 мм, число зубьев зубчатых колес механизма:
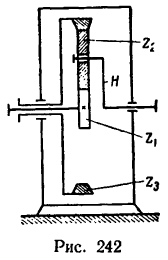
Определить: 1) с какой скоростью поднимается груз Р, если рукоятка / вращается с угловой скоростью я, =60 об/мин.
2) угловую скорость 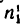
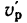
Решение.
1. Если рукоятка l, жестко соединенная с колесом 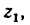
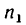
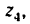
где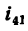
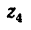
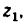
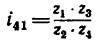
2. Так как барабан, вращаясь, делает 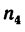
Скорость подъема груза Р равна окружной скорости и, следовательно,
3. Если нужно поднимать груз со скоростью 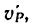
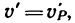
4. Если же барабан и вместе с ним колесо 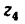
Такая угловая скорость рукоятки при ручном приводе, конечно, неосуществима.
Следующие две задачи рекомендуется решить самостоятельно.
Определение передаточных отношении простейших планетарных и дифференциальных передач
Планетарными называются передачи, в которых оси одного или нескольких колес закреплены в подвижном звене—водиле.
Любая планетарная передача состоит из трех групп элементов. Первая группа – центральные колеса (колеса, расположенные на неподвижных осях), вторая группа – сателлиты (колеса, расположенные на подвижном звене – водиле) и третья группа — водила.
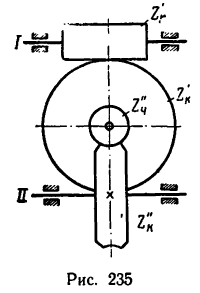
На рис. 237 показана схема передачи, состоящей из нейтрального колеса 1, сателлита 2 и водила H.
В общем случае центральное колесо и водило могут получать вращение от двух источников независимо друг от друга Такая
передача имеет две степени свободы и называется дифференциальной.
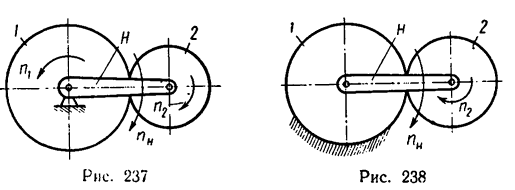
Если закрепить центральное колесо, то получается передача с одной степенью свободы — движение можно передавать либо от водила к сателлиту, либо от сателлита к водилу-• такая передача называется простой планетарной (рис. 238).
Чтобы в процессе решения задач глубже проанализировать кинематику планетарных передач, целесообразно не пользоваться готовыми выведенными в учебниках формулами, а применять метод сложения двух движений.
Сателлиты планетарных передач совершают сложное вращательное движение. Движение сателлитов относительно Земли (относительно неподвижной системы координат) складывается из вращения их вместе с водилом — переносного движения и вращения их вокруг осей, закрепленных в водиле, — относительного движения.
Метод сложения двух движений можно распространить и на центральные колеса. Так, например, закрепленное центральное жолесо простой планетарной передачи можно считать вращающимся вместе с воднлом и одновременно поворачивающимся на их общей оси в обратную сторону с такой же скоростью, что и водило.
Поэтому метод, который подробно изложен в решениях задач, включает следующие четыре этапа:
- 1. Мысленно закрепляем все колеса на водиле и придаем ему вращение с угловой скоростью водила относительно его собственной неподвижной оси – получаем первое движение.
- 2. Освобождаем колеса от водила. Водило мысленно закрепляем (превращаем планетарную передачу в обычную зубчатую передачу с неподвижными осями) и поворачиваем центральное колесо с угловой скоростью —
т. е. с угловой скоростью, равной разности абсолютных скоростей водила и центрального колеса, но в обратную сторону относительно направления вращения водила. В результате этого движения центрального колеса все остальные колеса передачи получают соответствующие угловые скорости, определяемые при помощи передаточных отношений. Так получается второе движение.
- 3. Угловые скорости всех элементов передачи, получившиеся в первом и втором движениях, складываем.
- 4. Из получившихся в результате сложения действительных зависимостей между угловыми скоростями определяем неизвестные в задаче величины.
Введем такие обозначения:
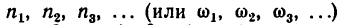
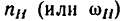
угловые скорости колес или водила в простой планетарной передаче (с закрепленным колесом) обозначим теми же буквами, но с верхними индексами в скобках, соответствующих закрепленному колесу, например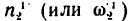
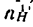
Аналогично обозначим и передаточные отношения:
передаточное отношение от колеса 1 к колесу 2 при неподвижном водиле;
—передаточное отношение от колеса 2 к водилу при неподвижном первом колесе;
— передаточное отношение от колеса 1 к водилу в дифференциальной передаче и т. д.
При решении задач с планетарными передачами необходимо очень внимательно следить за правильностью определения знаков передаточных отношений между отдельными элементами передачи.
Задача №5
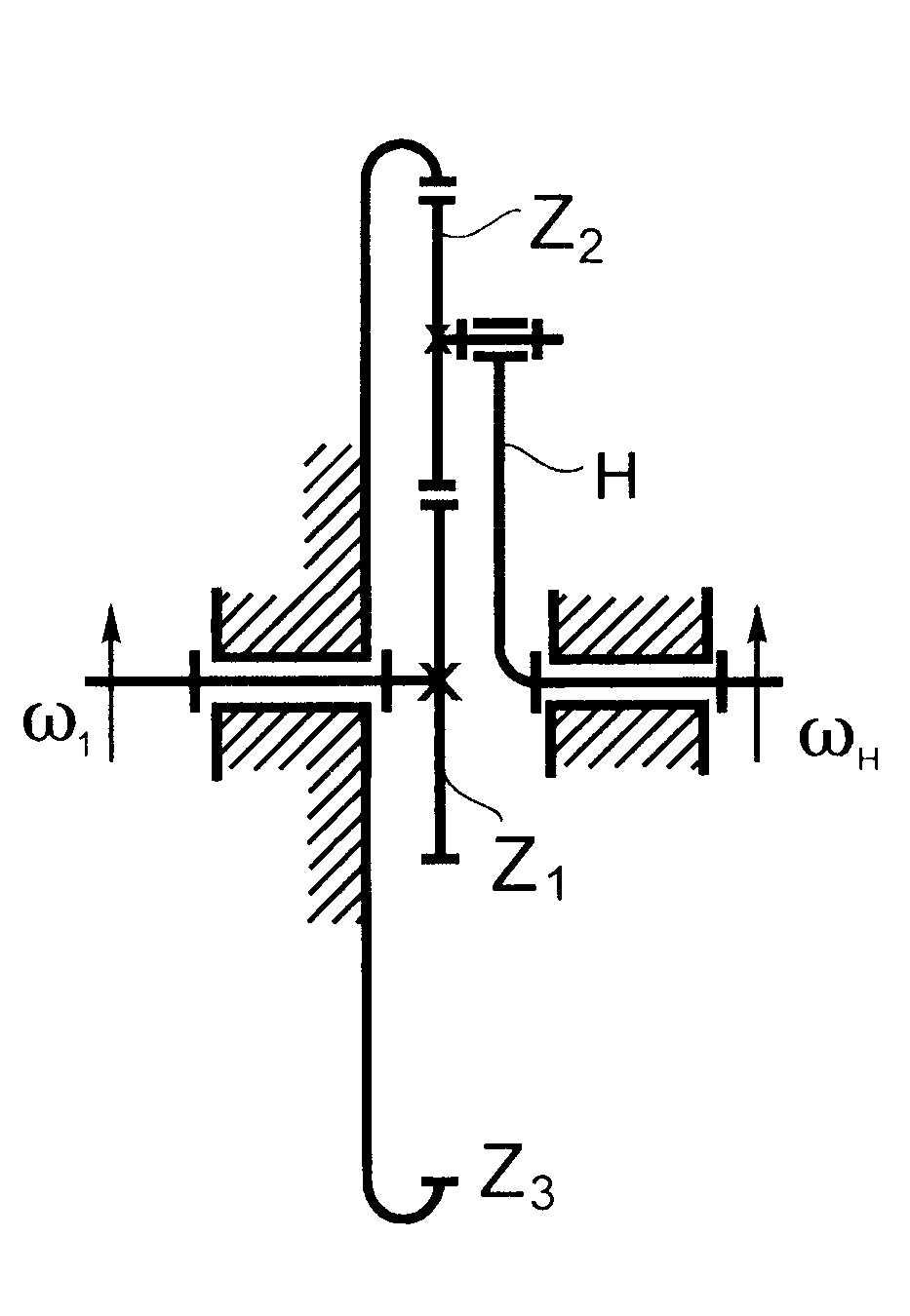
Определить передаточное отношение от сателлита 2 к водилу Н для простой планетарной передачи, показанной на рис. 238, если числа зубьев колес
Решение.
1. Осуществим первое движение. Закрепим колеса 1 и 2 на водиле и сообщим водилу вместе с колесами вращательное движение с угловой скоростью 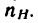
2. Осуществим второе движение. Освободим колеса от водила. Закрепим водило, т. е. превратим простую планетарную передачу в обычную зубчатую передачу, состоящую в данном случае из пары зубчатых колес.
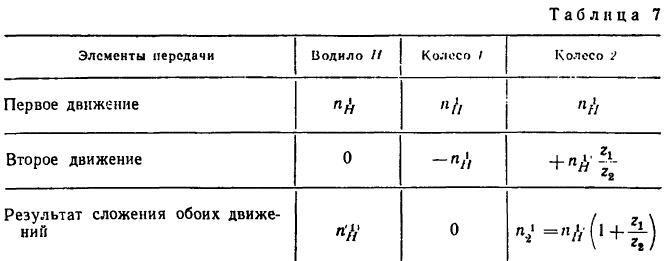
3. Угловая скорость центрального колеса в механизме 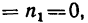
В результате вращения колеса1 колесо 2 приобретет угловую скорость
так как передаточное отношение от колеса 1, вращающегося со скоростью
ко второму колесу при закрепленном водиле отрицательное и равно
Приведенные результаты заносим в табл. 7, в нижней графе которой затем осуществляем третий этап — сложение обоих значений.
4. Находим передаточное отношение отсателлита 2 к водилу:
Таким образом,
Так как в данном случае передаточное отношение от колеса 2 к колесу 1 при закрепленном водиле имеет отрицательное значение
то окончательно
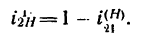
Но при помощи передачи, изображенной на рис. 238, неудобно передавать вращательное движение, так как необходимо дополнительное приспособление, чтобы сообщить угловую скорость сателлиту.
Аналогичная, но несколько видоизмененная простая планетарная передача рассматривается в следующей задаче.
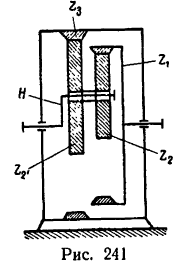
Задача №6
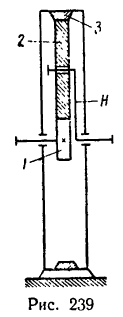
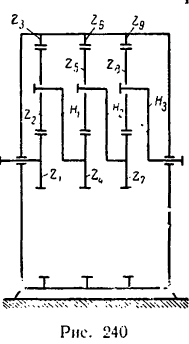
Определить передаточное отношение от колеса 2 к водилу Н простой планетарной передачи с закрепленным колесом внутреннего зацепления (рис. 239), если
Решение:
1. Так же как и в предыдущей задаче, осуществим сначала первое движение, и тогда все элементы механизма (водило H, колеса 1,. 2 и 3) получат угловую скорость
2. Превратим планетарную передачу в обычную, закрепив водило. Освободим колеса и осуществим
второе движение–сообщим колесу 3 угловую скорость — 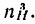
а колесо / – угловую скорость
3. Сведем результаты обоих движений в табл. 8 и произведем сложение угловых скоростей.
4. Найдем передаточное отношение
Подставим в (б) числовые значения чисел зубьев:
Таким образом, если к передаче подвести угловую скорость слева (к колесу 1), то справа (у водила Н) угловая скорость уменьшится в шесть раз.
Если в выражении передаточного отношения (б) заменить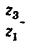
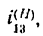
Сравнивая выражение (в) с выражением (а) из предыдущей задачи, замечаем, что они аналогичны.
Как видно, эти передачи не дают большого кинематического эффекта по сравнению с обычными передачами с неподвижными осями: передаточные отношения отличаются только на единицу.
Чтобы увеличить передаточное отношение, передачи, рассмотренные в задаче 202-40, соединяют последовательно.
Задача №7
Определить передаточное отношение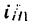
Решение.
1. Осуществим первое движение (см. табл. 9).
2. Осуществим второе движение при закрепленном водиле, сообщив вращение колесу 3 (см. табл. 9).
3 Записав угловые скорости каждого элемента в первом и втором движении, сложим их (табл. 9).
4. Находим передаточное отношение
Особенно большим получается передаточное отношение, если
близко к единице. Так, например, при
Следовательно, простая планетарная передача, состоящая всего из четырех колес, уменьшает угловую скорость в 10 тысяч раз.
Такие передачи создают большой кинематический эффект, но они имеют и крупный недостаток — крайне низкий коэффициент полезного действия (около 0,5%).
В следующей задаче рассматривается дифференциальная передача.
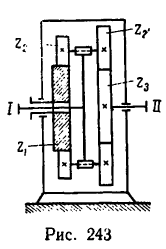
Задача №8
Определить угловую скорость водила Н и колеса 2 дифференциального зубчатого механизма (рис. 242), если число зубьев колес 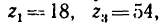
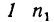
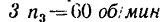
Решение.
1 Осуществим первое движение. Закрепив жестко все колеса на водиле, сообщим последнему угловую скорость 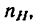
2. Освободив колеса от водила и закрепив его, сообщаем колесу 1 угловую скорость —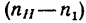
а колесо 3
3. Сведем все результаты в табл. 10.
4. Число оборотов в минуту водила найдем из равенства
откуда
Водило И вращается с угловой скоростью 15 об/мин в ту же сторону, что и колесо 3.
5. Число оборотов в минуту колеса 2 определяем из равенства
но предварительно необходимо определить число зубьев
Из рис. 242 ясно, что
или
Так как модули всех колес равны между собой, то
откуда
и теперь
Таким образом, бегающее колесо (сателлит) вращается вокруг своей оси со скоростью 150 об/мин в ту же сторону, что и водило, и колесо 3.
- Задачи на поступательное движение тела
- Задачи на вращательное движение тела
- Равновесие тяжелой рамы
- Расчет составной конструкции
- Равномерное вращательное движение
- Равнопеременное вращательное движение
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
В этой статье
- История
- Устройство ременной передачи
- Открытая, перекрестная и полуперекрестная передача
- Повышающая и понижающая передача
- Как посчитать передаточное отношение для ремённой передачи
- Передаточное число
- Передаточное отношение многоступенчатой ремённой передачи
- Виды приводных ремней
- Преимущества и недостатки ремённых передач
- Определения
- Вопросы
- Задачи
- Полезное видео
История
Ремённая передача – одна из древнейших и простых механических передач, в которой используются приводные ремни и специальные колеса — шкивы. По некоторым источникам, ременная передача впервые документально описана китайским философом, поэтом и политиком Ян Сюном (53 год до н. э. – 18 год н. э.) периода империи Хань в тексте «Словарь местных выражений». Описанное устройство использовали ткачи в своей работе с шелком.
Кстати, слово «ремённая» записывается через букву «ё», на которую и нужно ставить ударение. Но в печати, например, в нашем следующем заголовке, точки над «ё» могут опускать. Это не является ошибкой, но не забудьте ставить ударение правильно.
На средневековых картинах можно увидеть механизм — самопрялку, в которой принцип ремённой передачи используется для ускорения получения пряжи. Большое развитие ремённая передача вместе с другими механизмами получила во времена английской промышленной революции (1780-1830 гг.), которая началась с изобретения в 1769 году паровой машины. Небольшие кустарные ремесленные производства начали вытесняться фабричным трудом с большим количеством машин.


На приведенной ниже картинке показаны примеры использования ремённой передачи в современных технических устройствах – от двигателя внутреннего сгорания автомобиля до 3D-принтера.

Устройство ременной передачи
Ведущее и ведомое колесо – это шкивы. Их соединяет приводной ремень. Ведущий шкив — тот, который крутит мотор или другая внешняя сила, а ведомый – следующий за ним. Часто для предотвращения соскакивания ремня на ободе шкива делают канавку или бортики.
Чтобы ремень не проскальзывал, его нужно хорошо натянуть. Кто ездил на велосипеде хорошо знает проблему, что плохо натянутая цепь так и норовит слететь со звездочки, а если перетянешь – трудно ехать и она легко порвется. Для натяжения ремня или устранения его колебаний могут использоваться натяжные и прижимные ролики.
Диаметр ведущего шкива мы обозначим английской буквой d1, а ведомого — буквой d2. Нам это понадобится при расчетах.

Ремень является самым дешевым устройством в данном механизме. Но за счет него ремённая передача обеспечивает плавность хода и снижение шума. Такая передача способна амортизировать рывки и снижать нагрузку на мотор. Так, если на циркулярном станке резко заклинит диск при распиливании дубовой доски, электромотор остановится не сразу, а с задержкой за счет упругости ремня и его проскальзывания.
Рассмотрим следующую схему.

Ведущая ветвь ремня — та, которая набегает на ведущий шкив. Она при работе передачи испытывает растяжение.
Ведомая ветвь ремня — та, которая сходит с ведущего ремня и набегает на ведомый. Она при работе сжимается и расслабляется.
Сжатие и растяжение двух ветвей компенсируется. Иначе ремень рвется. При переходе с одной ветви на другую ремень упруго сжимается или растягивается. В этих зонах на шкиве происходит упругое скольжение ремня. Из-за изменения величины упругого скольжения передаточное отношение ремённой передачи непостоянное и может увеличиваться или уменьшаться в зависимости от нагрузки. При очень большой нагрузке ремень может упруго скользить по всей поверхности шкива.
Также важно знать про угол обхвата ремнём шкива. Чем больше угол обхвата, тем больше площадь контакта, тем больше полезная сила трения. При большой разнице в диаметрах шкивов этот угол может быть очень маленьким. Ремень при этом может проскальзывать. Чтобы увеличить угол обхвата без увеличения межосевого расстояния можно использовать прижимной ролик (смотри картинку ниже). В таком случае устанавливают ролик на ведомую ветвь, которая расслаблена, иначе ведущая ветвь растянется еще сильнее и износ ремня значительно вырастет.

Открытая, перекрестная и полуперекрестная передача
- В открытой ременной передаче шкивы расположены в одной плоскости параллельно друг-другу. Такая передача не меняет направления вращения ведомого шкива.
- В перекрестной ременной передаче приводной ремень закручен восьмеркой. Большой минус такого способа изменения направления вращения – большой износ ремня из-за дополнительного трения. Этот способ можно использовать при создании моделей из образовательного конструктора, но он редко используется в промышленных устройствах.
- В полуперекрестной ременной передаче ось вращения одного из шкивов повернута на некоторый угол относительно другой оси (например, на 90 градусов).
Повышающая и понижающая передача
Рассмотрим нижнюю картинку. Зеленый шкив с помощью ручки крутит персонаж с силой F. Это ведущий шкив. Синий шкив крутится за счет ремня. Это ведомый шкив. К нему на вал подвешен груз с максимально возможной массой, которую может поднять механизм.
- В первом случае диаметр ведущего и ведомого шкивов одинаковый. Скорость и сила на выходе не поменяется.
- Во втором случае диаметр ведущего шкива меньше ведомого. Скорость на выходе упадет. Такая передача называется понижающей. Сила при этом увеличится и механизм сможет поднять груз большей массы, чем первый.
- В третьем случае диаметр ведущего шкива больше ведомого. Скорость на выходе увеличится. Такая передача называется повышающей. Сила при этом уменьшится и механизм сможет поднять груз меньшей массы, чем первый и второй.
Почему так происходит? Любой сложный механизм можно представить через простые механизмы. В данном случае ручка, за которую тянет персонаж и радиус к точке на окружности, которую толкает приводной ремень, образуют рычаг. Посмотрите на следующий рисунок.
Короче плечо рычага к нагрузке (радиус шкива) – больше сила, но меньше пройденный путь.
Длиннее плечо рычага к нагрузке (радиус шкива) – меньше сила, но больше пройденный путь.
Эти схемы с понижающей и повышающей ремённой передачей наглядно демонстрируют работу золотого правила механики — за выигрыш в силе приходится платить таким же проигрышем в расстоянии (схема 1) или за выигрыш в расстоянии приходится платить таким же проигрышем в силе (схема 2).
Как посчитать передаточное отношение для ремённой передачи
При создании ремённой передачи нужно понимать, во сколько мы выиграем или проиграем в скорости и силе, чтобы собрать устройство с нужными характеристиками.
Передаточное отношение обозначается буквой i. Оно показывает, во сколько раз снизилась скорость вращения на выходе. Согласно золотому правилу механики, во столько же раз увеличится сила (крутящий момент).
Формулу для расчета передаточного отношения можно вывести из правила рычага. Передаточное отношение для ремённой передачи рассчитывается так:

Таким же образом передаточное отношение можно посчитать через соотношения радиусов.
Узнать размеры шкивов можно с помощью линейки. Самый точный метод измерения диаметра – с помощью штангенциркуля.

Передаточное отношение удобно записывать со знаком деления в виде i = 1 : 1. Эта запись показывает, что 1 оборот на входе даст 1 оборот на выходе. Передаточное отношение i = 5 : 1 показывает, что 5 оборотов на входе дает 1 оборот на выходе, то есть скорость упала в 5 раз (передача понижающая).
Если дробь можно сократить, её сокращают. Например, i = 5 : 25 = 1 : 5 (передача повышающая).
Передаточное число
Передаточное отношение можно записать в виде числа, поделив числитель на знаменатель. Например, i = 5 : 1 = 5, или i = 1 : 4 = 0,25. В данном случае говорят о передаточном числе.
Рассмотрим разные варианты передаточных чисел:

Передаточное отношение многоступенчатой ремённой передачи
Если передача многоступенчатая (двух-, трехступенчатая и т.д.), то общее передаточное отношение будет вычисляться как произведение отдельных передаточных отношений.

Эта формула справедлива для следующего рисунка:

Передаточное отношение для шкивов, жестко закрепленных на общей оси, не считается — скорость их вращения будет всегда одинаковой!
Виды приводных ремней
Видов ремней достаточно много, так как используются они в разных условиях. Где-то нужно передать очень большую мощность так, чтобы ремень не порвался и не растянулся. Где-то ремень не должен проскальзывать. Где-то ремень должен крутиться очень-очень быстро и мало изнашиваться со временем. А где-то нужно передать вращение на большое расстояние и под углом.
Очень распространенная классификация ремней – по поперечному сечению или форме. Основные виды: 1 — плоские ремни, 2 – клиновые ремни, 3 – ремни круглого сечения (пассики), 4 – многоручьевые ремни (или поликлиновые), 5 – зубчатые ремни.

В крупной промышленной технике самые распространенные ремни – клиновые и поликлиновые. Они достаточно толстые по сечению и имеют увеличенную за счет боковой поверхности площадь сцепления со шкивами.
В небольших электронных устройствах чаще используются плоские ремни и пассики (ремни с круглым сечением).

Плоские ремни широко использовались в 19-м и начале 20 века на фабриках для передачи движения на несколько машин с одного линейного вала (англ. line shaft). Они широко применялись и применяются в лесопильных станках, молотилках, электрогенераторах.
В станках с ЧПУ (3D-принтерах, плоттерах, лазерных станках) используются зубчатые ремни, так-так они сохраняют постоянное передаточное отношение и не проскальзывают.
Преимущества и недостатки ремённых передач
Как и у любого устройства, у ремённой передачи есть свои плюсы и минусы по сравнению с другими механизмами. Выделим важные из них.
Преимущества:
- простота конструкции;
- малая стоимость:
- малая шумность;
- плавность работы;
- сглаживание ударных перегрузок за счет упругости ремня;
- возможность менять направление вращения под разным углом;
- возможность передавать вращение на большое расстояние.
Недостатки:
- большие габариты конструкции;
- плохая работа на больших скоростях (появление вибраций);
- большая нагрузка на оси (валы, подшипники);
- непостоянное передаточное отношение при разной нагрузке (из-за упругого скольжения);
- малый срок службы ремня по сравнению с зубчатыми колесами;
- биение приводного ремня при его слабом натяжении;
- необходимость в дополнительных элементах при большой длине ремня или малом угле обхвата;
- увеличение износа приводного ремня или осей при неправильном натяжении.
Определения
- Ведущая ветвь ремня — набегает на ведущий шкив. При работе передачи растягивается.
- Ведомая ветвь ремня — сходит с ведущего ремня и набегает на ведомый. При работе передачи расслабляется.
- Межосевое (межцентровое) расстояние – кратчайшее расстояние между осями шкивов.
- Натяжной ролик (леникс, от нем. lenix, lenixrolle — натяжной ролик) – элемент ремённой или цепной передачи; свободно вращающееся на оси колесо (шкив, звездочка, ролик), которое используется для регулирования натяжения ремня или цепи. Например, используется в тракторах для натяжения гусениц или в двигателе автомобиля для натяжения ремня ГРМ (газораспределительного механизма).
- Пассик (от польского pasek — ремешок) – исторически вошедшее в наш оборот название приводного ремня круглого сечения. Слово «пассик» имеет польское происхождение. Его появление в русском словаре связывают с 80-ми годах 20-го века, когда им называли соответствующий элемент в импортном польском магнитофоне. Пассик, как правило, выполнен из резины или других полимерных материалов. Пассики использовались в устройстве протяжного механизма магнитной ленты старого кассетного магнитофона – он хорошо сглаживал рывки от электромотора и предохранял от искажений звука. «Пассики» входят в комплект конструктора Lego WeDo или ресурсного набора Lego MINDSTORMS Education EV3. В общем, всякий пассик — приводной ремень, но не каждый приводной ремень – пассик.
- Приводной ремень – гибкий замкнутый элемент (ремень) для передачи вращения между двумя шкивами. Вращение передается за счет силы трения (гладкий ремень) или силы зацепления (ремень с зубчиками). Может иметь разную форму: бывают плоские ремни, зубчатые ремни, клиновидные ремни.
- Ремённая передача (англ. belt drive)– механизм, предназначенный для передачи вращательного движения с помощью силы трения или зубчатого зацепления замкнутой гибкой связи (ремня) с помощью колес (шкивов), закрепленных на входном и выходном вале.
- Угол обхвата – угол прилегания ремня к шкиву.
- Шкив – фрикционное (англ. friction — трение) колесо с ободом или канавкой по окружности. Передает или принимает движение от приводного ремня. В отличие от блока, который имеет похожую форму, шкив всегда передавет усилие с оси на ремень, либо принимает усилие с ремня на ось. Блок же всегда свободно вращается на оси и обеспечивает изменение направления движения каната/троса, а также изменяет прикладываемую силу.
Вопросы
1. Что ты можешь сказать о ремённых передачах по этим двум изображениям? В чем их отличие и из каких элементов они состоят?

Задачи
1. Мальчик Ваня измерил штангенциркулем ведущий и ведомый шкив. Диаметр первого составил 12 миллиметров, второго – 32 миллиметра. Какое передаточное отношение у этой ремённой передачи?
2. Угловая скорость вращения вала мотора – 420 оборотов в секунду. Какая угловая скорость будет у ведомого шкива, если передаточное отношение i = 12 : 1?
3. Собери одноступенчатую понижающую ремённую передачу из деталей Lego. В качестве шкивов можно использовать диск узкого или большого колеса и желтые втулки. На ведущую ось установи ручку, на ось ведомого шкива установи стрелку, чтобы считать обороты.
Измерь с помощью линейки или штангенциркуля диаметры шкивов.
Заполни таблицу. Проверь опытным путем полученное значение с помощью стрелки.

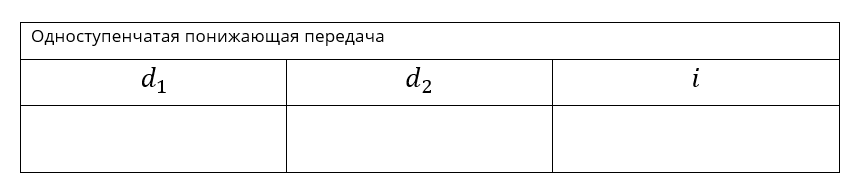
4. Собери двухступенчатую понижающую ремённую передачу с ручкой и стрелкой (пример — в 3 задаче). Посчитай передаточное отношение через диаметры. Проверь полученное значение опытным путем.


Полезное видео
- Э+М. Ременная передача. Урок №3
- GetAClass. Золотое правило механики
- Анимация. Прямая и перекрестная ременная передача
- Анимация. Ременная передача — работы различных механизмов с помощью ремня
Как рассчитать передаточное отношение шестерен механической передачи.
В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев. Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев.
Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.
Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.
Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.
Итак, рассмотрим пример расчета с использованием двух шестерен.
Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.
В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.
Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.
Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.
Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.
Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.
В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.
Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Определим теперь частоту вращения.
Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.
Будем использовать формулу: S1 × T1 = S2 × T2,
Где:
S1 – частота вращения желтой (ведущей) шестерни,
Т1 – количество зубьев желтой (ведущей) шестерни;
S2- частота вращения красной шестерни,
Т2 – количество зубьев красной шестерни.
В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.
340 rpm × 7 = S2 × 40
2 380 =S2 × 40
2 380 40 = S2
59,5 об/мин = S2
Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.















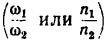
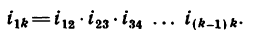
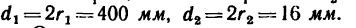
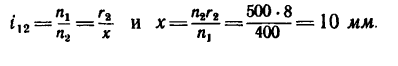
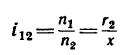
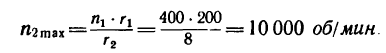
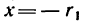
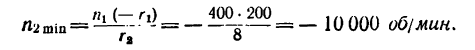
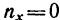
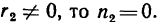
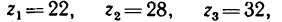
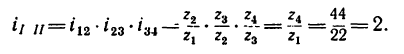
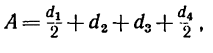
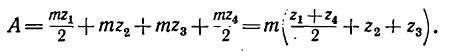
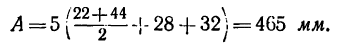
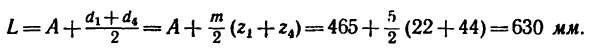
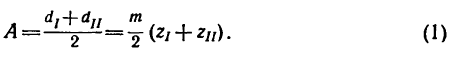

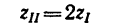
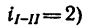
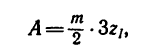
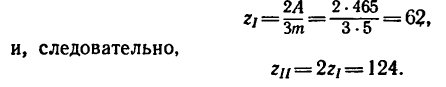
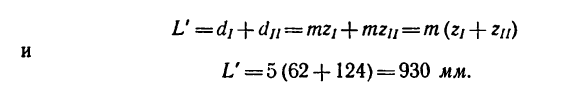
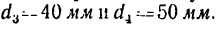
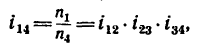
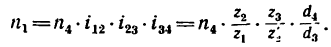
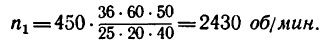
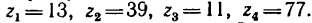
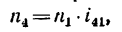
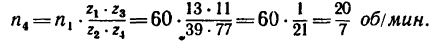
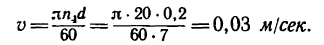
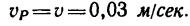
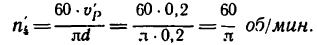
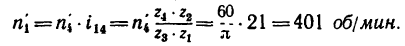
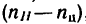 т. е. с угловой скоростью, равной разности абсолютных скоростей водила и центрального колеса, но в обратную сторону относительно направления вращения водила. В результате этого движения центрального колеса все остальные колеса передачи получают соответствующие угловые скорости, определяемые при помощи передаточных отношений. Так получается второе движение.
т. е. с угловой скоростью, равной разности абсолютных скоростей водила и центрального колеса, но в обратную сторону относительно направления вращения водила. В результате этого движения центрального колеса все остальные колеса передачи получают соответствующие угловые скорости, определяемые при помощи передаточных отношений. Так получается второе движение.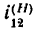 передаточное отношение от колеса 1 к колесу 2 при неподвижном водиле;
передаточное отношение от колеса 1 к колесу 2 при неподвижном водиле;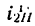 —передаточное отношение от колеса 2 к водилу при неподвижном первом колесе;
—передаточное отношение от колеса 2 к водилу при неподвижном первом колесе;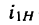 — передаточное отношение от колеса 1 к водилу в дифференциальной передаче и т. д.
— передаточное отношение от колеса 1 к водилу в дифференциальной передаче и т. д.