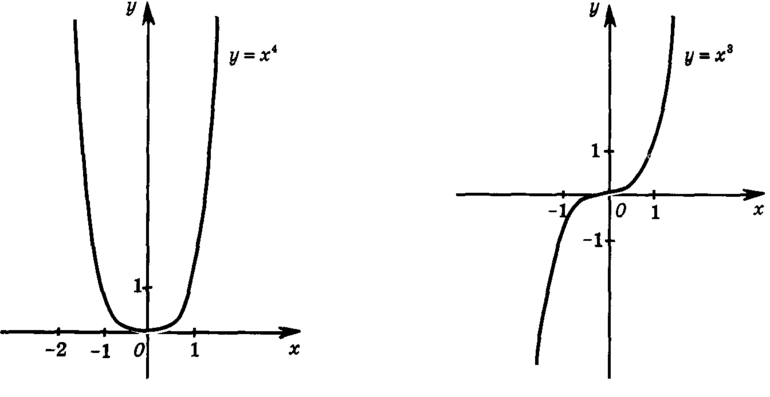Примеры как найти четность нечетность

Общие сведения

Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».

Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:

1. Область определения — D (f).
2. Виды.
3. Правила.
4. Свойства для четных и нечетных.
5. Классификация.

Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.

Область определения

Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.

D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.

Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.

Основные виды

Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:

• Простые: алгебраические, трансцендентные и тригонометрические.
• Составные или сложные.

Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.

Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.

Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.

Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.

Правила для выявления

Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.

Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:

• Разложить при необходимости на простые элементы.
• Определить D (z). Если ее график симметричный, то нужно переходить к следующему шагу. В противном случае результатом является функция общего вида.
• Проверить, подставив в выражение отрицательное значение аргумента w (-x).
• Выполнить сравнение: w (-x) = w (x).
• Сделать соответствующий вывод.

Если w (-x) = w (x), то это свидетельствует о четности. При выполнении тождества w (-x) = -w (x) функция является нечетной. Важно обратить внимание на D, поскольку в некоторых точках равенства и условия могут не выполняться. Это свидетельствует о том, что искомая функция принадлежит к общему виду, то есть не является четной и нечетной.

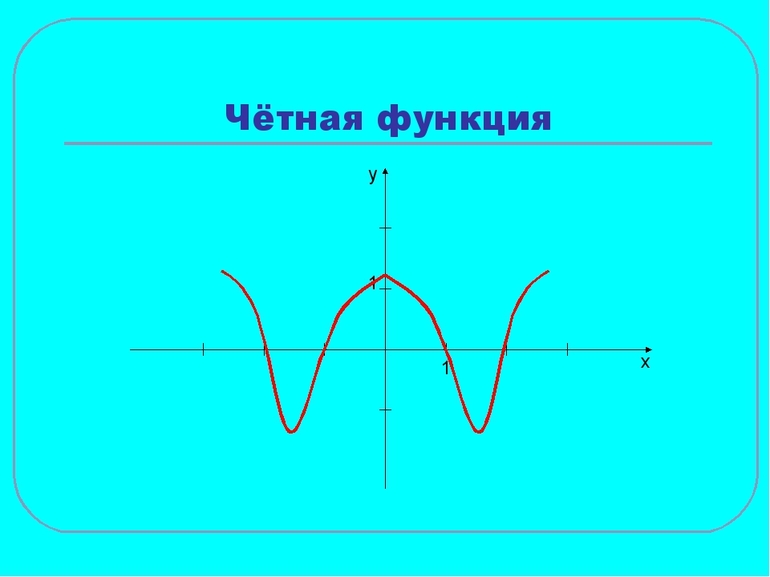
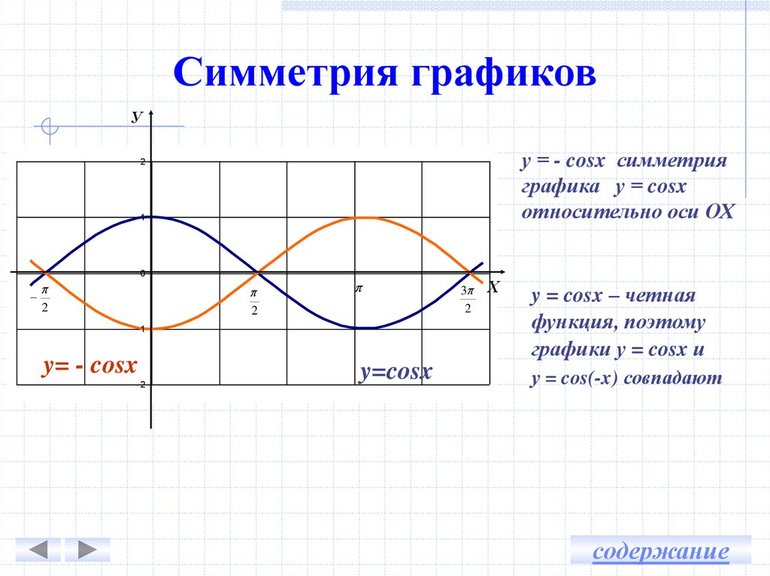
Одним интересным способом является графический метод (принцип). Для его реализации нужно выполнить построение графика. Если он будет симметричным относительно оси ординат ОУ, то равенство w (-x) = w (x) будет выполняться. В случае симметричности относительно начала системы координат (точка пересечения осей абсцисс и ординат), будет справедливым равенство w (-x) = -w (x).

Следствия из утверждений

Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:

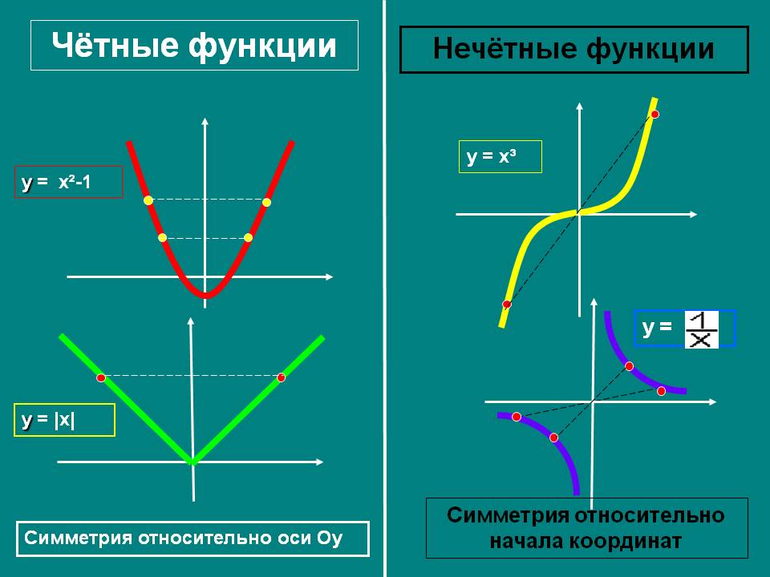
• Симметричность графика: четная — относительно ОУ, а нечетная — относительно начала координат.
• Функция эквивалентна сумме четной и нечетной.
• Результат комбинации четных эквивалентен четной, а нечетных — нечетной.
• Результирующее произведение: 2 четных — четное, 2 нечетных — четная, а 2 разной четности — нечетной.
• Композиция: 2 нечетных — нечетна, четная и нечетная — четна, любая с четной — четна (не наоборот).
• При взятии производной от четной результирующая является нечетной, а от нечетной — четной.
• Определенный интеграл вида ∫(g (x))dx с границами от -А до А равен двойным интегралам ∫(g (x))dx с границей от -А до 0 и от 0 до А: ∫(g (x))dx |(-A;A) = 2∫(g (x))dx |(-A;0) = 2∫(g (x))dx |(0;A).
• Определенный интеграл нечетной функции с границами -А и А равен 0.
• Ряд Маклорена: четные степени соответствуют четной и наоборот.
• Ряд Фурье: четная содержит только выражения с cos, а нечетная — sin.

Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.

Классификация по четности

Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):

• Возведение в степень, показатель которой является целым и нечетным.
• Сигнум (sgn) — кусочно-постоянный тип, который задан несколькими формулами, объединенными в систему.
• Радикал положительной нечетной степени.
• Тригонометрические: sin (x), tg (x), ctg (x) и cosec (x).
• Обратные тригонометрические: arcsin (x), arcctg (x), arcsec (x) и arccosec (x).
• Гиперболические и их обратные выражения: гиперболические синус и косинус, а также ареасинус, ареатангенс и ареакотангенс.
• Гудермана и обратная ей: gd (x) = arctg (sh (x)) и arcgd (x) = arch (sec (x)).
• Интегральный синус: Si (x).
• Матье: se (x).

Кроме того, существуют еще составные выражения, элементами которых являются простые функции. Для анализа необходимо руководствоваться свойствами. Следующий класс, который объединяет все четные выражения, состоит из следующего перечня:

• Возведение в четную и целую степень.
• Модуль аргумента.
• Константа.
• Тригонометрические: cos (x) и sec (x).
• Гиперболические: косинус и секанс.
• Дельта-функция Дирака: z (x) = δ(x).
• Гаусса: z (x) = a * exp[(-(x — b)^2) / 2c ² ].
• Кардинальный синус: sinc (x).

Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.

Пример решения

Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y ² — y — 2) / (y ² — 1). В этом случае следует действовать по алгоритму:

• Состоит из двух элементов: g (y) = y ² — y — 2 и h (y) = y ² — 1.
• Область значений: D (y ² — y — 2) = (-бесконечность; +бесконечность) и D (y ² — 1) = (-бесконечность; -1) U (-1;1) U (1; +бесконечность).
• График функции является симметричным, поскольку задан параболой.
• Выполнить анализ по формулам: g (-y) = (-y)^2 + y — 2 = y ² + y — 2 и h (-y) = (-y)^2 — 1 = y ² — 1.
• В двух случаях функции являются нечетными: в первом — изменение знака, а во втором — от четной отнимается 1. Следовательно, искомое выражение является нечетной функцией.

Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y ² отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.

Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.

Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.

Для начала вспомним свойства чётных и нечётных чисел.

Свойства чётных и нечётных чисел

1. Чётные числа делятся на 2 без остатка.

0, 2, 4, 6, 8, 10… – чётные числа.

2. Нечётные числа не делятся на 2 без остатка.

1, 3, 5, 7, 9, 11… – нечётные числа

3. У чётного числа последняя цифра всегда чётная.

110, 679232, 1000008 – чётные числа

4. У нечётного числа последняя цифра всегда нечётная.

123, 974341, 5234459 – нечётные числа

5. Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный

6∙5∙11 = 330, 4∙13∙15∙21 = 16380

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

6. Если в произведении нескольких чисел все числа нечётные, то результат всегда нечётный

3∙17∙7 = 357, 11∙23∙65 = 16445

7. Чётные числа при сложении и вычитании всегда дают чётное число.

22 + 46 = 68, 6 + 8 + 224 + 1284 = 1522, 56-44 = 12, 120 – 32 – 48 – 6 = 34

8. Сумма чётного количества нечётных чисел всегда чётная.

13 + 15 = 28, 7 + 9 + 21 + 33 = 70, 789 + 1003 + 611 + 1893 = 4296

9. Сумма нечётного количества нечётных чисел всегда нечётная.

11 + 21 + 43 = 65, 731 + 19 + 893 + 73 + 55 = 1771

10. При вычитании из нечётного числа нечётного всегда получается чётное.

13 – 7 = 6, 93 – 39 = 54

11. При вычитании из нечётного числа чётного всегда получается нечётное.

41 – 16 = 25, 139 – 122 = 17

12. При вычитании из чётного числа нечётного всегда получается нечётное.

20 – 9 = 11, 244 – 51 = 193

Задача 1

Петя купил в магазине 10 игрушек. Игрушки стоили 321, 259 и 411 рубль. Мог ли Петя заплатить за все 10 игрушек 3311 рублей?

Решение

Для решения этой задачи нам не нужно знать, сколько именно игрушек куплено за каждую из этих цен. Достаточно вспомнить свойство 8 из вышеприведённого списка свойств чётных и нечётных чисел: “Сумма чётного количества нечётных чисел всегда чётная”.

Куплено 10 игрушек, каждая из которых имеет нечётную цену. Таким образом, т.к. 10 – чётное число, а все цены нечётные, то мы имеем сумму чётного количества нечётных чисел, то есть эта сумма должна быть чётной. Но число 3311 – нечётное, поэтому 10 игрушек не могут столько стоить.

Ответ: нет, не мог, так как сумма его покупки должна быть чётным числом

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Задача 2

Вася купил в магазине несколько пирожных по 50 рублей, 2 коробки конфет, несколько йогуртов по 60 рублей. Продавец сказал, что Вася должен заплатить 931 рубль. Вася возмутился и сказал, что продавец не умеет считать. Действительно ли продавец ошибся?

Решение

У нас неизвестно либо количество купленного товара (несколько пирожных и несколько йогуртов), либо цена (цена конфет). Но то, что нам известно – цена пирожных (50 руб.), цена йогуртов (60 руб.) и количество коробок конфет (2 шт.) говорит о том, что если по отдельности посчитать суммарную стоимость пирожных, йогуртов и конфет, то везде получатся чётные суммы. Вспомним свойство 5 – “Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный”. Именно поэтому у нас везде будут чётные суммы.

И сложение этих чётных сумм тоже должно дать чётную сумму (свойство 7), а продавец насчитал нечётную.

Ответ: да, продавец ошибся, потому что сумма покупок должна быть чётным числом, а 931 руб. – нечётное число.

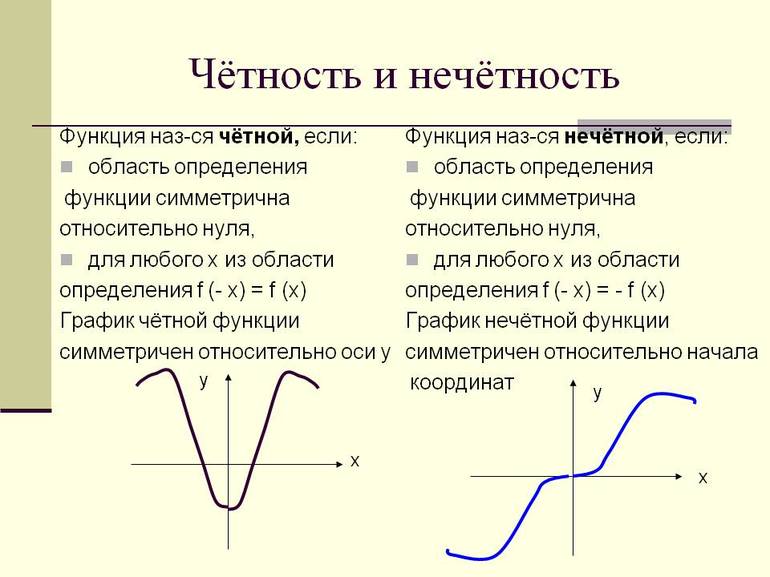
Функция  называется четной функцией, если для любого  из области определения выполняется равенство 

Функция  называется нечетной функцией, если для любого  из области определения выполняется равенство .

Если ни одно из условий  или  не выполняется, то говорят, что функция не является ни четной, ни нечетной (или функцией общего вида)

График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

При исследовании функции на четность и нечетность можно использовать следующие свойства:

1.  Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
2.  Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.
3.  Если функция  четная (нечетная), то и функция  четная (нечетная).

Пример

Задание	Исследовать функцию  на четность, используя свойства четных и нечетных функций.
Решение	Исследуем отдельно четность функции, которые находятся в числителе и знаменателе:    то есть функция  четная; аналогично    а тогда и функция  четная. По свойству 3, так как  — четная, то четной будет и функция . Тогда исходную функцию  можно представить в виде произведения четных функций , следовательно, по свойству 2,  — четная.
Ответ	Исследованная функция четная.