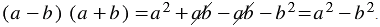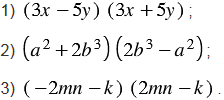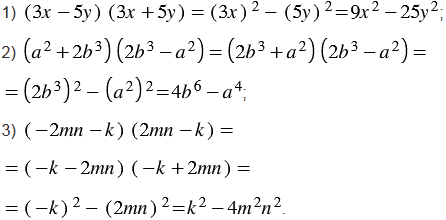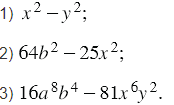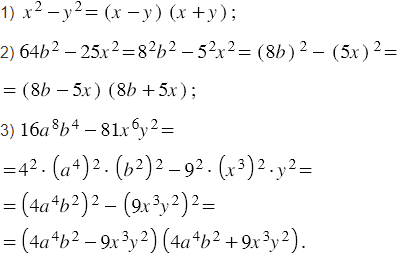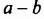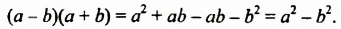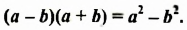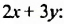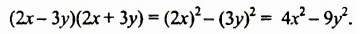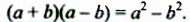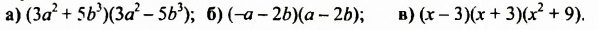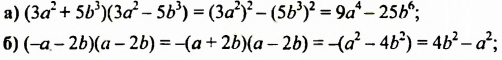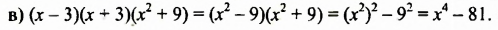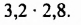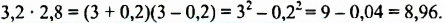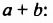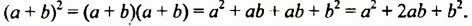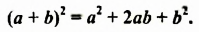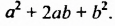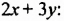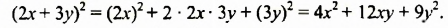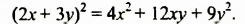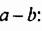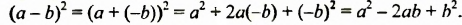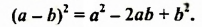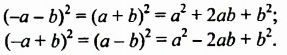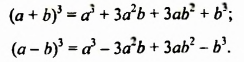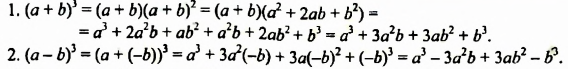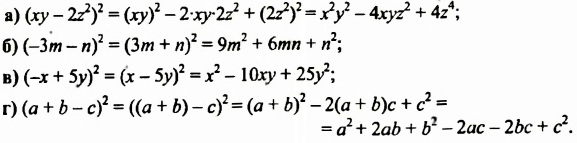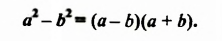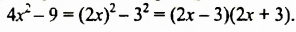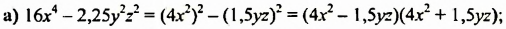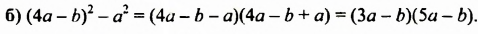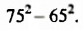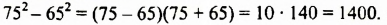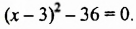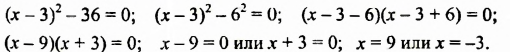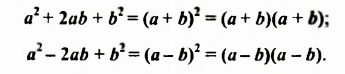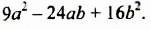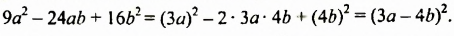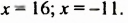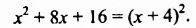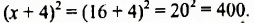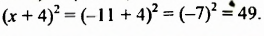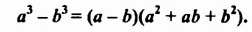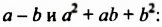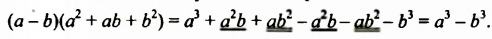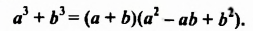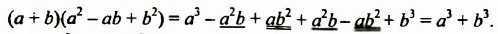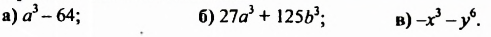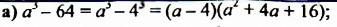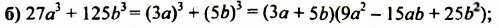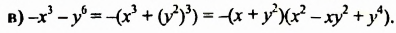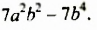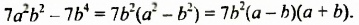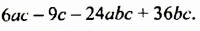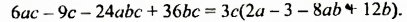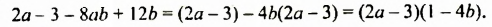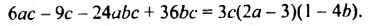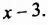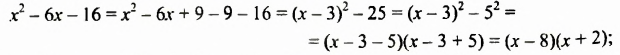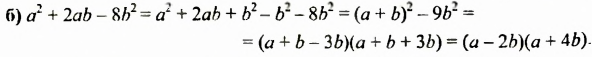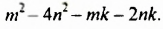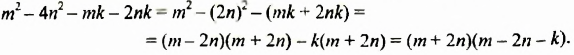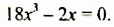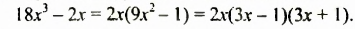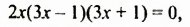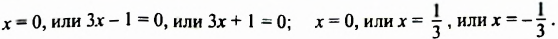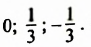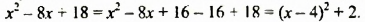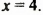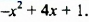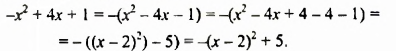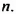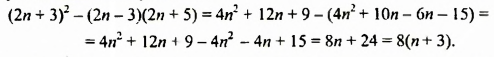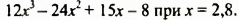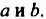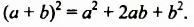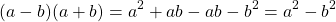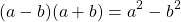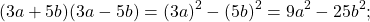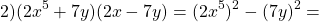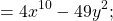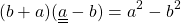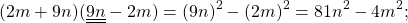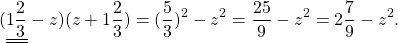Примеры задач как найти произведение суммы

Произведение разности и суммы двух выражений. Разность квадратов двух выражений.

Мы уже знаем правило умножения многочлена на многочлен. Но существуют правила, которыми удобно пользоваться при умножении многочленов в частных случаях.

Одним из таких частных случаев является произведение двух многочленов, один из которых представляет собой разность двух выражений, а другой – их сумму.

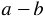
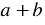
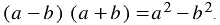
Умножим разность на сумму :

(1)

Следовательно, при умножении разности выражений на их сумму можно сразу записать результат – разность квадратов этих выражений. Поэтому полученное тождество называют формулой сокращенного умножения.

Правило:

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Обратите внимание, при возведении выражений в квадрат используем свойства степени с натуральным показателем.

Если выражение (1) переписать так

,

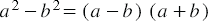
то мы получим тождество, которое называют формулой разности квадратов двух выражений.

Правило:

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

Разложите на множители:

Поделись с друзьями в социальных сетях:

Формулы сокращенного умножения с примерами решения

Содержание:

Формулы сокращенного умножения

Умножение разности двух выражений на их сумму

Умножим разность

Полученное тождество позволяет умножать разность двух выражений на их сумму не по правилу умножения двух многочленов, а сокращенно: сразу записывать произведение в виде 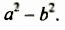Поэтому доказанное тождество называют формулой сокращенного умножения. Формулируют се так:

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Умножим по этому правилу разность 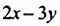на сумму

Из переместительного свойства умножения следует, что произведение суммы двух выражений и их разности равно разности квадратов этих выражений:

Примеры выполнения заданий:

Пример №135

Решение:

Пример №136

Вычислить

Решение:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений

Возведем в квадрат сумму

Полученное тождество называют формулой квадрата суммы. Оно является формулой сокращенного умножения, поскольку позволяет возводить в квадрат сумму любых двух выражений не по правилу умножения двух многочленов, а сокращенно: сразу записывать квадрат в виде трехчлена

Формулируют формулу квадрата суммы так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение этих выражений плюс квадрат второго выражения.

Возведем в квадрат сумму

При возведении суммы 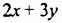в квадрат промежуточные преобразования можно выполнять устно:

Квадрат разности двух выражений

Возведем в квадрат разность

Итак, получили такую формулу квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения.

Квадрат суммы и квадрат разности двух выражений еще называют квадратом двучлена.

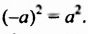
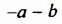
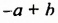
Квадраты противоположных чисел равны: Поэтому при возведении в квадрат выражений и можно пользоваться формулами:

Для тех, кто хочет знать больше

Чтобы возвести сумму или разность двух выражений в куб, можно использовать формулы куба суммы или куба разности:

Докажем эти формулы.

Формулируют формулу куба суммы так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

Формулу куба разности формулируют аналогично.

Примеры выполнения заданий:

Пример №137

Возвести в квадрат выражение:

Решение:

Разложение на множители разности квадратов двух выражений

В тождестве 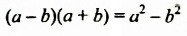поменяем местами левую и правую части:

Полученное тождество называют формулой разности квадратов двух выражений. Формулируют ее так:

Разность квадратов двух выражении равна произведению разности этих выражений и их суммы.

Формула разности квадратов позволяет разложить на множители двучлена 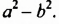Ее можно использовать при разложении на множители разности квадратов любых двух выражений. Например:

Примеры выполнения заданий:

Пример №138

Разложить на множители:

Решение:

Пример №139

Вычислить

Решение:

Пример №140

Решить уравнение

Решение:

Разложение многочленов на множители с использованием формул квадрата суммы и квадрата разности

Запишем формулы квадрата суммы и квадрата разности двух выражений (квадрата двучлена), поменяв в них левые и правые части:

Первая из этих формул дает разложение на множители трехчлена а вторая — трехчлена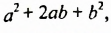

Примеры выполнения заданий:

Пример №141

Разложить на множители трехчлен

Решение:

Пример №142

Найти значение выражения 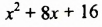при

Решение:

Запишем сначала трехчлен 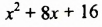в виде квадрата двучлена:

При 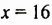получим:

При 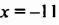получим:

Разность и сумма кубов двух выражений

Разность квадратов двух выражений можно разложить на множители по формуле разности квадратов. При разложении на множители разности кубов двух выражений используют формулу разности кубов:

Докажем это тождество, перемножив выражения

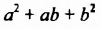
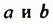
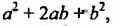
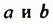
В формуле разности кубов трехчлен называют неполным квадратом суммы выражений (он напоминает трехчлен который является «полным» квадратом суммы выражений ). Поэтому формулу разности кубов можно сформулировать так:

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

При разложении на множители суммы кубов двух выражений используют формулу суммы кубов:

Докажем это тождество:

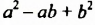
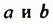
Трехчлен называют неполным квадратом разности выражений . Следовательно,

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Примеры выполнения заданий:

Пример №143

Разложить на множители:

Решение:

Применение нескольких способов для разложения многочленов на множители

Часто при разложении многочлена на множители нужно использовать несколько способов. Если это возможно, то разложение уместно начинать с вынесения общего множителя за скобки.

Рассмотрим несколько примеров:

1. Разложим на множители многочлен

Сначала вынесли общий множитель 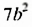за скобки, а потом применили формулу разности квадратов.

2. Разложим на множители многочлен

Все члены многочлена имеют общий множитель 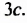Вынесем eго за скобки:

Многочлен 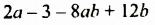разложим на множители способом группировки:

Примеры выполнения заданий:

Пример №144

Разложить на множители трехчлен:

Решение:

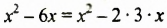
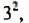
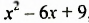
а) Если к выражению прибавить то есть 9, то получим выражение, которое является квадратом двучлена

Поэтому, выделив квадрат этого двучлена, получим:

Пример №145

Разложить на множители многочлен

Решение:

Пример №146

Решить уравнение

Решение:

Разложим левую часть уравнения на множители:

откуда:

Ответ:

Применение преобразований выражений

Нам уже встречались задачи, при решении которых нужно было преобразовывать то или иное выражение. Чаще всего мы использовали преобразования выражений при решении уравнений, доказательстве тождеств, нахождении значений выражении. Рассмотрим еще некоторые задачи, решение которых связано с преобразованием выражений.

Сравнение значений многочлена с нулем

Пример №147

Доказать, что многочлен 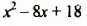принимает только положительные значения.

Решение:

Выделив из трехчлена 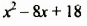квадрат двучлена, получим:

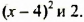
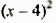
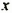
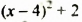
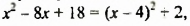
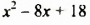
Мы представили многочлен в виде суммы двух слагаемых Слагаемое : при любых принимает только неотрицательные значения, слагаемое 2 — положительно. Поэтому выражение принимает только положительные значения. Поскольку то и выражение принимает только положительные значения.

Нахождение наибольшего и наименьшего значений выражений

Исходя из равенства 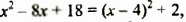полученного в примере 1, можно

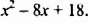
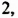
указать наименьшее значение многочлена Оно равно причем это наименьшее значение многочлен принимает при

Пример №148

Найти наибольшее значение многочлена

Решение:

Преобразуем данный многочлен так:

Наибольшее значение многочлена равно 5.

Решение задач на делимость

Пример №149

Доказать, что значение выражения 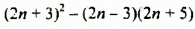делится на 8 при любом целом значении

Решение:

Упростим данное выражение:

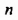
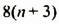
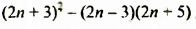
При любом целом значении произведение делится на 8, поэтому и значение выражения делится на 8.

Нахождение значений многочлена с помощью микрокалькулятора

Пример №150

С помощью микрокалькулятора найти значение многочлена

Решение:

Значение данного многочлена искать удобнее, если его предварительно преобразовать так:

При схема вычислений имеет вид:

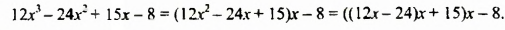
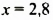
Выполнив вычисления, найдем значение многочлена. Оно равно 109,264.

Интересно знать

Античные математики использовали формулы сокращенного умножения задолго до нашей эры. В те времена формулы представлялись не в привычном нам символическом виде, а формулировались словами.

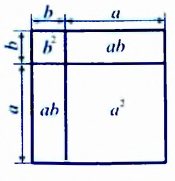
Ученые Древней Греции алгебраические утверждения, формулы, выражающие определенные зависимости между величинами, трактовали геометрически. Так, произведение 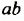они рассматривали как площадь прямоугольника со сторонами

Приведем пример алгебраического утверждения, которое было известно древнегреческим ученым и в геометрической терминологии формулировалось так: площадь квадрата, построенного на сумме двух отрезков, равна сумме площади квадратов, построенных на каждом из этих отрезков, плюс удвоенная площадь прямоугольника, построенного на этих отрезках.

Нетрудно догадаться, что речь идет о формуле квадрата суммы, которую мы символически записываем так:

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Разложение многочленов на множители
• Системы линейных уравнений с двумя переменными
• Рациональные выражения
• Квадратные корни
• Линейное уравнение с одной переменной
• Целые выражения
• Одночлены
• Многочлены

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Произведение суммы и разности

Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.

Найдем произведение суммы и разности двучленов непосредственным умножением:

-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.

Произведение суммы и разности двух выражений равно разности квадратов этих выражений.

Формула произведения суммы и разности:

Произведение суммы и разности двух выражений можно изобразить схематически так:

Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.

Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:

Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:

Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!

Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?

От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,

Выражения вида (-a-b)(a-b) также можно упрощать по формуле произведения суммы и разности. Вынесем -1 и из первых скобок, и из вторых:

[spoiler title=”источники:”]

http://www.evkova.org/formulyi-sokraschennogo-umnozheniya

[/spoiler]

Умножение числа на сумму

• Примеры

Умножить число на сумму можно двумя способами:

1) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат.

Например, чтобы найти значение выражения:

4 · (3 + 5),

можно сначала сложить числа  3  и  5:

3 + 5 = 8

и число  4  умножить на полученный результат:

4 · 8 = 32,  значит

4 · (3 + 5) = 4 · 8 = 32.

2) Для умножения числа на сумму, можно умножить данное число на каждое слагаемое отдельно и полученные результаты сложить.

Например, чтобы найти значение выражения:

4 · (3 + 5),

можно отдельно умножить число  4  на  3  и на  5:

4 · 3 = 12   и   4 · 5 = 20

и полученные произведения сложить:

12 + 20 = 32,  значит

4 · (3 + 5) = 4 · 3 + 4 · 5 = 12 + 20 = 32.

Данные способы умножения числа на сумму можно легко проверить, посчитав количество звёздочек на картинке:

Не важно как мы будем их считать:

• пересчитывать все по порядку;
• считать количество звёздочек в строке и умножать количество строк на полученный результат;
• считать сначала количество жёлтых звёздочек, затем зелёных, и складывать полученный результаты.

При любом способе счёта получится ровно  32  звёздочки.

Умножение числа на сумму можно представить в виде общей формулы:

a · (b + c) = a · b + a · c.

Данная формула выражает распределительный закон умножения.

Примеры

Как найти произведение суммы

Сложение и умножение – базовые математические операции, стоящие в одном ряду с вычитанием, делением, возведением в степень, и другими. Комбинируя эти операции между собой, можно получить новые, более сложные операции.

Инструкция

Чтобы умножить сумму на число, перемножьте каждое слагаемое с этим числом, полученные числа сложите между собой.Пример. (a+b+c)*p=a*p+b*p+c*p.Обратная операция – вынесение общего множителя за скобку: a*p+b*p+c*p=p(a+b+c).

Для перемножения двух скобок, содержащих в себе суммы каких-то переменных, существует определенная схема. Надо умножить сначала слагаемое первой скобки на каждое из слагаемых второй скобки, сложить полученные результаты, затем ту же операцию проделать со вторым и последующими слагаемыми первой скобки. Осталось сложить полученные числа между собой.Пример.(a+b)*(c+d)=a*c+a*d+b*c+b*d.Помните, что перемножаются также и знаки перед числами. Произведение одинаковых знаков дает плюс, разных знаков – минус. Например, (a-b)(c+d)=a*c+a*d-b*c-b*d; (a-b)(c-d)=a*c-a*d-b*c+b*d.Обратная операция – разложение суммы на множители.

Чтобы перемножить три скобки, являющиеся суммами некоторых переменных, надо перемножить сначала любые две скобки, затем полученный результат умножить на третью скобку. Умножение четырех и большего числа скобок происходит аналогично. Группируйте скобки так, чтобы считать было удобнее и проще.

Частный случай произведения сумм – возведение суммы в степень. Например, (a+b)^2, (c-d)^3, (p-k)^6. Можно представить возведение в степень в виде произведения нескольких одинаковых скобок и перемножать их по правилам, изложенным выше. А можно воспользоваться формулами сокращенного умножения, которые всегда полезно помнить.

Видео по теме

Полезный совет

Выведите самостоятельно формулы сокращенного умножения, последовательно перемножая скобки. Это позволит лучше понять суть происходящего, а заодно потренироваться в умножении сумм.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Пример: Найдите произведение чисел.

14×15=210

Здесь 14 и 15 называются — множители.

Свойства

Произведение цифр числа

Пример: найти произведение цифр числа 428

4×2×8=64

Произведение суммы и разности чисел

(23+14)×(23-14)=37×9=333

Наименьшее произведение чисел

При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.

Сумма двух произведений чисел

(7×8)+(9×3)=56+27=83

Ответ: 83

Пример: Найди сумму и произведение чисел 14 и 72

Решение:

14+72=86 — сумма

14×72=1008 — произведение