Многогранник, одна грань которого является (n)-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, (n)-угольник называется основанием пирамиды, а треугольники — боковыми гранями.
Общая вершина боковых граней называется вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок:
1. первым рисуется основание,
2. по условию задачи находится проекция вершины на плоскости основания,
3. вертикально проводится высота,
4. проводятся рёбра.
На рисунке изображена четырёхугольная пирамида (SABCD)
(первой пишут букву вершины).
Основание — четырёхугольник (ABCD).
Вершина проецируется в точку пересечения диагоналей (O) — основание высоты или проекция вершины.
(SA), (SB), (SC), (SD) — рёбра пирамиды,
(AB), (BC), (CD), (DA) — стороны основания.
В курсе средней школы в основном есть задачи, в которых даны:
– правильная пирамида (вершина проецируется в центр основания);
– пирамида, вершина которой проецируется в центр описанной окружности;
– пирамида, вершина которой проецируется в центр вписанной окружности;
– пирамида, высота которой совпадает с боковым ребром;
– пирамида, высота которой также является высотой боковой грани.
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды.
Двугранный угол между боковой гранью (SCD) и гранью основания равен линейному углу
∠
(OES). Этот угол образован отрезками (OE) и (SE), лежащими в этих гранях и перпендикулярных их общей прямой (CD). То есть (OE)
⊥CD
и (SE)
⊥CD
.
Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах.
Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания.
На рисунке
∠
(OCS).
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды.
Основные формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды:
S=S1+S2+S3+…
(Некоторые формулы годятся только для определённых видов пирамиды.)
Площадь полной поверхности
Sп.п.=S+Sоснования
.
Объём пирамиды (V =)
13Sоснования
(H), где (H) — высота пирамиды.
Формула объёма используется для пирамид любого вида.
Источники:
Рис. 1. Пирамида, © ЯКласс.
Метод проектов. Проекция вершины пирамиды на плоскость основания.
Тип: исследовательский.
Учебный предмет: геометрия
Участники: 10 класс
Продолжительность: краткосрочный (2 урока)
Внутри классный
Групповой: 3 группы
Проблема: Выяснить при каких условиях вершина пирамиды проектируется в центр окружности, вписанной в основание и описанной около основания пирамиды.
Задачи:
- Изучить свойства пирамид.
- Проанализировать применение данных свойств в других многогранниках. Найти многогранники обладающие данными свойствами.
- Научиться решать задачи по теме «Пирамида».
Продукт: таблица «Проекция вершины пирамиды на плоскость основания».
Оборудование: Ножницы, бумага, клей, мультимедийная доска, проектор, компьютер.
Ход проекта: класс делиться на три группы.
Задание для каждой группы:
1 – я группа: Выяснить при каких условиях вершина пирамиды проектируется:
- на биссектрису угла, лежащего в основании пирамиды;
- в центр окружности, вписанной в основание пирамиды.
2 – я группа: Выяснить при каких условиях вершина пирамиды проектируется:
- на серединный перпендикуляр к стороне основания пирамиды;
- в центр окружности, описанной около основания пирамиды.
3 – я группа: Выяснить при каких условиях вершина пирамиды проектируется:
- на сторону основания пирамиды;
- в вершину основания пирамиды.
Задачи для каждой группы:
- Сделать модели фигур.
- Найти условия.
- Провести доказательство.
- Найти применение данных свойств в других многогранниках (например, в призме).
- Составить задачу и решить ее.
Продукт: Каждая группа заполняет свою часть таблицы « Проекция вершины пирамиды на плоскость основания». Презентация своих результатов.
В данной публикации мы рассмотрим определение, виды (треугольная, четырехугольная, шестиугольная) и основные свойства правильной пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
-
Определение правильной пирамиды
-
Виды правильной пирамиды
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида
- Свойства правильной пирамиды
Определение правильной пирамиды
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Самые распространенные разновидности правильных пирамид: треугольная, четырехугольная и шестиугольная. Рассмотрим их подробнее.
Виды правильной пирамиды
Правильная треугольная пирамида

- Основание – правильный/равносторонний треугольник ABC.
- Боковые грани – одинаковые равнобедренные треугольники: ADC, BDC и ADB.
- Проекция вершины D на основание – точка O, которая является точкой пересечения высот/медиан/биссектрис треугольника ABC.
- DO – высота пирамиды.
- DL и DM – апофемы, т.е. высоты боковых граней (равнобедренных треугольников). Всего их три (по одной на каждую грань), но на рисунке выше изображено два, чтобы не перегружать его.
- ⦟DAM = ⦟ DBL = α (углы между боковыми ребрами и основанием).
- ⦟DLB = ⦟DMA = β (углы между боковыми гранями и плоскостью основания).
- Для такой пирамиды верно соотношение:
AO:OM = 2:1 или BO:OL = 2:1.
Примечание: если у правильной треугольной пирамиды все ребра равны, она также называется правильным тетраэдром.
Правильная четырехугольная пирамида

- Основание – правильный четырехугольник ABCD, другими словами, квадрат.
- Боковые грани – равные равнобедренные треугольники: AEB, BEC, CED и AED.
- Проекция вершины E на основание – точка O, является точкой пересечения диагоналей квадрата ABCD.
- EO – высота фигуры.
- EN и EM – апофемы (всего их 4, на рисунке в качестве примера изображено только два).
- Равные углы между боковыми ребрам/гранями и основанием указаны соответствующими буквами (α и β).
Правильная шестиугольная пирамида

- Основание – правильный шестиугольник ABCDEF.
- Боковые грани – равные равнобедренные треугольники: AGB, BGC, CGD, DGE, EGF и FGA.
- Проекция вершины G на основание – точка O, является точкой пересечения диагоналей/биссектрис шестиугольника ABCDEF.
- GO – высота пирамиды.
- GN – апофема (всего их должно быть шесть).
Свойства правильной пирамиды
- Все боковые ребра фигуры равны. Другими словами вершина пирамиды находится на одинаковом расстоянии от всех углов ее основания.
- Угол между всеми боковыми ребрами и основанием одинаковый.
- Все грани наклонены к основанию под одним и тем же углом.
- Площади всех боковых граней равны.
- Все апофемы равны.
- Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения перпендикуляров, проведенных к серединам боковых ребер.

- В пирамиду можно вписать сферу, центром которой будет точка пересечения биссектрис, берущих начало в углах между боковыми ребрами и основанием фигуры.

Примечание: Формулы для нахождения площади поверхности, а также объема пирамиды представлены в отдельных публикациях.
Геометрическая фигура пирамида: описание, основные виды, свойства, формулы
Содержание:
- Что такое пирамида в геометрии
- Виды пирамид
-
Свойства пирамиды
- Свойства правильной пирамиды
- Формулы вычисления объема и площади
Что такое пирамида в геометрии
Пирамидой называют многогранную объемную фигуру, которая ограничена плоским многоугольником в виде основы и треугольниками с общей вершиной, находящейся за пределами плоскости основания.
Боковой гранью пирамиды является треугольник, у которого один из углов лежит на вершине этой геометрической фигуры, а противоположная ему сторона соответствует стороне основания. Общие стороны, которыми обладают боковые грани, называются боковыми ребрами. Их количество в пирамиде соответствует числу углов многоугольника.
Высота пирамиды является перпендикуляром, который опустили из вершины к основанию пирамиды.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Перпендикуляр боковой грани пирамиды, который опустили из ее вершины на сторону основания, называют апофемой.
Диагональным сечением пирамиды называют сечение данной геометрической фигуры, которое пролегает через ее вершину и диагональ основания.
Построить геометрическую фигуру в виде пирамиды можно с помощью поэтапных действий:
- Нарисовать основание.
- Найти проекцию вершины геометрической фигуры на плоскости ее основания, исходя из условий задачи.
- Провести вертикальную высоту.
- Построить ребра геометрической фигуры.
На рисунке представлена пирамида с четырьмя углами SABCD. В первую очередь следует записывать вершину пирамиды. В основании лежит четырехугольник ABCD. Вершина изображенного многоугольника проецируется в точку О, где пересекаются диагонали. Данная точка представляет собой основание высоты или проекцию вершины. SA, SB, SC, SD представляют собой ребра пирамиды, а отрезки AB, BC, CD, DA являются сторонами ее основания.
Виды пирамид
Основными видами пирамид, которые наиболее часто встречаются при решении задач, являются:
- правильные пирамиды с вершиной, которая спроецирована в центральную точку основания фигуры;
- пирамида с вершиной, спроецированной в центральную точку окружности, которая вписана в геометрическую фигуру;
- пирамида с вершиной, спроецированной в центральную точку окружности, которая описана вокруг геометрической фигуры;
- пирамида с высотой, равной боковому ребру;
- пирамида, высота которой совпадает с высотой боковой грани этого многоугольника.
Свойства пирамиды
Среди свойств, которыми обладает многоугольник в виде пирамиды, можно отметить следующие:
- В случае равенства всех боковых ребер фигуры вокруг ее основания можно описать круг, центр которого совпадет с центром основания пирамиды. Кроме того, через эту точку пройдет перпендикуляр, который опустили из вершины многоугольника.
- Равенство всех ребер пирамиды говорит о том, что они расположены под равными углами к плоскости основания.
- Равенство боковых ребер будет соблюдаться в том случае, когда ими образованы равные углы с плоскостью основания, либо имеется возможность описать вокруг основания многоугольника круг.
- При наклоне боковых граней к плоскости основания под одинаковым углом можно вписать круг в основание пирамиды. При этом проекция вершины пирамиды будет совпадать с центральной точкой данной окружности.
- Равенство апофем боковых граней пирамиды возможно в том случае, когда углы наклона боковых граней к основанию равны.
Свойства правильной пирамиды
Правильную пирамиду характеризуют следующие особенности:
- вершина такой геометрической фигуры расположена на одинаковом расстоянии от всех углов основания;
- равенство всех боковых ребер;
- равенство углов наклона всех боковых ребер к плоскости основания;
- равенство апофем всех боковых граней;
- равенство площадей, которыми обладают все боковые грани;
- для всех граней характерно наличие одинаковых двугранных или плоских углов;
- вокруг такой пирамиды можно описать сферу, центром которой будет являться точка пересечения перпендикуляров, пересекающих середину ребер геометрической фигуры;
- в данный многоугольник можно вписать сферу с центром в точке, в которой пересекаются биссектрисы, выходящие из угла, разделяющего ребро и основание;
- при совпадении центра вписанной сферы с центральной точкой описанной сферы сумма плоских углов при вершине равна π (числу «пи», или 180-ти градусам), или наоборот, один угол соответствует π/n, где n является количеством углов в основании пирамиды.
Формулы вычисления объема и площади
Боковая поверхность пирамиды представляет собой общую площадь всех боковых граней данного многоугольника. Для расчета полной поверхности пирамиды необходимо определить сумму площадей боковой поверхности и основания многоугольника.
Площадь боковой поверхности правильной пирамиды можно рассчитать по формуле, зная периметр основания и апофему:
(Sb = 1/2 ph)
Объем данной геометрической фигуры определяют с помощью площади и высоты:
(V = 1/3 *SоснН)
Пирамида – объёмная фигура, обладающая характеристиками, которые позволяют легко рассчитать основные параметры: площадь поверхности граней и занимаемый ей объём пространства.
Пирамида является одной из основных фигур в геометрии. О её особенностях рассказано в статье.
Определение пирамиды в геометрии
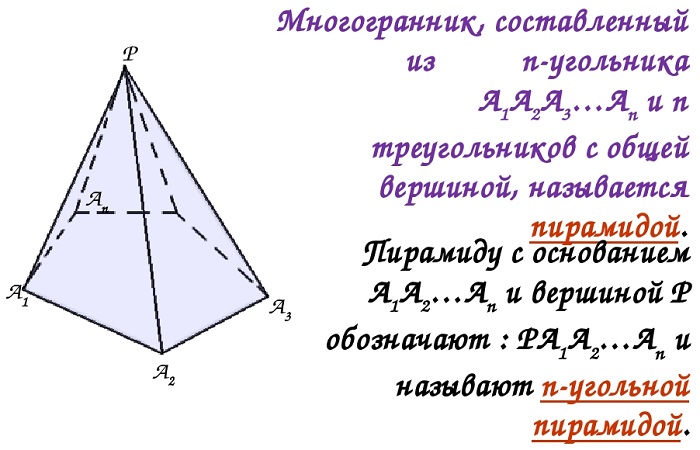
Эта стереометрическая фигура включает в себя часть пространства, отделённую плоскими многоугольниками: произвольным в основании и гранями — треугольниками, содержащими общую вершину и отрезок в виде общей стороны с ним.
Элементы пирамиды
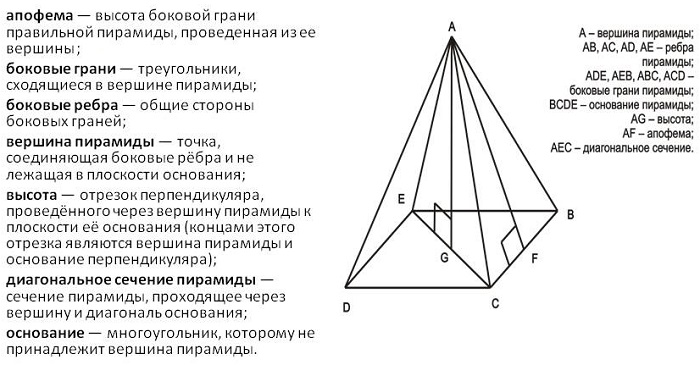
Элементами этой геометрической фигуры являются:
-
Место, куда сходятся все боковые грани фигуры, является вершиной.
-
Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.
-
Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.
-
Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.
-
На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.
-
Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.
-
У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.
Виды пирамид
Такие фигуры могут относиться к различным видам, в зависимости от типа основания и расположения вершины.
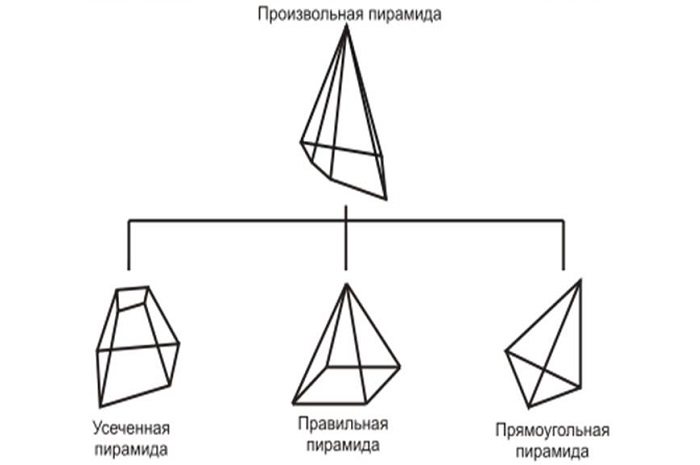
Можно указать следующие разновидности пирамид:
-
Правильной она будет в том случае, если в основании лежит правильный многоугольник. Проекция вершины на многоугольник основания должна приходиться на центр. Тетраэдр рассматривается как одна из разновидностей правильной пирамиды.
-
У прямоугольной фигуры одна из граней находится в плоскости, перпендикулярной многоугольнику, лежащему в основании.
-
Усеченная — это часть фигуры, находящаяся между пересекающей плоскостью и многоугольником основания. Причём эта плоскость должна располагаться горизонтально.
Свойства пирамиды
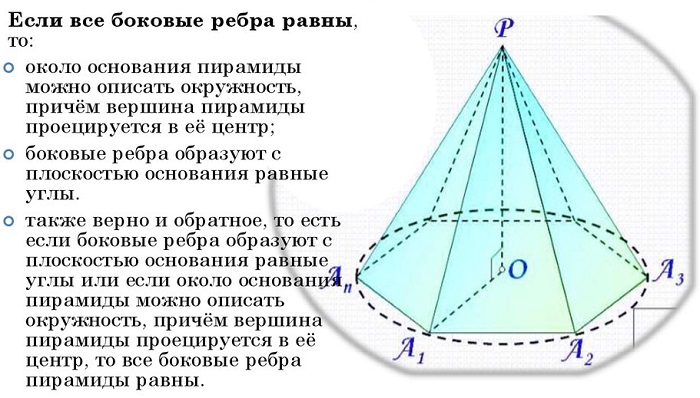
У этой объёмной геометрической фигуры имеются следующие свойства при условии равенства боковых рёбер:
-
круг возможно описать вокруг многоугольника основания;
-
угол, под которым наклонены боковые грани, будет таким же.
В том случае, когда треугольные грани имеют одни и те же углы с основанием, возможно сделать вывод о том, что их рёбра одинаковы.
Свойства правильной пирамиды
У такой фигуры можно отметить особые свойства.
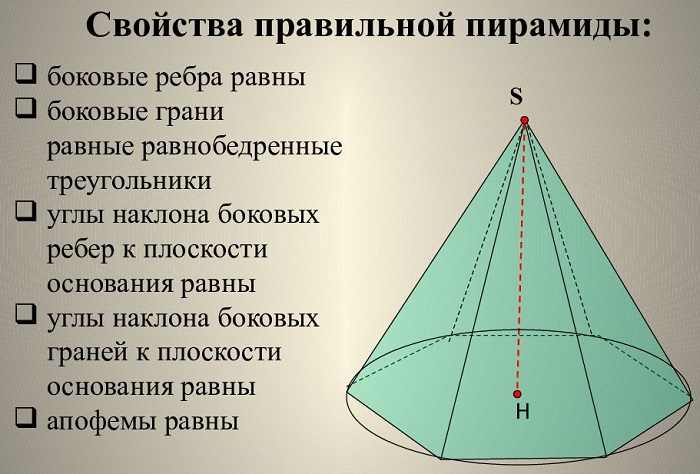
Вот их список:
-
У правильной пирамиды все боковые треугольники одинаковы.
-
Каждая из них является равнобедренным треугольником.
-
Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.
-
Снаружи возможна сфера, касающаяся всех вершин.
-
Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.
-
Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.
Формулы объема и площади поверхности пирамиды с примерами расчета
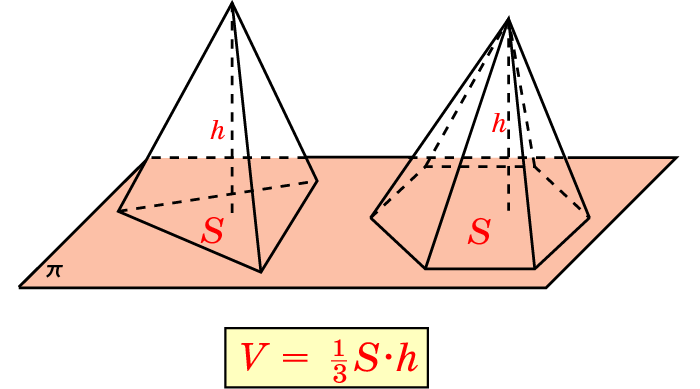
Вычислить объём можно с использованием следующей формулы.
V = (S * h) / 3,
где используются такие обозначения:
-
V – объём;
-
S – площадь основания;
-
h – высота фигуры.
Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.
Пример решения задачи
Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры.
Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата.
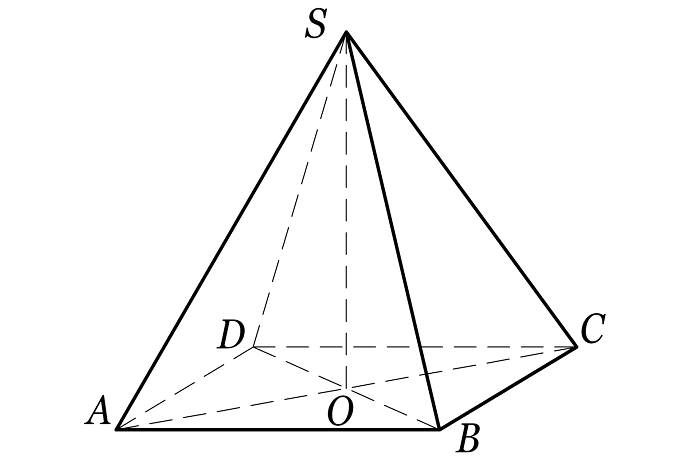
Здесь рассматривается четырехугольная пирамида.
По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.
Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.
V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.
Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см.
Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.
