|
1 / 1 / 0 Регистрация: 16.10.2014 Сообщений: 34 |
|
|
1 |
|
Как получить производную от выражения07.09.2015, 20:43. Показов 30658. Ответов 20
Здравствуйте. Есть выражение вроде ” sin(x^3) + x”. хотелось бы узнать как от этого выражения взять производную во время выполнения программы. Собственно такими выражениями заполнена матрица произвольного размера. Нужно получить новую матрицу где каждый элемент будет производной от одноименного выражения. Может существуют некомерчиские библиотеки для дифференцирования(будет круто если open source
0 |
|
553 / 361 / 206 Регистрация: 27.11.2014 Сообщений: 1,043 |
|
|
07.09.2015, 20:53 |
2 |
|
Апи вольфрам
0 |
|
2432 / 1832 / 404 Регистрация: 15.12.2013 Сообщений: 8,188 |
|
|
07.09.2015, 20:53 |
3 |
|
0 |
|
1673 / 1045 / 174 Регистрация: 27.09.2009 Сообщений: 1,945 |
|
|
07.09.2015, 21:00 |
4 |
|
Symbolic C++. И таки open source.
0 |
|
zss Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
||||
|
07.09.2015, 21:05 |
5 |
|||
|
Почему Вы делаете из дифференцирования проблему:
0 |
|
1 / 1 / 0 Регистрация: 16.10.2014 Сообщений: 34 |
|
|
07.09.2015, 21:16 [ТС] |
6 |
|
Почему Вы делаете из дифференцирования проблему Потому что все выражения будут формироваться на основе функциональной схемы. Там может быть почти все что угодно, и писать для каждого взятие производной это работа на месяцы
0 |
|
zss Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
||||
|
07.09.2015, 21:26 |
7 |
|||
|
Зачем для каждого? Если хотите использовать любое имя функции, то напишите так
1 |
|
1 / 1 / 0 Регистрация: 16.10.2014 Сообщений: 34 |
|
|
07.09.2015, 21:30 [ТС] |
8 |
|
Зачем для каждого? Это численное решение. Тоесть на выходе будет число. но ведь мне производную еще нужно в матрицу записать в строковом виде. Добавлено через 1 минуту
0 |
|
Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
|
|
07.09.2015, 21:31 |
9 |
|
нужно в матрицу записать Ну так в момент записи и вычисляйте нужное значение производной.
0 |
|
1 / 1 / 0 Регистрация: 16.10.2014 Сообщений: 34 |
|
|
07.09.2015, 21:32 [ТС] |
10 |
|
число как ответ это частный случай производной от х в первой степени Добавлено через 56 секунд
0 |
|
Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
|
|
07.09.2015, 21:34 |
11 |
|
Что-то Вы не то думаете…. Разница только в том, что значение dy/dx вычисляется приближенно. Чем меньше мы возьмем dx, тем более точно должно вычисляться dy. Однако, надо учесть, что числа double тоже приближенные. И при вычитании двух близких чисел может получится большая ошибка.
0 |
|
1 / 1 / 0 Регистрация: 16.10.2014 Сообщений: 34 |
|
|
07.09.2015, 21:36 [ТС] |
12 |
|
Вы правы, НО, производную придется брать еще раз, дифференциал высших степеней. А для этого нужно не конкретное значение в точке, а функция
0 |
|
zss Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
||||
|
07.09.2015, 21:49 |
13 |
|||
|
Для второй производной получается
f – Это исходная функция, для которой нужны первая и вторая производные.
0 |
|
2761 / 1915 / 569 Регистрация: 05.06.2014 Сообщений: 5,571 |
|
|
07.09.2015, 23:50 |
14 |
|
Почему Вы делаете из дифференцирования проблему: Если исходная функция известна заранее, это уже будет задача не на программирование, а на алгебру за одиннадцатый класс. Считаем производную на бумажке, вбиваем в код и вуаля, никакого численного дифференцирования вообще не надо. ТС же, как я понимаю, надо дифференцирование произвольной функции. Впрочем, это парсер+все та же алгебра за одиннадцатый класс.
0 |
|
_Ivana 4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
||||
|
08.09.2015, 00:25 |
15 |
|||
|
Здравствуйте. Есть выражение вроде ” sin(x^3) + x” Кто-то там из вредности Лисп рекомендовал?
Код Символьное дифференцирование: Функция (+ (sin (^ 3 x)) x) 1-я производная (+ (* (* 3 (^ 2 x)) (cos (^ 3 x))) 1) 2-я производная (+ (+ (* (* 3 (* 2 x)) (cos (^ 3 x))) (* (* 3 (^ 2 x)) (* (* 3 (^ 2 x)) (- 0 sin (^ 3 x)))))) 3-я производная (+ (+ (+ (* (* 3 2) (cos (^ 3 x))) (* (* 3 (* 2 x)) (* (* 3 (^ 2 x)) (- 0 sin (^ 3 x))))) (+ (* (* 3 (* 2 x)) (* (* 3 (^ 2 x)) (- 0 sin (^ 3 x)))) (* (* 3 (^ 2 x)) (+ (* (* 3 (* 2 x)) (- 0 sin (^ 3 x))) (* (* 3 (^ 2 x)) (- (* 3 (^ 2 x)))))))))
3 |
|
1391 / 1020 / 324 Регистрация: 28.07.2012 Сообщений: 2,809 |
|
|
08.09.2015, 02:37 |
16 |
|
Может существуют некомерчиские библиотеки для дифференцирования(будет круто если open source ) Я бы посоветовал воспользоваться GSL. Там и дифференцирование, и интегрирование, а также прочее-прочее-прочее. Плюс ко всему, у данной библиотеки отличная документация. Добавлено через 4 минуты
1 |
|
0 / 0 / 0 Регистрация: 30.07.2020 Сообщений: 1 |
|
|
30.07.2020, 17:44 |
17 |
|
zss, Подскажите пожалуйста как создать Dat файл с содержанием расчета производной при разных Х Необходимо на С++ (Visual Studio) написать программу расчета производной функции, допустим cos x2 при х от 1 до 20 ответы которые будут выводиться в Dat файл. Заранее благодарю
0 |
|
zss Модератор
13085 / 10362 / 6201 Регистрация: 18.12.2011 Сообщений: 27,707 |
||||
|
30.07.2020, 17:56 |
18 |
|||
|
как создать Dat файл Вывод в файл ничем не отличается от вывода на консоль:
1 |
|
Комп_Оратор)
8842 / 4585 / 618 Регистрация: 04.12.2011 Сообщений: 13,691 Записей в блоге: 16 |
|
|
30.07.2020, 18:44 |
19 |
|
Кто-то там из вредности Лисп рекомендовал?
Если выйдет что, сам кот морской, Лисп зелёный на горе у него… Вот.
0 |
|
4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
|
|
31.07.2020, 13:45 |
20 |
|
IGPIGP, проникновенно, за душу берет! ЗЫ на работе уже 3 года пишу на диалекте Лиспа, ощущения радости и удовольствия как у героя Вашего опуса
1 |
Yes, it is quite possible. However, the solution depends on your needs. If you need a simple numerical solution, the following will do (to a certain extent, with some constraints – naive implementation):
double derive(double (*f)(double), double x0)
{
const double delta = 1.0e-6; // or similar
double x1 = x0 - delta;
double x2 = x0 + delta;
double y1 = f(x1);
double y2 = f(x2);
return (y2 - y1) / (x2 - x1);
}
// call it as follows:
#include <math.h>
double der = derive(sin, 0.0);
printf("%lfn", der); // should be around 1.0
For more advanced numerical calculations, you can use the GNU Scientific Library.
However, if you need to analitically find the formula of the derivative of a given function, then you have to:
- Parse the input formula to some abstract data type, for example an AST;
- Derivate it using the identities and rules of derivation (there’s only a few of them, this part should be the easiest),
- Serialize the abstract data type you got as the result of the derivation process to a string and output that as the result.
However, you won’t need to do all this; there are great C mathematical libraries that provide such functionality.
Edit: after some Googling, I couldn’t find one. The closest solution for getting you started I can think of is having a look at GeoGebra’s source code – although it’s written in Java, it’s fairly easy to read for anybody fluent enough in a C-like language. If not, just go ahead and implement that algorithm yourself 🙂
Перейти к содержимому
Производная функции на C++ часто вычисляется с помощью разнообразных приближенных формул.
Например, есть следующие формулы для приближенного вычисления первой производной функции:
- левая разностная производная
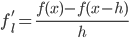 ,
, - правая разностная производная
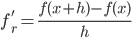 ,
, - центральная разностная производная
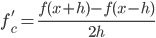 , эта формула точнее предыдущих.
, эта формула точнее предыдущих.
Есть также формула для приближенного вычисления второй производной функции 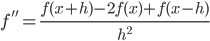 .
.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
#include <iostream.h> // подключаем функции ввода/вывода double f(double x) { //здесь функция, производную которой нужно найти, например, x^2 return x * x; } main() { double x, h, fl, fr, fc, f2; x = 1; // точка, в которой вычисляем производную h = 0.1; // шаг, с которым вычисляем производную // приближенно вычисляем первую производную различными способами fl = (f(x) – f(x – h)) / h; // левая fr = (f(x + h) – f(x)) / h; // правая fc = (f(x + h) – f(x – h)) / (2 * h); // центральная // приближенно вычисляем вторую производную f2 = (f(x + h) – 2 * f(x) + f(x – h)) / (h * h); // выводим результаты на экран cout<<“x = “<<x<<“n”; cout<<“fl = “<<fl<<“n”; cout<<“fr = “<<fr<<“n”; cout<<“fc = “<<fc<<“n”; cout<<“f2 = “<<f2<<“n”; system(“pause”); } |
Более сложный, но учитывающий различные особенности вычисления производных код можно найти в какой-нибудь стандартной программе для вычисления производной или какой-нибудь библиотеке численных методов.
Как на Python найти производную функции? В какой библиотеке есть необходимые для этого функции?
задан 20 фев 2017 в 5:59
![]()
Алексей ВороновАлексей Воронов
5413 золотых знака8 серебряных знаков24 бронзовых знака
1
2 ответа
SymPy (от слов Symbolic math и Python):
>>> from sympy import diff, symbols, cos, sin
>>> x, y = symbols('x y')
>>> diff(cos(x))
-sin(x)
>>> diff(cos(x) + 1j*sin(y), x)
-sin(x)
>>> diff(cos(x) + 1j*sin(y), y)
1.0*I*cos(y)
ответ дан 21 фев 2017 в 8:56
jfsjfs
51.8k11 золотых знаков107 серебряных знаков306 бронзовых знаков

 ) Это не обязательно должен быть С++, подойдет любой из популярных языков. или может быть где-то есть статьи с примерами реализации.
) Это не обязательно должен быть С++, подойдет любой из популярных языков. или может быть где-то есть статьи с примерами реализации.

