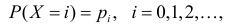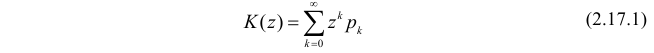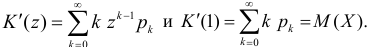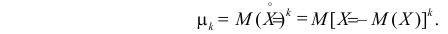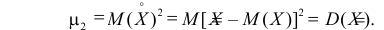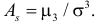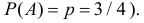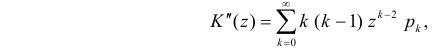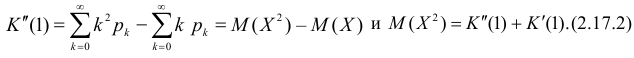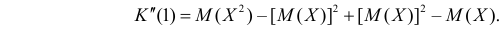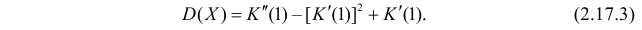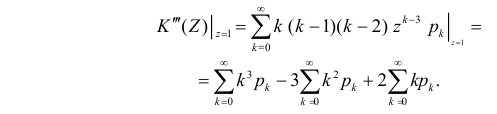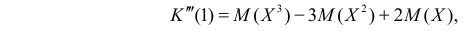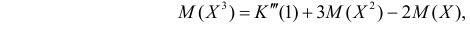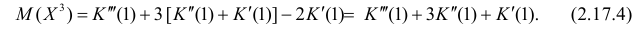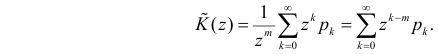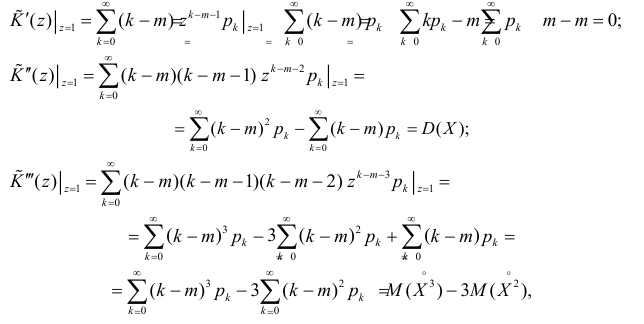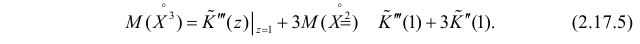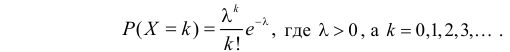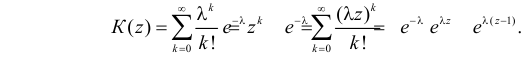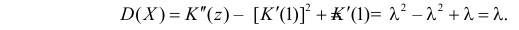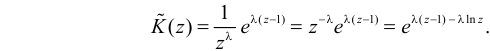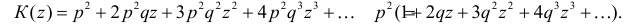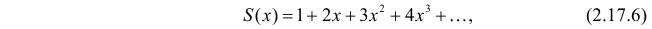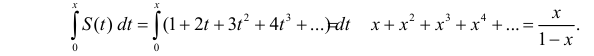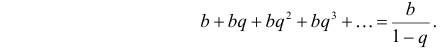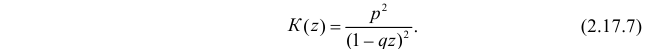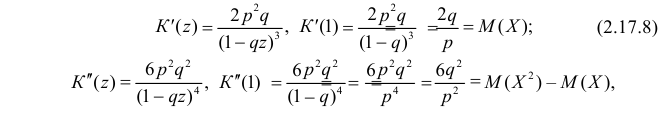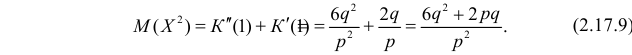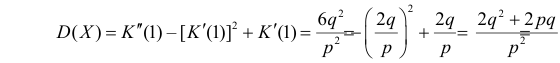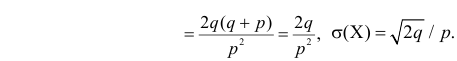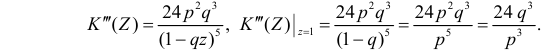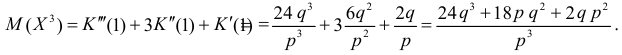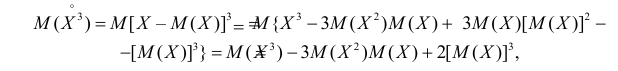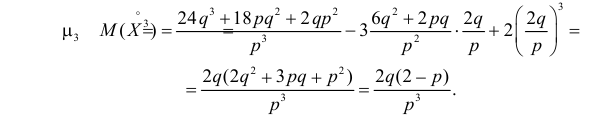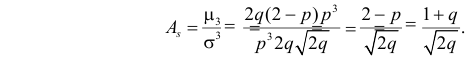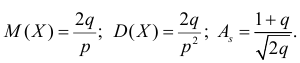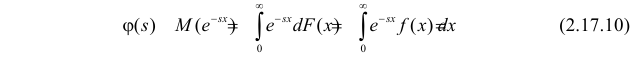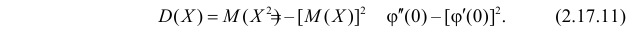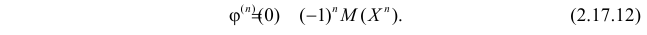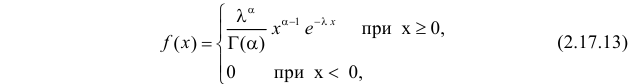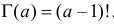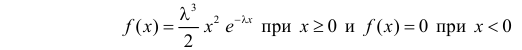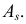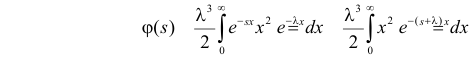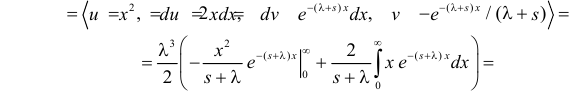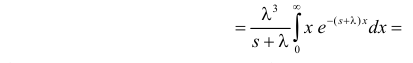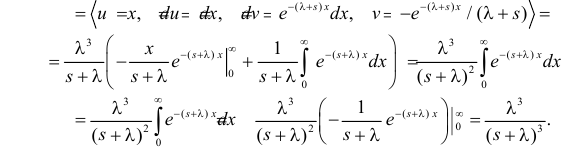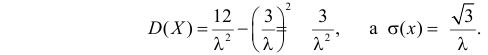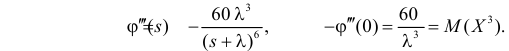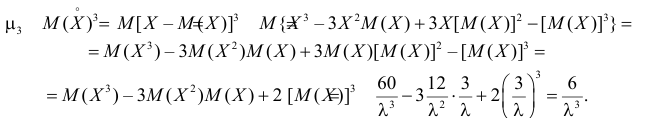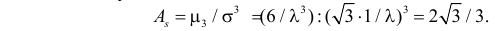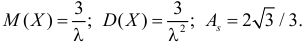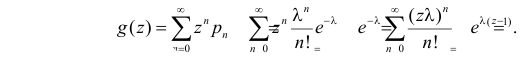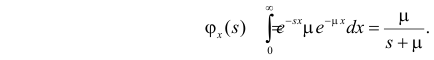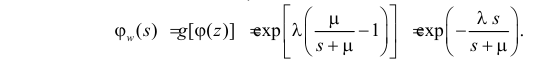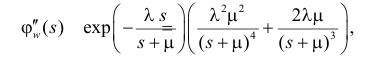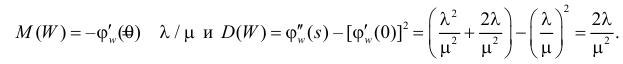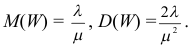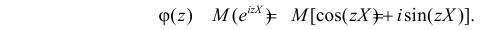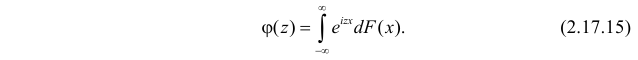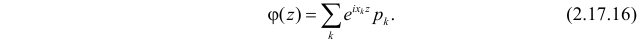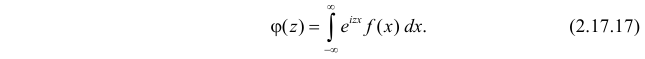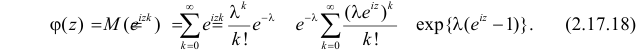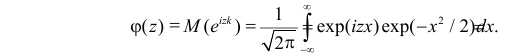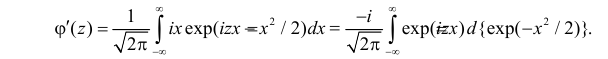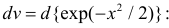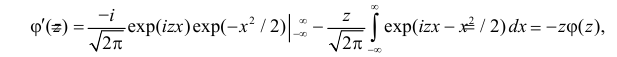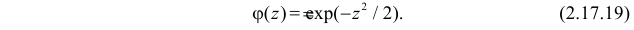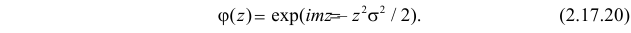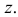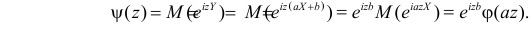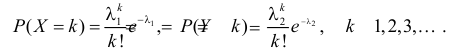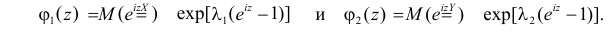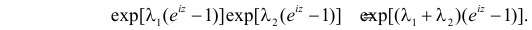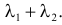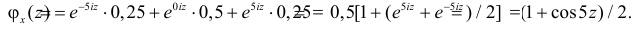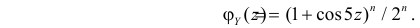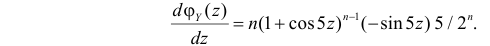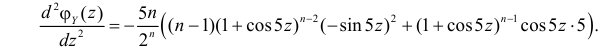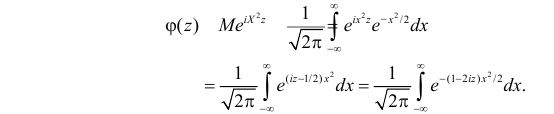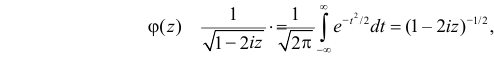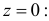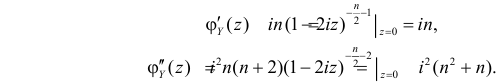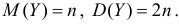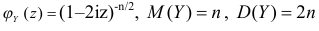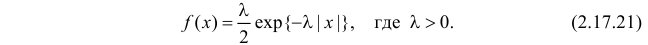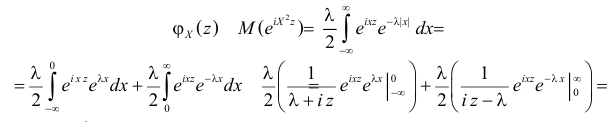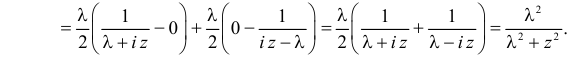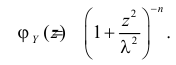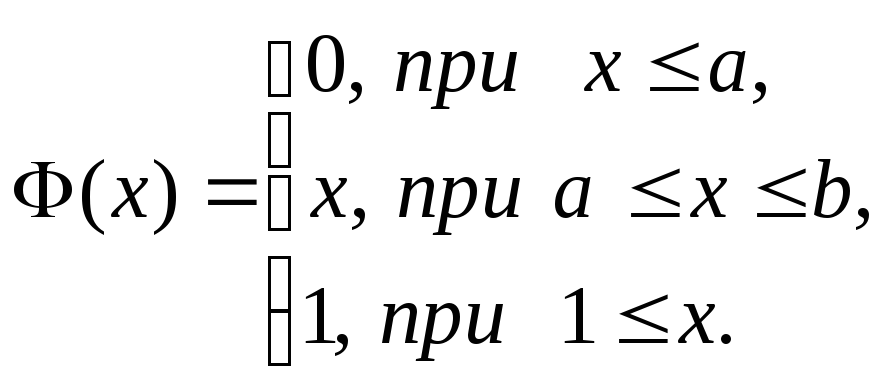Производящая функция вероятностей как найти - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 августа 2017 года; проверки требуют 5 правок.

В теории вероятностей, производящая функция вероятностей дискретной случайной величины представляет собой степенной ряд функции вероятности случайной величины. Производящие функции вероятностей часто используются для краткого описания их последовательности вероятностей P(X=i) для случайного величины Х, с возможностью применить теорию степенных рядов с неотрицательными коэффициентами.

Определение[править | править код]

Одномерный случай[править | править код]

Если Х является дискретной случайной величиной, принимающей неотрицательные целочисленные значения {0,1, …}, тогда производящая функция вероятностей от случайной величины Х определяется как

${displaystyle G(z)=M(z^{X})=sum _{x=0}^{infty }p(x)z^{x}}$

где p – это функция вероятности от Х. Заметим, что индексы обозначения G_X и p_X часто используются, чтобы подчеркнуть, что они относятся к конкретной случайной величине Х и ее распределению. Степенной ряд абсолютно сходится, по крайней мере, для всех комплексных чисел z, |z| ≤ 1; во многих примерах радиус сходимости больше.,c

Многомерный случай[править | править код]

Если X = (X₁,…,X_d) является дискретной случайной величиной, принимающей значения из d-мерной неотрицательной целочисленной решетки {0,1, …}^d, тогда производящая функция вероятностей от Х определена как

${displaystyle G(z)=G(z_{1},...,z_{d})=M(z_{1}^{X_{1}}...z_{d}^{X_{d}})=sum _{x_{1},...,x_{d}=0}^{infty }p(x_{1},...,x_{d})z_{1}^{x_{1}}...z_{d}^{x_{d}}}$

где p – это функция вероятности от Х. Степенной ряд абсолютно сходится по крайней мере для всех комплексных векторов z = (z₁,…,z_d ) ∈ ℂ^d с максимумом {|z₁|,…,|z_d |} ≤ 1.)

Свойства[править | править код]

Степенные ряды[править | править код]

Производящие функции вероятностей подчиняются всем правилам степенных рядов с неотрицательными коэффициентами. В частности, G(1⁻) = 1, где G(1⁻) = lim_z→1G(z) снизу, поскольку сумма вероятностей должна равняться 1. Таким образом, радиус сходимости любой производящей функции вероятностей должен быть как минимум 1, по теореме Абеля для степенных рядов с неотрицательными коэффициентами.

Вероятности и ожидания[править | править код]

Следующие свойства позволяют сделать вывод о различных базовых величинах, связанных с :

1. Функция вероятности от восстанавливается взятием производной

${displaystyle p(k)=P(X=k)={frac {G^{(k)}(0)}{k!}}}$

2. Из свойства 1 следует, что если случайные величины и имеют равные производящие функции вероятностей ( ${displaystyle G_{X}}$ = ${displaystyle G_{Y}}$ ), тогда ${displaystyle p_{X}(k)=p_{Y}(k)}$ .То есть, если и имеют одинаковые производящие функции вероятностей, то они имеют также и одинаковые распределения.

3. Нормализация функции плотности может быть выражена в терминах производящей функции

${displaystyle M(1)=G(1^{-})=sum _{i=0}^{infty }p(i)=1}$

Математическое ожидание X задается как

${displaystyle M(X)=G'(1^{-})}$

В более общем плане, k-ый факториальный момент,

от X задается как

${displaystyle Mleft({frac {X!}{(X-k)!}}right)=G^{(k)}(1^{-}),kgeq 0}$

Таким образом, дисперсия Х задается как

${displaystyle D(X)=G''(1^{-})+G'(1^{-})-[G'(1^{-})]^{2}}$

4. ${displaystyle G_{X}(e^{t})=M_{X}(t)}$ , где – это случайная величина. ${displaystyle G_{X}(t)}$ – это производящая функция вероятностей и ${displaystyle M_{X}(t)}$ – это производящая функция моментов.

Функции независимых случайных величин[править | править код]

Производящие функции вероятностей полезны в частности для работы с функциями независимых случайных величин. Например:

Если X₁, X₂, …, X_n представляет собой последовательность независимых (и не обязательно одинаково распределенных) случайных величин, и

${displaystyle S_{n}=sum _{i=1}^{n}a_{i}X_{i},}$

где a_i – константы, тогда производящая функция вероятностей определяется как

${displaystyle G_{S_{n}}(z)=M(z^{S_{n}})=M(z^{sum _{i=1}^{n}a_{i}X_{i}})=G_{x_{1}}(z^{a_{1}})G_{x_{2}}(z^{a_{2}})...G_{x_{n}}(z^{a_{n}})}$

Например, если

${displaystyle S_{n}=sum _{i=1}^{n}X_{i},}$

тогда производящая функция вероятностей, G_{S_n(z)}, определяется как

${displaystyle G_{S_{n}}(z)=G_{x_{1}}(z)G_{x_{2}}(z)...G_{x_{n}}(z)}$

Из этого также следует, что производящая функция разности двух независимых случайных переменных S = X₁ − X₂ определяется как

${displaystyle G_{S}(z)=G_{X_{1}}(z)G_{X_{2}}(1/z)}$

Предположим, что N также является независимой, дискретной случайной величиной, принимающая неотрицательные целочисленные значения, с производящей функцией вероятностей G_N. Если X₁, X₂, …, X_N независимы и одинаково распределены с общей производящей функцией вероятностей G_X, тогда

${displaystyle G_{S_{N}}(z)=G_{N}(G_{X}(z))}$

Это можно увидеть, используя закон полного математического ожидания следующим образом:

${displaystyle G_{S_{N}}(z)=M(z^{S_{N}})=M(z^{sum _{i=1}^{N}X_{i}})=M(M(z^{sum _{i=1}^{N}X_{i}}|N))=M((G_{X}(z))^{N})=G_{N}(G_{X}(z))}$

Этот последний факт полезен при изучении процессов Гальтона-Ватсона.

Пусть снова N также является независимой, дискретной случайной величиной, принимающей неотрицательные целочисленные значения, с производящей функцией вероятностей G_N и плотностью вероятности f_i=P{N=i}. Если X₁, X₂, …, X_n независимы, но неодинаково распределенные случайные величины, где G_{X_i} обозначает производящую функцию вероятностей от X_i, тогда

${displaystyle G_{S_{N}}(z)=sum _{igeq 1}{f_{i}}prod _{k=1}^{i}{G_{X_{i}}(z)}}$

Для одинаково распределенных X_i это упрощает тождественность указанную ранее. В общем случае иногда полезно получить разложение S_N с помощью производящих функций вероятностей.

Примеры[править | править код]

Производящая функция вероятностей для постоянной случайной величины принимающей одно значение c (P(X=c) = 1) есть

${displaystyle G(z)=z^{c}}$

Производящая функция вероятностей для случайной величины с биномиальным распределением есть

${displaystyle G(z)=[(1-p)+pz]^{n}}$

Очевидно, что это n-кратное произведение производящих функции случайной величины с распределением Бернулли с параметром p

Таким образом производящая функция случайной величины бросания честной монеты

Производящая функция вероятностей для случайной величины с отрицательным биномиальным распределением с вероятностью успеха p, проводимой до r-го успеха

${displaystyle G(z)={left({frac {p}{1-(1-p)z}}right)}^{r}}$

(Сходится при ${displaystyle left|zright|<{frac {1}{1-p}}}$

)

Очевидно, что это r-кратное произведение производящих функции случайных величин с геометрическим распределением с параметром (1-p)

Производящая функция вероятностей для случайной величины с распределением Пуассона с параметром λ есть

${displaystyle G(z)=e^{lambda {(z-1)}}}$

Ссылки[править | править код]

Johnson, N.L.; Kotz, S.; Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9 (Section 1.B9)

Источник

Производящие функции:

Пусть дискретная случайная величина Х имеет закон распределения

Функция

называется производящей функцией этого распределения.

Заметим, что

Напомним:

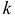
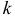
1) Начальным моментом порядка называется математическое ожидание -й степени случайной величины

Само математическое ожидание является начальным моментом первого порядка.

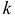
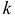
2) Центральным моментом -го порядка называется математическое ожидание -й степени соответствующей центрированной случайной величины

Дисперсия является центральным моментом второго порядка

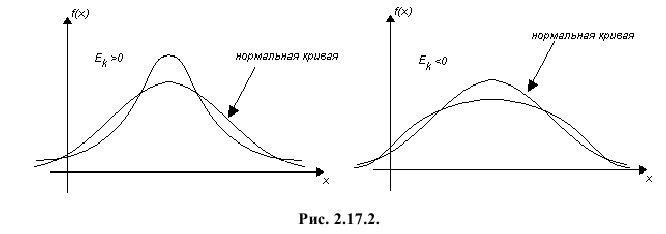
3) Асимметрией распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения случайной величины:

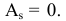
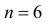
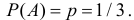
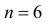
Если распределение симметрично, то На рис. 2.17.1 слева (в качестве примера закона равпределения с положительной асимметрией) изображен многоугольник распределения для биномиального закона распределения при и В правой части рис. 2.17.1 приведен пример закона распределения с отрицательной асимметрией (биномиальный закон при и

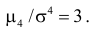
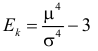
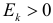
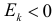
4) Для нормального закона распределения Безразмерный коэффициент называется эксцессом. Этот коэффициент характеризует «островерхость» распределения в сравнении с нормальным законом распределения. Например, если говорить о функциях плотности вероятности, то при график функции плотности вероятности более островерхий, чем график кривой нормального распределения (см. левую часть рис 2.17.2). При график плотности вероятности имеет более плоскую вершину, нежели нормальная кривая при тех же математическом ожидании и дисперсии (см. правую часть рис. 2.17.2).

Через производящую функцию можно выразить и другие начальные и центральные моменты случайной величины. Выразим через производящую функцию, например, дисперсию. Так как

то

Сформируем в правой части последнего равенства дисперсию. Для этого прибавим и отнимем квадрат математического ожидания:

Величина 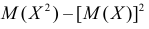равна дисперсии. Поэтому

Аналогично

Итак, при z =1 имеем

откуда

а с учетом (2.17.2)

Пусть 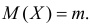Рассмотрим модифицированную производящую функцию

С помощью этой функции можно вычислять сразу центральные моменты случайной величины. Например

откуда

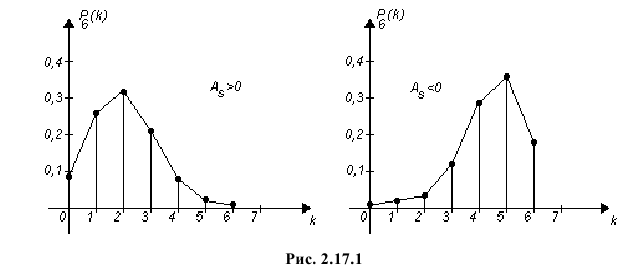
Пример:

Пусть Х имеет пуассоновский закон распределения:

Требуется найти математическое ожидание, дисперсию и коэффициент асимметрии этой случайной величины.

Решение. Производящая функция пуассоновского распределения имеет вид

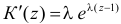
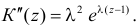
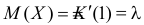
Заметим, что и Поэтому и, в соответствии с (2.17.3),

Для вычисления коэффициента асимметрии составим модифицированную производящую функцию. Так как 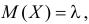то

Тогда

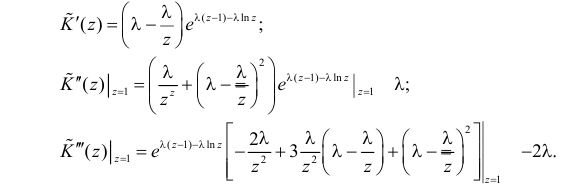
Поэтому по формуле (2.17.5) имеем

В итоге

Ответ.

Пример:

Пусть Х имеет закон распределения

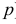
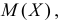
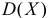
(Это частный случай отрицательного биномиального распределения или распределения Паскаля с параметрами 2 и ). Требуется найти и коэффициент асимметрии

Решение. Составим производящую функцию

Для вычисления суммы ряда в скобке рассмотрим сумму ряда

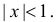
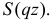
который абсолютно сходится при Легко видеть, что нас интересует Проинтегрируем почленно ряд (2.17.6) внутри его области сходимости:

В последней строке мы воспользовались формулой суммы бесконечной убывающей прогрессии:

Отсюда 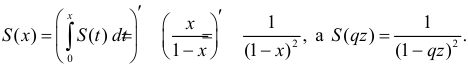Откуда

Воспользуемся теперь производящей функцией (2.17.7) для вычисления числовых характеристик случайной величины X:

откуда следует, что

По формуле (2.17.3)

По формуле (2.17.4) вычисляем

Так как

то с учетом (2.17.8) и (2.17.9) имеем

Учитывая это получаем значение коэффициента асимметрии

Ответ.

Преобразование Лапласа

Для непрерывной и неотрицательной случайной величины роль производящей функции может играть преобразование Лапласа.

Пусть Х – непрерывная, неотрицательная случайная величина с функцией распределения 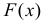. Тогда

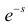
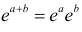
называется преобразованием Лапласа для этого распределения. (Фактически роль величины z в формуле (2.17.1) играет величина . Преимущество такого выбора состоит в том, что .)

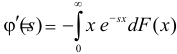
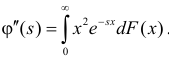
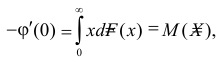
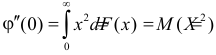
Отметим, что и Поэтому а и

Производная любого порядка от преобразования Лапласа связана с начальными моментами случайной величины соотношением

где 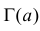– так называемая гамма-функция Эйлера, которая при целых положительных a принимает значения

Пример:

Случайная величина X имеет функцию плотности вероятности

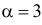
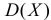
(гамма-распределение с параметрами и ). Требуется найти и коэффициент асимметрии

Решение. Соответствующее преобразование Лапласа имеет вид

(интегрируем по частям)

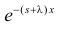
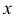
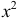
(первое слагаемое в скобке равно нулю, так как с увеличением убывает быстрее, чем растет )

(интегрируем еще раз по частям)

Вычислим начальные моменты распределения:

поэтому

Вычислим центральный момент третьего порядка:

Поэтому

Ответ.

Пример:

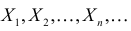
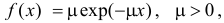
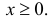
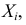
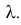
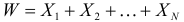
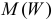
Пусть – последовательность независимых неотрицательных одинаково распределенных случайных величин с функцией плотности вероятности И пусть N – неотрицательная целочисленная случайная величина, независящая от величин и имеющая пуассоновский закон распределения с параметром Для случайной величины требуется найти и

Решение. Производящая функция пуассоновского закона распределения равна

Преобразование Лапласа показательного распределения равно

Поэтому по формуле (2.17.14) имеем

Так как 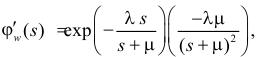а

то

Ответ.

Характеристические функции

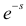
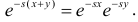
Замена z на в определении производящей функции позволила рассматривать непрерывные неотрицательные величины. Выгода от такой замены состоит в мультипликативном свойстве: Таким же свойством обладает и показательная функция чисто мнимого аргумента, которая для действительных x определяется равенством:

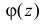
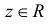
Характеристической функцией случайной величины X называется комплексно-значная функция, определенная при соотношением

Если 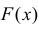– функция распределения случайной величины X, то

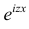
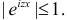
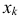
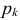
Существование интеграла, определяющего характеристическую функцию, вытекает из непрерывности функции и ее ограниченности: Для дискретной случайной величины X с возможными значениями и их вероятностями запись (2.17.15) расшифровывается как

Для непрерывной случайной величины X с функцией плотности вероятности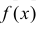

Пример:

Пусть случайная величина X имеет пуассоновский закон распределения, т.е.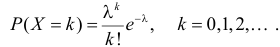 Тогда по формуле (2.17.11)

Пример:

Пусть 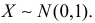Тогда в соответствии с формулой (2.17.12)

Вместо непосредственного вычисления интеграла, которое требует специальной математической техники, найдем его величину косвенным способом. Заметим, что

Полученный интеграл берем по частям, полагая 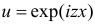и

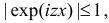
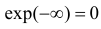
(первое слагаемое равно нулю так как а ).

В итоге для искомой характеристической функции получаем уравнение, которое при начальном условии 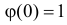имеет решение

Подобным же образом можно показать, что закон распределения 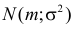имеет характеристическую функцию

Свойства характеристических функций.

1. для всех вещественных

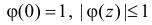
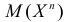
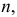
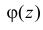
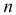
2. Если существует – момент порядка то функция имеет непрерывных производных и

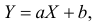
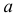
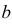
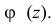
3. Пусть где и – постоянные величины, а X имеет характеристическую функцию Тогда характеристическая функция случайной величины Y имеет вид

4. Характеристическая функция однозначно определяет распределение случайной величины.

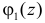
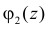
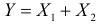
5. Если X₁ и X₂ – независимые случайные величины, а и – их характеристические функции, то характеристическая функция суммы равна произведению характеристических функций слагаемых:

Это следует из того, что в силу независимости слагаемых

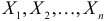
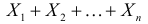
Можно показать, что для любого конечного числа независимых случайных величин характеристическая функция их суммы равна произведению характеристических функций слагаемых.

Пример:

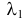
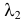
Случайные величины X и Y независимы и имеют пуассоновские законы распределения с параметрами и соответственно:

Требуется найти закон распределения случайной величины .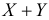

Решение. Согласно формуле (2.17.18) характеристические функции случайных величин X и Y имеют вид:

Сумме независимых случайных величин соответствует произведение характеристических функций слагаемых. Поэтому 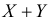имеет характеристическую функцию

Ответ. 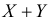имеет пуассоновский закон распределения с параметром

Полученный результат известен как факт устойчивости пуассоновского закона распределения. Этот результат можно обобщить на сумму любого конечного числа пуассоновских случайных величин.

Теорема. Если случайные величины Х₁ и Х₂ независимы и имеют соответственно нормальные законы распределения и то их сумма имеет тоже нормальный закон распределения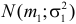

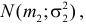
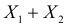
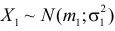
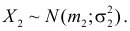
Доказательство. Пусть и Их характеристические функции в соответствии с формулой (2.17.15) имеют вид

Тогда характеристическая функция суммы :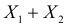

А это и означает, что

Пример:

Случайная величина 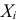имеет закон распределения.

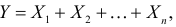
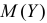
Требуется найти характеристическую функцию этой случайной величины. Используя свойства характеристических функций, найти характеристическую функцию случайной величины полагая слагаемые независимыми. Используя запись характеристической функции, найти и

Решение. По формуле (2.17.16)

Поэтому характеристическая функция случайной величины Y имеет вид

Для вычисления 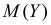находим

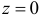
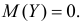
Последнее выражение при равно нулю. По свойству 2 это означает, что Так как вторая производная характеристической функции по z равна

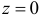
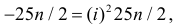
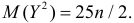
при равна то из свойства 2 следует, что Поэтому

Ответ.

Пример:

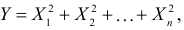
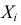
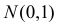
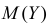
Требуется найти характеристическую функцию случайной величины где все имеют закон распределения независимы в совокупности. С помощью характеристической функции найти и

Решение. Найдем сначала характеристическую функцию для 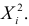В соответствии с формулой (2.17.7)

После замены переменных 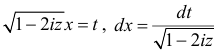получаем

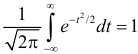
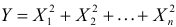
так как Из свойства 5 характеристических функций следует, что случайная величина имеет характеристическую функцию

Для вычисления числовых характеристик случайной величины Y найдем сначала первую и вторую производные характеристической функции при

Это означает, что

Ответ.

Пример:

Случайная величина Х имеет функцию плотности вероятности

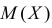
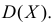
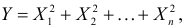
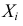
Требуется найти характеристическую функцию этой случайной величины и ее и Требуется также найти характеристическую функцию случайной величины где величины независимы и имеют распределение (2.17.21).

Решение. Найдем сначала характеристическую функцию:

(так как 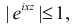то равенство можно продолжить следующим образом)

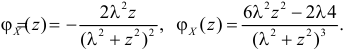
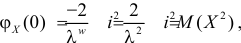
Тогда Откуда поэтому

Характеристическая функция случайной величины 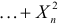имеет вид:

Ответ.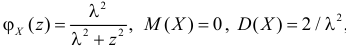

Теоремы теории вероятностей
Основные законы распределения дискретных случайных величин
Непрерывные случайные величины
Закон больших чисел
Центральная предельная теорема
Ковариация в теории вероятности
Функциональные преобразования двухмерных случайных величин
Правило «трех сигм» в теории вероятности

Источник

Кратко остановимся на понятие производящей
функции конечных дискретных случайных
величин.

Функцию определённую равенством
,
где
некоторый параметр называют
производящей функцией для
последовательности повторных независимых
опытов. Очевидно, что приимеет место равенство

для
любого натурального числа

Пусть производится
испытаний, причём в первом испытания
вероятность появления событияравнаво втором равнавм
испытании равнаи вероятностинепоявлениясобытиясоответственно равныЗаобозначим вероятность появления
событиявиспытаниях ровнораз.

Производящей функцией вероятностей
называют функцию, определяемую равенством

()

Таким образом, вероятность
равна коэффициенту прий
степени многочлена,
определённой равенством (),
т.е. равна коэффициенту прив разложении производящей функции по
степеням.

Замечание. Отметим, что придолжно выполняться равенство (обычно
называется контроль).

().

При
имеем равенство

Следовательно,
коэффициент при
равно,
приравнои при.

Следует заметить, что если в различных
испытаниях появляется различные события
(в первом испытании событие
,
во втором событиеи
т.д.), то изменяется лишь истолкование
коэффициентов при различных степенях.
Например, в равенстве ()
коэффициентопределяет вероятность появления двух
событийи.

Пример 8. Устройство состоит из трёх
независимо работающих элементов.
Вероятности безотказной работы элементов
(за время)
соответственно равныНайти вероятности того, что за времябудут работать безотказно:

а) все три элемента работают;

б) два элемента работают;

в) один элемент работает;

г) ни один из элементов не будет работать.

Решение. Вероятности безотказной
работы элементов соответственно равныСледовательно, вероятности того, что
элементы откажут, соответственно равны

Составим производящую функцию:

а) Вероятность того, что три элемента
будут работать безотказно, равна
коэффициенту при

б) Вероятность того, что два элемента
будут работать безотказно, равна
коэффициенту при

в) Вероятность того, что один элемент
будет работать безотказно, равна
коэффициенту при

г) Вероятность того, что ни один из
элементов не будет работать безотказно,
равна свободному члену:

Легко видет, что выполняется контроль:

Задания. Покажите, что

1. гдештрихозначаетю
производную функциипо
параметрупричём

3.,

гдечисло
размещений изэлементов по.

Заметим, что вероятности
,являются коэффициентами при степенив разложении

6. Плотность распределения вероятностей

непрерывной
случайной величины

Важнейшей характеристикой непрерывной
случайной величины (кроме функции
распределения) является так называемая
функция плотности распределения.Напомним, что «Случайную величину
называют непрерывной, если ее функция
распределениянепрерывна
в любой точке и дифференцируема всюду,
за исключением, может быть отдельных
точек».

Плотностью распределения вероятностейнепрерывнойслучайной величины
называют некоторую функциюпервую производную от функции
распределения:

(7)
.

Из этого определения следует, что
функция распределения является
первообразной функциейдля
функции плотности распределения.

Функцию
называют такжедифференциальной
функцией распределения: она выражает
одной из форм закона распределения
случайной величины, относящихся только
к непрерывным случайным величинам.

Следует заметить, что для описания
распределения вероятностей д.с.в.
понятие
плотность распределения неприменима.

Рассмотрим вероятностный смысл плотности
распределения. По определению производной
функции имеем

Далее,
согласно формуле (2), выполняется
равенство

Отношение
представляет собой «среднюю вероятность»,
которая приходится на единицу длины
участка.
Тогда получим

(8)
,

т.е.
плотность распределения
н.с.в.
равна
пределу отношения вероятности попадания
н.с.в.в
промежутокк длинеэтого промежутка, когда величинастремиться к нулю. Из равенства (8)
следует, что.

Тем самым, установлено, что плотность
вероятности н.с.в.
определяется
как функцияудовлетворяющая, условию.
Выражениеназываетсяэлементом вероятности.

Следует отметить, что понятие функции
плотности распределения вероятности
,
аналогично таким понятиям, как плотность
распределения масс на оси абсцисс или
плотность распределения электрического
тока в теории электричества в физике
и т.д.

Теперь, рассмотрим свойства функции
плотности распределения.

С.1.
.–
неотрицательная функция на всей числовой
оси.

С.2. Вероятность попадания
н.с.в.
в промежутокравна определенному интегралу от ее
функции плотности в пределах отдо,
т.е. верно равенство

(9)

С.3. Если
функция распределения н.с.в.и– функция плотности, то имеет место
равенство

(10)
.

С.4. Интеграл от функции плотности
вероятности н.с.в.
в бесконечных пределах равен единице
(условие нормировки – контроль)
т.е. еслиплотность распределения некоторой
с.в.,
тогда

.
(11).

Условие нормировки
для н.с.в. напоминает аналога условия
«контроля»
для случая д.с.в..

1.Функция плотности распределения–
неотрицательная функция потому, что
по определениюнеубывающая
и монотонна, а следовательно.
Это означает, что график функция
плотности, называемыйкривой
распределения, расположена не ниже
оси абсцисс, также следует отметить,
что функция плотности может принимать
сколь угодно большие значения.

2.Посколькуестьпервообразнаяфункцией для
функции,
тогда в соответствии с формулой
Ньютона-Лейбница справедливо равенство

(12)

Отсюда, согласно определению функции
получим

(13)
.

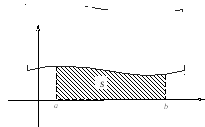
Геометрический смысл этого равенства
следующее: интеграл от элемента
вероятностиесть площадь фигуры
(),
ограниченной сверху кривой распределенияи опирающейся на отрезок [a;b]

рис.21-Письменный

3.На основании свойстваС.2. И
то, чтополучим:

(14)
.

4.Подставляя в формуле (13) соответственно,
получаем достоверное событиет.е.

(15)
.

Геометрическая трактовка свойство
С.4.(свойство нормировки) означает,
что площадь фигуры (S)
ограниченной функциейи числовой осью абсцисс,
равна единице.

Теперь, мы можем дать определение
непрерывной с.в. в связи с функцией
распределения плотности
:случайная величина
называетсянепрерывной, если существует
неотрицательная функция
такая, что при любом
её функция распределения
можно представить в виде

;

отсюда получим равенство
–дифференциальное равенство
(дифференциальный закон распределения).

Следовательно, функций
иявляются равноправными (эквивалентными)
характеристиками случайной величины.
Отметим, что на основании формулы (13)
непосредственно следует равенство

Отсюда,
также следуют равенства:

Пример 9. Пусть плотность распределения
с.в.задана функцией,.

1. Найти значение параметра
,
при которомбудет
функцией плотности,

2. Выписать функцию распределения
.

Решение. На основанииС.4. должно
выполняться равенство (см.(11))

Применяя метод подсчёта несобственных
интегралов, при этом воспользуюсь
табличным интегралом для функции
арктангенса с последующим применением
формулы Ньютона –Лейбница получим

Следовательно,
.
Далее, выпишем функцию распределения
с.в.плотность распределения которой равна.
Проведя обычные рассуждения на основании
формулы (14) получим

Такое
распределение называют распределением
Коши.

Задание. Проверьте справедливость
дифференциального закона распределения
и убедитесь, чтоявляется первообразной функцией.

Пример 9. Пусть плотность распределения
с.в.задана функцией,

1. Найти значение параметра
,
при которомбудет
функцией плотности,

2. Выписать функцию распределения
.

Решение. Аналогично как в примере
1 пользуясь равенством (11) получим

Следовательно,

Задание. 1. Проверьте
справедливость дифференциального
закона распределения
и убедитесь, что
является первообразной функцией для.

2. Пусть
и плотность распределения н.с.в.задана функцией

Найти значение параметра
C,
выписать явный вид функции распределения
и проверить выполнение дифференциального
закона.

Пример 10. Однородная проволока
длиной 1 м. растягивается за концы и
при этом разрывается. Пустьслучайная
величина, равная расстоянию от точки
разрыва до левого конца проволки.
Используя геометрические вероятности,
найдём, что

для
любых
Следовательно, функция распределения
и плотность распределения этой случайной
величины имеют вид:

Задание. Проверьте выполнения
дифференциального закона.

Соседние файлы в папке Теория вероятностей от исмоилова

#
#
#
#
#
#
#
#
06.02.20162.36 Mб71~WRL0002.tmp
#
06.02.20161.87 Mб67~WRL0005.tmp
#
06.02.20161.01 Mб66~WRL0205.tmp
#
06.02.20162.41 Mб65~WRL0264.tmp

Источник

Содержание:

Примеры с решением
Биномиальный закон
Геометрический закон
Закон Пуассона

Мы видели, что дискретные случайные величины, рассмотренные в предыдущих параграфах, принимали только целые значения Нахождение числовых характеристик таких величин упрощается, если рассмотреть производящие функции.

Определение. Производящей функцией дискретной целочисленной случайной величины с законом распределения называется функция, заданная степенным рядом

Поскольку все коэффициенты этого ряда не превосходят 1, то сравнение с геометрической прогрессией показывает, что этот ряд сходится, по крайней мере, для значений Из свойства закона распределения видно, что так что область сходимости ряда содержит точку

Теорема 4.4. Производящая функция суммы независимых случайных величин равна произведению производящих функций слагаемых

Доказательство. Имеем по определению

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Примеры с решением

Пример 4.8.

Найти производящую функцию для биномиального закона.

Решение:

Если вспомнить, что формула Бернулли получается из разложения бинома, то легко сообразить, что

Можно также вспомнить, что случайная величина распределенная по биномиальному закону, представляется в виде суммы независимых слагаемых – индикаторов появления события Очевидно, что для одного слагаемого производящая функция равна Теперь осталось применить (4.23).

Возможно вам будут полезны данные страницы:

Пример 4.9.

Найти производящую функцию для геометрического закона распределения.

Решение:

Имеем поэтому

Данное равенство справедливо для всех значений удовлетворяющих неравенству для которых мы применили формулу суммы бесконечно убывающей геометрической прогрессии. Таким образом,

Пример 4.10.

Найти производящую функцию для распределения Пуассона.

Решение:

Для пуассоновского закона с параметром имеем

Поэтому

причем все ряды сходятся для любых значений аргумента Окончательно

В качестве следствия получим теорему.

Теорема 4.5. Сумма независимых случайных величин, распределенных по закону Пуассона, распределена по тому же закону.

Доказательство. Пусть – независимые случайные величины, распределенные по закону Пуассона с параметрами Тогда их производящие функции находятся по формуле (4.26):

а производящая функция суммы находится согласно теореме 4.4

Отсюда видно, что сумма будет распределена по закону Пуассона с параметром что и требовалось доказать.

Зная производящую функцию дискретной случайной величины нетрудно найти ее математическое ожидание и дисперсию.

Теорема 4.6. Для дискретной случайной величины с производящей функцией выполняются следующие соотношения:

Доказательство. Дифференцируя почленно ряд (4.22) два раза, имеем

Подставляя получим

откуда легко получить формулы (4.25), (4.26).

Комбинируя полученные выражения для производящих функций биномиального, геометрического и пуассоновского законов (4.23), (4.24), (4.25) с формулами (4.26), (4.27), теперь нетрудно найти основные числовые характеристики этих законов.

Биномиальный закон

Из выражения (4.23) для производящей функции получим

Подставляя и учитывая, что имеем

Используя формулы (4.26), (4.27), получим

откуда

Геометрический закон

Дифференцируя два раза производящую функцию, имеем

Отсюда

откуда что и требовалось.

Закон Пуассона

Имеем

поэтому Подставляя найденные значения в формулы (4.26), (4.27), получим

Лекции:

Комбинаторные задачи: пример решения
Классическое определение вероятности
Геометрическое определение вероятности
Элементы комбинаторики
Действии над событиями
Количество сочетаний
Число сочетаний: формула, расчет
Сочетания с повторениями
Комбинаторика формулы: основные элементы
Элементы комбинаторики: примеры решения

Источник

Производящая функция

Для случайной величины $xi$ производящая функция моментов (сокращенно ПФМ) определяется следующим образом:

$$
M_{xi}(t)=M[e^{txi}].
$$

Для дискретной случайной величины с законом вида $(x_i,p_i)$ ПФМ выражается как

$$M_{xi}(t)=M[e^{txi}]=sum_i e^{tx_i}cdot p_i.$$

Для непрерывной случайной величины с плотностью распределения $f(x)$:

$$M_{xi}(t)=M[e^{txi}]=int_{-infty}^{infty} e^{tx}cdot f(x),dx.$$

Производящая функция моментов — это двустороннее преобразование Лапласа от плотности распределения случайной
величины.

По известной ПФМ можно вычислять моменты случайной величины по формуле:

$$M[xi^n] = frac{d^n}{dx^n} M_{xi}(t)|_{t=0} $$

ПФМ однозначно определяет распределение случайной величины. ПФМ суммы независимых случайных величин равна произведению их проиводящих функций моментов. Производящая функция существует только в случае существования всех моментов, а характеристическая функция – всегда.

В этом разделе вы найдете примеры нахождения производящей функции для разных законов распределения, в том числе для заданных произвольно случайных величины (см. задачи 3 и 4), а также пример решения обратной задачи – по имеющейся производящей функции восстановить закон распределения случайной величины.

Понравилось? Добавьте в закладки

Примеры решений: производящая функция

Задача 1. Найти производящую функцию моментов для случайной величины, имеющей геометрическое распределение. Вычислить с помощью найденной функции математическое ожидание и дисперсию.

Задача 2. Найти производящую функцию моментов для случайной величины, имеющей распределение Пуассона с параметром $lambda$. Вычислить с помощью найденной функции математическое ожидание и дисперсию.

Задача 3. Дискретная случайная величина X имеет ряд распределения.
x=-2 x=0 x=2
1/4 1/2 1/4
Найти производящую функцию моментов случайной величины X и с ее помощью вычислить математическое ожидание и дисперсию.

Задача 4. Абсолютно непрерывная случайная величина имеет плотность распределения
$$
p(x)=
left{
begin{array}{l}
sin(x)/2, x in[0;pi],\
0, x notin[0;pi] \
end{array}
right.
$$
Найти производящую функцию моментов.

Задача 5. Задана производящая функция вероятностей $p(t)=t(pt+q)^n$. Найти ряд и функцию распределения соответствующей случайной величины.

Мы отлично умеем решать задачи по теории вероятностей

Источник

Определение[править | править код]

Одномерный случай[править | править код]

Многомерный случай[править | править код]

Свойства[править | править код]

Степенные ряды[править | править код]

Вероятности и ожидания[править | править код]

Функции независимых случайных величин[править | править код]

Примеры[править | править код]

Ссылки[править | править код]

Преобразование Лапласа

Характеристические функции

6. Плотность распределения вероятностей

Примеры с решением

Пример 4.8.

Пример 4.9.

Пример 4.10.

Биномиальный закон

Геометрический закон

Закон Пуассона

Производящая функция

Примеры решений: производящая функция

Вам также может понравиться

Как найти новую жену для мужа

Как исправить вытянутое изображение на телевизоре самсунг

Нет mfc140 dll как исправить

Добавить комментарий Отменить ответ