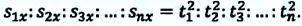Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 |
Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит
п.5. Как найти уравнение движения по графику движения?

п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости: 
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Как решать уравнения прямолинейного движения
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.


Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.


ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ: 
Задача № 6. По графикам на рисунке напишите уравнения движения x = x(t) . Из уравнений и графиков найдите координаты тел через 5 с , скорости движения тел, время и место встречи второго и третьего тел.

РЕШЕНИЕ: 
Задача № 7. ОГЭ Расстояние ( S ) между городами М и К = 250 км . Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч , из города К — со скоростью ν2 = 40 км/ч . Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.

Задача № 8. ЕГЭ Скорость течения реки vp = 1 м/с , скорость лодки относительно воды v0 = 2 м/с . Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м ?

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
Равномерное прямолинейное движение
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На предыдущих уроках мы познакомились с базовыми понятиями кинематики, которые позволят нам решать главную задачу механики. Для решения этой задачи нам необходимо записать законы изменения координат тела от времени. Для самого простого вида движения – равномерного прямолинейного движения – мы и получим этот закон.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/physics/10-klass/mehanikakinematika/ravnomernoe-pryamolineynoe-dvizhenie
[/spoiler]
Содержание:
Равномерное прямолинейное движение:
Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?
Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?
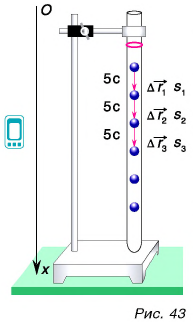
Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за 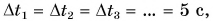
Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.
В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: 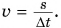 Это отношение показывает, как быстро движется тело, но ничего не говорит о направлении движения. Чтобы скорость характеризовала и быстроту движения, и его направление, ее определяют через перемещение.
Это отношение показывает, как быстро движется тело, но ничего не говорит о направлении движения. Чтобы скорость характеризовала и быстроту движения, и его направление, ее определяют через перемещение.
Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:

Из равенства (1) следует, что скорость 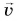 — векторная физическая величина. Ее модуль численно равен модулю перемещения за единицу времени, а направление совпадает с направлением перемещения (т. к.
— векторная физическая величина. Ее модуль численно равен модулю перемещения за единицу времени, а направление совпадает с направлением перемещения (т. к. 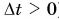 ).
).
Отношение 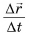 для всех участков движения на рисунке 43 одинаково:
для всех участков движения на рисунке 43 одинаково: 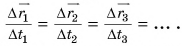 Значит, скорость
Значит, скорость 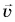 равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
Из формулы (1) легко найти перемещение:

и путь 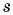 (равный модулю перемещения
(равный модулю перемещения 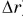 ):
):

А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени 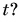 Рассмотрим пример. Автомобиль движется с постоянной скоростью по прямолинейному участку шоссе (рис. 44).
Рассмотрим пример. Автомобиль движется с постоянной скоростью по прямолинейному участку шоссе (рис. 44).
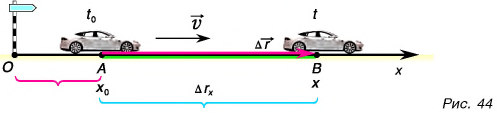
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время 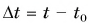 автомобиль совершил перемещение
автомобиль совершил перемещение 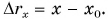 Подставляя
Подставляя 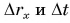 в равенство (4), получим:
в равенство (4), получим:
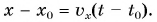
Приняв 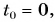 запишем формулу для координаты автомобиля:
запишем формулу для координаты автомобиля:

Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.

Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.

Для любознательных:
Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.

Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!
Главные выводы:
- При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
- При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
- Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Пример решения задачи:
Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением 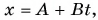 где
где 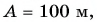
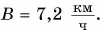
Определите: 1) проекцию скорости лодки 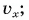 2) координату лодки
2) координату лодки 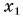 в момент времени
в момент времени 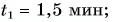 3) проекцию перемещения
3) проекцию перемещения 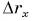 лодки на ось Ох и путь, пройденный лодкой за время от момента
лодки на ось Ох и путь, пройденный лодкой за время от момента 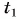 до момента
до момента 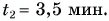

Решение
Сделаем рисунок к задаче.

По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив 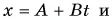
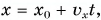 получим
получим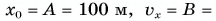
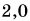
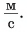
Найдем 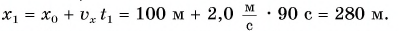
Из рисунка 49: проекция перемещения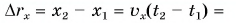
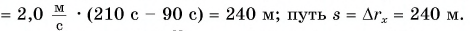
Ответ: 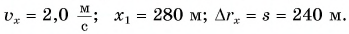
Графическое представление равномерного прямолинейного движения
Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.
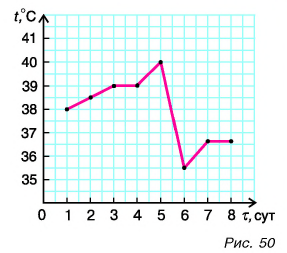
Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.
В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.
Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши 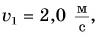 Тани
Тани 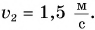 Как представить графически характеристики их движения?
Как представить графически характеристики их движения?
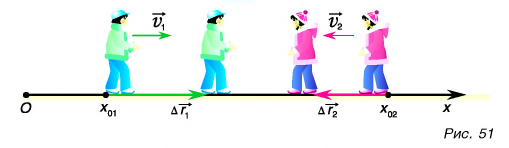
Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при 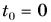 координата Леши
координата Леши 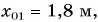 Тани
Тани 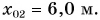
Построим графики зависимости проекции скорости 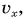 проекции перемещения
проекции перемещения 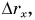 пути S и координаты X от времени t.
пути S и координаты X от времени t.
График проекции скорости
Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: 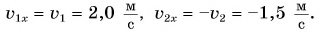 Так как проекции
Так как проекции 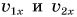 постоянны, то графики их зависимости от времени t — прямые, параллельные оси времени (прямые I и II на рисунке 52).
постоянны, то графики их зависимости от времени t — прямые, параллельные оси времени (прямые I и II на рисунке 52).
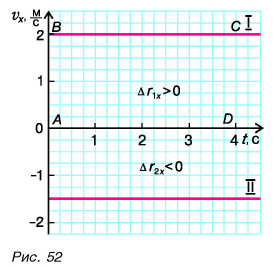
Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.
График проекции перемещения
Проекция перемещения 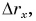 совершенного за время t, определяется формулой
совершенного за время t, определяется формулой 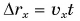 (см. § 6).
(см. § 6).
Зависимость проекции перемещения от времени для Леши 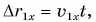 или
или 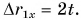 График
График 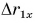 — наклонная прямая I (рис. 53).
— наклонная прямая I (рис. 53).
Для Тани 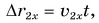 или
или 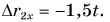 График
График 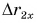 — наклонная прямая II, изображенная на рисунке 53.
— наклонная прямая II, изображенная на рисунке 53.
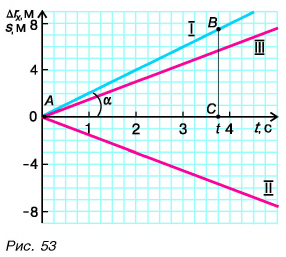
Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.
График пути
Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: 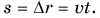 Поэтому при
Поэтому при 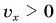 график пути совпадает с графиком проекции перемещения (прямая I), а при
график пути совпадает с графиком проекции перемещения (прямая I), а при 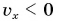 график пути (прямая III) является «зеркальным отражением» графика II (проекции перемещения) от оси времени.
график пути (прямая III) является «зеркальным отражением» графика II (проекции перемещения) от оси времени.
Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.
График координаты
Его называют также графиком движения.
По формуле 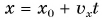 , используя данные из условия задачи и рисунок 51, находим зависимости координаты
, используя данные из условия задачи и рисунок 51, находим зависимости координаты 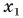 Леши и
Леши и 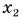 Тани от времени
Тани от времени 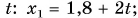
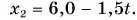 Графики этих зависимостей — прямые I и II на рисунке 54. Они параллельны соответствующим графикам проекций перемещения на рисунке 53.
Графики этих зависимостей — прямые I и II на рисунке 54. Они параллельны соответствующим графикам проекций перемещения на рисунке 53.
Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.
По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.
Что еще можно определить по графикам?
По графику проекции скорости можно найти проекцию перемещения и пройденный путь
Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна 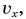 а основание — времени t. Значит, площадь прямоугольника равна
а основание — времени t. Значит, площадь прямоугольника равна 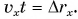 Таким образом, проекция перемещения численно равна площади прямоугольника между графиком проекции скорости и осью времени. При
Таким образом, проекция перемещения численно равна площади прямоугольника между графиком проекции скорости и осью времени. При 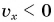 проекция перемещения отрицательна, и площадь надо брать со знаком «минус».
проекция перемещения отрицательна, и площадь надо брать со знаком «минус».
Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.
По углу наклона графика проекции перемещения можно оценить скорость движения
Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.
Главные выводы:
Для равномерного прямолинейного движения:
- График проекции скорости — прямая, параллельная оси времени.
- Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется скоростью движения.
- Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.
Пример №1
Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью 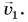 Через время
Через время 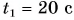 после проезда перекрестка он встречает едущего в город велосипедиста, движущегося равномерно со скоростью
после проезда перекрестка он встречает едущего в город велосипедиста, движущегося равномерно со скоростью 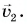 Определите расстояние между участниками движения через время
Определите расстояние между участниками движения через время 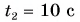 после их встречи, если
после их встречи, если 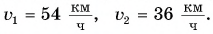 Запишите кинематические законы движения мотоциклиста и велосипедиста, постройте графики проекции и модуля скорости, проекции перемещения, координаты и пути для обоих участников движения.
Запишите кинематические законы движения мотоциклиста и велосипедиста, постройте графики проекции и модуля скорости, проекции перемещения, координаты и пути для обоих участников движения.
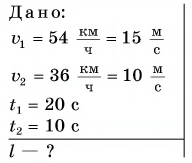
Решение
Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.

В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:
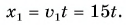
Найдем координату 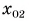 велосипедиста в начальный момент времени. Пусть точка С на оси Ох — место встречи участников движения (рис. 56).
велосипедиста в начальный момент времени. Пусть точка С на оси Ох — место встречи участников движения (рис. 56).
Тогда
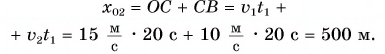
Кинематический закон движения велосипедиста имеет вид:
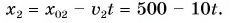
Расстояние между мотоциклистом и велосипедистом через время 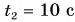 после их встречи равно сумме путей, которые они проделают за это время. Значит,
после их встречи равно сумме путей, которые они проделают за это время. Значит,
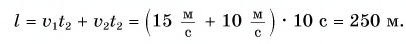
Пример №2
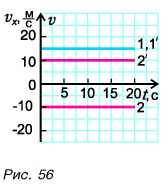
Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости 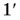 совпадают (рис. 56). Для велосипедиста график проекции скорости — прямая 2, а модуля скорости — прямая
совпадают (рис. 56). Для велосипедиста график проекции скорости — прямая 2, а модуля скорости — прямая 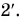 Объясните причину несовпадения.
Объясните причину несовпадения.
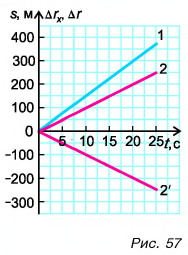
Графиками пути s, проекции 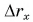 и модуля перемещения
и модуля перемещения 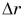 (рис. 57) будут прямые, выражающие прямую пропорциональную зависимость от времени t.
(рис. 57) будут прямые, выражающие прямую пропорциональную зависимость от времени t.
Для мотоциклиста:
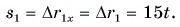
Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).
Для велосипедиста:
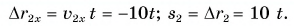
Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая 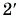 — графиком проекции его перемещения.
— графиком проекции его перемещения.
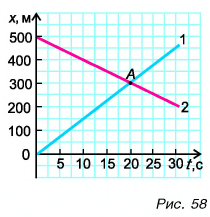
Графики координат представлены на рисунке 58. Они выражают зависимости 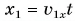 (прямая 1) и
(прямая 1) и 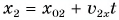 (прямая 2). Точка А определяет время встречи и координату места встречи.
(прямая 2). Точка А определяет время встречи и координату места встречи.
Ответ: 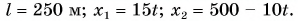
Прямолинейное равномерное движение и скорость
Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.
Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.
При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:
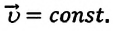
Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено: 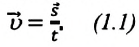
Так как отношение 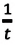 в формуле является положительной скалярной величиной, то направление вектора скорости
в формуле является положительной скалярной величиной, то направление вектора скорости 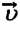 совпадает с направлением вектора перемещения
совпадает с направлением вектора перемещения 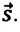 Единица измерения скорости в СИ – метр в секунду:
Единица измерения скорости в СИ – метр в секунду:
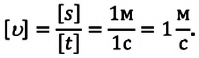
Если скорость 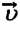 известна, то можно определить перемещение s материальной точки за промежуток времени
известна, то можно определить перемещение s материальной точки за промежуток времени 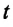 при прямолинейном равномерном движении:
при прямолинейном равномерном движении:

При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:
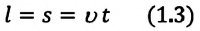
Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:
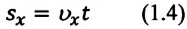
Можно получить формулу для вычисления координаты точки 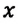 в произвольный момент времени (см.: тема 1.2):
в произвольный момент времени (см.: тема 1.2):
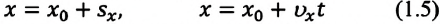
Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).
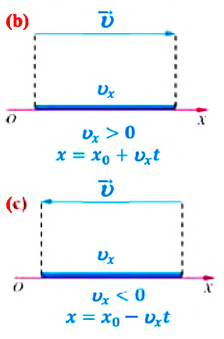
Из формулы (1.5) определяется выражение для проекции скорости:
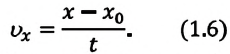
Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.
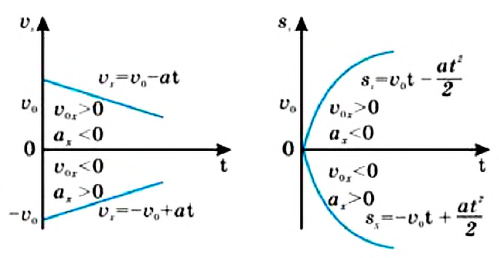
Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость – время будет представлять собой линию, параллельную оси времени — скорость такого движения не зависит от времени (е):
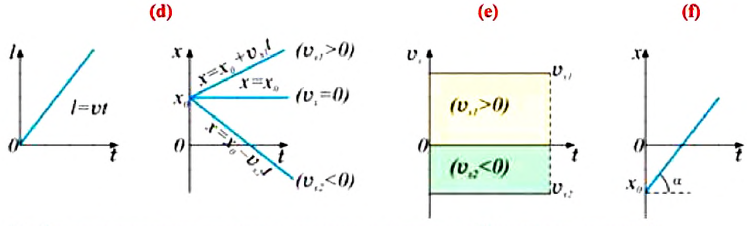
График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f): 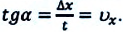
Пример №3
Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста 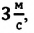 скорость второго велосипедиста
скорость второго велосипедиста 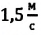 (g)?
(g)?
Определите: а) координату и время 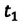 встречи велосипедистов; b) пройденные велосипедистами пути и совершенные ими перемещения к моменту встречи; с) время
встречи велосипедистов; b) пройденные велосипедистами пути и совершенные ими перемещения к моменту встречи; с) время 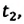 прошедшее с начала движения до момента, когда расстояние между ними стало 10 км.
прошедшее с начала движения до момента, когда расстояние между ними стало 10 км.
Дано:
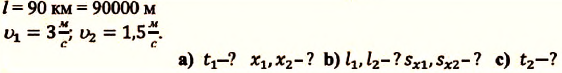
Решение:
a) При решении задачи соблюдается следующая последовательность действий:
I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).
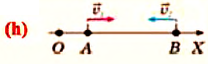
II действие. Уравнение движения записывается в общем виде: 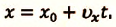
III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде: 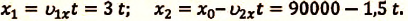
IV действие. Координаты велосипедистов при встрече равны: 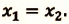 Это равенство решается для
Это равенство решается для 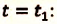
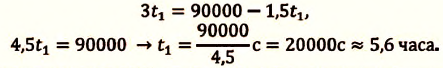
V действие. Для определения координат 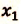 и
и 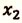 встречи велосипедистов необходимо решить уравнения их движения для времени
встречи велосипедистов необходимо решить уравнения их движения для времени 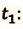
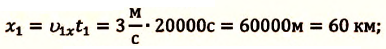
Так как 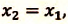 то
то 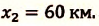
b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:
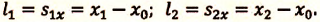
c) Время 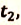 прошедшее с начала движения до момента, когда между ними осталось 10 км, вычисляется по нижеприведенному равенству:
прошедшее с начала движения до момента, когда между ними осталось 10 км, вычисляется по нижеприведенному равенству:
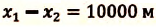 или
или 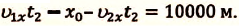
Скорость при равнопеременном прямолинейном движении
Из формулы (1.14) видно, что если известны ускорение 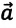 и начальная скорость тела
и начальная скорость тела 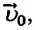 то можно определить его скорость в любой момент времени:
то можно определить его скорость в любой момент времени:
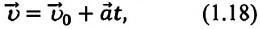
или ее проекцию на ось 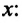
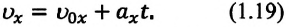
Если начальная скорость равна нулю 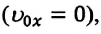 то:
то:

Из этих выражений видно, что скорость при равнопеременном движении является линейной функцией от времени. График зависимости скорости от времени – прямая линия, проходящая через начало координат (или через 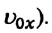 Эта линия, в соответствии с увеличением или уменьшением скорости, направлена вверх или вниз (с).
Эта линия, в соответствии с увеличением или уменьшением скорости, направлена вверх или вниз (с).
Перемещение при равнопеременном прямолинейном движении
Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком 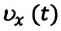 и осью времени.
и осью времени.
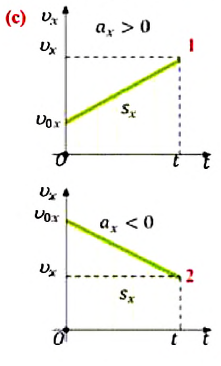
На приведенных графиках — это заштрихованная фигура трапеции (см: с):
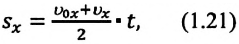
или в векторной форме:
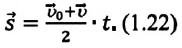
Если в последнюю формулу вместо 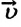 подставить выражение (1.18), то получим
подставить выражение (1.18), то получим
обобщенную формулу перемещения для равнопеременного движения:
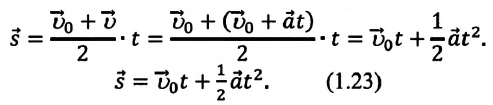
Таким образом, формула проекции перемещения (например, на ось 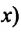 при равнопеременном прямолинейном движении будет:
при равнопеременном прямолинейном движении будет:
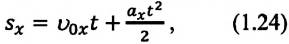
а формула координаты:
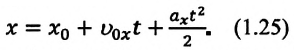
(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя 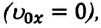 то:
то:
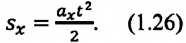
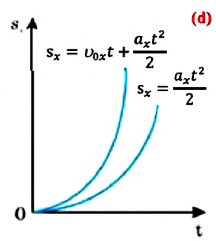
Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени 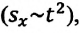 и его график представляет собой параболу, проходящую через начало координат (d).
и его график представляет собой параболу, проходящую через начало координат (d).
В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время 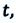 прошедшее от начала движения. Такую задачу можно решить тогда, когда известны ускорение, начальное и конечное значения скорости. Для получения этой формулы из выражения (1.19) получаем
прошедшее от начала движения. Такую задачу можно решить тогда, когда известны ускорение, начальное и конечное значения скорости. Для получения этой формулы из выражения (1.19) получаем 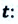
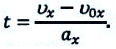
Это выражение подставляется в формулу (1.21):
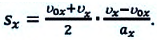
После простых преобразований получаем:

Для проекции конечной скорости получаем: 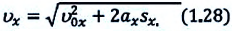 Если движение начинается из состояния покоя
Если движение начинается из состояния покоя 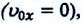 то проекции перемещения и скорости будут равны:
то проекции перемещения и скорости будут равны:
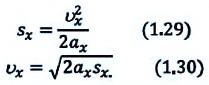
Равноускоренное и равнозамедленное движения
Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.
При равноускоренном движении векторы 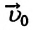 и
и 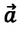 имеют одинаковые направления. В этом случае знаки у обеих проекций
имеют одинаковые направления. В этом случае знаки у обеих проекций 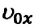 и
и 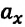 или положительные, или же отрицательные. Если материальная точка начнет движение из состояния покоя
или положительные, или же отрицательные. Если материальная точка начнет движение из состояния покоя 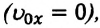 то независимо от направления движения, оно во всех случаях будет равноускоренным.
то независимо от направления движения, оно во всех случаях будет равноускоренным.
При равнозамедленном движении векторы 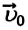 и
и 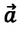 имеют противоположные направления. В этом случае проекции
имеют противоположные направления. В этом случае проекции 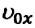 и
и 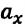 имеют противоположные знаки, если один из них отрицательный, то другой – положительный.
имеют противоположные знаки, если один из них отрицательный, то другой – положительный.
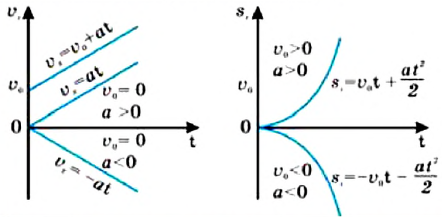
В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.
Таблица 1.3.
| Прямолинейное равноускоренное движение | |
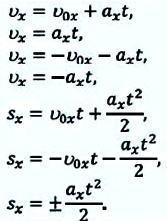 |
 |
|
Примечание: так как
Это соотношение иногда называется “правило путей”. |
|
| Прямолинейное равнозамедленное движение | |
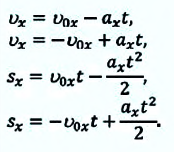 |
|
Кинематика прямолинейного движения
Физические величины бывают скалярные и векторные. Скалярные физические величины характеризуются только численным значением, тогда как векторные определяются и числом (модулем), и направлением. Скалярными физическими величинами являются время, температура, масса, векторными — скорость, ускорение, сила.
Мир вокруг нас непрерывно изменяется, или движется, т. е. можно сказать, что движение (изменение) есть способ существования материи.
Простейшая форма движения материи — механическое движение — заключается в изменении взаимного расположения тел или их частей в пространстве с течением времени. Наука, изучающая механическое движение, называется механикой (от греческого слова 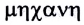 — подъемная машина).
— подъемная машина).
Даже самое простое движение тела оказывается достаточно сложным для изучения и исследования. Соответственно, для того чтобы в сложном явлении «увидеть» главное, в физике строится его адекватная упрощенная модель.
В механике широко используется простейшая модель реального тела, называемая материальной точкой (МТ). Под материальной точкой понимают тело, размерами и формой которого можно пренебречь при описании данного движения. Хотя МТ представляет собой абстрактное понятие, упрощающее изучение многих физических явлений, она, подобно реальному телу, «имеет» массу, энергию и т. д.
Кроме материальной точки, в механике используется модель абсолютно твердого тела. Под абсолютно твердым телом понимают модель реального тела, в которой расстояние между его любыми двумя точками остается постоянным. Это означает, что размеры и форма абсолютно твердого тела не изменяются в процессе его движения. В противном случае говорят о модели деформируемого тела.
В классической (ньютоновской) механике рассматривается движение тел со скоростями, намного меньшими скорости света в вакууме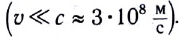
Классическая механика состоит из трех основных разделов: кинематики, динамики и статики. В кинематике (от греческого слова 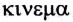 — движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова
— движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова 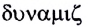 — сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова
— сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова 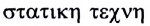 — искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.
— искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.
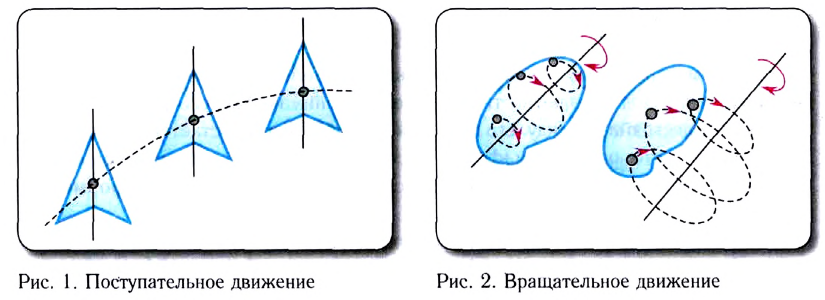
Всякое движение тела можно представить в виде двух основных видов движения — поступательного и вращательного.
Поступательным называется движение тела, при котором прямая, соединяющая в этом теле любые две точки, при перемещении остается параллельной самой себе (рис. 1).
Вращательным называется движение абсолютно твердого тела вокруг неподвижной прямой, называемой осью вращения, при котором все точки тела движутся по окружностям, центры которых лежат на этой оси (рис. 2).
Основными задачами кинематики являются:
описание совершаемого телом движения с помощью математических формул, графиков или таблиц;
определение кинематических характеристик движения (перемещения, скорости, ускорения).
Движение тела можно описать только относительно какого-либо другого тела. Тело, относительно которого рассматривается исследуемое движение, называют телом отсчета (ТО). Для описания движения используются формулы, графики и таблицы, выражающие зависимость координат, скоростей и ускорений от времени.
Основным свойством механического движения является его относительность: характер движения тела зависит от выбора системы отсчета (СО).
Систему отсчета, выбираемую для описания того или иного движения, образуют: тело отсчета, связанные с ним система координат (СК) и прибор для измерения времени (часы) (рис. 3).
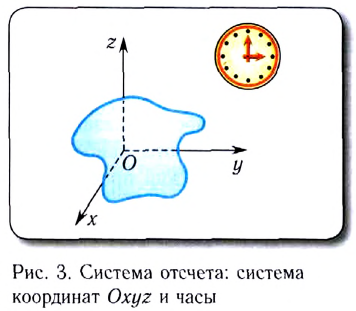
Система координат и часы необходимы для того, чтобы знать, как с течением времени изменяется положение тела относительно выбранного тела отсчета.
Для описания движения материальной точки в пространстве вводятся такие понятия, как траектория, перемещение, путь.
Линию, которую описывает материальная точка в процессе движения по отношению к выбранной СО, называют траекторией (от латинского слова trajectorus — относящийся к перемещению). Если траектория является прямой линией, то движение называется прямолинейным, в противном случае — криволинейным.
Длина участка траектории, пройденного МТ в процессе движения, называется путем (s).
Термин «скаляр», происходящий от латинского слова scalarus — ступенчатый, введен У. Гамильтоном в 1843 г.
Термин «вектор» произошел от латинского слова vector — несущий и введен У. Гамильтоном в 1845 г.
Перемещением называют вектор 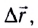 направленный из точки, заданной радиус-вектором
направленный из точки, заданной радиус-вектором 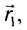 где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором
где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором 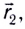 где МТ находится в рассматриваемый момент времени (рис. 4):
где МТ находится в рассматриваемый момент времени (рис. 4):
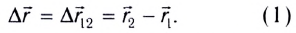
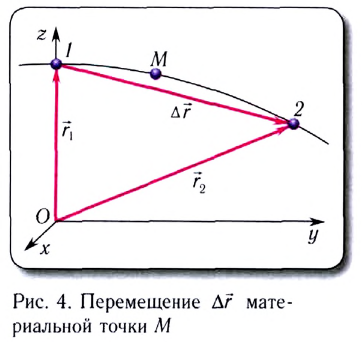
Для количественного описания механического движения тел (МТ) вводятся физические величины, характеризующие пространство и время: длина l, время t.
Длина l определяется как расстояние между двумя точками в пространстве. Основной единицей длины в Международной системе единиц (СИ) является метр (1м).
Время t между двумя событиями в данной точке пространства определяется как разность показаний прибора для измерения времени, например часов. В основе работы прибора для измерения времени лежит строго периодический физический процесс. В СИ за основную единицу времени принята секунда (1с).
В зависимости от вида движения могут выбираться следующие системы координат: одномерная (на прямой линии) (рис. 5), двухмерная (на плоскости) (рис. 6), трехмерная (в пространстве) (рис. 7).
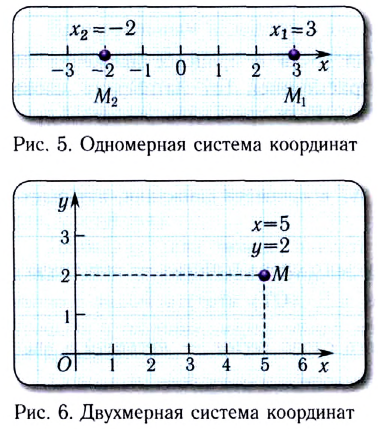
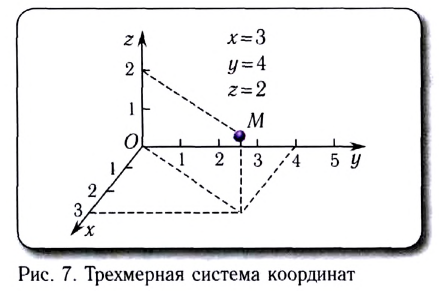
Произвольное движение материальной точки может быть задано одним из трех способов: векторным, координатным, траекторным (естественным).
При векторном способе описания положение движущейся МТ по отношению к выбранной системе отсчета определяется ее радиус-вектором 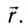
Радиус-вектор 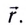 всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением
всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением 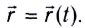
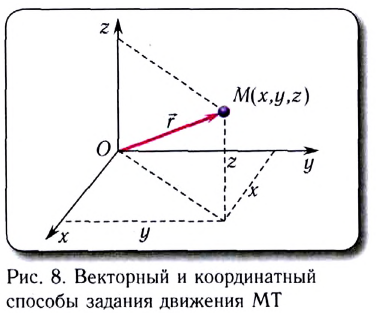
При координатном способе описания положение точки относительно СО определяется координатами х, у, z, а закон движения — уравнениями х = х(t), у = y(t), z = z(t) (см. рис. 8). Исключив из этих уравнений время /, можно найти уравнение траектории движения точки.
Траекторный (естественный) способ описания движения применяется, когда известна траектория движения материальной точки по отношению к выбранной СО (рис. 9).
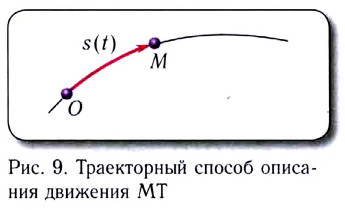
Текущее положение материальной точки в данном случае определяется расстоянием s, измеренным вдоль траектории от выбранного на ней начала отсчета (точка О на рисунке 9). Кинематический закон движения МТ при этом задается уравнением s = s(t).
Если положить в основу классификации движений характер изменения скорости, то получим равномерные и неравномерные движения, а если вид траектории, то — прямолинейные и криволинейные.
Для того чтобы описать быстроту изменения положения тела (МТ) и направление движения относительно данной СО, используют векторную физическую величину, называемую скоростью 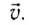
Чтобы охарактеризовать неравномерное движение тела (МТ), вводят понятие средней скорости 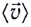 движения как отношение перемещения
движения как отношение перемещения 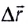 тела к промежутку времени
тела к промежутку времени 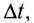 за который это перемещение произошло (рис. 10):
за который это перемещение произошло (рис. 10):

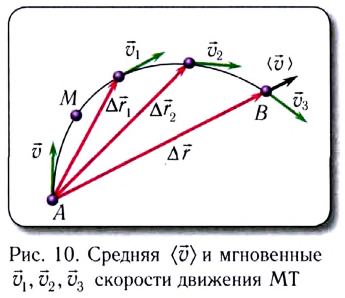
Средней путевой скоростью 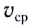 называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени
называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени 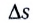 его прохождения:
его прохождения:

Средняя путевая скорость 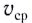 в отличие от средней скорости
в отличие от средней скорости 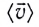 является скалярной величиной.
является скалярной величиной.
Однако средняя скорость 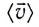 характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.
характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.
Для того чтобы отразить характер движения в данной точке траектории или в данный момент времени, вводится понятие мгновенной скорости 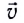 — это скорость тела (МТ), равная производной перемещения по времени:
— это скорость тела (МТ), равная производной перемещения по времени:

Вектор мгновенной скорости 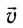 в любой точке траектории направлен по касательной к ней (см. рис. 10).
в любой точке траектории направлен по касательной к ней (см. рис. 10).
В СИ основной единицей скорости является метр в секунду 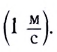
Простейший вид движения — равномерное. Равномерным называется движение МТ, при котором она за любые равные промежутки времени совершает одинаковые перемещения.
При прямолинейном движении в одном направлении модуль перемещения 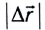 равен пройденному пути s. Скорость
равен пройденному пути s. Скорость 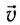 равномерного движения равна отношению перемещения тела
равномерного движения равна отношению перемещения тела 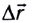 ко времени
ко времени 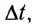 за которое это перемещение произошло:
за которое это перемещение произошло:

При равномерном движении скорость постоянна 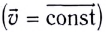 и равна средней скорости
и равна средней скорости 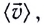 определяемой выражением (2).
определяемой выражением (2).
Зависимость перемещения от времени имеет вид 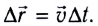 Вследствие того, что
Вследствие того, что 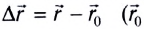 — радиус-вектор, задающий положение МТ в начальный
— радиус-вектор, задающий положение МТ в начальный
момент времени 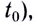 получаем кинематическое уравнение движения в векторном виде
получаем кинематическое уравнение движения в векторном виде

При проецировании радиус-вектора, например, на ось Ох получаем кинематическое уравнение для координаты при равномерном движении:
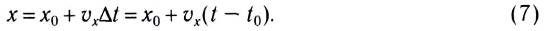
Здесь 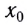 — координата тела (МТ) в начальный момент времени
— координата тела (МТ) в начальный момент времени 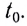 Если начальный момент времени
Если начальный момент времени 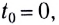 уравнение принимает вид
уравнение принимает вид
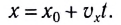
Для наглядности описания механического движения удобно представлять зависимости между различными кинематическими величинами графически.
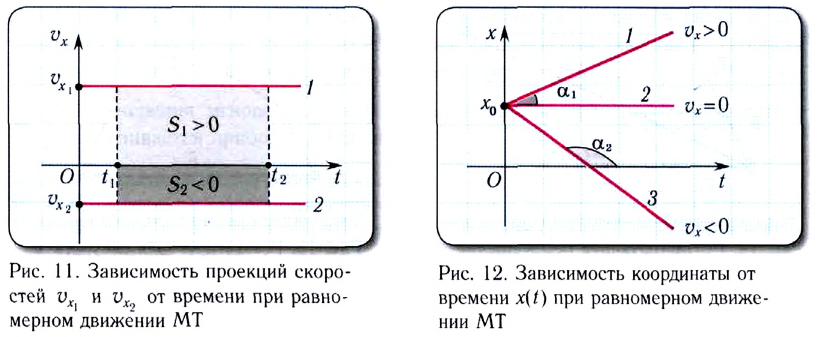
Скорость МТ при равномерном движении постоянна, поэтому график зависимости проекции скорости 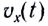 от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси
от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси 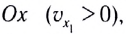 а 2 — в отрицательном
а 2 — в отрицательном 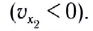 Площади
Площади 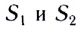 закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей
закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей 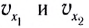 за промежуток времени
за промежуток времени 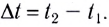
График зависимости координаты материальной точки, движущейся равномерно прямолинейно, от времени x(t) — линейная функция (рис. 12).
На рисунке отрезок / прямой соответствует равномерному движению в положительном направлении оси Ох; отрезок 2 прямой — покою материальной точки; отрезок 3 прямой — равномерному движению в отрицательном направлении оси Ох.
Проекция скорости движения численно равна угловому коэффициенту этой прямой линии: 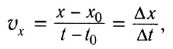
т. е. тангенсу угла наклона (tga) этой прямой к оси времени.
График зависимости пути (модуля перемещения|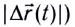 от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).
от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).
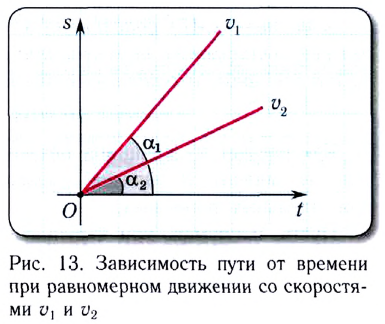
Угловой коэффициент (tga) этой прямой численно равен модулю скорости движения v. Поэтому на рисунке большей скорости у, соответствует больший угловой коэффициент (tg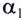 ).
).
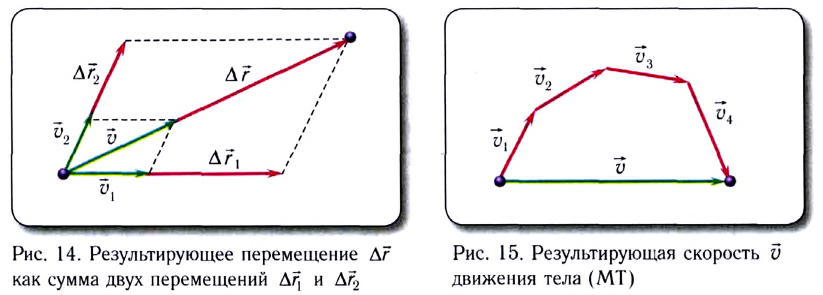
Для тел (МТ), участвующих в нескольких движениях одновременно, справедлив принцип независимости движений:
если тело (МТ) участвует в нескольких движениях одновременно, то его результирующее перемещение равно векторной сумме перемещений за то же время в отдельных движениях:

Как следует из принципа независимости движений, конечное перемещение тела не зависит от порядка (последовательности) суммирования перемещений при отдельных движениях.
Пусть, например, при переправе через реку, скорость течения которой 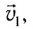 мы движемся на лодке со скоростью
мы движемся на лодке со скоростью 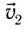 относительно воды. В этом случае результирующее перемещение
относительно воды. В этом случае результирующее перемещение 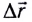 (рис. 14) лодки относительно берега будет складываться из собственного перемещения
(рис. 14) лодки относительно берега будет складываться из собственного перемещения 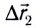 относительно воды и перемещения
относительно воды и перемещения 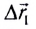 вместе с водой вследствие течения реки:
вместе с водой вследствие течения реки: 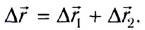
- Заказать решение задач по физике
На основе принципа независимости движений формулируется классический закон сложения скоростей:
результирующая скорость 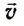 тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей
тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей 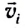 отдельных движений (рис. 15):
отдельных движений (рис. 15):

Этот закон справедлив только при условии, что скорость каждого отдельного движения мала по сравнению со скоростью света 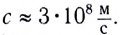
Так, для рассмотренного примера (см. рис. 14) результирующая скорость лодки 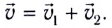
Равномерное движение по прямой линии в повседневной жизни встречается сравнительно редко. Например, различные транспортные средства (автомобиль, автобус, троллейбус и т. д.) равномерно и прямолинейно движутся лишь на небольших участках своего пути, в то время как на остальных участках их скорость изменяется как по величине, так и по направлению.
Для измерения мгновенной скорости движения на транспортных средствах устанавливается прибор — спидометр.
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
Школьный курс физики содержит раздел «кинематика». Большинство задач этого раздела можно решить, рассматривая движение вдоль одной оси — одномерное движение. Его еще называют прямолинейным движением.
Для некоторых задач нужно рассматривать движение на плоскости – двумерный случай.
Вообще, движение тела может происходить:
- вдоль оси – одномерный случай, ось часто именуют, как «Ox»;
- на плоскости;
- в трехмерном пространстве;
Здесь рассмотрим одномерный случай движения — движение тел вдоль оси.
Параметры, описывающие движение
Чтобы описать движение, используют:
- перемещение тела;
- время, в течение которого движение происходило;
- скорость тела;
- начальные и конечные координаты тела;
- траекторию тела;
Траектория – линия, вдоль которой двигалось тело.
Траектория – скаляр, в СИ длину траектории измеряют в метрах.
Для криволинейного движения траектория будет отрезком кривой.
Если движение прямолинейное, траектория – отрезок прямой линии.
Перемещение тела – это вектор. Он соединяет точки, в которых тело находилось в начале и конце движения, направлен из начальной точки в конечную.
Модуль этого вектора – его длину, в СИ измеряют в метрах.
Может ли перемещение тела равняться нулю, при том, что траектория имеет какую-либо протяженность?
Да, такое может быть. Когда тело движется так, что в конце движения оно вернется в начальную точку, в которой находилось перед началом движения.
Если в завершении движения тело окажется на каком-то расстоянии от начальной точки, длина вектора перемещения будет положительной.
Примечания:
- Модуль (длина) вектора не бывает отрицательным, он либо положительный, либо нулевой.
- Когда тело движется по прямой и не меняет направление, длина траектории совпадает с длиной (модулем) перемещения.
Уравнение движения — описывает характер движения.
Оно содержит:
- время движения,
- начальную и конечную координаты тела и
- его скорость.
Вместо координат тела уравнение движения может содержать перемещение.
Примечания:
- Координаты тела, время движения и траектория – это скалярные величины.
- А скорость тела, его ускорение и перемещение – это векторы.
- Когда движение равномерное, скорость тела не меняется.
- Скорость отвечает на вопрос: как быстро изменяется координата (или путь, перемещение).
Описанные параметры применяют и для равномерного и для неравномерного движения.
Прямолинейное движение вдоль оси
Рассмотрим движение по прямой, когда скорость тела не меняется. Это — равномерное прямолинейное движение.
На рисунке 1 представлено движение тела вдоль оси, назовем ее для определенности Ox:

Рис. 1. Перемещение – это разница между конечной и начальной координатами тела
Ось «Ox» на рисунке 1 обозначена большим символом «X».
Точка, в которой тело находилось в начале движения (x_{0} left( text{м} right)) — начальная координата тела;
В эту точку тело переместилось к концу движения (x left( text{м} right)) — конечная координата тела;
Расстояние между двумя точками (S left( text{м} right)) – это перемещение тела. Перемещение – это вектор.
Формула перемещения для одномерного случая
Для движения по оси (одномерный случай), длину перемещения находят так:
[ large boxed { S = left| x — x_{0} right| }]
Знак модуля нужен для того, чтобы длина перемещения оставалась положительной, даже, если движение происходит влево по оси, т. е. против направления оси Ox.
Сравним два случая движения тел. Первый – в положительном направлении оси Ox (рис 2а), второй – в направлении, противоположном оси (рис 2б).

Рис. 2. Перемещение вправо по оси – а) и влево по оси – б)
Чтобы найти длину вектора перемещения при движении в положительном направлении оси (рис. 2а), модуль раскрываем так:
[ S = left| x — x_{0} right| = x — x_{0} ]
Для движения в отрицательном направлении оси (рис. 2б), длина вектора перемещения выражается так:
[ S = left| x — x_{0} right| = — left( x — x_{0} right) = x_{0} — x ]
И в первом, и во втором случае, длина (модуль) вектора перемещения окажется положительной.
Скорость равномерного движения
В учебниках физики равномерному движению дают такое определение:
Движение равномерное, когда тело за одинаковые интервалы времени проходит равные расстояния.
Упростим формулировку:
Если каждую секунду тело проходит одинаковые расстояния – оно движется равномерно.
Слово «равномерное» состоит из двух частей.
Если разбить его на части, получим
«равно» — одинаковый, равный,
«мерное» — отмерять.
Или, другими словами: каждую секунду отмеряем одинаковые расстояния (рис. 2).

Рис. 3. Если тело проходит равные пути за одинаковые кусочки времени, движение будет равномерным
Для равномерного движения тела его
- перемещение,
- время движения и
- скорость,
связаны соотношением:
[ left|vec{S} right| = left|vec{v} right|cdot t ]
Эта формула называется уравнением движения. Или, развернуто: «уравнение равномерного прямолинейного движения».
Где ( left|vec{S} right| ) — длина (модуль) вектора перемещения и, (left|vec{v} right|) — длина (модуль) вектора скорости.
Уравнение движения можно записать проще:
[ large boxed { S = v cdot t }]
(S left( text{м} right)) – расстояние, пройденное телом (перемещение).
(t left( c right)) – промежуток времени, в течение которого тело двигалось.
(v left( frac{text{м}}{c} right)) – скорость, с которой двигалось тело.
Разделив обе части уравнения ( S = v cdot t ) на интервал времени ( t ), получим выражение для скорости тела:
[ large boxed { frac{S}{t} = v }]
График уравнения равномерного движения
Вспомним, что перемещение является разностью конечных и начальных координат тела
( S = left| x — x_{0} right| )
Воспользуемся тем, что при движении вдоль положительного направления оси модуль можно раскрыть так:
( left| x — x_{0} right| = x — x_{0} )
Тогда уравнение движения перепишем так:
[ large boxed { x — x_{0} = v cdot t }]
Прибавим к обеим частям уравнения величину ( x_{0} ). Получим такую запись
[ large x = v cdot t + x_{0}]
Это уравнение задает на плоскости tOx линию. Ее график на осях «x» и «t» — это прямая линия.
Вспомним, что для прямой линии в математике применяют такой вид записи:
( y = k cdot x + b)
Сравним два уравнения:
[ begin{cases} x = vcdot t + x_{0}\ y = kcdot x + b end{cases} ]
Видно, что число ( x_{0}) – начальная координата тела, выполняет роль коэффициента (b).
А скорость тела ( v) – играет роль углового коэффициента (k).
Сравним графики линий (рис. 4), описанных соотношениями ( y = k cdot x + b) и ( x = v cdot t + x_{0})

Рис.4. При равномерном движении тела координата изменяется по линейному закону
Видно, что линия на рисунке 4а, располагается и слева и справа от вертикальной оси.
Линия же, описывающая движение тела, представленная на рисунке 4б, располагается только лишь в правой полуплоскости. Это не с проста. На горизонтальной оси рисунка 4б отложено время, а в левой полуплоскости время будет отрицательным. При решении задач физики мы считаем, что в начальный момент задачи время равно нулю. Поэтому, область отрицательного времени в физике нас не интересует.
Рассмотрим теперь на графике равномерное движение двух тел, обладающих разными скоростями (рис. 5). Движение тела 1 на рисунке описывает синяя линия, а тела 2 – красная.

Рис.5. Равномерное движение двух тел, обладающих разными скоростями. Скорость тела 1 (синий цвет) больше скорости тела 2 (линия красного цвета).
Два тела стартуют из точки ( x_{0}) и двигаются равномерно воль оси Ox. За промежуток времени ( Delta t) тело 1, проходит больший путь, чем тело 2.
Примечание: Чем сильнее на графике x(t) прямая линия прижимается к вертикали, тем больше скорость, с которой движется тело!
Как отмечалось выше, тело может двигаться не только в положительном направлении вдоль оси, но и в отрицательном направлении.
На следующем рисунке представлены случаи движения тела в положительном (рис. 6а) и, в отрицательном (рис. 6б) направлениях оси Ox.
Когда скорость направлена по оси (рис. 6а) — координата «x» увеличивается,
а когда против оси (рис. 6б) — координата «x» уменьшается.

Перемещение тела в положительном направлении оси – а) и в отрицательном направлении по оси Ox – б)
На рисунке рядом с прямыми x(t) приведены уравнения движения. Когда скорость направлена против оси (рис. 6б), перед ней записывают знак «минус».
Угол (alpha) на рисунке связан со знаком скорости. Если скорость направлена по оси (рис. 6а), то угол будет острым. А если скорость направлена против оси (рис. 6б) – угол тупой.
Примечание: Скорость – это вектор. Когда вектор направлен против оси, его проекция на эту ось будет отрицательной. Читайте тут о проекциях векторов. Длина любого вектора – это положительная величина.
Как по графику перемещения определить скорость
Пользуясь графиком функций S(t), или x(t) равномерного движения можно определить скорость, с которой движется тело.
Примечания:
- График S(t) называют так: «зависимость перемещения S от времени t», или кратко — график перемещения от времени.
- А график x(t) — так: «зависимость координаты x от времени t», или кратко — график координат от времени.
Скорость находим за четыре шага (рис. 7):
- Выбираем две точки на линии, описывающей движение и определяем их координаты;
- Находим разность вертикальных координат;
- После находим разность координат по горизонтали;
- Делим «вертикаль» на «горизонталь»
Полученное число и будет скоростью тела.
Примечания:
- Когда просят найти скорость, обычно имеют ввиду, что нужно найти модуль вектора скорости.
- Скорость в системе СИ измеряют в метрах, деленных на секунду.
Обращаем внимание на то, в каких единицах на осях измерены расстояние S и время t. Если нужно, переводим расстояние в метры, а время — в секунды, чтобы получить скорость в правильных единицах измерения.

Рис.7. Две точки 1 и 2 выбраны для того, чтобы по графику x(t) найти скорость равномерного прямолинейного движения тела
Рассмотрим рисунок 7.
На рисунке первая точка имеет координаты ( left( t_{1} ; x_{1} right) ),
координаты второй точки: ( left( t_{2} ; x_{2} right) ).
Разницы между координатами находим, руководствуясь принципом («конечная» — «начальная») по формулам
( Delta t = t_{2} — t_{1} )
( Delta x = x_{2} — x_{1} )
Скорость вычислим из соотношения
[ v = frac{Delta x}{Delta t}]
Читайте далее о том, как переводить скорость из километров в час в метры в секунду и о равнопеременном движении
При
прямолинейном движении скорость и
ускорение точки все время направлены
вдоль одной и той же прямой. Так как
направление ускорения совпадает с
направлением действия силы, то отсюда
следует, что свободная материальная
точка будет двигаться прямолинейно
тогда, когда действующая на нее сила
имеет постоянное направление, а скорость
точки в начальный момент равна нулю или
направлена вдоль силы.
Рассмотрим
материальную точку, движущуюся
прямолинейно под действием приложенной
к ней силы ![]() .
.
 Положение
Положение
точки на траектории определяется ее
координатой х. Основная задача
динамики в этом случае состоит в том,
чтобы, зная
Рис. 3.1 ![]() ,
,
найти закон движения точки, то
есть ![]() .
.
Связь
между х и R дает
уравнение (3). Проектируя обе его части
на х, получим
![]()
так как ![]() ,
,
![]() (6)
(6)
Уравнение
(6) называется дифференциальным уравнением
прямолинейного движения точки.
Часто
уравнение (6) бывает удобнее заменить
двумя дифференциальными уравнениями,
содержащие первые производные:
![]() (7)
(7)
![]() (7/)
(7/)
В тех
случаях, когда при решении задачи надо
искать зависимость скорости от
координаты х, а не от времени t (когда
сами силы зависят от х) уравнение
(7) преобразуют к переменному х.
Так как ![]() ,
,
то
![]() (8)
(8)
Решение
основной задачи динамики сводится к
тому, чтобы из данных уравнений зная
силы, найти закон движения, то есть ![]() .
.
Для этого надо проинтегрировать
соответствующее дифференциальное
уравнение.
Входящие
в уравнение (6) силы могут зависеть от
времени t, от положения точки, то
есть х и от ее скорости, то
есть ![]() .
.
Следовательно, в общем случае уравнение
(6) с математической точки зрения
представляет дифференциальное уравнение
второго порядка.
![]() (9)
(9)
После того
как с помощью тех или иных математических
приемов уравнение (9) будет проинтегрировано,
в полученное решение войдут две постоянные
интегрирования С1 и С2 иобщее
решение будет иметь вид:
![]() (10)
(10)
Постоянные С1 и С2 определяют,
используя начальные условия.
Прямолинейное
движение — механическое движение,
происходящее вдоль прямой линии. То
есть, при прямолинейном движении
материальной точки траектория представляет
собой прямую линию.Сила и скорость
вдоль одной прямой. Движение
прямолинейное
Скорость
прямолинейного движения ![]() —
—
это векторная величина, совпадающая по
направлению с перемещением.
Работа ![]() постоянной
постоянной
силы ![]() при
при
прямолинейном перемещении ![]() вычисляется
вычисляется
по формуле скалярного произведения:
![]()
Принцип
инерции Галилея: если на тело не
действуют силы, оно сохраняет состояние
покоя или равномерного прямолинейного
движения. Инерциальные системы отсчета
(ИСО) — системы отсчета, в которых тело,
не взаимодействующее с другими телами,
сохраняет состояние покоя или равномерного
прямолинейного движения Преобразования
Галилея:

где х —
координата тела в ИСО X; х’ — координата
тела в ИСО X’, движущейся относительно
X со скоростью v
Закон
сложения скоростей:

где vx —
скорость тела в ИСО X; vx’— скорость
тела в ИСО Х’, движущейся относительно
X со скоростью V.
Принцип
относительности Галилея: во всех
инерциальных системах отсчета законы
механики имеют одинаковый вид
Первый
закон Ньютона: тело сохраняет состояние
покоя или равномерного прямолинейного
движения до тех пор, пока воздействие
со стороны других тел не заставит его
изменить это состояние Сила — векторная
физическая величина, являющаяся мерой
взаимодействия тела с другими телами,
в результате которого тело приобретает
ускорение (или изменяет свою форму и
размеры)
Инертность —
физическое свойство тела в отсутствие
трения оказывать сопротивление изменению
его скорости
Второй
закон Ньютона: в инерциальной системе
отсчета ускорение тела прямо пропорционально
векторной сумме всех действующих на
него сил и обратно пропорционально
массе тела

Третий
закон Ньютона: силы, с которыми два
тела действуют друг на друга, равны по
величине, противоположны по направлению
и приложены к разным телам:

Все
механические явления определяются
электромагнитным и гравитационным
взаимодействиями Электромагнитными
силами являются сила упругости и сила
трения. Упругое воздействие на тело —
воздействие, в результате которого тело
восстанавливает форму и размеры.
Закон
всемирного тяготения: гравитационная
сила притяжения материальных точек
пропорциональна произведению их масс
и обратно
пропорциональна
квадрату расстояния между ними.

где G = 6,67 •
10-11 Н • м2/кг2 –
гравитационная постоянная Сила тяжести
— гравитационная сила, действующая на
тело Вблизи поверхности Земли сила
тяжести, действующая на тело массой m,

Соседние файлы в папке Динамика билеты
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- калькулятор координаты тела при равномерном прямолинейном движении
- формула координаты тела при равномерном прямолинейном движении
Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.
Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:
Формула координаты тела при равномерном прямолинейном движении
x=x_0+ V cdot t
x0 – начальная координата тела
V – скорость тела
t – время движения
x – координата тела в текущий момент времени (в момент времени t)
Таким образом, для того, чтобы найти координату тела при равномерном прямолинейном движении необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат.
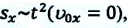 то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени: